Introduction

Optimization problems represent challenges with several possible solutions, one of which is the best choice. Accordingly, optimization is the process of achieving the best solution to the optimization problem. An optimization problem has three main parts: decision variables, objective function, and constraints1. Optimization aims to determine the values of the decision variables by considering the constraints so that the objective function is optimized2. Optimization problem-solving methods fall into two groups, deterministic and random approaches. Deterministic approaches deal well with linear, continuous, differentiable, and convex optimization problems. However, the disadvantage of these approaches is that their ability is lost in solving nonlinear, non-convex, non-differentiable, high-dimensional, NP-hard problems and discrete search spaces. These items, which have led to the inability of deterministic approaches, are among the features of real-world optimization problems. Stochastic algorithms, especially metaheuristic algorithms, have been introduced to meet this challenge. Metaheuristic algorithms can provide suitable solutions to optimization problems by using random search in problem-solving space and relying on random operators3. The critical thing about metaheuristic algorithms is that there is no guarantee that the solution obtained from these methods will be the best or global optimal. This fact has led researchers to develop numerous metaheuristic algorithms to achieve better solutions.

Metaheuristic algorithms are designed based on modeling ideas that exist in nature. Among the most famous metaheuristic algorithms can be mentioned Genetic Algorithm (GA)4, Particle Swarm Optimization (PSO)5, Ant Colony Optimization (ACO)6, and Artificial Bee Colony (ABC)7. GA is based on modeling the reproductive process. PSO is developed based on modeling the swarm movement of birds and fish in nature. ACO is designed based on simulating the natural behaviors of ants, and ABC is introduced based on modeling the activities of bee colonies in search of food.

Metaheuristic algorithms must have an acceptable ability for exploration and exploitation to deliver suitable optimization performance. Exploration is the concept of global search in different parts of the problem-solving space to find the main optimal area. Exploitation means a local search around candidate solutions to find better possible solutions that may be near them. In addition to having a high quality in exploration and exploitation, balancing these two indicators is the key to the success of metaheuristic algorithms8.

The main research question is, despite the large number of metaheuristic algorithms introduced so far, is there still a need to introduce newer methods? The answer to this question lies in the concept of the No Free Lunch (NFL) theorem9. According to the NFL, the excellent performance of an algorithm in solving a set of optimization problems does not guarantee the same performance of that algorithm in other optimization problems. This result is due to the random nature of metaheuristic algorithms in achieving the solution. In other words, the NFL states that it is impossible to claim that a particular algorithm is the best optimizer for dealing with all optimization issues. As a result, the NFL theorem has encouraged researchers to design new algorithms to provide more appropriate solutions closer to global optimization problems. The NFL has also motivated the authors of this study to be able to solve optimization problems more effectively by designing a new metaheuristic algorithm.

The novelty and innovation of this paper are in designing a new algorithm called Sewing Training-Based Optimization (STBO) for optimization applications. The main contributions of this article are as follows:

  • A new human-based metaheuristic algorithm based on sewing training modeling is introduced.

  • STBO is modeled in three phases: (i) training, (ii) imitation of the instructor's skills, and (iii) practice.

  • STBO performance is tested on fifty-two benchmark functions of unimodal, high-dimensional, fixed-dimensional multimodal types and from the CEC 2017 test suite.

  • STBO results are compared with the performance of eleven well-known metaheuristic algorithms.

  • STBO's performance in solving real-world applications is evaluated on four engineering design issues.

The rest of the paper is organized so that a literature review is presented in the section “Literature review”. Next, the proposed algorithm is introduced and modeled in the section “Sewing Training-Based Optimization”. Simulations and analysis of their results are presented in the section “Simulation Studies and Results”. The STBO's performance in solving real-world problems is shown in the section “STBO for real-world applications.” Finally, conclusions and several study proposals are provided in the section “Conclusion and future works”.

Literature review

Metaheuristic algorithms have been developed based on mathematical simulations of various natural phenomena, animal behaviors, biological sciences, physics concepts, game rules, human behaviors, and other evolution-based processes. Based on the source of inspiration used in the design, metaheuristic algorithms fall into five groups: swarm-based, evolutionary-based, physics-based, game-based, and human-based.

Swarm-based algorithms are derived from the mathematical modeling of natural swarming phenomena, the behavior of animals, birds, aquatic animals, insects, and other living organisms. For example, ant colonies can find an optimal path to supply the required food resources. Simulating this behavioral feature of ants forms the basis of ACO. Fireflies' feature of emitting flashing light and the light communication between them has been a source of inspiration in the design of the Firefly Algorithm (FA)10. Swarming activities such as foraging and hunting among animals are intelligence processes that are employed in the design of various algorithms such as PSO, ABC, Grey Wolf Optimizer (GWO)11, Whale Optimization Algorithm (WOA)12, Marine Predator Algorithm (MPA)13, Cat and Mouse based Optimizer (CMBO)14, Tunicate Swarm Algorithm (TSA)15,16, Reptile Search Algorithm (RSA)17, and Orca Predation Algorithm (OPA)18. Other swarm-based methods are Farmland Fertility19, African Vultures Optimization Algorithm (AVOA)20, Artificial Gorilla Troops Optimizer (GTO)21, Tree Seed Algorithm (TSA)22, Spotted Hyena Optimizer (SHO)23, and Pelican Optimization Algorithm (POA)24.

Evolutionary-based algorithms are inspired by the biological sciences, the concept of natural selection, and random operators. For example, Differential Evolution (DE)25 and GA are two of the most significant evolutionary algorithms developed based on the mathematization of the reproductive process, concepts of Darwin's theory of evolution, and random operators of selection, mutation, and crossover. Some other Evolutionary-based algorithms are Genetic Programming (GP)26, Memetic Algorithm (MA)27, Evolution Strategy (ES)28, Evolutionary Programming (EP)29, and Cultural Algorithm (CA)30.

Physics-based algorithms have been developed by simulating various laws, concepts, forces, and phenomena in physics. For example, the physical phenomenon of the water cycle has been the main idea in designing Water Cycle Algorithm (WCA)31. The employment of physical forces to design metaheuristic algorithms has been successful in designing algorithms such as Gravitational Search Algorithm (GSA)32, Spring Search Algorithm (SSA)33, and Momentum Search Algorithm (MSA)34. GSA is based on modeling the gravitational force that exists between masses at different distances from each other. SSA is inspired by the simulation of the spring tensile force and the Hook law between the weights connected by springs. MSA is developed based on the mathematization of the force of bullets' momentum that moves toward the optimal solution. Simulated Annealing (SA)35, Flow Regime Algorithm (FRA)36, Equilibrium Optimizer (EO)37, and Multi-Verse Optimizer (MVO)38 belong, e.g., among some other physics-based metaheuristic algorithms.

Game-based algorithms are formed by mathematical modeling of various game rules. For example, Volleyball Premier League (VPL) algorithm39 and Football Game-Based Optimization (FGBO)40 are game-based algorithms designed based on the simulation of club competitions in volleyball and football games, respectively. Likewise, the players' attempt in the tug-of-war game has been the main inspiration for the Tug of War Optimization (TWO)41 design. Likewise, the skill and strategy of the players in completing the puzzle pieces have been the idea behind the Puzzle Optimization Algorithm (POA)42 design.

Human-based algorithms have emerged inspired by human behaviors and interactions. This group's most widely used and well-known algorithm is Teaching–Learning-Based Optimization (TLBO). TLBO is introduced based on the mathematization of educational interactions between teachers and students43. The treatment process that the doctor uses to treat patients has been a central idea in the design of the Doctor and Patients Optimization (DPO)44. The relationships and collaboration of team members to perform teamwork and achieve the planned goal have been the source of inspiration for the Teamwork Optimization Algorithm (TOA) design45. Some other human-based metaheuristic algorithms are Society Civilization Algorithm (SCA)1, Seeker Optimization Algorithm (SOA)46, Imperialist Competitive Algorithm (ICA)47, Human-Inspired Algorithm (HIA)48, Social Emotional Optimization Algorithm (SEOA)49, Brain Storm Optimization (BSO)50, Anarchic Society Optimization (ASO)51, Human Mental Search (HMS)52, Gaining Sharing Knowledge based Algorithm (GSK)53, Coronavirus Herd Immunity Optimizer (CHIO)54, Ali Baba and the Forty Thieves (AFT)55, Human Mental Search (HMS)52, Multi-Leader Optimizer (MLO), Poor and Rich Optimization (PRO)56, Following Optimization Algorithm (FOA)57, and Election-Based Optimization Algorithm (EBOA)58.

Scientists' research in metaheuristic algorithm studies also includes improving existing algorithms59,60,61,62,63, extending hybrid algorithms by combining different algorithms to increase their efficiency64, developing binary versions of optimization algorithms65,66,67,68, and comprehensive survey studies69,70,71.

Several more recent or well-known metaheuristic algorithms published by researchers are listed in Table 1. In addition, this table specifies these algorithms' categories and sources of inspiration.

Table 1 A brief review of metaheuristic algorithms.
Full size table

Based on the best knowledge from the literature review, modeling the sewing training process has not been applied to designing any metaheuristic algorithm. However, sewing training by a training instructor to beginner tailors is an intelligent human activity that has the potential to simulate an optimizer. Therefore, a new human-based metaheuristic algorithm based on mathematical modeling of sewing training is designed in this paper to address this research gap. The design of this algorithm will be discussed in the next section.

Sewing training-based optimization

This section introduces the proposed Sewing Training-Based Optimization (STBO) algorithm and presents its mathematical model.

Inspiration and main idea of STBO

The activity of teaching sewing skills by a training instructor to beginner tailors is an intelligent process. The first step for a beginner is to choose a training instructor. Selecting the training instructor is essential in improving a beginner's sewing skills. Next, the instructor teaches sewing techniques to the beginner tailor. The second step in this process is the beginner tailor's efforts to mimic the skills of the training instructor. The beginner tailor tries to bring his skills to the level of the instructor as much as possible. The third step in the sewing training process is practice. The beginner tailors try to improve their skills in sewing by practicing. The interactions between beginner tailors and training instructors indicate the high potential of the sewing training process to be considered for designing an optimizer. Mathematical modeling of these intelligent interactions is the fundamental inspiration in the design of STBO.

Mathematical model of STBO

The proposed STBO algorithm is a population-based metaheuristic algorithm whose members are beginner tailors and training instructors. Each member of the STBO population refers to a candidate solution to the problem that represents the proposed values for the decision variables. As a result, each STBO member can be mathematically modeled with a vector and the STBO population using a matrix. The STBO population is specified by a matrix representation in Eq. (1).

$$ X = \left[ {\begin{array}{*{20}c} {X_{1} } \\ \vdots \\ {X_{i} } \\ \vdots \\ {X_{N} } \\ \end{array} } \right]_{N \times m} = \left[ {\begin{array}{*{20}c} {x_{1,1} } & \cdots & {x_{1,j} } & \cdots & {x_{1,m} } \\ \vdots & \ddots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots \\ {x_{i,1} } & \cdots & {x_{i,j} } & \cdots & {x_{i,m} } \\ \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \vdots & \ddots & \vdots \\ {x_{N,1} } & \cdots & {x_{N,j} } & \cdots & {x_{N,m} } \\ \end{array} } \right]_{N \times m} , $$
(1)

where \(X\) is the STBO population matrix, \(X_{i}\) is the ith STBO’s member, \(N\) is the number of STBO population members, and \(m\) is the number of problem variables. At the beginning of the STBO implementation, all population members are randomly initialized using Eq. (2).

$$ x_{i,j} = lb_{j} + r \cdot \left( {ub_{j} - lb_{j} } \right),\;i = 1,2, \ldots ,N,j = 1,2, \ldots ,m, $$
(2)

where \(x_{i,j}\) is the value of the jth variable determined by the ith STBO’s member \(X_{i}\), \(r\) is a random number in the interval \(\left[ {0,1} \right]\), \(lb_{j}\) and \(ub_{j}\) are the lower and upper bound of the jth problem variable, respectively.

Each STBO member represents a candidate solution to the given problem. Therefore, the problem's objective function can be evaluated based on the values specified by each candidate solution. Based on the placement of candidate solutions in the problem variables, the values calculated for the objective function can be modeled using a vector by Eq. (3).

$$ F = \left[ {\begin{array}{*{20}c} {F_{1} } \\ \vdots \\ {F_{i} } \\ \vdots \\ {F_{N} } \\ \end{array} } \right]_{N \times 1} = \left[ {\begin{array}{*{20}c} {F\left( {X_{1} } \right)} \\ \vdots \\ {F\left( {X_{i} } \right)} \\ \vdots \\ {F\left( {X_{N} } \right)} \\ \end{array} } \right]_{N \times 1} , $$
(3)

where \(F\) is the objective function vector and \(F_{i}\) is the objective function value for the ith candidate solution.

The values of the objective function are the main criterion for comparing candidate solutions with each other. The solution with the best value for the objective function is identified as the best candidate solution or the best member of the population \(X_{best}\). Updating the algorithm's population in each iteration leads to finding new objective function values. Accordingly, in each iteration, the best candidate solution must be updated. The design of the algorithm guarantees that the best candidate solution at the end of each iteration is also the best candidate solution from all previous iterations.

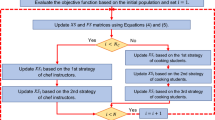
The process of updating candidate solutions in STBO is performed in three phases: (i) training, (ii) imitation of the instructor’s skills, and (iii) practice.

Phase 1: Training (exploration)

The first phase of updating STBO members is based on simulating the process of selecting a training instructor and acquiring sewing skills by beginner tailors. For each STBO member as a beginner tailor, all other members with a better value for the objective function are considered training instructors for that member. The set of all candidate members as the group of possible training instructors for each STBO member \(X_{i} , i = 1,2, \ldots ,N,\) is defined using the following identity

$$ CSI_{i} = \left\{ {X_{k} | F_{k} < F_{i} , k \in \left\{ {1,2, \ldots , N} \right\}} \right\} \cup \left\{ {X_{best} } \right\}, $$
(4)

where \(CSI_{i}\) is the set of all possible candidate training instructors for the ith STBO member. In the case \(X_{i} = X_{best}\) the only possible candidate training instructor is \(X_{best}\) itself, i. e., \(CSI_{i} = \left\{ {X_{best} } \right\}.\) Then, for each \(i \in \left\{ {1,2, \ldots ,N} \right\}\), a member from the set \(CSI_{i}\) is randomly selected as the training instructor of the ith member of STBO, and it is denoted as \(SI_{i}\). This selected instructor \(SI_{i}\) teaches the ith STBO member to sewing skills. Guiding members of the population under the guidance of instructors allows the STBO population to scan different areas of the search space to identify the main optimal area. This STBO update phase demonstrates the proposed approach's exploration ability in global search. At first, a new position for each population member is generated using Eq. (5) to update population members based on this phase of the STBO.

$$ x_{i,j}^{P1} = x_{i,j} + r_{i,j} \cdot \left( {SI_{i,j} - I_{i,j} \cdot x_{i,j} } \right) , $$
(5)

where \(x_{i,j}^{P1}\) is its dth dimension, \(F_{i}^{P1}\) is its objective function value, \(I_{i,j}\) are numbers that are selected randomly from the set \(\left\{ {1,2} \right\}\), and \(r_{i,j}\) are random numbers from the interval \(\left[ {0,1} \right]\).

Then, if this new position improves the objective function value, it replaces that population member's previous position. This update condition is modeled using Eq. (6).

$$ X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P1} ,} \hfill & {F_{i}^{P1} < F_{i} ;} \hfill \\ {X_{i} ,} \hfill & {else,} \hfill \\ \end{array} } \right. $$
(6)

where \(X_{i}^{P1}\) is the new position of the ith STBO member based on the first phase of STBO.

Phase 2: Imitation of the instructor skills (exploration)

The second phase of updating STBO members is based on simulating beginner tailors trying to mimic the skills of instructors. In the design of STBO, it is assumed that the beginner tailor tries to bring his sewing skills to the level of the instructor as much as possible. Given that each STBO member is a vector of the dimension \(m\) and each component represents a decision variable thus, in this phase of STBO, it is assumed that each decision variable represents a sewing skill. Each STBO member imitates \(m_{s}\) skills of the chosen instructor, \(1 \le m_{s} \le m.\) This process moves the population of the algorithm to different areas in the search space, which indicates the STBO exploration ability. The set of variables that each STBO member imitates (i.e., the set of skills of the training instructor) is specified in Eq. (7).

$$ SD_{i} = \left\{ {d_{1} , d_{2} , \ldots ,d_{{m_{s} }} } \right\}, $$
(7)

where \(SD_{i}\) is an \(m_{s} -\) combination of the set \(\left\{ {1,2, \ldots ,m} \right\}\), which represents the set of the indexes of decision variables (i.e., skills) identified to imitate by the ith member from the instructor and \(m_{s} = 1 + \frac{t}{2T}m\) is the number of skills selected to mimic, \(t\) is the iteration counter, and \(T\) is the total number of iterations.

The new position for each STBO member is calculated based on the simulation of imitating these instructor skills, using the following identity

$$ x_{i,j}^{P2} = \left\{ {\begin{array}{*{20}l} {SI_{i,j} , } \hfill & {j \in SD_{i} ;} \hfill \\ {x_{i,j} ,} \hfill & {else,} \hfill \\ \end{array} } \right. $$
(8)

where \(X_{i}^{P2}\) is the newly generated position for the ith STBO member based on the second phase of STBO, \(x_{i,j}^{P2}\) is the dth dimension of \(X_{i}^{P2} .\) This new position replaces the previous position of the corresponding member if it improves the value of the objective function

$$ X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P2} ,} \hfill & {F_{i}^{P2} < F_{i} ;} \hfill \\ {X_{i} ,} \hfill & {else,} \hfill \\ \end{array} } \right. $$
(9)

where \(F_{i}^{P2}\) is the objective function value of \(X_{i}^{P2}\).

Phase 3: Practice (exploitation)

The third phase of updating STBO members is based on simulating beginner tailoring practices to improve sewing skills. In fact, in this phase of STBO design, a local search is performed around candidate solutions with the goal to find the best possible solutions near these candidate solutions. This phase of the STBO represents the exploitation capability of the proposed algorithm in local search. In order to mathematically model this STBO phase (with a correction to stay the all newly computed population members in the given search space), a new position around each member of the STBO is first generated using Eq. (10).

$$ x_{i,j}^{P3} = \left\{ {\begin{array}{*{20}l} {lb_{j} ,} \hfill & {x_{i,j}^{*} < lb_{j} ;} \hfill \\ {x_{i,j}^{*} ,} \hfill & {x_{i,j}^{*} \in \left[ {lb_{j} , ub_{j} } \right];} \hfill \\ {ub_{j} , } \hfill & {x_{i,j}^{*} > ub_{j} ,} \hfill \\ \end{array} } \right. $$
(10)

where \(x_{i,j}^{*} = x_{i,j} + \left( {lb_{j} + r_{i,j} \left( {ub_{j} - lb_{j} } \right)/t} \right)\) and \(r_{i,j}\) is a random number from the interval \(\left[ {0,1} \right].\) Then, if the value of the objective function improves, it replaces the previous position of the STBO member according to Eq. (11).

$$ X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P3} ,} \hfill & {F_{i}^{P3} < F_{i} ;} \hfill \\ {X_{i} ,} \hfill & {else,} \hfill \\ \end{array} } \right. $$
(11)

where \(X_{i}^{P3}\) is the new generated position for the ith STBO member based on second phase of STBO, \(x_{i,j}^{P3}\) is its dth dimension, and \(F_{i}^{P3}\) is its objective function value.

Repetition process and pseudo-code of STBO

The first STBO iteration is completed after updating all candidate solutions based on the first to third phases. Then the update process is repeated until the last iteration of the algorithm, based on Eqs. (4) to (11). After the full implementation of the STBO on the given problem, the best candidate solution recorded during the algorithm iteration is introduced as the solution. Finally, STBO implementation steps are presented as pseudo-code in Algorithm 1.

figure a

Computational complexity of STBO

In this subsection, the computational complexity of STBO is investigated. Since the most time-consuming step in the entire algorithm is calculating the values of the objective function, which are very complicated in most real applications, the computational complexity of STBO can be estimated based on the number of population members generated in the algorithm. STBO initialization has a computational complexity equal to \(O\left(Nm\right),\) where \(N\) is the number of STBO members and \(m\) is the number of problem variables. In each STBO iteration, the candidate solution is updated in three phases. Thus, the computational complexity of the STBO update process is equal to \(O\left(3NmT\right),\) where \(T\) is the number of iterations of the algorithm. As a result, the total computational complexity of STBO is equal to \(O(Nm (1+3T))\).

Simulation Studies and Results

In this section, the ability of the proposed STBO algorithm in optimization applications and solution presentation is evaluated. In this regard, fifty-two standard benchmark functions consisting of twenty-three objective functions of unimodal, high-dimensional multimodal, fixed-dimensional multimodal types and twenty-nine benchmark functions from the CEC 2017 test suite77 are employed to test the STBO optimization capability29. The performance of DTBO is compared with the performance of eleven well-known metaheuristic algorithms GA, PSO, GSA, MPA, WOA, TLBO, RSA, MVO, GWO, AVOA, and TSA. Each of the competing metaheuristic algorithms and STBO is used in twenty independent runs, where each run contains 1000 iterations. The implementation results of metaheuristic algorithms are reported using six statistical indicators: mean, standard deviation (std), best, worst, median, and rank. The mean of rank is considered a ranking criterion of the performance of optimization algorithms for each objective function. The values of the control parameters of competitor metaheuristic algorithms are listed in Table 2.

Table 2 Assigned values to the control parameters of competitor algorithms.
Full size table

Evaluation of unimodal benchmark functions

The results of optimization of unimodal functions F1 to F7 using STBO and competitor algorithms are reported in Table 3. The optimization results show that STBO provides the exact optimal solution for functions F1 to F6. For optimization of function F7, STBO is the best optimizer compared to competing algorithms. The simulation results show that STBO has outperformed competitor algorithms in handling the F1 to F7 unimodal functions and has been ranked first among the compared algorithms.

Table 3 Evaluation results on unimodal functions.
Full size table

Evaluation of high dimensional multimodal benchmark functions

The results obtained using STBO and competitor algorithms in optimizing high-dimensional multimodal functions F8 to F13 are presented in Table 4. Based on the results, STBO has provided the exact optimal solution for optimizing functions F9 and F11. Furthermore, in solving the functions F8, F10, F12, and F13, the STBO has performed better than all competitor algorithms. Analysis of the simulation results indicates the superiority of STBO over competing algorithms in handling the high-dimensional multimodal functions of F8 to F13.

Table 4 Evaluation results on high-dimensional multimodal functions.
Full size table

Evaluation of fixed dimensional multimodal benchmark functions

The results of the implementation of STBO and competitor algorithms on fixed-dimensional multimodal functions F14 to F23 are released in Table 5. Compared to competitor algorithms, the optimization results show that STBO is the best optimizer in optimizing benchmark functions F14, F15, and F18. In optimizing functions F16, F17, and F19 to F23, the proposed STBO, and some competitor algorithms have a similar value in the "mean" index. However, STBO provides more efficient performance in these functions by providing better values of the "std" index. The simulation results show that STBO performs better than competitor algorithms in solving fixed-dimensional functions F14 to F23.

Table 5 Evaluation results on fixed-dimensional multimodal functions.
Full size table

The performance of STBO and competitor algorithms in optimizing F1 to F23 functions is presented as a boxplot in Fig. 1. Intuitive analysis of these boxplots shows that the proposed STBO approach has provided superior and more effective performance compared to competing algorithms by providing better results in statistical indicators in most of the benchmark functions.

Figure 1
figure 1

Boxplot of performance of STBO and competitor algorithms in solving F1 to F23.

Full size image

Statistical analysis

In this subsection, statistical analysis is presented to further evaluate the performance of the STBO compared to competitor algorithms. Wilcoxon sum rank test78 has been employed to determine whether there is a statistically significant difference between the results obtained from STBO and competing algorithms. In the Wilcoxon sum rank test, the p-value index determines the significant difference between the two data samples. The results of the Wilcoxon sum rank test on the performance of STBO and competitor algorithms are reported in Table 6. Based on these results, in cases where the \(p\)-value is calculated as less than 0.05, STBO has a statistically significant superiority over the competitor algorithm.

Table 6 Wilcoxon sum rank test results.
Full size table

Convergence analysis

In this subsection, the convergence analysis of the proposed STBO is presented in comparison with competitor algorithms. The convergence curves of STBO and competitor algorithms during the optimization of F1 to F23 functions are drawn in Fig. 2. In the optimization of unimodal functions F1 to F7, which lack local optima, it can be seen that STBO has converged towards better solutions with its high ability in local search and exploitation after identifying the position of the optimal solution. Especially in solving functions F1 to F6, STBO has converged to the global optimal of these functions.

Figure 2
figure 2

Convergence curves of STBO and competitor algorithms in solving F1 to F23.

Full size image

In the optimization of high-dimensional multimodal functions F8 to F13, which have a large number of local optima, it can be seen that STBO with high capability in global search and exploration has been able to identify the optimal global position well without getting stuck in local areas. With increasing iterations of the algorithm, it can be seen that STBO has converged towards better solutions. Especially in optimizing F9 and F11 functions, the proposed approach, with high ability in exploration and exploitation, has converged to the global optima. In the optimization of fixed-dimension multimodal functions F14 to F23, which have a smaller number of local optima (in comparison to F8 to F13 functions), it can be seen that STBO with high ability in balancing exploration and exploitation has provided a good performance in handling these functions. STBO first identified the main optimal area in solving these functions by providing an optimal global search. Then, by increasing the number of iterations of the algorithm, using local search, it converged towards suitable solutions. Convergence analysis shows that the proposed STBO approach, with its high ability to explore and exploit and balance during algorithm iterations, has better performance in handling functions F1 to F23 compared to competitor algorithms.

Scalability analysis

In this subsection, scalability analysis is presented to evaluate the proposed STBO approach and competitor algorithms in solving optimization problems under changes in the dimensions of the problem. In this analysis, the proposed STBO and each competing algorithm are used in optimizing the functions F1 to F13 for different dimensions \(m\) equal to 50, 100, 250, and 500. The results of the scalability analysis are reported in Table 7. These found simulation results show that the efficiency of the STBO's performance does not decrease much with the increase in the dimensions of the problem. Furthermore, the scalability analysis reveals that the performance of the proposed STBO is least affected by the increase in the dimensionality of search space in comparison to competitor algorithms. This superiority is due to the proposed STBO approach's better ability to balance exploitation and exploration during the search process than competing algorithms.

Table 7 The results of the scalability analysis of STBO.
Full size table

Evaluation of the CEC 2017 test suite benchmark functions

In this subsection, the performance of STBO in solving complex optimization problems of the CEC 2017 test suite is evaluated. This test suite has thirty standard benchmark functions consisting of three unimodal functions, C17-F1 to C17-F3, seven multimodal functions, C17-F4 to C17-F10, ten hybrid functions, C17-F11 to C17-F20, and ten composition functions C17- F21 to C17-F30. The C17-F2 function has been removed from this test suite due to unstable behavior. Full descriptions and details of the CEC 2017 test suite are available in the report78. The optimization results of the CEC 2017 test suite using the proposed STBO approach and competitor algorithms are reported in Table 8. Based on the optimization results, STBO is the first best optimizer in solving functions C17-F1, C17-F4 to C17-F6, C17-F8, C17-F10 to C17-F21, C17-F23 to C17-F25, and C17-F27 to C17-F30. The analysis of the simulation results found shows that the proposed STBO approach gives better results for most of the CEC 2017 test set features. It can be concluded that it performs better in solving this feature test set than the competing algorithms. Also, the results obtained from the Wilcoxon sum rank test show that the superiority of STBO against competitor algorithms in handling the CEC 2017 test suite is significant from a statistical point of view. The performance of STBO and competitor algorithms in solving the CEC 2017 test suite is presented as boxplot diagrams in Fig. 3. These diagrams intuitively show that STBO has performed more effectively in solving most of the benchmark functions of the CEC 2017 test suite by providing better results compared to competitor algorithms.

Table 8 Evaluation results on the CEC 2017 test suite functions.
Full size table
Figure 3
figure 3

Boxplot of performance of STBO and competitor algorithms in solving the CEC 2017 test suite.

Full size image

STBO for real-world applications

STBO's ability to optimize optimization problems in real-world applications is evaluated in this section. To this end, STBO and competitor algorithms have been implemented on four engineering optimization challenges. These engineering challenges are pressure vessel design (PVD)79, speed reducer design (SRD)80, welded beam design (WBD)12, and tension/compression spring design (TCSD)12. Schematics of these problems are presented in Fig. 4.

Figure 4
figure 4

Schematics of four real-world applications: (A) PVD, (B) SRD, (C) WBD, (D) TCSD.

Full size image

The optimization results of the four mentioned challenges are reported in Table 9. The simulation results show that STBO performs superior to competitor algorithms in optimizing all four studied engineering challenges. What is clear from the analysis of the simulation results is that STBO has an effective capability in dealing with real-world optimization applications. The convergence curves of STBO while optimizing the mentioned optimization challenges are presented in Fig. 5. The convergence curves show that STBO has identified the main optimal area in the initial iterations by providing a desirable global search. Then, by increasing the iterations of the algorithm based on the local search, it tries to get better solutions. Intuitive analysis of convergence curves shows that STBO has converged to suitable solutions with a high ability to balance exploration and exploitation.

Table 9 Evaluation results of four real-world applications.
Full size table
Figure 5
figure 5

Convergence curves of STBO on four real-world applications.

Full size image

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

Informed consent was not required as no human or animals were involved.

Conclusion and future works

This paper introduced a new metaheuristic algorithm called Sewing Training-Based Optimization (STBO) to solve optimization problems. The interactions between the training instructor and the beginner tailors are the main inspiration in the design of STBO. The proposed STBO was modeled and designed in three phases: (i) training, (ii) imitation of the instructor's skills, and (iii) practice. The STBO’s performance was tested on fifty-two objective functions of unimodal, high-dimensional multimodal, fixed-dimensional multimodal, and the CEC 2017 test suite. The optimization results of the benchmark functions showed that the proposed STBO approach has a good ability in exploration, exploitation, and balancing their proportion during the search process in the problem-solving space. Eleven well-known metaheuristic algorithms were employed to compare the performance of STBO in optimization. The simulation results showed that STBO has superior and competitive performance compared to some well-known metaheuristic algorithms, providing better results in most of the objective functions studied in this paper. STBO implementation on four engineering design challenges demonstrated the capability of the proposed algorithm in real-world applications.

Although the proposed STBO has provided good performance in most of the benchmark functions studied in this article, the proposed algorithm has some limitations. The first limitation of STBO is that it is always possible to devise newer algorithms that perform better than the proposed approach. The second limitation of STBO is that there is a possibility that the implementation of the proposed algorithm will fail in some optimization applications. Finally, the third limitation of STBO is that there is no guarantee that STBO can always provide a globally optimal solution since the proposed algorithm is based on a random search. Also, based on the concept of the NFL theorem, it is not claimed that STBO is the best optimizer for all optimization applications.

Introducing the STBO activates several research tasks for future studies. Developing binary and multimodal versions is a possible specific STBO research proposal. Employing STBO in various applications of optimization in science as well as in real-world applications are other suggestions for further studies.