Abstract
The setup, operational procedures and performance of a cryogen-free device for producing hyperpolarized contrast agents using dissolution dynamic nuclear polarization (dDNP) in a preclinical imaging center is described. The polarization was optimized using the solid-state, DNP-enhanced NMR signal to calibrate the sample position, microwave and NMR frequency and power and flip angle. The polarization of a standard formulation to yield ~ 4 mL, 60 mM 1-13C-pyruvic acid in an aqueous solution was quantified in five experiments to P(13C) = (38 ± 6) % (19 ± 1) s after dissolution. The mono-exponential time constant of the build-up of the solid-state polarization was quantified to (1032 ± 22) s. We achieved a duty cycle of 1.5 h that includes sample loading, monitoring the polarization build-up, dissolution and preparation for the next run. After injection of the contrast agent in vivo, pyruvate, pyruvate hydrate, lactate, and alanine were observed, by measuring metabolite maps. Based on this work sequence, hyperpolarized 15N urea was obtained (P(15N) = (5.6 ± 0.8) % (30 ± 3) s after dissolution).
Similar content being viewed by others
Introduction
Magnetic Resonance Imaging (MRI) has revolutionized modern diagnostics by providing high resolution anatomical and functional imaging in 3D without ionizing radiation1,2. Many of the biochemical processes in vivo, however, still elapse our best efforts, and accessing these remains a prime objective of much research.
Here, hyperpolarized contrast agents hold great promise as they provide a unique window into metabolism, non-invasively and in vivo. By boosting the signal of selected, often endogenous molecules, their fate can be followed—for a limited time—with high spatial and chemical resolution. These properties have allowed the identification of cancerous tissue before a tumor was apparent, and has helped monitoring treatment response.
Dissolution dynamic nuclear polarization (dDNP)3 is the most established technique for hyperpolarizing (HP) biomolecules for in vivo imaging, and it shares the applicability to humans4,5 only with hyperpolarized Xenon6. Other HP techniques include brute-force7, parahydrogen-induced polarization8, chemically induced dynamic nuclear polarization9 and, for noble gases, spin-exchange optical pumping10,11.
dDNP has allowed to polarize biomolecules to more than 50% in about 1 h12,13. The nuclear polarization of the target is achieved by polarizing electronic spin first, using low temperatures (≈ 1.4 K) and high magnetic fields (≈ 6.7 T). Then, the electron polarization is transferred to nuclear polarization using the interactions between the electronic and nuclear spin under the action of electromagnetic waves, transmitted at a frequency corresponding to the difference in Larmor frequency of the two electron spins involved14. The unpaired electron spins are added in the form of stable radicals: TEMPO15, TEMPOL, or trityl radicals16,17 or induced by UV radiation18. In addition, there are other types of sample formulations, for instance HYPOP19.
When the desired level of nuclear spin polarization is achieved, the frozen sample is rapidly melted, dissolved and ejected from the polarizer by pressurized overheated water, such that an injectable contrast agent results.
Overall, dDNP is a complex process combining nuclear magnetic resonance (NMR) electron spin resonance (ESR), radical chemistry, high magnetic fields, fast dissolution, and cryogenictemperatures. Making this process available for biomedical research routinely is not straight forward. Over the last decades, several experimental implementations of dDNP were presented such as a cryogen-consumption-free DNP 9.4 T polarizer20, a 129-GHz dynamic nuclear polarizer in an ultra-wide bore superconducting magnet21, a Dynamic Nuclear Polarization Polarizer for sterile Use Intent22 and a multisample 7 T dynamic nuclear polarization polarizer for preclinical hyperpolarized MR23. Moreover, a number of dDNP polarizer were commercialized: HyperSense by Oxford Instruments3, SpinLab by GE and SpinAligner by Polarize24.
Here, we present our first experiences with the latest addition to the family, a cryogen-free dissolution polarizer for preclinical applications (SpinAligner, Polarize, Denmark)24. We report on the installation of the device and the routine for 13C and 15N hyperpolarization. By implementing routine operational procedures, high and reproducible polarization was achieved.
Methods
DNP system
The polarizer used in this work (SpinAligner, Polarize, Denmark) is similar to a setup described in 201924, but features a different magnet (6.7–10.4 T) and dissolution module. The main components are a cryogen-free, superconducting magnet cooled by a closed-cycle helium cryostat, a variable temperature insert (VTI), a microwave source, an NMR spectrometer, a dissolution module, and control software (Figs. 1, 2). The superconducting magnet was driven by a 230 V/10 A power supply to reach max. 9.4 T (instead of 10.4 T as described in 201924) and was used at ~ 6.7 T here. It is relevant to point out that the fluid path for dissolution is optimized for pre-clinical and in-vitro applications.
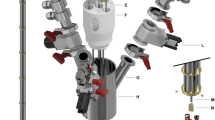
Photo (a,b) and diagram (c) of the polarizer used in this work. The polarizer consists of a dissolution module (a) mounted on the magnet (b section, magenta square) and a rack for auxiliary parts. The dissolution module (a) contains an inlet for the dissolution medium (DM), a heater for DM (5), a Swagelok manifold (1–4), a switch valve (6), the sample cup and an outlet. The magnet (b section, magenta square) is equipped with a variable temperature inset (VTI) which is cooled down to 1.4 K by evacuating a bath of liquid helium at the bottom of the VTI. The pressure of helium gas inside the VTI and in the inlet are shown by P1 (8) and P2 monitors respectively. The DNP probe inside the VTI consists of a tunnel for the sample cup, a waveguide to transmit the microwaves, and an NMR coil at the bottom. The sample is inserted into the VTI via an airlock (7) on top. The rack is used to house the pump circulating the Helium of the VTI, an NMR spectrometer, the magnet power supply, temperature controllers and the user interface. Figure c shows a schematic view of the polarizer naming all the main components.
For hyperpolarization, c.a. 22 mg of a formulation containing the radical and concentrated contrast agent was filled into a sample cup (PEEK, maximum filling volume is 400 µL), lowered into the magnet and polarized. Once the desired polarization was reached, the sample was dissolved, expelled, and diluted by injecting a superheated dissolution medium into the cup. The cup was connected to the polarizer’s fluid system using a disposable O-ring seal, inserted into the VTI via an airlock (Fig. 1), and lowered into the magnet using a centrally controlled mechanism. In the VTI, temperatures below 1.5 K were reached by pumping on a liquid helium bath. The helium was pumped from a 50 L storage cylinder into the closed cooling circuit to replenish the helium bath after condensation at the magnets cryo-cooler. It returns back to the tank through a charcoal filter (inside the magnets housing A needle valve was used to control the helium supply to the VTI, and volumes were chosen never to exceed atmospheric pressure assuring safety. P1 and P2 monitors are showing He pressure inside the VTI and just outside of the He tank respectively. The temperature of the sample was estimated by a ceramic thermistor on the outside of the copper microwave cavity and the pressure inside the VTI, measured below the airlock.
An NMR spectrometer (Cameleon, Spinit, RS2D) was connected to an Alderman-Grant coil inside the VTI to acquire NMR signal in situ. The frequency and impedance of the NMR probe were adjusted using variable capacitors of an LC-circuit in an aluminum box outside of the bore. Adjusting or exchanging the circuit allowed acquiring 1H, 13C, 15N, 63Cu, or 129Xe signals.
A microwave source with a maximum continuous output power of 100 mW provided constant or frequency modulated25 irradiation of the sample in the VTI as set by the control software.
All procedures were controlled by a central software and digital-analog converters (Polarize; LabVIEW, National Instruments). Notably, data of more than 4 sensors was constantly monitored and stored in a compressed fashion.
The dDNP system was set up close to a 7 T MRI (30 cm bore, BioSpec 70/30, Bruker), two 1 T benchtop NMR spectrometers (Spinsolve Carbon and Nitrogen, Magritek) and a 9.4 T high-resolution wide-bore NMR spectrometer (9 cm bore, WB400, Avance NEO, 5 mm BBFO probe, Bruker). Once installed, a series of calibrations was performed (Table 2).
Preparation of dDNP samples and dissolution medium
All the information about the standard sample are taken from the SpinAligner User Manual.
A general, step-by-step description of the preparation of contrast agent (CA)—radical concentrates is provided in Table 1; the procedure specifically for pyruvate is in Table 4 and can be adapted for other substances.
In general, a larger amount (e.g. 1.5 g) of CA-radical concentrate was prepared each time, split into smaller aliquots (e.g. 250 mg) and stored at − 22 °C. For a DNP experiment, one of these batches was warmed up, and the desired amount was retrieved (e.g. 22 mg).
All experiments were conducted using trityl radical (AH111501, molecular weight 1595 g/mol, POLARIZE) and one of the contrast agents described below.
Pyruvic acid 13C
About 1.5 mL Pyruvic acid radical concentrate was prepared and frozen in 250 µl aliquots at − 24 °C, containing 30 mM trityl radical and 14 M 1-13C-pyruvic acid (Table 2 1-13CPA, molecular weight 89.05 g/mol, Sigma-Aldrich, CAS: 99124-30-8). For each dDNP experiment, one aliquot was warmed up and the indicated amount of the concentrate was retrieved (typically 22 mg).
Urea 13C, 15N
51 mg of trityl radical and 250 mg 13C,15N2-urea (molecular weight 60.05 g/mol, Sigma-Aldrich, CAS: 58069-83-3) were solved in 500 mg of deionized water and 500 mg of glycerol (G7893-500 mL, MW 92.09 g/mol, CAS: 56-81-5, Sigma-Aldrich). The resulting concentrate contained 35.5 mM of trityl radical and 4.62 M of urea and was stored at − 24 °C. For each DNP experiment, the indicated amount of the concentrate (typically 54 mg) was taken from the stock and transferred into the sample cup.
Urea 13 N
51 mg of trityl radical and 250 mg of [1,3-15N] urea (molecular weight 60.05 g/mol, Sigma-Aldrich, CAS: 2067-80-3) were solved in 500 mg of deionized water and 500 mg of glycerol (G7893-500 mL, MW 92.09 g/mol, CAS: 56-81-5, Sigma-Aldrich). The resulting concentrate contained 35.5 mM of trityl radical and 4.62 M of urea and was stored at − 24 °C. For each DNP experiment, the indicated amount of the concentrate (typically 54 mg) was taken from the stock and filled into the sample cup.
Dissolution medium
The dissolution medium was prepared by mixing 1.51 g of Trizma pre-set crystals (pH 7.6, average molecular weight 149.0 g/mol Sigma-Aldrich, T7943) to buffer the sample to obtain a final pH close to 7, 27 mg of ethylendiamintetracetic acid (EDTA, SERVA, CAS: 9002-07-7), 0.756 g of NaCl (Sigma-Aldrich) and 0.81 g of NaOH (Sigma-Aldrich, CAS: 1310-73-2) in 250 mL of deionized water and stored at − 20 °C. Typically, 3.9 mL were used for one experiment. For the urea experiments, only H2O with 0.27 mM EDTA was used instead.
RF and µW frequency calibration
As indicated in the SpinAligner manual, after ramping up the magnet, the magnetic field strength was determined by detecting the solid-state 63Cu NMR signal of the NMR coil (B0 = 2π ν63Cu/γ63Cu) where ν63Cu is the frequency of the 63Cu resonance and γ63Cu/2π = 11.319 MHz/T is its magnetogyric ratio. With B0, the frequencies of 13C, 15N, 129Xe and e- were calculated correspondingly (νx = B0 γx/2π) (see other γx values in SI). A finer calibration of the frequencies was performed using the NMR signal of the nuclei.
The abbreviations used for NMR signal recording in Spinit
In the following, NA is number of averages per spectrum, NS is number of scans per spectrum, NX is number of excitations within the TR period, TR is the repetition time, and TX is the time between two consecutive excitations within one series of pulses. When we measured NMR spectra with DNP (Spinit, RS2D), we used often NS = 1 or 4, with TX < TR; the common parameters were TX = 217 µs and TR from 1 min to 1 h. When we measured NMR spectra with NMR spectrometers NS was 1 hence TX = TR.
NMR flip angle calibration
The RF flip angle α was calibrated by using a train of low-flip angle excitations to a DNP-enhanced sample. 490 excitations were applied in 10 s (TR = 1 s, TX = 217 µs, NX = 49, NS = 1) resulting in an average number of excitations every second N = NX/TR = 49 s−1. Each 49th free induction decay (FID) was recorded and processed. Then we fitted a mono-exponential decay function to the data.
(An extensive description of this approach is illustrated by Elliott et al.)26.
We will use the same function to fit the decay of polarization in liquid state to obtain apparent \(T_{1}^{obs}\) (explained in more details below).
Assuming that the polarization didn’t relax significantly during the course of the experiment it allowed us to obtain the flip angle applied (Eq. 2, details in SI):
where S(t) is the signal acquired at time point t, S0 is the initial signal, \({\uptau }\) is the fitted constant, NX is total number of excitations per TR period, N is number of excitations per second.
Assuming linearity of the RF power amplifier this calibration was used to set the excitation angle for other durations \(p_{d}^{RF}\) or power attenuation \(p_{a}^{RF}\) (in dB) using the settings for the calibrated angle:
Microwave power and frequency calibration
The polarization transfer from electrons to nuclei was optimized by acquiring the DNP-enhanced 13C- or 15N-NMR signal as a function of microwave power (in W) \(p_{w}^{{{\mathbf{\mu W}}}}\) (common increment of \(p_{w}^{{{\mathbf{\mu W}}}}\) was 5 mW) and frequency νµW (common increment of νµW was 10 MHz). After 1–2 min of microwave irradiation, the solid state, 13C (or 15N)-NMR signal of DNP polarized CA-radical concentrate using a constant 2°–5° excitation pulse was measured for different settings of the µW frequency or power. One thousand pulses with the same flip angle were applied after each acquisition to saturate the remaining polarization.
Optimization of sample position xs in the VTI
A pyruvate-radical concentrate was polarized for 40 min and moved to different positions in the VTI, where ~ 2° 13C-spectra were acquired.
Thermally polarized solid-state NMR and T1
To detect solid state 13C NMR signal in thermal equilibrium in the polarizer, 247.9 mg of pyruvate-radical concentrate (30 mM trityl-radical and 14 M 1-13C-PA) was prepared and inserted into the probe at ≈ 1.4 K. Every hour, several low-flip angle 13C NMR spectra were acquired to monitor the magnetization reaching the equilibrium (\(\alpha\) ~ 0.32°, \(p_{d}^{RF}\) = 2 us, \(p_{a}^{RF}\) = 38 dB, NS = 256, TS = 217 us, and TR = 1 h). The data was exported and processed offline (baseline, phase correction, zero-filling to 4096 and integration, MestReNova). A mono-exponential recovery function (Eq. 4) was fitted to the data to obtain the apparent equilibrium signal \(S_{inf}^{\alpha }\) and the apparent solid-state recovery time \(T_{1}^{obs}\):
Knowing excitation angle \(\alpha\) and number of excitations per second \(N\) we estimated real relaxation time and equilibrium signal (see SI for details) as
\(S_{inf}\) is the equilibrium signal when complete equilibrium of the signal without RF excitations is reached and as before \(N = NX/TR\) (Eq. 2).
DNP-enhanced solid state nuclear polarization build-up
The build-up of the solid-state, DNP-enhanced polarization was monitored in situ using \(\alpha \cong 0.7^\circ\) excitation with NS = 4 for 13C-DNP and about 3.5° for NS = 1 for 15N-DNP. The signals S(t) were automatically integrated and displayed on the polarizer along with an exponential recovery function fitted to the data. For a more detailed analysis, the spectra were processed offline (zero-filling, baseline correction, phase correction, integration; MestReNova). A mono-exponential recovery function (Eq. 5) was fitted to the data to obtain the build-up constant TDNP, taking the effect of the flip angle into account (Eq. 6).
DNP-enhanced solid state NMR enhancement and polarization
The DNP signal enhancement ε of the solid sample in the polarizer was calculated using the signal intensities of the thermally and hyperpolarized spectra, taking into account the acquisition parameters (Eq. 8).
where S are the integrals over corresponding NMR signals, \(NS_{{{\text{acq}}}}^{TP}\) and \(NS_{{{\text{acq}}}}^{HP}\) are the number of scans for the thermally and hyperpolarized sample, and \(\alpha_{HP}\) and \(\alpha_{TP}\) are the excitation flip angles used to acquire the hyperpolarized and thermal spectra, respectively. \(RG_{TP}\) and \(RG_{HP}\) are values of linear receiver gains (to notice that T1 therefore S values correction are shown in SI).
The absolute polarization was calculated by multiplying the enhancement by the thermal polarization (\(P^{{{\text{TP}}}}\), Eq. (9)): PTP(13C) (1 T, 295 K) = 0.8711 ppm, PTP(13C) (6.65 T, 1.4 K) = 1220 ppm, PTP(13C) (9.4 T, 295 K) = 8.187 ppm, (15N)PTP(15N) (9.4 T, 295 K) = 3.3 ppm.
where \(\hbar\) is the reduced Planck constant, ε is the enhancement factor, kB is the Boltzmann constant, B0 is the magnetic field and T is the temperature.
Thermally polarized liquid-state NMR
Liquid state NMR was acquired either by a 1 T benchtop NMR (Spinsolve Carbon, Magritek) or a 9.4 T high-resolution NMR (WB400, Avance NEO, 5 mm BBFO probe, Bruker). The 13C or 15N signal intensities were quantified using automatic baseline and manual phase correction prior to numerical integration (integration region around the signal was ± 1 ppm at 9.4 T and, ± 2 ppm at 1 T, using TopSpin or MestReNova).
To accelerate the acquisition of 13C NMR of thermally polarized samples at 1 T, 4 vol% Gd-contrast agent was added ([Gd], 1 mmol/mL, Gadovist, Bayer). We used 3600 averages, flip angle 20°, TR = 2 s and RG = 31 (note that the same RG was used to acquire liquid state NMR spectra of the hyperpolarized solution). Estimated T1 was 50 ms.
To obtain thermally polarized 13C-signal at 9.4 T, we used a single scan with 90° flip angle, with RG = 101, 20 min after dissolution (RG = 0.25 for liquid state NMR spectra of the hyperpolarized solution).
For 15N NMR, 3 vol% [Gd] was added and 128 acquisitions after 90° flip angle were collected at 9.4 T using TR = 17 s. No thermal 15N signal was observed at 1 T in 100.000 averages and TR = 2 s.
Liquid-state polarization decay
The hyperpolarized spectra were acquired after manual transfer to the respective device sequentially using fixed repetition time TR and a constant flip angle \(\alpha_{HP}\).
To quantify lifetime of hyperpolarization \(T_{1}^{HP}\), a mono-exponential decay function was fitted to the data yielding \(T_{1}^{obs}\) (Eq. 1). \(T_{1}^{obs}\) was corrected considering the polarization consumed by the repetitive RF excitations using Eq. (6) (Eq. 6, see details in SI).
Liquid-state enhancement and polarization
The signal enhancement \(\varepsilon\) and absolute polarization P was quantified with respect to the (averaged) signal from the thermally polarized samples using (Eqs. 5 and 7).
Note that all the experiments shown here were analyzed without any background subtractions.
Animals
Two male FVB.TgN(Ela1KRAS.G12D)9EPS.CEABAC were bred at the Central Animal Facility of the University Hospital Schleswig–Holstein, Kiel, Germany. The animals were measured at ~ 9 months and had a weight of ~ 35 g. This study was conducted in compliance with the German Animal Protection Law. The animal protection committee of the local authorities (Ministry of Energy, Agriculture, the Environment, Nature and Digitalization Schleswig–Holstein (MELUND)) approved all experiments (V242-18779/2021(2-1/21)).
This study is reported in accordance with ARRIVE guidelines.
HP-MRI in vivo
A mouse model for spontaneous pancreatic tumor was anaesthetized using intra peritoneal injection of 75 mg/kg ketamine and 0.5 mg/kg medetomidine. The anesthesia was diluted 1:5 with 0.9% NaCl yielding 155 µl solution per mouse. A tail vein catheter was used for injection of 200 µL HP 1-13C-PA solution. During the in vivo measurements the animals were heated via the bed and the vital parameters of the animals were monitored continuously. After the MRI measurements (~ 1 h), the animals were euthanized without awakening by cervical dislocation. Images were acquired on a 7 T, 30 cm MRI system (Biospec 70/30, Avance Neo, Bruker, Germany), equipped with a cylindrical, dual-tune 1H-/13C-volume transmit coil (72 mm diameter and 100 mm length and flexible 13C-surface receive coil (20 mm diameter, RAPID biomed, Germany)).
A T2-weighted 1H 2D RARE MRI was acquired for anatomical reference (acquisition time = 76.5 s, TR = 0.75 s, TE = 13 ms, 256 × 256 matrix size and field of view FOV = 33 mm × 33 mm, 9 slices with slice thickness = 4.26 mm, flip angle 90°/180°).
Free-induction decay 2D-chemical shift image (CSI) was acquired every 5 s for eight times in a row (acquisition time = 5 s, TR = 44.62 ms, TE = 0.489 ms, 11 × 11 matrix size, FOV = 33 mm × 33 mm, single slice, slice thickness = 4.26 mm, flip angle 5°)27,28,29.
13C-CSI images were processed using a script developed by Franz Schilling’s group (Matlab).
Results
DNP installation and initial calibration
Installation
The polarizer is mobile, mounted on wheels, (Fig. 1) and was placed at a distance of 3 m from the 7 T preclinical MRI, 2 m from two 1 T benchtop NMR spectrometers and 5 m from the 9.4 T NMR. The setup was provided with a 1-phase power outlet (10 A), dried and pressurized air (Atlas Copco 8F1 type air compressor), and Helium gas from a 50 L bottle (5.0 purity, Air Liquide). The helium compressor for cooling the magnet was installed at a distance of 9 m using a 20 m helium line. The He compressor requires cooling water and three phase electrical power (F-70H, Sumitomo).
The magnet was evacuated (HiCube 80 Classic vacuum pump, Pfeiffer Vacuum) before the closed-cycle He cooler was turned on (recommended pressure < 1 × 10−4 mbar). When a temperature of 1.5 K was reached (calculated from the pressure of the VTI outlet), the target field of 6.7 T was set in the polarizer user interface, and the magnet was ramped up in ~ 30 min to I = 72.811 A (using a factory calibration). The stabilizing period took around 20 min.
Calibration of RF frequency
The 63Cu-NMR signal of the NMR coil in the VTI was detected at ν63Cu = 75.259 MHz using 4 averages and flip angle of 32° (\(p_{a}^{RF}\) = − 2 dB, \(p_{d}^{RF}\) = 2 µs, see SI, Sect. 4.1.) resulting in B0 = 6.6489 T, 13C-frequency ν13C = 71.197 MHz and electron Larmor frequency νe− = 186.397 GHz. The full width at half maximum (FWHM) of the 63Cu signal was 0.25 MHz (the entire calibration procedure is described in the SpinAligner manual).
For a finer calibration of the carbon resonance frequency, ~ 22 mg of the pyruvate-radical concentrate (30 mM trityl-radical and 14 M 1-13C-PA) was filled in the sample cup and lowered to 10 mm above the bottom of the probe. After adjusting the LC circuit, DNP was commenced using continuous wave microwave irradiation (\(p_{a}^{MW}\) = 16 mW and νµW = 187.135 GHz), and solid state 13C NMR signal was detected at ν13C = 71.492 MHz (4 averages, the same RF parameters), resulting in a B0 = 6.6765 T and νe− = 187.17 GHz. 13C-FWHM was 0.16 MHz.
Calibration of sample position
The sensitive area of the NMR coil was determined by acquiring the solid state, DNP-enhanced 13C-signal as function of the sample’s position (Fig. 3a). A broad maximum was found around xs = 14 mm measured from the lowest position (bottom of probe). To assure a low sample temperature, we chose xS = 10 mm for all following experiments (within 90% of the maximum signal).
Calibration of the sample position and flip angle. (a) DNP-enhanced, solid-state 13C-NMR signal of pyruvate as a function of the position of the sample in probe. To ensure sufficient signal, the sample was first polarized for 40 min. Then the 13C signal was acquired at different positions xs every minute using a low flip angle of 2°. Moving the sample first down, then up, a broad maximum around xs = 14 mm was found. Straight lines were plotted to guide the eye. (b) DNP-enhanced 13C NMR signal acquired by a train of \(p_{d}^{RF}\) = 2 us, \(p_{a}^{RF}\) = 18 dB pulses with TX = 217 µs, TR = 1 s, NS = 1, NX = 49. By fitting a mono-exponential function to the data (red line, \(\tau =\) 13.3 s, Eq. 1), the flip angle was determined to α = 3.2° (Eq. 2).
Calibration of RF power
To calibrate the 13C flip angle, a standard sample was polarized by DNP and a train of low-angle free induction decays (FID) was acquired after turning off the microwaves (\(p_{d}^{RF}\) = 2 us, \(p_{a}^{RF}\) = 18 dB, TX = 217 µs, TR = 1 s, NS = 1, NX = 49 leading to N = 49 s−1 Fig. 3b). By fitting Eq. (1) to the signal, signal decay constant \(\tau =\) 13.3 s and α = 3.2° was obtained using Eq. (2). For many of the following experiments, a flip angle of ~ 0.32° was used (\(p_{d}^{RF}\) = 2 us, \(p_{a}^{RF}\) = 38 dB).
Microwave calibration
To optimize DNP, the polarization transfer from electrons to nuclei, the DNP-enhanced, solid state, 13C-NMR signal of pyruvate-radical concentrate was acquired using TR = 2 min as a function of µW frequency (Fig. 4a, 10 MHz steps, \(p_{a}^{RF} =\) 3 dB, NS = 4, with α = 18°) and fixed power \(p_{w}^{{{\mathbf{\mu W}}}}\) = 30 mW. Two extrema were found. The maximum at 187.135 GHz was chosen for the following dDNP experiments. After each acquisition, the polarization was saturated with a train of 1000 pulses with 18° excitation angle.
To calibrate the µW power, we repeated the experiment, keeping frequency constant and varying the power (Figs. 4b, 5 mW increments). The 13C signal was found to increase steeply between ≈ 5 and 15 mW, forming a slowly declining plateau that decreased for powers larger than ≈ 40 mW. To avoid heating the sample by µW irradiation, while maintaining a high polarization, we chose a power of 16 mW for the following dDNP experiments.
Optimization of 13C polarization transfer. DNP-enhanced, solid state 13C-NMR signal of pyruvate at ≈ 1.4 K as a function of microwave frequency (a, \(p_{w}^{MW}\) = 30 mW) and microwave power (b, νMF ≈ 187.135 GHz). When the frequency was varied (a), two extrema were observed, and the first maximum at ≈ 187.135 GHz was chosen for later experiments. For the power sweep, the signal was found to increase up to 20 mW; 16 mW was used in the subsequent experiments. Straight lines were added to guide the eye. 13C polarization was destroyed after each signal acquisition. Each data point corresponds to the 13C-signals acquired after 2 min of DNP. NMR acquisition parameters were \(p_{w}^{RF} =\) 2 µs, \(p_{a}^{RF} =\) 3 dB, NS = 4, and α ≈ 18°.
Quantification of solid-state polarization. Solid-state, 13C-NMR signals of 14 M 1-13C pyruvic acid mixed with 30 mM radical (112.3 mg total sample weight) monitored with low flip angle excitations (\(\alpha\) ~ 0.32°, NS = NX = 256, TR = 1 h (a) or TR = 5 min (b)) while reaching thermal equilibrium at ≈ 1.4 K and 6.7 T (a) and during DNP (b). Blue squares indicate the spectra shown below (c, d). By fitting a mono-exponential recovery function (Eq. 5) to the polarization build up without µW (a) and with µW (b) and correcting for the RF excitations (Eq. 6), a solid-state relaxation \(T_{1}^{ss} { } \approx { }\left( {5.45{ } \pm { }0.44} \right){\text{h }}\), signal at thermal equilibrium \({\text{signal }}S_{inf}^{ssTP } { } = { }\left( {4.07 \cdot 10^{4} \pm 0.1 \cdot 10^{4} } \right)\), DNP build-up time TDNP = (18.396 ± 0.49) min and equilibrium signal \(S_{inf}^{ssDNP}\) = (\(2.0 \cdot 10^{7}\) ± \(0.2 \cdot 10^{6}\)) a.u. were obtained (note that this build up is faster than for the standard sample). The polarization of the spectrum acquired after 110 min DNP was quantified to \(P^{obs,ssDNP}\) (110 min) = \(S_{ }^{ssDNP}\)(110 min) \(P^{{{\text{TP}}}}\)/\(S_{inf}^{ssTP }\) ≈ 64%. Without RF excitations the expected steady state signal is estimated to be \(P_{inf}^{ssDNP}\) = \(S_{inf}^{ssDNP}\) \(P^{{{\text{TP}}}}\)/\(S_{inf}^{ssTP }\) ≈ 61% The spectra (c) and (d) are the last measured thermal recovery and DNP spectra (marked on (a) and (b) with blue rectangles). The first six datapoints in (a) were neglected for the fit because of very low SNR.
DNP performance
Solid-state polarization of 1-13C-pyruvate
The pyruvic acid-radical concentrate was filled into the cup and lowered to xs = 10 mm above the bottom of the VTI at ≈ 1.4 K. While the sample was approaching the thermal equilibrium at B0 ≈ 6.7 T and T ≈ 1.4 K, thermal 13C signal was monitored for 24 h (Fig. 1). An asymptotic signal increase was observed, and a mono-exponential recovery function (Eq. 6) fitted to the data yielded an apparent solid-state relaxation time \(T_{1}^{obs,ss}\) = (4.98 ± 0.40) h and apparent steady state thermal signal \(S_{inf}^{obs,ssTP}\) = 3.9 × 104 (R2 = 0.969). Using the NMR acquisition parameters (\(\alpha\) ~ 0.32°, NS = NX = 256, and TR = 1 h) and Eqs. (3) and (6), the life-time corrected for the excitation was estimated to be \(T_{1}^{ss}\) ≈ (5.45 ± 0.44) h (Eq. 6, N = 256/3600 s−1) and thermally polarized signal \(S_{inf}^{ssTP }\) = 4.07 × 104 (R2 = 0.97) (Eq. 7). At the end, the thermal polarization was saturated with a train of 1000 pulses with 5° flip angle.
Next, DNP was commenced by turning on the microwave source in continuous wave mode using the above described optimized settings. The build-up of the DNP enhanced 13C signal SDNP(t) was monitored by acquiring an NMR spectrum every minute (Fig. 1, the same parameters as before but with TR = 1 min). The last spectrum, acquired tDNP = 110 min from the beginning of DNP, yielded a solid state polarization of Pobs,ssDNP = 64%. A mono-exponential recovery function was fitted to the data, yielding an apparent time constant of Tobs,DNP = (18.39 ± 0.50) min. The RF excitations almost did not affect the build-up of DNP signal: TDNP = (18.396 ± 0.49) min, that corresponds to polarization of ≈ 61%.
Dissolution and quantification of liquid state 13C-polarization
A standard sample was polarized as described above with a 22 mg sample. Once the desired polarization was reached, the dissolution medium (specific to the tracer and sample size) was filled into a heating chamber (Fig. 1a-1). The solution was heated until a pressure of 11 bar was reached, corresponding to temperature T ≈ 115 ºC. Right before the medium was injected into the sample cup, the cup was lifted 8 cm to reduce the impact of the hot solution on the helium bath in the VTI. The injection of the dissolution medium into the sample cup was commenced via the polarizer’s software. Within ca. 2 s, the sample was dissolved and transferred into the receiver vessel through a double-walled tubing assembly (injection via inner tube, ejection via outer tube). As hot and pressurized liquids were involved, care was taken and safety measures applied.
To quantify the liquid state polarization, the sample was split between 5 mm NMR tubes and transferred manually to 1 T and 9.4 T NMR spectrometers, where the hyperpolarized and (later) thermally polarized signals were acquired (Fig. 6). In this example, the polarization was quantified to 26% at 1 T, 26 s after dissolution, and 20% at 9.4 T, 30 s after dissolution. The lifetimes of the polarization were measured to 67 s for 1 T and 48 s for 9.4 T. Using the longest T1 which also corresponds to the lower field, we estimated the polarization at the time of dissolution to be 38% for the sample measured at 1 T, and ≈ 31% for the 9.4 T sample. Note that the sample was exposed to different, varying and much lower magnetic fields during the transfer, so that using the high-field T1 to estimate the polarization only provides a very rough estimate.
High resolution 13C-NMR spectra of hyperpolarized (black) thermally polarized (blue) 1-13C-PA measured at 1 T (a) and 9.4 T (b). (a) The hyperpolarized signal was measured in a single scan (NSDNP = 1) after approx. 26 s after dissolution (\(\alpha\) = 5°, pw = 3.05 µs, pa = − 5.6 dB, SDNP = 32.38 a.u.). The thermally polarized signal was acquired adding 4 vol% Gd contrast agent (\(\alpha\) = 20°, pw = 12.20 µs, pa = − 5.6 dB, SDNP = 4.18 × 10−4 a.u.). The resulting signal enhancement to SDNP was 1.09 × 109 (Eq. 8), and the polarization = 26% (Eqs. 9, 10). (b) At 9.4 T, the signal was acquired ≈ 30 s after dissolution using a 5° pulse (SDNP = 7.59 × 105 a.u., pw = 10 µs, pa = − 18.9 dB, RG = 0.25) and quantified with respect to the thermally polarized signal acquired with a single 90° pulse (STP = 1.41 × 105 a.u., pw = 0.55 µs, pa = − 18.9 dB, RG = 101) to an enhancement of 2.5 × 104 (Eq. 8) and polarization of 20% (Eqs. 9, 10). Note that due to the differences in the RG, both hyperpolarized spectra were normalized to 1 and the thermal spectrum measured at 1 T was multiplied by 5000 to fit in the scale.
Standard operational procedure, reproducibility and hyperpolarization yield
While performing more than 100 DNP experiments, the following procedure proved to be instrumental to obtain reproducible polarization for 1-13C-pyruvate. In addition to the initial calibrations during the setup (Table 2) we developed a more elaborate procedure which contains routine calibrations (Table 3), specific preparation of chemistry (Table 4), a 21-step polarization procedure (Table 5), and a weekly maintenance routine (Table 6). These procedures were developed for pyruvate polarization, but may serve as a starting point for other agents (e.g. below for 15N-urea), although some modifications will be necessary.
Using these procedures, we evaluated the reproducibility and yield for obtaining ≈ 4 mL solution with 60 mM hyperpolarized pyruvic acid, a composition suitable for animal experiments30,31,32. The dDNP process was repeated five times on different days using standard samples of (21.64 ± 0.15) mg and 3.9 mL dissolution medium and detection at 1 T (Table 7). On average, we obtained a build-up constant TDNP = (1032 ± 21.7) s and solid state polarization of (42.1 ± 3.7) a.u.. Depending on the transfer time ttrans (17–20 s), the liquid state polarization was quantified with respect to the thermally polarized sample to P ≈ 33%–46%, with a mean of (38 ± 5.7) %. To estimate the polarization right after dissolution, we used the T1 of the samples and obtained an average polarization of (47.2 ± 7.8) %33. The pH value of the sample inside the NMR tube was measured to be 8.51 ± 0.02.
dDNP duty cycle
In addition to reproducibility experiments, to evaluate how many samples can be polarized in a given time, we performed seven more 1-13C-PA DNP experiments every ≈ 90 min using the procedure described above: roughly 30 min were needed to prepare and clean the system, and ca. 60 min for dDNP. On average, measured liquid state polarization P(ttrans ≈26 s) = (33 ± 3.3) % was achieved that corresponds to the estimated value right after dissolution P(ttrans = 0) = (53.9 ± 12.4) %.
In vivo 13C MRI
To demonstrate the feasibility of metabolic imaging in vivo, we polarized 1-13C-PA with the procedure described above to P(ttrans = 0) ≈ 50%.
During the buildup of the polarization, a CEBAC-mouse was anesthetized, outfitted with a tail-vein catheter, and placed on the heated animal bed of the 7 T MRI system. The MRI coil was adjusted and anatomical images were acquired before dissolution (Fig. 7). No tumor was apparent on the conventional MRI.
High resolution 13C-NMR spectra of hyperpolarized (black) thermally polarized (blue) 1-13C-PA (sample 5 in the table) measured at 1 T. The hyperpolarized signal was measured in a single scan (NSDNP = 1) after approx. 17 s after dissolution (\(\alpha\) = 5°, pw = 3.05 µs, pa = − 5.6 dB). The thermally polarized signal was acquired adding 4 vol% Gd contrast agent (\(\alpha\) = 20°, pw = 12.20 µs, pa = − 5.6 dB, SDNP = 39.5 a.u.). The resulting signal enhancement to SDNP was 310 × 106 (Eq. 8), and the polarization = 43% (Eqs. 9, 10). The thermal spectrum measured was multiplied by 50,000 to fit in the scale.
After the dissolution with 5 mL medium, the contrast agent containing approx. 46 mM 1-13C-PA was rapidly transferred to the MRI and ≈ 100 uL were injected into the tail vein catheter of the mouse within 40 s after dissolution. About 10 s after the end of the injection, 13C-CSI was performed across an abdominal axial slice. Signals of pyruvate, lactate and alanine were observed, and maps of each metabolite were prepared (Fig. 8). Using the same geometry 1H T1w MRI was measured. We observed strong lactate and pyruvate signals in the liver and kidney. High SNR was observed in individual voxels as well in larger ROIs.
In vivo T1w 1H-MRI, maps of hyperpolarized 1-13C-PA and 1-13C-lactate (LA) and selected 13C spectra of a pancreatic tumor rat model acquired at 7 T. After the injection of 100 µl hyperpolarized contrast agent containing ~ 46 mM 1-13C-PA, eight CSI datasets were acquired. Prominent signal of lactate was found in the regions of kidney (ROI1), liver (ROI2), aorta and inferior vena cava branch (ROI3). Strong SNR was observed in the selected voxel (blue rectangle), exhibiting resonances of lactate, pyruvate and alanine (Ala) with a line width of ca. 84 Hz. The receive-only loop-coil was positioned ventral (yellow rectangle) and a small container filled with water was placed in the middle of the coil (green rectangle, phantom—Pha). Note that the tubes supplying warm water to the animal bed appeared on the top because of aliasing. The sum of eight consequent acquisitions is shown.
dDNP of other nuclei: demonstration with 15N
Exchanging the LC box allowed us to set the resonance frequency of the NMR coil in the polarizer to ≈ 28.83 MHz, the resonance frequency of 15N at 6.7 T. This allowed us to calibrate the 15N flip angle, µW frequency and power using a 200 mg sample of 4.16 mM 13C,15N2-urea and 35.7 mM radical (α = 3.5° at pw = 3 us, pa = 10 dB, ν(µW) = 187.18 GHz, p(µW) = 35 mW). DNP-enhanced solid state 15N-NMR signal was readily observed, and a build-up constant TDNP = (2140 ± 391) s was obtained for 13C,15N2-urea and (3358 ± 425) s for 15N2 urea.
Dissolution was performed using 5 mL of deionized H2O and 0.27 mM EDTA, leading to a nominal 45.4 mM urea concentration after dissolution. After transfer to the 9.4 T NMR spectrometer, sixty 5° 15N-spectra were acquired (TR = 3 s), and used to calculate T1 and quantify the polarization. The lifetime of the hyperpolarized sample was determined to T1(13C-15N urea) = (26.3 ± 1.0) s and T1(15N-urea) = (26.1 ± 0.7) s.
For 13C-15N2 urea, a 15N polarization of (4.5 ± 0.7) % was observed ttrans = (30 ± 1) s after dissolution (n = 4) and for 15N2-urea, the polarization was determined to (5.6 ± 0.8) % after (30 ± 3) s (n = 4), both with respect to the 15N-signal of each sample in thermal equilibrium (TR = 17 s, 128 averages, RG 101, α = 90°). The initial 15N-polarization at the time of dissolution (ttrans = 0 s) was estimated to P(15N) (t = 0 s) = (14.7 ± 1.7)% for 13C-15N2 urea and P(15N) (t = 0 s) = (18.4 ± 1.1)% for 15N2 urea34.
Discussion
In this paper, we describe our initial experience, operational routines and performance of a cryogen-free dDNP polarizer operated at 6.7 T.
Installation requirements
The polarizer requires ≈ 2–3 m2 footprint, standard single-phase electric power, compressed air and helium. The magnet is not actively shielded so safety has to be considered and some distance from other devices must be maintained. The helium compressor requires 3-phase power and cooling water;—prerequisites that are likely met by many NMR or MRI facilities. The noise of the helium pump at the polarizer and the cryo-expander may be an inconvenience for those working nearby for an extended time.
Safety
The main hazards of the setup include hot and cold pressurized fluids: water at 115 °C and 11 bar, liquid nitrogen, max. 2 bar helium and compressed air, acids and bases, magnetic fields (6.7 T) and electricity (230 V). In addition, the pressurized helium lines, standard gas bottles (e.g. 200 bar) as well as any chemical hazards have to be considered. The dissolution (heating, pressurization and extraction) takes place in a well-controlled manner behind closed, transparent doors, so that splash and splinter protection is provided (although no such event occurred). After the dissolution, the medium has sufficiently cooled to ≈ 37 °C, if necessary a jar of ice can be placed beneath the receiver vial. Cold temperatures are present while freezing the sample in liquid N2, and precautions include using appropriate safety gear (gloves, googles).
As the magnet contains no liquid cryogens, the safety precautions can be adjusted accordingly. A quench pipe is not needed, as the amount of gaseous helium used to cool the VTI is only 50 standard liters although there is more helium in the closed-cycle He-cryostat.
Handling and operation
The system provides full access to more than 4 sensor readouts, all of which are continuously stored for later retrieval. We found this to be an excellent and essential feature, allowing precise documentation and reconstruction of the experimental conditions. The software interface (LabView) provides control over many essential DNP parameters, and new features may be added by the user or manufacturer. It should be noted, however, that the temperature of the sample itself cannot be directly measured, and is estimated by measuring the temperature of the VTI.
Most parts are easily accessible for repairs or modifications, e.g. to adjust the amount of hyperpolarized substance, or to supply filtered air to the enclosure. As most valves are operated by compressed air, no heating and melting of the valves was observed.
Switching between different nuclei by tuning or exchanging the LC circuity was very convenient for monitoring the hyperpolarization of different nuclei.
Reproducibility
Using the polarization routines described above, robust and reliable liquid state hyperpolarization was achieved: P(13C ) with (ttrans = 19 s ± 1 s) = (38 ± 6)%, and an estimated polarization at dissolution of P(13C ) at t0 ≈ (47 ± 7)% (Table 7). Since, the actual decay of the sample during the transfer across strongly varying magnetic fields is not precisely known, the polarization at the time of dissolution is an estimate. The build-up of the solid-state polarization yielded a time constant of ~ 17 min, allowing for repetitive dissolutions with a duty cycle below two hours, which may be accelerated further if the need arises. The reported data were acquired after the level of the liquid helium in the VTI was raised by submerging a disk into the liquid. This modification resulted in less variable build-up times: cv(TDNP) = 2.1% and 22.8% with and without washer, respectively. It is relevant to point out that the temperature inside the VTI is not necessary the temperature of the sample inside the vial.
Interestingly, the 13C-NMR signal of pyruvate in the dissolved sample after hyperpolarization showed a relatively large variation, cv(SlsTH) = 13.1%. This result may indicate a varying pyruvate concentration, hinting at an inhomogeneous dissolution.
There is little data published with respect to reproducibility in the literature, but the absolute yield is comparable to what was reported before (1-13C-PA with trityl radical, i.e. 36–64%35). Of course, a faster and more reproducible sample transfer will improve the significance of these numbers; a dedicated delivery system will be presented elsewhere.
Polarization of other nuclei
Tuning the NMR coil of the DNP to other nuclei was easy as the LC circuit was placed in a shielded box outside the VTI. For resonance frequencies close to 13C (like 129Xe), it was sufficient to adjust the variable capacitors. For other nuclei, a different LC circuit was used. We demonstrated this by using 15N urea, whose gyromagnetic ratio is about 1/10 of that of 1H and 40% of 13C, and obtained a polarization of 5.6% at the spectrometer.
Pitfalls
During the course of this study, less than 5% of all experiments failed. Most of these were during the dissolution and before the cleaning procedures were in place. Among the issued encountered were:
Sample insertion failed
As the tubes for the dissolution have a smooth surface to assure a tight seal, the lowering mechanism was found to slip sometimes. This issue was easily addressed by gently assisting the insertion manually. A more serious problem occurred after three weeks of continuous using, when we experienced problems lowering the sample into the magnet. We assume that this was caused by ice starting to form inside the tube used to insert the sample, possibly caused by small leaks or the frequent insertion/ejection of the sample cup. The issue was resolved by warming up the VTI, so we implemented a weekly cleaning procedure (warming up the VTI to c.a. 180 K within ≈ 10 h and gas evacuation (1 h) by vacuum pump, followed by cooling to ≈ 1.4 K in ≈ 5 h). This procedure can be conducted automatically e.g. over the weekend.
Low solid-state polarization
To obtain consistent solid-state polarization, it turned out to be essential to freeze the sample in the cup (in liquid nitrogen) before inserting it in the magnet. This way, splashing of the sample during the pressurization was avoided, so that the sample stayed at the bottom of the cup. Furthermore, a mismatch of the (ESR and NMR) transmitter frequencies and the Larmor frequencies (caused by drifting of the magnetic field) may cause loss of polarization, so regular adjustments are needed. Additionally, it is relevant to underline the importance of keeping the sample vial in liquid He during the build-up, to assure the transfer of the highest electron polarization. Due to the relationship between hyperpolarization and T, any temperature higher than 3 K implies considerable losses in polarization.
Failed dissolution
To avoid any faulty dissolution, it was essential to dry the dissolution module two times by flushing all the tubes with compressed air for 7–10 min before starting the polarization procedure by inserting the sample. As the tubes and connectors for dissolution were exposed to highly varying temperatures and pressures, regular maintenance is required. In more than 100 dissolutions, we observed one material failure of the dissolution path so far (broken tube, unclear reason).
Varying liquid state polarization
Obviously, varying times and magnetic fields during transfer will cause varying polarizations. We ameliorated this issue by filling the NMR tubes on top of the magnet, where the field is ~ 10 mT, and by using a 12 mT resistive magnet to transfer the sample to the 9.4 T NMR. Using low-field NMR spectrometers to detect the enhanced 13C signal is advantageous as they can be placed close to the DNP system. However, quantification of the polarization is more difficult as the sensitivity is limited, requiring use of gadolinium relaxation agent and massive averaging to acquire sufficient SNR of the thermal 13C (no signal was observed for 15N).
Conclusion
In this paper, we share our experience, results and tips for operating the SpinAlinger polarizer of more than 100 experiments over the course of one year.
Overall, the polarizer turned out to be reliable, compact, easy in use and providing high polarization. Other advantages include the absence of liquid cryogens, a short duty cycle and an open, modular design that e.g. allows monitoring of solid-state signals of different nuclei. We estimated the liquid state polarization of 1-13C-PA after dissolution to (38 ± 5.7) % and 15N2-urea to (5.6 ± 0.8) %—well sufficient for metabolic imaging as was successfully demonstrated here.
Data availability
The datasets generated and/or analyzed during the current study are available in the Zenodo repository, at the following https://doi.org/10.5281/zenodo.5957503.
References
Katti, G., Ara, S. A. & Shireen, A. Magnetic resonance imaging (MRI): A review. Int. J. Dent. Clin. 3, 65–70 (2011).
Haase, A., Frahm, J., Matthaei, D., Hänicke, W. & Merboldt, K.-D. FLASH imaging: Rapid NMR imaging using low flip-angle pulses. J. Magn. Reson. 213, 533–541 (1986).
Ardenkjær-Larsen, J. H. et al. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. 100, 10158–10163 (2003).
Cunningham, C. H. et al. Hyperpolarized 13C metabolic MRI of the human heart: Novelty and significance. Circ. Res. 119(11), 1177–1182 (2016).
Lewis, A. J. M. et al. Noninvasive immunometabolic cardiac inflammation imaging using hyperpolarized magnetic resonance. Circ. Res. 122(8), 1084–1093 (2018).
Norquay, G., Collier, G. J., Rao, M., Stewart, N. J. & Wild, J. M. Xe 129 -Rb spin-exchange optical pumping with high photon efficiency. Phys. Rev. Lett. 121, 153201 (2018).
Hirsch, M. L., Kalechofsky, N., Belzer, A., Rosay, M. & Kempf, J. G. Brute-force hyperpolarization for NMR and MRI. J. Am. Chem. Soc. 137, 8428–8434 (2015).
Natterer, J. & Bargon, J. Parahydrogen induced polarization. Prog. Nucl. Magn. Reson. Spectrosc. 31, 293–315 (1997).
Kaptein, R. & Oosterhoff, J. L. Chemically induced dynamic nuclear polarization II: (Relation with anomalous ESR spectra). Chem. Phys. Lett. 4, 195–197 (1969).
Drullinger, R. E. & Zare, R. N. Optical pumping of molecules. J. Chem. Phys. 51(12), 5532–5542 (1969).
Lampel, G. Nuclear dynamic polarization by optical electronic saturation and optical pumping in semiconductors. Phys. Rev. Lett. 20, 491–493 (1968).
Jannin, S., Bornet, A., Melzi, R. & Bodenhausen, G. High field dynamic nuclear polarization at 6.7T: Carbon-13 polarization above 70% within 20min. Chem. Phys. Lett. 549, 99–102 (2012).
Capozzi, A. et al. Gadolinium effect at high-magnetic-field DNP: 70% 13 C polarization of [U- 13C] glucose using trityl. J. Phys. Chem. Lett. 10, 3420–3425 (2019).
Overhauser, A. W. Polarization of nuclei in metals. Phys. Rev. 92, 411–415 (1953).
Kurdzesau, F. et al. Dynamic nuclear polarization of small labelled molecules in frozen water–alcohol solutions. J. Phys. Appl. Phys. 41, 155506 (2008).
Reddy, T. J., Iwama, T., Halpern, H. J. & Rawal, V. H. General synthesis of persistent trityl radicals for EPR imaging of biological systems. J. Org. Chem. 67, 4635–4639 (2002).
Wolber, J. et al. Generating highly polarized nuclear spins in solution using dynamic nuclear polarization. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 526, 173–181 (2004).
Capozzi, A. et al. Metabolic contrast agents produced from transported solid 13C-glucose hyperpolarized via dynamic nuclear polarization. Commun. Chem. 4, 1–11 (2021).
El Daraï, T. & Jannin, S. Sample formulations for dissolution dynamic nuclear polarization. Chem. Phys. Rev. 2, 041308 (2021).
Baudin, M., Vuichoud, B., Bornet, A., Bodenhausen, G. & Jannin, S. A cryogen-consumption-free system for dynamic nuclear polarization at 9.4 T. J. Magn. Reson. 294, 115–121 (2018).
Lumata, L. L. et al. Development and performance of a 129-GHz dynamic nuclear polarizer in an ultra-wide bore superconducting magnet. Magn. Reson. Mater. Phys. Biol. Med. 28, 195–205 (2015).
Ardenkjaer-Larsen, J. H. et al. Dynamic nuclear polarization polarizer for sterile use intent. NMR Biomed. 24, 927–932 (2011).
Cheng, T. et al. A multisample 7 T dynamic nuclear polarization polarizer for preclinical hyperpolarized MR. NMR Biomed. 33, (2020).
Ardenkjær-Larsen, J. H. et al. Cryogen-free dissolution dynamic nuclear polarization polarizer operating at 3.35 T, 6.70 T, and 10.1 T. Magn. Reson. Med. 81, 2184–2194 (2019).
Bornet, A. et al. Microwave frequency modulation to enhance dissolution dynamic nuclear polarization. Chem. Phys. Lett. 602, 63–67 (2014).
Elliott, S. J. et al. Practical dissolution dynamic nuclear polarization. Prog. Nucl. Magn. Reson. Spectrosc. 126–127, 59–100 (2021).
Bliemsrieder, E. et al. Hyperpolarized 13C pyruvate magnetic resonance spectroscopy for in vivo metabolic phenotyping of rat HCC. Sci. Rep. 11, 1191 (2021).
Grashei, M., Hundshammer, C., van Heijster, F. H. A., Topping, G. J. & Schilling, F. pH Dependence of T2 for hyperpolarizable 13C-labelled small molecules enables spatially resolved pH measurement by magnetic resonance imaging. Pharmaceuticals 14, 327 (2021).
Hundshammer, C. et al. Hyperpolarized amino acid derivatives as multivalent magnetic resonance pH sensor molecules. Sensors 18, 600 (2018).
Flori, A. et al. DNP methods for cardiac metabolic imaging with hyperpolarized [1-13C]pyruvate large dose injection in pigs. Appl. Magn. Reson. 43, 299–310 (2012).
Golman, K. et al. Cardiac metabolism measured noninvasively by hyperpolarized 13C MRI. Magn. Reson. Med. 59, 1005–1013 (2008).
Lau, A. Z. et al. Rapid multislice imaging of hyperpolarized 13C pyruvate and bicarbonate in the heart. Magn. Reson. Med. 64, 1323–1331 (2010).
Dey, A. et al. Hyperpolarized NMR metabolomics at natural 13C abundance. Anal. Chem. 92, 14867–14871 (2020).
Milani, J. et al. Hyperpolarization of nitrogen-15 nuclei by cross polarization and dissolution dynamic nuclear polarization. Rev. Sci. Instrum. 88, 015109 (2017).
Jähnig, F., Kwiatkowski, G. & Ernst, M. Conceptual and instrumental progress in dissolution DNP. J. Magn. Reson. 264, 22–29 (2016).
Acknowledgements
We acknowledge support by the research unit miTarget (FOR 5042), the research training group “materials for brain” (GRK 2154/1-2019), Emmy Noether Program “metabolic and molecular MR” (HO 4604/2-2), DFG grant INST 257/616-1 (FUGG), the SFB “bulk-reaction” (TRR 287), the clusters of excellence “precision medicine in inflammation” (PMI 2167), and the German Federal Ministry of Education and Research (BMBF) within the framework of the e:Med research and funding concept (01ZX1915C) and DFG PR-1868/3-1 (TryIBD). Kiel University and the Medical Faculty are acknowledged for supporting the Molecular Imaging North Competence Center (MOIN CC) as a core facility for imaging in vivo. MOIN CC was founded by a grant from the European Regional Development Fund (ERDF) and the Zukunftsprogramm Wirtschaft of Schleswig-Holstein (Project no. 122-09-053). Additionally, we express our infinite gratitude to Dr. Andrea Capozzi for his support. Moreover, we acknowledge Mr. Thomas Griebenow and Prof. Dr. Rainer Herges for the UV-Vis Spectrometer measurements to define the real concentration of the dissolved sample. In addition, we want to express our deepest gratitude to Polarize for their constant assistance. We thank Franz Schilling and Geoffrey Topping for providing us the custom written Matlab based software for analysis and visualization of 13C-CSI. Franz Schilling can be inquired to make the software available. We thank Stephan Düwel for providing the software to process the CSI data.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A.F., J.P., M.A. and A.P. performed the experiments. A.P. helped with the set-up of the NMR and MRI experiments. O.W. and E.P. assisted with in-vivo experiments. A.F., J.P., M.A., A.P. and J.B.H. wrote the first draft of the article. J.B.H. designed, acquired and supervised the project. All the authors aided in revising the article critically and approved the final version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferrari, A., Peters, J., Anikeeva, M. et al. Performance and reproducibility of 13C and 15N hyperpolarization using a cryogen-free DNP polarizer. Sci Rep 12, 11694 (2022). https://doi.org/10.1038/s41598-022-15380-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-15380-7
This article is cited by
-
Nuclear spin polarization of lactic acid via exchange of parahydrogen-polarized protons
Communications Chemistry (2024)
-
Multi-sample/multi-nucleus parallel polarization and monitoring enabled by a fluid path technology compatible cryogenic probe for dissolution dynamic nuclear polarization
Scientific Reports (2023)
-
Parahydrogen-induced polarization and spin order transfer in ethyl pyruvate at high magnetic fields
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.