Abstract
Phase-change integrated photonics has emerged as a new platform for developing photonic integrated circuits by integrating phase-change materials like GeSbTe (GST) onto the silicon photonics platform. The thickness of the GST patch that is usually placed on top of the waveguide is crucial for ensuring high optical performance. In this work, we investigate the impact of the GST thickness in terms of optical performance through numerical simulation and experiment. We show that higher-order modes can be excited in a GST-loaded silicon waveguide with relatively thin GST thicknesses (<100 nm), resulting in a dramatic reduction in the extinction ratio. Our results would be useful for designing high-performance GST/Si-based photonic devices such as non-volatile memories that could find utility in many emerging applications.
Similar content being viewed by others
Introduction
Similarly to micro- and nano-electronics, silicon has become the mainstay material for developing photonic integrated circuits (PICs). Silicon photonics (SiPh) has been established as an appealing technology for a wide range of applications in the fields of telecom and datacom1, quantum computing2, or LiDAR3, to name a few. However, the active properties of silicon either based on nonlinearities4 or electro-optic effects5 are rather modest, thus imposing several trade-offs such as compactness and bandwidth. In such a way, there is a compelling interest in the integration of complementary metal-oxide-semiconductor (CMOS) compatible materials featuring a large refractive index modulation at telecommunication wavelengths to overcome those limitations and provide new functionalities to the SiPh platform.
In this context, a plethora of new materials have been proposed in recent years, namely: ferroelectrics, by relying on Pockels effect for enabling high-speed and loss-less refractive index modulation such as barium titanate (BTO)6 and lithium niobate (LiNbO\(_{3}\))7; two dimensional (2D) materials, which exploit their large electro-refractive index such as graphene8 and transition metal dichalcogenides (TMDs)9; transparent conducting oxides (TCOs) such as indium tin oxide (ITO) by leveraging the strong light-matter interaction (LMI) provided by the epsilon-near-zero (ENZ) regime10,11,12; and phase-change materials (PCMs) such as vanadium dioxide (VO\(_{2}\))13 and chalcogenides14 that stand out for enabling ultra-compact devices thanks to the dramatic change in the refractive index together with, in chalcogenides, a reversible non-volatile response at room temperature.
Ge\(_{2}\)Sb\(_{2}\)Te\(_{5}\) (GST) is one of the most widely used among the different chalcogenide compounds15. At telecom wavelengths, the refractive index of GST typically changes in the order of \(\Delta n \sim 2-3\) and \(\Delta \kappa \sim 1\) in the real and imaginary parts, respectively, between the amorphous (a-GST) and crystalline (c-GST) state16,17,18. To undergo the crystallization, the GST needs to be heated above \(\sim 180^{\circ }\)C, while for the amorphization, the material must reach the melting temperature (\(\sim 650^{\circ }\)C) followed by a rapid cooling (\(>1-10^{\circ }\) C/ns) to produce the melt-quench19. Otherwise, the GST is likely to be recrystallized. The phase change can be achieved on-chip by self-heating the material with optical pulses and evanescent-field coupling20 or placing a microheater near the GST21,22. On the other hand, the switching between both states can be achieved with sub-nanosecond times23, sub-picojoule energies24, and up to \(10^{15}\) cycles25.
Such appealing properties have led to developing high-performance and new kinds of waveguide-based photonic integrated devices such as modulators26,27,28,29,30, pass polarizers31, photonic memories32,33,34,35,36,37, reconfigurable devices38,39,40, switches41,42,43,44,45,46,47, or synapses48. Thereby, enabling new applications based on non-von Neumann architectures such as arithmetic49 and logic50 operations, in-memory computing51, neuromorphic computing52,53, or photonic tensor cores54. Moreover, the non-volatile characteristic of GST would be desirable for achieving silicon photonic devices with ultra-low power consumption55.
A waveguide loaded with a thin patch of GST is the basis of most GST-based photonic devices, which usually exploit the large change in the absorption. Therefore, minimizing insertion losses while maximizing the extinction ratio is the target for such absorption-based devices. In this context, the thickness of the GST layer directly impacts the optical performance of GST/Si waveguides. Compared to silicon, GST exhibits a larger real part in its refractive index in both states. Hence, the light can be confined and guided (with loss) in smaller cross-sections than their silicon counterparts. However, as we demonstrate in this work, the coupling and the guiding interplay between silicon and GST can reduce the expected optical performance in contrast to with the assumption of single-mode operation. Therefore, the analysis of the GST thickness in such terms is necessary to obtain optimal optical switching and provide a more in-depth insight into the optical behavior of such hybrid waveguides.
We demonstrate through numerical simulation and experiment that using relatively thick GST layers does not imply an enhancement of the optical performance. In fact, this is reduced compared to thinner layers because higher-order modes with a low extinction ratio are excited when the GST is crystalline.
Results
Description of GST-loaded silicon waveguides
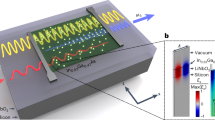
Figure 1 illustrates the working principle of the considered GST/Si waveguide used for optical switching. The waveguide comprises a standard silicon waveguide with a layer of GST on top (see inset of Fig. 1). Switching between amorphous and crystalline is achieved by triggering the phase change with an external or on-chip stimuli such as evanescent coupling or microheaters. For optical actuation, heating originates inside the GST patch, while for microheaters, the heat distribution depends on the heater design. Nevertheless, a full change in the GST patch is usually achieved by tailoring the shape of the optical or electrical pulses. The phase change is accompanied by a variation on both real and imaginary parts of the effective refractive index of the guided light. Therefore, at the output of the hybrid waveguide, the light is modulated in both phase and amplitude. On the other hand, the modulation strength is strongly dependent on the thickness of the GST patch, which can be tailored between a few and dozens of nanometers during the fabrication process.
Illustration of a GST-loaded silicon waveguide and its working principle for optical switching. The GST switches between crystalline and amorphous states upon an optical or electrical switching signal. Between both states, the refractive index of the GST suffers a dramatic change in both real and imaginary parts, resulting in an amplitude and phase modulation of the output light. Inset shows the cross-section and the dimensions of the GST/Si waveguide.
Optical modes coupling and propagation
For the materials used in this work, we consider the complex refractive indices (\(n+j\kappa\)) given in the "Methods" section. Those values are used for our numerical simulations, which unless otherwise stated, are given at 1550 nm and for the transverse electric (TE) polarization. Figure 2a depicts the power transfer between a silicon and GST/Si waveguide in the presence of a step discontinuity. Because of the refractive index profile mismatch between both structures, several optical modes may be excited in the GST/Si waveguide to fulfill the field continuity condition at the interface. In this regard, the normalized transmitted electric field along the propagation direction (z-axis) in the GST/Si waveguide can be approximated as a linear combination of the different supported modes or eigenmodes56 as
where \(\Gamma _{n}\) is the coupling coefficient between the optical mode of the silicon waveguide and the n\(^{th}\)-mode of the hybrid waveguide, \(\kappa _{\text {eff},n}\) is the corresponding effective extinction coefficient, and \(\lambda\) is the working wavelength.
To determine the value of \(\Gamma _{n}\), we exploited the reciprocity of the coupling process. Hence, we calculated the coupling by exciting the silicon waveguide with the supported optical modes of the GST/Si waveguide. Figure 2b illustrates this process when a GST/Si mode excites the silicon waveguide. Optical mismatch gives rise to uncoupled power comprised by reflection and radiation. In this manner, \(\Gamma _{n}\) can be obtained by assessing the amount of power that is transmitted, i.e., coupled to the TE mode of the silicon waveguide. To discriminate between radiated and transmitted power, we use the overlap integral:
where \(\mathbf{E }/\mathbf{H }_{n}\) is the field profile in the silicon waveguide at a certain length when is excited with the n\(^{th}\) GST/Si optical mode, and \(\mathbf{E }/\mathbf{H }_{in}\) is the TE fundamental mode of the silicon waveguide. Simulation details can be found in the "Methods" section.
(a) Illustration of the power transfer between a silicon and GST/Si waveguide. Due to the optical mismatch between both waveguides, the incident power (\(P_{in}\)) is radiated outside the waveguide (\(P_{rad}\)), reflected (\(P_{r}\)), and transmitted (\(P_{t}\)). (b) Illustration of the technique used to obtain the coupling efficiency between the optical modes of the GST/Si waveguide and the fundamental TE mode of the silicon waveguide by exploiting the reciprocity property of the coupling process.
Based on our simulations, the hybrid waveguide can support two optical modes (mode 0 and mode 1) in the amorphous state. Figure 3 shows the propagation losses and the associated power coupling coefficients as a function of the GST thickness. Mode 0 corresponds to the TE polarized fundamental mode of the GST/Si waveguide [Fig. 3a]. The light is mainly confined in the silicon waveguide for a very thin GST, giving rise to negligible coupling losses. As the GST thickness increases, the light is pushed up towards the GST [see insets of Fig. 3a]. However, the real part of the GST refractive index in the amorphous state is not high enough to allow guiding inside the GST patch. Consequently, a high percentage of the light remains in the silicon, and the optical coupling is still high. On the other hand, mode 1 corresponds to a hybrid optical mode with \(E_{x}\) and \(E_{y}\) components that has a cut-off around a thickness of 45 nm [Fig. 3b]. Although the propagation loss of this mode can be comparable to mode 0, the coupling is very weak since the light is mostly localized near the boundaries of the GST/Si waveguide.
For the crystalline state, the real part of the GST refractive index suffers a dramatic increase giving rise to additional higher-order optical modes [see Fig. 4]. The propagation loss of the fundamental mode (mode 0) can reach almost 40 dB/\(\upmu\)m for the highest thickness of GST [see Fig. 4a]. However, the coupling varies from near-perfect coupling to a high coupling loss for thickness values between 20 nm and 60 nm. Such a change arises because the GST becomes the core of the hybrid waveguide [see insets of Fig. 4a]. The hybrid mode (mode 1) has a lower cut-off thickness of around 20 nm [see Fig. 4b] in contrast to the amorphous state. This reduction is due to the larger refractive index contrast. The propagation loss is between 5 and 15 dB/\(\upmu\)m with a maximum coupling of \(\sim 0.2\). On the other hand, mode 2 has a cut-off thickness of around 55 nm [see Fig. 4c]. For this case, the light is guided through the silicon waveguide resembling the TE-like mode of a silicon waveguide [see insets of Fig. 4c]. Consequently, there is a weak interaction between the light and GST layer, yielding to the highest coupling values and lowest propagation losses among the three optical modes.
To verify the excitation and optical properties of such higher-order modes, we simulated the optical transmission between a silicon and GST/Si waveguide by using 3D-FDTD. Figure 5 shows the results obtained by 3D-FDTD (red line) and eigenmode expansion (EME) (blue line) using Eq. (1) together with values of Figs. 3 and 4. We considered a 5-\(\upmu\)m-long GST/Si waveguide like the shown in Fig. 2a ending in perfectly matched layer to avoid reflections [see inset of Fig. 5b]. The theoretical transmission considering only the propagation loss of the fundamental mode (mode 0) of the GST/Si waveguide is plotted for comparison (dotted line). Results show very good agreement between 3D-FDTD and EME simulations. Few discrepancies exist in the amorphous state since the fundamental GST/Si mode has small coupling losses and the propagation loss of the hybrid mode is similar to the fundamental (see Fig. 3). For the crystalline state, the influence of higher-order modes is notably for thicknesses higher than 20 nm. For lower values, modes 1 and 2 are cut-off and cannot be excited. As the GST patch is thickened, the coupling to the fundamental mode is reduced, and the values of modes 1 and 2 are increased (see Fig. 4). Higher-order modes have significantly lower propagation loss than the fundamental. Therefore, the discrepancies between the multimode behavior of the GST/Si waveguide and the single-mode assumption are enlarged.
Comparison between 3D-FDTD and eigenmode expansion (EME). Transmission of GST/Si waveguide as a function of the GST thickness in the (a) amorphous and (b) crystalline state. Simulations were carried out for a step discontinuity between a silicon and GST/Si waveguide. The fundamental TE mode of the silicon waveguide impinges into a GST/Si waveguide ending in perfectly matched layer (see inset). Results were obtained for a 5 \(\upmu\)m-long-GST/Si waveguide. The dotted line stands for the transmission considering a perfect coupling of the fundamental (mode 0) TE mode into the GST/Si waveguide.
Selection of optimal thickness
For optical switching purposes, the optimal thickness of the GST should maximize the figure of merit (FOM) that relates the extinction ratio (ER), the insertion loss (IL), and the length of the hybrid waveguide, i.e., FOM = ER/(IL\(\times\)Length). For GST-loaded silicon waveguides, the insertion loss and extinction ratio depend on the GST length due to the multimode behavior of the hybrid waveguide in the crystalline state. On the other hand, ultra-compact waveguides are desired since this feature enables higher chip density and reduces the energy consumption.
Figure 6 shows the optical performance (IL, ER, and FOM) of GST-loaded silicon waveguides calculated by EME as a function of the GST thickness and for different lengths. The insertion losses follow a similar trend like the propagation loss of the fundamental mode in the amorphous state due to its high coupling efficiency [see Fig. 3a]. Conversely, the response of the extinction ratio exhibits a maximum of around 30–40 nm, which stems from the multimode operation of the GST/Si waveguide. As the thickness of the GST increases, the contribution of the fundamental mode to total optical losses is reduced. These are mainly determined by the high-order modes (modes 1 and 2), which have much lower propagation losses than mode 0 (see Fig. 4). Such a response is transferred to the FOM, as shown in Fig. 6c. For thicknesses greater than 30-40 nm, the FOM suffers a dramatic reduction as the GST thickness increases.
Experimental characterization
We experimentally validated our simulations by fabricating and characterizing a multimode GST-loaded silicon waveguide in the amorphous and crystalline states (see "Methods" section for details about fabrication and characterization setup). We chose 70 nm for GST thickness to ensure the multimode operation in the GST/Si waveguide. Figure 7a shows the measured transmission spectrum of a 5-\(\upmu\)m-long GST/Si waveguide in the amorphous and crystalline state. The inset shows the fabricated waveguide’s scanning electron microscope (SEM) image. Results were normalized with respect to a silicon waveguide without GST. We obtained high insertion loss (\(\sim\)7 dB) and extinction ratio (\(\sim 30\) dB), resulting in a FOM value of around 4. These results are in good agreement with our simulations describing the multimode operation (see Fig. 6). Accordingly, the optical performance is in the crystalline state is not dominated by the propagation loss of the fundamental mode but by the higher-order modes. Otherwise, the extinction ratio would have drastically increased to values above 100 dB, i.e., the measured power would have been limited by the noise floor.
(a) Measured spectrum of the fabricated 70-nm-thick and 5-m-long GST/Si waveguide in the amorphous and crystalline state. The inset shows a scanning electron microscope (SEM) image of the waveguide. The scale bar is 2 \(\upmu\)m. The dashed line encloses the GST layer. (b) Simulated transmission and contribution of each mode along the 5-\(\upmu\)m-long GST/Si waveguide at a wavelength of 1550 nm. The experimental transmission value is also shown. The inset depicts a zoom-out of the plot.
To give a better insight into the multimode performance of the waveguide in the crystalline state, we simulated the transmission by EME as a function of the GST length, as shown in Fig. 7b. The transmission of each GST/Si optical mode and the experimental value (dot) are plotted for comparison. Discrepancies between simulation (solid red line) and experiment might be attributed to slight variations on the refractive index of the on-chip GST in the crystalline state compared to the thin film or a non-uniform crystallization of the GST layer. Nevertheless, as it can be noticed, the contribution of the fundamental mode (mode 0) is very small, mainly due to the extremely high propagation losses, and being negligible after a few nanometers [see inset of Fig. 7b]. Therefore, the transmission response of the 5-\(\upmu\)m-long GST/Si waveguide stems from the interplay between the high-order modes (modes 1 and 2), which have much lower propagation losses in comparison with the fundamental mode (mode 0).
Discussion
In conclusion, we have investigated and characterized the impact of GST thickness on GST-loaded silicon waveguides for optimal optical switching. Our results show that for thicknesses greater than \(\sim 30\) nm, GST/Si waveguides may work in a multimode regime arising from the large refractive index of GST. The multimode operation results in a reduction of the performance compared to the assumption of single-mode transmission, in which the light is mostly guided within the GST layer. Through numerical simulation, we unveil that the origin of such a multimode is the large step-index discontinuity between the silicon and GST/Si waveguide. Our experimental results confirm the optical performance’s multimode operation and the associated turndown. For a 70-nm-thick and 5-\(\upmu\)m-long GST patch, we obtain an insertion loss and extinction ratio of 7 dB and 30 dB, respectively, resulting in a FOM of around 4. Such values represent almost a six-fold reduction in the FOM value with respect to the assumption of single-mode operation. Hence, confirming that utilizing thick GST layers may not be optimal in GST-loaded silicon waveguides for optical switching purposes.
Our results are helpful for further developing and optimizing GST-based silicon photonic components and circuits that might apply in emerging fields such as non-volatile switching, photonic tensor cores, and neuromorphic computing.
Methods
Optical constants and GST refractive index characterization
For the materials used in this work, we consider the complex refractive indices (\(n+j\kappa\)) shown in Table 1. For GST, we experimentally determined the refractive index in both states from a 70-nm-thick Ge\(_{2}\)Sb\(_{2}\)Te\(_{5}\) thin film deposited in a gold substrate by using e-beam evaporation. As-deposited GST was amorphous, while crystallization was achieved by heating the sample with a hot plate at \(\sim 180^{\circ }\)C for 10 min. The complex refractive index was calculated from reflection measurements using Fourier-transform infrared (FTIR) spectroscopy.
Simulation of the optical modes and coupling
The optical modes and their associated effective complex refractive indices were obtained by using 2D finite element method (FEM) using FemSIM tool from RSoft57. We applied a non-uniform mesh of 20 nm \(\times\) 20 nm (x \(\times\) y) with a minimum division of 10 points in the GST thickness (y-axis). On the other hand, the mode coupling was obtained by 3D finite-difference time-domain (3D-FDTD) simulations using FullWAVE tool from RSoft58. We applied a non-uniform mesh of 20 nm \(\times\) 20 nm \(\times\) 20 nm (x \(\times\) y \(\times\) z) with a minimum division of 10 points in the thickness (y-axis) of the GST layer. Perfectly matched layers (PMLs) were utilized to all the boundaries, except at \(x=0\) in which symmetric boundary condition was used.
Fabrication and characterization setup
The photonic strucrures were fabricated in 220-nm-thick silicon-on-insulator (SOI) and patterned by e-beam. GST was deposited by e-beam evaporation from a Ge\(_{2}\)Sb\(_{2}\)Te\(_{5}\) source and etched by lift-off in acetone. As-deposited GST was amorphous, while crystallization was achieved by heating the samples above the crystallization temperature (\(\sim 180^{\circ }\)C) for several minutes. Grating couplers were used for fiber-to-chip coupling.
To characterize the sample, we used a continuous-wave tunable laser working in the C-band (Photonetics ECL-1600). Polarization was adjusted to TE with a polarization controller (Thorlabs FC032) before injecting it into the chip. At the output, optical power was recorded using a power meter (Thorlabs PM320E) and a high-sensitivity photodiode (Thorlabs S155C).
Data availibility
The datasets generated and/or analyzed during the current study are available in the Zenodo repository, https://doi.org/10.5281/zenodo.6201510.
References
Reed, G. T., Mashanovich, G., Gardes, F. Y. & Thomson, D. J. Silicon optical modulators. Nat. Photonics 4, 518–526. https://doi.org/10.1038/nphoton.2010.179 (2010).
Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. Nat. Photonics 14, 273–284. https://doi.org/10.1038/s41566-019-0532-1 (2020).
Heck, M. J. Highly integrated optical phased arrays: photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 6, 93–107. https://doi.org/10.1515/nanoph-2015-0152 (2017).
Leuthold, J., Koos, C. & Freude, W. Nonlinear silicon photonics. Nat. Photonics 4, 535–544. https://doi.org/10.1038/nphoton.2010.185 (2010).
Soref, R. & Bennett, B. Electrooptical effects in silicon. IEEE J. Quantum Electron. 23, 123–129. https://doi.org/10.1109/JQE.1987.1073206 (1987).
Abel, S. et al. Large Pockels effect in micro- and nanostructured barium titanate integrated on silicon. Nat. Mater. 18, 42–47. https://doi.org/10.1038/s41563-018-0208-0 (2019).
He, M. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s-1 and beyond. Nat. Photonics 13, 359–364. https://doi.org/10.1038/s41566-019-0378-6 (2019) (1807.10362.).
Romagnoli, M. et al. Graphene-based integrated photonics for next-generation datacom and telecom. Nat. Rev. Mater. 3, 392–414. https://doi.org/10.1038/s41578-018-0040-9 (2018).
You, J. et al. Hybrid/integrated silicon photonics based on 2D materials in optical communication nanosystems. Laser Photonics Rev. 14, 2000239. https://doi.org/10.1002/lpor.202000239 (2020).
Babicheva, V. E., Boltasseva, A. & Lavrinenko, A. V. Transparent conducting oxides for electro-optical plasmonic modulators. Nanophotonics 4, 165–185. https://doi.org/10.1515/nanoph-2015-0004 (2015).
Niu, X., Hu, X., Chu, S. & Gong, Q. Epsilon-near-zero photonics: a new platform for integrated devices. Adv. Opt. Mater. 6, 1701292. https://doi.org/10.1002/adom.201701292 (2018).
Wu, J., Xie, Z. T., Sha, Y., Fu, H. Y. & Li, Q. Epsilon-near-zero photonics: infinite potentials. Photonics Res. 9, 1616. https://doi.org/10.1364/PRJ.427246 (2021).
Cueff, S. et al. VO2 nanophotonics. APL Photonics 5, 110901. https://doi.org/10.1063/5.0028093 (2020).
Abdollahramezani, S. et al. Tunable nanophotonics enabled by chalcogenide phase-change materials. Nanophotonics 9, 1189–1241. https://doi.org/10.1515/nanoph-2020-0039 (2020).
Fang, Z., Chen, R., Zheng, J. & Majumdar, A. Non-volatile reconfigurable silicon photonics based on phase-change materials. IEEE J. Sel. Top. Quantum Electron. 28, 1–17. https://doi.org/10.1109/JSTQE.2021.3120713 (2022).
Shportko, K. et al. Resonant bonding in crystalline phase-change materials. Nat. Mater. 7, 653–658. https://doi.org/10.1038/nmat2226 (2008).
Wuttig, M., Bhaskaran, H. & Taubner, T. Phase-change materials for non-volatile photonic applications. Nat. Photonics 11, 465–476. https://doi.org/10.1038/nphoton.2017.126 (2017).
Zhang, Y. et al. Broadband transparent optical phase change materials for high-performance nonvolatile photonics. Nat. Commun. 10, 4279. https://doi.org/10.1038/s41467-019-12196-4 (2019).
Redaelli, A., Pirovano, A., Benvenuti, A. & Lacaita, A. L. Threshold switching and phase transition numerical models for phase change memory simulations. J. Appl. Phys. 103, 111101. https://doi.org/10.1063/1.2931951 (2008).
Rios, C. et al. Controlled switching of phase-change materials by evanescent-field coupling in integrated photonics [Invited]. Opt. Mater. Express 8, 2455. https://doi.org/10.1364/OME.8.002455 (2018).
Kato, K., Kuwahara, M., Kawashima, H., Tsuruoka, T. & Tsuda, H. Current-driven phase-change optical gate switch using indium-tin-oxide heater. Appl. Phys. Express 10, 072201. https://doi.org/10.7567/APEX.10.072201 (2017).
Taghinejad, H. et al. ITO-based microheaters for reversible multi-stage switching of phase-change materials: towards miniaturized beyond-binary reconfigurable integrated photonics. Opt. Express 29, 20449. https://doi.org/10.1364/OE.424676 (2021) (2003.04097.).
Loke, D. et al. Breaking the speed limits of phase-change memory. Science 336, 1566–1569. https://doi.org/10.1126/science.1221561 (2012).
Xiong, F., Liao, A. D., Estrada, D. & Pop, E. Low-power switching of phase-change materials with carbon nanotube electrodes. Science 332, 568–570. https://doi.org/10.1126/science.1201938 (2011).
Kim, I. et al. High performance PRAM cell scalable to sub-20nm technology with below 4F2 cell size, extendable to DRAM applications. In 2010 Symposium on VLSI Technology, 203–204, https://doi.org/10.1109/VLSIT.2010.5556228 (IEEE, 2010).
Tanaka, D. et al. Ultra-small, self-holding, optical gate switch using Ge2Sb2Te5 with a multi-mode Si waveguide. Opt. Express 20, 10283. https://doi.org/10.1364/OE.20.010283 (2012).
Rudé, M. et al. Optical switching at 1.55 \(\mu\)m in silicon racetrack resonators using phase change materials. Appl. Phys. Lett. 103, 141119. https://doi.org/10.1063/1.4824714 (2013).
Yu, Z., Zheng, J., Xu, P., Zhang, W. & Wu, Y. Ultracompact electro-optical modulator-based Ge2Sb2Te5 on silicon. IEEE Photonics Technol. Lett. 30, 250–253. https://doi.org/10.1109/LPT.2017.2783928 (2018).
Shadmani, A., Miri, M. & Mohammadi Pouyan, S. Ultra-wideband multi-level optical modulation in a Ge2Sb2Te5-based waveguide with low power consumption and small footprint.. Opt. Commun. 439, 53–60. https://doi.org/10.1016/j.optcom.2019.01.046 (2019).
Parra, J., Santome, A., Navarro-Arenas, J. & Sanchis, P. Fast volatile response in GST/Si waveguides for all-optical modulation. In 2021 IEEE 17th International Conference on Group IV Photonics (GFP), 1–2. https://doi.org/10.1109/GFP51802.2021.9673955 (IEEE, 2021).
Song, Y. & Xu, P. Design of ultra-low insertion loss active transverse electric-pass polarizer based Ge2Sb2Te5 on silicon waveguide. Opt. Commun. 426, 30–34. https://doi.org/10.1016/j.optcom.2018.05.034 (2018).
Rios, C., Hosseini, P., Wright, C. D., Bhaskaran, H. & Pernice, W. H. P. On-chip photonic memory elements employing phase-change materials. Adv. Mater. 26, 1372–1377. https://doi.org/10.1002/adma.201304476 (2014).
Ríos, C. et al. Integrated all-photonic non-volatile multi-level memory. Nat. Photonics 9, 725–732. https://doi.org/10.1038/nphoton.2015.182 (2015).
Zhang, H. et al. Miniature multilevel optical memristive switch using phase change material. ACS Photonics 6, 2205–2212. https://doi.org/10.1021/acsphotonics.9b00819 (2019) (1905.03163.).
Li, X. et al. Fast and reliable storage using a 5 bit, nonvolatile photonic memory cell. Optica 6, 1. https://doi.org/10.1364/OPTICA.6.000001 (2019).
Li, X. et al. Experimental investigation of silicon and silicon nitride platforms for phase-change photonic in-memory computing. Optica 7, 218. https://doi.org/10.1364/OPTICA.379228 (2020).
Feldmann, J. et al. Integrated 256 cell photonic phase-change memory with 512-bit capacity. IEEE J. Sel. Top. Quantum Electron. 26, 1–7. https://doi.org/10.1109/JSTQE.2019.2956871 (2020).
Stegmaier, M., Rios, C., Bhaskaran, H. & Pernice, W. H. P. Thermo-optical effect in phase-change nanophotonics. ACS Photonics 3, 828–835. https://doi.org/10.1021/acsphotonics.6b00032 (2016).
von Keitz, J. et al. Reconfigurable nanophotonic cavities with nonvolatile response. ACS Photonics 5, 4644–4649. https://doi.org/10.1021/acsphotonics.8b01127 (2018).
Zheng, J. et al. GST-on-silicon hybrid nanophotonic integrated circuits: a non-volatile quasi-continuously reprogrammable platform. Opt. Mater. Express 8, 1551. https://doi.org/10.1364/OME.8.001551 (2018).
Stegmaier, M., Ríos, C., Bhaskaran, H., Wright, C. D. & Pernice, W. H. P. Nonvolatile all-optical 1 2 switch for chipscale photonic networks. Adv. Opt. Mater. 5, 1600346. https://doi.org/10.1002/adom.201600346 (2017).
Xu, P., Zheng, J., Doylend, J. K. & Majumdar, A. Low-loss and broadband nonvolatile phase-change directional coupler switches. ACS Photonics 6, 553–557. https://doi.org/10.1021/acsphotonics.8b01628 (2019) (1811.08490.).
Wu, C. et al. Low-loss integrated photonic switch using subwavelength patterned phase change material. ACS Photonics 6, 87–92. https://doi.org/10.1021/acsphotonics.8b01516 (2019).
Hu, H. et al. Contra-directional switching enabled by Si-GST grating. Opt. Express 28, 1574. https://doi.org/10.1364/OE.381502 (2020).
Zhang, C. et al. Wavelength-selective 2 x2 optical switch based on a Ge2Sb2Te5-assisted microring. Photonics Res. 8, 1171. https://doi.org/10.1364/PRJ.393513 (2020).
Zheng, J. et al. Nonvolatile electrically reconfigurable integrated photonic switch enabled by a silicon PIN diode heater. Adv. Mater. 32, 2001218. https://doi.org/10.1002/adma.202001218 (2020).
Li, Y. et al. Design of an electric-driven nonvolatile low-energy-consumption phase change optical switch. Nanotechnology 32, 405201. https://doi.org/10.1088/1361-6528/ac0ead (2021).
Cheng, Z., Ríos, C., Pernice, W. H. P., Wright, C. D. & Bhaskaran, H. On-chip photonic synapse. Sci. Adv. 3, https://doi.org/10.1126/sciadv.1700160 (2017).
Feldmann, J. et al. Calculating with light using a chip-scale all-optical abacus. Nat. Commun. 8, 1256. https://doi.org/10.1038/s41467-017-01506-3 (2017).
Cheng, Z. et al. Device-level photonic memories and logic applications using phase-change materials. Adv. Mater. 30, 1802435. https://doi.org/10.1002/adma.201802435 (2018).
Ríos, C. et al. In-memory computing on a photonic platform. Sci. Adv. 5, eaau5759. https://doi.org/10.1126/sciadv.aau5759 (2019).
Feldmann, J., Youngblood, N., Wright, C. D., Bhaskaran, H. & Pernice, W. H. P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 569, 208–214. https://doi.org/10.1038/s41586-019-1157-8 (2019).
Brückerhoff-Plückelmann, F., Feldmann, J., Wright, C. D., Bhaskaran, H. & Pernice, W. H. P. Chalcogenide phase-change devices for neuromorphic photonic computing. J. Appl. Phys. 129, 151103. https://doi.org/10.1063/5.0042549 (2021).
Feldmann, J. et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58. https://doi.org/10.1038/s41586-020-03070-1 (2021).
Parra, J., Olivares, I., Brimont, A. & Sanchis, P. Toward nonvolatile switching in silicon photonic devices. Laser Photonics Rev. 15, 2000501. https://doi.org/10.1002/lpor.202000501 (2021).
Yariv, A. & Yeh, P. Optical waves in crystals: propagation and control of laser radiation (Wiley, London, 1984).
Synopsys. FemSIM RSoft.
Synopsys. FullWAVE RSoft.
Acknowledgements
This work is supported by grants PID2019-111460GB-I00, ICTS-2017-28-UPV-9F, and FPU17/04224 funded by MCIN/AEI/ 10.13039/501100011033, by “ERDF A way of making Europe” and “ESF Investing in your future”. Funding from Generalitat Valenciana (PROMETEO/2019/123). Funding for open access charge: Universitat Politècnica de València. The authors would like to thank Helen Urgelles for her help with the experimental measurements.
Author information
Authors and Affiliations
Contributions
J. P. performed the simulations, analyzed the experimental data, and wrote the initial draft. J.N.-A. helped to discuss the results. M.K. characterized the GST and fabricated the sample. P.S. conceived and supervised the project. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Parra, J., Navarro-Arenas, J., Kovylina, M. et al. Impact of GST thickness on GST-loaded silicon waveguides for optimal optical switching. Sci Rep 12, 9774 (2022). https://doi.org/10.1038/s41598-022-13848-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-13848-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.