Introduction

In glass industry, tubes are drawn through various manufacturing processes used to achieve the continuous production of glass tubes having correct wall thickness and diameter. The most commonly used are the Danner process and the Vello process1,2,3,4,5 having great importance in glass fabricating industry and are still in use today. In Danner process, glass is melted in a furnace to the stage where it is soft and pliable. Molten glass is then let to fall with low feeding speed \(v_{0}\) on the surface of a cylindrical device called mandrel kept in a temperature controlled tank called oven. Mandrel is slightly inclined and hollow such that the air can be blown through it. By continuous rotation of mandrel about its axis of symmetry, the molten glass falling downward creates a smooth layer around the mandrel. It cools down gradually and takes the shape of a thick-walled hollow glass tube with all desired properties at just below the end of mandrel. The length of hot-forming zone is taken as L. It is then pulled out by a drawing machine with a drawing speed \(v_{L}> v_{0}\). This ratio \(v_{L}/v_{0}>1\) is called the draw ratio. Keeping a constant temperature in the hot-forming zone leads to develop an isothermal tube drawing model. The drawn tube is then conveyed straight by rollers to further process of cutting, finishing, polishing and packaging at the end of the spinline. This manufacturing process is explained and illustrated in3. For the Vello process, we refer to1,2,3,4,5.

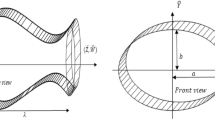
The geometry of the drawn tube is illustrated in Fig. 1. The length of hot forming zone is denoted by L. Inner and outer radii, inside pressure, feeding and take up speeds, axis of symmetry of the tube during the production process are shown in Figure. All other parameters involved along with their numerical values are illustrated in Table 1.

Table 1 Summary of parametric values appearing in the isothermal model (5).
Full size table

The shaping parameters such as the wall thickness and cross-sectional area (or diameter) are the main characterizations of the drawn tube. In either of the manufacturing processes, the required shape of the tube can be maintained by the stream of the air gently blown through the mandrel. Insufficient quantity of the air blown through the mandrel can disturb the desired shape of the glass tube. As a result, this insufficient balance collapse the walls of the glass tube. Moreover, the geometry of the glass tube can be controlled by the parameters involved herein such as the glass temperature, the composition of the raw material, the pressure of the blowing air in the mandrel and the rate of draw. We have added a Fig. 1 to better understand the geometry of the drawn glass tube.

Figure 1
figure 1

Diagram of a glass tube during production process.

Full size image

A variety of mathematical models both for the isothermal and non-isothermal tube drawing processes, with different levels of descriptions and needs, are available in the literature e.g., see1,2,3,4 and6,7,8,9,10,11. In1,2,3,7 numerical solutions of both the isothermal and non-isothermal models have been found and used to optimally control the geometry of the glass tube. In recent years, a variety of mathematical models representing physical and real world problems have been investigated for numerical solutions and stability analysis (for example see12,13,14,15,16,17,18,19,20,21,22,23,24). Thus, the concept of finding numerically accurate and exact solutions of real world problems has attracted attention from all over the world.

In this paper, we have considered an isothermal glass tube drawing model consisting of three coupled nonlinear partial differential equations of first and second order. The steady-state numerical solution of this model is required in order to investigate its stability. Recently, we have analyzed the stability of an isothermal tube drawing model and performed a complete mathematical analysis in3 by incorporating a steady state numerical solution. To better understand the physical model and to examine the accuracy of the obtained numerical solution, our objective here is to develop an analytical solution of the steady-state isothermal model. To start with, it is not possible to determine an analytical solution of this type of model with the given initial and boundary conditions. When we solve the second order ordinary differential equation appearing in the steady-state model, the difficulty lies in determining the constants of integrations. To overcome this concern, we utilize a numerical technique called shooting method to convert the boundary value problem into a set of initial value problems. An integrating technique is implemented to develop an analytical solution of the converted initial value problems. Similar approach has been suggested in10,22 to construct an analytical solution of a steady-state melt-spinning model. The semi-analytical approach developed in this paper has an advantage over other numerical methods that it may be applied directly to both linear and nonlinear systems of equations without the need for discretization, linearization, or perturbation.

The organization of the paper is as follows: In “Governing equations” section, we give a brief description of the mathematical model of an isothermal tube drawing process. A strategy converting a boundary value problem into a set of initial value problems is described in “Numerical approach” section. Analytical solution is developed in “Analytical solution” section and compared with the numerical solution in “Accuracy comparison” section. Conclusion is given in “Conclusions” section. We have included some leftover parts of the modeling of tube drawing process in the “Appendix”. In this section, we have included one example concerning the application of the analytical solution obtained through the implemented semi-analytic technique.

Governing equations

In the literature, different types of models for the drawing processes with different level of demands and descriptions are available. A considerable amount of work has been carried out by different researchers1,2,3,4,6,8,9 and11,25,26,27,28 to model the tube drawing process. In this section, we briefly explain the mathematical model for an isothermal tube drawing process.

To model the tube drawing process, we consider an incompressible Newtonian flow of a molten glass between two free surfaces \(r=r_{1}(z,t)\) and \(r=r_{2}(z,t)\) where \(r_{1}(z,t)\) and \(r_{2}(z,t)\) respectively denote the inner and outer radii of the glass tube, and assume that temperature remains constant throughout the forming zone. Glass tube during production process is illustrated in Fig. 1. In the draw-down zone, the surface tension force and the inertial force acting upon the molten glass are insignificant and hence can be neglected. This kind of flow is governed by the equations

$$\begin{aligned}&\frac{\partial u}{\partial z}+\dfrac{1}{r}\frac{\partial }{\partial r}(rv)=0, \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{\partial p}{\partial r}=\frac{\partial }{\partial z}\left( \mu \frac{\partial v}{\partial z}\right) +\mu \left( \frac{\partial ^{2}v}{\partial r^{2}}+\dfrac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^{2}}\right) +2\frac{\partial \mu }{\partial r}\frac{\partial v}{\partial r}+\frac{\partial \mu }{\partial z}\frac{\partial u}{\partial r}, \end{aligned}$$
(1b)
$$\begin{aligned}&\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left( \mu r\frac{\partial v}{\partial z}\right) +\frac{1}{r}\frac{\partial }{\partial r}\left( \mu r\frac{\partial u}{\partial r}\right) +\rho g+\frac{\partial }{\partial z}\left( 2\mu \frac{\partial u}{\partial z}\right) . \end{aligned}$$
(1c)

The Eqs. (1a)–(1c) are taken from4 and are known as the standard equations showing the axi-symmetric stokes flow. The first equation is the continuity equation and the last two equations are the momentum equations respectively in r and z directions. We denote the derivatives by subscripts r and z where z denotes the distance along the axis of the glass tube and r measures the distance perpendicular to it. The velocity of the molten glass is defined to be \(\bar{\mathbf{v }}=(u,v)\) where u and v are the components of velocity \(\bar{\mathbf{v }}\) along z and r direction respectively. The pressure, density and the acceleration due to gravity are denoted by p, \(\rho\) and g respectively.

Now, at the free surfaces \(r=r_{1}(z,t)\) and \(r=r_{2}(z,t)\), it is necessary to specify the stress conditions and the kinematic conditions.

On the inner and outer surfaces of the glass tube, the stress conditions are given as:

$$\begin{aligned} \tau {\hat{n}}_{i}&=-p_{s}{\hat{n}}_{i} \quad on \; r=r_{1}, \end{aligned}$$
(1d)
$$\begin{aligned} \tau {\hat{n}}_{o}&=0 \quad on \; r=r_{2}, \end{aligned}$$
(1e)

where \({\hat{n}}_{i}\) and \({\hat{n}}_{o}\) are the unit normals on the surfaces \(r=r_{1}\) and \(r=r_{2}\) of the tube respectively defined as

$$\begin{aligned} {\hat{n}}_{i}=\dfrac{1}{\sqrt{1+\left( \dfrac{\partial r_{1}}{\partial z}\right) ^{2}}}\left( 1,-\dfrac{\partial r_{1}}{\partial z}\right) \quad \text {and} \quad {\hat{n}}_{o}=\dfrac{-1}{\sqrt{1+\left( \dfrac{\partial r_{2}}{\partial z}\right) ^{2}}}\left( 1,-\dfrac{\partial r_{2}}{\partial z}\right) . \end{aligned}$$

and \(p_{s}\) is the inside pressure applied on the surface \(r=r_{1}\) of the glass tube and \(\tau\) is the stress tensor given as

$$\begin{aligned} \tau = \left( \begin{array}{cc} -p+2\mu \dfrac{\partial v}{\partial r} &{} \mu \left( \dfrac{\partial u}{\partial r}+\dfrac{\partial v}{\partial z}\right) \\ \mu \left( \dfrac{\partial u}{\partial r}+\dfrac{\partial v}{\partial z}\right) &{} -p+2\mu \dfrac{\partial u}{\partial z} \\ \end{array} \right) . \end{aligned}$$

The kinematic conditions are described as

$$\begin{aligned} v&=\frac{\partial r_{1}}{\partial t}+\frac{\partial r_{1}}{\partial z}u \quad on \; r=r_{1}, \end{aligned}$$
(1f)
$$\begin{aligned} v&=\frac{\partial r_{2}}{\partial t}+\frac{\partial r_{2}}{\partial z}u \quad on \; r=r_{2}, \end{aligned}$$
(1g)

and thus the stress conditions (1d)–(1e) can be expanded to give

$$\begin{aligned}&-\mu \left( \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right) \frac{\partial r_{1}}{\partial z}+\left( -p+2\mu \frac{\partial v}{\partial r}\right) =-p_{s} \quad on \; r=r_{1}, \end{aligned}$$
(1h)
$$\begin{aligned}&-\left( -p+2\mu \frac{\partial u}{\partial z}\right) \frac{\partial r_{1}}{\partial z}+\mu \left( \frac{\partial u}{\partial r}+\frac{\partial v}{\partial z}\right) =p_{s}\frac{\partial r_{1}}{\partial z} \quad on \; r=r_{1}, \end{aligned}$$
(1i)
$$\begin{aligned}&\mu \left( \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right) \frac{\partial r_{2}}{\partial z}=-p+2\mu \frac{\partial v}{\partial r}\quad on \; r=r_{2}, \end{aligned}$$
(1j)
$$\begin{aligned}&\left( -p+2\mu \frac{\partial u}{\partial z}\right) \frac{\partial r_{2}}{\partial z}=\mu \left( \frac{\partial u}{\partial r}+\frac{\partial v}{\partial z}\right) \quad on \; r=r_{2}. \end{aligned}$$
(1k)

where \(\mu\) denotes the viscosity of the molten glass which remains constant at the given temperature.

To take benefit of the small parameters present in the problem, it is now convenient to convert the Eq. (1) into dimensionless form. For the dimensional quantities, the appropriate scaling is defined as:

$$\begin{aligned} z&=L{\tilde{z}},\; r=\varepsilon L{\tilde{r}},\; r_{1}=\varepsilon L{\tilde{r}}_{1},\; r_{2}=\varepsilon L{\tilde{r}}_{2},\; \mu =\mu _{0}{\tilde{\mu }},\\ u&=U{\tilde{u}},\; v=\varepsilon U{\tilde{v}},\; t=\frac{L}{U}{\tilde{t}},\; p=\frac{\mu _{0}U}{L}{\tilde{p}},\; p_{s}=\frac{\mu _{0}U}{L}\tilde{p_{s}}, \end{aligned}$$

where \(\varepsilon =\dfrac{W}{L}\ll 1\). W is the width of the glass tube that has a very small value than the typical length of hot-forming zone L, U is the typical drawing speed and \(\mu _{0}\) is the typical melt glass viscosity which has a constant value for the isothermal case. After dropping the bar notation, the system of governing equations in dimensionless form is given as follows:

$$\begin{aligned}&0=\dfrac{1}{r}\frac{\partial }{\partial r}(rv)+\frac{\partial u}{\partial z}, \end{aligned}$$
(2a)
$$\begin{aligned}&\frac{\partial p}{\partial r}=\mu \left( \frac{\partial ^{2}v}{\partial r^{2}}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^{2}}\right) +\varepsilon ^{2}\frac{\partial }{\partial z}\left( \mu \frac{\partial v}{\partial z}\right) +\frac{\partial \mu }{\partial z}\frac{\partial u}{\partial r}+2\frac{\partial \mu }{\partial r}\frac{\partial v}{\partial r}, \end{aligned}$$
(2b)
$$\begin{aligned}&\varepsilon ^{2}\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left( \mu r\frac{\partial u}{\partial r}\right) +\varepsilon ^{2}\frac{\partial }{\partial z}\left( 2\mu \frac{\partial u}{\partial z}\right) +\varepsilon ^{2}\frac{1}{r}\frac{\partial }{\partial r}\left( \mu r\frac{\partial v}{\partial z}\right) +\varepsilon ^{2}{St}. \end{aligned}$$
(2c)

where \(St=\dfrac{\rho gL^{2}}{\mu _{0}U}\) is known as Stokes number.

The stress conditions (1h)–(1k) read as

$$\begin{aligned}&\left( -p+2\mu \frac{\partial v}{\partial r}\right) -\mu \left( \varepsilon ^{2}\frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right) \frac{\partial r_{1}}{\partial z}=-p_{s} \quad on \; r=r_{1}, \end{aligned}$$
(2d)
$$\begin{aligned}&\mu \left( \frac{\partial u}{\partial r}+\varepsilon ^{2}\frac{\partial v}{\partial z}\right) -\varepsilon ^{2}\left( -p+2\mu \frac{\partial u}{\partial z}\right) \frac{\partial r_{1}}{\partial z}=\varepsilon ^{2}p_{s}\frac{\partial r_{1}}{\partial z} \quad on \; r=r_{1}, \end{aligned}$$
(2e)
$$\begin{aligned}&-p+2\mu \frac{\partial v}{\partial r}=\mu \left( \varepsilon ^{2}\frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right) \frac{\partial r_{2}}{\partial z}\quad on \; r=r_{2}, \end{aligned}$$
(2f)
$$\begin{aligned}&\mu \left( \frac{\partial u}{\partial r}+\varepsilon ^{2}\frac{\partial v}{\partial z}\right) =\varepsilon ^{2}\left( -p+2\mu \frac{\partial u}{\partial z}\right) \frac{\partial r_{2}}{\partial z} \quad on \; r=r_{1}. \end{aligned}$$
(2g)

The kinematics conditions (1f)–(1g) become

$$\begin{aligned} v&=\frac{\partial r_{1}}{\partial t}+\frac{\partial r_{1}}{\partial z}u \quad on \; r=r_{1}, \end{aligned}$$
(2h)
$$\begin{aligned} v&=\frac{\partial r_{2}}{\partial t}+\frac{\partial r_{2}}{\partial z}u \quad on \; r=r_{2}. \end{aligned}$$
(2i)

The above model can be simplified by means of an asymptotic expansion, in which the inverse aspect ratio \(\varepsilon\) is used as scaling parameter. Assuming the glass flow as a thin layer flow and ignoring the large aspect ratio of the flow, one derives the simplified equations to model the isothermal tube drawing process. In this derivation, the surface tension and inertial forces acting upon the molten glass have also been ignored due to their insignificant contributions. For details, we refer to1,2,3,4,5,6 and9,27. However, we have included the remaining considerations of the modeling process in “Appendix A” and reach at the following model equations representing the isothermal process:

$$\begin{aligned}&\frac{\partial A}{\partial t}+\frac{\partial }{\partial z}(vA)=0, \end{aligned}$$
(3a)
$$\begin{aligned}&\frac{\partial }{\partial z}\left( 3\mu A\frac{\partial v}{\partial z}\right) +\rho gA=0, \end{aligned}$$
(3b)
$$\begin{aligned}&\frac{\partial }{\partial t}(R^{2})+\frac{\partial }{\partial z}(vR^{2})=\frac{p_{s}}{16\pi \mu A}\left( 16\pi ^{2}R^{4}-A^{2}\right) , \end{aligned}$$
(3c)

equipped with the initial conditions

$$\begin{aligned} A(z,0)=A_{0},\ R(z,0)=R_{0},\ \text {for}\ z\in {[0,L]}, \end{aligned}$$
(3d)

and the boundary conditions

$$\begin{aligned} A(0,t)=A_{0},\ R(0,t)=R_{0},\ v(0,t)=v_{0},\ v(L,t)=v_{L},\ \text {for}\ t\ge 0, \end{aligned}$$
(3e)

where \(A_{0}\) and \(R_{0}\) are the cross-sectional area and average radius of the glass tube at the time of entering the hot-forming zone, respectively. Acceleration due to gravity and density of the molten glass are denoted by g and \(\rho\), respectively. Average radius R of the tube is defined as

$$\begin{aligned} R=\dfrac{1}{2}\left( r_1+r_2\right) . \end{aligned}$$

Equations in system (3) give us cross-sectional area A, velocity v, and average radius R of the glass tube. Width W of the tube can be determined by the equation

$$\begin{aligned} A=2\pi RW. \end{aligned}$$

Since the temperature throughout the forming zone of the tubing process remains constant, the viscosity \(\mu\) of the melt glass also remains constant.

Dimensionless form

We introduce the following dimensionless quantities

$$\begin{aligned} z^{*}=\dfrac{z}{L},\ t^{*}=\dfrac{v_{0}t}{L},\ A^{*}=\dfrac{A}{A_{0}},\ R^{*}=\dfrac{R}{R_{0}},\ v^{*}=\dfrac{v}{v_{0}},\ p^{*}=\dfrac{Lp_{s}}{\mu _{0}v_{0}},\ \mu ^{*}=\dfrac{\mu }{\mu _{0}}, \end{aligned}$$

into the model (3) to get the dimensionless equations

$$\begin{aligned}&\frac{\partial A}{\partial t}+\frac{\partial }{\partial z}(vA)=0, \end{aligned}$$
(4a)
$$\begin{aligned}&\frac{\partial }{\partial z}(3A\frac{\partial v}{\partial z})+St A=0, \end{aligned}$$
(4b)
$$\begin{aligned}&\frac{\partial }{\partial t}(R^{2})+\frac{\partial }{\partial z}(vR^{2})=\frac{\pi c p}{A}\left( R^{4}-\frac{A^{2}}{(4\pi c)^{2}}\right) , \end{aligned}$$
(4c)

where we have removed the asterisk notation and

$$\begin{aligned} St=\frac{\rho gL^{2}}{\mu v_{0}}\quad \text {and}\quad c=\frac{R_{0}^{2}}{A_{0}}, \end{aligned}$$

are the dimensionless parameters.

The initial and boundary conditions are respectively transformed to

$$\begin{aligned}&A(z,0)=1,\ R(z,0)=1,\ \text {for all}\ z\in {[0,1]}, \end{aligned}$$
(4d)
$$\begin{aligned}&A(0,t)=1,\ R(0,t)=1,\ v(0,t)=1,\ v(1,t)=v_{d},\ \text {for} \ t\ge 0, \end{aligned}$$
(4e)

where \(v_{d}=\dfrac{v_{L}}{v_{0}}>1\) is the draw ratio.

The steady state form of the model (4) is written as

$$\begin{aligned}&\dfrac{d}{dz}(vA)=0, \end{aligned}$$
(5a)
$$\begin{aligned}&\dfrac{d}{dz}(3A\dfrac{dv}{dz})+StA=0, \end{aligned}$$
(5b)
$$\begin{aligned}&\dfrac{d}{dz}(vR^{2})=\dfrac{\pi c p}{A}\left( R^{4}-\dfrac{A^{2}}{(4\pi c)^{2}}\right) , \end{aligned}$$
(5c)

subject to the conditions:

$$\begin{aligned} A(0)=1,\ v(0)=1,\ v(1)=v_{d},\ R(0)=1. \end{aligned}$$
(5d)

The system (5) is a system of coupled nonlinear ordinary differential equations. We are interested in developing an analytical solution of the nonlinear system (5). However, we have already proved the existence and uniqueness of the solution of steady state isothermal tube drawing model (5) in3. For details, we refer the reader to3.

Numerical approach

There are different techniques available in the literature to solve boundary value problems analytically. The obtained general solutions contains arbitrary constant which can be determined by using boundary conditions. However, there exist some problems (e.g. problem (5) and see10,22) where it is not possible to find integration constants with the given conditions. It is interesting to mention that integration constants can be found if boundary value problem (BVP) is transformed to an initial value problem (IVP).

Shooting method is a technique that transforms a BVP of the form

$$\begin{aligned} \dfrac{d^2\phi }{dz^2}=f\Big (z, \phi , \dfrac{d\phi }{dz}\Big )\ \ \phi (a)=\alpha ,\ \phi (b)=\beta , \end{aligned}$$

into an IVP

$$\begin{aligned} \dfrac{d^2\phi }{dz^2}=f\Big (z, \phi , \dfrac{d\phi }{dz}\Big )\ \ \phi (a)=\alpha ,\ \dfrac{d\phi }{dz}(a)=s, \end{aligned}$$
(6)

where s is a guess to be determined in such a way that it shoots \(\phi (b)\).

We apply RK4 method to the second order differential Eq. (6) to determine approximation \(s_{i}, i = 1, 2, \ldots\) for \(\phi (b)\). Let the first guess \(s_{1}\) be taken as

$$\begin{aligned} s_{1}=\dfrac{d\phi }{dz}(a)\approx \dfrac{\phi (b)-\phi (a)}{b-a} \end{aligned}$$

RK4 method with \(s_{1}\) gives us an approximation \(\beta _{1}\) for \(\phi (b)\). If the absolute error \(|\beta _{1}-\phi (b)|\) is less than some pre-assigned tolerance, we stop, otherwise we refine our guess by considering

$$\begin{aligned} s_{2}=2s_{1}, \end{aligned}$$

and compute \(\beta _{2}\) by RK4 method. If the error \(|\beta _{2}-\phi (b)|\) agrees to pre-assigned tolerance, we stop. In the case of disagreement, we make further guesses using the secant formula

$$\begin{aligned} s_{i+1}=\dfrac{d\phi }{dz}(a)\approx s_{i}-e(s_{i})\Bigg [\dfrac{s_{i-1}-s_{i}}{e(s_{i-1})-e(s_{i})}\Bigg ],\ \ i=2,3,\ldots \end{aligned}$$
(7)

where

$$\begin{aligned} e(s_{j})=\beta _{j}-\phi (b),\ \ j=1,2,\ldots \end{aligned}$$

is the error of approximation. RK4 method is continued each time with a new guess \(s_{i}, i = 3, 4, \ldots\) computed from (7) until \(\beta _{i}\) agrees with the value \(\phi (b)\) to pre-set tolerance.

Once we able to compute a most suitable guess \(s_{i}\rightarrow s\), we are able to transform the BVP to IVP, and hence an analytical solution of the problem of type given in (6) can be found.

Analytical solution

With the initial conditions (5d), the Eq. (5a) is solved to get

$$\begin{aligned} A(z)=\dfrac{1}{v(z)},\quad v(z)>0,\quad z\in {\Omega }=[0, 1]. \end{aligned}$$
(8)

Equation (5b) can now be put in the form

$$\begin{aligned} \dfrac{d^{2}v}{dz^{2}}-\dfrac{1}{v}\left( \dfrac{dv}{dz}\right) ^{2}=-\dfrac{1}{3}St, \end{aligned}$$
(9a)

along with the conditions

$$\begin{aligned} v(0)=1,\ v(1)=v_{d}. \end{aligned}$$
(9b)

With the usual techniques, it is not an easy task to develop an analytical solution of the BVP (9). We use a non-conventional approach to build an analytical solution of the given nonlinear model. We convert the BVP (9) into two IVPs. For this purpose, we set

$$\begin{aligned} \dfrac{dv}{dz}=w, \end{aligned}$$
(10)

and

$$\begin{aligned} \dfrac{d^{2}v}{dz^{2}}=w \dfrac{dw}{dv}. \end{aligned}$$

Then the IVPs corresponding to BVP (9) are defined as

$$\begin{aligned} \dfrac{dv}{dz}&=w, \end{aligned}$$
(11a)
$$\begin{aligned} w\dfrac{dw}{dv}-\dfrac{1}{v}w^2&=-\dfrac{1}{3}St, \end{aligned}$$
(11b)

along with the conditions

$$\begin{aligned} v(0)=1,\ w(0)=w_0. \end{aligned}$$
(11c)

where \(w_{0}\) is approximated value determined by shooting the value of v at 1 i.e., \(v(1) = v_{d}\). (The process of finding the approximation \(w_{0}=s\) (say) by shooting method is explained in “Numerical approach” section).

The solution of first order non-linear ordinary differential Eq. (11b) is determined to give

$$\begin{aligned} w=\sqrt{c_{1}v^{2}+\dfrac{2St}{3}v}, \end{aligned}$$
(12)

where \(c_{1}\) is a constant of integration and is computed to give

$$\begin{aligned} c_{1}=(w_0)^{2}-\dfrac{2}{3}St, \end{aligned}$$
(13)

Solution (12) can be further re-written as

$$\begin{aligned} \dfrac{dv}{dz}=\sqrt{c_{1}v^{2}+\dfrac{2St}{3}v}. \end{aligned}$$
(14)

Separating the variables and then integrating, we reach at

$$\begin{aligned} \dfrac{1}{\sqrt{c_{1}}}\cosh ^{-1}(3c_{1}St^{-1}v+1)=z+c_{2}, \end{aligned}$$
(15)

where \(c_{2}\) is another constant of integration.

Solving for v, we obtain

$$\begin{aligned} v=\dfrac{1}{3c_{1}}St\Bigg (-1+\cosh \Big (\sqrt{c_{1}}(z+c_{2})\Big )\Bigg ). \end{aligned}$$
(16)

Equation (15) in view of condition (5d) gives us the value of \(c_{2}\), i.e.

$$\begin{aligned} c_{2}=\dfrac{1}{\sqrt{c_{1}}}\cosh ^{-1}\Big (3c_{1}St^{-1}+1\Big ). \end{aligned}$$
(17)

Equation (16) along with \(c_{1}\) and \(c_{2}\) respectively given in (13) and (17) represents an analytical solution of Eq. (5b).

Next we put the steady state solutions for A and v in Eq. (5c) to get

$$\begin{aligned} \dfrac{du}{dz}-(\pi c p)u^{2}+\left( \dfrac{\dfrac{St}{3\sqrt{c_{1}}}\sinh \sqrt{c_{1}}(z+c_{2})}{-\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \sqrt{c_{1}}(z+c_{2})}\right) u =\dfrac{-\pi c p}{\Bigg (4\pi c\Big (-\dfrac{St}{3c_{1}}+\dfrac{St}{3 c_{1}}\cosh \sqrt{c_{1}}(z+c_{2})\Big )\Bigg )^{2}}, \end{aligned}$$
(18)

where \(u=R^{2}\).

Equation (18) is a well-known Riccati’s equation29 whose solution is supposed to be of the form

$$\begin{aligned} u=u_{1}+\dfrac{1}{y}, \end{aligned}$$
(19)

where one solution \(u_{1}\), guessed by hit and trial procedure, is given as

$$\begin{aligned} u_{1}=\dfrac{1}{4\pi c\left( -\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \sqrt{c_{1}}(z+c_{2})\right) }. \end{aligned}$$

and y is any nonzero unknown function of z.

Differentiating (19) with respect to z and then putting the values of u and \(\dfrac{du}{dz}\) in Eq. (18), we reach at

$$\begin{aligned} \dfrac{dy}{dz}+\left( \dfrac{\dfrac{p}{2}-\dfrac{St}{3\sqrt{c_{1}}}\sinh \sqrt{c_{1}}(z+c_{2})}{-\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \sqrt{c_{1}}(z+c_{2})}\right) y=-\pi c p, \end{aligned}$$

which is a first order linear ordinary differential equation in y. After few steps of calculations, the solution of this differential equation is found to be

$$\begin{aligned} y=(-2\pi c)A+c_{3}B, \end{aligned}$$
(20)

where \(c_{3}\) is a constant of integration, and A(z), B(z) are given as

$$\begin{aligned} A(z)&=-\frac{St}{3c_{1}}+\frac{St}{3c_{1}}\cosh \sqrt{c_{1}}(z+c_{2}),\\ B(z)&=\dfrac{-\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh (\sqrt{c_{1}}(z+c_{2}))}{exp\Bigg ({-\frac{3\sqrt{c_{1}}p}{2St}\Big (\coth (\sqrt{c_{1}}(z+c_{2}))+csch(\sqrt{c_{1}}(z+c_{2}))\Big )}\Bigg )}. \end{aligned}$$

Using (19) and the condition (5d), we get

$$\begin{aligned} c_{3}=(4\pi c)k_{1}+(2\pi c)k_{2}, \end{aligned}$$
(21)

where

$$\begin{aligned} k_{1}&=\dfrac{exp\Bigg (\dfrac{-3\sqrt{c_{1}}p}{2St}\Big (\coth \sqrt{c_{1}}c_{2}+csch\sqrt{c_{1}}c_{2}\Big )\Bigg )}{\Bigg (4\pi c\Big (-\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \sqrt{c_{1}}c_{2}\Big )-1\Bigg )}, \end{aligned}$$

and

$$\begin{aligned} k_{2}&=exp\Bigg ({\frac{-3\sqrt{c_{1}}p}{2St}\Big (\coth \sqrt{c_{1}}c_{2}+csch\sqrt{c_{1}}c_{2}\Big )}\Bigg ). \end{aligned}$$

Substituting \(c_{3}\) in (20), we obtain

$$\begin{aligned} \dfrac{1}{y}=\dfrac{E}{(-2\pi c)D(z)\times E+(4\pi c)D(z)\times e^{g(z)}+(2\pi c)D(z)\times Ee^{g(z)}}. \end{aligned}$$

Therefore,

$$\begin{aligned} u=\dfrac{1}{(4\pi c)D(z)}+\dfrac{E}{(-2\pi C)E\times D(z)+(4\pi c)D(z)\times e^{g(z)}+(2\pi c)E\times D(z)\times e^{g(z)}}, \end{aligned}$$

where

$$\begin{aligned} D(z)&=-\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \Big (\sqrt{c_{1}}(z+c_{2})\Big ),\\ E&= 4\pi c\left( -\dfrac{St}{3c_{1}}+\dfrac{St}{3c_{1}}\cosh \sqrt{c_{1}}c_{2}\right) ,\\ g(z)&=\dfrac{3\sqrt{c_{1}}p}{2St}\Big (\coth \sqrt{c_{1}}(z+c_{2})+csch\sqrt{c_{1}}(z+c_{2})\Big )-\dfrac{3\sqrt{c_{1}}p}{2St}\Big (\coth \sqrt{c_{1}}c_{2}-csch\sqrt{c_{1}}c_{2}\Big ), \end{aligned}$$

and hence

$$\begin{aligned} R=\sqrt{u}, \end{aligned}$$
(22)

is an analytical solution of the Eq. (5c) along with \(c_{1}\) and \(c_{2}\) given respectively in (13) and (17). Thus, the solutions given in (8), (16) and (22) together constitute an analytical solution of the steady-state model (5).

Accuracy comparison

The developed analytical solution is plotted and compared with the numerical solution in Figs. 2, 3, 4. The parametric values used in the model are given in Table 1. The solutions obtained by RK4 method are reliable and competitive with the analytical solutions. We observe that the errors between numerical and analytical solutions for the steady state variables A, v and R are negligibly small (see Table 2). We also determine W, the width of the glass tube, by using the relation \(A=2\pi R W\). The steady state analytical and numerical solutions for W and the corresponding error are also shown in the Fig. 5. It is observed from Table 2 that error between the numerical and analytical solution for A, v, and R is maximum at \(z=0.2\), \(z=1.0\), and \(z=0.1\) respectively. Moreover, the error for the solution W is maximum at \(z=0.1\).

Figure 2
figure 2

Analytical and numerical solutions for the steady state variable A and the corresponding errors between the solutions with discretization step size \(h=0.1\).

Full size image
Figure 3
figure 3

Analytical and numerical solutions for the steady state variable v and the corresponding errors between the solutions with discretization step size \(h=0.1\).

Full size image
Figure 4
figure 4

Analytical and numerical solutions for the steady state variable R and the corresponding errors between the solutions with discretization step size \(h=0.1\).

Full size image
Table 2 Summary of errors in solutions for \(z\in [0,1]\) using step size \(h=0.1\).
Full size table
Figure 5
figure 5

Analytical and numerical solutions for the steady state variable W and the corresponding errors between the solutions with discretization step size \(h=0.1\).

Full size image

Conclusions

In this work, we have presented a numerical based approach to find analytical solution of a boundary value problem where one cannot find constants of integration with the given boundary conditions. The approach is to convert a boundary value problem into initial value problems and then to develop an analytical solution of the resulting problems with the usual methods. To explain the approach, we have developed an analytical solution of a steady-state model of the isothermal tube drawing process with the help of shooting method. The obtained analytical solution is almost in agreement with the numerical solution that justifies our approach.