Abstract
We have examined the uptake mechanisms of platinum-group-metals (PGMs) and molybdenum (Mo) ions into Prussian blue nanoparticles (PBNPs) in a nitric acid solution for 24-h sorption test, using inductively coupled plasma atomic emission spectroscopy, powder XRD, and UV–Vis-NIR spectroscopy in combination with first-principles calculations, and revealed that the Ru4+ and Pd2+ ions are incorporated into PBNPs by substitution with Fe3+ and Fe2+ ions of the PB framework, respectively, whereas the Rh3+ ion is incorporated into PBNPs by substitution mainly with Fe3+ and minorly with Fe2+ ion, and Mo6+ ion is incorporated into PBNPs by substitution with both Fe2+ and Fe3+ ions, with maintaining the crystal structure before and after the sorption test. Assuming that the amount of Fe elusion is equal to that of PGMs/Mo substitution, the substitution efficiency is estimated to be 39.0% for Ru, 47.8% for Rh, 87% for Pd, and 17.1% for Mo6+. This implies that 0.13 g of Ru, 0.16 g of Rh, 0.30 g of Pd, and 0.107 g of Mo can be recovered by using 1 g PBNPs with a chemical form of KFe(III)[Fe(II)(CN)6].
Similar content being viewed by others
Introduction
Recovery of precious metals from both nuclear wastes (N-wastes) and electronic wastes (E-wastes) plays one of key roles in solving energy and environmental issues in order to maintain our sustainable developing society. For the former one (N-wastes), the spent nuclear fuel generated from the power plants are vitrified at the reprocessing plant. After separating uranium (U) and plutonium (Pu) from the spent fuels by using the PUREX (Plutonium Uranium Redox EXtraction) method in order to re-use them as new fuels, the high-level radioactive liquid wastes (HLLW) are vitrified and geologically disposed1,2,3. In the vitrification processes, platinum-group metals (PGMs: especially, ruthenium: Ru, rhodium: Rh, and palladium: Pd) and molybdenum (Mo) cause serious problems: (1) PGMs tend to settle on the sidewall surface of a glass melter, giving rise to an inhomogeneous thermal distribution of the melter, and (2) Mo forms low-viscosity fluid compounds so-called “yellow phase” in the vitrified object4,5. These issues degrade the quality and stability of the vitrified objects due to heterogeneity, and increase both disposal spaces and costs in conjunction with additional vitrified rods produced by flushing the glass melter. Considering that Ru, Rh, and Pd with an amount of 2.09, 0.36, and 1.20 kg, respectively, are generated in 1 t of used nuclear fuels (burnup: 30,000 MWd/t, cooling period: 150 days) for light-water reactors (those generated amounts will increase by 1.5–2 times for fast breeder reactors), it is useful to recover PGMs from HLLW not only for the disposal of N-wastes but also for the recycling of precious metals from our alternative perspective. It is, of course, noted that it takes few decades to reduce their radioactive levels below safety standard except 107Pd long-lifetime nuclide (half-life: 6.5 million years) that is planned to be deleted using an extinction process with fast neutrons. In a similar manner to PGMs, Mo is also used both as Mo-Cu alloys and MoS2 materials for electronic and car industries, respectively, and also used as an alternative material for tungsten (W) because of its lower price.
For the latter case (E-wastes), the abundance of precious metals (Ru, Rh, Pd, rhenium: Re, osmium: Os, iridium: Ir, platinum: Pt, gold: Au) is much smaller by 10–6–10–9 times than that of rock-forming elements (sodium: Na, magnesium: Mg, aluminum: Al, silicon: Si, potassium: K, calcium: Ca, and iron: Fe)6. Although the precious elements are not uniformly dotted over the world in nature, the much amount of them has, however, been stored in E-wastes so far. For example, the amount of Au contained in 1 t of mobile phones is 300–400 g, which is much higher by 10–80 times than that in 1 t of natural ore. The other elements have a similar situation to Au. Consequently, the recovery of those precious elements from E-wastes is much more effective and efficient when compared to their collections from natural ore.
The aim of the present study is to solve the environmental and energy issues by utilizing the nanospace of Prussian blue (PB), which is one of metal hexacyanoferrates (MHCFs), as a sorbent7,8. Since MHCFs have a simple cubic lattice structure like a jungle gym (inset in Fig. 2), in which divalent (M2+) and trivalent (M3+) metal cations are cross-linked with each other via cyano-group anion (CN–), and exhibit many fascinating features9,10,11, they have been extensively investigated from viewpoints of both scientific and industrial aspects12,13,14,15,16,17,18. Recently, PB (FeHCF) has been applied to remove radioactive cesium-134 (134Cs) and 137Cs elements from contaminated soils caused by Fukushima nuclear plant accident in 201119,20,21,22,23, because PB has the jungle-gym cubic structure with a 0.5 nm-interstitial site (4c site in \(F\overline{4} 3m\) space group) that plays a role in trapping Cs ions efficiently. However, the uptake mechanisms of PB for multi-valent metal ions have been still unclear so far, though three possible sorption processes can be considered: (1) surface adsorption, (2) insertion or diffusion into interstitial sites (nanospace) in a similar manner to Cs ions, and (3) substitution of Fe with metals in the framework of PBs. In order to develop high-performance MHCF sorbents for recovery of the precious metals from N- and E-wastes, it is necessary to unravel the uptake characteristics of PB for those metal ions.
More recently, we have investigated the uptake mechanism of Pd (one of the most important elements in industry such as catalyst) ion into PB nanoparticles (PBNPs) in a nitric acid solution, and revealed that the Pd2+ ion is incorporated into PBNPs by substitution with Fe2+ ion of the PB framework with maintaining the crystal structure before and after Pd sorption, and the substitution efficiency was estimated to be 87% per PB unit cell24. This implies that 0.30 g Pd can be recovered by using 1 g PB with a chemical form of KFe(III)[Fe(II)(CN)6].
In the present study, we report here on the uptake characteristics of PBNPs for PGMs/Mo ions in a nitric acid solution as well as Pd ion. The uptake efficiency of PGMs/Mo into PBNPs and the elution efficiency of Fe from PBNPs were measured using inductively coupled plasma atomic emission spectroscopy (ICP-AES) before and after 24 h sorption test. We also examined changes in the structural and electronic properties of PBNPs before and after the sorption test, using powder x-ray diffraction (XRD) and ultraviolet–visible-Near IR (UV–vis-NIR) spectroscopy, in combination with first-principles calculations based on density functional theory. Furthermore, in order to understand the difference in the sorption efficiency among PGMs/Mo ions, we estimated the surface adsorption, diffusion, and substitution energies when PGMs/Mo ions are incorporated into PB unit cell, using the first-principles calculations.
Experimental and theoretical methods
Experimental methods
PBNPs were synthesized by mixing potassium hexacyanoferrate (II) (5 mmol, K4[Fe(CN)6]·3H2O, KANTO CHEMICAL) with Fe(III) nitrate (10 mmol, Fe(NO3)·9H2O, WAKO) in aqueous solution. PB precipitates thus formed were rinsed with ultrapure water after centrifugation (3000 rpm), which was performed for five times. Thereafter, PBNPs were dried at 75 °C for 12 h and thereafter kept in the vacuum desiccator for 3 h. We already confirmed the structural and physicochemical characteristics of PBNPs used in the present work elsewhere24.
Sorption test of PGMs/Mo ion (1 mM) for PBNPs (500 mg) were carried out in 1.5 M nitric acid solution (10 mL) upon shaking for 24 h. Subsequently, the mixtures were centrifuged to separate the PBNPs from the solution, and the concentration (C) of PGMs/Mo ion in the supernatant liquid was measured before (Cinitial) and after (Cfinal) the test, using ICP-AES (ICPE-9000, SHIMADZU), in order to estimate the sorption efficiency, [(Cinitial − Cfinal)/Cinitial × 100%], of PGMs/Mo ions into PBNPs. We also measured the concentration of Fe ion in the supernatant liquid after the sorption test, and estimated the elution efficiency of Fe ion when compared to the initial amount of PBNPs. Details of sorption test conditions have been described elsewhere25.
Powder XRD patterns and UV–vis-NIR diffuse reflectance spectra of the pristine and PGMs/Mo-sorbed PBNPs were measured using Rigaku RINT2200 (Cu Kα) and Shimazu UV-2600 spectrometer, respectively. The diffuse reflectance spectra thus obtained were converted to the corresponding absorption spectra in terms of the Kubelka–Munk conversion equation.
Theoretical methods
Theoretical absorption spectra of the pristine and PGMs/Mo-sorbed PBs were obtained using the relativistic configuration interaction (CI) method26,27, because the present method has been already confirmed to reproduce the experimental absorption spectra of Fe, Co, and Ni ferrocyanides quantitatively, using Fe(II)M(III)(CN–)116– (M = Fe, Co, Ni) cluster model28. 0 The multiplet energy levels and absorption spectra were calculated using Fe2+Fe3+(CN–)116–, MFe3+(CN–)116–, and Fe2+M(CN–)116– cluster models (M = Mo6+, Ru4+, Rh3+, Pd2+) (see Fig. 1), respectively, for the pristine and PGMs/Mo-sorbed PBNPs. Here, when the PBNPs are applied to the disposal of HLLW in a strong nitric acid solution (2–8 M), the present calculations were performed using an oxidation ionic valence of 6+, 4+, 3+, and 2+ for Mo, Ru, Rh, and Pd, respectively. The choice of the valence values for these ions is reasonable, because the valence of each ion in the nitric acid solution has been already clarified experimentally29,30,31,32,33. The structural parameters of these cluster models were determined from the optimized structures obtained using density functional theory (DFT) calculations. Details of the CI calculation method were described elsewhere26,27. As the active space for the CI calculations, all the electronic configurations of the d–d transitions for Fe and PGMs/Mo ions were explicitly treated. On the other hand, the electronic configurations for the charge transfer (CT) transitions from Fe2+/M to M were considered up to two electron excitations. The oscillator strength of the electric dipole transitions averaged over all directions was obtained using the general equation expressing the electric dipole transition. Theoretical absorption spectra were obtained by convolution of the oscillator strength replaced with a 0.30 eV full-width-at-half-maximum (FWHM) Gaussian function.
The surface adsorption, diffusion, and substitution energies of PGMs/Mo ions when incorporated into PBNPs were estimated using the CASTEP34 and QUANTUM-ESPRESSO35,36 based on DFT37,38. We adopted the Vanderbilt-type ultrasoft pseudopotentials39 throughout all the present calculations. The exchange–correlation potential was considered using the GGA (PBE)40. The cut-off energy of the plane wave was 550 eV, and the Brillouin zone was sampled on the 2 × 2 × 2 and 4 × 4 × 1 Monkhorst–Pack grid41 for the unit cell and (100) surface models of PB, respectively.
The adsorption energy of PGMs/Mo ions on the (100) surface of PB were calculated using a Fe(III)8Fe(II)8(CN)40 model (see Fig. 3) consisting of two layers of (100) surface (see Fig. 3a side view). In order to reproduce the surface environment, the 10 Å vacuum region was set on the (100) surface of PB model. The surface adsorption energy (Ead) was evaluated using the following equation,
Here, each term denotes the total energy of PGM/Mo-sorbed PBs, pristine PB, and PGMs/Mo themselves, respectively, which were calculated using CASTEP. The maximally-localized Wannier functions (MLWFs) of the C2p and N2p atomic orbitals (AOs) on the (100) surface of PB were obtained using Wannier9042.
The diffusion energy of PGMs/Mo ions through the nanospace of PBNPs was estimated for the unit cell model by using the Nudged elastic band (NEB) method implemented in QUANTUM-ESPRESSO. A diffusion pathway for PGMs/Mo ions in the nanospace of PBNPs was considered to be a route from the center of the square made of the four Fe ions in the (100) plane to the same site of the adjacent (100) plane via the 4c site (see the inset of Fig. 4).
The substitution energy (ES) of PGMs/Mo with Fe of PB was estimated for the unit cell model consisting of 60 atoms, which corresponds to 12.5% Fe ions substituted with PGMs/Mo ions. The ES was evaluated using the following equation,
Here, the first and second terms denote the total energy of the PGMs/Mo-sorbed and pristine PB models, respectively, whereas the third and fourth terms denote the chemical potentials of Fe and PGMs/Mo, respectively. In the present study, we used the chemical potential of the oxide at the oxidation limit and of the neutral atom at the reduction limit. These calculations were performed by DFT + U method43, using CASTEP. The U value was set to be 7.0 eV for the high-spin (HS) state of Fe3+ (Ionic radius: 0.645 Å for six coordination number), 3.0 eV for the low-spin (LS) state of Fe2+ (Ionic radius: 0.61 Å for six coordination number), and 2.0 eV for the LS state of PGMs/Mo (Ionic radius: 0.59 Å for Mo6+ with six coordination number, 0.62 Å for Ru4+ with six coordination number, 0.665 Å for Rh3+ with six coordination number, and 0.86 Å for Pa2+ with six coordination number)44,45,46. All calculations in the present study were performed until the residual forces and stresses below 0.01 eV/Å and 0.02 GPa, respectively. A uniformed background charge, so called the Jellium model, was used to accommodate the non-neutral states.
Results and discussion
Table 1 summarizes the sorption efficiency of PGM/Mo ions, the elution efficiency of Fe ion from PBNPs, the substitution efficiency of PGMs/Mo with Fe when incorporated into PBNPs, and the estimated amount of PGM/Mo recovery per 1 g PBNPs after 24 h sorption test. Since we already unraveled the uptake mechanism for Pd ion exhibiting the highest sorption and elution efficiencies24, we mainly discuss the mechanism for Ru, Rh, and Mo ions in relation to the results of Table 1.
UV–vis-NIR spectra
As shown in Table 1, the elution efficiency of Fe ion from PBNPs strongly supports that Ru, Rh, and Mo ions are also substituted with Fe ion of PBNPs when incorporated into PBNPs as well as Pd ion. In order to confirm the substitution of PGMs/Mo ions with Fe ion, we examined the UV–vis-NIR spectra of PBNPs before and after PGMs/Mo sorption in combination with first-principles calculations of theoretical spectra for the simple PB cluster model (see Fig. 1) by PGMs/Mo substitution with both Fe2+ and Fe3+ sites.
Figure 1 shows (a) the experimental spectra with respect to the absorption energy before (black) and after (red) 24 h sorption test [the intensity (absorbance) of the two spectra was normalized at 6 eV], and (b–d) theoretical spectra of the PB model before and after substitution with Fe2+ or Fe3+ for PGMs/Mo ions. For the pristine PBNPs, the three absorption band around 1.6 eV (weak), 2.1 eV (intense), 3.1 eV (weak), and 5.0 eV (middle) originate from the charge-transfer (CT) transitions from Fe2+ to Fe3+, which correspond to peaks A, B, C, and D, respectively28. For Pd ion (right hand), the theoretical spectra of the Pd ion substituted with Fe2+ (c) well explain the experimental spectral change (red shift) when compared to the spectra of the Pd ion substituted with Fe3+ (d). This is consistent with the previous results obtained using CASTEP24. For Rh ion (right-middle hand), comparison in theoretical spectra between before (b) and after (c, d) Rh substitution indicates that spectra (d) obtained for Rh substituted with Fe3+ reasonably explain the experimental spectral change after Rh sorption test. Thus, it is suitable to be concluded that Rh ion is mainly substituted with Fe3+ ion. For Ru ion (left-middle hand), comparison in theoretical spectra between before (b) and after (c, d) Ru substitution indicates that spectra (d) obtained for Ru substituted with Fe3+ obviously explain the experimental spectral change after Ru sorption test, because no red-shift in spectra after Ru sorption test was observed experimentally. For Mo ion (left hand), since the experimental spectra changed toward both a lower and a higher energy region after Mo ion sorption, it is found from theoretical spectral changes before (b) and after (c, d) Mo substitution that Mo6+ ion is substituted with both Fe2+ and Fe3+ ions.
In summary, it is reasonably concluded from the results of Fig. 1 that Ru4+ and Rh3+ ions are substituted with Fe3+ ion, and Pd2+ ion is substituted with Fe2+ ion, whereas Mo6+ ion is substituted with both Fe2+ and Fe3+ ions.
XRD
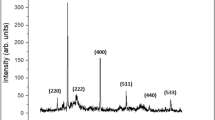
Figure 2 shows XRD patterns of the pristine (black) and PGM-sorbed (blue: Ru, pink: Rh, and red: Pd) PBNPs. Here, the inset shows the unit cell of PB crystal structure. The XRD pattern (black) shows that the pristine PBNPs have a face centered cubic (FCC) structure (space group: \(F\overline{4} 3m\)), which is consistent with the previous results obtained using high-resolution transmission electron microscope24. Table 2 summarizes the lattice constant and crystallite size of the PBNPs before and after 24 h PGMs/Mo sorption test, which were estimated by fitting the (200) diffraction peak with pseudo-Voigt function and by using the Scherrer equation47 with a constant of 1.5, respectively. Here, the constant value means an area-weighted effective diameter along the direction of the diffraction vector. The results of Fig. 2 and Table 2 indicate that PBNPs with a crystallite size of 16–17 nm were found to maintain the FCC structure before and after the PGMs/Mo sorption, and that the lattice constant was estimated to be 10.16 Å for the pristine PBNPs (10.13–10.18 Å range reported previously48,49,50), whereas 10.21 Å for the PGM/Mo-sorbed PBNPs.
Powder XRD patterns of the pristine and PGMs/Mo-sorbed PBNPs, along with the simulation results (stick bar) of FCC structure (space group: \(F\overline{4} 3m\)) for PB. The black, green, blue, pink, and red lines represent the pristine, Mo-, Ru-, Rh-, and Pd-sorbed PBNPs, respectively. The crystal structure of PB is shown in the inset.
For Pd ion sorption, since the ionic radius of Pd2+ ion (0.86 Å)46 is larger than that of Fe2+ (0.61 Å)46 and the substitution efficiency of Fe2+ with Pd2+ was 87.0% (Table 1), the lattice constant should be expanded significantly. For Rh ion sorption, the ionic radius of Rh3+ ion (0.665 Å)46 is larger than that of Fe3+ (0.645 Å)46 to some extent, and also the substitution efficiency of Fe3+ with Rh3+ was 47.8%, thus the lattice constant was expanded effectively. On the contrary, for the Ru sorption, despite the ionic radius of Ru4+ ion (0.62 Å)46 is smaller than that of Fe3+ (0.645 Å) with 39.0% of the substitution efficiency of Fe3+ with Ru4+, the lattice was expanded in a similar manner to Pd ion sorption. This is presumably because the Coulomb repulsion between Ru4+ and Fe2+ is stronger than that between Fe3+ and Fe2+, resulting in the expansion of the lattice constant. In a similar manner for the Mo sorption, although the ionic radii of 0.59 Å for Mo6+ is smaller than that of Fe3+ (0.645 Å) with 17.1% of the substitution efficiency of Fe2+/Fe3+ with Ru4+, a larger Coulomb repulsion between Mo6+ and Fe2+/Fe3+ stronger than that between Fe3+ and Fe2+ caused the expansion of the lattice constant, which is comparable to that for the PGMs. The reason why the lattice constant was expanded to be coincidently the same value after sorption of all PGMs/Mo ions is still unclear. It is necessary to be considered that the residual PGMs/Mo and Fe ions located in the nanospace of PB unit cell upon sorption play a role in expanding the lattice constant.
Elementary processes of PGMs sorption into PBNPs
To discuss the elementary processes of PGMs/Mo when incorporated into PBNPs, we next examined (1) the adsorption energy of PGMs/Mo ions on the PB surface, (2) the diffusion energy of PGMs/Mo ions into the nanospace of PBNPs, and (3) the substitution energy of PGMs/Mo ions with Fe ion, using first-principles calculations based on DFT.
We first discuss (1) the adsorption energy. Figure 3 shows (a) the optimized structure of PGMs/Mo ions on the (100) surface of PB, (b) the adsorption energy (Ead) of PGMs/Mo on the surface, and (c) the maximally-localized Wannier functions (MLWFs) of the C2p and N2p AOs for the CN group constructing the (100) surface. As shown in the side view of Fig. 3a, the (100) surface model was optimized to be the zig-zag structure which is stabler by 1.4 eV than the bulk flat surface structure. As shown in shown in the top view of Fig. 3a, it is found that all PGMs/Mo ions (red circle) are stably adsorbed on the center of the square consisting of the four Fe ions in the (100) plane. This is because PGMs/Mo ions surrounded by the four CN– anion groups became stable energetically due to the attractive Coulomb interactions. The optimized structural coordination was summarized in Tables S1–S5 (supporting materials). Figure 3b shows the plot of the Ead on the (100) surface with respect to the PGM elements. Here, a lager positive value of Ead implies a more difficulty to be adsorbed on the surface. It is found that the Ead seems to increase non-linearly with the valence number of PGMs ions: Ead = 0 eV for Pd2+ ion, ca. 0.2 eV for Rh3+ ion, ca. 1.8 eV for Ru4+ ion, and ca. 3.2 eV for Mo6+. This is partly because the repulsive Coulomb interactions between the adsorbed PGMs/Mo ions and their surrounding Fe2+/Fe3+ ions become greater than the attractive ones between the adsorbed ions and their surrounding CN– groups as the valence number of the adsorbed PGM/Mo ions increases, and partly because the latter attractive interactions become greater to cause a large distortion of the lattice with increasing the valence number as well. In addition, as show in in Fig. 3c, since the 2py and 2pz AOs of both C and N atoms are expanded within the (100) in-plane, the PGMs/Mo cations are easy to be trapped in the (100) in-plane. It is noted that the present study estimated the Ead in solid phase and in vacuum. For the practical HLLW system with metal ions in nitric acid solution, the metal ions are more easily transported to the PB surface via the solvent, and the electrostatic potential of the (100) surface should also be somewhat altered.
We next discuss (2) the diffusion of PGMs ions in the nanospace of PB unit cell, whose energy was calculated using the NEB method. Figure 4 shows the plot of the relative energy with respect to the five migration steps for PGMs/Mo. Inset schematically illustrates a snap shot at each migration step. The accurate structural parameters for each migration step were summarized in Tables S6.1–S9.5 (supporting materials). It is interesting to note that all PGMs/Mo ions become stable at the center of the square formed by the four Fe ions in the (100) plane, whereas the 4c site is a saddle point for those metal ions. The reason behind the stabilization of the PGMs/Mo ions in the (100) in-plane is the same as for their surface adsorption. In addition, it can be said that the space of the 4c site (5 Å) is too large for PGMs ions (Ionic diameter: 1.24 Å for Ru4+, 1.33 Å for Rh3+, 1.72 Å for Pd2+, 0.59 Å for Mo6+)45. Thus, the PGMs/Mo ions tend to be trapped at the (100) in-plane, where the substitution reaction between PGMs/Mo and Fe ions will take place.
We finally discuss the substitution energy (ES) of PGMs/Mo ions with the Fe2+/Fe3+ ions of PB, which was estimated using the unit cell model containing 60 atoms (inset of Fig. 2). Although it is supposed that the model corresponds to 12.5% Fe ions (one of eight) substituted with PGMs ions when applied to the solid state, we just focused on the substitution occurred locally using the unit cell. Figure 5 shows the ES of PGMs/Mo ions with the Fe ions of PB unit cell. When the ES is a negative value, the substitution takes place preferably. Since the ES was defined by Eq. (2) described above, the chemical potentials were required. In the present study, we used the chemical potential of each metal oxide at the oxidation limit, and of neutral metal atom at the reduction limit. At the oxidation limit, Pd2+ and Ru4+ ions are expected to be substituted energetical preferentially with the Fe2+ and Fe3+ sites, respectively. On the other hand, Rh3+ ion is expected to be substituted with both sites because of the small difference (ca. 0.4 eV) in Es between them. Although the results of Fig. 1 indicate that Rh3+ ion is substituted mainly with Fe3+ ion, Rh3+ ion would be substituted minorly with Fe2+ ion to some extent at temperatures around 353 K when applied to a practical HLLW containing the exothermic nuclides such as 137Cs and 90Sr. On the other hand, Mo6+ ion is preferable to be substituted with the Fe3+ site energetically, because the Coulomb repulsion between Mo6+ and the nearest surrounding Fe3+ ions for Mo6+ substitution with Fe2+ becomes much greater than that between Mo6+ and the nearest surrounding Fe2+ for Mo6+ substitution with Fe3+. However, comparison between the experimental and theoretical results (Fig. 1) indicates that Mo6+ is substituted not only with Fe3+ ion but also with Fe2+ ion, which is contradictory to that the Es of Fe2+ with Mo6+ is a large positive value of ca. 4.0 eV at the oxidation limit, as shown in Fig. 5. Since the present PB unit cell cluster model did not consider the Madelung potentials and the lattice relaxation, the Es may be overestimated when Fe2+/Fe3+ is substituted with the higher valent Mo6+ ion.
We examined the three elementary processes when PGMs ions are incorporated into PB: the adsorption on the (100) surface of PB, the diffusion in the nanospace of PB unit cell, and the substitution of PGMs ions with Fe ions. As summarized in Table 3, all the three processes are most easily to progress for Pd2+ ion, and subsequently for Rh3+ ion, whereas the surface adsorption process becomes the rate-determining step for Ru4+ ion. This is consistent with the results of the sorption and substitution efficiencies for these metal ions, as shown in Table 1. On the other hand, despite the order of the elusion and substitution efficiencies for Mo ion can be well explained using the results of Table 3 as well as PGMs ions, the sorption efficiency of Mo ion was higher than that for PGMs ions. Since Mo ion tends to be formed as polynuclear Mo oxide complexes in a nitric acid solution29, a part of them was presumably precipitated in the solution, which was not involved in the 24-h sorption test.
The findings in the present study provide us an important insight that these three processes mutually affect the sorption amount and the sorption efficiency, thus leading to develop a high-performance sorbent for recovery of rare metals not only from N-wastes but also from E-wastes.
The uptake amount of PGMs per 1 g PBNPs
As shown in Table 1, the uptake mechanism of PGMs/Mo ions when incorporated into PBNPs can allow us to estimate the substitution efficiency of PGMs/Mo with Fe by considering the PB unit cell (inset of Fig. 2) with inclusion of four Fe2+ and four Fe3+ atoms. Assuming that the amount of Fe elution is equal to that of PGMs/Mo substitution (namely, the amount of PGMs/Mo and Fe diffusion inside PBNPs is neglected), the substitution efficiency was obtained to be 39.0% for Ru ion, 47.8% for Rh ion, 87.0% for Pd ion, and 17.1% (Fe2+ and Fe3+ for each) for Mo ion. This implies that 0.13 g of Ru, 0.16 g of Rh, 0.30 g of Pd, and 0.11 g of Mo can be recovered by using 1 g PB with a chemical form of KFe(III)[Fe(II)(CN)6]. Furthermore, PBNPs were confirmed to exhibit several resistances against heat (up to 300 °C), nitric acid (up to 8 M), and γ-ray radiation (up to 1000 kGy), thus indicating that PBNPs are practically used not only for disposal processes of N-wastes but also for recycle processes of E-wastes.
Summary
We have examined the uptake mechanisms of platinum-group-metals (PGMs) and molybdenum (Mo) ions into PBNPs in a nitric acid solution for 24-h sorption test, using ICP-AES, powder XRD, and UV–Vis-NIR spectroscopy in combination with first-principles calculations, and revealed that the Ru4+ and Pd2+ ions are incorporated into PBNPs by substitution with Fe3+ and Fe2+ ions of the PB framework, respectively, whereas the Rh3+ ion is incorporated into PBNPs by substitution mainly with Fe3+ and minorly with Fe2+ ion, and Mo6+ ion is incorporated into PBNPs by substitution with both Fe2+ and Fe3+ ions, with maintaining the crystal structure before and after the sorption test. Assuming that the amount of Fe elusion is equal to that of PGMs/Mo substitution, the substitution efficiency is estimated to be 39.0% for Ru, 47.8% for Rh, 87% for Pd, and 17.1% for Mo6+. This implies that 0.13 g of Ru, 0.16 g of Rh, 0.30 g of Pd, and 0.107 g of Mo can be recovered by using 1 g PBNPs with a chemical form of KFe(III)[Fe(II)(CN)6].
Since PBNPs can be produced massively in liquid phase and exhibit nontoxic and stable up to 300 °C, they are well known to be used as pigments and paint color materials. Thus, the present findings demonstrate that PB (or its analogues) will be one of the hopeful candidates to develop the recycling of precious metals from N- and E-wastes when compared to conventional bio-based adsorbents/activated carbons.
References
Asano, H. & Aritomi, M. Long-term integrity of waste package final closure for HLW geological disposal, (I) points at issue concerning 1,000 years containment capability of overpack. J. Nucl. Sci. Technol. 42, 470–479 (2005).
Tochiyama, O. & Masuda, S. Building technical and social confidence in the safety of geological disposal in Japan. J. Nucl. Sci. Technol. 50, 665–673 (2013).
Gallardo, A. H., Matsuzaki, T. & Aoki, H. Geological storage of nuclear wastes: Insights following the Fukushima crisis. Energy Policy 73, 391–400 (2014).
Inoue, T. et al. Development of partitioning and transmutation technology for long-lived nuclides. Nucl. Technol. 93, 206–220 (1991).
Uruga, K., Sawada, K., Arita, Y., Enokida, Y. & Yamamoto, Y. Removal of platinum group metals contained in molten glass using copper. J. Nucl. Sci. Technol. 44, 1024–1031 (2007).
Haxel, G.B., Hedrick, J.B. & Orris, G.J. Rare Earth Elements: Critical Resources for High Technology. USGS Fact Sheet, 087-02 (2002).
Takeshita, K., Inaba, Y., Takahashi, T., Onoe, J. & Narita, H. Development of separation process of PGMs and Mo from high-level liquid waste for the stable operation of vitrification process. Proc. Glob. 2015, 20–24 (2015).
Onishi, T. et al. Adsorption of platinum-group metals and molybdenum onto aluminum ferrocyanide in spent fuel solution. Energy Procedia 131, 151–156 (2017).
Kitagawa, S., Kitaura, R. & Noro, S. Functional porous coordination polymers. Angew. Chem. Int. Ed. 43, 2334–2375 (2004).
Chang, Z., Yang, D., Xu, J., Hu, T. & Bu, X. Flexible metal-organic frameworks: Recent advances and potential applications. Adv. Mater. 27, 5432–5441 (2015).
Gangu, K. K., Maddila, S., Mukkamala, S. B. & Jonnalagadda, S. B. A review on contemporary metal-organic framework materials. Inorg. Chim. Acta 446, 61–74 (2016).
Gotoh, A. et al. Simple synthesis of three primary colour nanoparticle inks of Prussian blue and its analogues. Nanotechnology 18, 345609 (2007).
Yamamoto, T., Saso, N., Umemura, Y. & Einaga, Y. Photoreduction of Prussian blue Intercalated into Titania nanosheet ultrathin films. J. Am. Chem. Soc. 131, 13196–13197 (2009).
Middlemiss, D. S. et al. Spin crossover in the CsFeII[CrIII(CN)6] Prussian blue analog: Phonons and thermodynamics from hybrid functionals. Phys. Rev. B 81, 184410 (2010).
Tokoro, T. & Ohkoshi, S. Multifunctional material: Bistable metal-cyanide polymer of rubidium manganese hexacyanoferrate. Bull. Chem. Soc. Jpn. 88, 227–239 (2015).
Zhang, W. et al. Prussian blue nanoparticles as multienzyme mimetics and reactive oxygen species scavengers. J. Am. Chem. Soc. 138, 5860–5865 (2016).
Wu, X. et al. Low defect FeFe(CN)6 framework as stable host material for high performance Li-ion batteries. ACS Appl. Mater. Interfaces 8, 23706–23712 (2016).
Ishizaki, M. et al. Redox-coupled alkali-metal ion transport mechanism in binder-free films of Prussian blue nanoparticles. J. Mater. Chem. A 7, 4777–4787 (2019).
Mimura, H., Lehto, J. & Harjula, R. Selective removal of cesium from simulated high-level liquid wastes by insoluble ferrocyanides. J. Nucl. Sci. Technol. 34, 607–609 (1997).
Arisaka, M. et al. Cesium adsorption ability and stability of metal hexacyanoferrates irradiated with gamma rays. J. Radioanal. Nucl. Chem. 303, 1543–1547 (2015).
Vipin, A. et al. Cellulose nanofiber backboned Prussian blue nanoparticles as powerful adsorbents for the selective elimination of radioactive cesium. Sci. Rep. 6, 37009 (2016).
Ohnuki, T. et al. Direct accumulation pathway of radioactive cesium to fruit bodies of edible mushroom from contaminated wood logs. Sci. Rep. 6, 29866 (2016).
Tachikawa, H., Haga, K. & Yamada, K. Mechanism of K+, Cs+ ion exchange in nickel ferrocyanide: A density functional theory study. Comput. Theor. Chem. 1115, 175–178 (2017).
Onoe, J. et al. The uptake mechanism of palladium ions into Prussian-blue nanoparticles in a nitric acid solution toward application for the recycling of precious metals from electronic and nuclear wastes. RSC Adv. 11, 20701 (2021).
Mishima, R. et al. Sorption properties of aluminum hexacyanoferrate for platinum group elements. Chem. Lett. 49, 83–86 (2020).
Ogasawara, K. et al. Relativistic cluster calculation of ligand-field multiplet effects on cation L2,3 x-ray-absorption edges of SrTiO3, NiO, and CaF2. Phys. Rev. B 64, 115413 (2001).
Watanabe, S., Ogasawara, K., Yoshino, M. & Nagasaki, T. First-principles and experimental analysis of fn−fn−1d1 absorption spectra and multiplet energy levels of Pr3+, Nd3+, and U3+ in LiYF4. Phys. Rev. B 81, 125128 (2010).
Watanabe, S. et al. Intra- and inter-atomic optical transitions of Fe Co, and Ni ferrocyanides studied using first-principles many-electron calculations. J. Appl. Phys. 119, 235102 (2016).
Watanabe, S., Sato, T., Nakaya, M., Yoshida, T. & Onoe, J. Chemical forms of molybdenum ion in nitric acid solution studied using liquid-phase X-ray absorption fine structure, Ultraviolet–Visible absorption spectroscopy and first-principles calculations. Chem. Phys. Lett. 723, 76–81 (2019).
Verna, P. K., Gujai, R. B. & Mohapatra, P. K. Understanding the recovery of ruthenium from acidic feeds by oxidative solvent extraction studies. Radiochim. Acta 107, 423–429 (2019).
Samuels, A. C., Cherilynn, A. B., Clark, S. B., Wall, N. A. & Clark, A. E. Integrated computational and experimental protocol for understanding Rh(III) speciation in hydrochloric and nitric acid solutions. Inorg. Chem. 53, 12315–12322 (2014).
Watanabe, S. et al. Chemical forms of rhodium ion in pure water and nitric acid solution studied using ultraviolet–visible spectroscopy and first-principles calculations. IOP Conf. Ser. Mater. Sci. Eng. 835, 012001 (2020).
Watanabe, S. et al. Spectroscopic and first-principles calculation studies of the chemical forms of palladium ion in nitric acid solution for development of disposal of high-level radioactive nuclear wastes. AIP Adv. 8, 045221 (2018).
Clark, S. J. et al. First principles methods using CASTEP. Z. Kristallogr. Cryst. Mater. 220, 567–570 (2005).
Giannozzi, P. et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864-871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133-1138 (1965).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Mostofi, A. et al. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Cococcioni, M. & de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 71, 035105 (2005).
Wojdeł, J. C., Moreira, L. P. R., Bromley, S. T. & Illas, F. On the prediction of the crystal and electronic structure of mixed-valence materials by periodic density functional calculations: The case of Prussian Blue. J. Chem. Phys. 128, 044713 (2008).
Wang, L., Maxich, T. & Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 73, 195107 (2006).
Shannon, R. D. Effective ionic radii and systematic studies of interatomic distances in halides and chaleogenides. Acta Crystallogr. A32, 751–767 (1976).
Scherrer, P. Bestimmung der Größe und der inneren struktur von kolloidteilchen mittels röntgenstrahlen, Nachrichten von der Gesellschaft der Wissenschaften, Göttingen. Mathematisch-Physikalische Klasse, 2, 98–100 (Springer, 1918).
Buser, H. J. & Ludi, A. Single-crystal study of Prussian blue – Fe4[Fe(CN)6]2·14H2O. J. Chem. Soc. Chem. Commun., 1299–1299 (1972).
Buser, H. J., Schwarzenbach, D., Petter, W. & Ludi, A. Crystal structure of Prussian blue: Fe4[Fe(CN)6]3·xH2O. Inorg. Chem. 16, 2704–2710 (1977).
Herren, F., Ficher, P., Ludi, A. & Halg, W. Neutron-diffraction study of Prussian blue, Fe4[Fe(CN)6]3·xH2O: Location of water molecules and long-range magnetic order. Inorg. Chem. 19, 956–959 (1980).
Acknowledgements
The present work was financially supported partly by “The R&D program for advanced nuclear power systems” from MEXT (Ministry of Education, Culture, Sports, Science and Technology), and partly by Chubu Electric Power Co. Ltd. The CASTEP calculations were performed by using “Computer System for Nanostructure Design” of Venture Business Laboratory, Nagoya University.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Watanabe, S., Inaba, Y., Harigai, M. et al. The uptake characteristics of Prussian-blue nanoparticles for rare metal ions for recycling of precious metals from nuclear and electronic wastes. Sci Rep 12, 5135 (2022). https://doi.org/10.1038/s41598-022-08838-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-08838-1
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.