Abstract
Temporal dataset shift associated with changes in healthcare over time is a barrier to deploying machine learning-based clinical decision support systems. Algorithms that learn robust models by estimating invariant properties across time periods for domain generalization (DG) and unsupervised domain adaptation (UDA) might be suitable to proactively mitigate dataset shift. The objective was to characterize the impact of temporal dataset shift on clinical prediction models and benchmark DG and UDA algorithms on improving model robustness. In this cohort study, intensive care unit patients from the MIMIC-IV database were categorized by year groups (2008–2010, 2011–2013, 2014–2016 and 2017–2019). Tasks were predicting mortality, long length of stay, sepsis and invasive ventilation. Feedforward neural networks were used as prediction models. The baseline experiment trained models using empirical risk minimization (ERM) on 2008–2010 (ERM[08–10]) and evaluated them on subsequent year groups. DG experiment trained models using algorithms that estimated invariant properties using 2008–2016 and evaluated them on 2017–2019. UDA experiment leveraged unlabelled samples from 2017 to 2019 for unsupervised distribution matching. DG and UDA models were compared to ERM[08–16] models trained using 2008–2016. Main performance measures were area-under-the-receiver-operating-characteristic curve (AUROC), area-under-the-precision-recall curve and absolute calibration error. Threshold-based metrics including false-positives and false-negatives were used to assess the clinical impact of temporal dataset shift and its mitigation strategies. In the baseline experiments, dataset shift was most evident for sepsis prediction (maximum AUROC drop, 0.090; 95% confidence interval (CI), 0.080–0.101). Considering a scenario of 100 consecutively admitted patients showed that ERM[08–10] applied to 2017–2019 was associated with one additional false-negative among 11 patients with sepsis, when compared to the model applied to 2008–2010. When compared with ERM[08–16], DG and UDA experiments failed to produce more robust models (range of AUROC difference, − 0.003 to 0.050). In conclusion, DG and UDA failed to produce more robust models compared to ERM in the setting of temporal dataset shift. Alternate approaches are required to preserve model performance over time in clinical medicine.
Similar content being viewed by others
Introduction
The wide-spread adoption of electronic health records (EHRs) and the enhanced capacity to store and perform computation with large amounts of data have enabled the development of highly performant machine learning models for clinical outcome predictions1. The utility of these models critically depends on sustained performance to maintain safety2, end-users’ trust, and to outweigh the high cost of integrating each model into the clinical workflow3. However, this is hindered in the non-stationary healthcare environment by temporal dataset shift due to mismatch between the data distribution on which models were developed and the distribution to which models were applied4.
There has been limited research on the impact of temporal dataset shift in clinical medicine5. Recent approaches largely relied on maintenance strategies consisting of performance monitoring, model updating and calibration over certain time intervals6,7,8. Another approach grouped clinical features into their underlying concepts to cope with a change in the record-keeping system9. Generally, these approaches either require detection of model degradation or rely on explicit knowledge or assumptions about the underlying cause of the shift. Complementary to these approaches would be ones that attempt to proactively produce robust models that incorporate relatively few assumptions on the nature of the shift.
The past decade of machine learning research offered numerous algorithms that learn robust models by using data from multiple environments to identify invariant properties. These algorithms were often developed for domain generalization (DG)10 and unsupervised domain adaptation (UDA)11. In the DG setting, the goal is to learn models that generalize to new environments unseen at training time. In the UDA setting, the goal is to adapt models to target environments using labeled samples from the source environment as well as a limited set of unlabeled samples from the target environment. If we consider EHR data across discrete time windows as related but distinct environments, then both DG and UDA settings may be suitable to combat the impact of temporal dataset shift. To date, these approaches have not been evaluated on improving model robustness to temporal dataset shift for clinical prediction tasks. Therefore, the objective was to benchmark learning algorithms for DG and UDA on mitigating the impact of temporal dataset shift on machine learning model performance in a set of clinical prediction tasks.
Methods
Data source
We used the MIMIC-IV database12,13, which contains deidentified EHRs of 382,278 patients admitted to an intensive care unit (ICU) or the emergency department at the Beth Israel Deaconess Medical Center (BIDMC) between 2008 and 2019. For this cohort study, we considered ICU admissions sourced from the clinical information system MetaVision at the BIDMC, in which records from 53,150 patients were made available in the latest version of MIMIC-IV 1.0.
Data access
Data from MIMIC-IV was approved under the oversight of the Institutional Review Boards of BIDMC (Boston, MA) and the Massachusetts Institute of Technology (MIT; Cambridge, MA). Because of deidentification of protected health information, the requirement for individual patient consent was waived by the Institutional Review Boards of BIDMC and MIT. Data access was credentialed under the oversight of the data use agreement through PhysioNet13 and MIT. All experiments were performed in accordance with institutional guidelines and regulations.
Cohort
Each patient’s timeline in MIMIC-IV is anchored to a shifted (deidentified) year with which a year group and age are associated. The year group reflects the actual 3-year range (for example 2008–2010) in which the shifted year occurred, and age reflects the patient’s actual age in the shifted year. There are four available year groups in MIMIC-IV: 2008–2010, 2011–2013, 2014–2016 and 2017–2019. We included patients who were 18 years or older and randomly selected one ICU admission that occurred in the year group for each patient. As a result, each patient is represented once in our dataset and is associated with a single year group. We excluded ICU admissions less than 4 h in duration.
Outcomes
We defined four clinical outcomes. For each outcome, the task was to perform binary predictions over a time horizon with respect to the time of prediction, which was set as 4 h after ICU admission. Long length of stay (Long LOS) was defined as ICU stay greater than three days from the prediction time. Mortality corresponded to in-hospital mortality within 7 days from the prediction time. Invasive ventilation corresponded to initiation of invasive ventilation within 24 h from the prediction time. Sepsis corresponded to the development of sepsis according to the Sepsis-3 criteria14 within 7 days from the prediction time. For invasive ventilation and sepsis, we excluded patients with these outcomes prior to the time of prediction. Further details on each outcome are presented in the Supplementary Methods online.
Features
Our feature extraction followed a common procedure15 and obtained six categories of features including diagnoses, procedures, labs, prescriptions, ICU charts and demographics. Demographic features included age, biological sex, race, insurance, marital status and language. Clinical features were extracted over a set of time-intervals defined relative to the time of ICU admission as follows: 0–4 h after ICU admission, 0–7 days prior, 7–30 days prior, 30–180 days prior, and 180 days-any time prior. For each time interval, we obtained counts of unique concept identifiers for diagnoses, procedures, prescriptions and labs with the exception that identifiers for diagnoses and procedures were not obtained in the 0–4 h interval after admission as they were not available. We also obtained measurements for lab tests for each time interval, and measurements for chart events in the 0–4 h interval after admission. In addition, we mapped each measurement variable in each time interval to the patient-level mean, minimum and maximum. Number of extracted features for each category and time interval are listed in the Supplementary Methods online.
Feature preprocessing pruned features that had less than 25 patient observations, replaced non-zero count values with 1 s, encoded measurement features to quintiles, and one-hot encoded all but count features. This process resulted in binary feature matrices that were extremely sparse. All feature preprocessing procedures were fit on the training set (e.g., to determine the boundaries of each quintile) and were subsequently applied to transform the validation and test sets.
Model and learning algorithms
In all experiments, we leveraged fully connected feedforward neural network (NN) models for prediction, as they enable flexible learning for differentiable objectives across algorithms. The standard algorithm to learn models is the empirical risk minimization (ERM) algorithm in which the objective is to minimize average training error16 without considerations of environment annotations (year groups in our case).
In this study, we largely employ DG and UDA algorithms that learn to produce representations that exhibit certain invariances across environments by leveraging the training data and their corresponding year groups. One exception is Group distributionally robust optimization (GroupDRO)17, which does not “learn” invariances but instead minimizes training error in the worst-case training environment by increasing the importance of environments with larger errors. DG algorithms that learn invariant representations include Invariant risk minimization (IRM)18 and distribution matching. IRM aims to learn a latent representation (i.e., hidden layer activations) where the optimal classifier leveraging that representation is the same for all environments. Distribution matching algorithms include correlation alignment (CORAL)19, which seeks to match the mean and covariance of the distribution of the data encoded in the latent space across environments; maximum mean discrepancy (MMD)20, which minimizes distribution discrepancy between predictions belonging to different environments; and domain adversarial learning (AL)21,22, which matches the distributions using an adversarial network and an objective that minimizes discriminability between environments. The adversarial network used in this study is a NN model with one hidden layer of dimension 32. Since distribution matching algorithms (CORAL, MMD, and AL) do not require outcome labels, they can be leveraged for DG as well as UDA.
Model development
We conducted baseline, DG and UDA experiments. The baseline experiment consisted of several aspects. First, to characterize temporal dataset shift on model performance, we trained models with ERM on the 2008–2010 group (ERM[8–10]) and evaluated these models in each subsequent year group. Next, to describe the extent of temporal dataset shift, we compared the performance of ERM[8–10] in each subsequent year group with models trained using ERM on that year group. Difference in performance in the target year group (2017–2019) between ERM[8–10] and models trained and evaluated on the target year group (ERM[17–19]) described the extent of temporal dataset shift in the extreme scenario in which models were developed on the earliest available data and were never updated. All models in the baseline experiment used ERM.
For DG and UDA experiments, model training was performed on 2008–2016, with UDA also incorporating unlabelled samples from the target year group. Performance of DG and UDA models were compared with ERM models trained using 2008–2016 (ERM[8–16]) as these are the fairest ERM comparators for DG and UDA models. For models in the DG and UDA experiments, we focused on their performance in the target year group, but also described their performance in 2008–2016.
Data splitting procedure
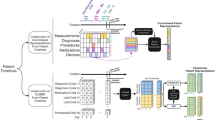
Data splitting procedure was performed separately for each task and experiment (see Fig. 1). The baseline experiment split each year group into 70% training, 15% validation and 15% test sets. In DG and UDA experiments, the training set included 85% data from 2008 to 2010 and 2011–2013, and 45% of data from 2014 to 2016. The validation set included 35% of data from 2014 to 2016 (chosen because of its temporal proximity to the target year group). The test set included the same 15% from each year group as the baseline experiment, which allowed us to compare model performance across experiments and learning algorithms on the same patients. For UDA, training year groups were combined into one group, and unlabeled samples of various sizes (100, 500, 1000, and 1500) from the target year group (2017–2019) were leveraged for unsupervised distribution matching.
Data splitting procedure for baseline, domain generalization (DG) and unsupervised domain adaptation (UDA) experiments. Different shades of the same color indicate that they were used to train or evaluate different models. For instance, in the baseline experiment, the training set of each year group was used to learn models for that year group. In the DG experiment, the training year groups were kept separate to allow DG algorithms to estimate invariance across the year groups. In comparison, in the UDA experiment, data from the training year groups were pooled, and unlabeled samples from the target year group were leveraged for unsupervised distribution matching between training and target year groups. In addition, ERM[8–16] models were learned on pooled data from the training year groups (2008–2016) to be used as ERM comparators for DG and UDA models.
Model training
We developed NN models on the training sets of each experiment for each task and selected hyperparameters based on performance in the validation sets. DG and UDA models used the same model hyperparameters as ERM[8–16], but involved an additional search over the algorithm-specific hyperparameter that modulated the impact of the algorithm on model learning. For all experiments, we trained 20 NN models using the selected hyperparameters for each combination of outcome, learning algorithm and experiment-specific characteristic (for example, year group in baseline experiment and size of unlabeled samples for UDA). Further details on the models, learning algorithms, as well as hyperparameter selection and model training procedures are presented in the Supplementary Methods online.
Model evaluation
We evaluated models on the test sets of each experiment. Model performance was evaluated using area-under-receiver-operating-characteristic curve (AUROC), area-under-precision-recall curve (AUPRC) and the absolute calibration error (ACE)23. ACE is a calibration measure similar to the integrated calibration index24 in that it assesses overall model calibration by taking the average of the absolute deviations from an approximated perfect calibration curve. The difference is that ACE uses logistic regression for approximation instead of locally weighted regression such as LOESS.
To aid clinical interpretation of the impact of temporal dataset shift and its mitigation strategies, we translated change in performance to interpretable threshold-based metrics (including sensitivity and specificity) across clinically reasonable threshold levels. We chose the task with the most extreme temporal dataset shift. Next, we set up a scenario with 100 hypothetical ICU patients and estimated the number of patients with and without a positive label using average prevalence from 2008 to 2019. We then estimated the number of false-positive (FP) and false-negative (FN) predictions using the average sensitivity and specificity for: (1) ERM[8–10] in 2008–2010, illustrating the results of initial model development with training and test sets in 2008–2010, and representing performance anticipated by clinicians applying the model to patients admitted in 2017–2019 if the model is not updated; (2) ERM[8–10] in 2017–2019, illustrating the actual performance of the earlier model on patients, or the impact of temporal dataset shift; (3) ERM[8–16] in 2017–2019, illustrating the ERM comparators for DG and UDA models; (4) models trained using a representative approach from DG or UDA; and (5) ERM[17–19] in which training and test sets are both using 2017–2019 data.
Statistical analysis
For each combination of outcome, experiment-specific characteristic (e.g., year group in the baseline experiment), and evaluation metric (AUROC, AUPRC and ACE), we reported the median and 95% confidence interval (CI) of the distribution over mean performance (across 20 NN models) in the test set obtained from 10,000 bootstrap iterations. To compare models (for example, learned using IRM vs. ERM[8–16]) in the target year group, metrics were computed over 10,000 bootstrap iterations and the resulting 95% confidence interval of the differences were used to determine statistical significance25.
Model training was performed on an Nvidia V100 GPU. Analyses were implemented in Python 3.826, Scikit-learn 0.2427 and Pytorch 1.728. The code for all analyses is open-source and available at https://github.com/sungresearch/mimic4ds_public.
Results
Cohort characteristics for each year group and outcome are presented in Table 1. Figure 2 shows performance measures (AUROC, AUPRC and ACE) of ERM[8–10] models in each year group vs. models trained on that year group. Largest temporal dataset shift was observed for sepsis predictions in 2017–2019 (drop in AUROC, 0.090; 95% CI 0.080–0.101).
Mean performance (AUROC, AUPRC, and ACE) of models in the baseline experiment. Solid blue lines depict models trained using 2008–2010 (ERM[8–10]) and evaluated in each year group. Dashed lines depict models trained and evaluated in each year group separately (comparators). Error bars indicate 95% confidence interval obtained from 10,000 bootstrap iterations. Black circles indicate statistically significant differences in performance based on the 95% confidence interval of the difference over 10,000 bootstrap iterations when comparing ERM[8–10] and comparators for each year group. The figure shows temporal dataset shift that is larger for Long LOS and Sepsis tasks. ERM: empirical risk minimization; LOS: length of stay; AUROC: area under the receiver operating characteristics curve; AUPRC: area under the precision recall curve; ACE: absolute calibration error.
Figure 3 illustrates change in the performance measures of DG and UDA models in the target year group (2017–2019) relative to ERM[8–16]. In addition, change in performance measures of ERM[8–10] and ERM[17–19] are plotted in grey for comparison. ERM[8–16] performed better than ERM[8–10] (largest gain in AUROC, 0.049; 95% CI 0.041–0.057; see Supplementary Table S1 online), but performed worse than ERM[17–19] (worst drop in AUROC, 0.071; 95% CI 0.062–0.081) with some exceptions in mortality and invasive ventilation predictions (see Supplementary Table S2 online). Performance of DG and UDA models was similar to ERM[8–16] and while some models performed significantly better than ERM[8–16], others performed significantly worse with all differences being relatively small in magnitude (see Supplementary Table S3). Correspondingly, shifts in the cumulative distribution of predicted probabilities across year groups were not reduced by DG and UDA relative to ERM (Supplementary Fig. S1), and model selection for DG and UDA algorithms tended to select small algorithm-specific hyperparameter values with little impact on model training (Supplementary Methods). However, increasing the magnitude of these hyperparameters did not result in performance gains (see Supplementary Fig. S2, S3, and S4).
Difference in mean performance of DG and UDA approaches relative to ERM[8–16] in the target year group (2017–2019). Performance of ERM[8–10] (train set 2008–2010 and test set 2017–2019, dashed line) and ERM[17–19] (train and test sets 2017–2019, solid line) models are also shown for comparison. Error bars indicate 95% confidence interval obtained from 10,000 bootstrap iterations. Here, we show results from three of the four experimental conditions using differing number of unlabelled samples for UDA—we did not observe meaningful differences across the number of unlabelled samples evaluated. Numerical representation of the performance measures relative to ERM[8–16] are presented in Supplementary Table S3. LOS: length of stay; ERM: empirical risk minimization; IRM: invariant risk minimization; AL: adversarial learning; GroupDRO: group distributionally robust optimization; CORAL: correlation alignment; MMD: maximum mean discrepancy; AUROC: area under the receiver operating characteristics curve; AUPRC: area under the precision recall curve; ACE: absolute calibration error; domain generalization: DG; unsupervised domain adaptation: UDA.
Table 2 illustrates a clinical interpretation of temporal dataset shift in sepsis prediction using a scenario of 100 consecutively admitted patients to the ICU between 2017 and 2019 with a risk threshold of 10% and an estimated outcome prevalence of 11% (see Supplementary Table S5 for results across thresholds from 5 to 45%). ERM[8–10] applied to 2017–2019 was associated with one additional FN among 11 patients with sepsis and 7 additional FP among 89 patients without sepsis when compared to the model applied to 2008–2010. FN with AL, as the representative mitigation approach, was similar to ERM[8–16].
Discussion
Our results revealed heterogeneity in the impact of temporal dataset shift across clinical prediction tasks, with the largest impact on sepsis prediction. When compared to ERM[8–16], DG and UDA algorithms did not substantially improve model robustness. In some cases, DG and UDA algorithms produced less performant models than ERM. We also illustrated the impact of temporal dataset shift and the effect of mitigation approaches for clinical audiences so that they can determine whether the extent of dataset shift precludes utilization in practice.
The heterogeneity of impact by temporal dataset shift as characterized by our baseline experiment echoes the mixed results in model deterioration across several studies that made predictions of clinical outcomes in various populations5. This calls for careful investigation of potential model degradation due to temporal dataset shift at both the population and task level. In addition, these investigations should translate model degradation, typically measured as change in AUROC, into change in clinically relevant performance measures29 or utility in allocation of resources30, and place its impact in the context of clinical decision making and downstream processes31,32,33,34.
This study is one of the first to benchmark the capability of DG and UDA algorithms on EHR data across multiple clinical prediction tasks to mitigate the impact of temporal dataset shift. Our findings align with recent empirical evaluations of DG algorithms demonstrating that they do not outperform ERM under distribution shift across data sources in real-world clinical datasets35,36 as well as non-clinical datasets37. The reasons underlying the failure of DG algorithms are topics of active research, with several recent works offering theory to explain why models derived with IRM and groupDRO are typically not more robust than ERM in practice38,39. Furthermore, other work has demonstrated that UDA objectives based on distribution matching, such as AL, CORAL, and MMD, failed to improve generalization to the target domain under shifts in the outcome rate or in the association between the outcome and features40,41. These findings highlight the difficulty of improving robustness to dataset shift with methods that estimate invariant properties without explicit knowledge of the type of dataset shift.
Future research should continue to explore methods that have demonstrated success in improving model robustness outside of clinical medicine and identify the types of shift for which these methods might be effective. For instance, models adapted from foundation models pre-trained on diverse datasets have displayed impressive performance gains in addition to robustness to various types of dataset shifts42. Domain adaptation methods that leverage distinct latent domains in the target environment43, data augmentation including the use of adversarial examples44, similarities between the source and target environments45,46, and semi-supervised learning that alternatively generate pseudo labels and incorporate them into re-training the model47,48 have all demonstrated success in various domains. In addition, domain knowledge as to which causal mechanisms are likely to be stable or change across time (for example, the causal effect of a disease on patient outcome versus the policy used to prescribe a specific drug) can be incorporated into learning robust models49. We observed heterogeneity across tasks in the impact of temporal dataset shift on model performance. While investigating the cause of the heterogeneity is beyond the scope of this work, it is an important issue to investigate in future research.
Strengths of this study include the use of multiple clinical outcomes and the illustration of temporal dataset shift and its mitigations using more clinically relevant metrics. There are several limitations in this study. First, the coarse characterization of temporal dataset shift did not offer insight about the rate at which model performance deteriorated. This was due to the deidentification in the MIMIC-IV database that left year group as the only time information that followed a correct chronological order across patients. Second, using data from the target year group to estimate best-case models is not realistic in real-world deployment as such data might not be available. Third, our assessment of clinical implications did not consider clinical use-cases in which the model alerts physicians of patients with the highest risks (i.e., acting on a threshold that is adaptively selected)50. In those scenarios, the amount of agreement in the ranking of risks between models need to be additionally considered. Finally, our choice of methods for DG and UDA algorithms were limited to those that estimate invariant properties across training data environments.
In conclusion, DG and UDA using methods that estimate invariant properties across environments failed to produce more robust models compared to ERM in the setting of temporal dataset shift. Alternate approaches are required to preserve model performance over time in clinical medicine.
Data availability
The MIMIC-IV dataset analyzed during the current study is available from https://mimic.mit.edu/docs/iv/. The code for all analyses is open-source and available at https://github.com/sungresearch/mimic4ds_public.
References
Rajkomar, A. et al. Scalable and accurate deep learning with electronic health records. NPJ Digit. Med. 1, 18. https://doi.org/10.1038/s41746-018-0029-1 (2018).
Seneviratne, M. G., Shah, N. H. & Chu, L. Bridging the implementation gap of machine learning in healthcare. BMJ Innov. 6, 45–47 (2020).
Sendak, M. P., Balu, S. & Schulman, K. A. Barriers to achieving economies of scale in analysis of EHR data. A cautionary tale. Appl. Clin. Inform. 8, 826–831. https://doi.org/10.4338/ACI-2017-03-CR-0046 (2017).
Moreno-Torres, J. G., Raeder, T., Alaiz-Rodríguez, R., Chawla, N. V. & Herrera, F. A unifying view on dataset shift in classification. Pattern Recognit. 45, 521–530. https://doi.org/10.1016/j.patcog.2011.06.019 (2012).
Guo, L. L. et al. Systematic review of approaches to preserve machine learning performance in the presence of temporal dataset shift in clinical medicine. Appl. Clin. Inform. 12, 808–815 (2021).
Davis, S. E., Greevy, R. A. Jr., Lasko, T. A., Walsh, C. G. & Matheny, M. E. Detection of calibration drift in clinical prediction models to inform model updating. J. Biomed. Inform. 112, 103611. https://doi.org/10.1016/j.jbi.2020.103611 (2020).
Davis, S. E. et al. A nonparametric updating method to correct clinical prediction model drift. J. Am. Med. Inform. Assoc. 26, 1448–1457. https://doi.org/10.1093/jamia/ocz127 (2019).
Siregar, S., Nieboer, D., Versteegh, M. I. M., Steyerberg, E. W. & Takkenberg, J. J. M. Methods for updating a risk prediction model for cardiac surgery: A statistical primer. Interact. Cardiovasc. Thorac. Surg. 28, 333–338. https://doi.org/10.1093/icvts/ivy338 (2019).
Nestor, B. et al. Feature robustness in non-stationary health records: Caveats to deployable model performance in common clinical machine learning tasks. In Proceedings of the 4th Machine Learning for Healthcare Conference 381–405 (Proceedings of Machine Learning Research, 2019).
Zhou, K., Liu, Z., Qiao, Y., Xiang, T. & Loy, C. C. Domain generalization: A survey. arXiv 1–21. https://arxiv.org/abs/2103.02503 (2021).
Wilson, G. & Cook, D. J. A survey of unsupervised deep domain adaptation. ACM Trans. Intell. Syst. Technol. 11, 1–46 (2020).
Johnson, A. et al. MIMIC-IV in PhysioNet (PhysioNet, 2021 Published).
Goldberger, A. L. et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals.
Singer, M. et al. The third international consensus definitions for sepsis and septic shock (Sepsis-3). JAMA 315, 801–810. https://doi.org/10.1001/jama.2016.0287 (2016).
Reps, J. M., Schuemie, M. J., Suchard, M. A., Ryan, P. B. & Rijnbeek, P. R. Design and implementation of a standardized framework to generate and evaluate patient-level prediction models using observational healthcare data. J. Am. Med. Inform. Assoc. 25, 969–975. https://doi.org/10.1093/jamia/ocy032 (2018).
Varnik, V. Principles of risk minimization for learning theory. In Advances in Neural Information Processing Systems Vol. 4 (eds Moody, J. E. et al.) 831–838 (NeurIPS, 1991).
Sagawa, S., Koh, P. W., Hashimoto, T. B. & Liang, P. Distributionally Robust neural networks for group shifts: On the importance of regularization for worst-case generalization. ArXiv. https://arxiv.org/abs/1911.08731 (2020).
Arjovsky, M., Bottou, L., Gulrajani, I. & Lopez-Paz, D. Invariant risk minimization. ArXiv. https://arxiv.org/abs/1907.02893 (2020).
Sun, B. & Saenko, K. Deep CORAL: Correlation alignment for deep domain adaptation. In European Conference on Computer Vision 443–450 (ArXiv, 2016).
Li, H., Pan, S. J., Wang, S. & Kot, A. C. Domain generalization with adversarial feature learning. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2018) 5400–5409 (IEEE, 2018).
Ganin, Y. et al. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 17, 1–35 (2016).
Pfohl, S. et al. Creating fair models of atherosclerotic cardiovascular disease. In AAAI/ACM Conference on AI, Ethics, and Society (AIES '19) 271–278 (ACM, 2019).
Pfohl, S. R., Foryciarz, A. & Shah, N. H. An empirical characterization of fair machine learning for clinical risk prediction. J. Biomed. Inform. 113, 103621. https://doi.org/10.1016/j.jbi.2020.103621 (2021).
Austin, P. C. & Steyerberg, E. W. The Integrated Calibration Index (ICI) and related metrics for quantifying the calibration of logistic regression models. Stat. Med. 38, 4051–4065. https://doi.org/10.1002/sim.8281 (2019).
Efron, B. & Tibshirani, R. An Introduction to the Bootstrap (Chapman & Hall, 1993).
Van Rossum, G. & Drake, F. Python Language Reference, Version 3.8 https://www.python.org/.
Pedregosa, F. et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Paszke, A. et al. PyTorch: An imperative style. High-performance deep learning library. NeurIPS 32, 8024–8035 (2019).
Shah, N. H., Milstein, A. & Bagley, D. S. Making machine learning models clinically useful. JAMA 322, 1351–1352. https://doi.org/10.1001/jama.2019.10306 (2019).
Ko, M. et al. Improving hospital readmission prediction using individualized utility analysis. J. Biomed. Inform. 119, 103826. https://doi.org/10.1016/j.jbi.2021.103826 (2021).
Char, D. S., Shah, N. H. & Magnus, D. Implementing machine learning in health care—Addressing ethical challenges. N. Engl. J. Med. 378, 981–983. https://doi.org/10.1056/NEJMp1714229 (2018).
Morse, K. E., Bagley, S. C. & Shah, N. H. Estimate the hidden deployment cost of predictive models to improve patient care. Nat. Med. 26, 18–19. https://doi.org/10.1038/s41591-019-0651-8 (2020).
Liu, V. X., Bates, D. W., Wiens, J. & Shah, N. H. The number needed to benefit: Estimating the value of predictive analytics in healthcare.
Li, R. C., Asch, S. M. & Shah, N. H. Developing a delivery science for artificial intelligence in healthcare. NPJ Digit. Med. 3, 107. https://doi.org/10.1038/s41746-020-00318-y (2020).
Koh, P. W. et al. WILDS: A benchmark of in-the-wild distribution shifts. ArXiv, 1–87. https://arxiv.org/abs/2012.07421 (2021)
Zhang, H. et al. An empirical framework for domain generalization in clinical settings. In ACM Conference on Health, Inference, and Learning (ACM CHIL ’21) 279–290 (ACM, 2021).
Gulrajani, I. & Lopez-Paz, D. In search of lost domain generalization. ArXiv https://arxiv.org/abs/2007.01434 (2020).
Rosenfeld, E., Ravikumar, P. & Risteski, A. The risks of invariant risk minimization. ArXiv https://arxiv.org/abs/2010.05761 (2020).
Rosenfeld, E., Ravikumar, P. & Risteski, A. An online learning approach to interpolation and extrapolation in domain generalization. arXiv (2021).
Wu, Y., Winston, E., Kaushik, D. & Lipton, Z. Domain adaptation with asymmetrically-relaxed distribution alignment. In Proceedings of the 36th International Conference on Machine Learning (eds Kamalika, C. & Ruslan, S.) 6872--6881 (PMLR, 2019).
Zhao, H., Combes, R. T. D., Zhang, K. & Gordon, G. On learning invariant representations for domain adaptation. In 36th International Conference on Machine Learning, ICML 2019 7523–7532 (PMLR, 2019).
Adeli, R. B. D. A. H. E. et al. On the Opportunities and Risks of Foundation Models. ArXiv 1–211. http://arxiv.org/abs/2108.07258 (2021).
Li, H., Li, W. & Wang, S. Discovering and incorporating latent target-domains for domain adaptation. Pattern Recognit. 108, 107536. https://doi.org/10.1016/j.patcog.2020.107536 (2020).
Che, Z., Cheng, Y., Zhai, S., Sun, Z. & Liu, Y. Boosting deep learning risk prediction with generative adversarial networks for electronic health records. In 2017 IEEE International Conference on Data Mining (ICDM) 787–792 (2017).
Pan, S. J., Tsang, I. W., Kwok, J. T. & Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 22, 199–210. https://doi.org/10.1109/TNN.2010.2091281 (2011).
Wu, H., Yan, Y., Ye, Y., Ng, M. K. & Wu, Q. Geometric knowledge embedding for unsupervised domain adaptation. Knowl.-Based Syst. 191, 105155. https://doi.org/10.1016/j.knosys.2019.105155 (2020).
Liang, J., Hu, D. & Feng, J. Domain adaptation with auxiliary target domain-oriented classifier. In 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 16627–16637 (2021).
Zou, Y., Yu, Z., Kumar, B. V. K. V. & Wang, J. Unsupervised domain adaptation for semantic segmentation via class-balanced self-training. In: Computer Vision—ECCV 2018. ECCV 2018 (eds Ferrari, V., Hebert, M., Sminchisescu, C. & Weiss, Y.) 297–313 (Lecture Notes in Computer Science, 2018).
Subbaswamy, A., Schulam, P. & Saria, S. Preventing failures due to dataset shift: Learning predictive models that transport. In Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics (eds Kamalika, C. & Masashi, S.) 3118--3127 (PMLR, 2019).
Manz, C. R. et al. Effect of integrating machine learning mortality estimates with behavioral nudges to clinicians on serious illness conversations among patients with cancer: A stepped-wedge cluster randomized clinical trial. JAMA Oncol. 6, e204759. https://doi.org/10.1001/jamaoncol.2020.4759 (2020).
Acknowledgements
LS is the Canada Research Chair in Pediatric Oncology Supportive Care.
Author information
Authors and Affiliations
Contributions
All authors conceptualized and designed the study. L.L.G., L.S., and A.J. acquired the data. L.L.G. and S.R.P. analyzed the data. All authors interpreted the data, drafted and revised the manuscript critically for important intellectual content, gave final approval of the version to be published, and agree to be accountable for all aspects of the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, L.L., Pfohl, S.R., Fries, J. et al. Evaluation of domain generalization and adaptation on improving model robustness to temporal dataset shift in clinical medicine. Sci Rep 12, 2726 (2022). https://doi.org/10.1038/s41598-022-06484-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-06484-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.