Abstract
We consider the case that four spin-3 atoms are confined in an optical trap. The temperature is so low that the spatial degrees of freedom have been frozen. Exact numerical and analytical solutions for the spin-states have been both obtained. Two kinds of phase-diagrams for the ground states (g.s.) have been plotted. In general, the eigen-states with the total-spin S (a good quantum number) can be expanded in terms of a few basis-states \(f_{S,i}\). Let \(P_{f_{S,i}}^{\lambda }\) be the probability of a pair of spins coupled to \(\lambda =0, 2, 4\), and 6 in the \(f_{S,i}\) state. Obviously, when the strength \(g_{\lambda }\) of the \(\lambda \)-channel is more negative, the basis-state with the largest \(P_{f_{S,i}}^{\lambda }\) would be more preferred by the g.s.. When two strengths are more negative, the two basis-states with the two largest probabilities would be more important components. Thus, based on the probabilities, the spin-structures (described via the basis-states) can be understood. Furthermore, all the details in the phase-diagrams, say, the critical points of transition, can also be explained. Note that, for \(f_{S,i}\), \(P_{f_{S,i}}^{\lambda }\) is completely determined by symmetry. Thus, symmetry plays a very important role in determining the spin-structure of the g.s..
Similar content being viewed by others
Introduction
It is recalled that, due to the realization of optical trapping about 20 years ago, the field of Bose–Einstein condensates has been greatly extended and the spin-degrees of freedom begin to play their roles. On the other hand, a notable progress in recent years is the technique in the trapping and manipulation of a few cold atoms (molecules)1. This technique could also extend the field greatly from traditional many-body systems to cold few-body systems. In the theoretical aspect, the former can only be solved approximately, while the latter can be solved exactly and detailed analysis on the spin-structures can be made. Thus the knowledge extracted from few-body systems would be a complement to those from many-body systems. Furthermore, for cold atoms, the temperature can be tuned so low (say, \({\text{ T }}<10^{-10}\) K) that the spatial degrees of freedom are nearly frozen. This leads to a kind of cold few-body systems having only spin-degrees of freedom. Note that all few-body systems are strongly constrained by symmetry so that the quantum states are governed by a few quantum numbers. Obviously, due to the difference in degrees of freedom, the effects of symmetry constraint imposing on usual and cold few-body systems are different (as shown in a previous paper2). Thus, the field of the study of few-body systems could also be thereby extended and rich physics would be involved. Therefore, the study of cold few-body systems, they are scarcely studied before, is meaningful.
For many-body systems, there are a number of literatures dedicated to the study of spin-13,4,5,6,7,8,9,10,11 and spin-2 cold atoms10,12,13,14,15,16,17,18,19. Those for spin-3 condensates are fewer, where the spin-structures appear to be complicated20,21,22,23,24,25,26. This paper, as a continuation of2, is dedicated to four-body systems with spin-3 cold atoms. The purpose is to find out the spin-structures of the ground states (g.s.). Note that the interaction contains four parameters \( \{g_{\lambda }\}\) (where \(\lambda \) is the coupled spin of two atoms). A negative \(g_{\lambda }\) would push a pair of atoms to form a [\(\lambda \)]-pair (\(\lambda =0\), 2, 4, and 6). We believe that, when \(g_{\lambda }\) is sufficiently negative, the [\(\lambda \)]-pairs would be important constituents. When two or more \(g_{\lambda }\) are negative, there is competition among them. We will see how the competition would be under the constraint from symmetry.
Spin-dependent Hamiltonian and the eigen-states
Let N spin-3 atoms (say, Cr, Mo, Sn, Pu) be confined in an optical trap. It is assumed that the temperature is so low and the binding is so strong that all the particles have condensed to a spatial state \(\phi (\mathbf {r})\) which is most favorable for binding. While all the spatial degrees of freedom are frozen, the spin-degrees of freedom remain free, therefore various spin-structures can be formed. These structures depend essentially on the spin-dependent Hamiltonian, which can be written as
where i (j) denotes a particle. \(\lambda =0\), 2, 4, and 6 is the coupled spin of a pair, \(P_{\lambda }^{ij}\) is the projector to the \(\lambda \) -channel. \(g_{\lambda }\) is the weighted strength which is a product of the strength and the integral \(\int \phi ^{4}d\mathbf {r}\). The latter embodies the effect of spatial profile. The dipole–dipole (d–d) coupling between a pair of atoms is relatively weak (for \(^{52}\)Cr as an example, the strength of the d–d coupling \(c_{dd}=0.004g_{6}\)), therefore is neglected. In fact, the calculation in21 demonstrates that the g.s. of \(^{52}\)Cr does not seem to depend on the d–d coupling. An important feature of \( H_{spin}\) is the conservation of the total spin S and its Z-component M . Thus the eigen-energies and eigen-states of \(H_{spin}\) are denoted as \( E_{SM}\) and \(\psi _{SM}\) (the subscript M might be neglected).
We introduce the Fock-states \(|\alpha \rangle \equiv |N_{3\alpha },N_{2\alpha },\ldots N_{-3,\alpha }\rangle \), where \(\alpha \) represents a set of seven numbers \(\{N_{\mu \alpha }\}\) (\(-3\le \mu \le 3\)), \(N_{\mu \alpha }\) is the number of particles in \(\mu \) magnetic component. Obviously, \(\Sigma _{\mu }N_{\mu \alpha }=N\) and \(\Sigma _{\mu }\mu N_{\mu \alpha }=M\). The Fock-states are adopted as basis-states for diagonalizing \(H_{spin}\). The matrix element is
where \(|\alpha ^{\prime }\rangle \equiv |N_{3\alpha }^{\prime },\cdot \cdot \cdot \rangle \), \(\delta _{\mu \nu }=1\) or 0 (if \(\mu =\nu \) or \(\ne \nu \) ), \(\overset{\_}{\delta }_{\mu \nu }=1-\delta _{\mu \nu }\), \(\delta _{[\beta ];[\alpha ]}=1\) (if all the seven numbers in \([\beta ]\) are one-to-one identical to those in \([\alpha ]\)) or 0 (otherwise), the Clebsch–Gordan coefficients have been introduced. Carrying out the diagonalization, \(E_{SM}\) together with
can be obtained. The total number of Fock-states is bound by N and M. Since no magnetic field is applied, S of an eigen-state can be known by its degeneracy. In particular, the lowest eigen-state (g.s.) is denoted as \(\Psi _{S(gs)}\) which we will focus on.
Spin-structures based on the pairs
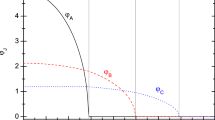
After the diagonalization of \(H_{spin}\), the parameter space can be divided into zones according to S, and the phase diagram thereby can be plotted. To reduce the complexity, we use three 2-dimensional subspaces to replace the 4-dimensional parameter space as shown in Fig. 1. In each of these subspaces \(g_{4}\) and \(g_{6}\) are variable, while \(g_{0}\) and \(g_{2}\) are fixed. There are three possible cases (1) \(g_{0}<g_{2}\), (2) \(g_{0}\simeq g_{2}\), and (3) \(g_{0}>g_{2}\). Note that the spin-structures will neither be changed when all the \(\{g_{\lambda }\}\) are shifted with the same value, nor when the unit for \(\{g_{\lambda }\}\) is changed. For case (1), let the set \(\{g_{\lambda }\}\) be shifted so that \((g_{0}+g_{2})/2=0\), then a unit is adopted so that \(g_{0}=-0.5\) and \(g_{2}=0.5\) (Fig. 1a). For case (2), as an approximation, we assume \(g_{0}=g_{2}\). Then, \(\{g_{\lambda }\}\) is shifted so that \(g_{0}=g_{2}=0\) (Fig. 1b). For case (3), similarly, we have \(g_{0}=0.5\) and \(g_{2}=-0.5\) (Fig. 1c). For all the three cases, the ranges of \(g_{4}\) and \(g_{6}\) are from \(-1\) to \(+1\). In the qualitative sense, the feature of a 4-dimensional diagram can be roughly illustrated via these three 2-dimensional diagrams.
To understand better the underlying physics, in addition to numerical solutions, we look for analytical solutions. Let

be a basis-state,where \(\mathfrak {S}\) is an operator for symmetrization and normalization, \( \chi (i)\) is the spin-state of the i-th particle, particles 1 and 2 (3 and 4) are coupled to \(\lambda _{a}\) (\(\lambda _{b}\)), \(\lambda _{a}\) and \( \lambda _{b}\) should be even and coupled to S. Note that
\(\overset{}{ \varphi }_{S;\lambda _{a}\lambda _{b}}\) has not yet been symmetrized, but  is. When S is fixed while \(\lambda _{a}\) and \(\lambda _{b}\) are variable, the set
is. When S is fixed while \(\lambda _{a}\) and \(\lambda _{b}\) are variable, the set  can also be used as (non-orthogonal) basis-states for \(\psi _{SM}\). It turns out that, for N = 4, the multiplicity of every \(\psi _{SM}\) is very small (\(\le 3\) ). Thus \(H_{spin}\) can be analytically diagonalized. Examples are given below.
can also be used as (non-orthogonal) basis-states for \(\psi _{SM}\). It turns out that, for N = 4, the multiplicity of every \(\psi _{SM}\) is very small (\(\le 3\) ). Thus \(H_{spin}\) can be analytically diagonalized. Examples are given below.
By recoupling the spins, we have

where
where \(\gamma \) is a coefficient for normalization, the quantity with {} is a 9-j symbol, and \(\overset{\_\_}{\lambda _{a}}\equiv \sqrt{2\lambda _{a}+1}\), etc.
The multiplicity of \(S=0\) states is two. Therefore, among the four basis-states  , it is sufficient to choose
, it is sufficient to choose  and
and  for the expansion of \(\psi _{SM}\). Other
for the expansion of \(\psi _{SM}\). Other  state is simply a linear combination of them. Note that these two basis-states are not exactly orthogonal to each other. Instead,
state is simply a linear combination of them. Note that these two basis-states are not exactly orthogonal to each other. Instead,  , where \(C_{0;\lambda \lambda ;\lambda ^{\prime }\lambda ^{\prime }}\) is given in the table.For \(S=0\) states, the associated matrix elements are
, where \(C_{0;\lambda \lambda ;\lambda ^{\prime }\lambda ^{\prime }}\) is given in the table.For \(S=0\) states, the associated matrix elements are

where the set \(\{C_{0;\lambda ^{\prime }\lambda ^{\prime };\lambda \lambda }\}\) are listed in the table:
The eigen-energy \(E_{0}\) is the root of a two-dimensional homogeneous linear equation,
Making use of Table 1, the eigen-energy of the lower \(S=0\) states is
where
The normalized spin-state of the lower \(S=0\) state is

where
\(a_{4}=1/\sqrt{1+x^{2}+2xO_{4,6}}\), \( x=(H_{4,4}-E_{0(-)})/(O_{4,6}E_{0(-)}-H_{4,6})\), and \(a_{6}=xa_{4}\).
The weight of  in \(\psi _{0(-)}\) is
in \(\psi _{0(-)}\) is  . Similarly, the weight of
. Similarly, the weight of  is equal to \( (a_{6}+a_{4}O_{4,6})^{2}\). If other
is equal to \( (a_{6}+a_{4}O_{4,6})^{2}\). If other  are chosen to replace
are chosen to replace  and/or
and/or  , the resultant \(E_{0(-)}\) and \(\psi _{0(-)}\) are not changed.
, the resultant \(E_{0(-)}\) and \(\psi _{0(-)}\) are not changed.
For \(S=2\) and 8 (both have multiplicity two), \(E_{S(-)}\) and \(\psi _{S(-)}\) can be similarly obtained. For \(S=4\) and 6 (both have multiplicity three), the analytical solutions are more complicated.
Whereas for \(S=3\), 5, 7, 9, 10 and 12 states, all of them have multiplicity one, thus the eigen-state is just  , where \(\lambda _{a}\) and \( \lambda _{b}\) are arbitrary even numbers adapted to S. For example, when \(S=7\) we choose \(\lambda _{a}=6\) and \(\lambda _{b}=4\), then we have
, where \(\lambda _{a}\) and \( \lambda _{b}\) are arbitrary even numbers adapted to S. For example, when \(S=7\) we choose \(\lambda _{a}=6\) and \(\lambda _{b}=4\), then we have

where \(C_{7;6,4;2,6}=.6362\), \(C_{7;6,4;4,6}=.3086\), \( C_{7;6,4;6,2}=-C_{7;6,4;2,6}\), \(C_{7;6,4;6,4}=-C_{7;6,4;4,6}\), otherwise \( C_{7;6,4;\lambda _{a}^{\prime }\lambda _{b}^{\prime }}=0\). The eigen-energy
The eigen-energies of other S-states with multiplicity can be similarly obtained.It is emphasized that, when other \(\lambda _{a}\) and \(\lambda _{b}\) are chosen, both \(\psi _{7M}\) and \(E_{S=7}\) remain the same. These states are strictly determined by symmetry. In particular, when \(S=3N\), we have \(E_{S=3N}=\frac{N(N-1)}{2}g_{6}\). With the help of the analytical solutions, the physics inherent in Fig. 1 can be better understood, we found
-
(1)
When \(g_{4}<0\) and \(g_{6}>0\) (up-left quadrant in Fig. 1) only \(S=0\) state is found.
Note that, when a \(g_{\lambda }\) is more negative than the others, two spins in the g.s. will prefer to be coupled to \(\lambda \) and form a [\(\lambda \)]-pair. Let \(\langle (\lambda _{a}\lambda _{b})_{S}|gs\rangle \) be a shortened label for the overlap
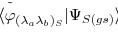 . We found that, at the point A (where \(g_{4}=-1\) and \(g_{6}=1\)) marked in Fig. 1a–c, \( \langle (4,4)_{0}|gs\rangle =0.9883\), 0.9996, and 0.9794, respectively. It implies that the g.s. is essentially composed of two [4]-pairs (due to the very negative \(g_{4}\)), and they are further coupled to zero, namely, they are lying opposite to each other (due to the very positive \(g_{6}\)). Besides, at C, B and A marked in Fig.1c (where \(g_{6}=0\), 0.5, and 1), \( \langle (4,4)_{0}|gs\rangle =\)0.9703, 0.9765, and 0.9883, respectively. It implies that, when \(g_{6}\) increases from 0, the structure (4,4)\(_{0}\) will be more dominant.
. We found that, at the point A (where \(g_{4}=-1\) and \(g_{6}=1\)) marked in Fig. 1a–c, \( \langle (4,4)_{0}|gs\rangle =0.9883\), 0.9996, and 0.9794, respectively. It implies that the g.s. is essentially composed of two [4]-pairs (due to the very negative \(g_{4}\)), and they are further coupled to zero, namely, they are lying opposite to each other (due to the very positive \(g_{6}\)). Besides, at C, B and A marked in Fig.1c (where \(g_{6}=0\), 0.5, and 1), \( \langle (4,4)_{0}|gs\rangle =\)0.9703, 0.9765, and 0.9883, respectively. It implies that, when \(g_{6}\) increases from 0, the structure (4,4)\(_{0}\) will be more dominant. -
(2)
When \(g_{4}\) and \(g_{6}\) are both negative (down-left quadrant), \(S=0\) , 8, and 12 states are found.
For Fig. 1c as an example, when \(g_{4}=-1\) and \(g_{6}=0\) (point C), \(-0.75\) (point D), and \(-1.1\), we found \(\langle (4,4)_{0}|gs\rangle =\)0.9703, \( \langle (4,4)_{8}|gs\rangle =0.966\), and \(\langle (6,6)_{12}|gs\rangle =1\), respectively. Thus S undergoes a transition as 0\(\rightarrow \)8\( \rightarrow \)12. It implies that the decrease of \(g_{6}\) causes first a change of the relative orientation of the two [4]-pairs (from being anti-parallel to parallel), then a succeeded breakdown of the [4]-pairs and leading to a full polarization. The transition of S takes place when either \(E_{0(gs)}=E_{8(gs)}\) or \(E_{8(gs)}=E_{12(gs)}\). Since the analytical expressions of the energies have been given, the critical points of transition can be analytically obtained.
-
(3)
In up-right quadrant with \(g_{4}>0\) and \(g_{6}>0\), if \(g_{0}\le 0\) (Fig. 1a,b), we found the [0]-pairs. For example,s at the point B, C and E in Fig. 1a, we have \(\langle (0,0)_{0}|gs\rangle =0.982\), 0.970, and 0.993, respectively. Whereas if \(g_{2}\le 0\) (1c) we found the [2]-pairs. For examples, at the point F2, E and F1, we have \(\langle (2,2)_{2}|gs\rangle =1.000\), \(\langle (2,2)_{2}|gs\rangle =0.993\), and \( \langle (2,2)_{4}|gs\rangle =\) 0.974, respectively. In these examples we see once more how the relative orientation of the two [\(\lambda \)]-pairs is adjusted by \(g_{6}\).
-
(4)
When \(g_{4}>0\) and \(g_{6}<0\) (down-right quadrant), the g.s. mostly has \(S=12\) and the g.s. is fully polarized.
-
(5)
Making use of the analytical solutions, all the boundaries in the phase diagrams can be analytically described via the equation \(E_{S(gs)}=E_{S^{ \prime }(gs)}\). For an example, in Fig. 1c, the boundary separating the zones with \(S=12\) and \(S^{\prime }=7\) satisfies \(g_{6}=0.1904,g_{4}=0.4048\). This explains why this boundary is a straight line up-rising slowly with \(g_{4}\).
Competition in the formation of pairs
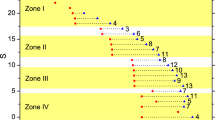
From the above section we know that, when a \(g_{\lambda }\) is more negative than the others, the [\(\lambda \)]-pairs will be important. The relative orientation of the spins of pairs depends on \(g_{6}\) and will be changed from being anti-parallel to parallel. It is expected that, when \(g_{\lambda } \) and \(g_{\lambda ^{\prime }}\) are both more negative, there would be a competition between the [\(\lambda \)]- and [\(\lambda ^{\prime }\)]-pairs. To clarify, we introduce another kind of phase diagrams as shown in Fig. 2.
The dominant component(s) in the spin-structure of the g.s. The label of the component \((\lambda _{a},\lambda _{b})_{S}\) is marked above the horizontal lines, each is for a given \(g_{6}\) marked at the left end of the line. For 2a, \(g_{0}=0\), the abscissa is for \(g_{4}\), and \(g_{2}=-1-g_{4} \). For 2b, \(g_{2}=0\), the abscissa is also for \(g_{4}\), and \(g_{0}=-1-g_{4}\). For 2c, \(g_{4}=0\), the abscissa is for \(g_{2}\), and \( g_{0}=-1-g_{2}\).
In Fig. 2a both \(g_{4}\) and \(g_{2}\) are negative, thus there is a competition between the [4]- and [2]-pairs
When \(g_{6}=-1\) (horizontal black line), due to the strong attraction caused by \(g_{6}\), no [\(\lambda \)]-pairs (\(\lambda \ne 6\)) would emerge. Instead, all the spins are aligned and the g.s. is fully polarized.
When \(g_{6}=-0.5\) (dash), both [4]-, [2]-, and [6]-pairs might emerge. When \( g_{4}<g_{2}\), the g.s. is dominated by (4,4)\(_{8}\) (say, when \(g_{4}=-0.75\), \(\langle (4,4)_{8}|gs\rangle _{g_{4}=-0.75} =0.966\)). There is a critical point p\(_{8\rightarrow 4}\) located at \(g_{4}=g_{2}=-0.5\), at which S transits from 8 to 4. Afterward, when \( g_{4}\) \((g_{2})\) increases (decreases) further so that \(g_{2}<g_{4}\), the g.s. is dominated by (2,2)\(_{4}\) (say, \(\langle (2,2)_{4}|gs\rangle _{g_{4}=-0.25}=0.967\)). Thus the negative \(g_{6}=-0.5\) is not sufficient to form the [6]-pairs, but sufficient to bring the spins of the two [4]-pairs or the two [2]-pairs to be parallel.
When \(g_{6}=0\) (dash–dot). Due to the vanish of the attraction from \(g_{6}\), the two [4]- or [2]-pairs are no more parallel. There is a critical point p\( _{0\rightarrow 2}\) (where \(g_{4}=-0.333\)) and a point of balance B\(_{1}\) (where \(g_{4}=-0.391\) ). When \(g_{4}<{\text{ p }}_{0\rightarrow 2}\), the g.s. is composed of (4,4)\(_{0}\) and (2,2)\(_{0}\). The pair (4,4)\(_{0}\) would be more important if \(g_{4}\) < B\(_{1}\), whereas (2,2)\(_{0}\) would be if \(g_{4}\) > B\(_{1}\), and they would arrive at a balance at B\(_{1}\), i.e., \(\langle (4,4)_{0}|gs\rangle _{g_{4}=-0.391}=\langle (2,2)_{0}|gs\rangle _{g_{4}=-0.391}=0.874\) (note: \( \langle (4,4)_{0}|(2,2)_{0}\rangle \ne 0\)). The point p\(_{0\rightarrow 2}\) marks the transition of S from 0 to 2. When \(g_{4}>{\text{ p }}_{0-2}\), the g.s. is essentially (2,2)\(_{2}\) (say, \(\langle (2,2)_{2}|gs\rangle _{g_{4}=-0.32}=0.986\), \(\langle (2,2)_{2}|gs\rangle _{g_{4}=-0.1}=1.000\)).
The case with \(g_{6}=0.5\) (solid line in orange) is similar to the case with \(g_{6}=0\), except p\(_{0\rightarrow 2}=-0.163\), and the balance point B\(_{2} =-0.274\). Thus, both p\(_{0\rightarrow 2}\) and B\(_{2}\) shift to the right.
When \(g_{6}=1\) (dot), the case is also similar to the above case, however the critical point shifts to the right and beyond the range \(-1{<} g_{4}\le 0\) (therefore it can not be seen). The repulsion caused by \(g_{6}\) is sufficiently strong so that the pairs kept to be anti-parallel, and therefore the g.s. is composed of \((4,4)_{0}\) and \((2,2)_{0}\) with the balance point B\(_{3}\) at \(g_{4}=-0.157\). Say, \(\langle (4,4)_{0}|gs\rangle _{g_{4}=-1}=1.000\), \(\langle (4,4)_{0}|gs\rangle _{g_{4}=-0.157}=\langle (2,2)_{0}|gs\rangle _{g_{4}=-0.157}=0.874\), and \(\langle (2,2)_{0}|gs\rangle _{g_{4}=0}=0.942\).
We found B\(_{1}< {\text{ B }}_{2}< {\text{ B }}_{3}\). Note that, when \(g_{6}\) is positive, the formation of [6]-pairs is unfavorable to the energy. Let the probability of two spins coupled to \(\lambda \) in a state \(\Phi \) be \(\ P_{\Phi }^{\lambda }\). Then, \(P_{(\lambda \lambda )_{0}}^{6}=(C_{0;\lambda \lambda ;6,6})^{2}=(0.4598)^{2}\) (if \(\lambda =2\)) and \(=(0.0540)^{2}\) (if \( \lambda =4\)). Thus the appearance of the [6]-pairs in (4,4)\(_{0}\) is much less probable than in (2,2)\(_{0}\). Therefore, the structure (4,4)\(_{0}\) would be more favorable than (2,2)\(_{0}\) when \(g_{6}\) becomes more positive. This explains the reason that the balance point shifts to the right.
Furthermore, when \(g_{6}\) increases, the critical point also shifts to the right. This is due to a similar reason that the appearance of the [6]-pairs in (2,2)\(_{0}\) is less probable than in (2,2)\(_{2}\).
In Fig. 2b both \(g_{0}\) and \(g_{4}\) are negative.
Figure 2b is comparable with Fig. 2a, but the following distinctions are noticeable.
-
(1)
In this case the [0]-pairs and [4]-pairs are competing. Accordingly, when \(g_{6}\ge 0\), the two important and competing component are (4,4)\(_{0}\) and (0,0)\(_{0}\) (rather than (2,2)\(_{0}\)).
-
(2)
When \(g_{6}\ge 0\), \(g_{0}\) and \(g_{4}\) are both negative. Thus, both the [4]-pair and [2]-pair are important and they are competing. Meanwhile, \( g_{6}\) is sufficiently positive to keep the two [\(\lambda \)]-pairs anti-parallel so that S is kept to be zero and the transition of S from 0 to 2 does not appear.
-
(3)
When \(g_{6}\) becomes negative, there is competition among the [6], [4], and [0]-pairs. Say, when \( g_{6}=-0.5\) and \(-0.51<g_{4}<-0.29\), the [6]-pairs emerge in the middle segment of the dash-line. They will be changed to the [4]-pairs if \(g_{4}\) becomes more negative, or to the [0]-pairs if \(g_{0}\) becomes more negative. For the dash-line, due to the negative \(g_{6}\), either the two [4]-pairs or the two [6]-pairs are parallel to each other. This leads to the transition of S as \(8\rightarrow 12\rightarrow 0\) when \(g_{4}\) increases (\(g_{0}\) decreases).
-
(4)
The shift of the balance point to the right appears again (i.e., B\(_{1} {<} {\text{ B }} _{2}< {\text{ B }}_{3}\)). Note that \(C_{0;0,0;6,6}=0.5245\). Thus the appearance of the [6]-pairs in (4,4)\(_{0}\) is also much less probable than in (0,0)\(_{0}\). This causes the shift as before.
In Fig. 2c both \(g_{0}\) and \(g_{2}\) are negative.
When \(g_{6}=-1\), the g.s. is fully polarized as before. Otherwise, the g.s. is essentially composed of \((2,2)_{\lambda _{b}}\) and \((0,0)_{0}\) (where \( \lambda _{b}=4\), 2, and 0). When \(g_{6}=-0.5\) we see a chain of transitions: S=\(4\rightarrow 2\rightarrow 0\rightarrow 12\rightarrow 0\).When \(g_{0}\), \(g_{2}\) and \( g_{6}\) are all close to \(-0.5\), there is a small segment in bold black line where (6,6)\( _{12}\) emerges (similar to the case in Fig. 2b). When \(g_{6}=0,\) 0.5, and 0.8 (dotted line), we see the transition of \(S=2\rightarrow 0\). Where the critical point shifts to the left when \(g_{6}\) increases. It implies that the appearance of the [6]-pairs in (2,2)\(_{0}\) is less probable than in (2,2)\( _{2}\). Whereas the balance point shifts to the right when \(g_{6}\) increases. It implies that the appearance of the [6]-pairs in (2,2)\(_{0}\) is less probable than in (0,0)\(_{0}\).
Final remarks
The spin-structures of \(N=4\) condensates have been studied, both numerical and analytical solutions have been obtained. Thereby two kinds of phase-diagrams for the g.s. have been plotted and explained. From dynamical aspect, the [\(\lambda \)]-pairs would be important constituents when \( g_{\lambda }\) is more negative. However, the probability of the appearance of a [\(\lambda \)]-pair in a particular component \((\lambda _{a}\lambda _{b})_{S}\) is determined by symmetry. Thus the structure of the g.s. depends not only on the strengths but also on the symmetry constraint. We have calculated the probabilities \(P_{(\lambda _{a}\lambda _{b})_{S}}^{\lambda }\) for finding out the important components. The importance is further confirmed by the calculation of the amplitudes \( \langle (\lambda _{a}\lambda _{b})_{S}|\Psi _{S(gs)}\rangle \). Obviously, for cold few-body systems, the very small multiplicity of a state is a remarkable feature, thereby the states are tightly (or even completely) constrained by symmetry.
When two or more \(g_{\lambda }\) are negative and close to each other, there is competition between various [\(\lambda \)]-pairs and the most important pair is thereby determined. Note that the magnitude of S depends on the relative orientation of the pair-spins \(\lambda _{a}\) and \( \lambda _{b}\) (if they are nonzero), while the orientation is determined by the strengths. In particular, the sign of \(g_{6}\) is crucial which determines whether the two pair-spins are parallel or anti-parallel. Thus the variation of \(\{g_{\lambda }\}\) will cause the change of the most important pair and the relative orientation of the pair-spins. This leads to the shift of the balance point and the critical point. The chain of transitions is thereby explained.
The approach of this paper can be generalized to systems with a larger N. When N is larger, if \(g_{\lambda }\) is more negative, the [\(\lambda \)]-pairs would also be more important in the g.s. There would also be competitions among various [\(\lambda \)]-pairs. The study of the probability \(P_{\Phi }^{\lambda } \) where \(\Phi \) is an assumed basis-state would also be helpful for finding out the important component(s) and their alternation. In particular, some very stable spin-structures found in few-body systems could be building blocks for large N systems. This is a point to be clarified.
References
Meyer, G. et al. Controlled manipulation of atoms and small molecules with a low temperature scanning tunneling microscope. Single Molecules 1(1), 79 (2000).
Liu, Y. M., He, Y. Z. & Bao, C. G. A stable spin-structure found in a 3-body system with spin-3 cold atoms and its role in N-body condensates. Sci. Rep. 11, 1792 (2021).
Stenger, J. et al. Spin domains in ground-state Bose–Einstein condensates. Nature 396, 345 (1998).
Stamper-Kurn, D. M. et al. Optical confinement of a Bose–Einstein condensate. Phys. Rev. Lett. 80, 2027 (1998).
Ho, T. L. Spinor Bose condensates in optical traps. Phys. Rev. Lett. 81, 742 (1998).
Ohmi, T. & Machida, K. Bose–Einstein condensation with internal degrees of freedom in alkali atom gases. J. Phys. Soc. Jpn. 67, 1822 (1998).
Law, C. K., Pu, H. & Bigelow, N. P. Quantum spins mixing in spinor Bose–Einstein condensates. Phys. Rev. Lett. 81, 5257 (1998).
Goldstein, E. V. & Meystre, P. Quantum theory of atomic four-wave mixing in Bose–Einstein condensates. Phys. Rev. A 59, 3896 (1999).
Ho, T. L. & Yip, S. K. Fragmented and single condensate ground states of spin-1 bose gas. Phys. Rev. Lett. 84, 4031 (2000).
Koashi, M. & Ueda, M. Exact Eigenstates and magnetic response of spin-1 and spin-2 Bose–Einstein condensates. Phys. Rev. Lett. 84, 1066 (2000).
Li, Z. B., Yao, D. X. & Bao, C. G. Spin-thermodynamics of ultra-cold spin-1 atoms. J. Low Temp. Phys. 180, 200 (2015).
Ciobanu, C. V., Yip, S. K. & Ho, T. L. Phase diagrams of F = 2 spinor Bose–Einstein condensates. Phys. Rev. A 61, 033607 (2000).
Ueda, M. & Koashi, M. Theory of spin-2 Bose–Einstein condensates: Spin correlations, magnetic response, and excitation spectra. Phys. Rev. A 65, 063602 (2002).
Van, Isacker P. & Heinze, S. Bose–Einstein condensates of atoms with arbitrary spin. J. Phys. A Math. Theor. 40, 14811 (2007).
Chacon, E., Moshinsky, M. & Sharp, R. T. U(5)\(\subseteq \)O(5)\( \subseteq \)O(3) and the exact solution for the problem of quadrupole vibrations of the nucleus. J. Math. Phys. 17, 668 (1976).
Gheorghe, A. & Raduta, A. A. New results for the missing quantum numbers labelling the quadrupole and octupole boson basis. J. Phys. A Math. Gen. 37, 10951 (2004).
Kawaguchi, Y. & Ueda, M. Spinor Bose–Einstein condensates. Phys. Rep. 520, 253 (2012).
Stamper-Kurn, D. M. & Ueda, M. Spinor Bose gases: Symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 85, 1191 (2013).
He, Y. Z., Liu, Y. M. & Bao, C. G. Generalized Gross–Pitaevskii equation adapted to the U(5)\(\supset \)SO(5)\(\supset \) SO(3)symmetry for spin-2 condensates. Phys. Rev. A 91, 033620 (2015).
Santos, L. & Pfau, T. Spin-3 chromium Bose–Einstein condensates. Phys. Rev. Lett. 96, 190404 (2006).
Makela, H. & Suominen, K.-A. Ground states of spin-3 Bose–Einstein condensates for conserved magnetization. Phys. Rev. A 75, 033610 (2007).
Uchino, S., Otsuka, T. & Ueda, M. Dynamical symmetry in spinor Bose–Einstein condensates. Phys. Rev. A 78, 023609 (2008).
Huhtamaki, J. A. M. et al. Spin textures in condensates with large dipole moments. Phys. Rev. A 81, 063623 (2010).
Pasquiou, B. et al. Thermodynamics of a Bose–Einstein condensate with free magnetization. Phys. Rev. Lett. 108, 045307 (2012).
Situ, S. P. & He, Y. Z. The spin evolution of spin-3 \(^{52} \) Cr Bose–Einstein condensate. Chin. Phys. B 20, 010310 (2011).
He, Y. Z., Chen, Z. F., Li, Z. B. & Bao, C. G. Evaluation of the 52Cr–52Cr interaction via spin–flip scattering. Few-Body Syst. 46, 257 (2009).
Acknowledgements
Supported by the National Natural Science Foundation of China under Grants nos. 11372122 and 10874122; Key Scientific Research Platforms and Projects of Ordinary Universities of Guangdong of China (2020KCXTD024).
Author information
Authors and Affiliations
Contributions
Y.M.L. is for theoretical derivation and numerical calculation, C.G.B. propose the idea and write the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Y.M., Bao, C.G. Spin structures of the ground states of four body bound systems with spin 3 cold atoms. Sci Rep 11, 17999 (2021). https://doi.org/10.1038/s41598-021-97521-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-97521-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



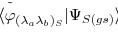 . We found that, at the point A (where
. We found that, at the point A (where 