Abstract
Aurora kinase B plays an important role in the cell cycle to orchestrate the mitotic process. The amplification and overexpression of this kinase have been implicated in several human malignancies. Therefore, Aurora kinase B is a potential drug target for anticancer therapies. Here, we combine atom-based 3D-QSAR analysis and pharmacophore model generation to identify the principal structural features of acylureidoindolin derivatives that could potentially be responsible for the inhibition of Aurora kinase B. The selected CoMFA and CoMSIA model showed significant results with cross-validation values (q2) of 0.68, 0.641 and linear regression values (r2) of 0.971, 0.933 respectively. These values support the statistical reliability of our model. A pharmacophore model was also generated, incorporating features of reported crystal complex structures of Aurora kinase B. The pharmacophore model was used to screen commercial databases to retrieve potential lead candidates. The resulting hits were analyzed at each stage for diversity based on the pharmacophore model, followed by molecular docking and filtering based on their interaction with active site residues and 3D-QSAR predictions. Subsequently, MD simulations and binding free energy calculations were performed to test the predictions and to characterize interactions at the molecular level. The results suggested that the identified compounds retained the interactions with binding residues. Binding energy decomposition identified residues Glu155, Trp156 and Ala157 of site B and Leu83 and Leu207 of site C as major contributors to binding affinity, complementary to 3D-QSAR results. To best of our knowledge, this is the first comparison of WaterSwap field and 3D-QSAR maps. Overall, this integrated strategy provides a basis for the development of new and potential AK-B inhibitors and is applicable to other protein targets.
Similar content being viewed by others
Introduction
The Aurora kinase family is a group of serine/threonine kinases that regulate various aspects of mitosis including centrosome duplication, chromosomal rearrangement spindle formation, activation of mitotic checkpoint and cytokinesis1,2. Any kind of disturbance in these processes eventually leads to cell death or aneuploidy. Human aurora kinases are functionally and structurally categorized into three subtypes, aurora A, B and C. All three isoforms contain a conserved catalytic domain, a variable N-terminal domain, and a short C-terminal extension. Despite significant similarity among these kinases, the location and functions are different from one another3,4,5,6,7.
Aurora A is found on chromosome 20q13.2 (a region amplified in various cancers) and expressed in initial mitosis at G2/M phase. Ajuba, BRCA-1, CDC25B, Eg5, TPX2 and p53 are reported as substrates for Aurora A kinase It is necessary for multiple key events in cell division including maturation of centrosome, segregation and assembly of spindles8,9. It acts as an oncogene and its over expression is found in several tumours such as colon, breast, pancreatic, ovarian and bladder cancers10,11,12. Aurora B is located on 17p13 chromosome and acts as a chromosomal passenger protein13 along with its two substrates, INCENP and Survivin14,15,16. Each of these proteins is required for AK-B to correct chromosome location in mitosis process. Similar to AK-A, it regulates different processes in mitosis. AK-B activity is based on the phosphorylation of its residue Thr232 and Ser10 of its substrate Histone H315,16. necessary for accurate completion of mitosis Inhibition of AK-B activity can lower the H3 phosphorylation, as a result of which improper condensation of chromosome and in-complete cytokinesis occurs, ultimately leading to cell apoptosis. Its over-expression is found in multiple human cancers such as mesothelioma, malignant endometrium, glioblastoma, non-small cell lung carcinoma, hepatocellular carcinoma, testicular germ cell tumours, oral cancer, thyroid, ovarian, colorectal and prostate cancer17,18,19,20.
Aurora kinase C particularly is found in the testes and plays an important role in spermatogenesis and regulates the movement of flagella and cilia21.
Structurally, Aurora kinases are comprised of three domains: the N-terminal domain, followed by a conserved kinase domain, and a C–terminal domain. The N-terminal domain exhibits sequence dissimilarity thus providing selectivity for protein–protein interactions. The kinase domain constitutes a β-stranded lobe and an α-helical lobe on the N-terminal and C-terminal respectively connected by a hinge region. The autophosphorylation of Thr 288 (AurA), Thr232 (AurB) and Thr195 (AurC) in the catalytic T-loop region of the kinase domain’s C-terminal lobe results in conformational changes thereby activating the kinase domain22,23. Aurora kinases are considered as potential drug targets for tumour remedy due to their strong association with tumorigenesis24.
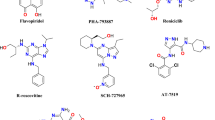
A number of small molecules inhibitors against AK-B have been reported to date. A classification for such compounds has been reported by Yan and colleagues who utilized a machine learning algorithm (Self-Organizing Map and Support Vector Machine) to classify Aurora kinase inhibitors into three classes, namely dual Aurora-A and Aurora-B inhibitors, Aurora-A selective inhibitors and selective inhibitors of Aurora-B25. Aurora kinases are effectively inhibited in numerous preclinical cell line and animal models. Several small molecule inhibitors have been developed and are indifferent stages of clinical trials. Uptil now only ten clinical trials have been reported, using inhibitors targeting specifically AK-B and most of them are still in phase I stage26 such as AK-B selective inhibitors Barasertib (AZD1152)27,28,29,30,31, Chiauranib32,33, BI84732534, PF-0381473535,36, GSK107091637,38,39, TAK-90140 and hesperidin41 and the pan Aurora A/B inhibitors VX-68019 and ZM44743917,18,19,29. Most of these inhibitors are ATP-competitive with a planar heterocyclic ring system that can reside in the adenine-binding region and mimic adenine–kinase interactions. These inhibitors are derivatives of indole, bis-indole, pyrrolopyrazole, pyrimidine, thiazolo-quinazoline, quinazolin, pyrazoloquinazoline, fused tricyclic structures, and some other structures42. In addition, the prospect of designing potent allosteric inhibitors for AK-B appears very promising from the clinical perspective, because it may generate selective inhibitors43. Recently, Colombo and colleagues proposed a new possibility in pursuit of designing selective chemical tools by perturbing the intermolecular interaction between chaperone and kinases thus, targeting protein folding and rendering it inactive44. Unfortunately, despite intensive efforts, no small molecule inhibitor of AK-B has been approved by the FDA, thus demanding the development of new inhibitors.
In the current study, a multiplex computational approach including molecular docking, 3D-QSAR, pharmacophore-based screening, MD simulation and binding free energy calculation was performed to investigate the binding mechanism of AK-B inhibitors. The 3D-QSAR model was built using CoMFA and CoMSIA approaches to explore the structural requirements of inhibitors impacting their inhibitory activities. Furthermore, to investigate the conformation and contribution of key residues to the potency of compounds, docking, MD simulations and binding free energy calculations were performed. In this study our main focus is to demonstrate a combined computational approach: the combination of QSAR with simulation, specifically in combination with the WaterSwap45 method. This is first such combined application according to best of our knowledge. By understanding the binding mode of aurora kinase B inhibitors, we can get deeper insights into the structural requirements that may produce more selective and potential AK-B inhibitors.
Materials and methods
Data set
A structurally diverse dataset of 57 compounds was collected from literature to perform 3D-QSAR studies probing the effect of inhibition against AK-B46,47. On the basis of structural diversity and activity, 45 out of 57 compounds were randomly selected as the training set however, the remaining 12 compounds were used as the test set. The training set was used to build the 3D-QSAR model while the test set compounds were used for the verification of the developed models. The test compounds evenly covered the range of biological activity and structural diversity of the dataset. Observed biological activities (IC50) were changed to negative logarithm (pIC50) before 3D-QSAR model generation. The chemical structures and the experimental activities of compounds are presented in Table S1 (supplementary material).
Structure preparation
The crystal structures of Aurora kinase B crystallized with inhibitors were taken from the protein data bank (Table 1). The structure preparation was performed in MOE48 and the missing loops, steric clashes and missing atom names were corrected. The hydrogen atoms were added, water molecules were removed, and the energy minimization was performed using Amber99 force field. The protonation state of every titratable residue within the complexes was assigned at physiological conditions using the Protonate-3D module of MOE48 and their conformations were produced with default parameters by using the Conformation Search option. Finally, the protein complex was minimized (giving a RMSD of 0.3 Å by selecting heavy atoms) using the force field AMBER9949,50.
Pharmacophore modeling
The MOE option in LigandScout56 was used to build the pharmacophore models on the basis of available crystal structures of AK-B complex (Table 1). Hydrophobic (HY), hydrogen-bond donor (HBD), hydrogen-bond acceptor (HBA) and exclusion volume features were considered for the generation of pharmacophore model. Numerous pharmacophore models were generated with significant statistical parameters. The best model was designated on the basis of a good correlation coefficient (r) and rmsd values. Moreover, the developed model was further validated by actives, decoys and random sets of molecules.
Molecular docking
The MOE software package (Molecular Operating Environment, 2015.01) was used to perform docking. The crystal structure of human AK-B complex (PDB ID: 4AF3) was retrieved from the Protein Data Bank51 and used for docking studies as it is the only available crystal structure of human Aurora kinase B. The generated conformations were minimized using the MMFF94 × force field (Merck Molecular Force Field 94 × gradient: 0.05 kcal/mol). The Triangle Matcher placement method was used for molecular docking with London dG and Generalized-Born Volume Integral/Weighted Surface area (GBVI/WSA) scoring function48. All compounds presented in Table S1 were docked successively in the binding cavity of AK-B using default parameters. The lowest score docked pose of every compound was considered for protein–ligand interactions and QSAR modeling.
CoMFA and CoMSIA analysis
The CoMFA57 potential fields (steric and electrostatic) were calculated at every point of regular grid spacing lattice of 2.0 Å. A probe of sp3 carbon atom was used to calculate the electrostatic and steric field energies with contributions trimmed to 30 kcal/mol and the remaining default parameters were used. For CoMSIA58 studies, five different descriptor fields such as electrostatic (E), steric (S), hydrophobic (H), hydrogen bond donor (HBD) and acceptor (HBA) were calculated. Descriptors used for CoMSIA were obtained by the same lattice box as used for CoMFA method. Both CoMFA and CoMSIA methods use the same function depicted by Gaussian function and raises the hydrogen bond donor, acceptor and hydrophobic fields. CoMSIA results illustrate a comparatively small effect from molecule corresponding rules and can more instinctively clarify a compound's SAR relationship. The intrinsic defects of CoMFA method can be overcome by CoMSIA method but this does not essentially obtain better results59. Thus, in the current study, CoMFA and CoMSIA methods can validate and complement each other to achieve consistent predicted models.
Partial least square analyses (PLS)
To associate the CoMFA or CoMSIA fields of 3D-QSAR utilizing AK-B inhibitors and their biological activities, partial least square (PLS) analysis (regression analysis) was performed. The optimal number of components that produces most promising extrapolative models was recognized by using cross-validation leave-one-out (LOO) method. The column filtering value was set at 2.0 kcal/mol to make better signal to noise ratio, by removing some lattice points, with less difference in energy than threshold value. The PLS analysis was performed using no column filtering with non-cross-validation method. The mean values for cross-validation correlation coefficient q2 and the resultant standard error of prediction (SEP) values were achieved by reiterating every random run of cross-validation.
Validation of CoMFA and CoMSIA models
The robustness and internal prediction power of the generated models was assessed by cross-validation leave one out (LOO) method. The q2 and r2 values showed the internal prediction power and sturdiness of the model respectively. The average values of r2 (rboot2) and SEE (SEE boot)) were calculated, a bootstrapping analysis of 60 runs was also performed to measure the biasness of the calculation. It has been reported that only q2 value is not enough to assess the predictive quality of 3D-QSAR model thus external validation must be applied. For this purpose, a total of eleven test set compounds that were not utilized previously to build the QSAR model were used for the external validation. The external test set validation is considered as the most reliable validation method to evaluate the extrapolative capability of the developed model. The predictive ability of CoMFA and CoMSIA models was assessed externally by forecasting the biological activity of independent set of test compounds. The model prediction power was expressed by r2 (rpred2 > 0. 6), variance in prediction (Qext2 > 0. 5), standard error of prediction (SEP) and external standard deviation error of prediction (SDEPext).
The given equation was used to calculate \(R_{pred}^{2}\).
where PRES indicates the sum of squared deviations between biological and predicted activity values while SD indicate the sum of squared deviations between average biological activity of compounds in the training set and experimental activity of the test set compounds.
The cross-validated coefficient (q2) was calculated by the following given formula:
where yi and \(\tilde{y}_{i}\) are the experimental and the predicted values, respectively; and \(\overline{y}\) is the averaged value for the variables of the training set.
Molecular dynamics simulations
To test the stability of the docked complexes, and for insight into the binding interactions in the inhibitor complexes, molecular dynamic simulations were performed with the AMBER 12 simulation software package49 using the ff14SB60 and ff99SB force field61. The Acyl-54 (most active), Acyl-24 (inactive), ZINC11253730, ZINC42019540, ZINC65618522 and ZINC07046484 compounds bound in target structures were obtained from molecular docking, as described above. The atomic charges of the compounds were calculated based on the electrostatic potential from single point HF/6-31G* calculations using Gaussian 03 and fitted using RESP in the Antechamber module62. The GAFF force field63 was used to parametrize the compounds. LEaP module was used to assign Hydrogen atoms by setting default protonation states of ionizable residues at a neutral pH. The systems were solvated using the TIP3P water model and a minimum of 10 Å solute-wall distance was used to cover every complex. Each complex was neutralized with chloride counter ions. The solvated systems were energy minimized by following two stages of steepest descent algorithm and conjugate gradient algorithm. The molecular dynamic simulations were performed using heating, density equilibration and production run in Berendsen isothermal isobaric ensemble MD. The systems were gradually heated up to 300 K in 500 ps at constant volume and constant pressure (1 atm) with a Langevin thermostat that was used to maintain a temperature of 300 K. While an isotropic pressure scaling algorithm was used to maintain the pressure of 1 bar, using a pressure relaxation time of 1 ps. Then every system underwent production run of 200 ns. The particle mesh Ewald method was used for calculating long-range electrostatic interactions, with a 10 Å cutoff. The SHAKE algorithm was used to constrain bonds involving hydrogen atoms to their equilibrium length. After equilibration, coordinates were saved every 50 ps. These collected trajectories were used for structural and energetic analysis of each system.
Binding free energy calculations
Binding free energy of all systems was calculated by two different methods: WaterSwap45,64 and MM(PB/GB)SA65. WaterSwap is an absolute binding free energy method that avoids the cavitation and some other issues of double-decoupling methods45. WaterSwap calculates the free energy for exchanging a bound ligand with a flexible water cluster of similar shape and size. The free energy difference is calculated by Monte Carlo replica exchange simulations along the Water Swap Reaction Coordinate. It uses an explicit treatment of water, so includes the detail of protein–water, protein–water–ligand and ligand–water interactions that are missing in continuum solvent methods64. WaterSwap uses a reaction coordinate which swaps the bound ligand with an equivalent volume and shape of water, moving the ligand from the protein into bulk solvent, with simulations at points along this WaterSwap Reaction Coordinate, using a dual topology algorithm. It uses an identity constraint66 to define the water cluster: this identity constraint places identity points in space instead of labelling water molecules to define water molecules in the binding site. The absolute binding free energy is calculated by replica exchange thermodynamic integration method67. The end points are a pair of simulation boxes (coupled to the same thermostat), one being a water box (box of water molecules) and the other is protein box contain protein–ligand complex solvated in periodic boundary box of explicit water molecules.
With the identified cluster, the total energy of the system is assessed using the following equation,
where Eproteinbox is the energy of all the molecules in the protein box except the ligand, Ewaterbox is the energy of all the molecules except the water cluster identified in the water box, Eligand represents the intramolecular energy of the ligand, Ecluster is the intermolecular energy between all the water molecules present in the water cluster, Eligand:protein box is the energy of interaction between the ligand and all atoms of the protein box, Ecluter:water box is the resultant energy of interactions between all water molecules and water clusters of the water box, λ is the WaterSwap Reaction Coordinates, used to scale Ecluster:water box by 1 − λ.
The decoupling of the ligand from the protein box is associated with decoupling of water cluster from water box. Simultaneously, cluster of water coupled to the protein box and ligand is coupled to the water box. This energy calculation between water molecules and the ligand in the protein box is represented by Eligand:water box, and the molecules and water cluster in the box is presented as Ecluster:protein box and scaling by λ. The λ is a single coordinate reaction that is changed from λ = 0 (ligand bound to the protein in protein box) to λ = 1 (unbound ligand and is in bulk water). Moreover, it corresponds to a transferred of water cluster to the protein box for filling the resulting cavity.
The absolute binding free energy is calculated by thermodynamic integration (TI) using the gradient of energy calculations with respect to λ,
The ensemble average is calculated at different values of λ to obtain free energy gradient across λ,
To get average free energy gradients, Monte Carlo (MC) sampling for each λ must be achieved. The binding free energy is finally obtained by integrating the gradient across λ,
WaterSwap calculations of absolute binding free energy were performed with the Sire package using the WSRC module45, these calculations used the same forcefield and solvent model as in the molecular dynamics simulations67. For each system, five WaterSwap calculations were performed of absolute binding free energies. The starting structures for WaterSwap calculation taken from clustering of the 100 ns trajectories. Errors were calculated from standard errors on these averages. The WaterSwap binding free energies were calculated by replica-exchange thermodynamic integration over 16 λ windows (0.005, 0.071, 0.137, 0.203, 0.269, 0.335, 0.401, 0.467, 0.533, 0.599, 0.665, 0.731, 0.797, 0.863, 0.929, 0.995) across the WaterSwap Reaction Coordinate. For each window, 50 million Monte Carlo steps were performed, and absolute free energies calculated by Free Energy Perturbation (FEP), Thermodynamic Integration (TI), and Bennetts algorithm, from the free energy gradient calculated over the last 30 million steps. The “Set A” soft-core parameters are used in the simulations with 15 Å Lennard–Jones and coulomb non-bonded cutoff, the shifted force field used to account long range electrostatics and reflection sphere used to restrict sampling within 15 Å radius of compound. VMD 1.9.168 used to visualize the trajectories. Analysis and visualization were carried out with alignment of protein backbone using RMSD tool in VMD.
The binding free energy of the system was also calculated separately by a completely different approach, namely the MM(PB/GB)SA method implemented in AMBER 1669. This is an implicit solvent approach, which can give useful results in some cases. 1000 frames were extracted from the simulation trajectories and MMPBSA.py module of AMBER was used for calculation analysis. In the MM(PB/GB)SA approach, the binding free energy is calcualted as the difference between the free energy of complex, and that of the ligand and receptor.
Furthermore, the binding free energy was decomposed into residue contributions to identify amino acids that contribute to binding affinity70,71. The binding interaction of each inhibitor–residue pair includes four terms:
where the van der Waals contribution (ΔGvdw) and the electrostatic contribution (ΔGele) are calculated using the Pmemd.cuda program72 in Amber 16. The nonpolar solvation contribution (ΔGnonpol) is the contribution of nonpolar to the solvation free energy and calculated from the solvent accessible surface area (SASA) model by the LCPO method: (ΔGSA = 0.0072 × ΔSASA). The polar solvation contribution (ΔGpol) was computed using the generalized Born module in Amber16.
Results and discussion
Molecular docking
Before starting the docking, all available crystal structures of AK-B protein were assessed to evaluate the degree of similarity in their binding sites. The results indicate that most of the binding site residues are conserved within the binding site (Figure S1). After evaluating the degree of similarity, all compounds were docked to the binding site of 4AF3 protein. The docking produced 30 conformations for each compound. The clusters were examined, and the final docked conformation was selected on the basis of scores. The binding pocket of AK-B is composed of residues Leu83, Phe88, Val91, Ala157 and Leu207. The docked conformation of VX-680, which is a cognate ligand of aurora kinase B, is shown in the Fig. 1. It was observed that compound acyl-54 was well located within the binding pocket of AK-B and showed similar type of interaction with the active site residues of AK-B as presented by cognate ligand. The amino group of Ala157 forms two hydrogen bonds with pyrazolidine and linker nitrogen of VX-680 at a distance of 1.92 and 2.39 Å. Additionally Leu83, Val91 and Phe88 are involved in hydrophobic interaction while Phe88 forms pi–pi interaction with the benzene ring of VX-680. In case of acyl-54, a hydrogen bonding interaction is found between amino group of Ala157 and carbonyl group of acyl-54 at a distance of 1.85 Å. Another hydrogen bond is found between Glu155 and NH group of Acyl-54 at a distance of 3.05 Å. These hydrophilic interactions have been already reported in the literature73. As well as docking with the 4AF351 structure, the selected compounds were also docked to the active site of other AK-B crystal structures (Table 1). Further, these docked conformations were used in receptor-guided 3D-QSAR studies.
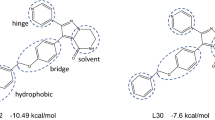
Docking of compounds into the binding site of Aurora kinase B. (A) Compound VX-680, (B) Acyl-54. Compounds and active site residues for Ligands and the important residues for binding interaction are represented by stick and line models 1 (A), while in 1 (B) non-polar and polar residues are presented in green and pink circles; hydrogen bond interaction is indicated by green dotted arrows; the shape of the binding site indicated by the proximity contour (dotted lines) surrounding the ligand.
Molecular alignment
In CoMFA and CoMSIA studies, 3D structures of the molecules are required to be aligned based on a suitable conformational template and its substructure, which taken as a “bioactive” conformation. Molecular alignment based on the common scaffold has been extensively used74,75; conversely it is thought to be more reasonable if the model is developed and evaluated on the active conformations. Moreover, the alignment based on docked conformations will help in the contour map analysis of the models in a structure-based manner. In the present study, molecular alignment was achieved via molecular docking (Fig. 2). As a result, all the compounds were aligned in the active site for building 3D-QSAR models.
CoMFA and CoMSIA statistics
The CoMFA and CoMSIA models were built using Sybyl7.3 to assess the changes in three-dimension structural features of chemical substitution affects the anticancer activity of acylureidoindolin derivatives. The statistical values of these models are summarized in Table 2. These statistics obtained after omitting three outliers Acyl-43, Indoline-24B and Indoline-25H. The cross-validation coefficient value of 0.68 was achieved for CoMFA model with optimum number of component 6 having standard error of prediction 0.021 while non-cross validation coefficient analysis was done with 6 number of optimal component in conventional r2 of 0.971, a standard error of estimation (SEE) value of 0.203 and F value of 253.86. The resultant field contributions were 63.6% and 36.4% for steric and electrostatic field respectively, displaying a higher effect of the steric field. As compared to CoMFA, CoMSIA model based on five different fields (steric, electrostatic, hydrophobic, hydrogen bond donor and acceptor fields) gave a q2 (cross validation coefficient) value of 0.641 and r2 value of 0.933 with 6 optimum number of components, standard error of estimation (SEE) of 0.2110 and F value of 122.544. The field contributions of electrostatic, steric, hydrophobic, donor and acceptor fields were 0.252, 0.160, 0.189, 0.101 and 0.298, respectively. These values indicate that hydrophobic field made greater contribution in ligand–protein binding and inhibitory activity of AK-B. Our developed models predicted the correlation coefficients r2pred values 0.733 and 0.947, respectively. Relatively, the CoMSIA model presented better competency in predicting the biological activity of external test set compounds (Fig. 3). The statistical results indicate that these developed models are robust enough to design novel and potent inhibitors. Observed and predicted pIC50 values of CoMFA and CoMSIA model was shown in Table 3.
CoMFA and CoMSIA model analysis based on predicted pIC50 of AK-B inhibitors
The CoMFA and CoMSIA model results are summarized in Table 2. The generated 3D-QSAR models were found to be reliable and satisfactory if q2 value is greater than 0.50 and r2 value is greater than 0.90, These statistical keys, representing that both models have a robust extrapolative power by demonstrating a good correlation between the predicted and experimental log IC50 values. The stability and robustness of the model is further confirmed by bootstrapping technique for 60 runs. The average r2 (r2boot) and SEE (SEE boot) of these analyses of CoMFA and CoMSIA model are 0.9649, 0.013 and 0.941, 0.021 respectively. The greater value of r2boot and lowest value of SEE describe the robustness of generated CoMFA and CoMSIA model. Further robustness of these model was tested by shuffling the log IC50 values. The resulting q2 and r2 values were in the range of − 0.059 to 0.085 and − 0.006 to 0.030 respectively. The predicted pIC50 values of acyl and indoline derivatives are listed in Table 3. The correlations between calculated and predicted pIC50 values for the training and the test sets are depicted in Fig. 3. External validation (using a test set) was also carried out to evaluate the stabilities and the predictive capability of the generated QSAR model. These statistical calculations validated the good ability of our CoMFA and CoMSIA model to predict the external dataset.
CoMFA and CoMSIA contour map analysis
To visualize the effects of CoMFA and CoMSIA fields on acyl and indoline derivatives in three dimensional spaces, the contour plots for the final model of CoMFA and CoMSIA are shown in Fig. 4. The contour analysis might be effective in recognizing the significant areas where changes in all five fields around the molecule describe the differences in IC50 values. The field type “standard deviation and coefficient” (stdev*-coeff) was used for building the contour maps. The compound acyl-54 (most active compound) was overlaid on contour plots for visualization.
CoMFA and CoMSIA contour maps with combination of active and least active compounds. The active site residues, most active and inactive compound are presented for the comparison of their position with respect to contour maps position. The steric contour depicted in green and yellow contour indicates sterically favour and disfavour group (A,B). Electrostatic maps depicted in red and blue color shows favoured level for electron withdrawing and donating group respectively (C,D). Similarly, Hydrophobic contour depicted in Yellow and white maps indicate favoured and disfavoured regions for hydrophobicity (E,F). Hydrogen bond donor field presented in cyan and purple maps indicates the favoured and disfavoured areas for donating substituents. Hydrogen bond acceptor field presented in magenta and red contour indicates the favoured and disfavoured areas for hydrogen bond acceptor group (G,H).
In CoMFA model, the sterically favorable and unfavorable areas are highlighted by green and yellow colors respectively. While electrostatic map of CoMFA model shows blue and red color for electron donating and withdrawing group respectively. The CoMFA contour map is shown in Fig. 4(A–D).
It is shown that the sterically favorable contour is present near the linker which is adjacent to the core structure of biologically most active compound (acyl-54) indicating that the bulky substitution at that position is favorable (Fig. 4A). This is observed for two compounds, acyl-52 and acyl-53. Another green contour found near the carbonyl group of linker region also explains the sterically favorable substitution at this position. One of the green contours found near the methoxy group of flouro-benzoyl around Phe88 indicates that the methoxy group at this position is favorable for the activity of indoline derivatives, while in the case of indoline-14, 24a, 24c, 24g, 25a, 25h many fold decrease in inhibition is observed due to absence of methoxy group as compared to most active compound. A yellow contour is present near the CH2 of NH(CH2)2pyrrolidin-1-yl methyl group which indicates that the less bulky substitution is suitable for this position.
The CoMFA electrostatic maps displayed in Fig. 4(C,D), represented by red and blue color contours, indicate electron withdrawing and donating groups respectively. Two red contours found near the carbonyl oxygen of the ureido moiety and the side chain the of pyrrole ring indicate that electron withdrawing group around these areas is responsible for increasing the AK-B inhibitory activity. This is verified experimentally by the compounds indoline 24a–24i and 25h where decreased in activity is observed in the absence of these carbonyl oxygens. A blue contour is found near the NH which is adjacent to 2-floro-4-methoxybenzoyl group which indicates that electron donating group at this position is favorable for increasing inhibitory activity. Presence of another red contour indicating that 2-fluoro substituent on 4-methoxy benzoyl was required for optimum activity of aurora kinase B. Similar results can be observed in case of compound acyl-32a, 32b, 32c, 34 and 35 that do not contain fluorine atom at the aforementioned position which is might be responsible for their reduced activity in comparison to acyl-54.
The steric and electrostatic contour map analysis of CoMSIA model showed similar results to CoMFA. Therefore, the remaining three fields of CoMSIA model (hydrophobic, hydrogen bond donor and acceptor) are discussed in this section. The hydrophobic contour analysis of CoMSIA model is represented in Fig. 4(E,F), in which white contour is favorable for hydrophilic character while yellow areas were favorable for hydrophobic features. A white contour was found near the NH of pyrrole ring demonstrating that the hydrophilic substitution at this position was favorable for enhancing its inhibitory activity. At the same time, another large white region was observed near ureido moiety which is complementary to the pocket requirement. A yellow contour was observed near methyl of pyrrole ring suggesting the significance of non-hydrophobic character at pyrrole ring for AK-B inhibition activity as shown in Fig. 4(E,F).
The hydrogen bond donor and acceptor analysis represented in Fig. 4(G,H), the cyan and purple contour represent the maps where hydrogen bond donor groups favored and disfavored the activity respectively. Two medium sized cyan contours were observed near NH of pyrrole ring and indoline scaffold indicating that it fulfils the pocket requirement and responsible for inhibitory activity of indoline derivatives. A purple contour was found around the methoxy group of 2-floro-4-methoxybenzoyl indicating that the hydrogen bond donor substituent is not favorable in this zone. The structure of compound 32a (pIC50 = 7.8) and 32b (pIC50 = 8.2) presented the similar results, the only difference in their structure is the replacement of methoxy group by hydrogen in 32b, which shows better activity than 32a.
The magenta and red contour of Fig. 4(G,H) revealed the areas where hydrogen bond acceptor groups increase and decrease activity, respectively. A red contour near NH of indoline core structure suggested that hydrogen bond acceptor group is unfavorable at this position which is also proved experimentally. Another red contour appeared near NH of ureido moiety, suggesting that the hydrogen bond donor groups are favorable at this position. Two magenta contours were found near the carbonyl oxygen of ureido moiety indicating the importance of a hydrogen bond acceptor group at this position for better activity. Here, compounds acyl-32a-32j, 34, 38–53 with ureido moiety show better activity than those which do not contain ureido moiety such as indol-14-14b, 24a, 25h. The biological activities of these compounds are lower, consistent with the contour analysis, showing that our model is robust enough and can be used for future predictions.
Identification of hits via structure-based pharmacophore
A pharmacophore can be defined as “a collection of electronic and steric features which is required for optimum molecular interaction with a specific biological target, to block its biological response76.” For successful structure-based pharmacophore virtual screening one should know the maximum information about target of interest. To meet this point, we developed a robust pharmacophore model by using eight crystal structures of AK-B to identify novel compounds that may inhibit AK-B activity. For this purpose, eight basic pharmacophore models were generated, then aligned to produce number of shared and merged pharmacophore models to identify the best model with true and high active hit rate. The selected model was produced by combination of 4AF351, 2VGO53 and 2VGP55 features i.e. two hydrophobic (yellow color), one donor (green), one acceptor (red) and three exclusion volume (grey). The selected pharmacophore model with desired features is represented in Fig. 5. The generated pharmacophore model was then assessed for its capability to discriminate between true positive and true negative by actives, random and decoys dataset. The hit rate of the best model with these three datasets is 70%, 3% and 10% respectively. Compound libraries from ChemBridge77, MayBridge78, NCI79 and ZINC80 databases (> 30 million) were first filtered via drug-like and lead-like parameters to give 17.4 million molecules that were further decreased in number (16.9) by removing duplicates. The selected model was used to screen filtered databases and ~ 23,000 hits were obtained. The 70% of active lie in top 25% of the dataset which shows the reliability of pharmacophore model, these results were also supported by statistical techniques i.e., AUC and enrichment factor. ROC curve was calculated to measure the sensitivity and specificity between active and decoys in order to avoid false positive prediction on the basis of pharmacophore fitness score and the value of AUC was found to be 0.73. Further dataset was reduced by similarity signature technique via ROC software with 0.6 cut-off. After similarity search, > 2000 compounds were used for biological activity prediction by previous developed 3D-QSAR model. Finally, 17 compounds were considered as hits on the basis of pharmacophore fit score, docking interaction and 3D-QSAR predictions.
Binding mode prediction for active compounds by docking
Molecular docking was performed using the Dock suite in MOE48 to predict the most plausible binding conformation of the compounds. Docking is a computational technique that aims to predict the binding position poses of small molecules in protein binding sites, with scoring functions used to evaluate which poses are best matches to the protein binding site. In this study, two aspects are analysed to measure the quality of docking method: first is docking program should be able to reproduce the experimentally determined crystal pose and second the scoring function should be able to discriminate between true binders and non-binders (active and inactive).
Primarily acylureidoindolin derivatives as potential Aurora-B inhibitors are docked in the active site, to investigate the binding site of AK-B.
After prediction of hit compounds by the 3D-QSAR model, seventeen compounds were selected based on pharmacophore fit score, docking scores (London dG and GBVI/WSA dG) and prediction by 3D-QSAR models. As the most representative sample, the binding mode of AK-B (PDB ID: 4AF351) was selected to continue with further docking analysis. This analysis included assessing the compounds position inside the binding cavity and their hydrogen bond formation pattern. It is evident that these compounds bind in the catalytic pocket of AK-B. The interactions specifically with Lys106, Glu155 and Ala157 in the hinge region and Leu83, Val91 and Leu207 in the conserved hydrophobic region are consider for the binding affinity. Only four compounds from the ZINC database showed hydrogen bond interactions with Lys106, Glu155 and Ala157 as shown in the Fig. 6. The proposed binding modes of the compounds ZINC11253730, ZINC42019540, ZINC65618522 and ZINC7046484 are shown in Fig. 6. Analysis of the binding mode of compound ZINC11253730 showed that it interacted via hydrogen bond between the carbonyl oxygen of the carbamoyl acetamide and the NH of Ala157 with the distance of 2.64 Å. Another hydrogen bond was observed between the side chain of Glu155 and carbonyl oxygen of ZINC11253730 at a distance of 2.36 Å. Asn206 also attached via hydrogen bond that radiated from its side chain oxygen and targeted the CN of compound with the distance of 3.5 Å. Besides hydrogen bonds, the molecule also interacted to the target protein via hydrophobic interaction through its benzonitrile ring to the phenyl ring of Lys106. Similarly, compounds with zinc identification code ZINC65618522 and ZINC7046484 interacted efficiently with Ala157 and Glu155 through hydrogen bond of ~ 3.0 and ~ 2.5 Å respectively. These compounds also bound through hydrophobic interaction via their phenyl ring with the five-membered ring of Pro158. Another compound, ZINC42019540 (which is similar to ZINC11253730) interacted through two hydrogen bonds with the backbone NH of Ala157 and carbonyl oxygen of compound mentioned in the Fig. 6, however, Leu83, Phe88, Pro158 and Leu207 residues formed CH-π and π-π interactions with all these compounds.
2D Ligand interaction diagrams for the top scored pose of selected compounds for docking into the binding site of the AK-B using MOE software; non-polar and polar residues are presented in green and pink circles; hydrogen bond interaction is indicated by green dotted arrows; Shape of the binding site indicated by the proximity contour (dotted lines) surrounding the ligand and available space to the more outward-facing parts of the ligand.
Stability of complexes and binding mode analysis
Initially, replicates of 200 ns MD simulations were performed with both forcefields to explore the binding of the reported inhibitors to AK-B protein. In this regard a total of eight simulations were performed using crystal complex (4AF3) and the reported most active inhibitor (Acyl-54) of acyl ureido indoline derivative. The results indicate that ff14SB force field is more suitable for AK-B system than ff99SB due to excessive structural drift in the activation loop of AK-B. Detailed results for both forcefields are provided in the SI (Figure S2–S3). After analyzing the results with both force fields, the ff14SB force field was finally used to run the 200 ns MD simulations of remaining complexes with Acyl-24, ZINC11253730, ZINC42019540, ZINC65618522 and ZINC07046484. Simulation convergence and system stability were monitored by computing root mean square deviation (RMSD) of backbone atoms C, Cα, N and O with respect to the starting structure (Fig. 7). The RMSD plot showed stability of all systems at around 5 ns. The RMSD values of all systems initially increased during equilibration phase and indicate convergence after 10 ns. The active site residues show stability with less deviation. The RMSF plot was also analyzed from 0 to 200 ns for the regions which show higher flexibility (Fig. 8). The largest fluctuations were observed in the loop region. The binding of compounds did not affect the proteins overall conformational diversity. The interaction analysis in terms of hydrogen bonding and hydrophobic interactions and their occupancy were calculated during simulation (Figure S4–S5).
The reference compound VX-680 binds deeply within the active site of AK-B via a number of hydrophilic and hydrophobic interactions with the residues Lys106, Glu155 and Ala157 (hinge region) and Leu83, Val91 and Leu207 of hydrophobic region respectively. The amino group linking the pyrazole and pyrimidine ring show hydrogen bonding to the carbonyl oxygen atom of Ala157 throughout simulation with 99% occupancy. Another hydrogen bond which is not found during docking is observed between the Ala157 and N atom of pyrazole ring. The rest of the hydrophobic interactions observed in docking remain stable during the MD simulation. The benzene ring of VX-680 forms a pi–pi interaction with residue Phe88. Initially the cyclopropyl ring formed hydrophobic interaction with Leu207 but after 2 ns simulation it projected out towards the solvent. The piperazine ring is placed in a solvent-exposed region of the cavity and encircled by Arg81, Leu83, and Gly160. In case of the most active compound acyl-54, most of the hydrophobic interactions found by docking were conserved during MD simulation, while changes were observed for a number of hydrogen bonds. The NH of Ala157 formed hydrogen bond with double bonded oxygen of indoline-2-one moiety with 100% occupancy. Another new hydrogen bond was observed during MD simulation between the linker oxygen of acyl-54 and the sidechain of Arg82. The strong interaction of important residues with acyl-54 suggested its contribution to their inhibitory activity. Similarly, for compounds ZINC65618522 and ZINC7046484, hydrophobic interactions are conserved during MD simulation while hydrogen bonds with Glu155 and Ala157 remain unstable throughout the MD simulation. The phenyl ring of both compounds undergoes hydrophobic interaction with the side chain residues Phe88, Leu83, Lys106, Pro158 and Leu207. ZINC11253730 and ZINC42019540 showed similar interactions with the active site of AK-B. The carbonyl oxygen of benzamide is found in the vicinity of hinge region and forms hydrogen bond with the backbone and side chain of Ala157 and Glu155 respectively. The benzonitrile ring of ZINC42019540 shows CH- π and T-shaped π–π stacking interaction with Phe219. In the case of ZINC11253730, this CH–π interaction was found between benzonitrile ring and Lys106.
Binding free energy calculations
The interactions were also analyzed by calculation of absolute binding free energies using the WaterSwap45,64,81,82,83,84,85,86,87 and MM(GB/PB)SA65 methods. Generally, the MM(GB/PB)SA method is used to compute the binding free energy by selecting snapshots at regular intervals from the trajectory of entire MD simulation. This method does not consider the protein: solvent and ligand: solvent interaction details as it uses an implicit water model. Information concerning bridging interactions of solvent molecule between protein and ligand is of great importance. This problem can be avoided by using advanced and more convenient assay of WaterSwap, which uses explicit water model, so does not suffer with such limitations. The WaterSwap and MMGBSA calculations produce binding free energies in the range of − 20 to − 35.3 and − 36.2 to − 14 kcal/mol, respectively indicating that all inhibitors bind strongly to the AK-B protein (Table 4). For the selected AK-B inhibitor complexes, the range of IC50 is very narrow which is challenging for computational methods. If VX-680 is ignored as an outlier, then the docking score show good correlation coefficient with MMGBSA and WaterSwap with correlation value 0.58 and 0.68 respectively. A good correlation (R = 0.662) is observed between MMGBSA and WaterSwap, if compound ZINC42019540 is removed as an outlier. Overall, the binding free energies obtained from WaterSwap, MMGBSA and MMPBSA do not differ significantly. If VX-680 is ignored as an outlier then the MM(GB/PB)SA results predict the correct order of the compounds. The most potent compound showed results similar to the reference compound in case of MM(GB/PB)SA method. This might be because of hydrogen bonding to the hinge region which is necessary for the inhibition of kinases73. WaterSwap absolute binding free energy calculations for all seven compounds were performed on five representing structures after clustering of 200 ns MD simulation. The resulting binding free energy per compound obtained from FEP, Bennett and TI method (which were combined to produce an average value) can be compared with the experimentally derived binding free energy. The average absolute binding free energy of all systems is presented in Table 4. Further, the binding free energy is decomposed into individual residue contributions (Figs. 9–10). The decomposition analysis, highlight the major contributing residues for binding of AK-B inhibitors. For visualization of this residue decomposition, the CHEWD88 plugin for Chimera was used.
Comparison of 3D-QSAR (left) and WaterSwap(right) maps. The WaterSwap map shows the contributions to the free energy, with red values indicating preference of that residue for the electrostatic interaction, and blue indicating residues that favour binding of the ligand by van der Waals interactions.
Upper panel: WaterSwap45 residue energy contributions. Positive values indicate stabilization of the water cluster, while negative values indicate stabilization of the protein–ligand complex. Lower panel indicate the MMGBSA decomposition results of total binding free energy per residue.
Here, the WaterSwap residue-based binding energy decompositions were investigated to highlight the residue which significantly contributed to the inhibitor binding throughout the course of MD simulations. The time-averaged values of the total (ΔGresidue) components for all crucial residues that display good binding affinity towards the short listed compounds are shown in the Fig. 10. The Residues with positive values from the WaterSwap decomposition analysis favour binding of the water cluster, while negative values indicate that the residue contributes favourably to ligand binding. This shows that in case of reference compound 4af3, acyl-54 and acyl-24 charged residues (Lys106 and Glu161) stabilise the water cluster, while these compounds are stabilised by promising hydrophobic contacts with the neighbouring residues Leu83, Phe88, Val91, Pro158, Gly160 and Leu207 of the binding site, and all these come into direct contact with the large compounds, as some of these contacts are missing in case acyl-24 which is the least compound of the series and also smaller in size. This is realized that the binding contribution is increasing with ligand size. Similarly, the short-listed compounds ZINC11253730, ZINC42019540, ZINC65618522 and ZINC7046484, are stabilized by hydrophobic contact with the surrounding residues Leu83, Phe88, Tyr156, Leu207 and Phe219. Besides hydrophobic interactions, these compounds also show negative contribution with the charged residues Glu155 and Ala157 because of their involvement in hydrogen bond interaction. The interaction between the compound and Lys165 is unfavourable in all complexes except 4af3 and acyl-54, where it is slightly favourable due to its participation in van der Waals interactions. After computing residue-based binding free energy decomposition, the results of WaterSwap and 3D-QSAR maps were correlated. For this purpose, the components of ΔGresidue value were visualised by modifying them into a score which is used to colour each corresponding residue differently in molecular viewer. Snapshot from the resulting movie of acyl-54 (most active compound) are shown in Fig. 9. The trajectory displays that the residue based free energy components are fairly stable throughout the simulation. The residues are coloured by their total, van der Waals and electrostatic free energy components.
Additionally, Fig. 9 shows that the charged residues Lys106, Glu155 and Ala157 in the hinge region provides strong electrostatic stabilization (highlighted in red); this result is consistent with the 3D-QSAR maps in which two red contours found near the carbonyl oxygen of the ureido moiety of acyl-54 indicate that electron withdrawing group around these areas is responsible for increasing the AK-B inhibitory activity. Additionally, the compound attains promising van der Waals stabilisation by residues Leu83, Val91 and Leu207 (shown in blue). This decomposition reveals the experimental observation that the compound mostly binds via hydrophobic interactions. This observation is also well correlated with 3D-QSAR maps. The decomposition result also indicates that binding affinity of compound may be improved by adding a hydrogen bond donor group to get the same hydrogen bonding interactions that are observed to stabilise the swapped water cluster. To best of our knowledge, this study provides the first comparison of WaterSwap fields and 3D-QSAR maps.
To get further insight into inhibitor binding, MM/GBSA free energy decomposition analysis was used to decompose the total binding free energies into per residue components (Fig. 10). Table 4 lists the binding free energies for all inhibitor complexes. The residue decomposition approach suggested that major binding contribution comes from Glu155, Trp156 and Ala157 of site B and Leu83 and Leu207 of site C that play an important role in the binding. Free energy decomposition also shows favourable electrostatic contributions by Glu155 and Ala157 in both the WaterSwap and 3D-QSAR results.
Conclusions
AK-B is a promising target in the field of oncology7. The current study employed structure-based pharmacophore modelling and an atom-based 3D-QSAR analysis of acylureidoindolin derivatives as AK-B inhibitors, followed by MD simulation and free energy calculations. The selected CoMFA and CoMSIA model exhibited good extrapolative power and strong correlation between theory and experiment with cross-validation values (q2) of 0.68, 0.641 and linear regression values (r2) of 0.971, 0.933 respectively. The contour maps of 3D-QSAR indicate that electrostatic and hydrophobic fields explain the activity of acylureidoindolin derivatives. Structural requirements including the carbonyl group of ureido moiety and the methoxy of the fluorobenzoyl in the vicinity of Phe88 are important for activity. Multiple crystal structures (Table 1) of AK-B inhibitor complexes were used to generate structure based pharmacophoric hypothesis to facilitate the identification of novel compound from commercial database. All compounds that satisfied the structural pharmacophoric features were analyzed with our 3D-QSAR model. To remove false positives, and refine the hits, 7 compounds were evaluated by MD simulation and binding free energy analysis. Decomposition of overall binding energy showed that major contributions came from Glu155, Trp156 and Ala157 of site B and Leu83 and Leu207 of site C. These results could help in understanding AK-B inhibition and in designing more specific and potent inhibitors against AK-B protein to treat various malignant disorders.
Data availability
Data created during this research is provided as supplementary information accompanying this paper.
References
Goldenson, B. & Crispino, J. D. The aurora kinases in cell cycle and leukemia. Oncogene 34, 537 (2015).
Fu, J., Bian, M., Jiang, Q. & Zhang, C. Roles of aurora kinases in mitosis and tumorigenesis. Mol. Cancer Res. 5, 1–10 (2007).
Brown, J. R., Koretke, K. K., Birkeland, M. L., Sanseau, P. & Patrick, D. R. Evolutionary relationships of Aurora kinases: Implications for model organism studies and the development of anti-cancer drugs. BMC Evol. Biol. 4, 39 (2004).
Giet, R. & Prigent, C. Aurora/Ipl1p-related kinases, a new oncogenic family of mitotic serine-threonine kinases. J. Cell Sci. 112, 3591–3601 (1999).
Hu, H.-M., Chuang, C.-K., Lee, M.-J., Tseng, T.-C. & Tang, T. K. Genomic organization, expression, and chromosome localization of a third aurora-related kinase gene, Aie1. DNA Cell Biol. 19, 679–688 (2000).
Manning, G., Whyte, D. B., Martinez, R. & Hunter, T. The protein kinase complement of the human genome. Science (80-) 298, 1912–1934 (2002).
Vankayalapati, H. et al. Targeting Aurora2 kinase in oncogenesis: a structural bioinformatics approach to target validation and rational drug design 1. Mol. Cancer 2, 283–294 (2003).
Carmena, M. & Earnshaw, W. C. The cellular georgraphy of aurora kinases. Nat. Rev. Mol. Cell. Biol. 4, 842–854 (2003).
Kufer, T. A., Nigg, E. A. & Silljé, H. H. W. Regulation of Aurora-A kinase on the mitotic spindle. Chromosoma 112, 159–163 (2003).
Terada, Y., Uetake, Y. & Kuriyama, R. Interaction of Aurora-A and centrosomin at the microtubule-nucleating site in Drosophila and mammalian cells. J. Cell Biol. 162, 757–763 (2003).
Bolanos-Garcia, V. M. Aurora kinases. Int. J. Biochem. Cell Biol. 37, 1572–1577 (2005).
Hupp, T. R., Meek, D. W., Midgley, C. A. & Lane, D. P. Regulation of the specific DNA binding function of p53. Cell 71, 875–886 (1992).
Adams, R. R., Carmena, M. & Earnshaw, W. C. Chromosomal passengers and the (aurora) ABCs of mitosis. Trends Cell Biol. 11, 49–54 (2001).
Chen, J. et al. Survivin enhances aurora-B kinase activity and localizes aurora-B in human cells. J. Biol. Chem. 278, 486–490 (2003).
Honda, R., Körner, R. & Nigg, E. A. Exploring the functional interactions between Aurora B, INCENP, and survivin in mitosis. Mol. Biol. Cell 14, 3325–3341 (2003).
Bolton, M. A. et al. Aurora B kinase exists in a complex with survivin and INCENP and its kinase activity is stimulated by survivin binding and phosphorylation margaret. Mol. Biol. Cell 13, 3064–3077 (2002).
Keen, N. & Taylor, S. Mitotic drivers-inhibitors of the Aurora B Kinase. Cancer Metastasis Rev. 28, 185–195 (2009).
Yoon, M. J. et al. Aurora B confers cancer cell resistance to TRAIL-induced apoptosis via phosphorylation of survivin. Carcinogenesis 33, 492–500 (2012).
Harrington, E. A. et al. VX-680, a potent and selective small-molecule inhibitor of the Aurora kinases, suppresses tumor growth in vivo. Nat. Med. 10, 262–267 (2004).
Gordon, D. J., Resio, B. & Pellman, D. Causes and consequences of aneuploidy in cancer. Nat. Rev. Genet. 13, 189–203 (2012).
Sasai, K. et al. Aurora-C kinase is a novel chromosomal passenger protein that can complement Aurora-B kinase function in mitotic cells. Cell Motil. Cytoskeleton 59, 249–263 (2004).
Borah, N. A. & Reddy, M. M. Aurora kinase B inhibition: A potential therapeutic strategy for cancer. Molecules 26, 1981 (2021).
Willems, E. et al. The functional diversity of Aurora kinases: A comprehensive review. Cell Div. 13, 7 (2018).
Katayama, H., Brinkley, W. R. & Sen, S. The Aurora kinases: Role in cell transformation and tumorigenesis. Cancer Metastasis Rev. 22, 451–464 (2003).
Yan, A., Nie, X., Wang, K. & Wang, M. Classification of Aurora kinase inhibitors by self-organizing map (SOM) and support vector machine (SVM). Eur. J. Med. Chem. 61, 73–83 (2013).
Du, R., Huang, C., Liu, K., Li, X. & Dong, Z. Targeting AURKA in Cancer: Molecular mechanisms and opportunities for Cancer therapy. Mol. Cancer 20, 1–27 (2021).
Collins, G. P. et al. A phase II trial of AZD1152 in relapsed/refractory diffuse large B-cell lymphoma. Br. J. Haematol. 170, 886–890 (2015).
Kantarjian, H. M. et al. Stage i of a phase 2 study assessing the efficacy, safety, and tolerability of barasertib (AZD1152) versus low-dose cytosine arabinoside in elderly patients with acute myeloid leukemia. Cancer 119, 2611–2619 (2013).
Wilkinson, R. W. et al. AZD1152, a selective inhibitor of Aurora B kinase, inhibits human tumor xenograft growth by inducing apoptosis. Clin. Cancer Res. 13, 3682–3688 (2007).
Marampon, F. et al. Close correlation between MEK/ERK and Aurora-B signaling pathways in sustaining tumorigenic potential and radioresistance of gynecological cancer cell lines. Int. J. Oncol. 44, 285–294 (2014).
Gully, C. P. et al. Antineoplastic effects of an Aurora B kinase inhibitor in breast cancer. Mol. Cancer 9, 42 (2010).
Zhou, Y. et al. Antitumor and immunomodulatory effects of a novel multitarget inhibitor, CS2164, in mouse hepatocellular carcinoma models. Anticancer Drugs 30, 909–916 (2019).
Zhou, Y. et al. CS2164, a novel multi-target inhibitor against tumor angiogenesis, mitosis and chronic inflammation with anti-tumor potency. Cancer Sci. 108, 469–477 (2017).
Sini, P. et al. Pharmacological profile of BI 847325, an orally bioavailable, ATP-competitive inhibitor of MEK and Aurora kinases. Mol. Cancer Ther. 15, 2388–2398 (2016).
Schöffski, P. et al. Phase I, open-label, multicentre, dose-escalation, pharmacokinetic and pharmacodynamic trial of the oral aurora kinase inhibitor PF-03814735 in advanced solid tumours. Eur. J. Cancer 47, 2256–2264 (2011).
Jani, J. P. et al. PF-03814735, an orally bioavailable small molecule aurora kinase inhibitor for cancer therapy. Mol. Cancer Ther. 9, 883–894 (2010).
Hardwicke, M. A. et al. GSK 1070916, a potent Aurora B/C kinase inhibitor with broad antitumor activity in tissue culture cells and human tumor xenograft models. Mol. Cancer Ther. 8, 1808–1817 (2009).
McNeish, I. et al. A phase I pharmacokinetic (PK) and pharmacodynamic (PD) study of the selective aurora kinase inhibitor GSK1070916A. J. Clin. Oncol. 31, 2525–2525 (2013).
Adams, N. D. et al. Discovery of GSK1070916, a potent and selective inhibitor of aurora B/C kinase. J. Med. Chem. 53, 3973–4001 (2010).
Farrell, P. et al. Biological characterization of TAK-901, an investigational, novel, multitargeted aurora B kinase inhibitor. Mol. Cancer Ther. 12, 460–470 (2013).
Hauf, S. et al. The small molecule Hesperadin reveals a role for Aurora B in correcting kinetochore—microtubule assembly checkpoint. Cell https://doi.org/10.1083/jcb.200208092 (2002).
Garuti, L., Roberti, M. & Bottegoni, G. Small molecule aurora kinases inhibitors. Curr. Med. Chem. 16, 1949–1963 (2009).
Juillet, C. et al. From synthetic simplified marine metabolite analogues to new selective allosteric inhibitor of aurora B kinase. J. Med. Chem. 64, 1197–1219 (2021).
Paladino, A. et al. Chemical perturbation of oncogenic protein folding: from the prediction of locally unstable structures to the design of disruptors of Hsp90–client interactions. Chem. A Eur. J. 26, 9459–9465 (2020).
Woods, C. J. et al. Rapid decomposition and visualisation of protein–ligand binding free energies by residue and by water. Faraday Discuss. 169, 477–499 (2014).
Wang, H. C. et al. Bioisosteric replacement of an acylureido moiety attached to an indolin-2-one scaffold with a malonamido or a 2/4-pyridinoylamido moiety produces a selectively potent Aurora-B inhibitor. Eur. J. Med. Chem. 84, 312–334 (2014).
Jagtap, A. D. et al. Novel acylureidoindolin-2-one derivatives as dual Aurora B/FLT3 inhibitors for the treatment of acute myeloid leukemia. Eur. J. Med. Chem. 85, 268–288 (2014).
Inc., C. C. G. Molecular operating environment (MOE) (2016).
Pearlman, D. A. et al. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 91, 1–41 (1995).
Pérez, A. et al. Refinement of the AMBER force field for nucleic acids: Improving the description of α/γ conformers. Biophys. J. 92, 3817–3829 (2007).
Elkins, J. M., Santaguida, S., Musacchio, A. & Knapp, S. Crystal structure of human aurora B in complex with INCENP and VX-680. J. Med. Chem. 55, 7841–7848 (2012).
Kwiatkowski, N. et al. Selective aurora kinase inhibitors identified using a taxol-induced checkpoint sensitivity screen. ACS Chem. Biol. 7, 185–196 (2012).
D’Alise, A. M. et al. Reversine, a novel Aurora kinases inhibitor, inhibits colony formation of human acute myeloid leukemia cells. Mol. Cancer Ther. 7, 1140–1149 (2008).
Sessa, F. & Villa, F. Structure of Aurora B-INCENP in complex with barasertib reveals a potential transinhibitory mechanism. Acta Crystallogr. Sect. FStruct. Biol. Commun. 70, 294–298 (2014).
Andersen, C. B. et al. Discovery of selective aminothiazole aurora kinase inhibitors. ACS Chem. Biol. 3, 180–192 (2008).
Wolber, G. & Langer, T. LigandScout: 3-D pharmacophores derived from protein-bound ligands and their use as virtual screening filters. J. Chem. Inf. Model. 45, 160–169 (2005).
Cramer, R. D., Patterson, D. E. & Bunce, J. D. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J. Am. Chem. Soc. 110, 5959–5967 (1988).
Klebe, G. & Abraham, U. Comparative molecular similarity index analysis (CoMSIA) to study hydrogen bonding properties and to score combinatorial libraries. J. Comput. Aided. Mol. Des. 13, 1–10 (1999).
Du, M., Gu, W., Li, X., Fan, F. & Li, Y. Modification of hexachlorobenzene to molecules with lower long-range transport potentials using 3D-QSAR models with a full factor experimental design. In Advances in Marine Biology vol. 81, 129–165 (Elsevier, 2018).
Maier, J. A. et al. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 11, 3696–3713 (2015).
Lindorff-Larsen, K. et al. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinforma. 78, 1950–1958 (2010).
Wang, J., Wang, W., Kollman, P. A. & Case, D. A. Antechamber: an accessory software package for molecular mechanical calculations. J. Am. Chem. Soc. 222, U403 (2001).
Wang, J., Wolf, R. M., Caldwell, J. W., Kollman, P. A. & Case, D. A. Development and testing of a general Amber force field. J. Comput. Chem. 25, 1157–1174 (2004).
Woods, C. J., Malaisree, M., Hannongbua, S. & Mulholland, A. J. A water-swap reaction coordinate for the calculation of absolute protein-ligand binding free energies. J. Chem. Phys. 134, 054114 (2011).
Genheden, S. & Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 10, 449–461 (2015).
Tyka, M. D., Sessions, R. B. & Clarke, A. R. Absolute free-energy calculations of liquids using a harmonic reference state. J. Phys. Chem. B 111, 9571–9580 (2007).
Woods, C. J., Malaisree, M., Long, B., McIntosh-Smith, S. & Mulholland, A. J. Computational assay of h7n9 influenza neuraminidase reveals r292k mutation reduces drug binding affinity. Sci. Rep. 3, 7–12 (2013).
Humphrey, W., Dalke, A. & Schulten, K. V. M. D. Visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
Case, D.A., Betz, R.M., Cerutti, D.S., Cheatham, T.E., III, Darden, T.A., Duke, R.E., et al. Amber 2016. Univ. California, San Fr. (2016).
Yan, C. et al. Comparative molecular dynamics simulations of histone deacetylase-like protein: Binding modes and free energy analysis to hydroxamic acid inhibitors. Proteins Struct. Funct. Bioinforma. 73, 134–149 (2008).
Gohlke, H., Kiel, C. & Case, D. A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes. J. Mol. Biol. 330, 891–913 (2003).
Salomon-Ferrer, R., Götz, A. W., Poole, D., Le Grand, S. & Walker, R. C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh ewald. J. Chem. Theory Comput. 9, 3878–3888 (2013).
Xiong, R., Cai, X.-M., Wei, J. & Ren, P.-Y. Some insights into the binding mechanism of Aurora B kinase gained by molecular dynamics simulation. J. Mol. Model. 18, 4591–4601 (2012).
Verma, J., Khedkar, V. M. & Coutinho, E. C. 3D-QSAR in drug design—a review. Curr. Top. Med. Chem. 10, 95–115 (2010).
Fang, Y. et al. 3D-QSAR and docking studies of flavonoids as potent Escherichia coli inhibitors. Sci. Rep. 6, 23634 (2016).
Gimeno, A. et al. The light and dark sides of virtual screening: What is there to know?. Int. J. Mol. Sci. 20, 1375 (2019).
Eugene, V., Sergey, A. and Gala, V. ChemBridge. US Priv. Co. (2010).
Scrguide. The Maybridge Screening Collection-Maybridge... Bringing Life to Drug Discovery. Fisher Scientific. https://www.google.com.pk/search?q=ScrGuide,+2004+Maybridge&hl=en&authuser=0 (2004).
Voigt, J. H., Bienfait, B., Wang, S. & Nicklaus, M. C. Comparison of the NCI open database with seven large chemical structural databases. J. Chem. Inf. Comput. Sci. 41, 702–712 (2001).
Sterling, T. & Irwin, J. J. ZINC 15—ligand discovery for everyone. J. Chem. Inf. Model. 55, 2324–2337 (2015).
Callegari, D. et al. L718Q mutant EGFR escapes covalent inhibition by stabilizing a non-reactive conformation of the lung cancer drug osimertinib. Chem. Sci. 9, 2740–2749 (2018).
Rinaldi, S., Van Der Kamp, M. W., Ranaghan, K. E., Mulholland, A. J. & Colombo, G. Understanding complex mechanisms of enzyme reactivity: the case of limonene-1,2-epoxide hydrolases. ACS Catal. 8, 5698–5707 (2018).
Thai, K. M. et al. Computational assay of Zanamivir binding affinity with original and mutant influenza neuraminidase 9 using molecular docking. J. Theor. Biol. 385, 31–39 (2015).
Ahmad, S., Raza, S., Abbasi, S. W. & Azam, S. S. Identification of natural inhibitors against Acinetobacter baumannii D-alanine-D-alanine ligase enzyme: a multi-spectrum in silico approach. J. Mol. Liq. 262, 460–475 (2018).
Ahmad, S. et al. From phylogeny to protein dynamics: a computational hierarchical quest for potent drug identification against an emerging enteropathogen “Yersinia enterocolitica”. J. Mol. Liq. 265, 372–389 (2018).
Ahmad, S., Raza, S., Abro, A., Liedl, K. R. & Azam, S. S. Toward novel inhibitors against KdsB: a highly specific and selective broad-spectrum bacterial enzyme. J. Biomol. Struct. Dyn. 37, 1326–1345 (2019).
Ahmad, S., Murtaza, U. A., Raza, S. & Azam, S. S. Blocking the catalytic mechanism of MurC ligase enzyme from Acinetobacter baumannii: an in Silico guided study towards the discovery of natural antibiotics. J. Mol. Liq. 281, 117–133 (2019).
Raza, S. et al. Visualizing protein–ligand binding with chemical energy-wise decomposition (CHEWD): application to ligand binding in the kallikrein-8 S1 Site. J. Comput. Aided. Mol. Des. 33, 461–475 (2019).
Acknowledgements
A.J.M. thanks EPSRC for funding (Grant Number EP/M022609/1, CCP-BioSim, http://www.ccpbiosim.ac.uk and AJM and K.E.R thank BBSRC for funding (Grant Number BB/M000354/1). Simulations were conducted using computational facilities of the Advanced Computing Research Centre, University of Bristol.
Author information
Authors and Affiliations
Contributions
S.A. conducted in silico studies and wrote the manuscript. K.E.R provided the guidance in running molecular dynamic simulation and binding free energy calculation. K.E.R, A.J.M and Z.U.H edited the manuscript. A. J. M and Z.U.H. designed and supervised the project. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ashraf, S., Ranaghan, K.E., Woods, C.J. et al. Exploration of the structural requirements of Aurora Kinase B inhibitors by a combined QSAR, modelling and molecular simulation approach. Sci Rep 11, 18707 (2021). https://doi.org/10.1038/s41598-021-97368-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-97368-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.