Abstract
Soil properties, such as organic carbon, pH and clay content, are critical indicators of ecosystem function. Visible–near infrared (vis–NIR) reflectance spectroscopy has been widely used to cost-efficiently estimate such soil properties. Multivariate modelling, such as partial least squares regression (PLSR), and machine learning are the most common methods for modelling soil properties with spectra. Often, such models do not account for the multiresolution information presented in the vis–NIR signal, or the spatial variation in the data. To address these potential shortcomings, we used wavelets to decompose the vis–NIR spectra of 226 soils from agricultural and forested regions in south-western Western Australia and developed a wavelet geographically weighted regression (WGWR) for estimating soil organic carbon content, clay content and pH. To evaluate the WGWR models, we compared them to linear models derived with multiresolution data from a wavelet decomposition (WLR) and PLSR without multiresolution information. Overall, validation of the WGWR models produced more accurate estimates of the soil properties than WLR and PLSR. Around 3.5–49.1% of the improvement in the estimates was due to the multiresolution analysis and 1.0–5.2% due to the integration of spatial information in the modelling. The WGWR improves the modelling of soil properties with spectra.
Similar content being viewed by others
Introduction
Soil properties are critical indicators of ecosystem function1,2. They can directly indicate the quality of ecosystem services, including food and energy production, plant growth, carbon storage, regulation of greenhouse gas emissions and climate change3,4,5,6,7. Soil organic carbon, clay content and pH are essential soil properties affecting soil nutrient supply and plant development8. However, the measurement of these soil properties remains challenging because conventional analytical methods are time-consuming and expensive9,10. Diffuse reflectance soil spectroscopy, for example, using visible and near infrared (vis–NIR) spectra, has been proposed as a means to overcome those issues. The physcial basis of vis–NIR spectroscopy relies on overtones and combination bands from fundamental molecular vibrations of bonds in molecules of soil consituents, which occur in the mid infrared region11,12. Increasingly, the method has been used to estimate soil properties and to estimate their values more rapidly and cost-efficiently than conventional laboratory analytical methods13,14. Another advantage of the method is that a vis–NIR spectrum can be used to simultaneously characterise multiple soil properties4.
Methods for modelling continuous soil properties with highly collinear spectra include multivariate statistics and machine learning. The most common statistical methods are principal component regression (PCR)15,16 and partial least squares regression (PLSR)17,18. Different machine learning algorithms also have been used, including support vector machines, artificial neural networks, random forests and other regression trees19. More recently, convolutional neural network (CNN) and other deep learning architectures are also being developed20,21,22.
Wavelets have been successfully used with spectra in soil science and other fields of research4,23,24. Studies have demonstrated that the discrete wavelet transform (DWT) can improve the analysis of soil diffuse reflectance spectra for the prediction of soil properties14. They showed that multiresolution analysis (MRA) of soil diffuse reflectance spectra could identify different spectral features that occurred over different resolutions (or scales). They also showed that the highly collinear spectra could be transformed into a smaller number of orthogonal wavelet coefficients that produced more parsimonious and accurate multivariate calibrations.
Soil properties, like other natural phenomena, vary spatially and at different scales25,26,27. This variability is due to complex interactions between the environmental factors that affect the formation and distribution of soil28. The incorporation of spatial information in aspatial models can improve the accuracy of their predictions29. Spectroscopic modelling of soil properties often ignores geography and the spatial dependence of soil properties. Only a few studies have tried to account for geography in spectroscopic modelling. For example, the states or territories of Australia were used as categorical variables to account for any variance in the modelling of Australian soil spectra resulting from geography30. Sila et al.31 used regression–kriging to predict soil properties with mid-infrared spectra of soil samples, where residuals from a regression fit were informed using variograms.
Geographically weighted regression (GWR) might be a useful tool for modelling spectra and accounting for the geographic relationships and spatial non-stationarity in the data32. GWR, developed by33, supports locally varied regression parameter estimates for each explanatory variables across space34,35. The recent advances in the methodology and applications of GWR have helped to acquire new understanding of spatial processes. For example, basic GWR has been adapted for improved local inference of soil property data36, it has been adapted to a multiscale form37,38, to address issues of local multicollinearity39, and to down-weight the influence of outliers for robustly estimating the variability of local coefficients in social data40,41. These studies demonstrate the power and versatility of GWR for measuring spatial non-stationarity37,38,42,43. As such, GWR has been used in various fields of research, including ecology and environment44, climate45, social science46 and public health47.
Here, we propose to combine wavelets with geographically weighted regression (WGWR). Our hypothesis is that the spectral modelling of soil properties can be improved by accounting for the multiresolution information in the spectra and the spatial variations of the data. Thus, our aim is to demonstrate the implementation of WGWR for modelling soil properties with vis–NIR spectra and to evaluate the performance of the WGWR by comparing its predictions to those from PLSR and WLR. Experiments were conducted using a spectral library from the south-western West of Australia (WA).
Results
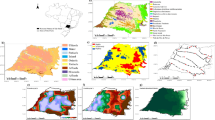
The spatial distributions of the organic carbon, clay content and pH data at the sampling locations are shown in Fig. 1a–c. The statistical summary of soil properties is shown in Table 1. In the study area, the mean soil organic carbon is 1.61%, mean clay content is 16.64% and mean pH is 5.77. Maps of spatial distributions, density figures, and statistical summaries of soil properties indicate their spatial variation across the study area.
Figure 1d, e shows the measured and transformed spectra. The broad absorptions between 350–1100 nm are associated with the iron oxides hematite or goethite, but also with organic carbon48. The wavelengths near 1412 nm are generally associated with the first overtone of hydroxyl stretching modes of water and minerals49. The wavelengths near 1917 nm are linked with hydroxyl and H-bonding hydroxyl stretching vibrations of water molecules and mineral constituents of water50. The neighbouring wavelengths near 2207 nm are related to clay minerals51,52.
Wavelet Geographically Weighted Regression (WGWR) of soil properties
Multiresolution analysis
The MRA of a vis–NIR spectrum shows six scales with detailed coefficients and a smooth component at the coarsest scale (Fig. 2a). The details at the different wavelet scales reveal the multiresolution features of soil spectra. At the finest scales \(\lambda\) = 2 and 4, the high frequency elements of the spectra occur at the interface between the three detectors in the spectroscopic sensor, where the signal is ‘noisier’. At the medium scales \(\lambda\) = 8 and 16, the wavelet coefficients depict the edges of the absorptions of the soil constituents near 595 nm, 1007 nm, 1415 nm, 1831 nm, 1903 nm, and 2207 nm. At the coarse scales \(\lambda\) = 32 and 64, the wavelet coefficients represent the broader absorptions of soil consituents primarily near 1400 nm and 1900 nm. The MRA results indicate that wavelet transformation can effectively identify the multiresolution local features of soil spectra.
Optimal identification of wavelets
Figure 2b shows the absolute correlations (|R|) between soil organic carbon, clay and pH, and the wavelet coefficients at the different wavelet scales. The larger |R| values occur at different wavelengths and wavelet scales, showing the multiresolution features in the spectra. For organic carbon, the largest |R| values at the smooth and detail components occur near 632 nm, 1894 nm, 1984 nm, 1953 nm, 985 nm, 1004 nm and 1003 nm. For clay content the largest |R| values occur near 2246 nm, 2399 nm, 2455 nm, 1927 nm, 1893 nm, 1892 nm and 1890 nm, and for pH near 1940 nm, 1949 nm, 1862 nm, 1906 nm, 1905 nm, 1892 nm and 1890 nm. The wavelets around these wavelengths show greater correlations with the soil properties as they represent absorptions due to the mineral and organic composition of soil53.
Figure 3 illustrates the procedure for selecting the optimal combinations of wavelet coefficients for soil organic carbon. The selection of optimal coefficients for soil clay and pH followed a similar processes. According to the distributions of |R| values, wavelets are ranked from the highest to the lowest |R| values (Fig. 3a). Figure3b shows the frequency of the ranked wavelets grouped by wavelet scales. The statistical summaries indicate that the wavelets at coarse scales tend to be more correlated with soil organic carbon compared with the wavelets at fine scales.
Process of selecting optimal combinations of wavelets for soil organic carbon prediction: (a) Ranked wavelets by the absolute values of correlation coefficients; (b) Statistical summary of wavelet scales by the rank of wavelets; (c) Wavelets selected by a multicollinearity analysis where the maximum VIF is lower than 10; (d) Ten-fold cross validation for selecting wavelets with the maximum testing R\(^2\); and (e) Selected optimal combinations of wavelets for explaining soil organic carbon.
Figure 3 c shows the wavelets selected by the multicollinearity analysis with the threshold that the maximum variance inflation factor (VIF) value is lower than 10 (see "Methods" section). In this step, 17 wavelet coefficients were selected. This shows that vis–NIR spectra are highly collinear and redundant. The number of explanatory wavelets are much reduced and the multicollinearity is eliminated. Figure 3 d shows the result of the fitness of the wavelet coefficient selection, which we performed by a ten-fold cross validation. With increases in the number of wavelet coefficients, the fitness of training data gradually increased, but that of testing data increased initially and decreased after four coefficients. This shows that the combination of the four coefficients was optimal for modelling soil organic carbon (Fig. 3e). The selected optimal combinations of wavelet coefficients for clay and pH are shown in Fig. 4.
Geographically weighted regression
Due to the spatial non-stationarity of soil properties, GWR is used to model the relationships between soil properties and the selected optimal combinations of wavelets. Figure 5 shows spatial distributions of local coefficients of wavelets in WGWR models, where significance of local coefficients were tested but not shown on the maps. The coefficients of both training and testing data are combined on maps of Fig. 5. The maps of local coefficients indicate spatially variable coefficients of wavelets across the study area for predicting soil organic carbon, clay and pH values. The spatially variable local coefficients also reveal the spatial non-stationarity of the relationships between soil properties and spectra data.
Comparing WGWR to other methods
Figure 6 shows maps of the PLSR, WLR, and WGWR residuals calculated on the test dataset for soil organic carbon, clay and pH, respectively. The maps indicate that the absolute values of the residuals are smaller for WLR and WGWR, respectively, compared with PLSR, due to the wavelet-based multi-resolution analysis. In addition, compared to the WLR, the residuals from the WGWR are smaller.
The validation results of the PLSR, WLR and WGWR are given in Table 2. In the PLSR, the (R\(^2\)) of the models derived using the training data of soil organic carbon, clay and pH are 0.547, 0.674 and 0.445, and the R\(^2\) of the models when generalised on the test data are 0.477, 0.389 and 0.347, respectively. Due to the incorporation of multi-solution information, the WLR models performed better than PLSR. Compared to PLSR, the R\(^2\) of the WLR of organic carbon, clay and pH increased by 22.4%, 49.1% and 3.5%, and the RMSE reduced by 10.8%, 17.1% and 0.9%, respectively. The incorporation of geographical information helped to improve the accuracy of the spectroscopic soil property estimates. In the WGWR, the training R\(^2\) of soil organic carbon, clay and pH are 0.702, 0.678 and 0.414, and the test set R\(^2\) values are 0.590, 0.587 and 0.378, respectively. Compared to WLR, the R\(^2\) of the WGWR estimates of organic carbon, clay and pH increased by 1.0%, 1.2% and 5.2%, and the RMSE decreased by 0.7%, 0.8% and 1.5%, respectively. Thus, compared to PLSR, the R\(^2\) of the WGWR estimates of organic carbon, clay and pH increased by 23.6%, 50.9% and 8.8%, and their RMSE decreased by 11.4%, 17.8% and 2.4%, respectively.
In addition, the Akaike information criterion (AICc) also demonstrate the improved accuracy and parsimony of WGWR.
Discussion
This study proposes a WGWR to more accurately estimate soil properties using reflectance spectra. We demonstrate that the integration of an MRA of reflectance spectra and spatial non-stationarity in the relationships between soil properties and spectra can improve the spectroscopic modelling of soil properties. The advantages of WGWR are the improved prediction accuracy, fewer spectral variables with reduced multicollinearity, and more robust estimates compared to PLSR and WLR.
The assessments of the soil organic carbon, clay and pH estimates indicate that the multiresolution features of spectra modelled by wavelet-based MRA can improve the skill of the modelling by 3.5–49.1%. Viscarra Rossel & Lark14 developed the modelling of soil properties with wavelets using an MRA. Compared to the approach by Viscarra Rossel & Lark, this study provides an alternative framework for the selection of coefficients. Here, we use correlation rather than variance for the ranking of coefficients and the VIF for eliminating multicollinearity, followed by ten-fold cross validation to minimise overfitting. As a result, the number of predictors were much reduced for modelling with WLR and WGWR. Two-thousand-one-hundred-and-fifty-one vis–NIR wavelengths were used in the PLSR, but only 4, 7 and 6 wavelets were selected for modelling soil organic carbon, clay and pH with WLR and WGWR.
The consideration of spatial non-stationarity in the WGWR, reduced errors and improved the accuracy of the models. Thus we show that WGWR can improve the modelling of soil properties with spectra by accounting for both multi-resolution information and spatial non-stationarity.
Our results suggest that, if spatial information is available, geographical characteristics of soil properties should be considered and used in spectroscopic modelling of soil properties.
Reflectance spectroscopy is an efficient and cost-efficient approach for rapidly estimating soil properties. We developed the WGWR that effectively integrates the multiresolution characteristics of soil vis–NIR spectra, the process of optimal wavelets identification and the spatial variations of soil properties and the spectra. Compared to PLSR and WLR, WGWR produced more accurate estimates of soil organic carbon, clay content and pH. The models were more parsimonious and thus the danger of multicollinearity of spectral variables and overfitting was eliminated. Improved modelling of soil properties with spectra, like we have done here, can also provide insights of geographical characteristics in soil-related ecosystems services, climate responses and sustainable development. Future studies might investigate the use of other geospatial methods for use with soil spectra, such as as kriging with external drift54.
Methods
Study area and soil observations
The study region in the south west of WA covers about 252,100 km\(^2\). It represents diverse land uses, including cropping, native forests and nature conservation. It is one of the primary agricultural production regions in Australia55. In 2018–2019, the gross value of agricultural production (GVAP) in WA, primarily in the South West Agricultural Area, was about 18% of the national GVAP56. The primary grains produced in this area include wheat, barley, canola, lupins, oats, and field peas, where wheat account for 65% of annual grains in WA57. Understanding the soil properties is essential for agricultural and environmental management.
We used a set of 226 soil samples collected within the study area. The shortest distances between soil samples and their nearest neighbours vary from 0.24 to 84.16 km. Among the samples, 20.4% of the sample points have neighbour samples within 1 km, and 33.2% of the sample points are the only samples within a radius of 10 km. At each sampling location, samples were taken at multiple depths from the surface down to 135 cm. The soil properties measured included soil organic carbon, clay content and pH measured in water. The analytical methods used to measure these soil properties are described in Rayment58,59,60. To derive a more consistent dataset for the modelling (described below), at the each sampling location, we took a weighted average of the soil properties from different depths, using the depths as weights.
The statistical distributions of soil organic carbon and clay content were negatively skewed so they were transformed to approximate normality using logs. Outliers were identified by setting thresholds of 2.5 standard deviations from the mean values61. Values that exceeded the threshold were removed. As a result, 4, 6 and 3 outliers were removed from the organic carbon, clay and pH data, respectively.
vis–NIR spectroscopy
The vis–NIR reflectance spectra of 226 soil samples were measured with a Labspec vis–NIR spectrometer (PANalytical Company, Boulder, CO., USA). The spectral range of the spectrometer spans from 350 to 2500 nm, and it has a spectral resolution of 3 nm at 700 nm and 10 nm at 1400 and 2100 nm. Measurements were made with a high-intensity contact probe (also from PaNalytic) that uses a halogen bulb (\(2901\pm 10\) K) for illumination. The contact probe measures a spot of diameter 10 mm, and it is designed to minimize errors associated with stray light. The sensor was calibrated with a Spectralon® white reference panel once every ten measurements. For each soil sample, 30 spectra were averaged to minimize noise and so to maximize the signal-to-noise ratio. The measurements were made following the protocols described in Rossel4. Spectra were recorded with a sampling resolution of 1 nm so that each spectrum comprised reflectances at 2151 wavelengths. The measured reflectances, R, were first converted to apparent absorbance as log10(1/R).
Wavelet geographically weighted regression
To improve the modelling of soil properties with spectra, we developed a WGWR model. It integrates the multiresolution information in the spectra and the spatial variations of soil properties. The WGWR model consists of three steps: (1) decomposition of the vis–NIR spectra with a DWT and MRA, (2) selection of an optimal set of wavelet coefficients for the regression, and (3) GWR. The workflow is shown in Fig. 7.
First, we decomposed each vis–NIR spectrum using the DWT and MRA to reveal the multiresolution nature of the spectra. For the decomposition, we used the Daubechies wavelet with 4 vanishing moments. The MRA is implemented via a pyramid algorithm62, in which a spectrum is decomposed into the detail components (\(D_i\)) at different wavelet scales (\(\lambda _i\)) up to a coarsest scale, when a smooth or approximation component (S) is obtained. In this study, the spectrum beyond its boundaries, including the start and end of the data, is assumed to be a symmetric reflection of the spectrum63. The sum of the detail and smooth components is the original spectrum. Viscarra Rossel and Lark14 provide a description of the approach for the analysis of soil spectra. The decomposition was performed, as above, for the vis–NIR spectra of all samples.
Second, to identify the optimal wavelet coefficients for modelling, we correlated the soil properties to the wavelet coefficients and recorded the Pearson correlation coefficient. We then ranked the wavelet coefficients according to the absolute values of correlation coefficients (|R|). A multicollinearity analysis was then performed using a VIF, a measure of multicollinearity of variables in a regression model, to discard wavelet coefficients that were highly correlated. Highly correlated explanatory variables can lead to unstable coefficients and a less accurate regression64,65. From the ranked set of coefficients, the wavelet with the largest |R| was selected as the first explanatory variable to use in the regression to estimate the multicollinearity among wavelets. Then, wavelet coefficients from the ranked list were sequentially added to the first, and a linear regression performed. If the VIF was smaller than 10, that wavelet coefficient is selected, but if it was larger than 10, then that coefficient was removed. The procedure continued sequentially and the final selected coefficients are uncorrelated and with a VIF smaller than 10. The remaining selected wavelet coefficients, were sequentially added one at a time to perform regressions using a ten-fold cross validation. We did this to eliminate overfitting in the assessments and modelling. The average cross validation R\(^2\), and the number of wavelet coefficients were compared to derive the optimal number of coefficients with the highest average cross validation R\(^2\). Thus, the final selected wavelet coefficients were the optimal combination for each of the modelled soil properties.
Third, a GWR is applied to characterise geographically local relationships between soil property and the optimal combination of wavelets derived from reflectance spectra. Soil properties are spatially correlated66,67. The GWR models enable locally varied estimates of coefficients for all explanatory variables in the regression. The spatial non-stationarity of soil properties is examined using the Monta Carlo technique with the randomisation variability test of local coefficients and the coefficient of variations of local coefficients68,69,70. In the GWR model, the location-wise coefficients of the selected wavelets are estimated with distance-decay spatial weights. The GWR model for estimating the geographically local relationships is computed as:
where s is the observation of a soil property (e.g. organic carbon) at the location \(\varvec{u}\), \(w_i(i=1,\ldots ,m)\) is the ith selected optimal wavelet at the location \(\varvec{u}\), \(\beta _i (\varvec{u})\) is the location-wise regression coefficient, and \(\epsilon\) is the normally distributed random error. The spatially adaptive Gaussian kernel function is applied in the weighting scheme, where the optimal bandwidth is determined through the adaptive process, and the number of neighbour observations is optimised by minimising the AICc of the model32.
Model comparison and validation
We compared the WGWR to PLSR and WLR. Our implementation of PLSR used the iterative singular value decomposition algorithm. The explanatory variables in the PLSR are the selected optimal combination of the PLS components of wavelet transformed spectra. To select the optimal number of PLS factors to use in the regression we used a cross validation and selected as many factors as necessary to produced the the smallest error71. For the WLR, the selection of the optimal wavelet coefficients to use was the same as that for the WGWR (see above).
The methods were evaluated with an external validation process. It involved selecting, at random, 70% of the observations to train the models and the remained 30% of the observations to test the estimates. To evaluate the performance of the methods we used the coefficient of determination (R\(^2\)), the mean absolute error (MAE) to assess bias and root mean squared error (RMSE) to assess inaccuracy. In the cross validation, values of soil properties have been back-transformed, since they have been transformed before modelling. To further compare AICc values of different models, relative likelihood of the models was computed as:
where \(\eta _j\) and \(AICc_j\) are the relative likelihood and AICc value of jth model, respectively; and \(AICc_{min}\) is the minimum AICc value among optional models. The \(\eta _j\) is used to explain the probability that the minimised information loss in the jth model72.
All computations were performed in the R software version 4.0.373. The wavelet analysis was performed using the package “waveslim”63, the PLSR was performed using the package “pls”74, and the GWR was performed using the package “spgwr”75.
References
Schmidt, M. W. et al. Persistence of soil organic matter as an ecosystem property. Nature 478, 49–56 (2011).
Drobnik, T., Greiner, L., Keller, A. & Grêt-Regamey, A. Soil quality indicators-from soil functions to ecosystem services. Ecol. Ind. 94, 151–169 (2018).
Bradford, M. A. et al. Managing uncertainty in soil carbon feedbacks to climate change. Nat. Clim. Change 6, 751–758 (2016).
Viscarra Rossel, R. et al. A global spectral library to characterize the world’s soil. Earth Sci. Rev. 155, 198–230 (2016).
Amundson, R. & Biardeau, L. Opinion: Soil carbon sequestration is an elusive climate mitigation tool. Proc. Natl. Acad. Sci. 115, 11652–11656 (2018).
Smith, P. et al. How to measure, report and verify soil carbon change to realize the potential of soil carbon sequestration for atmospheric greenhouse gas removal. Glob. Change Biol. 26, 219–241 (2020).
Zhang, S., Yu, Z., Lin, J. & Zhu, B. Responses of soil carbon decomposition to drying-rewetting cycles: A meta-analysis. Geoderma 361, 114069 (2020).
Bot, A. & Benites, J. The Importance of Soil Organic Matter: Key to Drought-Resistant Soil and Sustained Food Production. 80 (Food & Agriculture Org., 2005).
Rawles, W. J. & Brakensiek, D. Estimating soil water retention from soil properties. J. Irrig. Drain. Div. 108, 166–171 (1982).
Zhao, D., Zhao, X., Khongnawang, T., Arshad, M. & Triantafilis, J. A Vis–NIR spectral library to predict clay in Australian cotton growing soil. Soil Sci. Soc. Am. J. 82, 1347–1357 (2018).
Demattê, J. A., Campos, R. C., Alves, M. C., Fiorio, P. R. & Nanni, M. R. Visible–NIR reflectance: A new approach on soil evaluation. Geoderma 121, 95–112 (2004).
Viscarra Rossel, R. Fine-resolution multiscale mapping of clay minerals in Australian soils measured with near infrared spectra. J. Geophys. Res. Earth Surf. 116 (2011).
Viscarra Rossel, R., Walvoort, D., McBratney, A., Janik, L. J. & Skjemstad, J. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 131, 59–75 (2006).
Viscarra Rossel, R. & Lark, R. Improved analysis and modelling of soil diffuse reflectance spectra using wavelets. Eur. J. Soil Sci. 60, 453–464 (2009).
Abdi, H. & Williams, L. J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2, 433–459 (2010).
Næs, T. & Martens, H. Principal component regression in NIR analysis: Viewpoints, background details and selection of components. J. Chemom. 2, 155–167 (1988).
Geladi, P. & Kowalski, B. R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 185, 1–17 (1986).
Rossel, R. V. Robust modelling of soil diffuse reflectance spectra by “bagging-partial least squares regression”. J. Near Infrared Spectrosc. 15, 39–47 (2007).
Viscarra Rossel, R. & Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 158, 46–54 (2010).
Tsakiridis, N. L., Keramaris, K. D., Theocharis, J. B. & Zalidis, G. C. Simultaneous prediction of soil properties from VNIR–SWIR spectra using a localized multi-channel 1-d convolutional neural network. Geoderma 367, 114208 (2020).
Yang, J., Wang, X., Wang, R. & Wang, H. Combination of convolutional neural networks and recurrent neural networks for predicting soil properties using Vis–NIR spectroscopy. Geoderma 380, 114616 (2020).
Shen, Z. & Viscarra Rossel, R. A. Automated spectroscopic modelling with optimised convolutional neural networks. Sci. Rep. 11, 208. https://doi.org/10.1038/s41598-020-80486-9 (2021).
Li, F., Wang, L., Liu, J., Wang, Y. & Chang, Q. Evaluation of leaf n concentration in winter wheat based on discrete wavelet transform analysis. Remote Sens. 11, 1331 (2019).
Meng, X. et al. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 89, 102111 (2020).
Jiang, B. Geospatial analysis requires a different way of thinking: The problem of spatial heterogeneity. GeoJournal 80, 1–13 (2015).
Song, Y., Wang, J., Ge, Y. & Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GISci. Remote Sens. 57, 593–610 (2020).
Yang, Z. et al. The effect of environmental heterogeneity on species richness depends on community position along the environmental gradient. Sci. Rep. 5, 1–7 (2015).
Jenny, H. Factors of Soil Formation (McGraw-Hill, 1941).
Ye, H. et al. Effects of different sampling densities on geographically weighted regression kriging for predicting soil organic carbon. Spat. Stat. 20, 76–91 (2017).
Viscarra Rossel, R. & Webster, R. Predicting soil properties from the Australian soil visible-near infrared spectroscopic database. Eur. J. Soil Sci. 63. https://doi.org/10.1111/j.1365-2389.2012.01495.x (2012).
Sila, A., Pokhariyal, G. & Shepherd, K. Evaluating regression-kriging for mid-infrared spectroscopy prediction of soil properties in western Kenya. Geoderma Reg. 10, 39–47 (2017).
Fotheringham, A. S., Brunsdon, C. & Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships (Wiley, 2003).
Brunsdon, C., Fotheringham, A. S. & Charlton, M. E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 28, 281–298 (1996).
Bidanset, P. E. & Lombard, J. R. The effect of kernel and bandwidth specification in geographically weighted regression models on the accuracy and uniformity of mass real estate appraisal. J. Prop. Tax Assess. Admin. 11, 5–14 (2014).
Brunsdon, C., Fotheringham, A. & Charlton, M. Geographically weighted summary statistics? A framework for localised exploratory data analysis. Comput. Environ. Urban Syst. 26, 501–524 (2002).
Comber, A. et al. The GWR route map: A guide to the informed application of geographically weighted regression. arXiv preprint arXiv:2004.06070 (2020).
Fotheringham, A. S., Yang, W. & Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 107, 1247–1265 (2017).
Yu, H. et al. Inference in multiscale geographically weighted regression. Geogr. Anal. 52, 87–106 (2020).
Wheeler, D. & Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 7, 161–187 (2005).
Harris, P., Fotheringham, A. S. & Juggins, S. Robust geographically weighted regression: A technique for quantifying spatial relationships between freshwater acidification critical loads and catchment attributes. Ann. Assoc. Am. Geogr. 100, 286–306 (2010).
Harris, P., Brunsdon, C., Lu, B., Nakaya, T. & Charlton, M. Introducing bootstrap methods to investigate coefficient non-stationarity in spatial regression models. Spat. Stat. 21, 241–261 (2017).
Cho, S.-H., Lambert, D. M. & Chen, Z. Geographically weighted regression bandwidth selection and spatial autocorrelation: An empirical example using Chinese agriculture data. Appl. Econ. Lett. 17, 767–772 (2010).
Lu, B., Yang, W., Ge, Y. & Harris, P. Improvements to the calibration of a geographically weighted regression with parameter-specific distance metrics and bandwidths. Comput. Environ. Urban Syst. 71, 41–57 (2018).
Arabameri, A., Pradhan, B. & Rezaei, K. Gully erosion zonation mapping using integrated geographically weighted regression with certainty factor and random forest models in gis. J. Environ. Manag. 232, 928–942 (2019).
Li, X. et al. Mapping soil organic carbon and total nitrogen in croplands of the corn belt of northeast china based on geographically weighted regression kriging model. Comput. Geosci. 135, 104392 (2020).
Cao, K., Diao, M. & Wu, B. A big data-based geographically weighted regression model for public housing prices: A case study in Singapore. Ann. Am. Assoc. Geogr. 109, 173–186 (2019).
Ge, Y. et al. Geographically weighted regression-based determinants of malaria incidences in northern China. Trans. GIS 21, 934–953 (2017).
Viscarra Rossel, R. A. & Hicks, W. S. Soil organic carbon and its fractions estimated by visible–near infrared transfer functions. Eur. J. Soil Sci. 66(3), 438–450 (2015).
Wight, J. P., Ashworth, A. J. & Allen, F. L. Organic substrate, clay type, texture, and water influence on NIR carbon measurements. Geoderma 261, 36–43 (2016).
Costa, L. R., Tonoli, G. H. D., Milagres, F. R. & Hein, P. R. G. Artificial neural network and partial least square regressions for rapid estimation of cellulose pulp dryness based on near infrared spectroscopic data. Carbohyd. Polym. 224, 115186 (2019).
Murphy, R. J., Schneider, S., Taylor, Z. & Nieto, J. Mapping clay minerals in an open-pit mine using hyperspectral imagery and automated feature extraction. In Vertical Geology, From Remote Sensing to 3D Geological Modelling. Proceedings of the first Vertical Geology Conference, Lausanne, Switzerland, 5–7 (2014).
Todorova, M. H. & Atanassova, S. L. Near infrared spectra and soft independent modelling of class analogy for discrimination of chernozems, luvisols and vertisols. J. Near Infrared Spectrosc. 24, 271–280 (2016).
Stenberg, B., Viscarra Rossel, R., Mouazen, A. & Wetterlind, J. Visible and Near Infrared Spectroscopy in Soil Science, vol. 107 (Academic Press, 2010).
Harris, P., Fotheringham, A., Crespo, R. & Charlton, M. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Math. Geosci. 42, 657–680 (2010).
Department of Primary Industries and Regional Development, Western Australia. South West Agricultural Region (dpird-008) (2020).
Australian Bureau of Statistics. Value of Agricultural Commodities Produced, Australia (2020).
Department of Primary Industries and Regional Development, Western Australia. Western Australian Wheat Industry (2019).
Rayment, G. E. & Lyons, D. J. Soil Chemical Methods—Australasia (CSIRO Publishing, 2010).
Dolui, S. et al. Structural correlation-based outlier rejection (score) algorithm for arterial spin labeling time series. J. Magn. Reson. Imaging 45, 1786–1797 (2017).
Pollet, T. V. & van der Meij, L. To remove or not to remove: The impact of outlier handling on significance testing in testosterone data. Adapt. Hum. Behav. Physiol. 3, 43–60 (2017).
Leys, C., Ley, C., Klein, O., Bernard, P. & Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 49, 764–766 (2013).
Mallat, S. G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11, 674–693 (1989).
Whitcher, B. waveslim: Basic Wavelet Routines for One-, Two-, and Three-Dimensional Signal Processing (2020).
O’brien, R. M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 41, 673–690 (2007).
Akinwande, M. O. et al. Variance inflation factor: As a condition for the inclusion of suppressor variable (s) in regression analysis. Open J. Stat. 5, 754 (2015).
Webster, R. & Oliver, M. A. Sample adequately to estimate variograms of soil properties. J. Soil Sci. 43, 177–192 (1992).
Atteia, O., Dubois, J.-P. & Webster, R. Geostatistical analysis of soil contamination in the Swiss Jura. Environ. Pollut. 86, 315–327 (1994).
Brunsdon, C., Fotheringham, S. & Charlton, M. Geographically weighted regression-modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D (The Statistician) 47, 431–443 (1998).
Gollini, I., Lu, B., Charlton, M., Brunsdon, C. & Harris, P. Gwmodel: An r package for exploring spatial heterogeneity using geographically weighted models. arXiv preprint arXiv:1306.0413 (2013).
Lu, B., Harris, P., Charlton, M. & Brunsdon, C. The GWmodel R package: Further topics for exploring spatial heterogeneity using geographically weighted models. Geo Spat. Inf. Sci. 17, 85–101 (2014).
Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Springer Science & Business Media, 2009).
Burnham, K. P. & Anderson, D. R. A practical information-theoretic approach. Model selection and multimodel inference 2 (2002).
R Core Team. R: A Language and Environment for Statistical Computing. (R Foundation for Statistical Computing, Vienna, Austria 2020).
Mevik, B.-H., Wehrens, R., Liland, K. H. & Hiemstra, P. pls: Partial Least Squares and Principal Component Regression (2020).
Bivand, R., Yu, D., Nakaya, T. & Garcia-Lopez, M. spgwr: Geographically weighted regression. R Package Version 0.6-34. http://cran.r-project.org/web/packages/spgwr/. Accessed August 30th 2020 (2020).
Acknowledgements
This work was supported by funding from Curtin University.
Author information
Authors and Affiliations
Contributions
Y.S. and R.A.V.R. designed the experiments and data analyses. R.A.V.R. supervised the research. Y.S. and Z.S. carried out the experiments and Y.S. drafted the manuscript. R.A.V.R., Z.S., and P.W. revised the manuscript. All authors reviewed the manuscript before submitting.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Song, Y., Shen, Z., Wu, P. et al. Wavelet geographically weighted regression for spectroscopic modelling of soil properties. Sci Rep 11, 17503 (2021). https://doi.org/10.1038/s41598-021-96772-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-96772-z
This article is cited by
-
Geographically Optimal Similarity
Mathematical Geosciences (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.