Abstract
In recent years the intermetallic ternary RE2MgGe2 (RE = rare earth) compounds attract interest in a variety of technological areas. We therefore investigate in the present work the structural, electronic, magnetic, and thermodynamic properties of Nd2MgGe2 and Gd2MgGe2. Spin–orbit coupling is found to play an essential role in realizing the antiferromagnetic ground state observed in experiments. Both materials show metallicity and application of a Debye-Slater model demonstrates low thermal conductivity and little effects of the RE atom on the thermodynamic behavior.
Similar content being viewed by others
Introduction
The examination of intermetallic compounds with Mo2FeB2 structure type (space group P4/mbm), as ordered variant of the U3Si2 structure type, has been the subject of many studies in recent years due to a variety of intriguing physical properties1. Examples reach from superconductivity to heavy fermion behavior, Kondo lattices, and magnetocalorics2. Well-known members of the material class are U2SnCo2 and U2InPt2, non-Fermi liquid systems on the verge of long-range magnetic ordering, and the hybridization-gap semiconductor U2SnRu23. Y1.6Ce0.4InPd2 and Lu1.6Ce0.4InPd2 show heavy fermion behavior and in Ce2InRh2 the Ce atoms realize a mixed valent state with high spin fluctuation temperature4. Yb2AlSi2, on the other hand, shows an intermediate valent state5. More than 300 intermetallic compounds M2XT2 (M = rare earth or actinoid metal; X = Mg, In, Sn, Cd; T = transition metal) are known. The X and T atoms constitute planar [XT2] networks such that each X atom is coordinated to four T2 dumb-bells6,7. The crystal structure can be understood as packing of distorted fragments of AlB2 and CsCl structure types, which form a network of octahedra and trigonal bipyramids with interstitial sites favorable for H allocation. The M atoms form a planar structure with triangular motif, which, depending on the exchange interaction, can lead to magnetic frustration, as described by the two-dimensional Shastry-Sutherland Hamiltonian \(H = J\sum\nolimits_{NN} {S_{i} S_{j} } + J^{\prime } \sum\nolimits_{NNN} {S_{i} S_{j} }\), where Si represents the magnetic moment at site i8. Magnetic frustration exists when the nearest neighbor interaction J and next nearest neighbor interaction J′ are both antiferromagnetic (AF)9. Since J > J′, nearest neighbor atoms form a network of J-coupled dimers that are coupled by J′. The ground state is a disordered spin liquid with energy gap between the singlet and triplet states or an antiferromagnet with gapless magnetic excitations. Transition is predicted for J′/J ≈ 0.6–0.7 at 0 K10, although symmetry arguments suggest that an intermediate state is required, such as a helical magnet or a spin density wave11.
Cermets with Mo2FeB2 structure type show excellent wear resistance, low friction to non-ferrous metals, and thermal expansion coefficients close to those of steel. While they are not as strong as the commonly used hard metals12, the mechanical properties can be improved by Cr and Ni additions. B, V, and Mn additions reduce the grain size and remarkably increase the transverse rupture strength13. RE2MgT2 (RE = rare earth) compounds are used for lightweight construction in the automobile and aerospace industries14. They show high corrosion resistance and thus have been investigated intensively with respect to their microstructure and mechanical properties15. The compounds play an essential role as bio-compatible materials for healing or replacing natural bone16. They are also able to absorb large amounts of H, up to 8 atoms per formula unit, which weakens the magnetism, as the RE–RE exchange interaction and magnetic coupling via the conduction electrons are suppressed (while for U2MgT2 the upper limit of H absorption is 2 atoms per formula unit and hydrogenation enhances the magnetism)17,18. Interstitial doping with H atoms, which induces internal pressure and/or modifies the bonding between the other atoms, can be used to tune the crystal and electronic structures, particularly the magnetism, which depends critically on details of the hybridization and charge localization19.
M2XT2 compounds can be magnetocaloric with field-induced magnetic and/or structural transitions, where for M = RE the magnetic structure is determined mainly by the (i) RKKY (Ruderman, Kittel, Kasuya, and Yosida) interaction and (ii) crystalline electric field (which is responsible for magnetic phase transitions, for example, for RE = Nd)20. In magnetocaloric ferromagnets/antiferromagnets the entropy change during isothermal magnetization is negative/positive (termed positive/negative magnetocaloric effect). A positive magnetocaloric effect is interesting for magnetic refrigerators and a negative magnetocaloric effect for heat pumps21.
In U2SnT2 compounds (non-magnetic or magnetic depending on T) the interatomic distance between U and T increases from U2SnFe2 to U2SnCo2 and U2SnNi2, even though the atomic radius decreases from Fe (1.27 Å) to Co (1.25 Å) and Ni (1.24 Å), and the spin–orbit coupling plays an important role for the electronic states22. While in U2SnNi2 the a lattice parameter increases with the temperature and the c lattice parameter decreases, in the cases of U2SnCo2 and U2SnPd2 both lattice parameters increase22. U2SnNi2 shows AF ordering below 25 K with the U moments aligned parallel to the c-axis23. The band width of the U 5f. states decreases for heavier T = Co, Ni, Rh, Pd, Ir, and Pt24. Giant magnetoresistance is predicted for U2SnPd2 and U2InPd225, and specific heat data classify single crystalline U2SnCo2 and U2InPt2 as non-Fermi-liquid materials26. Enhanced hybridization between the U 5f. and Ni 3d states leads in U2Sn(Ni1-xCox)2 solid solutions for increasing x to a loss of AF ordering at x = 0.3 and in U2Sn(Ni1-xPdx)2 solid solutions to a decrease of the Neel temperature (TN) up to x = 0.3, which is reproduced by the RKKY model22. At 1.5 K the U magnetic moments switch from in-plane ordering in U2SnPd2 (2 μB) to out-of-plane ordering in U2Sn0.65Pd2.35 (0.9 μB) due to enhanced hybridization between the U 5f. and Pd 4d states (reduced U-Pd distance)22.
The magnetic behavior of the Ce2InT2 compounds is determined by the filling of the T d bands, with Ce being trivalent in Ce2InCu2 and Ce2InAu2 but not in Ce2InPd227. First principles calculations demonstrate that in Ce2SnPd2 the hybridization between the Ce 4f. and Pd 4d states is weak (strong localization of the Ce 4f. states and large Ce magnetic moments)26. Ce2(In/Sn)Pd2 alloys display transitions between AF and ferromagnetic (FM) ground states as a function of the Sn/In ratio28,29. Ce2PbPt2 realizes AF ordering below 3.4 K30. Tb2InCu2 is FM up to 81 K29, and Nd2InAu2 and Tb2InAu2 are ferrimagnetic and FM up to 36 and 73 K with magnetic moments of 3.5 and 9.31 μB, respectively30. Pr2InNi2 and Nd2InNi2 undergo second order FM to paramagnetic transitions at 7.5 and 10.5 K, respectively, according to Ref. 31, whereas Ref. 32 reports Nd2InNi2 to be AF with TN = 8 K. Nd2InNi2 can absorb up to 7 H atoms per formula unit at room temperature, which leads to expansion of the unit cell along the a- and c-axes and compression along the b-axis (orthorhombic structure with space group Pbam)33. The Nd magnetic moment of 3.55 μB resembles that of a free Nd3+ ion (3.62 μB)34,35. Nd2InNi2 is an Ising antiferromagnet36.
Tb2InPd2 shows a significantly higher TN = 32 K than Pr2InPd2 (5 K) and Nd2InPd2 (8 K)37, with a spin-reorientation transition at μ0Hc = 4 T. Ref. 38 confirms TN = 29.4 K for Tb2InPd2. Based on neutron powder diffraction, the Tb magnetic moments of μeff = 10.54 μB (aligned along the c-axis) ecxeed the theoretically predicted value of 9.72 μB35,37. Substitution of In by Pd in Ce2InPd2 results in a transition from FM to AF ordering39. The fact that the specific heat of Yb2InPd2 is one order of magnitude larger than that of Yb2InAu2 is due to a high Yb 4f. density of states at the Fermi level, the intermediate valence of Yb being explained by hybridization with the Pd 4d states40. RE2PbPd2 compounds with RE = Ce, Nd, Sm, Gd, Tb, Dy, Ho, Er, and Tm show AF ordering at low temperatures (TN in the range of 3.6–35 K), Pr2PbPd2 is a Curie–Weiss paramagnet down to 1.72 K, and Y2PbPd2 and La2PbPd2 are weak Pauli paramagnets41. Ce2PbPd2 is subject to a weak Kondo effect with a Ce magnetic moment of 2.61 μB, and RE magnetic moments of 4.05 and 9.85 μB are found for Nd2PbPd2 and Tb2PbPd2, respectively41. Ce2MgSi2 shows helical AF ordering at TN = 12 K with magnetocrystalline anisotropy and a Ce magnetic moment of 2.47 μB42. An anomaly in the electrical resistivity of Nd2InGe2 at 9 K points to AF ordering with a small FM component43.
In the case of the RE2SnNi2 compounds the smaller RE elements Ho, Er, Tm, Lu, and Sc result in a Mo2FeB2 structure, whereas the larger RE elements Ce, Pr, Nd, Sm, Gd, Tb, Dy, and Y result in an orthorhombic W2CoB2 structure (space group Immm)44,45. Nd2SnNi2 exhibits AF ordering below TN = 21 K (which can be turned into FM ordering by a moderate magnetic field of 0.25 T) and two further magnetic transitions at 17.7 and 14–15 K20. Ce2SnNi2 is a Kondo system with TN = 4.7 K and TK ≈ 8 K, and Gd2SnNi2 and Tb2SnNi2 show oscillatory magnetocaloric effects20. Tb2SnNi2 transforms under high pressure (8 GPa) and high temperature (1470 K) to the Mo2FeB2 structure44. In the W2CoB2 structure it shows AF ordering below TN = 66 K (Tb magnetic moment of 8.7 μB; very close to a free Tb3+ ion) with magnetic transitions at 42 and 8 K (probably coexistence of FM and AF ordering), and a Curie–Weiss behavior above 80 K (Tb magnetic moment of 7.7 μB)20. In the temperature range of 5–220 K, Nd2SnNi2 and Tb2SnNi2 do not reach their theoretical saturation magnetization in a magnetic field of 100 kOe, which may be attributed to a canted magnetic structure20. For the isothermal magnetic entropy change in a magnetic field of 50 kOe values of 7.2, 0.1, 4.6, and 2.8 J/kg K are reported for Nd2SnNi2, Sm2SnNi2, Gd2SnNi2, and Tb2SnNi2, respectively20. Tb2SnNi2 shows striking similarities to (Pr,Ca)MnO3, since both these compounds are subject to coexistence of AF and FM ordering at low temperature with a magnetocaloric effect that switches from negative to positive when the temperature increases46.
Replacing the transition metal with a main group element has a drastic effect on the RE element and thus on the magnetic properties. To give an example, TN grows from 49 K in Gd2MgNi2 (additional magnetic transitions at 20.7 and 4.5 K47) to 150 K in Gd2MgGe248. The RE2MgGe2 compounds with RE = Nd, Gd, Tb, Dy, Ho, Er, and Tm show Curie–Weiss paramagnetism at high temperature, while Y2MgGe2 and Lu2MgGe2 display Pauli-like temperature independent paramagnetism49. AF ordering at 14, 13, 32, 55, 24, and 14 K is found for Nd2MgGe2, Sm2MgGe2, Gd2MgGe2, Tb2MgGe2, Dy2MgGe2, and Ho2MgGe2, respectively, while Er2MgGe2 and Tm2MgGe2 do not undergo magnetic ordering at least down to 5 K49. Since the type of magnetic ordering and ordering temperature are determined by the atomic interactions50 and there is a lack of detailed understanding, the present work addresses the class of RE2MgGe2 compounds from a first principles perspective.
Results and discussion
We use the full potential linear augmented plane wave plus local orbitals software WIEN2k51, which provides highly accurate results due to the fact that it is an all-electron implementation of density functional theory. The electronic wave functions are expanded in spherical harmonics (up to lmax = 10) within non-overlapping muffin-tin spheres centered at the nuclear sites and plane waves (limited by Kmax = 7/RMT,min) in the remaining space (interstitial region). The generalized gradient approximation is chosen for the exchange–correlation functional52. We employ 6 × 6 × 11 and 6 × 6 × 5 Monkhorst–Pack k-grids in the structural optimizations of unit cells and 1 × 1 × 2 supercells, respectively. The unit cells are non-primitive with two formula units (Fig. 1a). In the supercell calculations spin-polarization is taken into account with the RE atoms coupled ferromagnetically within the ab-plane and antiferromagnetically along the c-axis (Fig. 1b). Densities of states are calculated using a refined 10 × 10 × 9 Monkhorst–Pack k-grid and adding spin–orbit coupling by the polarized orbital method to obtain correct magnetic moments53,54.
In the tetragonal unit cell of RE2MgGe2 (Fig. 1a) the atoms occupy the Wykhoff positions RE 4 h (xRE, xRE + 1/2, 1/2), Ge 4 g (xGe, xGe + 1/2, 0), and Mg 2a (0, 0, 0). Both for non-magnetic and AF configurations, we relax xRE and xGe at different volumes and fit the total energy to the Murnaghan equation of state55 in order to obtain the equilibrium volume (Fig. 2a,b). Then we relax xRE and xGe at different c/a ratios and again fit the total energy to the Murnaghan equation of state in order to obtain the equilibrium c/a ratio (Fig. 2c,d) as well as the bulk modulus and its pressure derivative. Table 1 shows that AF ordering significantly modifies the unit cell volume for Nd2MgGe2 but not for Gd2MgGe2. It turns out that AF ordering results in energy gain of 0.5 eV per unit cell for Nd2MgGe2 and 2.3 eV per unit cell for Gd2MgGe2 with respect to the non-magnetic solution. We do not further investigate Sm2MgGe2, Tb2MgGe2, Dy2MgGe2, and Ho2MgGe2, as no qualitative difference can be expected. Y2MgGe2 and Lu2MgGe2 are not of interest, because no magnetic ordering is obtained, in agreement with Ref. 49. For Er2MgGe2 and Tm2MgGe2 our calculations predict magnetic ground states. However, absence of magnetic ordering above 5 K implies that the compounds undergo low temperature phase transitions, i.e., our results are not of experimental relevance and therefore excluded from the following discussions.
The obtained AF lattice constants in Table 1 deviate from the experimental values by less than 0.4% (a) and 2.3% (c)48,49. They turn out to be smaller for Gd2MgGe2 than Nd2MgGe2 though Gd is heavier than Nd (lanthanide contraction) and the shortest RE–RE distances within the ab-plane (3.72 Å for Nd2MgGe2, 3.66 Å for Gd2MgGe2) are significantly smaller than those along the c-axis (4.46 Å for Nd2MgGe2, 4.30 Å for Gd2MgGe2). This confirms the magnetic structure model of Ref. 49 that the localized RE 4f. spins realize FM ordering within the ab-plane and AF ordering mediated by RKKY interaction along the c-axis. As expected, we find B ∝ V0‒1, where V0 is the equilibrium unit cell volume. Rather small values of B reflect softness of the compounds under study. The magnetic moment \(M = g \sqrt {J\left( { J + 1 } \right)}\) depends on the Landé factor \(g = 1 + \frac{{J\left( {J + 1} \right) + S\left( {S + 1} \right) - L\left( {L + 1} \right)}}{{2J\left( {J + 1} \right)}}\) with J = L ± S for a less/more than half-filled shell56. Comparison of the obtained magnetic moments with experiment in Table 2 confirms the validity of our theoretical approach. The fact that they are almost purely of 4f. origin and close to those of free atoms demonstrates localized magnetism.
To study the nature of the chemical bonding, we evaluate the electronic density of states (DOS) in Figs. 3 and 4. We note that the local density approximation yields qualitatively the same behavior (Figure S1 in the Supporting Information) and that the wave function expansions are well converged (Figure S2 in the Supporting Information). For both the non-magnetic and AF configurations of the two compounds we obtain similar results, in particular a finite DOS at the Fermi level, i.e., a metallic state. The high non-magnetic DOS at the Fermi level (mainly Nd/Gd 4f. states) points to magnetism according to the Stoner criterion57. The symmetric shape of the AF DOS is due to the absence of a total magnetic moment. The AF DOS shows strong contributions of the Ge 4 s states at low energy, the Ge 4p states below the Fermi level, and the Nd/Gd 4f. states above the Fermi level. The Nd 4f. states are found from − 2 eV to 4 eV, whereas the Gd 4f. states give rise to pronounced peaks around − 4 eV and just above the Fermi level. As the compounds are isostructural, the nature of the chemical bonding is similar (except for the splitting of the Nd/Gd 4f. states) and the physical properties thus are expected to be comparable.
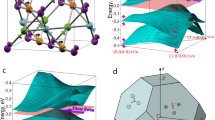
To better understand the magnetism, we evaluate as dominant perturbation the crystal field splitting of the localized and correlated 4f. states. We follow the methodology of Refs.58,59,60,61,62 to extract the crystal field parameters from our first principles calculations and obtain the ground state multiplet energies 0, 2, 13, 15, and 16 meV (first excited state: 245 meV) for the Nd3+ ions and 0, 0.01, 0.03, and 0.05 meV (first excited state: 3980 meV) for the Gd3+ ions. Nd3+ (4f3 electronic configuration) and Gd3+ (4f7 electronic configuration) are Kramer ions. While the ground state of Nd3+ (4I9/2, S = 3/2, L = 6, J = 9/2) is split by the crystal field into five Kramer doublets (in agreement with Ref. 63), Gd3+ has zero orbital moment in the ground state (8S7/2, S = 7/2, L = 0, J = 7/2) and, consequently, is not influenced by the crystal field in first approximation. The angular dependence of the ground state multiplet energies in a magnetic field aligned within the ab-plane (Fig. 5a,b) shows that a is the easy magnetic axis and b is the hard magnetic axis. The obtained magnetic susceptibilities approach the experimental curve for increasing temperature (Fig. 5c,d).
We analyze the electron density in terms of the quantum theory of atoms in molecules64 (CRITIC code65) by means of the critical points (CPs), which are categorized into nuclear, bond, ring, and cage CPs according to the Hessian matrix. Table 3 lists the locations and characteristics of all the symmetry-inequivalent CPs. As expected, the CPs are very similar for the two compounds. In Fig. 6 we represent the bond CPs (same order as in Table 3) by red spheres to identify the atoms linked by them. For Nd2MgGe2 the Ge-Mg bond CP is closer to Mg (2.03 Å) than Ge (3.41 Å), while the Ge–Nd bond CP is more centered. The electron density at the bond CPs is small and the Laplacian is close to zero (positive in the cases of the Ge-Mg and Ge–Nd bonds, negative in the cases of the Mg-Mg and Ge–Ge bonds; Table 3). For Gd2MgGe2 the Ge-Gd bond CP is closer to Gd (2.86 Å) than Ge (3.00 Å). Again the electron density at the CPs is small and the Laplacian is close to zero (positive in the case of the Ge-Gd bonds, negative in the cases of the Ge–Ge and Mg-Mg bonds; Table 3).
Table 4 lists the atomic volumes and corresponding integrated charges. 48% and 51% of the unit cell volume is filled by Ge for Nd2MgGe2 and Gd2MgGe2, respectively, 40% and 38% by RE, and 11% by Mg. We find a net transfer of charge from Nd/Gd and Mg to Ge, in agreement with the Pauling electronegativity. The obtained oxidation states deviate significantly from the nominal values of + 3 (Nd/Gd), + 2 (Mg), and ‒4 (Ge), confirming a metallic nature48, in contrast to the semiconducting charge distribution with neutral Mg proposed in Ref. 66. The global charge transfer is described by the ionicity \(c = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\frac{{\Delta Q_{i} }}{{OS_{i} }}}\)67, where N is the number of atomic sites i and \(\Delta Q_{i}\)/OSi is the ratio of the actual and nominal oxidation states. The values of 37% and 39% for Nd2MgGe2 and Gd2MgGe2, respectively, are indicative of dominant covalent bonding. Indeed, the electron localization function demonstrates strong covalent Mg-Mg bonds (Fig. 7a,c) and the electronic charges in Table 4 in conjunction with Fig. 7b,d point to polarized covalent Mg-Ge bonds. We estimate the degree of metallicity in terms of the electron density flatness f = ρmin/ρmax, where ρmin is the minimum electron density (at the cage1 CP) and ρmax is the maximum electron density (at the bond5 CP)65. As f = 1 represents metallic bonding and f = 0 represents localized bonding, the obtained values of 20% and 18% for Nd2MgGe2 and Gd2MgGe2, respectively, show that metallic bonding plays a limited role.
We use a Debye-Slater model to drive the thermodynamic properties68. Table 5 indicates that the two compounds behave similarly although Nd2MgGe2 shows slightly larger bulk modulus and Debye temperature. The heat capacity at constant pressure (Cp) turns out to be larger than the heat capacity at constant volume (CV), consistent with the relation Cp − CV = (αV)2BVpT, where αV, B, Vp, and T are the thermal expansion coefficient at constant volume, bulk modulus, volume of the primitive unit cell (Nd2MgGe2: ½ × 1592.4 Bohr3; Gd2MgGe2: ½ × 1590.2 Bohr3), and absolute temperature, respectively. According to Fig. 8a, CV ∝ T3 at low temperature and the Dulong-Petit limit is approached at high temperature. Low Debye temperatures reflect low thermal conductivities and melting temperatures. According to Fig. 8b, the volume expansion starts to become linear in T at about 150 K.
Conclusions
The structural, electronic, magnetic, and thermodynamic properties of the intermetallic compounds Nd2MgGe2 and Gd2MgGe2 have been investigated by full potential linearized augmented plane wave plus local orbitals calculations, employing the generalized gradient approximation for the exchange–correlation potential. The calculated lattice constants agree well with the available experimental data. Accounting for the spin–orbit coupling turns out to be mandatory to obtain correct magnetic moments and evaluate the electronic properties. Both compounds are found to combine metallicity with an AF ground state with localized magnetic moments. The chemical bonding turns out to be predominantly covalent. According to a Debye-Slater model, the thermal conductivity is low and the choice of the RE atom hardly affects the thermodynamic behavior.
References
Villars, P. & Calvert, L. D. (eds.), 2nd edn. https://searchworks.stanford.edu/view/2016804 (American Society for Metals, 1991).
Szytula, A. & Leciejewicz, J. Handbook of Crystal Structures and Magnetic Properties of Rare Earth Intermetallics (CRC Press, 1994).
Kaczorowski, D. & Gulay, L. D. Magnetic and electrical properties of a novel compound U2Pd2Pb. J. Alloys Compd. 419, 11–14 (2006).
Mallik, R., Sampathkumaran, E. V., Dumschat, J. & Wortmann, G. Magnetic ordering and spin fluctuation behavior in compounds of the type Ce2(Pd, Rh)2In. Solid State Commun. 102, 59–64 (1997).
Gannon, W. J. et al. Intermediate valence in single crystalline Yb2Si2Al. Phys. Rev. B 98, 075101 (2018).
Zaremba, V. I., Johrendt, D., Rodewald, U., Nychyporuk, P. & Pöttgen, R. Structure and chemical bonding of Ce2Ge2In and Ce2Pt2In. Solid State Sci. 7, 998–1002 (2005).
Wang, B., Liu, Y., Ye, J. & Wang, J. Electronic, magnetic and elastic properties of Mo2FeB2: first-principles calculations. Comput. Mater. Sci. 70, 133–139 (2013).
Shastry, B. S. & Sutherland, B. Exact ground state of a quantum mechanical antiferromagnet. Phys. B 108, 1069–1070 (1981).
Miyahara, S. & Ueda, K. Theory of the orthogonal dimer Heisenberg spin model for SrCu2(BO3)2. J. Phys. Condens. Matter 15, R327–R366 (2003).
Havela, L., Mašková, S., Daniš, S., Stelmakhovych, O. & Miliyanchuk, K. Large H absorption in Nd2Ni2In; magnetism in a new structure type. Mater. Res. Soc. Symp. Proc. 1216, W03-W12 (2010).
Carpentier, D. & Balents, L. Field theory for generalized Shastry–Sutherland models. Phys. Rev. B 65, 024427 (2002).
Sun, C., Yu, H. & Liu, W. Microstructure, mechanical properties and first-principles calculations of Mo2FeB2-based cermets with Mn addition. J. Ceram. Soc. Jpn. 125, 677–680 (2017).
Xuming, P., Yong, Z., Shaogang, W. & Qiuhong, W. Effect of Mn on valence-electron structure and properties of hard phase in Mo2FeB2-based cermets. Int. J. Refract. Met. Hard Mater. 27, 777–780 (2009).
Aghion, E., Bronfin, B. & Eliezer, D. The role of the magnesium industry in protecting the environment. J. Mater. Process. Technol. 117, 381–385 (2001).
Kraft, R., Fickenscher, T., Kotzyba, G., Hoffmann, R. & Pottgen, R. Intermetallic rare earth (RE) magnesium compounds REPdMg and RE2Pd2Mg. Intermetallics 11, 111–118 (2003).
Staiger, M., Pietak, A., Huadmai, J. & Dias, G. Magnesium and its alloys as orthopedic biomaterials: a review. Biomaterials 27, 1728–1734 (2006).
Ourane, B. Recherche Exploratoire de Nouveaux Intermétalliques Ternaires à Base de Magnésium, Application au Stockage d’Hydrogène, Doctoral Thesis, Bordeaux University (2014).
Miliyanchuk, K., Maskova, S., Havela, L. & Gladyshevskii, R. Influence of hydrogenation on the magnetic properties of Er2Ni2Al. Chem. Met. Alloys. 9, 169–173 (2016).
Mašková, S. Structure and Magnetic Properties of F-Electron Compounds and Their Hydrides, Doctoral Thesis, Charles University in Prague, Faculty of Mathematics and Physics (2013).
Kumar, P., Singh, N. K., Suresh, K. G. & Nigam, A. K. Magnetocaloric and magnetotransport properties of R2Ni2Sn compounds (RE = Ce, Nd, Sm, Gd, and Tb). Phys. Rev. B 77, 184411 (2008).
Proceedings of the First International Conference on Magnetic Refrigeration at Room Temperature, edited by P. W. Egolf, International Institute of Refrigeration, Paris, France (2005).
Lafargue, D. Structures Magnétiques de Nouveaux Stannures Ternaires a Base d'Uranium ou de Terres Rares T2M2Sn (T = RE, U et M = Ni, Pd), Doctoral Thesis, Sciences et Technologies University, Bordeaux I (1997).
Mašková, S. et al. U2Ni2Sn and the origin of magnetic anisotropy in uranium compounds. Phys. Rev. B 99, 064415 (2019).
Prokeg, K., Brfick, E., Nakotte, H., de Chfitel, P. F. & de Boer, F. R. Simple calculation of hybridization effects in UTX and U2T2X compounds. Phys. B 206(207), 8–10 (1995).
Richter, M., Zahn, P., Divis, M. & Mertig, I. Giant magnetoresistance in uranium intermetallics: ab initio calculations for U2Pd2In and U2Pd2Sn. Phys. Rev. B 54, 11985–11988 (1996).
Lukachuk, M. & Pöttgen, R. Intermetallic compounds with ordered U3Si2 or Zr3Al2 type structure-crystal chemistry, chemical bonding and physical properties. Z. Kristallogr. 218, 767–787 (2003).
Hulliger, F. On tetragonal M2Au2In and related compounds. J. Alloys Compd. 232, 160–164 (1996).
Sereni, J. G., Roberts, J., Gastaldo, F. & Giovannini, M. Suppression of the Shastry–Sutherland phase driven by electronic concentration reduction in magnetically frustrated Ce2.15Pd1.95(Sn1−yIny)0.9 alloys. Phys. Rev. B 100, 054421 (2019).
Sereni, J. G., Roberts, J., G-Bastaldo, F., Gerisso, M. & Giovannini, M. Shastry–Sutherland phase formation in magnetically frustrated Ce2Pd2In1−xSnx alloys. Mater. Today Proc. 14, 80–83 (2019).
Kabeya, N. et al. Antiferromagnetic ground state and heavy-fermion behavior in Ce2Pt2Pb. Phys. Rev. B 98, 035131 (2018).
Zhang, Z., Wang, P., Ronga, H. & Li, L. Structural and cryogenic magnetic properties of RE2Ni2In (RE = Pr, Nd, Dy and Ho) compounds. Dalton Trans. 48, 17792–17799 (2019).
Maskova, S., Danis, S., Llobet, A., Nakotte, H. & Havela, L. Large magnetocaloric effect in Nd2Ni2In. Acta Phys. Pol. A 126, 282–283 (2014).
Mašková, S. et al. Impact of hydrogen absorption on crystal structure and magnetic properties of geometrically frustrated Nd2Ni2In. J. Alloys Compd. 566, 22–30 (2016).
Mašková, S., Havela, L. & Daniš, S. Enormous Hydrogen Absorption in Nd2Ni2In, in WDS'09 Proceedings of Contributed Papers, Part III 109–112 (2009).
Maškova, S. et al. Magnetic properties of Tb2Pd2In. Single Cryst. Study Solid State Phenom. 194, 58–61 (2013).
Sala, G., Mašková, S. & Stone, M. B. Frustrated ground state in the metallic ising antiferromagnet Nd2Ni2In. Phys. Rev. Mater. 1, 054404 (2017).
Fischer, P. et al. Antiferromagnetic rare-earth ordering in the intermetallic compounds R2Pd2In (R = Pr, Nd). J. Phys. Condens. Matter 12, 7089–7098 (2000).
Maskova-Cerna, S. et al. New type of magnetic structure in the R2T2X group: Tb2Pd2In. J. Phys. Condens. Matter 32, 345801 (2020).
Giovannini, M. et al. Effect of nonstoichiometry on the transition from ferromagnetism to antiferromagnetism in the ternary indides Ce1.95Pd2+2xIn1−x and Ce2+xPd1.85In1−x. Phys. Rev. B 61, 4044–4053 (2000).
Giovannini, M. et al. Characterization and physical properties of the indides Yb2T2In (T = Cu, Pd, Au). Intermetallics 9, 481–485 (2001).
Kaczorowski, D. & Gulay, L. D. Magnetic and electrical properties of RE2Pd2Pb (RE = Y, La-Sm, Gd-Tm) compounds. J. Alloys Compd. 442, 169–171 (2007).
Dhar, S. K., Manfrinetti, P. & Palenzona, A. Magnetic ordering in CeMg2Si2 and Ce2MgSi2. J. Alloys Compd. 252, 24–27 (1997).
Zaremba, V. I., Kaczorowski, D., Nychyporuk, G. P., Rodewald, U. C. & Pöttgen, R. Structure and physical properties of RE2Ge2In (RE = La, Ce, Pr, Nd). Solid State Sci. 6, 1301–1306 (2004).
Heymann, G. et al. High-pressure phases of Tb2Ni2Sn and Dy2Ni2Sn. Monatsh. Chem. 145, 863–867 (2014).
Heying, B., Rodewald, U., Chevalier, B. & Pottgen, R. The stannides RE2Ni2Sn (RE = Pr, Ho, Er, Tm)—structural transition from the W2B2Co to the Mo2B2Fe type as a function of the rare earth size. Z. Naturforsch. B 68, 10–16 (2014).
Gomes, A. M., Garcia, F., Guimarães, A. P., Reis, M. S. & Amaral, V. S. Field-tuned magnetocaloric effect in metamagnetic manganite system. Appl. Phys. Lett. 85, 4974–4976 (2004).
Łatka, K., Kmiec, R., Pacyna, A. W., Mishra, R. & Pöttgen, R. Magnetism and hyperfine interactions in Gd2Ni2Mg. Solid State Sci. 3, 545–558 (2001).
Choe, W., Mille, G. J. & Levin, E. M. Crystal structure and magnetism of Gd2MgGe2. J. Alloys Compd. 329, 121–130 (2001).
Suen, N., Tobash, P. H. & Bobev, S. Synthesis, structural characterization and magnetic properties of RE2MgGe2 (RE = Rare-Earth Metal). J. Solid State Chem. 184, 2941–2947 (2011).
Kraft, R. & Pottgen, R. Ternary germanides RE2Ge2Mg (RE = Y, La-Nd, Sm, Gd, Tb). Monatsh. Chem. 135, 1327–1334 (2004).
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, D. & Luitz, J. WIEN2k: An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties (Technische Universität Wien, 2001).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Brooks, M. S. S. Calculated ground state properties of light actinide metals and their compounds. Phys. B 130, 6–12 (1985).
Eriksson, O., Johansson, B. & Brooks, M. S. S. Meta-magnetism in UCoAl. J. Phys. C 1, 4005–4011 (1989).
Murnaghan, F. D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 30, 244–247 (1944).
Buschow, K. H. J. & de Boer, F. R. Physics of Magnetism and Magnetic Materials (Kluwer Academic Publishers, 2003).
Stoner, E. C. Collective electron specific heat and spin paramagnetism in metals. Proc. R. Soc. A 154, 656–678 (1936).
Novák, P., Knížek, K. & Kuneš, J. Crystal field parameters with wannier functions: application to rare-earth aluminates. Phys. Rev. B 87, 205139 (2013).
Mihóková, E., Novák, P. & Laguta, V. Crystal field and magnetism with Wannier functions: rare-earth doped aluminum garnets. J. Rare Earth 33, 1316–1323 (2015).
Novák, P., Kuneš, J. & Knížek, K. Crystal field of rare earth impurities in LaF3. Opt. Mater. 37, 414–418 (2014).
Novák, P., Knížek, K., Maryško, M., Jirák, Z. & Kuneš, J. Crystal field and magnetism of Pr3+ and Nd3+ ions in orthorhombic perovskites. J. Phys. Condens. Matter 25, 446001 (2013).
Novák, P., Nekvasil, V. & Knížek, K. Crystal field and magnetism with Wannier functions: orthorhombic rare-earth manganites. J. Magn. Magn. Mater. 358–359, 228–232 (2014).
Popova, M. N. et al. Optical spectra, crystal-field parameters, and magnetic susceptibility of multiferroic NdFe3(BO3)4. Phys. Rev. B 75, 224435 (2007).
Bader, R. F. W. Atoms in Molecules (Oxford University Press, 1990).
Otero-de-la-Roza, A., Blanco, M. A., Martin Pendas, A. & Luana, V. Critic: a new program for the topological analysis of solid-state electron densities. Comput. Phys. Comm. 180, 157–166 (2009).
Whangbo, M.-H., Lee, C. & Köhler, J. Transition-metal anions in solids and their implications on bonding. Angew. Chem. 45, 7465–7469 (2006).
Sanchez, P. M., Pendas, A. M. & Luana, V. A classification of covalent, ionic, and metallic solids based on the electron density. J. Am. Chem. Soc. 124, 14721–14723 (2002).
Otero-de-la-Roza, A., Abbasi-Pérez, D. & Luana, V. Gibbs2: a new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 182, 2232–2248 (2011).
Acknowledgements
The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST).
Author information
Authors and Affiliations
Contributions
S.M. and O.M.A. conducted the calculations. U.S. contributed to the analysis of the results and writing of the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Menouer, S., Abid, O.M., Benzair, A. et al. First principles calculations of the structural, electronic, magnetic, and thermodynamic properties of the Nd2MgGe2 and Gd2MgGe2 intermetallic compounds. Sci Rep 11, 10870 (2021). https://doi.org/10.1038/s41598-021-89042-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-89042-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.