Abstract
Habitat selection is a basic aspect of the ecology of many species, yet often the term is conflated or confused with both habitat preference and habitat use. We argue that each term fits within a conceptual framework that can be viewed in Bayesian terms and demonstrate, using long-term data on occupancy patterns of a grassland grouse, how prior probability profiles can be estimated. We obtained estimates by specifically focusing on whether and to what extent the Lesser Prairie-Chicken (Tympanuchus pallidicinctus) avoids anthropogenic features such as roads, powerlines, petroleum wells, fences, and buildings, in two study areas, one with denser and one with sparser incidence of features. Grouse strongly avoided large features such as outbuildings and tended to avoid tall features such as powerlines; by contrast, grouse did not or only slightly avoided low, unobtrusive features such as fences. We further examined co-location of pairs of anthropogenic features and found that certain features were avoided so strongly that avoidance distance may be shorter for other features; that is, birds were “pushed toward” some features because they are “pushed away” from others. In each case, our approach points toward a means to incorporate avoidance behavior directly into analytic studies of habitat selection, in that data on use (the posterior, as it were) could be used to infer the selection process provided data on preference (the prior, as it were) could be obtained.
Similar content being viewed by others
Introduction
Habitat selection, preference, and use are not equivalent terms. Selection refers to non-random occupancy of habitat bearing some consequences on individual fitness1, preference is conceptualized as a probability distribution of an individual’s selection for a habitat when offered alternatives2, and use describes resultant patterns, which may be mitigated by factors outside of preference, such as competition pressure or predation risk. Habitat selection itself is active, not passive, with a prerequisite of cognitive assessment among available choices (Fig. 1).
Conceptual schematic of distinctions and relationships between habitat preference (here with an example of a probability distribution for a single cue, i.e., landscape feature), habitat selection, and habitat use. For the example of use, availability is considered to be near zero, so the patch (the hatched box) is unoccupied.
A key aspect of cognitive assessment inherent to habitat selection is the possibility of avoidance, a type of assessment that has its own consequences3. Avoidance is both an outcome of intrinsic negative preference and a complex reaction attenuated by an individual's ecological context. Even so, avoidance is not merely an individual's maintenance of negative preference for a given habitat, even though patterns of use may appear equivalent in a binary case. For example, if an organism prefers habitat B to habitat A (Fig. 2), it may select habitat B every time when only A and B are available, but it may not avoid habitat A in another context, as when the second option is habitat D. In that case, the organism may select habitat A every time given those two options but always avoid habitat D regardless of the alternative, even against an option for which an individual has no preference (habitat C in Fig. 2).
Conceptual schematic of habitat preference viewed as a probability distribution. Four habitats, (A–D) are available to the organism, which has a moderate preference for (A), strong preference for (B), low preference for (D), and no preference for (C). We posit that such distributions can be used as priors in a Bayesian framework.
It is tempting, then, to conclude that preference and subsequent selection are relative, with preference expected to be “hard wired” to the extent it is under natural selection4, meaning some aspect of individuals’ habitat selection will reflect the landscape’s contextual history5. In this view, an organism will assess particular cues, such as vegetation structure or water availability (among many possibilities), to build its probability distribution of preference. Human alteration of the landscape’s fragmentation, biotic interactions, and physical structure (our focus in this study) can disconnect cues from outcomes (i.e., fitness components) either by leaving cues unchanged but reducing fitness (ecological traps6) or leaving fitness unchanged but altering cues (perceptual traps3). Potential fitness consequences have received the bulk of attention in the literature, including the role of habitat avoidance in speciation7, yet altered cues matter a great deal given that otherwise suitable habitat may be avoided.
Habitat avoidance falls under the purview of sensory ecology, “the study of how organisms acquire and respond to information in their environment”8, with avoidance comprising an outcome of “acquisition of information from the abiotic environment (cues) by a single organism”8 and subsequent processing of that information. Estimating the extent and magnitude of avoidance is a challenge precisely because an organism will either not occur in or occur in low densities in habitats perceived to be unsuitable (e.g., habitat D in Fig. 2). Here avoidance must be identified by absence of certain habitat cues, which assumes sufficient knowledge of a species’ ecology, such as consistent presence of cues in occupied habitat. Despite this complication, we can make substantial inroads toward understanding what information matters to an individual’s avoidance with rigorous evaluation of patterns of habitat use and exploration of cues that vary across the landscape.
We suggest a conceptual approach to model and analyze the overall process grounded in Bayesian thinking. Frequentist statistics test how well data fit an established model (e.g., a t distribution); Bayesian statistics test how well models fit data at hand and explicitly take into account prior knowledge of data distributions or parameter estimates. We posit that preference can be treated as an informative prior, a statistical distribution of preference grounded in existing knowledge of a species’ habitat preferences and habitat selection cues. It is standard in Bayesian models to update the prior (i.e., a parameter estimate) with subsequent information. Our approach resembles the concept that habitat preference, selection, and use form a feedback loop resulting from individual behavior across generations. Treating preference as a prior suggests a direct utility of analyses of avoidance behavior such as ours, in that results could be used to build a probability distribution across selected cues rather than beginning with an assumption of flat priors, an assumption that animals have no initial preference (e.g., Fig. 2C). We further posit that selection, as we restrict its definition (Fig. 1), can be treated as the likelihood. It is the process that, combined with the prior, determines extrinsic behavior. The endpoint of such a Bayesian formulation is a posterior distribution (the model estimate) that can be viewed as use (Fig. 1).
We use long-term tracking data in an anthropogenically modified landscape to assess patterns of avoidance and four potential causal processes of it. In our system, cues were altered in that humans placed objects on a landscape, objects such as powerlines, roads, or oil wells. On the basis of research on avoidance behavior in grouse9,10, it is expected such objects (hereafter called features) would affect the sensory ecology of our focal species, the Lesser Prairie-Chicken (Tympanuchus pallidicinctus), a rare and declining grouse endemic to arid grasslands of the south-central United States (see “Focal species”, below). We postulated four novel hypotheses that explain how and why individual grouse avoid these man-made features.
-
(1)
“Proportional use” posits that grouse will, on average, distribute themselves across the landscape at distances directly in proportion to the spatial density of any anthropogenic feature. In essence, then, this idea corresponds to a null expectation and as such implies no avoidance.
-
(2)
“Egalitarian avoidance” posits demonstrable equitable non-use of areas near to any anthropogenic feature; i.e., all anthropogenic features are avoided equally. Under this hypothesis, avoidance distance from feature A is the same as it is to feature B, regardless of the spatial density of either feature.
-
(3)
“Selective avoidance” differs from “egalitarian avoidance” in that grouse avoid some features more than others. Perhaps they avoid roads more (i.e., avoidance at a greater distance) than fences because the former is noisier, or perhaps they avoid powerlines or outbuildings more than oil or gas wells because these features are more prominent (both taller and seemingly more massive). As with the first two hypotheses, “selective avoidance” does not consider spatial density of a given feature.
-
(4)
“Rather be elsewhere” posits that apparent avoidance of a feature reflects either a preference for another feature or a density-dependent—in terms of the features, not of the grouse—response such that stronger avoidance of feature A “pushes” a grouse nearer to feature B, which it otherwise would avoid but cannot given its situation.
Grouse that avoid a feature ought to occur farther (statistically) from a feature than realizations of random points would in the same context. A corollary to this simple decision rule is that statistically nearer distances could be considered preference for proximity to a feature. This rule and associated analyses led us to key statistical predictions for a distance parameter, d[], for each hypothesis with regard to random points (R) and grouse locations (G):
-
H1: no difference; i.e., d[R] = d[G].
-
H2: d[G] > d[R], with d[Gi] = d[Gj] for any feature i or j.
-
H3: d[G] > d[R], with d[Gi] > d[Gj] for some features i and j, i ≠ j.
-
H4: d[Gij]/d[Rij] < 1, = 1, or > 1 if, respectively, nearer to, the same distance from, or farther from feature i versus feature j, i ≠ j, for grouse occurrences relative to random points.
The final prediction indicates whether bird occurrences are clustered, randomly placed, or dispersed relative to random points for any two features (i.e., covariation in feature avoidance). We tested each prediction with a suite of Bayesian models.
Methods
Focal species
The Lesser Prairie-Chicken is a medium-sized grouse endemic to, broadly, the shortgrass prairie ecosystem of the south-central United States, where it is found only in southwestern Colorado, western Kansas, northwestern Oklahoma, the Texas panhandle, and eastern New Mexico. As with almost all open-country grouse of temperate environments, the Lesser Prairie-Chicken forms leks at which a cluster of males (in this species, usually 5–12 individuals) display vigorously and female visit to assess males with an intent to secure sperm to fertilize her eggs, which she will lay and raise without male help. Outside of male lekking (mid-March to mid-May) and female nesting (late April to early July), birds congregate is small flocks to forage, at times on grain remains in farmed fields but typically, as through the rest of the life cycle, restricting themselves to native prairie. Accordingly, this species has three distinct aspects of habitat selection: general occurrence, lek placement, and nest placement.
Data
Lesser Prairie-Chicken were tracked at two study sites, one in Roosevelt County in east-central New Mexico, U.S.A., the other in Beaver, Harper, and Ellis Counties in northwestern Oklahoma, U.S.A. Birds tagged with VHF transmitters were tracked from April 1999–March 2006 in New Mexico and from March 1999–July 2013 in Oklahoma11,12,13,14. Study periods differed chiefly because of funding, which for New Mexico was insufficient after 2006. The study sites differ markedly in land tenure history. Parcel size in New Mexico averages 1300 ha versus 180 ha in Oklahoma11. The difference largely stems from settlement patterns over the past two centuries. New Mexico was part of the Spanish land grant system, which tended to yield huge parcels. In our study area, parcels approach 8 km2 (> 1900 acres). By contrast, during the “land rush” era of the late 19th Century most of northwestern Oklahoma was parceled into 65-ha (160-acre) plots as part of the United States’ Homestead Act. Smaller parcels translate to a higher density of roads, fences, buildings, and powerlines11.
Radiotracking typically yielded a triplet of coordinate readings, from which we had to triangulate a grouse’s location. We estimated latitude and longitude using a maximum likelihood estimator (MLE), although it some cases the MLE algorithm failed to converge. If it failed, we instead used the Andrew and Huber methods15. R code for the estimation procedure can be found at https://github.com/henry-dang/triangulation/blob/master/lenth_triang.R.
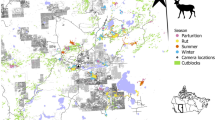
From these data we used kernel density methods (R package ks16) to estimate annual home ranges (235 in New Mexico, 263 in Oklahoma). Tracking data included lek (12 in New Mexico, 23 in Oklahoma) and nest (122 in New Mexico, 128 Oklahoma) locations. For home range centroids, the outer contour of home ranges, leks, and nests, we estimated distance to seven anthropogenic features: roads (highways, primary, and secondary roads only; small farm roads or one-lane gravel roads were excluded), powerlines (overhead only, with buried or trunk lines excluded; https://hifld-geoplatform.opendata.arcgis.com/datasets/electric-power-transmission-lines), oil wells, gas wells (for both types of wells, http://www.occeweb.com and http://www.emnrd.state.nm.us/ocd), outbuildings (barns, grain silos, poultry houses, and similar large structures; chiefly the TIGER database), and fences (Bureau of Land Management) in both states, plus private houses in New Mexico and railroad tracks in Oklahoma. We placed 2000 random points on each study area to estimate distances to each of these same anthropogenic features, which provided an estimate of feature density on the landscape.
Analyses
The initial step was to estimate the probability of a grouse occurring a certain distance from a feature. We treated New Mexico and Oklahoma data separately, giving us a replicate assessment because these populations have been isolated from each other for > 100 years17 and, as noted above, land tenure history differs strikingly between the states11. We estimated probabilities of grouse occurrence, πi, via a Bayesian model with binomial likelihood and flat prior (i.e., no assumption of the central tendency of occurrence probability at a given distance from a feature):
yi ~ binomial (πi, n) with yi the cumulative count of grouse at distance i (i.e., the data) and n the total number of home ranges, leks, or nests. Distances, i, were binned to the smallest extent possible, from 10 to 100 m, to allow the Markov chain Monte Carlo (MCMC) algorithm to converge in a reasonable number of iterations (e.g., < 100,000). (In Bayesian statistics, MCMC is used to build a posterior probability distribution from the product of the prior and the likelihood without having to integrate the often intractable denominator in the Bayes’ theorem formulation. The algorithm “allows one to characterize a distribution without knowing all of the distribution’s mathematical properties by randomly sampling values out of the distribution”18.) We used the same process for random points to estimate probability of feature occurrence at a given distance, the idea being to establish a null expectation of density of class in each study area. We plotted resultant bird and random curves to get an idea of whether grouse avoided the feature (Fig. 3A). If grouse neither avoided nor preferred a feature, then its curve and the random curve would trace similar arcs (within credible intervals; see below). If instead grouse avoided a feature, then its curves would intersect the random one at some distance from the origin (Fig. 3A); the converse holds for preference.
Analytic process used to determine presence and magnitude of avoidance thresholds. All examples use data for home range centroids. (A) Probabilities (± Bayesian highest density credible intervals) of occurrence of an individual Lesser Prairie-Chickens and random points at a given distance from an feature (in this case roads in New Mexico, binned at 100 m). (B) Difference in random and prairie-chicken points for the same data set. The point at which the difference curve crosses 0 is the threshold. (C) The search window (small box) to estimate the threshold often was unambiguous (fences, New Mexico, binned at 10 m). (D) For unclear cases, we conservatively searched for the threshold at the shorter distance (left box, where credible intervals cross 0) rather than the direct point (right box) crossed (fences, Oklahoma, binned at 10 m).
To assess if and to what extent grouse avoid a feature, we extended the Bayesian model to calculate a difference in probabilities between random points and grouse occurrence (Fig. 3B19). (At root, our method resembles a resource selection ratio20, but it was derived independently within a Bayesian framework.) We used the posterior probability distributions of these differences to search for the point at which grouse and random curves converged, the threshold distance (T). Our algorithm was.
-
(1)
calculate differences per bin, πRi–πGi, with associated posteriors;
-
(2)
use the extent (q) to which a posterior distribution overlapped 0 to estimate the probability (p) that the threshold occurred in bin k, with pk = 1 − 2|qk − ½|;
-
(3)
locate the apparent crossover region given calculated differences; usually the crossover was unambiguous (Fig. 3C), but if credible intervals overlapped 0 before the bulk of the distribution crossed (Fig. 3D), we conservatively used the region with the shorter distance so as not to overestimate distance;
-
(4)
estimate T as a weighted average of probabilities pk ± 500 m of apparent crossover, with pk as weights and for the kth bin (small boxes in Fig. 3C,D).
This algorithm yielded an estimate of T as a posterior probability distribution, from which we calculated threshold distance as the median and uncertainty as the highest density credible intervals, the broadest probability density that includes the mode. (A Bayesian credible interval is calculated directly from the posterior distribution and states that, say, 95% of parameter estimates lie between upper and lower bounds.) If the lower interval overlapped or closely approached 0, we could reasonably conclude the feature was not avoided. We supplemented threshold analyses with a Bayesian estimate, with log-normal likelihood and flat prior, of prediction intervals for grouse occurrence relative to a feature. From these estimates we calculated a coefficient of variation to evaluate whether areas with higher feature density had greater uncertainty for distance estimates. Lastly, we compared feature density at each study site by means of a Bayesian analog to a two-sample t-test21, with t likelihood and flat prior.
Our final analysis assessed the extent to which avoidance of one feature might suggest preference for another or an instance of “co-avoidance”; i.e., it assesses colocation in a manner related to a cross-K function22. Available data were distance from a grouse (home range centroid only; sample size was otherwise too low) or random point to a given feature. We estimated distance, d, between one feature and another feature by means of the cosine rule:
where A is the distance from a grouse to the first feature, B is the distance from a grouse to the second feature, and θ is the angle between them (Fig. 4). We built a Bayesian model to estimate d for grouse (dG) and for random points (dR), with log-normal likelihood and θ as a flat prior. We used estimated distances to estimate a dispersion ratio, dG/dR, for which values less than one (i.e., below the lower credible interval of the estimate) implied a clumped distribution, values greater than one (i.e., beyond the upper credible interval) implied a dispersed distribution, and values between (i.e., within the credible intervals) implied a random distribution. The logic behind this ratio is that if avoidance of one feature was stronger than avoidance of another, then the ratio would increase: if B is unchanged, a decrease in A will increase d (Fig. 4), implying that strong aversion of B “pushes” organisms nearer to A as an effect of their preferences. The reverse situation implies that an organism is equally averse to the features or prefers one feature to another even if both are avoided (i.e., they are “lesser evils”).
Each of our Bayesian models was coded in JAGS and run via package rjags23 in R, with associated R code to support hierarchical flow (i.e., to manage data between some stages of the analyses).
Results
Density of all features across the landscape was markedly higher in Oklahoma than in New Mexico (Table 1). Even in the case of road density, for which the 95% highest density credible intervals of the difference overlapped 0, it remained that with probability 0.93 the true and underlying mean distance to a road from a random point in New Mexico was farther than a random point in Oklahoma.
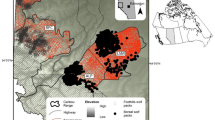
Regardless of the density of a feature, we found evidence of avoidance, although estimated threshold distances were shorter in Oklahoma (Table 2, Fig. 5). Estimated thresholds varied across features, often messily. Even so, outbuildings were avoided at a considerable distance (> 1 km) in either state, whereas fences were avoided at a slighter distance (< 100 m) in either state (Fig. 5). State-for-state, estimated thresholds were similar for leks, nests, or home range centroids but were, as logic would dictate, shorter for home range contours (Table 2). Prediction intervals and associated coefficients of variation implied greater uncertainty of distance estimates in Oklahoma irrespective of feature (Appendix S1).
Estimated threshold avoidance distance ± Bayesian highest density credible intervals (gray ellipses) for the Lesser Prairie-Chicken, with, for comparative purposes, Bayesian 95% prediction intervals (black lines, with the tick marking the median) and the minimum recorded distance from a feature (x). Results are for centroids of home ranges for the Oklahoma (top) and New Mexico (bottom) study sites. Note the logarithmic scale on the x-axis.
We found evidence for colocation effects, i.e., where a relationship with one feature might suggest preference or avoidance with another feature. For example, at the Oklahoma study site, grouse consistently avoided outbuildings at a greater distance than other features (Fig. 5), such that estimates of avoidance distances to some features may have been shorter than if outbuildings were removed from the landscape; i.e., the dispersion ratio was consistently > 1.0, implying strong avoidance of one feature (outbuildings) relative to other features. Conversely, gas wells and fences were viewed as more benign, all else being equal (Fig. 6). The latter pattern held in New Mexico, too, where in some circumstances oil wells appeared to be “lesser evils” (Fig. 6). At that study site, though, grouse avoided powerlines (in particular) and roads at a greater distance than they did in Oklahoma (Fig. 5), such that higher dispersion ratios were estimated when response to a more “severe” feature (e.g., a road) was compared to a more “benign” feature (e.g., a fence).
Depiction of clustered (ratio ± Bayesian highest density credible intervals < 1), random (ratio ± CI = 1), or dispersed (ratio ± CI > 1) occurrence of Lesser Prairie-Chickens relative to two features considered jointly (see Fig. 5 for a key to symbols used). Results are for centroids of home ranges for the Oklahoma (top) and New Mexico (bottom) study sites and are assumed symmetrical (i.e., mean distance from, say, fence to road is assumed to be the same as from road to fence) as opposed to a model that allowed for weighted (asymmetrical) ratios.
Discussion
Avoidance behavior
Many organisms are reported to avoid anthropogenic features9,10,24,25,26, yet the “unintended but potentially profound consequences of infrastructure on animals remain poorly understood”27. The nature of avoidance exacerbates its study because observed absence of use must be relied upon as an indication of putative avoidance behavior; hence, we analyzed binned data of habitat use to elucidate feature avoidance. In doing so, we add to evidence that the Lesser Prairie-Chicken avoids various man-made features9,28,29,30, but our analyses go further because they provide estimates of avoidance distances. A quantified animal behavior such as avoidance distance can inform conservation planning, concerns about transferability among sites and species notwithstanding31. Such concerns may have merit in this system in light of distinct differences in avoidance distances between our two study sites, which differ fundamentally in both land tenure (see “Methods”: Data) and floristic composition and structure11,12.
Leveraging Markov chain Monte Carlo to approximate a posterior habitat preference distribution for models considering animals’ exposure to dis-amenity or negative cues constitutes a novel way to describe influences that lead to avoidance. Research that used animal locations to infer habitat use has informed spatial ecology, movement ecology, and conservation planning. Following the early logic of bounding extent methods that examined habitat availability and use from known animal locations, improvements to understanding habitat use have incorporated approaches from computational geometry32, probabilistic approaches33,34, simulation35,36,37, and methods adapted from time geography38,39,40 in their estimation of utilization distributions. Methods that combine and connect ideas among these themes are emergent, too41. Combination of the action and effect of preference in these estimates generally is limited. Modeling behavioral influences on the expression of habitat avoidance represents an unexplored and promising avenue for growth in this pursuit.
Our analyses allowed us to reject our first hypothesis: rather than distribute themselves randomly across the landscape, Lesser Prairie-Chickens avoid anthropogenic features. We likewise were able to reject our second hypothesis: anthropogenic features are not avoided uniformly. Instead, some features were avoided at a greater distance than others, even when accounting for differences in feature density, a pattern that held in both study areas and whether we considered home range centroid, lek location, or nest placement. Features avoided the most tended to be tall, imposing, or noisy, such as powerlines, outbuildings, and roads, whereas those avoided the least tended to be small and static, such as gas wells and fences, a result that lent support to our third hypothesis. Even so, this result is complicated by apparent covariation in avoidance, corresponding to our fourth hypothesis, which is not mutually exclusive of the third. We suggest that strong avoidance of large, imposing features reduced estimates of avoidance to other, less imposing features.
Our specific findings contradict those reported in a review paper on avoidance behavior in grouse10. Across 8–9 species of grouse, including the Lesser Prairie-Chicken, they “found that oil and gas structures had the greatest negative effect on displacement behaviour”, yet our data for a single species indicated that oil well and gas wells had among the shortest avoidance distances, and avoidance distances were less than the median distances from random points to the features, indicating that the threshold occurred well before feature density saturated on the landscape. Likewise, the review10 reported a low effect of displacement from powerlines and outbuildings, yet we found that outbuildings, especially, had among the highest avoidance thresholds at our two study sites. Our results correspond better to those of two subsequent studies focused on the Lesser Prairie-Chicken29,30, which reported strong avoidance of tall features such as powerlines and wind turbines; e.g., “[d]istance to powerline [was] the single most consistent variable negatively affecting nest placement,” and oil wells had no effect on placement of home ranges or nests29. We found that grouse avoided oil wells, as did one study29 when data were pooled, and both that study and ours found that avoidance of oil wells was of a smaller magnitude (i.e., shorter distance) than avoidance of other features. Across all studies, including the important meta-analysis10, it is clear that grouse avoid man-made features, with avoidance distance varying with feature type.
We caution that our estimates of avoidance distance, as with those in many studies, are based on best available data but nonetheless may suffer from exactly where the study area was sited. Perhaps a study area was selected that had numerous long-standing leks but in or near which no development had occurred. Compared to a study area embedded in an area of intensive land use, estimates of avoidance distance would necessarily be higher. We are confident that our methods elucidate relative avoidance distances well, but if we assume an estimable parameter for avoidance distance exists, then such estimates are highly uncertain (Fig. 5). After all, apparent avoidance could result from human preference to build in certain parts of a landscape (e.g., in valley floors) or a legacy of haphazard settlement patterns. Our model did not incorporate as a covariate variation across the landscape in vegetation or geography, because we only sampled two non-overlapping ecoregions for a species with extremely specific structural preferences. Nonetheless, our model could be modified readily to accommodate such covariates in other study systems that include more types of land cover, ecoregions in common between study sites, or in species with a wider range of remotely detectable vegetation differences (or with more local vegetation data obtained). Short of controlled experiments, which are nearly impossible in studies of avoidance of large features, the ideal is a before-after/control-impact (BACI) design42. Even so, comparisons between areas with striking differences in feature density, as in our system (Table 1), are valuable, too, in the same way that the comparative method is valuable in evolutionary studies.
Habitat selection and avoidance
Our analytic approach points toward a means to incorporate avoidance behavior directly into studies of habitat selection. At root, we focus on providing a model of animal perception, an intrinsic aspect of an organism that governs how cues are assessed to judge habitat suitability, the very substance of habitat preference (Figs. 1, 2). The probability distribution2 of preference is not fixed but is shaped by fitness consequences of habitat use. It is a feedback loop: observed habitat use by individuals is a result of preference and pressures and context that shape selection, with use in turn affecting preference visible in populations. Habitat selection is itself a complex and temporally dynamic process driven initially by preference but shaped by various extrinsic factors, from competition to predation and from disturbance to availability.
It is imperative that we begin to link sensory ecology, including avoidance, to basic aspects of habitat occupancy and associated aspects of conservation biology43. Yet where an organism settles in space is only part of its overall life history. There are consequences to habitat use, good or ill. Such fitness consequences—whether effects to mate acquisition, reproductive output, or survival—will inform and update the prior to the extent that perception of and action on cues ultimately are heritable. In this light, an organism’s small and routine daily decisions manifest over evolutionary time.
References
Jones, J. Habitat selection studies in avian ecology: A critical review. Auk 118, 557–562 (2001).
Beyer, H. L. et al. The interpretation of habitat preference metrics under use-availability designs. Philos. Trans. R. Soc. B 365, 2245–2254 (2010).
Patten, M. A. & Kelly, J. F. Habitat selection and the perceptual trap. Ecol. Appl. 20, 2148–2156 (2010).
Martin, T. E. Are microhabitat preferences of coexisting species under selection and adaptive?. Ecology 79, 656–670 (1998).
Knick, S. T. & Rotenberry, J. T. Ghosts of habitats past: Contribution of landscape change to current habitats used by shrubland birds. Ecology 81, 220–227 (2000).
Hale, R. & Swearer, S. E. Ecological traps: Current evidence and future directions. Proc. R. Soc. B 283, 20152647 (2016).
Forbes, A. A., Fisher, J. & Feder, J. L. Habitat avoidance: Overlooking an important aspect of host-specific mating and sympatric speciation?. Evolution 59, 1552–1559 (2005).
Madliger, C. L. Toward improved conservation management: A consideration of sensory ecology. Biodivers. Conserv. 21, 3277–3286 (2012).
Pruett, C. L., Patten, M. A. & Wolfe, D. H. Avoidance behavior by prairie grouse: Implications for development of wind energy. Conserv. Biol. 23, 1253–1259 (2009).
Hovick, T. J., Elmore, R. D., Dahlgren, D. K., Fuhlendorf, S. D. & Engle, D. M. Evidence of negative effects of anthropogenic structures on wildlife: A review of grouse survival and behaviour. J. Appl. Ecol. 51, 1680–1689 (2014).
Patten, M. A., Wolfe, D. H., Shochat, E. & Sherrod, S. K. Habitat fragmentation, rapid evolution and population persistence. Evol. Ecol. Res. 7, 235–249 (2005).
Patten, M. A., Wolfe, D. H., Shochat, E. & Sherrod, S. K. Effects of microhabitat and microclimate selection on adult survivorship of the Lesser Prairie-Chicken. J. Wildl. Manag. 69, 1270–1278 (2005).
Wolfe, D. H., Patten, M. A., Shochat, E., Pruett, C. L. & Sherrod, S. K. Causes and patterns of mortality in Lesser Prairie-Chickens Tympanuchus pallidicinctus and implications for management. Wildl. Biol. 13(Suppl. 1), 95–104 (2007).
Larsson, L. C., Pruett, C. L., Wolfe, D. H. & Patten, M. A. Fine-scale selection of habitat by the Lesser Prairie-Chicken. Southwest. Nat. 58, 135–149 (2013).
Lenth, R. V. On finding the source of a signal. Technometrics 23, 149–154 (1981).
Duong, T., Wand, M., Chacon J. & Gramacki, A. ks: Kernel smoothing, ver. 1.11.6. https://CRAN.Rproject.org/package=ks (2019).
Oyler-McCance, S. J. et al. Rangewide genetic analysis of Lesser Prairie-Chicken reveals population structure, range expansion, and possible introgression. Conserv. Genet. 17, 643–660 (2016).
van Ravenzwaaij, D., Cassey, P. & Brown, S. D. A simple introduction to Markov Chain Monte-Carlo sampling. Psychom. Bull. Rev. 25, 143–154 (2018).
Agresti, A. & Hitchcock, D. B. Bayesian inference for categorical data analysis. Stat. Methods Appl. 14, 297–330 (2005).
Manly, B. F., McDonald, L. L., Thomas, D. L., McDonald, T. L. & Erickson, W. P. Resource Selection by Animals: Statistical Design and Analysis for Field Studies (Kluwer, Dordrecht, 2002).
Kruschke, J. K. Bayesian estimation supersedes the t test. J. Exp. Psychol. Gen. 142, 573–603 (2013).
Huang, Y., Shekhar, S. & Xiong, H. Discovering colocation patterns from spatial data sets: A general approach. IEEE Trans. Knowl. Data Eng. 16, 1472–1485 (2004).
Plummer, M. rjags: Bayesian graphical models using MCMC, ver. 4-6. https://CRAN.R-project.org/package=rjags (2016).
Leblond, M., Dussault, C. & Ouellet, J.-P. Avoidance of roads by large herbivores and its relation to disturbance intensity. J. Zool. 289, 32–40 (2013).
Thompson, S. J., Johnson, D. H., Niemuth, N. D. & Ribic, C. A. Avoidance of unconventional oil wells and roads exacerbates habitat loss for grassland birds in the North American great plains. Biol. Conserv. 192, 82–90 (2015).
Remon, J., Chevallier, E., Prunier, J. G., Baguette, M. & Moulherat, S. Estimating the permeability of linear infrastructures using recapture data. Landsc. Ecol. 33, 1697–1710 (2018).
Beyer, H. L. et al. ‘You shall not pass!’: Quantifying barrier permeability and proximity avoidance by animals. J. Anim. Ecol. 85, 43–53 (2016).
Hagen, C. A. et al. Impacts of anthropogenic features on habitat use by Lesser Prairie-Chickens. Stud. Avian Biol. 39, 63–75 (2011).
Plumb, R. T. et al. Lesser Prairie-Chicken space use in relation to anthropogenic structures. J. Wildl. Manag. 83, 216–230 (2019).
Peterson, J. M. et al. Estimating response distances of Lesser Prairie-Chickens to anthropogenic features during long-distance movements. Ecosphere 11, e03202 (2020).
Johnson, C. J. Identifying ecological thresholds for regulating human activity: Effective conservation or wishful thinking?. Biol. Conserv. 168, 57–65 (2013).
Downs, J. A. & Horner, M. W. A characteristic-hull based method for home range estimation. Trans. GIS 13, 527–537 (2009).
Worton, B. J. A review of models of home range for animal movement. Ecol. Model. 38, 277–298 (1987).
Worton, B. J. Kernel methods for estimating the utilization distribution in home-range studies. Ecology 70, 164–168 (1989).
Carter, N., Levin, S., Barlow, A. & Grimm, V. Modeling tiger population and territory dynamics using an agent-based approach. Ecol. Model. 312, 347–362 (2015).
Ahearn, S. C., Dodge, S., Simcharoen, A., Xavier, G. & Smith, J. L. D. A context-sensitive correlated random walk: A new simulation model for movement. Int. J. Geogr. Inform. Sci. 31, 867–883 (2017).
Anderson, J. H., Downs, J. A., Loraamm, R. & Reader, S. Agent-based simulation of Muscovy duck movements using observed habitat transition and distance frequencies. Comp. Environ. Urban Syst. 61, 49–55 (2017).
Downs, J. A., Horner, M. W. & Tucker, A. D. Time-geographic density estimation for home range analysis. Ann. GIS 17, 163–171 (2011).
Downs, J. A., Horner, M. W., Hyzer, G., Lamb, D. & Loraamm, R. Voxel-based probabilistic space–time prisms for analysing animal movements and habitat use. Int. J. Geogr. Inform. Sci. 28, 875–890 (2014).
Long, J. A. Modeling movement probabilities within heterogeneous spatial fields. J. Spat. Inform. Sci. 16, 85–116 (2018).
Loraamm, R. W. Incorporating behavior into animal movement modeling: A constrained agent-based model for estimating visit probabilities in space–time prisms. Int. J. Geogr. Inform. Sci. 34, 1607–1627 (2020).
Colman, J. E. et al. Wildlife response to infrastructure: The problem with confounding factors. Polar Biol. 40, 477–482 (2017).
Dominoni, D. M. et al. Why conservation biology can benefit from sensory ecology. Nat. Ecol. Evol. 4, 502–511 (2020).
Acknowledgements
Trapping and tracking efforts were funded largely by the New Mexico Department of Game and Fish, Oklahoma Department of Wildlife Conservation, and the U.S. Fish and Wildlife Service, with additional support from the U. S. Fish and Wildlife Foundation, Wolfe Creek Foundation, and private donors. Donald H. Wolfe of the Sutton Avian Research Center helped to oversee data collection. We thank a small army of field technicians for their hard work. Brittany Benson (BRBFineArt, https://dancingfemora.wixsite.com/brbfineart/) provided the icons used in the figures. We thank the handling editor and two reviewers for their helpful feedback and comments.
Author information
Authors and Affiliations
Contributions
M.A.P. formulated the idea and conducted statistical analyses. C.M.C., with H.D., built and proofed the databases. H.D. crafted the triangulation code. A.A.B. performed all GIS work, including deriving data from it. M.A.P. wrote the initial draft, with key contributions from R.W.L.; all other authors provided editorial advice.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patten, M.A., Barnard, A.A., Curry, C.M. et al. Forging a Bayesian link between habitat selection and avoidance behavior in a grassland grouse. Sci Rep 11, 2791 (2021). https://doi.org/10.1038/s41598-021-82500-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-82500-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.