Introduction

Lanthanides have revolutionised the modern science and technology and are present in almost any device1. The global value of lanthanide-containing products estimated in 2014 was 1.5–2 trillion dollars2, and this number has been continuously increasing since that time. Moreover, the use of lanthanides in phosphors accounts for approximately 3% of the total market share1. Considering lanthanide applications in phosphors, researchers focus on luminescent properties, which make these compounds unique among other luminescence centres. Owing to the characteristic electronic configuration of trivalent lanthanide ions, their luminescence due to 4f–4f electronic transitions is characterised by the narrow emission and absorption bands, host-independent transition energies, and plethora of emissions spanning across the ultraviolet–near infrared (NIR) spectral range with long emission decays and high quantum efficiencies3.

From the viewpoint of the quantum theory developed in the 1920–1930s, the spectral properties of lanthanides were puzzling as summarised by Van Vleck in his famous article ‘The Puzzle of Rare-earth Spectra in Solids’ published in 19374. In particular, the high intensities of intra-configurational 4f transitions contradicted the parity (Laporte) selection rule5. Owing to development of Racah’s algebra in 1949 and first computers allowing the tabulation of many required coefficients, two equivalent articles were published almost simultaneously in 1962 by Judd in Physical Review6 and Ofelt in The Journal of Chemical Physics7 which were characterised by B. Wybourne in the following words8:

‘The two papers of 1962 represent the paradigm that has dominated all future work…up to the present time’

What was later coined as the Judd–Ofelt theory (JO) provided the first quantum–mechanical explanation of the intensities of induced electric dipole transitions. The centrepiece of this theory includes three intensity parameters Ωλ, λ = 2, 4, 6, from which many ‘derived quantities’ with high practical importance (such as radiative transition probabilities, radiation lifetimes, branching ratios, cross-sections, and intrinsic quantum yields) can be simply obtained. These parameters may be subsequently used to calculate the intensities of the entire emission or absorption spectra9.

Considering the capability of the JO theory and spectroscopic importance of lanthanides, it is not surprising that the research interest in this theory is rapidly growing (Fig. 1).

Figure 1
figure 1

Numbers of published papers with the expression “Judd–Ofelt” determined for 5-year intervals by Google Scholar (accessed in July 2021).

Full size image

The ongoing research studies in this field can be classified into three categories: (i) theory improvement and development of alternate JO parametrisation methods5,10,11,12,13,14,15,16,17, (ii) JO parametrisation of lanthanides in different hosts doped at various concentrations and analysis of lanthanide-activated phosphors synthesised by different methods (see Tables 10–21 in Ref.18), and (iii) applications of JO theory and JO parameters by constructing various models in other areas of science related to luminescence19,20. The majority of research works on these topics fall into categories (ii) and (iii), demonstrating that the practical implementation of the JO theory does not require its deep understanding. For category (ii), it is necessary to know the methods for calculating JO parameters, while for research category (iii), such parameters can be obtained from the literature.

Previous JO parametrisation studies

JO parameters are traditionally determined by analysing the absorption spectra of trivalent lanthanide-activated materials. This method is described in detail in Refs.5,9; therefore, only its brief description is provided below. It is based on fitting the experimental oscillator strengths obtained from the absorption spectrum with theoretical equations derived for selected transitions of a given lanthanide ion. The experimental oscillator strength (Pexp) is equal to18

$$\begin{array}{c}{P}_{\text{exp}}\left[\text{/}\right]=4.32\cdot \frac{{10}^{-9}\Xi }{{X}_{A}},\end{array}$$
(1)

where

$$\begin{array}{c}\Xi =\int \varepsilon \left(\nu \right)d\nu ,\end{array}$$
(2)

is the integrated molar absorptivity, \(\nu\) is the wavenumber (cm−1), and XA is the fractional thermal population at the initial level. ε (mol−1 L cm−1) is the molar extinction coefficient (molar absorptivity), which can be calculated from absorbance by the following formula:

$$\begin{array}{c}\varepsilon =Cd/A.\end{array}$$
(3)

Here, C (mol/L) is the concentration, and d (cm) is the length of the optical path in a given material.

At temperatures above the absolute zero, the higher-lying energy levels of lanthanide ions are thermally populated with probabilities specified by the Boltzmann distribution. If the energy separation to the next level is larger than 2000 cm−1, the thermalisation of the current energy level is not efficient and may not follow the Boltzmann distribution (in this case, it can be even neglected due to its low contribution). The ratio of the optical centres at a selected level to the total number of optical centres is represented by the fractional thermal population18,21:

$$\begin{array}{c}{X}_{A}=\frac{{g}_{A}\mathrm{exp}\left(-\frac{\Delta {E}_{A}}{kT}\right)}{\sum_{i}{g}_{i}\mathrm{exp}\left(-\frac{\Delta {E}_{i}}{kT}\right)},\end{array}$$
(4)

where T (K) is the temperature, gi is the level of degeneracy, ΔEi is the energy difference between level i and the ground state (in cm−1), and k = 0.695 cm−1·K−1·is the Boltzmann constant. According to the fractional thermal population of the Eu3+ ground multiplet 7FJ, the 7F1 level is significantly populated even at room temperature due to the low energy separation between the 7F0,1 levels, which can be verified by the excitation or absorption spectra that contain transitions originating from the Eu3+ 7F1 level22.

Unlike the oscillator strength, dipole strength is independent of the photon energy and related to the oscillator strength via the following expression:

$$\begin{array}{c}{P}_{\text{th}}\left[\text{/}\right]=4.702\cdot {10}^{29} \tilde{\nu } {D}_{th},\end{array}$$
(5)

where \(\tilde{\nu }\) is the transition barycentre energy (in cm−1), and Dth is the dipole strength. The dipole strength of the electric dipole (ED) transition is defined as9

$$\begin{array}{*{20}c} {D_{{th}}^{{ED}} \left[ {{\text{esu}}^{2} {\text{cm}}^{2} } \right] = e^{2} \sum\limits_{\lambda } {\Omega _{\lambda } } U^{\lambda } ,} \\ \end{array}$$
(6)

where Uλ are the squared reduced matrix elements (RMEs), and e = 4.803 × 1010 esu is the elementary charge. RMEs are often considered host-independent; for this reason, many researchers have consorted to using the values tabulated by Carnall et al.23 instead of calculating them for a particular host by employing Slater integrals and spin–orbit coupling parameters24. The magnetic dipole (MD) transition has a dipole strength that is also host-independent. The tabulated values for all MD transitions of all trivalent lanthanides are provided in Ref.25.

The experimental oscillator strength is compared to the theoretical strength by the formula

$$\begin{array}{c}{P}_{\text{exp}}=\frac{\chi }{g}{P}_{\text{th}},\end{array}$$
(7)

where χ is the local field correction, and g = 2 J + 1 is the degeneracy of the J level, from which the transition originates. The Lorenz field correction for the ED transition and local field correction for the MD transition during absorption are computed as follows26:

$$\begin{array}{c}{\chi }_{ED}^{ab}=\frac{{\left({n}^{2}+2\right)}^{2}}{9n}, { \chi }_{MD}^{ab}=n,\end{array}$$
(8)

where n is the wavelength-dependent refractive index. Ideally, the refractive index is calculated using the dispersion relation.

To obtain JO parameters, all Pexp magnitudes should be fitted to Pth using Eq. (7) for the observed transitions, thereby minimising the discrepancies between the theoretical and experimental values. Ultimately, this will produce Ωλ values closest to the experimental data. As pointed out by Blasse and co-workers, a drawback of this method is the necessity to accurately measure the density of ions in the analysed sample. In addition, absorption intensity can be routinely measured only for glasses, transparent solutions, and crystals, leaving out non-transparent materials and crystalline powders13. Another drawback of the described approach is a high error of ~ 20%27 caused by the absence of higher-order contributions, whose inclusion significantly complicates the calculation procedure (see Ref.28). The third problem arises with the parametrisation of the Pr3+ ion as the proximity of the 4f5d levels mixes with the 4f levels, leading to a case that cannot be treated by the original JO method. As a result, complex alternative parameterisation methods with questionable accuracies were developed for Pr3+ ions11. Parametrisation using crystal field parameters is called ab initio parameterisation; however, it suffers from high complexity and limited accuracy, as stated by L. Smentek10:

‘Indeed, there are objective, or rather technical reasons, why it is still impossible to perform ab initio calculations that would provide reliable results.’

The readers interested in this method are referred to Refs.18,29,30.

Various techniques similar to the absorption-based one, which utilise excitation15 or diffuse-reflectance31 spectra, have been proposed in recent years. Their development was motivated by the limited application of the absorption method for powders and non-transparent materials. The methods are based on the comparison of the theoretical line strengths, Scalc = ΣΩλUλ, with the measured line strengths which are proportional to the peaks in the diffuse-reflectance or excitation spectrum. Although these techniques can be used for any material, they produce only relative JO parameters, which must be calibrated against the radiative transition probability of a selected level that is approximately equal to the inverse of the experimentally measured lifetime. By this spectrum calibration, the unknown parameter c vanishes, and the absolute values of the JO parameters are obtained. This assumption inherently introduces an error into the calculated values. For this reason, the authors of both the above-mentioned methods have chosen the first excited level of Er3+ for the calibration by the excited-level lifetime value (because it is almost purely radiative) and Nd3+ ion for the diffuse-reflectance method. Luo et al. have predicted that their excitation method parametrisation can be used on 10 lanthanide ions, among which is not the Eu3+ ion15. In recent years, this method has been tested on Dy3+ ion with success32,33.

Sytsma and Blasse were the first researchers who performed spectrum calibration using an excited-level lifetime for the JO parametrisation of the Gd3+ emission spectrum13 assuming that the deexcitation of its first excited level, which lied high above the ground level, was purely radiative. A similar approach was explored in our previous research study12 describing a JO parametrisation method that utilised the Pr3+ emission spectrum. Because the emissive 3P0 level is non-degenerate, parametrisation can be performed using the low-temperature emission spectrum with negligible temperature quenching. At low Pr3+ concentrations, the depopulation of the excited states through the interionic processes was very small, and the radiative lifetime of the 3P0 level was equal to the experimentally measured value. This allowed conducting more accurate spectrum calibration and JO parameterisation than the corresponding procedures of the alternative absorption methods mentioned above.

In 1966, shortly after Judd and Ofelt had published their articles, Krupke developed a JO parametrisation method using the emission spectrum of the Eu3+ ion17. Because this method includes the higher-order contributions not considered in the traditional parametrisation of the absorption spectrum, it remains the most accurate JO parameterisation technique. Unlike the methods that require calibration with the excited level lifetime, Krupke exploited the fact that Eu3+ had a pure host-independent MD transition 5D0 → 7F1, to which other intensities could be compared. In the method proposed in our previous work16, the pure MD 5D1 → 7F0 emission is used for spectral calibration and, as will be demonstrated later, the same energy levels are utilised in the novel parametrisation technique developed in this study. Owing to the use of an accurate dispersion relation for the refractive index, the JO parameterisation methods based on the emission spectra of the Eu3+ ion are unbeatable in terms of accuracy and simplicity. However, in such spectra, the only transition that can be used to calculate the Ω6 parameter lies in the NIR region outside the detection limits of most traditional detectors and is also very weak due to the low U6 = 0.0002 RME34. Only a limited number of studies have reported the 5D0 → 7F6 emission35,36,37,38,39. Thus, JO parameterisations performed using Eu3+ emission spectra are often incomplete. Furthermore, because U6 has a low value, it is estimated with relatively large error and variations34,40, making the parameterisation of the Ω6 value based on the emission spectrum unreliable and difficult to perform. Despite its low importance for Eu3+ emission, Ω6 is the most important parameter in the absorption/excitation spectrum, as the most intense absorption, 7F0 → 5L6, depends solely upon its value. The Ω6 magnitude is related to the rigidity of a medium where ions are incorporated41,42, which in turn depends on the Debye temperature43,44. Consequently, there is experimental and theoretical incompleteness of the JO parametrisation of Eu3+-activated materials that are not glasses, crystals, or solutions.

Self-calibrated JO parametrisation of the Eu3+ excitation spectrum (JOEX)

Therefore, to perform accurate JO parameter determination and avoid the limitations of the methods described above, we propose a novel technique for the JO parametrisation of Eu3+-doped materials, which enables the estimation of all three Ωλ parameters from a single excitation spectrum. Unlike the other methods that rely on spectrum calibration by the excited-level lifetime, this approach utilises the pure MD transition 7F0 → 5D1 at 525 nm for calibration purposes. The proposed method simultaneously facilitates the determination procedure and increases the reliability of the obtained results. The versatility of this technique allows its application to non-transparent and powder materials, for which other methods are not suitable. It includes all higher-order contributions to the JO parameters (the original absorption spectrum-based method utilised only a static coupling model)45. Owing to the high U6 value obtained for the 7F0 → 5L6 electronic transition of Eu3+ ions, U6 was used with low relative uncertainty. In addition, due the high intensity of the band associated with the 7F0 → 5L6 transition, its integrated intensity was also estimated with low uncertainty, contrary to the 5D0 → 7F6 emission in Krupke’s method.

In order to verify the reliability of the data obtained by the proposed method, the latter was applied to two different (from the chemical and morphological perspectives) materials: well-known Eu3+-activated Y2SiO5 microcrystalline phosphor and β-NaYF4 nanoparticles. The determined parameters were compared with the results obtained by Krupke’s parametrisation technique and the emission spectrum calculated by the JOES application software (https://omasgroup.org/joes-software/)46.

Theoretical approach

The experimental dipole strength of a randomly oriented system (e.g., powder) in its absorption spectrum is equal to18.

$$\begin{array}{c}{D}_{\text{exp}}\left[{\text{esu}}^{2}{\text{cm}}^{2}\right]=\frac{\Xi }{108.9\cdot {10}^{36}\tilde{\nu }{X}_{A}}.\end{array}$$
(9)

The experimentally obtained dipole strength can be compared with the theoretical value using the formula.

$$\begin{array}{c}{D}_{\text{exp}}=\frac{\chi }{g}{D}_{\text{th}}.\end{array}$$
(10)

These equations are suitable for both ED and MD transitions; therefore, local field corrections must be applied accordingly. For pure MD and ED transitions, Eq. (10) can be modified as follows:

$$\begin{array}{c}\frac{{\Xi }_{\mathrm{MD}}}{108.9\cdot {10}^{36}{\tilde{\nu }}_{MD}{X}_{A}^{MD}}=\frac{{\chi }_{MD}}{{g}_{MD}}{D}_{\text{MD}}^{th},\end{array}$$
(11)
$$\begin{array}{*{20}c} {\frac{{\Xi _{{{\text{ED}}}} }}{{108.9 \cdot 10^{{36}} \tilde{\nu }_{{ED}} X_{A}^{{ED}} }} = \frac{{\chi _{{ED}} }}{{g_{{ED}} }}e^{2} \sum\limits_{\lambda } {\Omega _{\lambda } } U^{\lambda } .} \\ \end{array}$$
(12)

In the case of the 4f–4f lanthanide transitions, the excitation spectrum is assumed to be identical to the corresponding absorption spectrum multiplied by a constant. Because absolute values cannot be obtained from excitation spectra, only \(c{D}_{\text{exp}}\) may be calculated via Eq. (9) as follows:

$$\begin{array}{c}c{D}_{\text{exp}}\left[{\text{esu}}^{2}{\text{cm}}^{2}\right]=\frac{\Gamma }{108.9\cdot {10}^{36}\tilde{\nu }{X}_{A}},\end{array}$$
(13)

where Γ = cΞ is the integrated intensity in the excitation spectrum for the corresponding transition, which is equal to the integrated molar absorptivity multiplied by the unknown c coefficient. Thus, the knowledge of c would allow JO parameterisation using Eq. (12). For the pure Eu3+ ED transitions 7F0 → 5D4 (λ = 4), 7F0 → 5L6 (λ = 6), and 7F0 → 5D2 (λ = 2), the theoretical dipole strength can be expressed as

$$\begin{array}{c}{D}_{\lambda }={e}^{2}{\Omega }_{\lambda }{U}^{\lambda },\end{array}$$
(14)

considering that all RMEs other than Uλ are equal to zero (see Table 1). In this case, Eq. (13) becomes

Table 1 RMEs of various transitions relevant for the JO parametrisation of the Eu3+ excitation spectrum.
Full size table
$$\begin{array}{c}\frac{{\Gamma }_{\lambda }}{108.9\cdot {10}^{36}{\tilde{\nu }}_{\lambda }{X}_{A}\left({{}_{ }{}^{7}F}_{0}\right)}=c{\chi }_{\lambda }{e}^{2}{\Omega }_{\lambda }{U}^{\lambda }.\end{array}$$
(15)

Note that the degeneracy term is absent from this formula because J = 0 for the initial level.

In our recent article16, we exploited the pure MD emission 5D1 → 7F0 with an MD strength of 1.8 × 10−42 esu2 cm2. Because the dipole strength values determined for the emission and absorption/excitation processes are identical, the same dipole strength holds for the 7F0 → 5D1 transition (further abbreviated as DMD). As a result, Eq. (13) for the MD transition can be written in the following form:

$$\begin{array}{c}\frac{{\Gamma }_{MD}}{108.9\cdot {10}^{36}{\tilde{\nu }}_{MD}{X}_{A}\left({{}_{ }{}^{7}F}_{0}\right)}=c{\chi }_{MD}{D}_{MD}.\end{array}$$
(16)

After dividing Eq. (15) by Eq. (16), the fractional level populations vanish because the initial levels for calibrating the MD and ED transitions are the same. The unknown c parameter also disappears from the equation. As a result, a set of three equations for the determination of the JO parameters from the excitation spectrum is obtained:

$$\begin{array}{c}{\Omega }_{\lambda }\left[{\text{cm}}^{2}\right]=\frac{{\chi }_{MD}}{{\chi }_{\lambda }}\frac{{\tilde{\nu }}_{MD}}{{\tilde{\nu }}_{\lambda }}\frac{{D}_{MD}}{{e}^{2}{U}^{\lambda }}\frac{{\Gamma }_{\lambda }}{{\Gamma }_{MD}}, \quad \lambda =2, 4, 6.\end{array}$$
(17)

Note that a similar equation can be derived by using the 7F1 → 5D0 pure MD transition with a dipole strength 9.56 × 10−42 esu2 cm225, but it would require the inclusion of degeneracies and fractional thermal populations.

Parametrisation procedure

A straightforward algorithm for obtaining JO intensity parameters from the excitation spectrum of Eu3+ is outlined below.

  1. 1.

    The excitation spectra of Eu3+-activated materials can be obtained by monitoring the emission from the 5D0 level (from 350 to 550 nm). Monitoring the 5D0 → 7F2 emission at approximately 612 nm is the best option due to its high intensity. The emission from the 5D0 → 7F4 transition can be also used; however, one should be aware of the overlap with the second harmonic at 700 nm (for 350 nm excitation). The excitation band of the 7F0 → 5D4 transition is observed at approximately 364 nm, while that of 7F0 → 5L6 is detected at approximately 395 nm, 7F0 → 5D2—at 467 nm, and 7F0 → 5D1—at 525 nm.

  2. 2.

    The intensities of the excitation bands must be integrated, and their barycentres should be determined. It is easier to obtain the barycentre wavelength (sometimes called a centroid). In this case, the integrated intensities are equal to Γ2 = Γ(7F0 → 5D2), Γ4 = Γ(7F0 → 5D4), Γ6 = Γ(7F0 → 5L6), and ΓMD = Γ(7F0 → 5D1). The wavelength barycentres are denoted by symbol \(\tilde{\lambda }\). Owing to the nature of the Eu3+ excitation spectrum, they are almost equal to the wavelengths of the peak maxima. In some hosts the charge-transfer band may overlap with the 7F0 → 5D4, 5L6 excitations. Then the charge-transfer band must be subtracted by spectrum deconvolution prior to peak integration.

  3. 3.

    A refractive index value should be determined for each transition using the dispersion relation (if possible). For several hundred materials, dispersion relations are stored in a refractive index online database47. The values of the refractive index are computed by the formulas n2 = n(467 nm), n4 = n(364 nm), n6 = n(395 nm), and nMD = n(525 nm).

  4. 4.

    The following three simplified equations can be used for parametrisation:

    $$\begin{array}{c}{\Omega }_{2}=7.803\frac{{n}_{2}{n}_{MD}}{{\left({n}_{2}^{2}+2\right)}^{2}} \frac{{\tilde{\lambda }}_{2}}{{\tilde{\lambda }}_{MD}}\frac{{\Gamma }_{2}}{{\Gamma }_{MD}}\cdot {10}^{-20}{\text{cm}}^{2},\end{array}$$
    (18)
    $$\begin{array}{c}{\Omega }_{4}=6.384\frac{{n}_{4}{n}_{MD}}{{\left({n}_{4}^{2}+2\right)}^{2}} \frac{{\tilde{\lambda }}_{4}}{{\tilde{\lambda }}_{MD}}\frac{{\Gamma }_{4}}{{\Gamma }_{MD}}\cdot {10}^{-20}{\text{cm}}^{2},\end{array}$$
    (19)
    $$\begin{array}{c}{\Omega }_{6}=0.459\frac{{n}_{6}{n}_{MD}}{{\left({n}_{6}^{2}+2\right)}^{2}} \frac{{\tilde{\lambda }}_{6}}{{\tilde{\lambda }}_{MD}}\frac{{\Gamma }_{6}}{{\Gamma }_{MD}}\cdot {10}^{-20}{\text{cm}}^{2}.\end{array}$$
    (20)

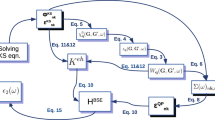
The developed parametrisation procedure is illustrated in Fig. 2 (left) and compared with the Krupke method (right) using the Eu3+ emission spectrum.

Figure 2
figure 2

JO parametrisation schemes using the excitation and emission spectra of the Eu3+ ion: JOEX (left) and Krupke’s method (right).

Full size image

To facilitate the described procedure and make it universally accessible, a user-friendly web application for the JO parameter calculations via Eqs. (18)–(20) was developed. It can be accessed at https://omasgroup.org/judd-ofelt-from-excitation-spectrum-of-eu/ (Fig. 3) and represents a free open-source web application written in PHP. After inputting the integrated intensities of the excitation bands of relevant transitions, their barycentre wavelengths, and refractive index values, the program outputs the calculated JO parameters.

Figure 3
figure 3

Web application for calculating JO parameters from an excitation spectrum, which is available at https://omasgroup.org/judd-ofelt-from-excitation-spectrum-of-eu/.

Full size image

Experimental verification of the JOEX method

For comparison, JO parameters were estimated from the emission spectrum of the Eu3+-activated Y2SiO5 microcrystalline phosphor and β-NaYF4 nanoparticles using the JOES software46. The relative deviation from the average value of the JO parameters obtained using the excitation (\({\Omega }_{\uplambda }^{\text{ex}}\)) and emission (\({\Omega }_{\uplambda }^{\text{em}}\)) spectra were calculated by the following formula48:

$$\begin{array}{c}{\delta }_{\lambda }\left[\%\right]=\left|1-\frac{2{\Omega }_{\uplambda }^{\text{em}}}{{\Omega }_{\uplambda }^{\text{em}}+{\Omega }_{\uplambda }^{\text{ex}}}\right|\cdot 100\%.\end{array}$$
(21)

Y2SiO4:Eu3+ microcrystalline powder

The emission and excitation spectra of Y2SiO4:Eu3+ are shown in Fig. 4. The refractive index values of Y2SiO5 at the barycentre wavelengths of relevant transitions were calculated via the dispersion relation provided in Ref.49. The parameters used for calculating JO parameters from the excitation spectrum (Fig. 4b), JO parameters, and their deviations from the values estimated by utilising the emission spectrum (Fig. 4a) are listed in Table 2.

Figure 4
figure 4

Emission spectrum of Y2SiO5:Eu3+ obtained for the excitation to the 5L6 level (a) its excitation spectrum obtained by monitoring the 5D0 → 7F2 emission (b).

Full size image
Table 2 JO parameters determined from the excitation spectrum of Y2SiO5:Eu3+ and their comparison with the values obtained from its emission spectrum.
Full size table

The Ω2 and Ω6 values estimated by the excitation and emission parametrisation methods matched very well (the largest deviation of ~ 12% was obtained for the Ω4 parameter). Given that the error in estimation of JO parameters is up to 20%5, the mismatch of the Ω4 parameter is acceptable.

β-NaYF4:Eu3+ nanoparticles

The emission and excitation spectra of β-NaYF4:Eu3+ are shown in Fig. 5. The refractive index values were calculated using the Cauchy formula provided in Ref.50, and the parametrisations data obtained from the spectra depicted in Fig. 5 are presented in Table 3. Similar to the Y2SiO5:Eu3+ parameters, the resulting Ω2,6 values are very close to each other, while the Ω4 magnitudes differ by 13%.

Figure 5
figure 5

Emission spectrum of β-NaYF4:Eu3+ obtained for the excitation to the 5L6 level (a) its excitation spectrum obtained by monitoring the 5D0 → 7F2 emission (b).

Full size image
Table 3 JO parameters estimated from the excitation spectrum of β-NaYF4:Eu3+.
Full size table

Conclusion

In this study, we developed a comprehensive self-referenced method for estimating all JO intensity parameters of Eu3+-doped compounds from their excitation spectra (JOEX).

With the current method for parametrization from emission spectrum the Ω6 parameter is difficult or impossible to obtain. The traditional JO parametrization from absorption spectrum does not include the higher-order contributions (e.g. dynamic-coupling) in its standard form, thus the error in the JO parameters estimation is greater than by employing luminescence. Furthermore, it requires fitting procedure, making it more complex and difficult to apply. The absolute absorption spectrum is difficult or impossible to obtain on non-transparent or powder materials. JOEX, like parametrisation from emission spectrum, includes all the higher-order contributions, it is self-referenced meaning that only one spectrum is sufficient for parametrisation (unlike other methods from the excitation of diffuse-reflectance spectra), and can be applied to any material form.

The accuracy and suitability of the described approach were experimentally verified for phosphors with different chemical compositions and morphologies. Excellent matching of the obtained Ω2 and Ω6 parameters was observed with a slight difference between the Ω4 values whose origin has not been established yet. The proposed method facilitates a simple derivation of Ω6 intensity parameters, which are difficult to calculate by the parametrisation of emission spectra and, therefore, frequently omitted in related studies.

One should note that the presented work is not extending the JO theory to explain its shortcomings but provides a new theoretical and computational tool for its practices. For an easier, faster, and reliable computational procedure, we have also developed a special web application available at https://omasgroup.org/judd-ofelt-from-excitation-spectrum-of-eu/. The direction of future work is the calculation of JO intensity parameters for many important phosphors for which available parametrisation approaches were not feasible or sufficiently precise.