Abstract
To identify risk factors and develop a simple model to predict early prognosis of acute paraquat (PQ) poisoning patients, we performed a retrospective cohort study of acute PQ poisoning patients (n = 1199). Patients (n = 913) with PQ poisoning from 2011 to 2018 were randomly divided into training (n = 609) and test (n = 304) samples. Another two independent cohorts were used as validation samples for a different time (n = 207) and site (n = 79). Risk factors were identified using a logistic model with Markov Chain Monte Carlo (MCMC) simulation and further evaluated using a latent class analysis. The prediction score was developed based on the training sample and was evaluated using the testing and validation samples. Eight factors, including age, ingestion volume, creatine kinase-MB [CK-MB], platelet [PLT], white blood cell [WBC], neutrophil counts [N], gamma-glutamyl transferase [GGT], and serum creatinine [Cr] were identified as independent risk indicators of in-hospital death events. The risk model had C statistics of 0.895 (95% CI 0.855–0.928), 0.891 (95% CI 0.848–0.932), and 0.829 (95% CI 0.455–1.000), and predictive ranges of 4.6–98.2%, 2.3–94.9%, and 0–12.5% for the test, validation_time, and validation_site samples, respectively. In the training sample, the risk model classified 18.4%, 59.9%, and 21.7% of patients into the high-, average-, and low-risk groups, with corresponding probabilities of 0.985, 0.365, and 0.03 for in-hospital death events. We developed and evaluated a simple risk model to predict the prognosis of patients with acute PQ poisoning. This risk scoring system could be helpful for identifying high-risk patients and reducing mortality due to PQ poisoning.
Similar content being viewed by others
Introduction
The non-selective contact herbicide paraquat (PQ) is predominantly used in developing agricultural countries1,2. PQ is lethal when ingested orally, and there are still no effective and specific antidotes. Patients with acute PQ poisoning usually die within several days to weeks after exposure due to hypoxemia or multiple organ failure. PQ poisoning results in increased medical resource use, causing a considerable economic impact3,4,5,6. Therefore, timely clinical outcome evaluation and risk assessment for critically ill PQ poisoning patients and essential for appropriate medical resource allocation, which has become an important public health and social security agency issue concerning doctors and patients.
To our knowledge, several systems have been reported to predict the prognosis of patients with PQ poisoning, including the Acute Physiology and Chronic Health Evaluation II (APACHE II) score7, Sequential Organ Failure Assessment (SOFA) score8, the Severity Index of PQ Poisoning (SIPP)9, Poisoning Severity Score (PSS)10, and several equations and nomograms based on large cohort studies11,12,13. Most of these models are suitable for critically ill patients rather than patients with minimal exposure or early-stage patients with mild symptoms. Moreover, these scoring systems can fail to predict mortality and conduct risk assessment for PQ poisoning patients instantly because of their complicated calculations or the unavailability of laboratory tests. Thus, establishing an effective, simple, and universal predictive model based on common laboratory tests would be invaluable for risk stratification and therapeutic regimen adjustment for patients with acute PQ poisoning of all stages.
Here, based on data from 1199 patients with PQ poisoning from two large academic hospitals in China, we developed and evaluated a simple risk model by identifying significant clinical risk factors to predict in-hospital death. Data for our study were collected from the medical records of acute PQ poisoning patients from different time periods and geographic regions. This study describes a well-designed and easy to administer tool for predicting in-hospital death of PQ poisoning patients using a combination of simple and clinically relevant variables.
Methods
Study samples and data sources
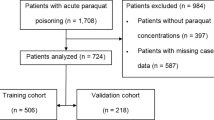
The PQ poisoning study included 932 patients from January 1, 2011 to December 31, 2018. Patient information was collected during January and February of 2019. An additional 207 cases from Zhengzhou 2019 and 79 from Shenyang Shengjing hospital were collected as external validation samples. Patients with missing information on sex (n = 11) and prognosis (n = 22) were excluded. The final sample included 913 unique patients who were randomly divided into two mutually exclusive training (66.7% [609 patients]) and test (33.3% [304 patients]) sets. The training sample was used to select risk factors, and the test sample was used for evaluation. Cases from Zhengzhou 2019 (n = 207) were used as a validation sample from a different time period and 79 cases from Shenyang as a validation sample from a different hospital (Fig. 1).
Study design. A total of 932 patients were enrolled during January and February 2019. An additional 207 patients from Zhengzhou 2019 and 79 from Shenyang Shengjing hospital were included as the external validation data sets. Patients without sex (n = 11) and prognosis (n = 22) information were excluded. Then, 913 unique patients were randomly divided into two mutually exclusive samples for training (66.7% [609 patients]) and testing (33.3% [304 patients]). All analyses were conducted using SAS® statistical software version 9.4 (https://www.sas.com).
Ethical statement
This study was approved by the Institutional Review Board of the First Affiliated Hospital of Zhengzhou University (2017-XY-002), and all experimental protocols of the study were approved by the ethics committee. Written informed consent was obtained from all enrolled patients. This study was conducted in accordance with the ethical standards of the Declaration of Helsinki 1975.
Potential risk factors and outcome
We selected candidate risk factors that were clinically meaningful, reliable, and easily collected, which occurred with a frequency of more than 1%. Initial factors included patient demographic characteristics (age, sex), PQ ingestion time and volume, and laboratory test results (blood urea nitrogen [BUN], creatine kinase [CK], CK-MB, gamma-glutamyl transferase [GGT], mean platelet volume [MPV], procalcitonin [PCT], platelet [PLT], white blood cell [WBC], and neutrophil [N] counts, aspartate aminotransferase [AST], alanine aminotransferase [ALT], and creatinine [Cr]). Detailed information on these variables in the 1199 samples is shown in “Supplementary file S1”, Table S1. To facilitate the risk score calculation, we examined the nonlinear relationship of each continuous factor with the outcome and categorized it using a cut-off point while taking into account both in-hospital death rates and sample sizes (“Supplementary file S1”, Fig S1). Parameters with missing data rate > 15% were excluded. Factors with missing values were imputed using ten imputations. The final imputed value was the average of the ten imputations. Missing values ranged from 1.1% (age) to 13.3% (CK-MB). The primary outcome was in-hospital death, which defined as death during hospitalization.
Statistical analysis
Risk factor selection and evaluation
Using the training sample with all candidate risk factors, we fit a logistic model with Markov Chain Monte Carlo (MCMC) simulation, and we calculated a posterior probability for each factor14. The posterior probability could assess the association strength between a factor and the outcome. Factors with a posterior probability > 0.95 (or < 0.05 for factors with estimates < 0.0) were considered significant for predicting the outcome and were included in the final risk factor list15. Then, we developed the final risk model to predict the outcome by fitting a logistic regression to the training sample data using the selected risk factors identified by the MCMC method.
We used the following indicators to evaluate the risk model performance: the Harrell C statistic to assess the overall predictive accuracy16,17, the McFadden R square to assess explained variation18, and the Hosmer–Lemeshow goodness-of-fit test to assess calibration19. Discrimination was assessed between the observed outcomes in strata defined by the predictive probabilities’ deciles. As described previously, we divided patients in the training sample into five mutually exclusive risk classes based on the deciles, ranking them from lowest (class 1) to highest risk (class 5) for evaluation20.
To further evaluate the selected risk factors, we used the training data to conduct a latent class analysis by an unsupervised machine learning algorithm that does not require a specified outcome14. Conceptually, unsupervised learning algorithms can assign patients to risk classes if the selected risk factors are substantially associated with the outcome. Thus, we used latent class analysis to classify patients into five mutually exclusive classes and ranked them from lowest (class 1) to highest risk (class 5) based on the observed outcome. We chose five classes to align with the decile-specific classes based on the risk model described previously. We calculated a Spearman correlation coefficient between the risk classes based on the risk model and the risk classes determined by the latent class analysis. A high coefficient was indicative of good agreement between the classified results, thereby providing information on the robustness of the selected risk factors.
We further validated the risk model by comparing its performance with the training sample, test sample and 2 independent validation samples.
Risk score
As described previously15, to facilitate the use of the selected risk factors and the risk model, we developed a simple risk score for each patient based on the regression coefficients estimated from the risk model with the training sample. Points for each risk factor were calculated by dividing the risk factor’s coefficient by the sum of all coefficients in the model, multiplying by 100, and rounding to the nearest integer. We stratified patients into 3 risk groups based on the distribution of the risk score: low (< 25th percentile), average (25th–75th percentile), and high (> 75th percentile).
All analyses were conducted using SAS® software version 9.4 (SAS Institute Inc.). Latent class analysis was conducted using the PROC LCA method (version 1.3.2 beta). Nonlinear relationships were assessed using the PROC GAM method. This study followed the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) reporting guideline. All 22 items of the TRIPOD statement were addressed.
Results
Study sample
A total of 1199 (609 training, 304 test, 207 validation by time, and 79 validation by site) participants were included in this study. The mean (SD) age was 35.1 (16.4) years, and 599 patients (50.0%) were female. There were some differences in the basic clinical characteristics of patients in training, test, and two validation samples. The differences between the training, test, and validation samples demonstrate the predictability and extrapolation of the model (Table 1).
In-hospital death events
In-hospital death rates were 40.6% (95% CI 36.6–44.6%) and 38.5% (95% CI 33.0–44.2%) for the training and test samples. The average in-hospital death rate was 37.9%. The median (interquartile range [IQR]) hospital stay was 5 (2–11) days (Table 1).
Risk factor selection and testing
The MCMC simulation identified eight candidate factors with a posterior probability of at least 0.95 (Table 2), including age, ingestion volume, CK-MB, PLT, WBC, N, GGT, and Cr (Fig. 2). The risk model based on the eight risk factors and the training sample demonstrated good discrimination, calibration, and fit. The overall C statistic was 0.926 (95% CI 0.891–0.924) for the risk model (Fig. 3). The mean observed in-hospital death rate ranged from 3.3% in the lowest predicted quintile to 99.2% in the highest predicted quintile, with a range of 95.9% and variation of 0.4999 (Fig. 4). Moreover, the P-values of the Hosmer–Lemeshow goodness-of-fit test were 0.4262 in the training sample and 0.9078 in the test sample, indicating a good fit with the test cohort (Fig. 5).
Risk factors associated with in-hospital death based on the training sample. Eight candidate factors, including age, ingestion volume, CK-MB, PLT, WBC, N, GGT, and Cr, were identified using the MCMC simulation. Factors with a posterior probability > 0.95 were considered significant for predicting the outcome.
ROC analyses for the evaluation and validation of the risk model in the training, test, validation_time, and validation_site samples. Model performance in the test, validation_time, and validation_site samples was comparable to that in the training sample. The overall C statistics were 0.926 (95% CI 0.891–0.924), 0.895 (95% CI 0.855–0.928), 0.891 (95% CI 0.848–0.932), and 0.827 (95% CI 0.455–1.000) for the training, test, validation_time, and validation_site samples, respectively.
Additionally, model performance with the test sample was comparable to that with the training sample. The overall C Statistic was 0.895 (95% CI 0.855–0.928) in the test sample (Fig. 3). The observed in-hospital death rate ranged from 4.6% in the lowest predicted quintile to 98.2% in the highest predicted quintile, and the explained variation was 0.4182 for the test sample (Fig. 4).
Furthermore, in the latent class analysis, 609 patients in the training sample were assigned into five classes based on the combination of the eight risk factors (Fig. 6). For this analysis, the area under the receiver operating curve (ROC) curve was 0.877 (95% CI 0.832–0.906), and the mean observed in-hospital death rate ranged from 0.0% in the lowest- to 99.2% in the highest rating group. The Spearman’s correlation coefficient between the predicted quintile based on the logistic model and the latent class analysis was 0.754 (95% CI 0.715–0.874).
Risk score system
The risk factor-specific points ranged from 19 (WBC ≥ 20) to 6 (PLT < 80) (Table 2). WBC ≥ 20, CK-MB ≥ 50, N ≥ 80, ingestion volume ≥ 100, and Cr ≥ 150 were the top five factors with odds ratios > 5.0 (Fig. 2). The training sample had a mean (SD) risk score of 26.6 (21.6). The mean (SD) score of the test sample was 24.8 (21.1). Further, in the training sample, 18.4%, 59.9%, and 21.7% of patients were stratified into the high, average, and low-risk groups, with corresponding probabilities of 0.985, 0.365, and 0.03 for in-hospital death, respectively (Fig. 7). The stratification of the test sample was not markedly different from that of the training sample (Fig. 7, Table 3).
Risk stratification by risk scores. For the training, test, validation_time, and validation_site samples, respectively, the predicted probabilities of in-hospital death for PQ poisoning patients were 98%, 99%, 98%, and 97% in the highest risk group (46+), 59.9%, 62.2%, 59.4%, and 60.8% in the average-risk group (15–45), and 21.7%, 22.4%, 27.1%, and 36.7% in the lowest risk group (0–14).
Risk model validation
The in-hospital death events rates were 42.0% (95% CI 35.2–49.1%) and 3.8% (95% CI 0.8–10.7%) for the time and site validation samples, respectively (Table 1). The observed in-hospital death rates ranged from 2.3% and 0.0% in the lowest predicted quintiles to 94.9% and 12.5% in the highest predictive quintiles, and the explained variations were 0.3798 and 0.2421 for the time and site validation samples, respectively. The overall C statistics were 0.891 (95% CI 0.848–0.932) and 0.827 (95% CI 0.455–1.000) (Fig. 3), and the P-values of the Hosmer and Lemeshow's Goodness of Fit Test were 0.9671 and 0.9999 for the two independents samples (Fig. 5).
The mean (SD) risk scores were 23.5 (19.7) and 16.3 (14.1) for the time and site validation samples, respectively. In the validation_time sample, 27.1%, 59.4%, and 13.5% of patients were classified into the low-, average-, and high-risk groups, respectively, with corresponding probabilities of 0.98, 0.38, and 0.03 for in-hospital death events (Fig. 7 and Table 3). In the validation_site group, 36.7%, 60.8%, and 2.5% of patients were classified into the low-, average-, and high-risk groups, with corresponding probabilities of in-hospital death events of 0.03, 0.33, and 0.97. The probabilities for in-hospital death events of the validation samples were identical to those of the training sample (Fig. 7 and Table 3).
Discussion
In this study, we evaluated 609 patients with acute PQ poisoning, and we identified eight prognostic factors for survival after PQ poisoning. Furthermore, a random forest risk model and a scoring system based on these risk factors were developed to predict the in-hospital death probability for patients diagnosed with PQ poisoning. Importantly, our model was tested both in internal and external validation samples. The risk factors were selected based on data from medical records and ease of collection and availability after discharge and during long-term follow-up. Furthermore, the statistical algorithms used in this study are robust. The risk prediction model and its corresponding risk scoring system may help clinicians to identify the patients at highest risk of in-hospital death after PQ poisoning.
PQ exposure is a major cause of fatal poisoning in most Asian nations. PQ can cause severe multiple organ damage, such as lungs and gastrointestinal tract, which are the main causes of death after PQ poisoning21,22,23. Although therapeutic strategies for the management of acute PQ poisoning have been extensively investigated, PQ poisoning remains poor24,25. Generally, the severity and prognosis of acute poisoning are determined by the ingested dose. Previous studies have reported that plasma PQ concentrations can be used to predict clinical outcomes for patients with PQ poisoning26,27. In view of plasma PQ concentration is quantitatively measured using radioimmunoassay or liquid chromatography-mass spectrometry methods, which cannot be done in most hospitals, we used PQ ingestion volume rather than PQ plasma concentration at present medical situation. Moreover, Patients with PQ poisoning were conscious on admission, including critical PQ poisoning patients. Clinicians can easily obtain PQ ingestion volume data from the patients or their relatives. Identifying potential risk factors to predict the clinical outcome of PQ poisoning patients at an early stage may improve early diagnosis and facilitate rapid medical intervention for patients who have the highest risk of in-hospital death. Therefore, there is an urgent need to develop a reliable and universal risk prediction model based on available laboratory data to evaluate the early prognosis of PQ poisoning patients. Furthermore, validating and classifying the risk of in-hospital death based on a multi-clinical factor index model is an important innovation in emergency medical research, which could aid in risk stratification and therapeutic regimen adjustment for patients with acute PQ poisoning.
The MCMC algorithm was used to evaluate the association strength between the risk factors and the outcome. Compared with prior studies, the clinical indicators included in this model were routine and inexpensive, and every hospital could easily acquire the data. Our model had better predictive accuracy based on two external validation samples from a different time and site, which were used to validate our scoring system. The SIPP has been recognized as a valuable prognostic model for PQ poisoning patients in previous studies9,28. The unavailability of SIPP indicators in many hospitals makes it difficult to apply the scoring system routinely, limiting the accurate evaluation of PQ poisoning severity. The APACHE II scoring system is also in clinical settings to evaluate the prognosis of PQ poisoning patients29,30. However, this scoring system might underestimate mortality in critically ill patients. Our prediction model was developed using the baseline clinical indicators of PQ poisoning patients. It is easy to use and allows the exclusion of terminally-ill or minimally affected patients from needless aggressive therapy.
Hidden factors used for risk model development may affect the efficiency of the model in different contexts. Effective risk prediction factors must be supported by clinical research, and the data must be easily collected and available during hospitalization as well as after discharge. The risk factors in our study were tested and validated and had good agreement with the training results. Notably, the eight risk factors selected for this study meet all the criteria listed above. Our risk model includes age, ingestion volume, CK-MB, PLT, WBC, N, GGT, and Cr. Previous studies demonstrated that WBC and neutrophil counts were essential indexes for the prognosis of PQ poisoning patients31,32. Creatinine, one of the risk factors associated with a poor prognosis, could be induced by direct oxidative injury in renal tubules33. Elevated serum Cr level is closely associated with acute kidney injury (AKI). Further, PQ poisoning patients with AKI had a higher mortality risk than those with normal kidney function34. Through risk stratification, we found that in the training sample, the proportion of patients at high risk or moderate risk of in-hospital death after PQ poisoning was 98% and 36%, respectively. The eight risk factors we identified could help clinicians make medical interventions that may improve the prognosis and reduce unnecessary treatment of PQ poisoning patients. Improving the clinical outcomes of PQ poisoning patients and reducing in-hospital death rates would decrease the economic burden on the healthcare system.
Conclusion
The early clinical outcomes for PQ poisoning patients have been difficult to evaluate. The novel risk model we developed is easy to use and can exclude the terminally-ill or minimally affected PQ poisoning patients from needless aggressive therapy better than conventional scoring systems such as APACHE II, SOFA, and SIPP. This risk score system is suitable for clinical use for recognizing high-risk PQ poisoning patients and for predicting the probability of in-hospital death.
References
Lee, K. et al. Occupational paraquat exposure of agricultural workers in large Costa Rican farms. Int. Arch. Occup. Environ. Health 82, 455–462. https://doi.org/10.1007/s00420-008-0356-7 (2009).
Klein-Schwartz, W. & Smith, G. S. Agricultural and horticultural chemical poisonings: Mortality and morbidity in the United States. Ann. Emerg. Med. 29, 232–238. https://doi.org/10.1016/s0196-0644(97)70274-9 (1997).
Jones, A. L., Elton, R. & Flanagan, R. Multiple logistic regression analysis of plasma paraquat concentrations as a predictor of outcome in 375 cases of paraquat poisoning. QJM Monthly J. Assoc. Phys. 92, 573–578. https://doi.org/10.1093/qjmed/92.10.573 (1999).
Min, Y. G. et al. Prediction of prognosis in acute paraquat poisoning using severity scoring system in emergency department. Clin. Toxicol. (Philadelphia, Pa.) 49, 840–845. https://doi.org/10.3109/15563650.2011.619137 (2011).
Khazraei, S., Marashi, S. M. & Sanaei-Zadeh, H. Ventilator settings and outcome of respiratory failure in paraquat-induced pulmonary injury. Sci. Rep. 9, 16541. https://doi.org/10.1038/s41598-019-52939-3 (2019).
Wu, L. et al. Metformin activates the protective effects of the AMPK pathway in acute lung injury caused by paraquat poisoning. Oxidative Med. Cell. Longevity 2019, 1709718. https://doi.org/10.1155/2019/1709718 (2019).
Huang, J. et al. The value of APACHE II in predicting mortality after paraquat poisoning in Chinese and Korean population: A systematic review and meta-analysis. Medicine 96, e6838. https://doi.org/10.1097/md.0000000000006838 (2017).
Wang, W. J., Zhang, L. W., Feng, S. Y., Gao, J. & Li, Y. Sequential organ failure assessment in predicting mortality after paraquat poisoning: A meta-analysis. PLoS ONE 13, e0207725. https://doi.org/10.1371/journal.pone.0207725 (2018).
Sawada, Y. et al. Severity index of paraquat poisoning. Lancet (London, England) 1, 1333. https://doi.org/10.1016/s0140-6736(88)92143-5 (1988).
Persson, H. E., Sjoberg, G. K., Haines, J. A. & de Garbino, J. P. Poisoning severity score. Grading of acute poisoning. J. Toxicol. Clin. Toxicol. 36, 205–213. https://doi.org/10.3109/15563659809028940 (1998).
Lee, E. Y., Hwang, K. Y., Yang, J. O. & Hong, S. Y. Predictors of survival after acute paraquat poisoning. Toxicol. Ind. Health 18, 201–206. https://doi.org/10.1191/0748233702th141oa (2002).
Hong, S. Y., Lee, J. S., Sun, I. O., Lee, K. Y. & Gil, H. W. Prediction of patient survival in cases of acute paraquat poisoning. PLoS ONE 9, e111674. https://doi.org/10.1371/journal.pone.0111674 (2014).
Hu, X., Guo, R., Chen, X. & Chen, Y. Increased plasma prothrombin time is associated with poor prognosis in patients with paraquat poisoning. J. Clin. Lab. Anal. 32, e22597. https://doi.org/10.1002/jcla.22597 (2018).
Wang, Y. et al. Risk factors associated with major cardiovascular events 1 year after acute myocardial infarction. JAMA Netw. Open 1, e181079. https://doi.org/10.1001/jamanetworkopen.2018.1079 (2018).
Lichtman, J. H., Leifheit-Limson, E. C., Jones, S. B., Wang, Y. & Goldstein, L. B. Preventable readmissions within 30 days of ischemic stroke among Medicare beneficiaries. Stroke 44, 3429–3435. https://doi.org/10.1161/strokeaha.113.003165 (2013).
Hu, Z. et al. An in-hospital mortality risk model for patients undergoing coronary artery bypass grafting in China. Ann. Thoracic Surg. https://doi.org/10.1016/j.athoracsur.2019.08.020 (2019).
Wang, Y. A multinomial logistic regression modeling approach for anomaly intrusion detection. Comput. Security 24, 662–674. https://doi.org/10.1016/j.cose.2005.05.003 (2005).
Schemper, M. & Henderson, R. Predictive accuracy and explained variation in Cox regression. Biometrics 56, 249–255. https://doi.org/10.1111/j.0006-341x.2000.00249.x (2000).
O’Quigley, J. & Flandre, P. Predictive capability of proportional hazards regression. Proc. Natl. Acad. Sci. USA 91, 2310–2314. https://doi.org/10.1073/pnas.91.6.2310 (1994).
Wei, Z. et al. Development and validation of a simple risk model to predict major cancers for patients with nonalcoholic fatty liver disease. Cancer Med. https://doi.org/10.1002/cam4.2777 (2019).
Sun, B. & He, Y. Paraquat poisoning mechanism and its clinical treatment progress. Zhonghua wei zhong bing ji jiu yi xue 29, 1043–1046. https://doi.org/10.3760/cma.j.issn.2095-4352.2017.11.018 (2017).
Tai, W. et al. Rapamycin attenuates the paraquat-induced pulmonary fibrosis through activating Nrf2 pathway. J. Cell. Physiol. 235, 1759–1768. https://doi.org/10.1002/jcp.29094 (2020).
Li, Y. et al. Abnormal pancreatic enzymes and their prognostic role after acute paraquat poisoning. Sci. Rep. 5, 17299. https://doi.org/10.1038/srep17299 (2015).
Oghabian, Z. et al. Clinical features, treatment, prognosis, and mortality in paraquat poisonings: A hospital-based study in Iran. J. Res. Pharm. Practice 8, 129–136. https://doi.org/10.4103/jrpp.JRPP_18_71 (2019).
Wang, Y. et al. Radiomics nomogram analyses for differentiating pneumonia and acute paraquat lung injury. Sci. Rep. 9, 15029. https://doi.org/10.1038/s41598-019-50886-7 (2019).
Zhang, J. et al. The significance of serum uric acid level in humans with acute paraquat poisoning. Sci. Rep. 5, 9168. https://doi.org/10.1038/srep09168 (2015).
Gil, H. W., Kang, M. S., Yang, J. O., Lee, E. Y. & Hong, S. Y. Association between plasma paraquat level and outcome of paraquat poisoning in 375 paraquat poisoning patients. Clin. Toxicol. (Philadelphia, Pa.) 46, 515–518. https://doi.org/10.1080/15563650701549403 (2008).
Xu, S. et al. APACHE score, Severity Index of Paraquat Poisoning, and serum lactic acid concentration in the prognosis of paraquat poisoning of Chinese Patients. Pediatr. Emerg. Care 31, 117–121. https://doi.org/10.1097/pec.0000000000000351 (2015).
Jacobs, S., Chang, R. W. & Lee, B. One year’s experience with the APACHE II severity of disease classification system in a general intensive care unit. Anaesthesia 42, 738–744. https://doi.org/10.1111/j.1365-2044.1987.tb05319.x (1987).
Huang, N., Lin, S., Hung, Y., Hung, S. & Chung, H. Severity assessment in acute paraquat poisoning by analysis of APACHE II score. J. Formosan Med. Assoc. Taiwan yi zhi 102, 782–787 (2003).
Gil, H. W. et al. Plasma level of malondialdehyde in the cases of acute paraquat intoxication. Clin. Toxicol. (Philadelphia, Pa.) 48, 149–152. https://doi.org/10.3109/15563650903468803 (2010).
Liu, H. et al. High-dose acute exposure of paraquat induces injuries of swim bladder, gastrointestinal tract and liver via neutrophil-mediated ROS in zebrafish and their relevance for human health risk assessment. Chemosphere 205, 662–673. https://doi.org/10.1016/j.chemosphere.2018.04.151 (2018).
Kim, S. J., Gil, H. W., Yang, J. O., Lee, E. Y. & Hong, S. Y. The clinical features of acute kidney injury in patients with acute paraquat intoxication. Nephrol. Dialysis Transplant. Off. Publ. Eur. Dialysis Transpl. Assoc. Eur. Renal Assoc. 24, 1226–1232. https://doi.org/10.1093/ndt/gfn615 (2009).
Mohamed, F. et al. Kidney damage biomarkers detect acute kidney injury but only functional markers predict mortality after paraquat ingestion. Toxicol. Lett. 237, 140–150. https://doi.org/10.1016/j.toxlet.2015.06.008 (2015).
Acknowledgements
We thank the medical doctors from the Precision Medicine Center and Emergency Department of the First Affiliated Hospital of Zhengzhou University who participated in this study.
Funding
This work was supported by the National Natural Science Foundation of China (81701893 and U2004121), National S&T Major Project of China (2018ZX10301201-008 and 2017ZX10103005-009), Key Scientific Research Projects of Higher Education Institutions in Henan Province (20A320046 and 20A320056), and the Joint Construction Project of Henan Province Medical S&T Research (SB201901006).
Author information
Authors and Affiliations
Contributions
Z.R., Y.G., and Y.L. designed the study. Y.G., T.L., D.Y., Y.W., Z.X., L.H., Y.Z., G.D., C.S., L.C., S.L. and P.S. collected clinical data; Z.R., and Y.G. analyzed the data and developed the model; Z.R., L.L., and Y.G. wrote the manuscript. All authors reviewed and approved the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, Y., Liu, L., Li, T. et al. A novel simple risk model to predict the prognosis of patients with paraquat poisoning. Sci Rep 11, 237 (2021). https://doi.org/10.1038/s41598-020-80371-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-80371-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.