Abstract
Reactive power dispatch is a vital problem in the operation, planning and control of power system for obtaining a fixed economic load expedition. An optimal dispatch reduces the grid congestion through the minimization of the active power loss. This strategy involves adjusting the transformer tap settings, generator voltages and reactive power sources, such as flexible alternating current transmission systems (FACTS). The optimal dispatch improves the system security, voltage profile, power transfer capability and overall network efficiency. In the present work, a fractional evolutionary approach achieves the desired objectives of reactive power planning by incorporating FACTS devices. Two compensation arrangements are possible: the shunt type compensation, through Static Var compensator (SVC) and the series compensation through the Thyristor controlled series compensator (TCSC). The fractional order Darwinian Particle Swarm Optimization (FO-DPSO) is implemented on the standard IEEE 30, IEEE 57 and IEEE 118 bus test systems. The power flow analysis is used for determining the location of TCSC, while the voltage collapse proximity indication (VCPI) method identifies the location of the SVC. The superiority of the FO-DPSO is demonstrated by comparing the results with those obtained by other techniques in terms of measure of central tendency, variation indices and time complexity.
Similar content being viewed by others
Introduction
The optimal reactive power dispatch (ORPD) problem in coordination with flexible alternating current transmission system (FACTS) devices became a topic of growing research interest for the cost-effective operation and security of power systems1,2,3,4,5. The aim of the ORPD is to attain a fine tuning of the control variables for obtaining minimum transmission losses and acceptable voltage profiles while reducing the operational cost. Several voltage controlling devices are integrated in the power systems for voltage profile improvement, such as tap changing transformers6, shunt capacitors7, static VAR compensators (SVC), thyristor-controlled series compensators (TCSC) and thyristor-controlled phase shifters (TCPS)8. However, optimal allocation of the FACTS and setting their control variables poses a complex constraint optimization problem. Furthermore, such optimization has considerable influence on the effectiveness in system performance, by providing loss reduction, voltage profile improvement, network load ability enhancement, increased voltage stability and fuel cost reduction through optimal power flow9,10,11,12.
Due to these reasons we verify a growing interest to reach these objectives, namely with the incorporation of FACTS in legacy power systems. In power systems, weak buses were identified for the installation of FACTS through modal analysis. Moreover, the voltage collapse proximity indicator (VCPI) was tested for improving the voltage stability index. Optimal power flow (OPF) problems were solved by means of analytical methods13, genetic algorithms (GA)14,15, current injection16 and power injection model of FACTS17. Indeed, FACTS were installed at optimal locations to reduce voltage deviation18, active power loss19 and reactive power control20, or for security purposes such as in margin21 and congestion22 management. Several computational techniques were proposed for the optimal allocation of FACTS, namely fuzzy GA23, gravitational search algorithms24 and population-based techniques, such as differential evolution25, artificial bee colony with firefly26, quasi-oppositional chemical reaction optimization27, improved gravitational search algorithm28, ant lion optimizer29, whale optimization algorithm30, adaptive particle swarm optimization31 and chaotic krill herd algorithm32. These schemes have their own pros and cons and, therefore, it is important to explore the fractional swarming/evolutionary techniques, because these algorithms have not yet been exploited in the viewpoint of ORPD including FACTS.
In recent years, the implementation of fractional swarming and evolutionary computational strategies including fractional calculus in the internal structure of the optimizers was proposed. We can cite the PSO with fractional order velocity, fractional particle swarm optimization (FPSO), fractional order Darwinian PSO (FO-DPSO) and fractional order robotic PSO33,34,35,36,37,38. These methods were successfully applied in several problems including robot path controllers design39, image processing40, classification of hyperspectral images41,42, feature selection43, estimation of electromagnetic plane wave parameters44, adaptation of parameter for Kalman filtering algorithms45, localization and segmentation of optic disc46, design of discretized fractional order filters47 and land-cover monitoring48. Beside these application, we find also the design of PID controllers for AVR systems49, non-linear systems identification50, fractional robust control of coupled tank systems51, continuous nonlinear observer using sliding mode PID52 and design of power system stabilizer using GA-PSO53. These works point toward embedding the fractional calculus tools with the evolutionary strategies for optimization problems in the energy sector. This study explores the application of FO-DPSO for ORPD incorporating FACTS in electric power networks.
In various contingency situations, weak buses provide substantial evidences that they are responsible for voltage collapse. We start by applying power flow analysis and VCPI methods to detect the weak buses in the interconnected power system. Then, a new fractional version of the PSO, the FO-DPSO, is implemented as an efficient solver for ORPD problems. The algorithm involves the computation of control variables, including the values of SVC, TCSC, transformer tap positions and bus voltages, while satisfying the power demand. The voltage deviation, line loss minimization and system overall cost are considered as the objective functions, while observing the FO-DPSO execution. The highlights of the contribution can be summarized as:
-
Novel application of the fractional swarming scheme for reliable solution of ORPD incorporating FACTS with optimization by means of the FO-DPSO.
-
Application of the FO-DPSO on ORPD problems for reducing the overall cost, voltage deviation, and line loss minimization, while fulfilling of the load demand and operational constraints.
-
Performance analysis of the FO-DPSO with different fractional orders conducted with ORPD problems.
-
Statistical analysis, in terms of histograms, probability plots and learning curves, demonstrating the consistency, robustness, and stability of the proposed FO-DPSO.
The paper is structured as follows. “Objective functions of ORPD problem with FACTS devices” section formulates the fitness function for ORPD. “Mathematical model of FACTS” Section describes the mathematical modeling of FACTS and its influence in power system. “Weak bus detection for optimal positioning of FACTS” Section presents methods for the identification of weak buses. “Proposed methodology” Section gives an overview of the designed FO-DPSO, pseudocode and work flow diagram of the scheme. "Results and discussion" and "Statistical analysis" sections analyse several simulations with the proposed algorithm including a detailed comparison with other strategies and a statistical evaluation. Finally, the last “Conclusions” section summarizes the main conclusions.
Objective functions of ORPD problem with FACTS devices
The locations of the SVC and the TCSC can be found by using the VCPI and the load flow analysis, respectively. Then the FO-DPSO is applied to optimize the control variables. This includes the reactive power generation, tap changer settings, and size of the TCSC and SVC considering the system evaluation functions. The expressions of the objective functions and constraints are given in the follow-up.
Fitness function for power loss minimization
The fitness function for real power losses in power system is expressed as
where \(x_1\) and \(x_2\) are defined as:
In expressions (1) to (3) we have following variables and symbols:
-
\(F_1(x_1,x_2)\) consists of the loss minimization function.
-
R represents the total number of transmission lines.
-
\(V_i\) and \(V_j\) are the sending and receiving end voltages, respectively.
-
\(g_r\) stands for the line conductance.
-
\(\delta _i\) and \(\delta _j\)are the sending and receiving end voltage angles, respectively.
-
\(x_2\) denotes the vector of control variable consisting of transformers tap positions \(\left( {{T_1},{T_2},\ldots ,{T_{{N_T}}}} \right) \), generators voltage magnitude \(\left( {{V_{G1}},{V_{G2}},\ldots ,{V_{G{N_{PV}}}}} \right) \), reactive power compensators \(\left( {{Q_{C1}},{Q_{C2}},\ldots ,{Q_{C{N_C}}}} \right) \), static VAR compensators \(\left( {SV{C_1},SV{C_2},\ldots ,SV{C_{{N_{SVC}}}}} \right) \), thyristor controlled series capacitors \(\left( {TCS{C_1},TCS{C_2},\ldots ,TCS{C_{{N_{TCSC}}}}} \right) \).
-
\(x_1\) denotes the vector of dependent variables that include the generator reactive power \(\left( {{Q_{G1}},{Q_{G2}},\ldots ,{Q_{G{N_{PV}}}}} \right) \), load voltages \(\left( {{V_{L1}},{V_{L2}},\ldots ,{V_{L{N_L}}}} \right) \) and line loading \(\left( {{S_{L1}},{S_{L2}},\ldots ,{S_{L{N_L}}}} \right) \).
The allowable limits of the SVC and the TCSC are provided in Table 1. The equality constraints are defined as:
The inequality constraints consist of the transformer’s tap position settings, generators voltage and reactive power, and the SVC and TCSC boundaries as:
here, \(P_{G_i}\) and \(P_{D_i}\) are the ith bus active power supply and demand, respectively, \(Q_{G_i}\) and \(Q_{D_i}\) represent the ith bus reactive power supply and demand, respectively, \(N_T\), \(N_{TCSC}\), \(N_{SVC}\) and \(N_c\) correspond to the number of transformers, TCSCs, SVCs and fixed shunt capacitors, respectively.
Fitness function for voltage deviation (\(V_D\))
Keeping a steady voltage profile in power system for secure operation is a challenging objective. Mathematically, the reduction of (\(V_D)\) can be characterized as:
here, \(V_i\) is the voltage at ith and \(N_{BUS}\) is number of buses.
Fitness function for overall operating cost minimization
The fitness function for overall operating cost minimization combines two parts. The first part incorporates the investment of FACTS devices, whereas the second part represents the cost due to energy loss. Therefore, the aim is not only to reduce the cost of energy losses associated with the TCSC and SVC during minimization of power loss, but also to minimize the initial investment of these devices. Hence, the overall fitness function for cost minimization can be formulated as:
where
Hereafter, we fix the following values: cost due to energy loss 0.06 $/kWh, capital cost of shunt capacitor 1000$, hours in a day 24, days in a year 365. The provided cost data for \(C_{Energy}\) is taken from reference1,30. The cost \(C_{FACTS}\) of the FACTS devices is taken from the Siemens AG database20 and is specified as
where \(\alpha \), \(\beta \), and \(\gamma \) are the cost coefficients and S is the operating range of the FACTS devices in MVAR. The limits and values can be seen in Tables 1 and 2.
Mathematical model of FACTS
The solid-state devices provide an innovative concept in load flow control through network branch, fault reduction and reduced line losses, while keeping desired level of voltages30. This can be implemented by governing the network parameters including the current, voltage, phase angle, series and shunt impedances by incorporating FACTS in the electric power network. From the family of the FACTS, the TCSC and the SVC are used as stunt and series compensating devices, respectively. The mathematical model of TCSC and SVC along their influence after integrating into the network is discussed in the next sub-section.
TCSC modelling
The TCSC provides a variable reactive impedance equation \(jX_c\) that can be altered above and below of the original impedance line. The power system static model equipped with TCSC between the mth to nth buses can be seen in Fig. 1. The power flow equations for the active and reactive components after coupling the TCSC are expressed, respectively, as30
likewise, the power (real and reactive) flow equations from the nth to mth buses can be formulated as
where the susceptance and conductance of the transmission line are given by \({B_{mn}} = \frac{{ - X - {X_{TCSC}}}}{{{R^2} + {{(X - {X_{TCSC}})}^2}}}\) and \({G_{mn}} = \frac{R}{{{R^2} + {{(X - {X_{TCSC}})}^2}}}\), respectively.
The modified \(Y_{bus}\) equation matrix after the installation of the TCSC between the buses of the network is given by:
Here, \(\Delta {y_{sr}}\), is the change in admittance value after the installation of TCSC. These new entries of the line reactance affect the branch data due to the presence of TCSC.
SVC modelling
The SVC can inject and absorb reactive power to and from the bus bar by coupling different topologies of inductors and capacitors in shunt. The reactive power flow is governed by the phase-controlled operation of thyristor valve to quickly remove or add parallel connected capacitor and reactors. The equivalent model of the SVC that can also be implemented as a parallel integrated variable susceptance \(B_{SVC}\) at any given bus-k is depicted in Fig. 2. The reactive power flow from the SVC into the bus can be written as30:
where V is the amplitude of bus voltage where the compensator is installed. The modified admittance (\(Y_{bus}\)) matrix after installation of the SVC at a given bus is expressed as:
Here, \(\Delta {Y_{shunt}}\), is the shunt admittance of SVC. These modified values in the admittance matrix due to the SVC affects the bus data.
Weak bus detection for optimal positioning of FACTS
The main aim of a weak bus recognition is to obtain the best possible position of the FACTS devices for providing proper reactive power provision at the suitable locations. This action affects the natural characteristics of the electrical transmission lines, provides better voltage profile, increases the power transfer capacity, reduces line losses and solves problems related to voltage instability31. The method used in the present work for weak bus identification involves the load flow analysis through single line diagram.
Voltage collapse proximity indication (VCPI)
The maximum power transfer theorem provides the basis of the VCPI technique30 for a line. Consider a constant voltage source \(V_{s}\) with internal impedance \(Z_s \angle \theta \) that is feeding a load with impedance \(Z_L \angle \varphi \). According to this theorem, the maximum power flow occurs when the ratio of impedances \(Z_L/Z_s\) equals 1. This result is used as voltage collapse predictor.
In order to simplify the problem and to maintain the accuracy level it is useful to keep \(\varphi \) constant while considering a variable load impedance. For each increase of the load demand, it results that the current increases and \(Z_L\) decreases. These combined effects further increase the line drop and decrease the voltage at the receiving end as follows:
For
the line power loss is given by
and the receiving end power by
The maximum power \({P_r}\) can be attained by applying the boundary conditions \((\partial {P_r}/\partial {Z_L}) = 0\), which implies that \({Z_L}/{Z_s} = 1\). By replacing this in Eq. (27), the maximum power transfer capacity results
the line maximum power transfer forms the conceptual basis of VCPI and, therefore, it can be written as
with a value that should be lower than one for a stable system. When this value is approaching the unity, for any bus, it means that it is getting closer to instability. This bus is identified as weak bus and designated as the best possible location for the SVC installation.
Load flow analysis
The reactive power flow can be computed and those lines that transfer the higher value can be identified. The buses where the branch ends are referred as weak buses and the TCSC are installed between such buses.
The procedural steps for finding the TCSC locations are as follow:
-
1.
Load bus and line of the test system.
-
2.
Generate the Y-bus matrix.
-
3.
Compute the angle and voltage of each bus using the Newton Raphson technique.
-
4.
Compute the reactive power (Q) and active power (P) in each line using load-flow technique.
-
5.
Pick the line/branch with maximum Q.
-
6.
Conditional check: If the designated branch is a slack bus (reference bus), or if it is linked to a generator (generator bus), then repeat step 5, else switch to step 7.
-
7.
The branch end-point or bus is designated for the position of the TCSC.
Proposed methodology
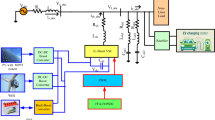
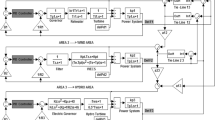
The proposed methodology includes two phases. In the first, an introductory overview of the FO-DPSO is presented. In the second phase the computational strategy in terms of the processing block structure and pseudocode are provided for ORPD incorporating FACTS. The overall workflow schematic of the presented technique is depicted in Fig. 3. The idea is to develop a technique based on the FO-DPSO for optimal sizing of the SVC and TCSC with appropriate placement in the inter connected power system, while minimizing the overall operational cost, power loss and voltage deviation of the IEEE standard test systems.
Introduction of the FO-DPSO
The Darwinian PSO (DPSO) is an evolutionary mechanism that improves the standard PSO by increasing its capability to escape from local optimum either by natural assortment, or by persisting those with high fitness values. The performance of DPSO is superior to the one exhibited by the PSO, but has the disadvantage of a higher computational complexity. Pires et al. combined the DPSO with the concept of fractional calculus (FC) to improve learning ability of the DPSO mechanism by designing the Fractional Order Darwinian PSO (FO-DPSO)54.
The development of FC and its application in engineering problems has proved its importance due to heredity and long memory effects in many phenomena and systems36. The integro-differential operator defined by the Grünwald-Letnikov, Caputo and Riemann–Liouville formulations are classical expressions that are adopted in science and engineering. The Grüwald-Letnikov interpretation of the fractional derivative can be expressed as35
hereafter, h is sampling interval, \(\alpha \) denotes the fractional order and \(\Gamma \) stands for the Euler gamma function. In the present study we adopt the discrete time approximation
where T corresponds to the sampling period and r is the truncation order. Considering \(r = 4\), that is, adopting the first four terms for the expression (5.4.2) of differential derivatives, the velocity update equation for FO-DPSO is transformed from that of conventional PSO and is given for nth particle as:
and position update is given as:
where x is the position vector of nth particle with velocity v, t is the flight index, and \(\Phi _1\) and \(\Phi _2\) are the personal best and global best acceleration constant, respectively. Moreover, S represents the swarm consisting of m particles, i.e., \(x_1, x_2, x_m\), \(r_1\) and \(r_2\) are random numbers between 0 and 1, and G and L are the global and local best position vector in the swarm, respectively.
Equation (32) shows that the canonical PSO is a particular scenarios of the FO-DPSO with order of derivative \(\alpha = 1\), i.e., without “memory”. In the literature, there is no specific method to find out the best fractional orders \(\alpha \). The searching of the appropriate fractional order \(\alpha \) for optimal performance of the fractional evolutionary/swarming techniques for a specific objective function is usually conducted by means of a stochastic procedure, i.e., the best performance of order \(\alpha \) based on the statistics. The interpretation of the fractional order \(\alpha \) used in the optimization using the fractional PSO and a possible justification through physics is always a complex task. The traditional practice is to adopt the Monte-Carlo simulations-based statistics to select the order \(\alpha \) that perform best on a problem-oriented specific fitness function.
In addition, the results depend on the fractional order \(\alpha \) depending on the problem and function convergence rate varies for different \(\alpha \) and each scenario. In55, the convergence rate with respect to \(\alpha \) was studied. In this case, the best results were obtained at lower orders for different test functions. In35, a faster convergence rate was attained at \(\alpha \) in the range [0.5, 0.8]. In spite of these difficulties, all studies endorsed that adopting a fractional order provides better results in comparison with the integer case. In addition, each optimization scenario may have a different optimal value of \(\alpha \). Afterwards, the FO-DPSO is adopted as a significant fractional evolutionary strategy considering the best \(\alpha \), that is evaluated and selected using Monte-Carlo simulations-based statistics for each objective function.
Application of FO-DPSO for ORPD incorporating FACTS
The key modification adopted in the FO-DPSO is the velocity update in the standard PSO since the fractional derivative is included in the algorithm. The global optimization effectiveness of FO-DPSO is explored for finding the best size of the TCSC, SVC, tap values and generators reactive power output in the IEEE-30, IEEE-57 and IEEE-118 buses power systems, while reducing the line losses, voltage deviation and overall cost.
The steps for the evaluation of control variables using FO-DPSO are given in Algorithm 1, and the parameter settings of FO-DPSO are documented in Table 3.

Results and discussion
The validity and applicability of the FO-DPSO is analyzed for the reactive power scheduling in the IEEE 30, IEEE 57 and IEEE 118 buses while incorporating the SVC and TCSC devices at weak buses. We tested the performance of designed fractional order DPSO technique on a consistent similar strategy as reported in recent articles35,55 where the fractional order is taken between 0 and 1 (i.e., [0.1, 0.2,..., 1.0]). The theoretical and simulation analyses are presented for 10 values of the fractional order including the integer order case, i.e., \(\alpha \) = 1, where the fractional DPSO transformed to standard DPSO. The search for the fractional order for optimal performance of fractional evolutionary/swarming technique is normally conducted on stochastic procedure, namely on the basis of statistics. Indeed the selection of \(\alpha \) with a clear justification through physics is always difficult and Monte-Carlo statistics are used to select the order which performs best. To evaluate the optimization robustness of the FO-DPSO, a statistical analysis is performed for 100 trials during all test cases.
Test case 1
As a first case, the IEEE 30 bus system is adopted with the numerical values documented in Table 4. The initial operating cost without reactive power planning is \(3.737016 \times 10^6\)USD and the active power loss is 7.11 MW. Weak buses are identified through the power flow analysis method and according to that criterion the TCSC are installed in the 5th, 28th, 25th, and 41th lines. Using the VCPI method, the SVC are installed at the 4th, 20th, 22th and 28th buses. After that, the FO-DPSO is implemented for computing the optimal settings of the SVC, TCSC, tap changer position and reactive power generation, while considering all the fitness functions. The number of particles is taken as 80. The learning behavior of the FO-DPSO for line loss \(P_{Loss}\) minimization using the orders \(\alpha = [0.1, 0.2, \ldots , 1.0]\) is depicted in Fig. 4a, where the minimum loss is obtained at \(\alpha \) = 0.6. The learning behavior for the voltage deviation and overall cost function are shown in Fig. 4b,c, respectively. The optimized settings of control variables including reactive power generation, tap value, size of the TCSC and SVC by mean of the FO-DPSO, are listed in Table 5 along with different optimization methods. The results of the FO-DPSO can be compared with those exhibited by other schemes including the GWO30, WOA30, QOGWO30, DE23, fuzzy DE23, SPSO31, APSO31, EPSO31 and QODE30 algorithms. The corresponding results are documented in Table 5, where one can observe that the FO-DPSO evaluated for the minimum losses, and compares well with the other optimization schemes.
The FO-DPSO computes real power loss of 0.04683 p.u and an operating cost as \(2.4528 \times 10^6\) USD, that is inferior values with 0.0243 p.u and \(1.284216 \times 10^6\) USD less than the base case, respectively. The comparative analysis for the line loss and operating cost reduction in relation with the other cases can be seen in Table 6. We observe that the strategy for ORPD incorporating FACTS provides a better solution than the other optimization mechanisms in terms of minimum losses and minimum overall operating cost.
To highlight the optimization strength of presented technique, we have also applied fractional evolutionary computing FO-DPSO to solve the ORPD problem in IEEE 30 bus system with 13 control variables without FACTS devices. The results are documented in Table 7. We verify that the results yielded by FO-DPSO are superior to the state of art solvers reported in literature including MICA-IWA56, PSO57, MFO56, HSA57, ICA56, GA58, IWO59, DE57, GWO60 and NMFLA61. The line loss reduction from presented scheme as compared to counterparts can be seen in Table 8 where it is endorsed that FO-DPSO is the best.
Test case 2
The second test case addresses the \(P_{Loss}\) of the IEEE 57 bus system. This standard power system comprises 80 transmission lines with the tap changing transformers installed at seventeen links, 7 generating stations synchronized at buses 1, 2, 3, 6, 8, 9 and 12, and three shunt capacitors. Bus# 1 represents the slack bus, that is the reference bus. The cumulative power demand for the real and reactive load is 12.5170 MW and 3.3570 MVAR, respectively, at base power of 100 MVA. Initially, the cost of operation is \(1.471 \times 10^7\) USD and the \(P_{Loss}\) is 27.99 MW without ORPD. The SVC are installed at the \(23^{rd}\), 38th, 39th, and 48th, buses, that are identified as weak buses by means of the VCPI method. The TCSC are installed in 13th, 37th, 57th, and \(61^{st}\) lines that are found as the weak links based on the power flow technique. The FO-DPSO is tested to evaluate the best values of the dependent variables, namely the size of the SVC and TCSC along with the tap changer position and reactive power generation while reducing the network evaluation fitness functions including \(P_{Loss}\), \(V_{D}\) and \(C_{overall}\) minimization. The behavior of FO-DPSO using different differential orders \(\alpha = [0.1, 0.2,\ldots , 1.0]\) can be seen in Fig. 5a for the line loss \(P_{Loss}\), in Fig. 5b for the voltage deviation \(V_D\), and in Fig. 5c for the overall cost \(C_{overall}\). The superiority of the new approach is again endorsed when comparing the results of the FO-DPSO and those of the SPO31, APSO31, EPSO31, DE23, QODE30 and GWO30 algorithms. The results are listed in Table 9. The system operating cost and the real power loss reduction for different solvers is documented in Table 10 that highlights the significance of the FO-DPSO as both quantities are considerably smaller than those obtained when adopting other optimization strategies. Additionally, from these results, we verify that the \(P_{Loss}\), \(V_{D}\) and \(C_{overall}\) converge smoothly and with a less iterations for the FO-DPSO with respect to the other optimization algorithms.
Test case 3
The 3rd test case consists of the standard IEEE 118 bus network for validating the FO-DPSO in the case of large scale power systems. This system contains 186 lines, 9 transformer, 64 load buses, and 54 generator buses. Here, the system restrictions and settings were derived from57. Bus# 1 is considered as the slack/reference bus and the base power is 100 MVA. The FO-DPSO is tested to evaluate the optimum values of the dependent variables while reducing the fitness functions. The effectiveness of FO-DPSO is again endorsed by mean of a comparative analysis between the results of the proposed technique and those provided by the OGSA, WCA and NGBWCA56,57. The results are documented in Table 11, one may observe that FO-DPSO achieved losses inferior than those provided by other optimization mechanisms. The setting of the control variables for the FO-DPSO and other optimization strategies can also be seen in Table 11. The comparative learning behavior of the FO-DPSO using different differential orders \(\alpha = [0.1, 0.2,\ldots , 1.0]\) can be seen in Fig. 6a for line loss (i.e \(P_{loss}\)), in Fig. 6b for voltage deviation (i.e., \(V_{D}\)) and in Fig. 6c for overall cost (i.e., \(C_{overall}\)). We can verify again that, all the minimization functions converge for a smaller number of iterations and evolve more smoothly for the FO-DPSO with respect to other methods.
It is important to mention that the statistical analysis has been performed for 100 independent trials and for each independent run the population (i.e., the swarm), is initialized with pseudo random real numbers between the allowable bounds of decision variables. Different initial populations/swarms are used for each independent trial and the robustness of FO-DPSO is endorsed by the optimization of the control variable with reasonable accuracy for each trail. The difference in performances depicted by Figs. 4, 5 and 6, is due to some better initial population which is completely formulated on random process. Therefore, the main concern/intention for multiple runs is to prove/certify the reliability, effectiveness and stability of the FO-DPSO on standard ORPD problems.
Statistical analysis
In this section, a comprehensive statistical investigation is conducted to demonstrate consistent implications of the FO-DPSO evolution for all the test cases and the three fitness functions of ORPD problems. The performance of the FO-DPSO with fractional order \(\alpha \) = 0.6 revealed the best results on average among the set \(\alpha = [0.1, 0.2,\ldots , 1.0]\) for the IEEE 30 and IEEE 57 bus systems, while fractional order \(\alpha \) = 0.3 for the IEEE 118 bus system. Therefore, a sample of 100 independent runs are conducted with the FO-DPSO using \(\alpha \) = 0.6 for the test cases 1 and 2, while \(\alpha \) = 0.3 for the test case 3, considering \(P_{Loss}\), \(V_{D}\) and \(C_{overall}\) minimization functions as the objectives of ORPD system incorporating FACTS. The statistics from the three fitness measures, in term of stair plot, probability metric for box plot, cumulative distribution function (CDF), histogram, and convergence curves for the best, worst and mean gauges, are demonstrated in Figs. 7, 8 and 9, Figs. 10, 11, 12 and Figs.13, 14 and 15 for the IEEE 30, 57 and 118 bus networks, respectively. The minimum value of the fitnesses in all the test cases are depicted in Figs. 7a, 8a, 9a, 10a, 11a, 12a, 13a, 14a and 15a. The probability plots for the CDF are illustrated in Figs. 7b, 10b and 13b showing that 80% of the independent flights yield line losses inferior to 4.85 MW, 20.4 MW and 132.7 MW for the test cases 1, 2 and 3, respectively. The histograms represented in Figs. 7c, 8c, 9c, 10c, 11c, 12c, 13c, 14c and 15c reveal that most of the autonomous simulations of the FO-DPSO yield minimum values of the three fitness functions. The values of box plots in Figs. 7d, 10d and 13d demonstrate that the median of line losses is approximately 4.8 MW and 20.3 MW for the three test cases, respectively. The learning behavior for the best, average and worst cases are included in Figs. 7e, 8e, 9e, 10e, 11e, 12e, 13e, 14e and 15e that demonstrate the consistency of the FO-DPSO for an effective optimization. In brief, all statistics of the ORPD cases demonstrate the stability, robustness, and consistency of the FO-DPSO as a significant, reliable and accurate optimization strategy.
The scalability of the FO-DPSO is further extended on a very large power system i.e. IEEE 300 bus which contains 304 transmission lines, 60 tap changing transformers, and 69 generators. This study proposes the earliest solution for a single objective of ORPD which is line loss minimization, \(P_{Loss}\). As IEEE-300 bus system is challenging problem, the solutions for reactive power dispatch problems published in the literature are very rare, and so the comparison of results is not possible at this stage. However, when the FO-DPSO is applied to tune the variables, better and consistent results than the base case values are obtained. The computed \(P_{Loss}\) from proposed strategy are 403.259 MW, which are 1.2% less than the base case i.e. 408.316MW. The statistical results obtained for 100 independent trial are depicted in Fig. 16. The Fig. 16a demonstrates that for 95 times, the minimum fitness values obtained by the FO-DPSO are below the base case value (408.316 MW). The CDF based probability plot in Fig. 16b reveals that 90% of the independent runs computed \(P_{Loss}\) values less than 407 MW. The histogram represented in Fig. 16c shows that maximum of the independent trials provide minimum gauge of the fitness function. The values of box plot in Fig. 16d reveal that median of \(P_{Loss}\) is approximately 405.8 MW with relative small spread of data. The learning curves for the best, average and worst cases can be seen in Fig. 16e that demonstrate the consistency of the FO-DPSO for an effective computation.
The time complexity of FO-DPSO is presented in the box plots of Fig. 17 for all the evaluated fitnesses. The calculated time of the algorithm execution for 100 independent runs in term of median gauge adopting test case 1 for \(P_{Loss}\), \(V_{D}\), and \(C_{overall}\) minimization are around 42 s, 68.3 s and 68.5 s, respectively, for case 2 the respective values are around 55 s, 75.75 s, 84.25 s, while for case 3 the values are around 60 s, 80.3 s and 91.5 s, respectively. The small difference between the calculated time for each independent trial (i.e., results of the first quartile and third quartile) show the smooth and consistency operation of proposed FO-DPSO technique for solving the ORPD problems.
The computational complexity of the FO-DPSO is also compared with the other algorithms implemented to solve the ORPD problems. The reported results of time complexity of seeker optimization algorithm (SOA), simple GA (SGA)62, PSO, multi agent PSO (MAPSO)63, improved evolutionary programming (IEP), evolutionary programming EP64, self-adaptive real coded GAs, SARGA65 and the FO-DPSO are documented in Table 12 along with the available specification of the system and number of independent trials used for the analysis. The results show that there is no noticeable variation in the computational time requirements of the FO-DPSO versus those for the rest of the algorithms. However, the complexity performance is difficult to compare because reported results are based on machines with different hardware specification, i.e., RAM, CPU, cloud and parallel processing platform, operating algorithms (i.e., swarm intelligence, evolutionary computing) with different initial settings of swarm size, population, flights and generations, and software environment (i.e., operating systems, MATLAB, MATHEMATICA, etc.).
Conclusions
A fractional evolutionary computing algorithm was designed to solve the ORPD problem in power systems using shunt and series FACTS devices. The FO-DPSO was explored for the minimization of the active power losses and the operating costs, together with the installation cost of FACT, while the voltage profile is maintained within the allowable limits through minimizing voltage deviation index in the standard IEEE-30, 57 and 118 bus systems. The results using the FO-DPSO are compared with those reported in the literature adopting the GWO, WOA, QOGWO, DE, fuzzy DE, SPSO, APSO, EPSO, QODE, OGSA, WCA and NGBWCA schemes. The results demonstrated the superior performance of the FO-DPSO for all objectives of ORPD with FACTS devices. The validation of the FO-DPSO is supported by statistics that include the probability distribution functions, histogram and boxplot representations as measures of the central tendency and diversity indices for ORPD problems solved for the standard test systems.
In future, one may exploit the strength of the fractional swarming/evolutionary computing paradigm as an alternative optimization solver for multi-model nonlinear problems including robust wind power prediction66, forecasting of air temperature67, design of optical metasurfaces68, nonlinear active noise control69, parameter estimation of photovoltaic models70, optimization of design for desalination plant71, multi-objective classification problems72 and prediction of blast-induced ground vibrations73. In addition, the power system performance should be investigated further by incorporating the second generation FACTS devices including the STATCOM, UPFC and TCPS while operating in steady and dynamic states by exploiting the optimization legacy of proposed fractional swarming technique with orders \(\alpha \le 0\), \(0<\alpha <1\) and \(\alpha > 1 \). The selection of appropriate fractional order \(\alpha \) in FO-DPSO with theoretical justification of the physics for a particular optimization problem looks promising to be explore by research community as a further related work.
References
Gerbex, S., Cherkaoui, R. & Germond, A. J. Optimal location of multi-type FACTS devices in a power system by means of genetic algorithms. IEEE Trans. Power Syst. 16, 537–544 (2001).
Mei, R. N. S., Sulaiman, M. H., Mustaffa, Z. & Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 59, 210–222 (2017).
Heidari, A. A., Abbaspour, R. A. & Jordehi, A. R. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 57, 657–671 (2017).
Biswas, P. P., Suganthan, P. N., Mallipeddi, R. & Amaratunga, G. A. J. Optimal reactive power dispatch with uncertainties in load demand and renewable energy sources adopting scenario-based approach. Appl. Soft Comput. 75, 616–632 (2019).
Biswas, S., Mandal, K. K. & Chakraborty, N. Pareto-efficient double auction power transactions for economic reactive power dispatch. Appl. Energy 168, 610–627 (2016).
Montoya, F. G. et al. Minimization of voltage deviation and power losses in power networks using Pareto optimization methods. Eng. Appl. Artif. Intell. 23, 695–703 (2010).
Tushar, M. H. K. & Assi, C. Volt-VAR control through joint optimization of capacitor bank switching, renewable energy, and home appliances. IEEE Trans. Smart Grid 9, 4077–4086 (2017).
Mathur, R. M. & Varma, R. K. Thyristor-based FACTS Controllers for Electrical Transmission Systems (Wiley, Hoboken, 2002).
Awad, N. H., Ali, M. Z., Mallipeddi, R. & Suganthan, P. N. An efficient differential evolution algorithm for stochastic OPF based active-reactive power dispatch problem considering renewable generators. Appl. Soft Comput. 76, 445–458 (2019).
Sayah, S. Modified differential evolution approach for practical optimal reactive power dispatch of hybrid AC-DC power systems. Appl. Soft Comput. 73, 591–606 (2018).
Sang, Y. & Sahraei-Ardakani, M. Effective power flow control via distributed FACTS considering future uncertainties. Electr. Power Syst. Res. 168, 127–136 (2019).
Naderi, E., Pourakbari-Kasmaei, M. & Abdi, H. An efficient particle swarm optimization algorithm to solve optimal power flow problem integrated with FACTS devices. Appl. Soft Comput. 80, 243–262 (2019).
Belati, E. A., Nascimento, C. F., de Faria, H., Watanabe, E. H. & Padilha-Feltrin, A. Allocation of static VAR compensator in electric power systems considering different load levels. J. Control Autom. Electr. Syst. 30, 1–8 (2019).
Salkuti, S. R. Optimal power flow based congestion management using enhanced genetic algorithms. Int. J. Electr. Comput. Eng. 9, 875 (2019).
Osman, M. S., Abo-Sinna, M. A. & Mousa, A. A. A solution to the optimal power flow using genetic algorithm. Appl. Math. Comput. 155, 391–405 (2004).
Padhy, N. P. & Moamen, M. A. A. Power flow control and solutions with multiple and multi-type FACTS devices. Electr. Power Syst. Res. 74, 341–351 (2005).
Xiao, Y., Song, Y. H. & Sun, Y. Z. Power flow control approach to power systems with embedded FACTS devices. IEEE Trans. Power Syst. 17, 943–950 (2002).
Ravi, K. & Rajaram, M. Optimal location of FACTS devices using improved particle swarm optimization. Int. J. Electr. Power Energy Syst. 49, 333–338 (2013).
Bamigbola, O. M., Ali, M. M. & Oke, M. O. Mathematical modeling of electric power flow and the minimization of power losses on transmission lines. Appl. Math. Comput. 241, 214–221 (2014).
Bhattacharyya, B. & Gupta, V. K. Fuzzy genetic algorithm approach for the optimal placement of flexible AC transmission systems devices in a power system. Electr. Power Compon. Syst. 42, 779–787 (2014).
Gitizadeh, M. & Kalantar, M. A novel approach for optimum allocation of FACTS devices using multi-objective function. Energy Convers. Manag. 50, 682–690 (2009).
Phichaisawat, S., Song, Y. H., Wang, X. L. & Wang, X. F. Combined active and reactive congestion management with FACTS devices. Electr. Power Compon. Syst. 30, 1195–1205 (2002).
Bhattacharyya, B. & Gupta, V. K. Fuzzy based evolutionary algorithm for reactive power optimization with FACTS devices. Int. J. Electr. Power Energy Syst. 61, 39–47 (2014).
Bhattacharyya, B. & Kumar, S. Loadability enhancement with FACTS devices using gravitational search algorithm. Int. J. Electr. Power Energy Syst. 78, 470–479 (2016).
Sakr, W. S., El-Sehiemy, R. A. & Azmy, A. M. Adaptive differential evolution algorithm for efficient reactive power management. Appl. Soft Comput. 53, 336–351 (2017).
Shareef, S. K. M. & Rao, R. S. Optimal reactive power dispatch under unbalanced conditions using hybrid swarm intelligence. Comput. Electr. Eng. 69, 183–193 (2018).
Dutta, S., Paul, S. & Roy, P. K. Optimal allocation of SVC and TCSC using quasi-oppositional chemical reaction optimization for solving multi-objective ORPD problem. J. Electr. Syst. Inf. Technol. 5, 83–98 (2018).
Chen, G., Liu, L., Zhang, Z. & Huang, S. Optimal reactive power dispatch by improved GSA-based algorithm with the novel strategies to handle constraints. Appl. Soft Comput. 50, 58–70 (2017).
Rajan, A., Jeevan, K. & Malakar, T. Weighted elitism based ant lion optimizer to solve optimum VAR planning problem. Appl. Soft Comput. 55, 352–370 (2017).
Raj, S. & Bhattacharyya, B. Optimal placement of TCSC and SVC for reactive power planning using whale optimization algorithm. Swarm Evol. Comput. 40, 131–143 (2018).
Bhattacharyya, B. & Raj, S. Swarm intelligence based algorithms for reactive power planning with flexible AC transmission system devices. Int. J. Electr. Power Energy Syst. 78, 158–164 (2016).
Mukherjee, A. & Mukherjee, V. Chaotic krill herd algorithm for optimal reactive power dispatch considering FACTS devices. Appl. Soft Comput. 44, 163–190 (2016).
Ghamisi, P., Couceiro, M. S. & Benediktsson, J. A. A novel feature selection approach based on FODPSO and SVM. IEEE Trans. Geosci. Remote Sens. 53, 2935–2947 (2014).
Ates, A., Alagoz, B. B., Kavuran, G. & Yeroglu, C. Implementation of fractional order filters discretized by modified fractional order Darwinian particle swarm optimization. Measurement 107, 153–164 (2017).
Couceiro, M. S., Rocha, R. P., Ferreira, N. M. F. & Machado, J. A. T. Introducing the fractional-order Darwinian PSO. Signal Image video Process. 6, 343–350 (2012).
Shahri, E. S. A., Alfi, A. & Machado, J. A. T. Fractional fixed-structure controller design using augmented Lagrangian particle swarm optimization with fractional order velocity. Appl. Soft Comput. 77, 688–695 (2019).
Taş, K., Machado, J. A. T. & Baleanu, D. Mathematical Methods in Engineering (Springer, Berlin, 2007).
Ghamisi, P., Couceiro, M. S., Martins, F. M. L. & Benediktsson, J. A. Multilevel image segmentation based on fractional-order Darwinian particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 52, 2382–2394 (2013).
Łegowski, A. & Niezabitowski, M. Robot path control based on PSO with fractional-order velocity. In 2016 International Conference on Robotics and Automation Engineering (ICRAE), 21–25 (IEEE, 2016).
Wang, Y.-Y., Peng, W.-X., Qiu, C.-H., Jiang, J. & Xia, S.-R. Fractional-order darwinian PSO-based feature selection for media-adventitia border detection in intravascular ultrasound images. Ultrasonics 92, 1–7 (2019).
Paliwal, K. K., Singh, S. & Gaba, P. Feature selection approach of hyperspectral image using GSA-FODPSO-SVM. In 2017 International Conference on Computing, Communication and Automation (ICCCA), 1070–1075 (IEEE, 2017).
Ghamisi, P., Couceiro, M. S. & Benediktsson, J. A. Classification of hyperspectral images with binary fractional order Darwinian PSO and random forests. In Image and Signal Processing for Remote Sensing XIX, vol. 8892, 88920S (International Society for Optics and Photonics, 2013).
Wang, Y.-Y., Zhang, H., Qiu, C.-H. & Xia, S.-R. A novel feature selection method based on extreme learning machine and fractional-order Darwinian PSO. Computational Intelligence and Neuroscience 2018, (2018).
Akbar, S., Zaman, F., Asif, M., Rehman, A. U. & Raja, M. A. Z. Novel application of FO-DPSO for 2-D parameter estimation of electromagnetic plane waves. Neural Comput. Appl. 31, 3681–3690 (2019).
Zhu, Q. et al. Research and application on fractional-order Darwinian PSO based adaptive extended Kalman filtering algorithm. IAES Int. J. Robot. Autom. 3, 245 (2014).
Guo, F., Peng, H., Zou, B., Zhao, R. & Liu, X. Localisation and segmentation of optic disc with the fractional-order Darwinian particle swarm optimisation algorithm. IET Image Process. 12, 1303–1312 (2018).
Ates, A., Kavuran, G., Alagoz, B. B. & Yeroglu, C. Improvement of IIR filter discretization for fractional order filter by discrete stochastic optimization. In 2016 39th International Conference on Telecommunications and Signal Processing (TSP), 583–586 (IEEE, 2016).
Yokoya, N. & Ghamisi, P. Land-cover monitoring using time-series hyperspectral data via fractional-order Darwinian particle swarm optimization segmentation. In 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), 1–5 (IEEE, 2016).
Li, X. et al. Optimal fractional order PID controller design for automatic voltage regulator system based on reference model using particle swarm optimization. Int. J. Mach. Learn. Cybern. 8, 1595–1605 (2017).
Kosari, M. & Teshnehlab, M. Non-linear fractional-order chaotic systems identification with approximated fractional-order derivative based on a hybrid particle swarm optimization-genetic algorithm method. J. AI Data Mining 6, 365–373 (2018).
Katal, N. & Narayan, S. Design of robust fractional order PID controllers for coupled tank systems using multi-objective particle swarm optimisation. Int. J. Syst. Control Commun. 8, 250–267 (2017).
Azar, A. T. & Serrano, F. E. Fractional order sliding mode PID controller/observer for continuous nonlinear switched systems with PSO parameter tuning. In International Conference on Advanced Machine Learning Technologies and Applications, 13–22 (Springer, 2018).
Abdulkhader, H. K., Jacob, J. & Mathew, A. T. Fractional-order lead-lag compensator-based multi-band power system stabiliser design using a hybrid dynamic GA-PSO algorithm. IET Gener. Transmission Distrib. 12, 3248–3260 (2018).
Pires, E. J. S., Machado, J. A. T. & de Moura Oliveira, P. B. Fractional particle swarm optimization. In Mathematical Methods in Engineering, 47–56 (Springer, 2014).
Pires, E. J. S., Machado, J. A. T., de Moura, Oliveira, P. B.., Cunha, J. . B. . & Mendes, L. . Particle swarm optimization with fractional-order velocity. Nonlinear Dyn. 61, 295–301 (2010).
Ghasemi, M., Ghavidel, S., Ghanbarian, M. M. & Habibi, A. A new hybrid algorithm for optimal reactive power dispatch problem with discrete and continuous control variables. Appl. Soft Comput. 22, 126–140 (2014).
El Ela, A. A. A., Abido, M. A. & Spea, S. R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 81, 458–464 (2011).
Mahadevan, K. & Kannan, P. S. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 10, 641–652 (2010).
Mandal, B. & Roy, P. K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization. Int. J. Electr. Power Energy Syst. 53, 123–134 (2013).
Sulaiman, M. H., Mustaffa, Z., Mohamed, M. R. & Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 32, 286–292 (2015).
Khorsandi, A., Alimardani, A., Vahidi, B. & Hosseinian, S. H. Hybrid shuffled frog leaping algorithm and Nelder-Mead simplex search for optimal reactive power dispatch. IET Gener. Transm. Distrib. 5, 249–256 (2011).
Dai, C., Chen, W., Zhu, Y. & Zhang, X. Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 24, 1218–1231 (2009).
Zhao, B., Guo, C. X. & Cao, Y. J. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst. 20, 1070–1078 (2005).
Yan, W., Lu, S. & Yu, D. C. A novel optimal reactive power dispatch method based on an improved hybrid evolutionary programming technique. IEEE Trans. Power Syst. 19, 913–918 (2004).
Subbaraj, P. & Rajnarayanan, P. N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 79, 374–381 (2009).
Zameer, A., Arshad, J., Khan, A. & Raja, M. A. Z. Intelligent and robust prediction of short term wind power using genetic programming based ensemble of neural networks. Energy Convers. Manag. 134, 361–372 (2017).
Ratnam, J. V. et al. Improving seasonal forecasts of air temperature using a genetic algorithm. Sci. Rep. 9, 1–11 (2019).
Jafar-Zanjani, S., Inampudi, S. & Mosallaei, H. Adaptive genetic algorithm for optical metasurfaces design. Sci. Rep. 8, 1–16 (2018).
Khan, W. U., Ye, Z., Altaf, F., Chaudhary, N. I. & Raja, M. A. Z. A novel application of fireworks heuristic paradigms for reliable treatment of nonlinear active noise control. Appl. Acoustics 146, 246–260 (2019).
Biswas, P. P., Suganthan, P. N. & Amaratunga, G. A. J. Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 148, 1194–1207 (2017).
Abdelshafy, A. M., Hassan, H. & Jurasz, J. Optimal design of a grid-connected desalination plant powered by renewable energy resources using a hybrid PSO-GWO approach. Energy Convers. Manag. 173, 331–347 (2018).
Zhang, Y., Gong, D.-W., Sun, X.-Y. & Guo, Y.-N. A PSO-based multi-objective multi-label feature selection method in classification. Sci. Rep. 7, 1–12 (2017).
Bui, X.-N., Jaroonpattanapong, P., Nguyen, H., Tran, Q.-H. & Long, N. Q. A novel hybrid model for predicting blast-induced ground vibration based on k-nearest neighbors and particle swarm optimization. Sci. Rep. 9, 1–14 (2019).
Author information
Authors and Affiliations
Contributions
Y.M. carried out simulations and writeup, R.A. provided financial support and resources, R.K. has role in supervision and administration, F.U. involved in software and methodology, M.A.Z.R. conceptualization and review, J.A.T.M validation and review.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Muhammad, Y., Akhtar, R., Khan, R. et al. Design of fractional evolutionary processing for reactive power planning with FACTS devices. Sci Rep 11, 593 (2021). https://doi.org/10.1038/s41598-020-79838-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-79838-2
This article is cited by
-
A mini review on optimal reactive power dispatch incorporating renewable energy sources and flexible alternating current transmission system
Electrical Engineering (2024)
-
Real power loss reduction by monitor lizard optimization algorithm based on class room learning
Energy Systems (2022)
-
Multi-objective-based reactive power planning and voltage stability enhancement using FACTS and capacitor banks
Electrical Engineering (2022)
-
Real power loss reduction by enhanced Apple Maggot optimization algorithm
International Journal of System Assurance Engineering and Management (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.