Abstract
Stemborers (Busseola fusca, Sesamia calamistis and Chilo partellus), the fall armyworm (Spodoptera frugiperda) and associated parasitoids constitute an interacting system in maize fields in Kenya. This work aims at developing and evaluating models that represent the evolution of those interactions by applying system thinking and system dynamics approaches with its archetypes [causal loop diagram (CLD), reinforcing (R) and balancing (B)] to analyse the population of these multi-species systems. The software Vensim PLE 8.0.9 was used to implement the models and carry out the simulations of single- and multi-species systems. The results showed that when a single pest species with its associated parasitoids interact with the host plant, the species was able to establish and sustain by cyclical relationship between populations of the pest and the associated parasitoids. However, in multi- pest species systems, dominance of S. frugiperda and C. partellus over B. fusca and S. calamistis was observed, but without extinction. However, there was a likelihood for B. fusca being displaced by C. partellus. Overall, the models predict the co-existence of fall armyworm with stemborer species as an additional pest of maize in Africa that need to be considered henceforth in designing IPM strategies in maize.
Similar content being viewed by others
Introduction
Globally, maize Zea mays L. (Poaceae) production was estimated at 1.3 billion tons in 20181. Maize is one of the most important cereal crops in sub-Saharan Africa (SSA)2. In Kenya, maize is grown predominantly by smallholder farmers3 and constitutes a vital source for household livelihoods4. The productivity of maize is affected by a wide array of biotic and abiotic stresses that reduce the quantity and quality of its yields. Insect pest pressure is among the major threats that constrain maize crop from reaching its maximum potential yields. A complex of lepidopteran stemborers and the recent invasive fall armyworm Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae) are the primary pests of maize crop in many parts of the world, including Kenya, causing yield losses ranged from 30 to 70%3,5. These pests are responsible for significant losses of maize upon infestation. Evidence to date suggests that with climate change, these pests are continuing to spread to new areas6,7,8.
In SSA, the noctuid stemborers Busseola fusca (Fuller) and Sesamia calamistis (Hampson) (Lepidoptera: Noctuidae), and the crambid stemborer Chilo partellus (Swinhoe) (Lepidoptera: Crambidae) are economically the most important lepidopteran pest species that severely limit maize productivity as a result of a continuous infestation of the crop throughout its growth stages9,10. In maize fields, these stemborers may occur as single species or as a community of mixed species11,12. Among these stemborers, C. partellus is exotic and invaded eastern Africa in the 1930s9. This species has competitively displaced B. fusca in the highlands of South Africa13. It has also displaced Chilo orichalcociliellus Strand (Lepidoptera: Crambidae) in the coastal region of Kenya14 and might get an advantage over S. calamistis in the utilization of maize in the context of future climate change6,15. Recently, S. frugiperda invaded SSA, where it seriously limits maize yields16,17. Field observations indicated that it interacts strongly with maize stemborer systems18 and might also displace them.
Invasive insect herbivores have the prospective to significantly hamper with prevailing insect parasitoids species in invaded areas; this mechanism can occur in different ways: (1) interferences with the volatiles that attract the insect parastoids to unsuitable the host; if the plants can be infested by both the native and invader, the later produces volatiles that are less attractive to parasitoids19; and (2) the parasitoids can attempt to parasitize the invasive insect, with low chance to complete their development. This is considered as a waste of time and energy that can negatively affect the fitness of the parasitoids19,20. These interferences can therefore have detrimental consequences on a pre-existing biological control process21.
Although stemborer species and the fall armyworm have been considered a serious constraint to maize production, few studies have illustrated the interactions among these complexes of pest species. System dynamics, first developed by Forrester21, offers a useful method to understand and describe such interactions. That approach, that was originally developed for engineering and administration studies is increasingly been applied to other fields such agriculture, health, economic, and social science21,22. The method takes in consideration a set of elements that interact continuously as a component with structure, which undergoes changes22,23. The analysis of the system structure (model) by scenarios provides an understand the system behaviour with time. Using differential equations and the Routh–Hurwitz criteria, Mwalusepo et al.24 studied the stability of insect species competing for resource. The study revealed that when a species feeds on a resource, the species will be able to establish and sustain a stable population that fluctuates based on the resource availability. However, in a competing context with many species feeding on a single resource, it is observed that the combinations of three parameters (half-saturation, growth rate and mortality rate) determine which species has the upper edge on the resource. In another study, Neill25 applied matrix model of the competition coefficients to study the community of species to reveal different patterns of interspecific interactions and estimate the maximum number of interacting species expected in a community. This work therefore aims at developing and evaluating models that represents the interactions of maize stemborer species and S. frugiperda populations and their associated parasitoids in a multi-species community in maize fields.
System components and structure of the models
The stemborers, B. fusca, S. calamistis and C. partellus are the most important pests of maize in Kenya9. The three stemborers frequently occur as single or mixed species communities11,12 whose structure varies with agro-ecological zones. Busseola fusca is generally the dominant species in the highlands, while C. partellus dominates in the lowlands6,26, and S. calamistis occurs at all altitudes27. These stemborer species often occur as a mixed community of the three species in the mid-altitudinal regions7,12. Spodoptera frugiperda, since its first report in the western region of Kenya in 2017, has been confirmed throughout the different agro-ecological zones by the early cropping season in 201828.
Several studies have documented parasitoids associated with the three stemborers in the different agroecological zones29,30,31. In cultivated habitats in Kenya, the most common parasitoids of all three species are the larval parasitoids Cotesia flavipes Cameron and Cotesia sesamiae (Cameron) (Hymenoptera: Braconidae) followed by the pupal parasitoids Xanthopimpla stemmator (Hymenoptera: Ichneumonidae) and Pediobius furvus Gahan (Hymenoptera: Eulophidae), and the tachinid Siphona sp. (Diptera: Tachinidae)29,30,31. Since its invasion, research for development efforts has highlighted the effectiveness of several integrated pest management strategies for S. frugiperda, including new association of indigenous natural enemies with S. frugiperda such as the larval parasitoids Cotesia icipe Fernandez‐Triana & Fiaboe (Hymenoptera: Braconidae), Charops sp. Holmgren (Hymenoptera: Ichneumonidae) , Coccigydium luteum Brullé (Hymenoptera: Braconidae), Palexorista zonata Curran (Diptera: Tachinidae); the egg-larval parasitoid Chelonus curvimaculatus Szépligeti (Hymenoptera: Braconidae) and the egg parasitoids Telenomus remus Dixon (Hymenoptera: Platygastridae) and Trichogramma chilonis Ishii (Hymenoptera: Trichogrammatidae)28,32.
Busseola fusca and S. calamistis females deposit the eggs between the leaf sheath and the stem of plant as a protection strategy against the environment and the natural enemies, whereas C. partellus and S. frugiperda females deposit eggs directly on leaf surfaces33,34. Upon emergence, the young larvae are dispersed by ballooning while older larvae disperse by crawling, resulting in a redistribution of the insect infestations within and between plants in maize fields35. The stemborer larvae feed on young leaves until the third instar and later bore into maize stems. Spodoptera frugiperda larvae feed only on leaves during their whole development, especially the central leaves in the plant whorl36,37. In addition, in maize fields at tasseling stage, S. frugiperda larvae can be found feeding on the tassels and subsequently on the ear, silk, cob and even in stemborer's holes36,38. Therefore, S. frugiperda and stemborer larvae may interact by sharing the same niche at young developmental stages and even when the stemborer larvae migrate from the leaves to stems.
The four pest species (three stemborers + S. frugiperda), in addition to their associated parasitoids and the maize plants that serve as the resource for the pests, constitute the system under study. Several cases are considered because these insects occur at different spatial distributions aross different agroecological zones. The analyses were subdivided in four cases: (1) a single pest species feeding on maize plants and its parasitoids, (2) two species competing on maize plants and their parasitoids, (3) three species competing on maize plants and their parasitoids, and (4) four pest species together on maize plants and their parasitoids.
Results
One pest species and its parasitoids and the resource (maize plants)
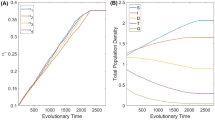
For each pest species and its associated parasitoid populations, the outcomes of the models showed that both populations marginally increased at the beginning. After 4 months, the relationship became cyclical between a host (pest) and its associated parasitoids (Fig. 1A–D). As the population of parasitoids increased, the pest population decreased, which in turn caused parasitoids population to decrease. As parasitoids population decreased, the pest population was able to recover, and its population increased. Subsequently, the parasitoids population increased and the cycle began again. The three stemborer species had similar populations with a maiximum peak after 6 months of about 4900 individuals (Fig. 1A–C) while the maximum peak of S. frugiperda poplulation (Fig. 1D) was 17% less than those of stemborers. The peaks of the populations of parasitoids of the three stemborers species reach a level above 4500 individuals after 7 months while the population of parasitoids associated with S. frugiperda was below 4000 individuals during the same period (Fig. 1A–D).
Two pest species and associated parasitoids and the resource (maize plants)
In a two species system, a strong unilateral competitive interaction was revealed in the C. partellus and B. fusca system (Fig. 2A) representing 81.18% and 18.82%, respectively of the total pest populations in the system. The population of B. fusca was largely outcompeted by C. partellus after 6 months and its population was drastically reduced in a two species system as compared to when it was the sole species in the system. In the system of either B. fusca and S. calamistis (Fig. 2B) or C. partellus and S. frugiperda (Fig. 2C), bilateral competitive interactions were strong, leading to the decline of both the species populations but without dominance. Although bilateral competitive interactions were revealed in other two multi- pest species systems, C. partellus was most prevalent to S. calamistis (Fig. 2D) representing 66.08% and 33.92%, respectively and S. frugiperda was most prevalent to B. fusca (Fig. 2E) and S. calamistis (Fig. 2F) after 6 months and represented 60.53% and 39.47%, respectively of the total pest populations in the system. In addition, the model showed that the populations of each pest species in two pest species systems (Fig. 2A–F) declined as compared to those in sole pest species systems (Fig. 1A–D). However, the average total pest populations (population size of each pest) in sole-pest species systems represented only 85.36% of total average pest populations in two-pest species systems (population size of any given combination of two pest species). In each combination, the associated parasitoid populations proportionally varied with their respective host population fluctuation as parasitoid population tracked the peaks of the pest population.
Populations of Chilo partellus, Busseola fusca, Sesamia calamistis and Spodoptera frugiperda and their associated parasitoids in two multi- pest species competitive systems. (A) C. partellus + B. fusca (Cp + Bf) system; (B) B. fusca + S. calamistis (Bf + Sc) system; (C) S. frugiperda + C. partellus (Sf + Cp) system; (D) C. partellus + S. calamistis (Cp + Sc) system; (E) S. frugiperda + B. fusca (Sf + Bf) system; (F) S. frugiperda + S. calamistis (Sf + Sc) system.
Three and four pest species and associated parasitoids and the resource (maize plants)
In three species systems after 6 months, C. partellus and S. frugiperda co-exist representing 45.45% and 40.42% of the total pest populations in the system but competitively dominated B. fusca population that represented only 14.13% (Fig. 3A). However, in C. partellus + S. calamistis + S. frugiperda three species system, S. calamistis became dominant over S. frugiperda (Fig. 3B). They represented 44.80%, 31.43% and 23.77% , respectively of the total pest populations in the system. The system of the three stemborer species (Fig. 3C) showed the dominance of C. partellus (47.93%) followed by S. calamistis (31.70%) and B. fusca(20.37%), respectively. Spodoptera frugiperda was the dominant species followed by B. fusca and S. calamistis in three pest species system (Fig. 3D). In each system, the parasitoid population fluctuation evolved according to its host population fluctuation. Furthermore, the model showed that the population of each pest species in three pest species systems (Fig. 3A–D) declined as compared to those in two pest species systems (Fig. 2A–F). However, the average total pest populations in two-pest species systems represented only 70.07% of total average pest populations in three-pest species systems.
Populations of Chilo partellus, Busseola fusca, Sesamia calamistis and Spodoptera frugiperda and their associated parasitoids in three and four multi-species competitive systems. Three multi-species: (A) S. frugiperda + B. fusca + C. partellus (Sf + Bf + Cp); (B) S. frugiperda + S. calamistis + C. partellus (Sf + Sc + Cp); (C) B. fusca + S. calamistis + C. partellus (Bf + Sc + Cp) and (D) S. frugiperda + B. fusca + S. calamistis (Sf + Bf + Sc) systems. Four multi-species: (E) B. fusca + C. partellus + S. calamistis + S. frugiperda (Bf + Cp + Sc + Sf) and (F) their associated parasitoids systems.
In four pest species system, C. partellus was the dominant species (48.79%), followed by S. calamistis (28.34%), S. frugiperda (14.85%) and B. fusca (8.02%), respectively (Fig. 3E), with the same trend of their associated parasitoids (Fig. 3F). Comparing four pest species system populations to those in three pest species systems, the population of each pest species declined except that of C. partellus. The total average pest populations in three-pest species systems represented only 89.88% of those in four pest species system.
Discussion
In this study, we modeled the dynamics and interactions of populations of three maize stemborer species and the fall armyworm, as well as their associated parasitoids, in either single or multi-species systems. The population dynamics of single pest species systems presented S-shaped growth with overshoot logistic form of the well-known Lotka–Volterra prey predator system39,40. The S-shaped form could be due to the negative feedback in the loop diagram that slowly limits the growth as the growth rate reaches the limit. However, the negative feedback contains time delays due to the variability of available resources (host plants) leading to intra-specific competitive interaction that affected the abundance of the pest. The time delay in the negative feedback causes the system to exceed the limit value and exhibit oscillation behavior around the limit value as previously reported by Sterman41. Furthermore, the presence of parasitoids influences the host population dynamics leading to a cyclical relationship between a host (pest) and its associated parasitoids as previously demonstrated by the Lotka-Volterra predator–prey model function39,40. For each of the three stemborer species systems, the associated parasitoids populations grew faster than their respective host populations. Din and Donchev42 reported that in a host-parasite interaction, if a host population is a pest, then according to the Leslie–Gower model, a fast-growing parasite population with a growth rate larger than that of the host significantly reduces the host population. Therefore, the present model indicates a significant effect of parasitoid on stemborers population regulation. Despite high outbreaks reported for S. frugiperda, its population dynamics in our single-species system was actually the lowest which might be due to its high cannibalism rate reported in the literature43,44 and also because the high outbreaks across SSA was reported during the first months of infestation when equilibrium was not yet established; whereas stemborers have been present for decades.
Within stemborer species in multi-species systems (either in two or three species systems), C. partellus exhibited dominance whenever involved in a system. Several previous studies have reported the dominance of C. partellus over B. fusca and S. calamistis when they co-exist15,19,24. In two-species system with C. partellus and B. fuca, the model showed that C. partellus has displaced B. fusca population with time. Those competitive interactions may justify the spatial distribution of these stemborer species in Kenya. Previous studies have reported that B. fusca and S. calamistis co-exist in the highlands with dominance of B. fusca species, while C. partellus and S. calamistis co-habituate in the lowlands with dominance of C. partellus6,25,26. These three stemborer species were reported to occur as a mixed system in the mid-altitudinal regions with dominance of C. partellus7,12. Furthermore, studies in South Africa showed that C. partellus has expanded its distribution into highland region and has competitively displaced B. fusca population in that area13.
On the other hand, the model demonstrated that bilateral competitive interactions were strong in B. fusca + S. calamistis and C. partellus + S. frugiperda two-species systems where both species populations fluctuate and dropped considerably. Those behaviours may be explained by the overlapped ecological niches of these pest species. The females of B. fusca and S. calamistis deposit the eggs between the leaf sheath and the stem of plant, whereas C. partellus and S. frugiperda deposit eggs directly on leaf surfaces33,34. Therefore, the interactions in those systems might start at neonate stage when the eggs hatched or even at egg stage by sharing the same ecological niches. Sokame et al.35 have also demonstrated that the larvae of pest species in those respective systems shared the same behaviour in terms of ballooning and crawling. All those common life traits might lead them to strong competition. Zhou et al45 have demonstrated that in the nature, species that are living together in the same or similar niches because they have one or several kinds of similar behaviours are highly competitive. The dominance of S. frugiperda species in the system of either B. fusca or S. calamistis in two species systems or with both species in three species system in the present model might be the intraguild predation preference of S. frugiperda to the detriment of cannibalism in interspecific systems which is reflected in competition coefficients of S. frugiperda in multi-species systems used in our study. Bentivenha et al.46 demonstrated that S. frugiperda in multi-species system with Helicoverpa zea (Boddie) (Lepidoptera: Noctuidae), its cannibalism decreases to the detriment of intraguild predation of the other species.
Overall, the outputs of the simulations indicated that C. partellus and S. frugiperda species were competitively superiors over B. fusca and S. calamistis. However, in three or four multi-species involving C. partellus with S. calamistis and S. frugiperda, S. calamistis took the advantage and dominated S. frugiperda. Chilo partellus and S. frugiperda are exotic species in Africa while B. fusca and S. calamistis are indigenous. Invasive insect pest species have the potential to rapidly establish and spread to new areas47. The organisms that arrive and establish themselves in a new range of hosts are positioned to have adverse effects on the surrounding fauna and also results in the extinction of other species48. They often affect native species populations and systems by competing for the same resource49. For example, the Asian adelgid, Pineus boemeri Annand, has been shown to be competitively superior and to displace a native congener, P. coloradensis (Gilette) in red pine (Pinus resinosa Aiton) plantation in Eastern USA, possibly through the reduction of host plant quality and forcing P. coloradensisto to less suitable sites50. The invasive fruit fly Bactrocera invadens Drew, Tsuruta & White (Diptera: Tephritidae), has displaced the indigenous mango fruit fly, Ceratitis cosyra Walker (Diptera: Tephritidae) 4 years after invasion in Kenya and become the dominant fruit fly pest of mango51. Temperature and resource pre-emption were demonstrated to be key factors contributing to the competitive success of the invasive fruit fly B. invadens over the indigenous mango fruit fly, C. cosyra in Kenya52. Fabre et al.53 demonstrated a form of resource competition between native and exotic seed chalcids, Megastigmus spp. and displacement of the native species. Similarly, the African stemborer B. fusca seems to have been displaced from sorghum fields by the Asian invasive stemborer C. partellus13 possibly due to deterrence of the native species by the invasions or due to differences in host plant phenology.
The comparison of sole pest species systems with multi-pest species systems of the models showed that the population of each species declined in multi-pest species systems and more the number of pest species involved in the system increased more the population of each species declined. In contrary, the total number of pest populations in the systems increased with the number of pest species involved in the system. Therefore, the reduction of stemborer populations in maize fields with the arrival of S. frugiperda was even overtaken up by that latter. Those results indicate the overall pest abundance increasing in maize fields with the invasion of fall armyworm in maize stemborer systems with more infestations and damages, leading to the increasing of the smallholder incomes losses in maize production. However, the fact that no competition between parasitoid species was considered might have effect on the system dynamics model.
In conclusion, the present models predict the co-existence of S. frugiperda with stemborer species in maize fields. Spodoptera frugiperda and C. partellus dominate over B. fusca and S. calamistis but without extinction, except that B. fusca seems to be displaced by C. partellus. Therefore, the invasion of S. frugiperda in maize fields in Africa constitutes an additional pest to maize crop that need to be considered within the context of integrated pest management strategy. However, the underpinning mechanisms surrounding the co-existence and possible displacement of other species warrant additional studies.
Methods
Modelling and simulations assumptions
To develop the model, the following assumptions have been made:
-
1.
Data obtained under laboratory conditions were used to reproduce and simulate what may occur under field conditions.
-
2.
The growth of insect pest species is limited by a single maize resource, and the parasitoids only depend on their host pests for survival.
-
3.
During the non-cropping season, only 10% of the pest found in maize fields survived on alternative host plants and will give rise to a new pest population in maize field during the subsequent cropping season.
-
4.
A 3-month maize variety (Duma 43, Kenya Seed Company, Nairobi, Kenya) was considered to be used and grown from April to June and from October to December, periods corresponding to the yearly cropping seasons in Kenya.
-
5.
Insect pests were recorded for the first time in the maize field 1 month after planting date.
-
6.
Pest population growth is assumed to follow the Lotka–Volterra competition function39.
-
7.
The parasitism level of a given pest species is recorded from the second generation of the pest, thus with an average of 2 months of delay after maize planting.
-
8.
The parasitism level of all parasitoid species on a given host were lumped together and no competition between parasitoid species was taken into account.
-
9.
Simulations were carried out assuming that each system was at the equilibrium state.
Models simulations and data sources
Before the simulations, a multiple regression procedure was conducted using the R software version 3.5.1 (R Foundation for Statistical Computing, Vienna, Austria) with experimental data from Sokame56 on density-dependent of species interaction in laboratory conditions to estimate the competition coefficients of each studied case of species combination as presented in Table 1.
In addition, the parasitism level of all parasitoids species on a given host that were lumped together and other constants in Table 2 were used for the model simulations. Units and models’ commodities were well checked prior to the simulations.
The models were implemented and simulated using the Vensim PLE 8.0.9 platform (Ventana Systems, Harvard, USA), which consists of a graphical environment that permits users to draw the CLD, stocks and flows diagrams and carry out simulations55. The dynamics of pest and associated parasitoids populations were considered as stocks and the in/out flows were defined. The inflows were composed of pest or parasitoid population growth rates while the outflows were represented by decrease rates of the pests that have been parasitized or the parasitoids that have completed their life cycle.
As mentioned in the assumptions section, all simulations were conducted at the equilibrium state of each system that is characterized by:
where Ki is the column vector of the total number of larvae survived, Ni is the column vector of the total number of survived larvae of a given species, and aijNj is the “system matrix’’ of the interaction coefficients.
The absolute value of any (a) reflects the intensity of the interaction on a given species. The system matrix therefore characterizes the first order (linear) relationship of each species with each other in the system.
Models formulation
Ordinary differential equation developed to study species population dynamics under competitions were used in this study. All the models used have the generic formulation displayed in Eq. (2). Considering N(t) as a state variable to denote the insect population abundance at time t; the population growth for the ith species is defined with the Lotka–Volterra competition equations, which was later modified by MacArthur and Levins54 as:
where the Ni is the species abundance, ri is the intrinsic rate of population natural increase, Ki is the species carrying capacity (the maximum attainable population size), m is the number of pest species in the system, and aij is the effect that an individual species characterized by jth can cause to another species characterized with ith. The translation of this generic mathematical expression was applied to formulate the equations used to simulate each case studied. The model expressions can be found in Supplementary Appendix.
Models implementation
The methodology here is rooted in system thinking approach with its archetypes [causal loop diagram (CLD), reinforcing (R) and balancing (B)] by a mental and holistic conceptual framework used to map how the variables, issues and processes are influencing each other in the complex competitions and interactions among and between insect species and the impacts. Although these archetypes are qualitative in nature, they help to disclose and elucidate the fundamental feedback configurations that occur in maize fields when insect pests are competing for resource and associated parasitoids are hunting for hosts. The CLD obtained were converted into a dynamic modelling using stocks, flows, auxiliary links and clouds; which in turn were translated into coupled differential equations for simulations.
One pest species and associated parasitoids and the resource (maize plants)
The diagram of causalities represents the basic structure of the system of a given pest species with its associated parasitoids, where arrows show the cause–effect relations. A positive sign indicates direct proportionality of cause and effect, and the negative sign indicates a relation of inverse proportionality. The system is characterized by two negative feedbacks (Fig. 1, Loops B1 and B2) and one positive feedbacks (Fig. 1A, Loop R1) leading to three main relationships:
-
a)
as the resource (maize plants) increases, the growth of the pest increases to occupy the available resource resulting in the pest population increase;
-
b)
as host availability increases, the probability that the parasitoid encounters its host increases, resulting in higher parasitism, increased host mortality rate and decreased pest population;
-
c)
as host mortality rate increases, parasitoid growth rate increases, and parasitoid population increases.
Figure 4B showed the stocks and flows diagram and auxiliary variables obtained from causal loop diagram displayed in Fig. 4A. The single pest species (PSi) and associated parasitoids are the stocks in the system, representing the population size of pest species and parasitoids, respectively, at a given point in time. The growth rates represented the inflows while the decrease rates represented the outflows of the diagram. The auxiliary as well as constant variables that drive the behaviour of the system were connected using information arrows within them and to flows and stocks to represent the relations among variables in terms of equations.
Two pest species and associated parasitoids and the resource (maize plants)
In two multi-pest species system (Fig. 5A), the three previous relationships intervened for each species (Fig. 5A, Loops B1, B2, and R1 for species 1 and Loops B3, B4, and R2 for species 2). In addition, relationship (d: Loop R3, Fig. 5A) described inter-specific competition effect of involved pest species on each other. The stocks and flows diagram of each of the two species occurred with level of discrepancy between the carrying capacity (K) and the population size, which additionally is dependent on the intra and inter-specific competition and interations among and between these species (Fig. 5B).
Three pest species and associated parasitoids and the resource (maize plants)
In three multi-pest species system and associated parasitoids system (Fig. 6A), we have the three relationships (a, b and c) previously described for each species (Loops B1, B2, and R1 for species 1; Loops B3, B4, and R2 for species 2 and Loops B5, B6, and R3 for species 3). The relationship (e) represented the inter-specific competitive influence exercised by each of the three species on each other (Fig. 6A,B7). The stocks and flows diagram of individual species in the system occurred with a level of discrepancy between the carrying capacity (K) and the population size, which additionally is dependent on the intra- and inter-specific competition and interations among and between these species (Fig. 6B).
Four pest species and associated parasitoids and the resource (maize plants)
In four multi-pest species system (Fig. 7A), the relationships (a, b and c) existed for each of the four species (species 1: Loops B1, B2, and R1; species 2: Loops B3, B4, and R2; species 3: Loops B5, B6, and R3 and species 4: Loops B7, B8, and R4). The relationships (f) represented by the Loops B9, B10, B11 and R5 showed interaction relationships between the four species. The stocks and flows diagram obtained from the system made by four species occurred with a level of discrepancy between the carrying capacity (K) and the population size of individual species, which additionally is dependent on the intra and inter-specific competition and interations among and between these species (Fig. 7B).
Models evaluation
The model equations used in this study are standard with Lotka–Volterra like formulation. These equations have been used by others authors39,57 to study biological species involving multiple species interactions. Lack of adequate time series data did not allow to use the conventional evaluation technique that consists of plotting the observed data and simulated outputs for measuring the goodness fit of the models. However, we leveraged on the popularity and enormous amount of studies produced from the famous Lotka Volterra competitive equations. To measure the model’s performance and ensure that the obtained outputs are authentic, we compiled the population densities of all pest species (stemborers and S. frugiperda) and parasitoids to establish an interacting system with only two species (pest and parasitoids). The obtained new model was simulated, and the parasitoid-host phase diagram is presented in Fig. 8. The two species competition models produced circular isoclines as phase diagram, as revealed by Lotka–Volterra equations therefore, we concluded the validity of the developed models using stock and flow diagram. The curve of the graph is identical to shape found in literature39,40 and used to describe the co-evolution of two species under interactions.
References
FAO Food and agriculture data [Internet]. www.fao.org/faostat/en/#home. Accessed 17 July 2019 (2018).
Badu-Apraku, B. & Fakorede, M. Maize in Sub-Saharan Africa: Importance and Production Constraints. Advances in Genetic Enhancement of Early and Extra-Early Maize for Sub-Saharan Africa 3–10 (Springer, Cham, 2017).
Jin, Z. et al. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 228, 115–128 (2019).
De Groote, H. et al. Spread and impact of fall armyworm (Spodoptera frugiperda J.E. Smith) in maize production areas of Kenya. Agric. Ecosyst. Environ. 292, 106804 (2020).
Mumo, L., Yu, J. & Fang, K. Assessing impacts of seasonal climate variability on maize yield in Kenya. Int. J. Plant Prod. 12, 297–307 (2018).
Mwalusepo, S. et al. Predicting the impact of temperature change on the future distribution of maize stem borers and their natural enemies along East African mountain gradients using phenology models. PLoS One 10, e0130427 (2015).
GuoFa, Z., Overholt, W. A. & Mochiah, M. B. Changes in the distribution of lepidopteran maize stemborers in Kenya from the 1950s to 1990s. Int. J. Trop. Insect Sc. 21, 395–402 (2001).
Tounou, A. K., Agboka, K., Agbodzavu, K. M. & Wegbe, K. Maize stemborers distribution, their natural enemies and farmers’ perception on climate change and stemborers in southern Togo. J. Appl. Biosci. 64, 4773–4786 (2013).
Kfir, R., Overholt, W. A., Khan, Z. R. & Polaszek, A. Biology and management of economicaly important lepidopteran cereal stem borers in Africa. Annu. Rev. Entomol. 47, 701–731 (2002).
Nwilene, F. E., Nwanze, K. F. & Youdeowei, A. Impact of integrated pest management on food and horticultural crops in Africa. Entomol. Exp. Appl. 128, 355–363 (2008).
Krüger, W., Van den Berg, J. & Van Hamburg, H. The relative abundance of maize stem borers and their parasitoids at the Tshiombo irrigation scheme in Venda, South Africa. S. Afr. J. Plant Soil 25, 144–151 (2008).
Ongamo, G. et al. Distribution, pest status and agro-climatic preferences of lepidopteran stem borers of maize in Kenya. Ann. Soc. Entomol. Fr. 42, 171–177 (2006).
Kfir, R. Competitive displacement of Busseola fusca (Lepidoptera: Noctuidae) by Chilo partellus (Lepidoptera: Pyralidae). Ann. Entomol. Soc. Am. 90, 619–624 (1997).
Ofomata, V. C., Overholt, W. A., Lux, S. A., Van Huis, A. & Egwuatu, A. R. I. Comparative studies on the fecundity, egg survival, larval feeding, and development of Chilo partellus and Chilo orichalcociliellus (Lepidoptera: Crambidae) on five grasses. Ann. Entomol. Soc. Am. 93, 492–499 (2000).
Ntiri, E. S., Calatayud, P.-A., Van den Berg, J., Schulthess, F. & Le Ru, B. P. Influence of temperature on intra- and interspecific resource utilization within a community of lepidopteran maize stemborers. PLoS One 11, e148735 (2016).
Fotso-Kuate, A. et al. Spodoptera frugiperda Smith (Lepidoptera: Noctuidae) in Cameroon: Case study on its distribution, damage, pesticide use, genetic differentiation and host plants. PLoS One 14, e0215749 (2019).
Goergen, G., Kumar, P. L., Sankung, S. B., Togola, A. & Tamò, M. First report of outbreaks of the fall armyworm Spodoptera frugiperda (J E Smith) (Lepidoptera, Noctuidae), a new alien invasive pest in West and Central Africa. PLoS One 11, e0165632 (2016).
Sokame, B. M. et al. Influence of temperature on the interaction for resource utilization between Fall Armyworm, Spodoptera frugiperda (Lepidoptera: Noctuidae), and a community of lepidopteran maize stemborers larvae. Insects 11, 73 (2020).
Sokame, B. M. et al. Impact of the exotic fall armyworm on larval parasitoids associated with the lepidopteran maize stemborers in Kenya. Biocontrol https://doi.org/10.1007/s10526-020-10059-2 (2020).
Chabaane, Y., Laplanche, D., Turlings, T. C. & Desurmont, G. A. Impact of exotic insect herbivores on native tritrophic interactions: A case study of the African cotton leafworm, Spodoptera littoralis and insects associated with the field mustard Brassica rapa. J. Ecol. 103, 109–117 (2015).
Forrester, J. W. Industrial Dynamics (The MIT Press, Cambridge, 1961).
Sapiri, H., Zulkepli, J., Abidin, N. Z., Ahmad, N. & Hawari, N. N. Introduction to System Dynamics Modelling and Vensim Software 173 (Universiti Utara Malaysia, Malaysia, 2016).
Maani, K. E. & Cavana, R. Y. System Thinking and Modelling: Understanding Change and Complexity (Prentice Hall, Auckland, 2000).
Mwalusepo, S., Tonnang, H. E. Z., Massawe, E. S., Johansson, T. & Le Ru, B. P. Stability analysis of competing insect species for a single resource. J. Appl. Math. 20, 2014 (2014).
Neill, W. E. The community matrix and interdependence of the competition coefficients. Am. Nat. 108, 399–408 (1974).
Calatayud, P.-A. et al. Can climate-driven change influence silicon assimilation by cereals and hence the distribution of lepidopteran stem borers in East Africa?. Agric. Ecosyst. Environ. 224, 95–103 (2016).
Ntiri, E. S., Calatayud, P.-A., Van den Berg, J. & Le Ru, B. P. Spatio-temporal interactions between maize lepidopteran stemborer communities and possible implications from the recent invasion of Spodoptera frugiperda (Lepidoptera : Noctuidae) in sub-Saharan Africa. Environ. Entomol. 48, 573–582 (2019).
Sisay, B. et al. First report of the fall armyworm, Spodoptera frugiperda (Lepidoptera: Noctuidae), natural enemies from Africa. J. Appl. Entomol. 142, 800–804 (2018).
Mailafiya, D. M., Le Ru, B. P., Kairu, E. W., Calatayud, P.-A. & Dupas, S. Species diversity of lepidopteran stem borer parasitoids in cultivated and natural habitats in Kenya. J. Appl. Entomol. 133, 416–429 (2009).
Mailafiya, D. M., Le Ru, B. P., Kairu, E. W., Calatayud, P.-A. & Dupas, S. Geographic distribution, host range and perennation of Cotesia sesamiae and Cotesia flavipes Cameron in cultivated and natural habitats in Kenya. Biol. Control 54, 1–8 (2010).
Mailafiya, D. M., Le Ru, B. P., Kairu, E. W., Dupas, S. & Calatayud, P.-A. Parasitism of lepidopterous stemborers in cultivated and natural habitats. J. Insect Sci. 11, 1–19 (2011).
Sisay, B. et al. Fall armyworm, Spodoptera frugiperda infestations in East Africa: Assessment of damage and parasitism. Insects 10, 195 (2019).
Pitre, H. N., Mulrooney, J. E. & Hogg, D. B. Fall armyworm (Lepidoptera: Noctuidae) oviposition: Crop preferences and egg distribution on plants. J. Econ. Entomol. 76, 463–466 (1983).
Polaszek, A. African Cereal Stem Borers: Economic Importance, Taxonomy, Natural Enemies and Control 530 (CAB International, Wallingford, 1998).
Sokame, B. M., Subramanian, S., Kilalo, D. C., Juma, G. & Calatayud, P.-A. Larval dispersal of the invasive fall armyworm, Spodoptera frugiperda, the exotic stemborer, Chilo partellus, and the indigenous maize stemborers in Africa. Entomol. Exp. Appl. 168, 322–331 (2020).
Morrill, W. L. & Greene, G. L. Distribution of fall Armyworm larvae. 1. Regions of field corn plants infested by larvae. Environ. Entomol. 2, 195–198 (1973).
Van den Berg, J. Economy of Stem Borer Control in Sorghum. ARC-Crop Protection Series no 2 4 (South Africa, Potchefstroom, 1997).
CAB International. How to Identify Fall Armyworm. Poster. Plantwise, http://www.plantwise.org/FullTextPDF/2017/20177800461.pdf. Accessed 23 Nov 2018 (2017).
Bischof, R. & Zedrosser, A. The educated prey: Consequences for exploitation and control. Behav. Ecol. 20, 1228–1235 (2009).
Boukal, D. & Kivan, V. Lyapunov functions for Lotka–Volterra predator-prey models with optimal foraging behavior. J. Math. Biol. 39, 493–517 (1999).
Sterman, J. Business Dynamics: Systems Thinking and Modeling for a Complex World (Irwin/McGraw-Hill, Boston, 2000).
Din, Q. & Donchev, T. Global character of a host-parasite model. Chaos Soliton Fract. 54, 1–7 (2013).
Sarmento, R. D. A. et al. Biology review, occurrence and control of Spodoptera frugiperda Smith (Lepidoptera: Noctuidae) in corn in Brazil. Biosci. J. 18, 41–48 (2002).
Chapman, J. W., Williams, T., Martínez, A. M. & Cisneros, J. Does cannibalism in Spodoptera frugiperda (Lepidoptera: Noctuidae) reduce the risk of predation?. Behav. Ecol. Sociobiol. 48, 321–327 (2000).
Zhou, S. Z., Chen, Z.-P. & Xu, Z.-F. Niches and interspecific competitive relationships of the parasitoids, Microplitis prodeniae and Campoletis chlorldeae, of the oriental leafworm moth, Spodoptera litura, in tobacco. J. Insect Sci. 10, 10 (2010).
Bentivenha, J. P. F., Baldin, E. L. L., Hunt, T. E., Paula-Moraes, S. V. & Blankenship, E. E. Intraguild competition of three noctuid maize pests. Environ. Entomol. 45, 999–1008 (2016).
Richardson, D. M., Allsopp, N., D’Antonio, C. M., Milton, S. J. & Rejmanek, M. Plant invasions—the role of mutalists. Biol. Rev. 75, 65–93 (2000).
Sujay, Y. H., Sattagi, H. N. & Patil, R. K. Invasive alien insects and their impact on agroecosystem. Karnatka J. Agric. Sci. 23, 26–34 (2010).
Reitz, S. & Trumble, J. Competitive displacement among insects and arachnids. Annu. Rev. Entomol. 47, 435–465 (2002).
McClure, M. S. Biology, population trends, and damage of Pineus boerneri and P. coloradiensis (Homoptera: Adelgidae) on red pine. Environ. Entomol. 18, 1066–1073 (1989).
Ekesi, S., Billah, M. K., Nderitu, P. W., Lux, S. A. & Rwomushana, I. Evidence for competitive displacement of Ceratitis cosyra by the invasive fruit fly Bactrocera invadens (Diptera: Tephritidae) on mango and mechanisms contributing to the displacement. J. Econ. Entomol. 102, 981–991 (2009).
Rwomushana, I., Ekesi, S., Ogol, C. K. P. O. & Gordon, I. Mechanisms contributing to the competitive success of the invasive fruit fly Bactrocera invadens over the indigenous mango fruit fly, Ceratitis cosyra: The role of temperature and resource pre-emption. Entomol. Exp. Appl. 133, 27–37 (2009).
Fabre, J. P., Auger-Rozenberg, M. A., Chalon, A., Boivin, S. & Roques, A. Competition between exotic and native insects for seed resources in trees of a Mediterranean forest ecosystem. Biol. Invas. 6, 11–22 (2004).
Macarthur, R. & Levins, R. The limiting similarity, convergence, and divergence of coexisting species. Am. Nat. 101, 377–385 (1967).
Ventana. Ventana Systems Incl. Vensim software PLE 8.0.9. https://vensim.com/download/ (2019).
Sokame, B. M. Functioning of a community of lepidopteran maize stemborers and associated parasitoids following the fall armyworm invasion in Kenya 276 (PhD thesis, University of Nairobi, Kenya, 2020).
Tonnang, H. E. Z., Nedorezov, L. V., Ochanda, H., Owino, J. & Löhr, B. Assessing the impact of biological control of Plutella xylostella through the application of Lotka–Volterra model. Ecol. Model. 220, 60–70 (2009).
Kroschel, J., Mujica, N., Carhuapoma, P. & Sporleder, M. Pest Distribution and Risk Atlas for Africa-Potential Global and Regional Distribution and Abundance of Agricultural and Horticultural Pests and Associated Biocontrol Agents Under Current and Future Climates (International Potato Center (CIP), Lima, 2016).
Prasanna, B. M., Huesing, J. E., Eddy, R. & Peschke, V. M. Fall Armyworm in Africa: A Guide for Integrated Pest Management. First Edition, Mexico (CDMX: IMMYT, Mexico, 2018).
Sokame, B. M. et al. Carry-over niches for lepidopteran maize stemborers and associated parasitoids during non-cropping season. Insect 10, 191 (2019).
Acknowledgments
This research was funded by the ‘Institut de Recherche pour le Développement’ (IRD)-France through the IRD Collaborative Research project (Grant number B4405B) and the integrated pest management strategy to counter the threat of invasive fall armyworm to food security in eastern Africa (FAW-IPM) (Grant number DCI-FOOD/2017/) financed through the European Union. The authors wish to acknowledge the financial support for this research by the following organizations and agencies: the UK’s Department for International Development (DFID), the Swedish International Development Cooperation Agency (SIDA), the Swiss Agency for Development and Cooperation (SDC), and the Kenyan Government.
Author information
Authors and Affiliations
Contributions
Initiated the study: H.E.Z.T., P.A.C., S.S., A.Y.B., B.M.S., T.D., S.E. Conceived and designed the experiments: H.E.Z.T., B.M.S., A.Y.B. Contributed reagents/materials/analysis tools: P.A.C., S.S., T.D., S.E. Analysed the data: B.M.S., H.E.Z.T., A.T.B. Wrote the paper: B.M.S., H.E.Z.T., S.S., A.Y.B., P.A.C., T.D., S.E. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sokame, B.M., Tonnang, H.E.Z., Subramanian, S. et al. A system dynamics model for pests and natural enemies interactions. Sci Rep 11, 1401 (2021). https://doi.org/10.1038/s41598-020-79553-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-79553-y
This article is cited by
-
Combining Milpa and Push-Pull Technology for sustainable food production in smallholder agriculture. A review
Agronomy for Sustainable Development (2023)
-
Cannibalism and intraguild predation involved in the intra- and inter-specific interactions of the invasive fall armyworm, Spodoptera frugiperda, and lepidopteran maize stemborers
Journal of Pest Science (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.