Abstract
Determination of crystal system and space group in the initial stages of crystal structure analysis forms a bottleneck in material science workflow that often requires manual tuning. Herein we propose a machine-learning (ML)-based approach for crystal system and space group classification based on powder X-ray diffraction (XRD) patterns as a proof of concept using simulated patterns. Our tree-ensemble-based ML model works with nearly or over 90% accuracy for crystal system classification, except for triclinic cases, and with 88% accuracy for space group classification with five candidates. We also succeeded in quantifying empirical knowledge vaguely shared among experts, showing the possibility for data-driven discovery of unrecognised characteristics embedded in experimental data by using an interpretable ML approach.
Similar content being viewed by others
Introduction
Crystal structure characterisation is one of the most important tasks in materials development because crystal structure determines material properties1,2. A crystal structure is defined in terms of lattice symmetry, lattice parameters, the types and positions of atoms, and site occupancy. Powder X-ray diffraction (XRD) and powder neutron diffraction are principal experimental techniques to elucidate crystal structures; data obtained using these techniques are stored in various databases for specific classes of materials, for instance, inorganic materials and proteins3. Decoding powder diffraction patterns to crystal structure information involves several steps, such as peak indexing, space group determination, initial parameter estimation for the crystal structure, and structure refinement4,5,6,7,8,9. While the most arduous step is structure refinement using the Rietveld method10, which typically requires manual optimisation of tens of parameters, space group determination at the initial stage of structure analysis also needs manual trial-and-error operations frequently. Given that a large number of powder XRD patterns are generated daily at synchrotron facilities around the world, these time-consuming processes performed manually by human experts are obvious bottlenecks in materials research11,12,13. Excluding human involvement in these processes as far as possible improves the situation and helps realise high-throughput (HiTp) experiments. Therefore, we focus on the classification of crystal systems and space groups using machine learning (ML) approaches, inspired by the fact that experienced researchers can guess the crystal system from a given diffraction pattern.
Application of ML and related techniques for diffraction data analysis is a hot research topic in recent times13,14. Among various subtopics such as pattern decomposition and phase identification15,16,17,18 cluster analysis and phase mapping19,20,21,22,23, similarity metrics for comparison of diffraction data24,25,26 classification of a crystal symmetry27,28,29,30,31,32,33, a paper by Park et al.34 is relevant to this work. Park et al. classified crystal systems and space groups by applying a convolutional neural network (CNN) to simulated powder XRD patterns. They achieved high classification performance despite data deterioration due to Poisson noise and instrumental resolution. However, the complexity of CNN, or deep neural network, makes it difficult to interpret its internal processes to extract meaningful insights. While most materials informatics (MI) studies aim high classification or prediction accuracy, we believe that maintaining the possibility of data-driven knowledge discovery by using a human-interpretable model is important as well. If an ML model can classify the crystal class and the space group based on a diffraction pattern, it must have classification rules. By analysing the model, we could quantitatively specify the rules of thumb that experienced researchers have.
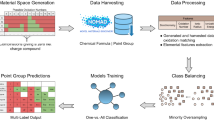
In this paper, we show that a simple and fast ML technique (Fig. 1) can classify crystal systems (seven classes) and space groups (230 classes) with high accuracy based on powder XRD patterns and that data-driven quantification of empirical expert knowledge is possible using an interpretable ML model. We emphasise that the purpose of this work is neither to replace conventional methods nor to achieve state-of-the-art accuracy among other emerging ML-based techniques but to demonstrate the potential of simple ML techniques suitable for knowledge discovery and real-world experiments. Although this study is in a proof of concept (POC) stage using ML models trained on ideal simulated diffraction data (i.e. noise-free, no peak-broadening, no peak superposition, no impurity peaks), it provided some interesting findings described in following sections.
Results
Data preparation and feature extraction
199,391 powder XRD patterns were calculated as training datasets (see “Methods” section for details) from Inorganic Crystal Structure Database (ICSD) entries using Pymatgen middleware. The patterns were not used as they were for the following reason. Typical powder XRD patterns have several thousand data points, and, if used as they are, ML models treat them as several-thousand-dimensional vectors. Training an ML model using such extremely high-dimensional data inevitably suffers from “the curse of dimensionality”35, the fact that the amount of data required for training increases exponentially with increasing data dimensions. To avoid this problem, we reduced the thousands of data points into a handful of numbers characterising each XRD pattern. These quantities are usually called “features” or “descriptors”13, and we use the former term in this paper. In areas where a large amount of quality-controlled data is available, such as ImageNet dataset with about 14 million labelled images used for image recognition36, it has become mainstream to build feature extractors simultaneously with classification models by training deep neural networks with the huge dataset36,37,38. However, such approach is often inappropriate in MI due to two reasons: a limited amount of available data and difficulty in data quality control. In our case, while low quality data are eliminated as much as possible the data size is roughly two orders of magnitude smaller than ImageNet. Additionally, automatically-selected features are not always in a simple form for humans to understand. Therefore, we chose to select features manually using human expert knowledge. An XRD pattern (Fig. 1 left) has many peaks that together act as a fingerprint of a crystal structure. Among the peak characteristics, intensity (height) is mostly determined by the atomic positions and with a few exceptions, not to symmetry of crystal, which is the target of this study. Therefore, the following eleven features were selected for this study: (1) the positions of the first ten peaks in the lower-angle range. (2) the total number of peaks in \(2\theta\) range from \(0^\circ\) to \(90^\circ\). Considering only the lower-angle peaks and ignoring the rest is justified because the peaks in the higher-angle range heavily overlap in real experimental data and it is impossible to identify individual peak positions, especially for low-symmetry cases. To examine the feature space, we have used Stochastic Neighbour Embedding with t-distribution (t-SNE)39, which is a popular method to visualise multi-dimensional data on a two-dimensional plane, preserving the local structure in the original multi-dimensional space. Figure 2 shows the result of the dimensionality reduction of eleven-dimensional data to two-dimensional space using t-SNE. The XRD patterns are distributed in the feature space and form loose clusters for each crystal system, implying that eleven features capture the characteristics of the XRD patterns at least in terms of crystal systems.
Here we mention ambiguity in the unit for peak positions. In most diffraction experiments, the horizontal axis of a diffraction pattern describes \(2\theta\), which is the angle between the incident beam and the scattered beam. Through Bragg’s law \(2d \sin \theta = \lambda\) and the definition of scattering vector length \(Q = 4\pi \sin {\theta }/\lambda\) where d and \(\lambda\) represent the separation of scattering planes and the wavelength of incident beam, respectively, \(2\theta\) is occasionally converted to d, 1/d, \(1/d^2\), or Q. We investigated the influence of these peak position notations on the classification accuracy and found that the difference is negligible (Table 1). Thus, herein we use \(2\theta\) for Cu \(\hbox {K}_{\alpha }\), which is the most commonly measured variable, and hence, the most familiar for many readers. It should be noted that the proposed method is applicable to any XRD patterns with arbitrary wavelength using wavelength-independent expressions above.
Classification of crystal systems and space groups
Even though it is a POC, it is favorable to choose a algorithm satisfying some realistic requirements such as fast training speed, easy hyperparameter tuning, and an ability to provide multiple candidates so that researchers can tailor the model to meet their experimental conditions such as \(2\theta\) range and wavelength, and choose the most reasonable candidate with the help of supplemental information.
Among various ML algorithms for classification tasks, random forest (RF) and its related algorithms satisfy all requirements mentioned above40. Table 1 shows the performance comparison of RF and other representative ML algorithms (Extremely randomised trees (ExRT)41, k-nearest neighbour (KNN)42, logistic regression43, and decision tree44,45) on the crystal system classification task. ExRT is an RF-based ML algorithm in which variables used for decision-making are chosen randomly in contrast to the significance-based selection criterion in normal RF. This randomness in ExRT reduces overfitting to the training data and improves the classification performance for unknown data. Additionally, we note the robustness of majority-voting algorithms including ExRT and RF. In actual experiments, some weak peaks are hard to recognise, or we may miss peaks outside the measurement range. Such deficiencies may cause wrong decisions for some of individual decision trees, but a majority decision taken by an ensemble of trees is often insensitive to such perturbations. Following the comparison result, we choose ExRT because it satisfies the requirements and exhibits the best performance. The computation time for the model training was a few minutes, and the classification for one XRD pattern only took several milliseconds with a general workstation (3.3 GHz 10-core CPU and 96 GB RAM), showing that the entire process can be performed even on an ordinary laptop computer within a reasonable time length.
Classification performance for each crystal system with test dataset is shown in Table 2 and Fig. 3. Values in Fig. 3 represent the ratio of a crystal system classified by the ExRT model (predicted label) to a given crystal system dataset (actual label). The values along the diagonal correspond to the accuracy. Our model succeeded in classifying crystal systems with accuracy about 90%, which is higher than our expectation, except for triclinic cases.
The low accuracy for triclinic cases may be attributed to the rarity of the triclinic structure in ICSD (only 4%), which hinders the classification.
Along with the crystal system, we evaluated the performance of the space group classification as well. The classification accuracy of the most likely candidate proposed by the model was 80.46% (Fig. 4a). Considering that the number of training data for each space group is considerably smaller than that for each crystal system, this accuracy significantly lower than that of the crystal system classification is reasonable. However, if we consider a list of multiple candidates proposed by our model, the accuracy defined as the probability that the list includes the correct answer increases to 92.42% and 94.35% for five and ten most likely candidates, respectively. These values are more relevant to actual space group determination tasks compared to the accuracy with a single candidate because the multiple candidate approach is often applied in conventional space group determination methods as well.
In Fig. 4a, besides the diagonal line indicating the correct prediction, there are other noteworthy features and we conclude that two major causes showing the shortcomings of our model and one trivial cause are responsible for those features. First, we point out the trivial and less important one. There are some isolated non-diagonal thick blue pixels [e.g. (50, 12), (97, 139), (132, 116) in (row, column) notation]. These are false predictions of space groups with a few test structures deceptively emphasised by normalisation with the number of test data. Next, we describe the one of the two major cause, that is, overfitting, a common issue in machine learning. The overfitting issue is visible as thicker blue pixels aligned vertically at some space groups (2, 12, 14, 15, 62, and 139 in Fig. 4a and b), which means our ML model tends to pick up specific space groups for prediction. This issue is caused by the uneven distribution of space groups in the ICSD data used for training shown in Fig. S1 in Supplementary Information as the histogram of our training data, that is, our model is biased to give an answer from what it have learnt frequently. The second major cause is an inherent defect in our approach itself which attempts to determine space groups only from the number and positions of peaks. To determine whether a crystal structure is centrosymmetric or not from a diffraction pattern, peak intensity is essential. Therefore, our ML model which ignores the peak intensity is intrinsically unable to determine the existence of centrosymmetry from a diffraction pattern.
Careful examination of the confusion matrix allows us to find some traces of this limitation. For example, in Fig. 4b, noncentrosymmetric space groups 1, 4, 6, 8, and 9 in test data are frequently predicted as their centrosymmetric minimal isomorphic supergroups 2, 11, 10, 12, and 15, respectively. Statistics also indicates the significance of this limitation in single-candidate prediction, that is, about 30% of false predictions (6% of test data) occur for centro- and noncentrosymmetric pairs.
We note that the identifying some false predictions as the centrosymmetric/noncentrosymmetric misclassification issue is exceptionally straightforward which is theoretically evident. For other misclassified results that are not relevant to centrosymmetry issue, we conclude that it is difficult to analyse the reasons from crystallographic points of view due to potential superposition of multiple causes mentioned above as well as the luck of our experience in such type of analysis.
Since there is a hierarchical relationship between space groups and crystal systems, the performance of space group prediction may be improved by using predicted crystal systems as the features for space group prediction. This idea to combine multiple ML models is called stacking46. Aguiar et al.32,33 reports that stacking improves the prediction accuracy for space group determination by electron diffraction. However, for our case, stacking did not improve the performance, i.e., the prediction performance was deteriorated. A possible reason is that misidentification in the crystal system prediction negatively affected the learning of the space group predictor as noise.
Normalised confusion matrix for space group classification. Normalisation is done in the horizontal direction. Tick labels represent space group numbers. (a) The overall confusion matrix. Some space groups lacked in the test data are shown as grey horizontal lines. (b) The confusion matrix of triclinic and monoclinic crystal systems [the upper left corner of (a)].
Classification performance for new materials and actual experimental data
We perform two types of tests to assess the efficacy of our model on crystal structure classification tasks for new materials. The first one, whose results are already shown in Table 2, uses the powder XRD patterns calculated from a subset of ICSD. The subset consists of materials not included in the training datasets, that is, crystal structures unknown for the model (see “Methods” section for details). This test represents the performance of the model against new materials. As evident from Table 2, our model scores satisfactory performance except for the triclinic system, which is intrinsically difficult because of the lack of the triclinic structure data in ICSD as previously discussed.
So far, we have used only simulated patterns which are not deteriorated by statistical and experimental noises. The second test is meant to assess the model in a more practical situation. Instead of calculated peak positions, we use peak search results of two actual measured XRD patterns of \(\hbox {Ca}_{1.5}\hbox {Ba}_{0.5}\hbox {Si}_{5}\hbox {N}_{6}\hbox {O}_{3}\) and \(\hbox {BaAlSi}_{4}\hbox {O}_{3}\hbox {N}_{5}{:}\hbox { Eu}^{2+}\) taken from supplementary tables in Ref.34. We chose these two materials because their structures are so unique that they belong to none of over nineteen thousand prototype structures in ICSD as described in Ref.34. The auto peak search was performed in a conventional manner according to the explanation by the authors, which means using its results is practically equal to starting from raw XRD patterns that we do not have in our hands. Due to the limited 2\(\theta\) range shown in the tables, we could not obtain the number of detected peaks suitable for our model. With this situation, we retrained our model without the total number of peaks and used only the ten lowest peak positions for classification. Nonetheless, the retrained model correctly classified not only the crystal systems of both compounds but also the space group of \(\hbox {BaAlSi}_{4}\hbox {O}_{3}\hbox {N}_{5}:\hbox {Eu}^{2+}\). The CNN model in Ref.34 did succeeded in crystal system prediction for both compounds, but failed in space group prediction for both.
We analysed these benchmark materials with several standard peak-indexing programs in Crysfire2020 (ITO47, FJZN48, TREOR49, KOHL50, DICVOL51, LZON48) as well. However, none of them were able to give proper indexing results for both materials with the default settings. The comparison result is shown in Table S1 in the supplementary material. In Ref.34 the two materials were analysed with TREOR, and the authors of the paper also concluded that TREOR could not give proper results without human intervention. This fact indirectly shows that, at least for these specific cases, our method is more suitable for crystal system and space group estimation tasks than an existing software if less human intervention is preferred. Nonetheless, this comparison is not intended to claim superiority of our method. While both take peak positions as input, the type of output is different: the primal purpose of conventional peak-indexing programs is to give lattice constants and our method aims to estimate only crystal systems and space groups. This difference means that our model cannot be a substitute for long-lived existing peak-indexing programs.
Although the test size is extremely limited (only two) and our model failed one of the two space group prediction tasks, it is still worth noting that our model with only ten features gives a better result in space group prediction than the CNN model using ten thousand data points as features which failed for two test compounds. This indicates that appropriate feature selection is important for this task. Additionally, the success of the ExRT model trained without the total number of peaks may broaden the target range of our approach because some XRD patterns are not suitable for correctly counting the number of peaks because of impurity peaks, the bad signal-to-noise ratio, or severe peak overlapping.
Knowledge extraction from machine learning models
In terms of prediction performance, there was no significant difference between KNN and ExRT as shown in Table 1. However, tree-based models such as ExRT and decision tree provide more information to us than KNN. That is, our ML model may provide an insight into the relevant tasks as an additional advantage through careful analysis. Such knowledge may help in designing a minimum but effective measurement setup and an experiment plan for a specific purpose.
In this regard, we investigate the following points to exploit our ML model: (1) evaluation of feature importance, (2) classification performance dependency on the number of features (peak positions), (3) quantification and visualisation of decision rules for crystal system classification.
Table 3 shows the feature importances of eleven features used in our model for the crystal system classification task. Feature importance quantifies the contribution of a feature to the improvement of the splitting quality. We use Gini impurity46 as a split criterion in this study.
Larger importance on the number of peaks and peak positions at lower angles can be interpreted as follows. Because most lattice constants of the crystal structures stored in ICSD are available within a certain range, the main factor that determines the number of peaks within a 2\(\theta\) window that we use is the symmetry of a crystal structure. Similarly, under the same experimental condition, the positions of the ten lowest-angle peaks primarily depend on the extinction rule determined by the symmetry of the structure. For example, simple cubic structures whose symmetry is the highest among the seven crystal systems have three reflections, 001, 011, and 111 in this order in the lowest \(2\theta\) range. If the structure changes from cubic to orthorhombic, both 001 and 011 reflections of the original cubic structure split into three reflections, and in some cases, even high-order reflections appear in the lower \(2\theta\) side of the 111 reflection. As a result, most of the ten lowest-angle peaks are dominated by such split peaks and their positions shift to a lower \(2\theta\) range, compared to the cubic case. A similar argument is also valid for general cases related to the comparison between two crystal systems not involving a structural phase transition. Therefore, if many peaks appear in the low \(2\theta\) region, it implies that the symmetry is low and vice versa. These inferences are consistent with the first impression of experts. Notably, these inferences could be extracted quantitatively from the ML model, which we will discuss later.
Next, we evaluate the importance of lower peaks in the actual classification task by plotting the dependency of classification accuracy on the number of peak positions used in model training (Fig. 5). Here, the total number of diffraction peaks was omitted from the features to extract the effect of peak positions. The accuracy saturates at five or six lowest peak positions for most of the crystal systems, and adding higher peak positions in training only gives a marginal improvement. Here, the qualitative tendency was revealed that more complex crystal systems require more information for identification.
As discussed in the Introduction, experienced researchers can estimate the crystal system from a given XRD pattern without any additional information, mostly when the symmetry of the crystal structure is high. In general, such expert knowledge obtained through experience is vague and difficult to quantify. Here, we present an attempt to quantify expert knowledge on a simplified crystal system classification task, i.e. binary classification of cubic and non-cubic systems.
Because classification results by ExRT are based on the majority vote of several hundred decision trees with their maximum depth as a hyperparameter, it is difficult to extract the classification rules from our ExRT model in a reasonable way. Instead, we repeatedly train a single decision tree for a binary classification task (cubic or non-cubic system) and a crystal system classification task (seven classes) with different random seeds. Two representative decision trees and their splitting rules for the binary classification are shown in Fig. 6.
The splitting rules of the two trees consist of only two features in total, and the accuracy is surprisingly high despite such simple tree structures of depth one or two. The number of peaks, which is employed by both trees, is a reasonable criterion to distinguish cubic and non-cubic crystal structures because higher symmetry crystal structures have less Bragg peaks in their diffraction patterns in general. On the contrary, it is not as straightforward as the case for the number of peaks to interpret how the other criterion, the position of peak 3, contributes to the binary classification task. A hint is found in Fig. 6b and d where the splitting rules are visualised in a scatter plot, i.e. the wider distribution of data points for the cubic system along the horizontal axis representing the position of third lowest-angle peak (peak 3). As already discussed, the feature importance indicates that lower-angle peak positions are more important in the crystal system classification task. The difference in the distribution of peak 3 between cubic and non-cubic systems implies that an effective threshold exists for the binary classification task, which is the exact strategy that the decision tree in Fig. 6a takes. This argument can be regarded as a case showing the importance of lower peaks for a specific task, that is “cubic-or-not” classification, and also an example of quantitative knowledge extraction using an ML model.
We confirmed the similar trend in the crystal system classification. The decision tree is visualised in Fig. S3 in the supplemental material.
Visualisation of the decision tree classifier for cubic system identification. The ML model was trained with \(2\theta\) features (see in “Data preparation and feature extraction” section). In this figure, the peak position is represented by the length of the scattering vector Q for wavelength-independency.
Discussion
The highlight of this study is quantitative knowledge extraction enabled by the analysis of a trained ML model, which is hard to realise only with physical principles. We expect this idea is relevant to experimental setup optimisation because many experiments in material science still rely on conventional rules-of-thumb parameters. For example, experimental parameters such as scanning ranges, data point intervals, and measurement time can be objectively tailored for a specific purpose if an ML model indicates guidelines for these parameters to assure minimal but sufficient data quality for the purpose. An efficient experimental design is particularly crucial for experiments using synchrotron X-rays and neutron beams, where the efficient use of the measurement time is essential because of limited beamtime available52,53,54.
Another highlight is that our ML model does not require large computational resources: training two ExRT models for crystal system and space group classification tasks will only take a few minutes on a modern laptop computer in contrast to the CNN model proposed in Ref.34 which requires more than a day for training even with one of the currently fastest GPUs (Nvidia TITAN RTX). This advantage is crucial for on-site customisation because measurement parameters such as wavelength and \(2 \theta\) range may vary in each diffraction experiment and sample.
A noticeable flaw in our model, that is, the low accuracy for non-cubic systems, especially for triclinic cases, presumably stems from the shortage of training data in these crystal systems. This type of problem is called the class imbalance and is resolved by a technique called “data augmentation” in some fields in ML such as image and speech recognition tasks37,38,55,56. Data augmentation for a crystal-system learning task is theoretically possible in a straightforward way as well; by distorting or expanding actual crystal structures, we can generate any number of artificial low-symmetry crystal structures. However, due to the enormous amount of the possible combinations of artificial structures, the improvement of the classification accuracy using data augmentation is beyond the scope of this paper and left as a future issue.
The scope of this paper is limited to proposing a new method using ML, and we do not expect our current models to work well with real data at this moment. However, it is interesting to check the current performance of our approach for real-world data, so we did some tests. Please refer to “Classification performance for new materials and actual experimental data” sectiion in the main text and Section S4 in Supplementary Information. To apply this method to real-world data, the ML model should be flexible about imperfections such as peak overlap and impurity peaks under practical measurement conditions, but we did not address these issues at this moment. In future work, we will update our models and verify them on real experimental data.
Methods
XRD datasets
XRD patterns were generated from the crystal structures registered in ICSD (2018.1) using Pymatgen middleware. The X-ray wavelength was set to 1.54184 Å (Cu \(\hbox {K}_{\alpha 1}\)), and the \(2\theta\) range was \(0^\circ\) to \(90^\circ\). It is well known that removing “bad data” from training data is crucial to avoid detrimental effects on a trained ML model57. We excluded about 30k structures exhibiting one of the following issues:
-
1.
Missing information (i.e., null in the atom position): 19967 samples.
-
2.
Mismatch in space groups between those calculated from the crystal structure using spglib58 and those registered in ICSD: 8540 samples. One of the possible reasons for the mismatch is rounding because some of these structures have 0.67 in one of atomic positions, which is close to a special value 2/3. We chose not to investigate the cause of the mismatch in detail because it is difficult to investigate over 8000 samples whether the disagreement is due to wild rounding or a valid shift from a special value. We simply excluded all structures showing this space group mismatch. We note that the impact of this exclusion on the hexagonal structures is limited. The number of excluded hexagonal structures due to this space group mismatch is 2067, which corresponds to 9.0% of 22,953 hexagonal structures registered in ICSD.
-
3.
R factor larger than 20%: 948 samples. Large R factor implies that the refined crystal structure is not reliable.
-
4.
Huge lattice constants (> 50 Å): 1022 samples. These structures are exceptionally complex and seem to be approximated expressions for amorphous materials. They are inappropriate for our purpose because we do not focus on amorphous materials and such outliers deteriorate ML models.
-
5.
Tiny lattice constants (< 2.5 Å): 173 samples. Assumed to be crystal structures under high pressure. These structures have only a few Bragg peaks and are inappropriate likewise.
In all, 169,563 XRD patterns were used in this study. The distributions of crystal systems in ICSD and reduced dataset is shown in Figs. S1 and S2 in the supplementary information.
For generalisation performance evaluation, we employed a date-based data-splitting policy instead of the conventional random data-splitting policy to reduce the possibility of data leakage. As a nature of materials science research, there are many systematic works reporting a series of compounds with different compositions showing almost identical crystal structures. If we choose crystal structures randomly, the test data likely contains a certain amount of structures from those works, which results in data leakage. We expect this issue is partly alleviated by splitting the database with a chronological threshold. In our case, the data registered in ICSD until 2014 (123,495 samples) were used as the training data, and those registered after 2014 (46,068 samples) were used as the test data. We confirmed that both datasets have a similar composition of crystal classes.
A non-cubic dataset for binary classification in Fig. 6 was undersampled so that the numbers of cubic structures and non-cubic structures were equal, and the prediction performance of the trained model was evaluated with 10CV as well. For the visualisation of crystal system classification rules (Fig. S2), the decision tree was trained using the randomly sampled dataset to include 2000 entries of each crystal system from the training data. The prediction performance of the decision tree was verified using the test data.
Machine learning models
The following ML algorithms were employed in this study: Logistic Regression43, K-Nearest Neighbour42, Decision Tree44,45, Random Forest40, Extremely randomised trees41. These algorithms are available in scikit-learn59. Hyperparameters of ML models were determined by random search, and the classification performance was evaluated using 10-fold cross-validation (10CV) with the training data. The parameter showing the best performance was used in this study.
For Logistic Regression, feature standardisation, which makes the values of each feature in the data have zero-mean and unit-variance, was performed to standardise the range of independent features.
For the classification performance measure, we use accuracy, recall, precision, and F1-score60. The first three measures are defined as follows with the number of true positive (TP), true negative (TN) false positive (FP), and false negative (FN) predictions:
And using precision and recall, F1-score is defined as follows:
Data availability
The dataset and codes that support the findings of this study are available at https://github.com/quantumbeam/xrd-symmetry-prediction.
References
Callister, W. D. & Rethwisch, D. G. Materials Science and Engeneering (Wiley, Hoboken, 2010).
De Graef, M. & McHenry, M. E. Structure of Materials. An Introduction to Crystallography, Diffraction and Symmetry (Cambridge University Press, Cambridge, 2012).
Hofmann, D. W. M. & Kuleshova, L. N. (eds) Data Mining in Crystallography. (Springer, Berlin, 2009).
Habershon, S., Cheung, E. Y., Harris, K. D. M. & Johnston, R. L. Powder diffraction indexing as a pattern recognition problem: a new approach for unit cell determination based on an artificial neural network. J. Phys. Chem. A 108, 711–716 (2004).
Le Bail, A. Monte Carlo indexing with McMaille. Powder Diffr. 19, 249–254 (2004).
Neumann, M. A. X-Cell: a novel indexing algorithm for routine tasks and difficult cases. J. Appl. Crystallogr. 36, 356–365 (2003).
Pawley, G. S. Unit-cell refinement from powder diffraction scans. J. Appl. Crystallogr. 14, 357–361 (1981).
Le Bail, A., Duroy, H. & Fourquet, J. L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 23, 447–452 (1988).
Altomare, A. et al. Space-group determination from powder diffraction data: a probabilistic approach. J. Appl. Crystallogr. 37, 957–966 (2004).
Rietveld, H. M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 2, 65–71 (1969).
Gregoire, J. M. et al. High-throughput synchrotron X-ray diffraction for combinatorial phase mapping. J. Synchrotron Radiat. 21, 1262–1268 (2014).
Lookman, T., Alexander, F. J. & Rajan, K. Information Science for Materials Discovery and Design (Springer, Berlin, 2015).
Lookman, T., Eidenbenz, S., Alexander, F. & Barnes, C. Materials Discovery and Design: By Means of Data Science and Optimal Learning. Springer Series in Materials Science (Springer, Berlin, 2018).
Ludwig, A. Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods. Comput. Mater. 5, 70 (2019).
Kusne, A. G., Keller, D., Anderson, A., Zaban, A. & Takeuchi, I. High-throughput determination of structural phase diagram and constituent phases using GRENDEL. Nanotechnology 26, 444002–10 (2015).
Bunn, J. K. et al. Generalized machine learning technique for automatic phase attribution in time variant high-throughput experimental studies. J. Mater. Res. 30, 879–889 (2015).
Bunn, J. K., Hu, J. & Hattrick-Simpers, J. R. Semi-supervised approach to phase identification from combinatorial sample diffraction patterns. JOM 68, 2116–2125 (2016).
Long, C. J., Bunker, D., Li, X., Karen, V. L. & Takeuchi, I. Rapid identification of structural phases in combinatorial thin-film libraries using x-ray diffraction and non-negative matrix factorization. Rev. Sci. Instrum. 80, 103902–7 (2009).
Kusne, A. G. et al. On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets. Sci. Rep. 4, 191–7 (2014).
Xue, Y. et al. Phase-Mapper: An AI platform to accelerate high throughput materials discovery. In Twenty-Ninth IAAI Conference (2017).
Suram, S. K. et al. Automated phase mapping with AgileFD and its application to light absorber discovery in the V–Mn–Nb oxide system. ACS Comb. Sci. 19, 37–46 (2017).
Li, S., Xiong, Z. & Hu, J. Inferring phase diagrams from X-ray data with background signals using graph segmentation. Mater. Sci. Technol. 34, 315–326 (2018).
Stanev, V. et al. Unsupervised phase mapping of X-ray diffraction data by nonnegative matrix factorization integrated with custom clustering. Comput. Mater. 4, 43 (2018).
Baumes, L. A., Moliner, M. & Corma, A. Design of a full-profile-matching solution for high-throughput analysis of multiphase samples through powder X-ray diffraction. Chem. A Eur. J. 15, 4258–4269 (2009).
Hernández-Rivera, E., Coleman, S. P. & Tschopp, M. A. Using similarity metrics to quantify differences in high-throughput data sets: application to X-ray diffraction patterns. ACS Comb. Sci. 19, 25–36 (2017).
Iwasaki, Y., Kusne, A. G. & Takeuchi, I. Comparison of dissimilarity measures for cluster analysis of X-ray diffraction data from combinatorial libraries. NPJ Comput. Mater. 3, 1–8 (2017).
Ziletti, A., Kumar, D., Scheffler, M. & Ghiringhelli, L. M. Insightful classification of crystal structures using deep learning. Nat. Commum. 9, 2775 (2018).
Ryan, K., Lengyel, J. & Shatruk, M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 140, 10158–10168 (2018).
Vecsei, P. M., Choo, K., Chang, J. & Neupert, T. Neural network based classification of crystal symmetries from x-ray diffraction patterns. Phys. Rev. B 99, 245120 (2019).
Oviedo, F. et al. Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks. NPJ Comput. Mater. 5, 60 (2019).
Ke, T. W. et al. A convolutional neural network-based screening tool for X-ray serial crystallography. J. Synchrotron Radiat. 25, 655–670 (2018).
Aguiar, J. A., Gong, M. L., Unocic, R. R., Tasdizen, T. & Miller, B. D. Decoding crystallography from high-resolution electron imaging and diffraction datasets with deep learning. Sci. Adv. 5, 1949 (2019).
Aguiar, J. A., Gong, M. L. & Tasdizen, T. Crystallographic prediction from diffraction and chemistry data for higher throughput classification using machine learning. Comput. Mater. Sci. 173, 109409 (2020).
Park, W. B. et al. Classification of crystal structure using a convolutional neural network. IUCrJ 4, 486–494 (2017).
Bishop, C. M. Pattern Recognition and Machine Learning (Springer, Berlin, 2006).
Russakovsky, O. et al. ImageNet large scale visual recognition challenge. International Journal of Computer Vision (IJCV) 115, 211–252 (2015).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems - Volume 1, 1097–1105 (Curran Associates Inc., USA, 2012).
Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, Cambridge, 2016).
Maaten, L. V. D. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
Breiman, L. Random Forests. Mach. Learn. 45, 5–32 (2001).
Geurts, P., Ernst, D. & Wehenkel, L. Extremely randomized trees. Mach. Learn. 63, 3–42 (2006).
Dasarathy, B. V. Nearest neighbor (NN) norms: nn pattern classification techniques (IEEE Computer Society Press, Washington, 1991).
Cox, D. R. The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B (Methodol.) 20, 215–242 (1958).
Breiman, L., Friedman, J., Stone, C. J. & Olshen, R. A. Classification and Regression Trees. The Wadsworth and Brooks-Cole statistics-probability series (Taylor & Francis, 1984).
Quinlan, J. R. C45: Programs for Machine Learning (Morgan Kaufmann Publishers Inc., Burlington, 1993).
Hastie, T., Tibshirani, R. & Friedman, J. The elements of statistical learning: data mining, inference and prediction. Data Mining, Inference, and Prediction (Springer, Berlin, 2009)
Visser, J. W. A fully automatic program for finding the unit cell from powder data. J. Appl. Crystallogr. 2, 89–95 (1969).
Shirley, R. A modified version of Visser’s ITO zone-indexing program, using the Ishida & Watanabe PM criterion for zone evaluation. Unpublished work .
Werner, P. E., Eriksson, L. & Westdahl, M. TREOR, a semi-exhaustive trial-and-error powder indexing program for all symmetries. J. Appl. Crystallogr. 18, 367–370 (1985).
Kohlbeck, F. & Horl, E. M. Indexing program for powder patterns especially suitable for triclinic, monoclinic and orthorhombic lattices. J. Appl. Crystallogr. 9, 28–33 (1976).
Boultif, A. & Louër, D. Indexing of powder diffraction patterns for low-symmetry lattices by the successive dichotomy method. J. Appl. Crystallogr. 24, 987–993 (1991).
Ueno, T. et al. Adaptive design of an X-ray magnetic circular dichroism spectroscopy experiment with Gaussian process modelling. NPJ Comput. Mater. 4, 4 (2018).
Saito, K. et al. Accelerating small-angle scattering experiments on anisotropic samples using kernel density estimation. Sci. Rep. 9, 1526 (2019).
Suzuki, Y., Hino, H., Kotsugi, M. & Ono, K. Automated estimation of materials parameter from X-ray absorption and electron energy-loss spectra with similarity measures. NPJ Comput. Mater. 5, 39 (2019).
Shorten, C. & Khoshgoftaar, T. M. A survey on image data augmentation for deep learning. J. Big Data 6, 60 (2019).
Cubuk, E. D., Zoph, B., Mane, D., Vasudevan, V. & Le, Q. V. AutoAugment: Learning Augmentation Strategies From Data. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2019).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
Togo, A. & Tanaka, I. Spglib: a software library for crystal symmetry search. arXiv cond-mat.mtrl-sci, arXiv:1808.01590 (2018).
Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT Press, Cambridge, 2012).
Acknowledgements
This work is partly supported by JST-Mirai Program, Grant Number JPMJMI19G1. Y.S. is supported by JST ACT-I grant number JPMJPR18UE. K.O. and T.H. are partly supported by the Elements Strategy Initiative Center for Magnetic Materials (ESICMM), Grant Number 12016013, through the Ministry of Education, Culture, Sports, Science and Technology (MEXT). H.H. is partly supported by JST CREST grant number JPMJCR1761. K.S. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 701647. K.O. and K.S. gratefully acknowledge the financial support by Toyota Motor Corporation.
Author information
Authors and Affiliations
Contributions
K.O. conceived the idea for the present work. Y.S., K.O. and H.H. carried out the computation. T.H. and K.S. examined the obtained knowledge as experts in materials science. Y.S., H.H., T.H., K.S, M.K. and K.O. discussed the results and wrote the manuscript together.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Suzuki, Y., Hino, H., Hawai, T. et al. Symmetry prediction and knowledge discovery from X-ray diffraction patterns using an interpretable machine learning approach. Sci Rep 10, 21790 (2020). https://doi.org/10.1038/s41598-020-77474-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-77474-4
This article is cited by
-
Towards end-to-end structure determination from x-ray diffraction data using deep learning
npj Computational Materials (2024)
-
Semantic segmentation in crystal growth process using fake micrograph machine learning
Scientific Reports (2024)
-
Enhanced accuracy through machine learning-based simultaneous evaluation: a case study of RBS analysis of multinary materials
Scientific Reports (2024)
-
Deep learning for symmetry classification using sparse 3D electron density data for inorganic compounds
npj Computational Materials (2024)
-
Advances of machine learning in materials science: Ideas and techniques
Frontiers of Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.