Introduction

Phononic crystals (PnCs) and metamaterials can be considered as engineered materials with designed macroscopic periodic or non-periodic structures that exhibit acousto/elastic responses not achievable in natural materials1. A universally accepted distinction between PnCs and metamaterials does not yet exist. Some researchers define metamaterials as artificially structured media showing novel acousto/elastic effects for wavelengths much greater than their periodicities. Others extend the concept of metamaterials to include PnCs.

PnCs with periodic structures are the mechanical analog of well-known photonic crystals in optics and have been studied since the pioneering work of Lord Rayleigh in 18872. However, only recently, PnCs have received widespread interest because their design can be supported by modern optimizers with high computing performance and innovative additive manufacturing (3D-printing) processes, which provide unprecedented manufacturing freedom for the fabrication of intricate parts and geometries.

From a structural viewpoint, PnCs are an arrangement of many elementary cells, each containing an inclusion or a cavity inducing non-conventional dispersion properties3. Depending upon their geometry and constituents, PnCs include: (a) structures made of two or more materials with different mechanical properties in a periodic repetition, (b) structures with enclosed periodic units such as holes containing fluids and (c) waveguide structures characterised by periodic surface profiles4,5,6,7. A distinguishing peculiarity of PnCs is that they can be designed and manufactured to inhibit the propagation of acoustic/elastic waves in specific frequency ranges known as phononic band gaps or stop bands8. Outside these band gaps, waves can propagate in any direction. So, PnCs can be considered as material-enabled signal filters. This property allows PnCs to be used for frequency-dependent control of the trajectory and dissipation characteristics of acoustic and stress waves9. As a result, PnCs have found natural applications in research areas such as acoustic lenses10, wave filters11, frequency modulators5, acoustic cloaks12, and thermal insulators4.

The two broadly accepted physical mechanisms at the origin of phononic band gaps are the Bragg-scattering and local resonance effects3,13. In the former mechanism, stop bands are generated by the destructive interference of both incident and reflected waves in specific frequency bands, which are excited resonantly when the wave-vector is equal to 2 \(\pi \) /\(\Lambda \), where \(\Lambda \) is the periodicity of the PnC structures. The Bragg-scattering effect enables phononic band gaps with broader frequency ranges. However, Bragg-scattering stop bands strongly depend on the geometry of the lattice and the shape of scattering. In the local resonance effect, instead, stop bands are induced by local resonances of the internal oscillating inclusions of the PnC3. However, the width of a local resonant band gap is typically narrow14,15.

A theoretical and experimental study of longitudinal wave propagation in a rod structure including periodic PnC local resonators was presented by Wang et al.16. The authors showed that the band gap attenuation was influenced by the stiffness and mass ratios of the local resonator. However, their work did not fully explore the band gap formation mechanism. A more systematic study was provided by Xiao et al.17, who investigated stop bands of metamaterial rods combined with periodically attached local resonators through a Finite Element (FE) approach, their work showed that the wave attenuation is efficient only at the resonator eigen frequencies and dramatically decreases away from them18.

That is why regardless of numerous PnCs proposed in recent decades, few have been shown to possess simultaneously wide and robust stop bands19. Hence, a broadband control of low-frequency waves using lightweight structures remains a challenge. This consideration led to the new three-dimensional (3D) rainbow-trapping design. Originally proposed in the context of optical waves20, this concept has been further developed for acoustic and elastic waves. Zhu et al.21 have proposed the first experimental demonstration of acoustic rainbow trapping, i.e. a metamaterial containing non-periodic grooves that trap broadband acoustic waves. Chen et al.22 have applied this concept to a gradient metamaterial beam to observe the enhancement of flexural waves in beams. Also, Beli et al.23 have experimentally shown that the wave trapping effect can also arise from manufacturing variability in printed metamaterials and that the mistuning of the resonators can also prevent the band formation, thus requiring careful design of the spatial profile of the rainbow metamaterial. This effect is shown to be more relevant in Bragg-scattering of resonators24. Moreover, it has been shown that both spatially graded and random arrangements result in bandgap widening in locally resonant metamaterials25. Recently, Meng et al.26 have proposed a multi-frequency broadband rainbow metamaterial with one-dimensional bandgaps. Meng et al.27 have also shown that optimal spatial distribution of the tuning frequency of each resonator can be further explored for different performance criteria in multi-frequency metamaterials, thus opening new and innovative possibilities for metamaterial design.

Motivated by these results, this report investigates the attenuation performance of a novel 3D rainbow PnC produced using addtive manufacturing (AM) processes. The proposed design is based on spatially distributed cubic blocks connected by two curved beams. Internal holes in the cubic block tessellated in the structural design are used to adjust the local masses and create a spatial gradient profile. Consequently, broadband attenuation can be achieved for x, y and z directions in the structure, i.e. a 3D attenuation band, as a result of the rainbow PnC design. It is later shown, by experimental and numerical results, that the proposed approach can produce PCs with attenuation bandwidths more than two times larger than the periodic design with the same mass. Practical aspects of the employed AM technology are also discussed.

Results and discussion

To explore the effect of non-periodicity on the frequency response functions (FRFs), 3D PnCs structures consisting of spatially distributed blocks connected by two curved struts as shown in Fig.1a are investigated. To deliver the rainbow structural design, the mass of each block is changed by opening a cylindrical hole in the middle of it which would allow for a mass reduction between 0% and 70%. This upper limit is set in order to preserve the structural integrity of the blocks and to maintain the assumption that blocks act as rigid bodies. The masses of blocks are set as sinusoidally varying over the x, y and z periodicity directions of the rainbow structure with the aim of inducing a smooth near-periodicity and avoiding rapid mechanical impedance changes for consecutive masses. The two curved struts between blocks are inverted towards each other. Curvature can both enhance stability and reduce transmission rigidity compared to straight beams. The cross-section of the connecting beams and consequently connecting stiffness is fixed. The equivalent periodic structure is straightforward to derive by calculating the diameter of a periodic set of holes in the vibrating masses that would induce a structure of equal mass to the rainbow one.

The dynamic properties of the rainbow PnCs were investigated both numerically and experimentally. The material has a density of 1000 kg/m3, Young’s modulus of 1.75 GPa, and Poisson’s ratio of 0.35. The proposed rainbow PnC structure has a periodicity of seven in 3D (i.e. forming a 7 × 7 × 7 rainbow PnC). The side length of cubic blocks is Q = 20 mm, the distance between blocks is S=20mm, the radius of the curved beam is R = 20 mm and the cross-section dimensions of the curved beams are \(C_a\)=\(C_b\)= 2.5 mm. The mass m of the rainbow PnC can be calculated using the following sinusoidal distribution in 3D: \(m_{ijk}=(0.675+0.115\sin ((i-1)\pi /3)+0.115\sin ((j-1)\pi /3)+0.115\sin ((k-1)3\pi /3))M\), where M is the mass of original non-opening blocks and i, j, k = 1,2,…,7 represent the number of cuboid blocks in x, y and z directions. The block mass of corresponding periodic PnC is equal to the average block mass of the rainbow PnC and is given by: \(m_{ijk}=0.675M\). The block mass distributions of periodic and rainbow PnCs are depicted in Fig. 1b and c.

A FE approach was employed to compute the FRFs of the 3D nearly-periodic PnCs. Elastic PnCs and metamaterials can be modelled by analytical and numerical methods, such as plane-wave expansion methods28,29,30,31, finite-difference time-domain32,33,34,35, layer-multiple scattering method36,37,38 and FE approaches39,40,41,42. Compared to other modelling schemes with a range of limitations, the FE method is the most pertinent one for non-periodic structures and able to elaborate accurately on their internal dynamics and interactions. In the FE modelling, forces in x, y and z directions are exerted on one vertex of the PnCs and displacements of the diagonal vertex are then computed, with which the receptances of the structures in all directions can be obtained by \(R_x=20\log 10|D_x/F_x|\), \(R_y=20\log 10|D_y/F_y|\), \(R_z=20\log 10|D_z/F_z|\), where \(F_x\), \(F_y\), and \(F_z\) are the excitation forces, and \(D_x\) , \(D_y\), and \(D_z\) are the acquired displacements in the three directions. More details of the FE modelling scheme are given in the “Methods” section.

Figure 1
figure 1

Design of the investigated 3D PnC: (a) schema of the 3D rainbow PnC, the labels show the geometric parameters block side length (Q), blocks distance (S), radius of the curved beam (R), cross-section dimensions of the curved beams (\(C_{a}\), \(C_{b}\)). Block mass distributions (\(m_{ijk}\)) of (b) periodic and (c) rainbow PnCs by bubbles of different dimensions.

Full size image
Figure 2
figure 2

FE simulated displacement FRFs for the rainbow PnC in (a) x, (c) y and (e) z directions. Simulated response for the periodic PnC in (b) x, (d) y and (f) z directions. The stopbands are marked within grey areas.

Full size image

The calculated receptance values of the rainbow and periodic PnCs are shown in Fig.2a–f. It can be seen that the rainbow PnC has broader bandgaps than that of the periodic structure of the same mass . The bandgaps of the periodic PnC occur at the frequency range 550–638 Hz, within which the receptance values are significantly reduced. The mode shapes of the periodic PnC at the starting and ending frequencies of the bandgaps are shown in Fig. 3c and d. It can be seen that the bandgaps are formed by local resonance of the mass blocks. Wavelengths at bandgaps are also much larger than the lattice dimensions of the PnC. In contrast, the rainbow PnC has bandgaps within the frequencies 452–698 Hz. Mode shapes of the rainbow PnC at the starting and ending frequencies of the bandgap are shown in Fig. 3a and b. The rainbow PnC has enhanced bandgaps more than two times broader than that of periodic lattice. The extension of bandgaps should be attributed to the block mass variations in the rainbow PnCs, which will bring in local resonance at different frequencies. Meanwhile, it can also be observed that the reduction of receptance values within the bandgaps of the rainbow PnC is smaller than that of the periodic PnC. As discussed by Meng et al.26, the enlarged bandwidth could simultaneously induce smaller attenuation amplitude and thus smaller reduction of receptance values.

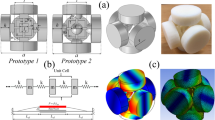
With the purpose of exploring further the effects of non-periodicity and verifying the above mentioned numerical results, experimental analysis was conducted on a rainbow and a periodic PnCs as shown in Fig. 4a and b. The two prototypes were realised through AM process. AM has become one of the most popular manufacturing methods for PnCs and metamaterials. It is more time-saving and less costly for the generation of objects with complex geometric shapes and enhanced precision than traditional subtractive manufacturing processes26,27,43,44,45,46,47,48. Numerous AM technologies have been employed for PnCs, including laser sintering, binder jetting and stereolithography49,50. Given the geometric dimensions, the structural physical parameter requirements, as well as the factor of cost, a Selective Laser Sintering (SLS) method was selected for the fabrication of the 3D PnCs. In-depth description of the fabrication process can be found in the “Methods” section.

Figure 3
figure 3

Mode shapes of PnCs at the starting and ending frequencies of the bandgaps: rainbow PnC at (a) 452 Hz and (b) 698 Hz, periodic PnC at (c) 550 Hz and (d) 639 Hz.

Full size image

The geometric parameters of the structures are identical to the ones employed in the numerical calculation. It should be stressed that 7 unit cells in each dimensions is considered as a low to moderate number for vibration stopband generation. Increasing the number of unit cells51 would imply deeper stopbands within the measured FRF structures. The choice of 7 unit cells resulted as a compromise between the maximum available dimensions for manufacturing the PnCs through AM (27 cm per direction). Besides, it is noted that an oblique cylinder was printed on the vertex of PnCs for the purpose of adhering the testing system which would exert the required excitation force on the PnCs. This oblique cylinder was also numerically modelled within the computations exhibited above.

Figure 4
figure 4

Photographs of the manufactured (a) periodic PnC and (b) rainbow PnC by laser sintering.

Full size image

The samples were tested through the experimental setup presented in Fig. 5. A mechanical shaker was employed to excite the PnCs on the end face of the oblique cylinder with an input signal over the frequency range of 20–1000 Hz. The excitation forces on the PnCs were tested by an impedance head which was bolted to the mechanical shaker on the opposite end. Displacements in three directions at the diagonal corner of the excitation point were measured with the laser Doppler vibrometer. Due to the large dimensions and masses of the structures, the PnCs were suspended on a metallic truss using rubber bands and plastic hooks to simulate free boundary conditions. The approach of suspending the tested structures has been discussed and proved effective by Elmadih et al.41,52,53,54. More details of the experiment process are described in the “Methods” section.

Figure 5
figure 5

Experimental setup for dynamic testing of the 3D PnCs.

Full size image

The measured receptance values of the two samples are shown in Fig.6a–f. It can be seen that the experimental results display the same trends as the numerical ones. The rainbow and periodic PnCs have evident vibration attenuation in the frequency ranges of circa 515–620 Hz and 620–670 Hz respectively, as marked in grey areas in Fig.6a–f. The bandgaps of rainbow PnC are thus more than two times broader than those of the equivalent periodic PnC. It should be noted that the measured receptance values have reasonable differences in bandgap frequencies and bandwidths compared with the simulated results shown in Fig. 2a–f, which might be caused by the non-ideal experimental conditions and simulation models, especially the uncertainties introduced by the AM process. It has been found that the physical parameters (density, elastic modulus, etc.) in structures printed by AM technologies could have variabilities of up to more than 10%, which would change the bandgap frequencies and bandwidths of PnCs and metamaterials remarkably23,46. Despite the reasonable differences, both the experimental and numerical results proved the design method of enlarged bandgaps due to nonperiodic design, which could inspire future researchers to produce structures with enhanced vibration attenuation.

Figure 6
figure 6

Experimental displacement FRFs of the rainbow PnC in x (a), y (c) and z (e) directions, and the periodic PnC in x (b), y (d) and z (f) directions.

Full size image

Methods

Finite element modelling

A commercial FE tool was employed in order to numerically model the 7x7x7 structures. Due to non-periodicity, unit cell computational approaches were not applicable and the complete structure had to be modelled to simulate its broadband harmonic response. Linear hexahedra elements were employed for modelling the geometry of the structures. A mesh convergence study was performed in order to ensure accuracy and stability of the obtained results with a convergence criterion of 0.1% being employed for the maximum divergence between two mesh configurations as shown in Fig. 7a and b. A global damping lost factor of 0.03 was considered throughout the simulation process. The structural boundary conditions were assumed to be free-free with no structural displacement conditions imposed in order to emulate the physical experiment to a maximum degree. The input force was a 1 N force applied in a broadband spectrum between 0 and 1000 Hz. Each broadband frequency analysis consisted of 2000 steps in total with a total running time of 3830 s on a 2.2 GHz processor with 8 GB of RAM memory.

Figure 7
figure 7

Mesh convergence study of finite element modelling with different element numbers with respect to the average displacement at the sampling point in the considered frequency range for (a) Rainbow PnC and (b) Periodic PnC.

Full size image

Additive manufacturing technology employed

The structural samples were fabricated by a Laser Sintering 3D printer using PA12 material. The 3D printer employed a CO2 laser having a scan speed and hatch spacing of 0.35 m/s and 0.3 mm, respectively. The nominal spot size of the laser was 0.46 mm and the layer thickness 0.12 mm. A powder bed with dimensions of 375 mm × 375 mm × 430 mm was filled with PA12 powder at a temperature of 170. The accuracy of the printed geometries was related to the laser spot size, the layer thickness, the size of the powder and the laser scanning strategy etc. The minimum feature size by the 3D printer was 1 mm, below which considerable mechanical properties would be introduced owing to the existence of unsolidified powder55. The Young’s modulus and material density of the printed structures were measured on small fabricated samples based on the ASTM standard56 and found to be 1.75 GPa and 1000 kg/m3 respectively.

Experimental process

During the experiment, a chirp wave with the frequency range of 20–1000 Hz was used as excitation signals. It was first generated by the computer and sent to a junction box (Polytec VIB-E-400), and afterwards amplified by a Modal Shop 2050E09 unit. The mechanical shaker (Modal Shop 2060E) excited the sample according to the received signals. An impedance head (PCB 288D01) mounted on the shaker was applied to test the force signals at the exciting point and a laser Doppler vibrometer (Polytec PSV-400) employed to measure displacement signals at sampling points. The collected displacements and forces were sent back to the junction box and calculated by the software to solve out the FRFs. All measurements were taken with a frequency resolution of 1.25 Hz and are complexly averaged over 100 spectral sweeps. The schematic illustration of the experiment setup is shown in Fig. 8.

Figure 8
figure 8

Caption of the experimental setup exhibiting connectivity between the signal generator, amplifier, structure under investigation, laser vibrometer and the signal acquisition unit.

Full size image