Abstract
Large trees are disproportionately important in terms of their above ground biomass (AGB) and carbon storage, as well as their wider impact on ecosystem structure. They are also very hard to measure and so tend to be underrepresented in measurements and models of AGB. We show the first detailed 3D terrestrial laser scanning (TLS) estimates of the volume and AGB of large coastal redwood Sequoia sempervirens trees from three sites in Northern California, representing some of the highest biomass ecosystems on Earth. Our TLS estimates agree to within 2% AGB with a species-specific model based on detailed manual crown mapping of 3D tree structure. However TLS-derived AGB was more than 30% higher compared to widely-used general (non species-specific) allometries. We derive an allometry from TLS that spans a much greater range of tree size than previous models and so is potentially better-suited for use with new Earth Observation data for these exceptionally high biomass areas. We suggest that where possible, TLS and crown mapping should be used to provide complementary, independent 3D structure measurements of these very large trees.
Similar content being viewed by others
Introduction
Some of the highest values of forest above ground biomass (AGB) ever reported, up to \(5190\,\hbox { t ha}^{-1}\), are from groves of Sequoia sempervirens and Sequoiadendron giganteum in Northern California1,2,3. These trees are also the tallest trees on Earth, routinely exceeding 100 m4,5,6. Estimating the size and mass of such trees is an extremely difficult task and is very rarely, if ever, done directly via destructive harvest of complete trees, for a variety of reasons7,8. The most compelling of these is of course the undesirability of damaging such magnificent and ancient trees, very often in protected areas. Even if harvest is possible e.g. in conjunction with timber operations, it is still very challenging due to the sheer size of the trees and so is done typically for trees \(< 50\) m height. Destructive harvesting also requires great care to minimise damage during felling, and then sub-sampling of component volumes and masses that are then extrapolated to the whole tree9. Even when larger trees have been sampled, the measurements have been affected by the crowns being destroyed during felling10.
The importance of big trees, (typically defined as \(> 70\) cm diameter-at-breast height, DBH), is widely-recognised in terms of carbon storage, demographics and impact on their surrounding ecosystems11,12,13,14. Unfortunately the importance of big trees is in direct proportion to the difficulty of measuring them, particularly for AGB. As a result, AGB is estimated using indirect approaches, the most widely-used being calibrated empirical allometric models relating DBH, height H (if available) to volume and then, via wood density or specific gravity, to AGB15. These allometric relationships represent the assumption of the general scale-invariance of the often (but not always) strong correlations between DBH, H and AGB, and are calibrated against destructively harvested data15,16. However even these destructively-harvested calibration data are very often only sub-samples of full trees, extrapolated using estimates of form and shape, particularly for large trees. For the very largest trees there are virtually no destructive harvest measurements at all and so AGB is inferred from allometric extrapolations based on much smaller trees. A key assumption of allometric models is that provided scale-invariance holds, then the distribution of tree size in the calibration data is irrelevant. However if scale-invariance is not true, then predictions for under-represented trees, likely to be the largest ones18, will be biased17.
An additional challenge when measuring very large trees is that the particular growth and survival strategies that allow for such size and age may also lead to departure from allometric models based on smaller trees7,18. For example, it has been observed that trees with main trunks that are large compared to their crowns (relative to other, smaller trees) produce more wood annually19. Specific traits of Sequoia sempervirens include shade tolerance, fire and and disease resistance, and a high capacity for sprouting and trunk reiteration. These traits may also mean that they are not well-represented by generalised allometries8. Longevity also implies that older, larger trees have encountered very different histories of fire, disease and climate variation than their smaller neighbours, presumably leading not only to potentially different growth forms but also greater variance.
To overcome some of the limitations of DBH:H allometry when measuring very large trees, a second indirect approach is to use either ground-based measurements of standing trees2 or far more detailed tree-climbing measurements, referred to as ‘crown mapping’ (see18,19,20 for example). The latter approach can be used to quantify the size of different components of an individual tree in situ (trunk, major branches, crown etc.), as well as potentially providing core samples of wood tissue from the different components. This provides a much more detailed 3D structural picture of a particular individual tree, but requires skilled and potentially difficult climbing activities. In addition, various choices are needed as to what to measure, where and how, and then how to combine the resulting measurements in to a more complete map of 3D structure and volume20.
The uncertainties of any indirect estimate of AGB are compounded by the need for values of wood density to convert volume to mass. The importance of wood density as a key plant trait that in some senses integrates form and function21,22 have led to published databases of values. These have been widely-used in estimating AGB from plot measurements of DBH22. Given the long history of commercial forestry management of Sequoia sempervirens, values of wood density (and specific gravity) have been published for some time23. However, even with reliable values of wood density, uncertainty in allometric estimates of AGB will also be a function of the variability of density within an individual tree. This can vary substantially in the radial direction, with height and wood type (cambium, heartwood, sapwood, compression or tension tissue etc). In addition the fraction of bark can vary substantially in large Sequioa sempervirens, making up 18% of the total wood volume in some cases24,25.
A fundamental issue when applying indirect models of this sort to estimating AGB is that at no stage are the resulting estimates directly validated i.e. by harvest and weighing. This makes it all the more important (but also difficult) to quantify estimated uncertainties, particularly when moving to larger scales (see the discussion by26 of this problem).
When moving up in scale e.g. via Earth Observation (EO), either at the tree-scale using airborne lidar, or at larger scales using satellite estimates of canopy height, some of the allometric uncertainties relating to random errors in individual tree size, form and wood density may average out27,28. Satellite estimates of AGB are based on area-averaged canopy height estimates (typically weighted by stem basal area) rather than individual tree heights30, which again will tend to reduce errors arising from using allometries derived from individual tree measurements. However, the accuracy of these estimates relies more generally on conformity of the wider sample to the underlying allometric harvest data17. Ultimately, all EO estimates are based on field estimates, and in turn on the allometric models applied to tree measurements. Uncertainties and biases in individual tree estimates that result from allometric models therefore potentially propagate to uncertainties and biases in EO products. When considering the biomass of plots containing exceptionally large individual trees, uncertainties are likely to be compounded because of the importance of these trees in the overall biomass budget13. This has implications for wide-area estimates of AGB from EO, which typically rely on H-based allometry and estimates of stem density or basal area. This requires calibration of these allometries (potentially using H to estimate DBH and then AGB), as well as specific ground measurements to validate the resulting EO-derived estimates of AGB, something that is currently very rarely done29,30.
One way to at least partially address the problem of validating indirect estimates, is by comparing methods that are independent, having totally different underlying assumptions, strengths and weaknesses. Terrestrial laser scanning (TLS) offers one such alternative, by providing estimates of detailed 3D tree structure and volume in even tall, dense forests31,32. While TLS estimates of tree volume (and AGB) are also indirect, they do not rely on the assumptions of allometric models. TLS estimates of volume and AGB have also been shown to agree closely with destructive harvest measurements of full trees33 as well as with harvested sub-components of larger tropical trees34,35. As a non-destructive technique, TLS data can also be collected in established forest plots, making them particularly suited for EO calibration and validation activities36,37.
Here, we aim to test whether TLS can provide accurate estimates of volume and hence AGB of large Sequioa sempervirens trees. We compare TLS measurements to an independent 3D crown-mapping approach, and to both species-specific and generalised allometric estimates of volume and AGB8,9,19. We develop a new allometric relationship spanning a far greater size-range of trees than currently possible.
Results
Point clouds of trees extracted from a single plot (CAL-01, below) are shown in Fig. 1, illustrating the diversity of tree size and form of trees growing within a few m of each other under the same environmental conditions. Cross sections through the point clouds of two trees are shown in Figs. 2 and 3. This illustrates the potential variety of trunk and crown shapes and nature of the bark roughness. Note the different scales in each case.
The Colonel Armstrong tree shown in Fig. 3 is the largest tree we scanned. The TLS point cloud has 14.5 M points, and the tree as measured by TLS is ~88 m tall, with DBH of 3.39 m. The mean and SD of the TLS-estimated volume of the tree is \(321\pm 27\,\hbox { m}{^3}\) (see “Methods” below for details). Of this volume, \(216\,\hbox { m}{^3}\) is from the trunk, with the remainder in the branches. The total surface area of the woody part of the tree is \(2358\,\hbox { m}{^2}\).
Tree 6 from site CAL-02 (described below): (left) side elevation; (right) cross section through point cloud at location of dotted line in the (left) panel i.e. 1.2–1.4m. The grid shows an alpha shape fit to the TLS cross-section (described below), with the resulting RMSE of fit; and fDBH, the so-called functional DBH, defined as the DBH of a circle of equivalent area to the estimated non-circular trunk cross-sectional area.
The largest Sequoia by volume anywhere (estimated from trunk diameter) is apparently the General Sherman, with a reported volume of \(1487\,\hbox { m}{^3}\). Interestingly, while the Colonel Armstrong would not even get close to the list of the top 30 largest Sequoia sempervirens by volume, at only 35% of the 30th placed tree, it is taller than every one of those trees. This is indicative of the variation in H:DBH that these trees can encompass. It also rather raises the question of how well an allometry based on DBH, or DBH and H, is able to predict AGB of large trees.
Figure 4 shows the various allometric model estimates of AGB varying with DBH as well as the TLS-derived AGB values. The variation in allometric AGB is much greater (in an absolute sense; the Sillett et al.19 estimate is 78% larger than the Jenkins et al.52 estimate) for the largest tree than for the others, varying between 70 (Jenkins et al.52 and 103 tons (Sillett et al.19), against a TLS-derived value of 106 tons. Larger relative differences occur, particularly for trees between 10 and 30 tons—up to nearly 100% in some cases. It is also clear that the TLS and crown-mapping estimates are higher than the species-specific or generalised allometries, the latter being considerably lower.
Figure 5 shows the regressions of TLS and species-specific allometric estimates of AGB. Figure 6 shows the comparison between TLS-derived and allometric AGB estimated from generalised allometries only. Table 1 summarises the resulting model fits from all allometric models both including and excluding the Colonel Armstrong tree, to quantify the impact of a single large tree on an allometric regression model. The species-specific allometric and generalised allometry results are grouped separately. Plot-level AGB density (AGBD) values for all plots are given in Table 2, for both TLS-derived and allometric estimates. AGBD is the total AGB for all trees in each plot divided by plot area.
To demonstrate how crown mapping and TLS might be used to estimate additional canopy properties related to AGB and function, we used the crown depth and volume approximation of Sillett et al.8 to estimate crown volume (CV), and the number and mass of needles for the Colonel Armstrong tree. The resulting crown volume (CV) is \(5378\,\hbox { m}{^3}\), with 168 million needles, needle mass 320 kg, needle area \(2100\,\hbox { m}{^2}\). The tree most comparable in size measured by19 is their tree SESE21, with \(\hbox {H} = 86.10\) m and functional DBH, \(\hbox {fDBH} = 349\) cm, weighing 55.59 tons. That tree has \(\hbox {CV} = 7755\hbox { m}{^3}\), needle mass = 546.3 kg, needle area of \(3068\hbox { m}{^2}\) and 298 million needles.
Discussion
This is (we believe) the first time that TLS has been used to make full volume measurements of large Sequoia sempervirens trees. Our results suggest that TLS is well-suited to making detailed 3D structural measurements of the size and volume of these trees. The TLS measurements were collected in a few days per ha and sample the full size range of trees in each plot.
Our TLS-derived estimates of volume and AGB agree closely with an allometric model developed from detailed crown mapping measurements of large Sequoia sempervirens trees19. In this case TLS-derived and allometric AGB agree to within 2% AGB and, crucially, with no difference in regression slope. All other allometric models tested, based on samples of smaller trees and/or from more indirect measurements, tend to under-estimate AGB compared to both TLS and crown-mapping estimates, with generalised allometries being 30–40% lower. The fit in each of these case is unsurprisingly similar given the form of the allometric models, but the slope and intercept differences indicate calibration data with different properties to those provided by TLS and crown mapping. The fact that TLS and crown mapping agree so closely is encouraging. The estimates of volume are completely independent (AGB estimates share wood density) with their own pros and cons, but that also means their uncertainties will be uncorrelated. It has been suggested that crown mapping has two key advantages over TLS: the ability to estimate leaf components from crown dimensions and branch allometries; and the ease with which it can be applied to giant trees in remote areas8. However, TLS measurements also allow retrieval of crown and branch size information38. As we show above, there is also the possibility to use TLS with crown mapping to estimate crown volume, needle mass and number. By definition, these numbers are impossible to validate—much more so than the woody volume and mass—based as they are on very large extrapolation, and should be considered as indicative at best. However, if validated these properties are potentially useful in developing allometries based on crown volume, accounting for foliar biomass in AGB, and relating to photosynthesis and transpiration. In terms of the difficulty of collecting TLS data, it has already been used to measure the structure of very large trees (H up to 100 m) in remote tropical forest34,35,39.
Verbeeck et al.40show that large trees may have more variable architecture than smaller ones on a so-called structural economics spectrum (SES), due to greater variations of crown morphology. Routinely combining the structural information provided by TLS with the type of branch-level allometry developed via crown mapping for leaf material8, would potentially provide the best of both worlds in terms of understanding relationships between architecture and function in these very large trees.
Our results suggest that TLS is well-suited to characterising the size and mass of Sequoia sempervirens trees, particularly if other measurements are hard to make. This is of particular importance when attempting to calibrate and validate estimates of AGB which are made from EO30,41. Our results also suggest that allometries developed from less detailed or non species-specific measurements, are likely to significantly underestimate biomass in these tall forests with exceptionally high AGBD. The TLS-derived estimates of AGBD include all trees in a plot, whereas allometric estimates are based on selected individuals are not spatially explicit. This is of particular importance to upscaling from tree-based to area-based estimates of AGB, for both EO and census-based estimates. While uncertainty in the individual tree AGB estimates will be reduced at these aggregate scales, bias in the estimates would not. If allometric models yield biased estimates of plot-level AGB, these biases will naturally be passed to the satellite models. Our results suggest that the TLS individual tree estimates do not have biases with respect to species-specific allometric models, but show systematic bias with respect to the generalized allometries that are used to train satellite products (e.g. Jenkins et al.52).
As discussed above, larger trees have a wider range of AGB, but are rarely measured in allometric samples due to the difficulty of measurement. Samples of much smaller harvested trees will not represent this greater variance with size. In addition, partial measurement of felled or fallen trees will tend to underestimate branch mass. Using measurements of other, smaller species to infer the mass of Sequoia sempervirens is also a potential source of underestimate, given they are seemingly exceptionally massive for given DBH.
Table 1 demonstrates the difference a single large tree can have on allometric predictions. The regression \(\hbox {r}^2\) values are all higher with the Colonel Armstrong tree included and the slopes are all closer to one, increasing by up to 7% in the case of Fujimori2 for example. This shows how a few particularly large trees may dominate an allometric regression model. Or conversely, how failing to sample the full range of tree size risks a biased regression model. Most of the trees we measured here have DBH greater than the largest tree in the sample of Kizha and Han9 (max DBH 85 cm). A key advantage of the TLS approach is that it removes the need to select trees a priori a i.e. all trees within a given plot are captured. So trees of \(< 85\) cm DBH are not representative of the size distribution in the plots measured here. This is perhaps not surprising given that Kizha and Han9 measured in commercial forestry plots. But an allometry calibrated using these measurements and then applied to trees in non-commercial forest plots will be extrapolating well outside the DBH:AGB calibration range. This is fine as long as the fundamental allometric assumption of a scale-invariant size-mass relationship holds; if not, this will fail to capture AGB variance of larger trees.
Care needs to be taken in considering the effects of sampling on allometric model selection and uncertainty17,42. Even if observations from a particular size class, species or type are present in allometric calibration data, the resulting model is not necessarily suitable for predictions even within those groups if the calibration data are overwhelmed by observations from other types (e.g. far more trees of one size class than another)17.
And whilst it is true that out-of-sample predictions of trees outside the range of the in-sample (calibration) data may in general be ‘a bad thing’, particularly if the assumptions of allometric regression are violated, this raises an interesting question: how do we resolve the seeming contradiction between these warnings on the one hand, and the fundamental assumption of scale-invariance that underpins the concept of allometry on the other i.e. that big trees have the same diameter-mass relationship as smaller ones43,44? That aside, the disproportionate impact of large trees also indicates that more estimates of the volume of large trees are needed, at least commensurate with their contribution to AGB if that is the property of interest. Whether these are obtained by TLS, crown mapping or other methods, they will help avoid errors caused by undersampling and allow better characterisation of variance in allometric predictions of AGB at larger DBH. This is of particular importance for EO estimates of AGBD, given the relatively weaker relationship between H and AGB than between DBH and AGB45.
Methods
Study sites
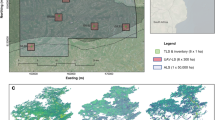
TLS data were collected during a campaign in 3 locations in Sonoma County, California during 2017 at three sites, listed below.
-
Grove of Old Trees, CAL-01: 38.4, − 123.0;
-
Armstrong Redwoods State Natural Reserve, CAL-02: 38.5, − 123.0;
-
Sea Ranch, CAL-07: 38.7, − 123.5
See https://mattbv.github.io/tls-data-map/ for more location details. The climate in Sonoma County is broadly temperate coastal, with annual average rainfall of 80 cm, annual average temperature of \(15 \,^\circ \hbox {C}\), with mean low of \(7 \,^\circ \hbox {C}\) and mean high of \(23\, ^\circ \hbox {C}\). Prevailing westerly winds bring a large amount of moisture inland as sea mist, which is crucial to the existence of Sequoia sempervirens9.
TLS data collection and processing
TLS data were collected with a Riegl VZ-400 TLS (RIEGL Laser Measurement Systems GmbH, Austria) using \(0.04^\circ\) scan resolution, and upright and \(90^\circ\) tilt scans at each location, with the scanner mounted at 1.5 m on a tripod. The scanner range is ~700 m, with beam divergence 0.35 mrad leading to a footprint diameter of 42 mm at 100 m. Scans were taken on a 12.5 m grid using multiple reflectance targets to enable co-registration of scans, following the protocol of46. For the Colonel Armstrong tree, scans were collected at five locations around the tree at a distance of 10–20 m. All TLS scans were then co-registered into plot-level point clouds using the Riegl RiSCAN PRO software package (v 2.7.1). Clusters of tree points were extracted from each plot point cloud for further analysis using the treeseg tool47. All tree measurements referred to here are Sequoia sempervirens only.
Grove of Old Trees, CAL-01
The Grove of Old Trees is a 13.5 ha region of old-growth redwoods, privately-owned and managed by non-profit local organisations. The site is in the so-called Petaluma Wind Gap that carries cooler, wetter air from the coast inland and provides the moist climate required for large Sequoia sempervirens growth. A 1 ha area was scanned within the larger site and of this the central 0.25 ha was used, with twenty six trees extracted from the resulting point cloud. The tree dimensions derived from the TLS point clouds are given in Supplementary Table S1.
Armstrong Redwoods State Natural Reserve, CAL-02
This plot was located within Armstrong State Natural Reserve near Guerneville, and was one of five 0.25 ha plots that were positioned to avoid roads, pedestrian paths, enclosed areas and river beds. Thirty six trees were extracted from the resulting point cloud. The Colonel Armstrong tree was just outside the plot and was scanned separately.
The Sea Ranch, CAL-07
The Sea Ranch is a privately-owned reserve along 16 km of the Sonoma County coast (https://www.tsra.org). A 1 ha plot was scanned and the central 0.25 ha was extracted for further analysis. Eighty two trees were extracted from the resulting point cloud. This plot contained characteristic ‘fairy ring’ structures of secondary growth stems growing around the site of an older, absent tree. Fairy rings have generally been thought to arise mainly (but not exclusively) from clonal spread, a key (and unusual in conifers) reproductive strategy for Sequoia sempervirens48.
TLS and allometric estimates of volume and AGB
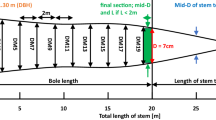
The volume of each tree was estimated by fitting Quantitative Structural Models (QSM) using the TreeQSM approach of49. This provides an estimate of tree volume (as well as branch and trunk size distributions) of each extracted tree point cloud. For each tree, multiple QSMs were fitted to each point cloud, using the parameter optimisation approach of47, resulting in a mean and standard deviation of QSM volume estimation. To estimate DBH from the TLS point clouds, a cross-section was taken through each point cloud at 1.2–1.4m above the lowest point (indicated by the dotted lines in Figs. 2 and 3). Each 20 cm thick slice was collapsed onto a plane and a least squares circle-fitting algorithm applied50. The RMSE of the circle fit was used in the subsequent allometric equations to estimate the uncertainty in AGB due to DBH estimation.
We convert TLS-derived estimates of volume (via QSM fitting) to AGB using the same wood density values as those in five allometric models developed specifically for Sequoia sempervirens, and two general (non species-specific) models. We then compare our TLS-derived estimates of tree AGB with these allometric model estimates of AGB. To generate the latter, we fit the published forms of these models (i.e. using the specified model parameter values), to size and shape variables derived from TLS i.e. DBH and variants thereof, as well as tree height, H. H here is taken from the highest point of the original point cloud in each case. The explicit form of each model, and the parameter values used in each case, are given in Supplementary Table S1.
Species-specific models
Fujimori2 and Parks10 developed species-specific DBH, H allometries based on volume estimates of larger trunk and branch components sampled from fallen trees i.e. non-destructive, partial samples. We also compare with two more recent allometric models developed by Sillett et al.8,19, which predict AGB and total volume. The 2015 model was developed from detailed 3D crown mapping via tree-climbing measurements. These were used to generate estimates of 3D volume of as many of the components of large Sequoia sempervirens trees as possible, and also included multiple cores for wood density and specific gravity. Empirical relationships between sampled branch volume and leaf mass were also generated. The later model used the previous crown mapping structural data to develop an allometry of the same form, but using ground-based measurements of DBH, H and crown size.
For the19 model of predicted AGB, the independent variables are diameter at the top of buttress (DTB) and functional DBH (fDBH). Total wood volume is predicted using the same form but with different coefficients. The TLS-derived values of DTB, fDBH are given in Supplementary Tables S2–S4. Across all trees, the difference between DBH and fDBH varies by mean − 6.9%, stdev 2.6% (i.e. fDBH > DBH). Figure 2 shows that the difference between DBH and fDBH may only be a few % by chance despite potentially large departures from the assumption of a circular cross-section. For the8 model, the independent variables are DTB and H.
To estimate DTB, Sillett et al.19 plotted their measurements of tree circumference (x, y) and then estimated the resulting cross-sectional area via an image-processing approach. Here, we estimate DTB by taking a circle fitted to points in the range 4–4.5 m up the trunk to guarantee being above buttresses. We estimate fDBH by fitting a concave hull (alpha shape) (Python alphashape toolbox v 1.0.151). We used an alpha parameter of 4.0 determined as a balance between fitting more (higher alpha) or less (lower alpha) tightly, to the cloud sections. The resulting alpha shape areas are shown in blue hatching in Figs. 2 and 3, and the circle of equivalent area is then used to estimate fDBH. The RMSE of fit is used as the uncertainty in the resulting fDBH and propagated through the allometric volume estimates. We also fitted the8 model to the TLS-derived estimates of volume, to generate a new set of model parameters based on the 146 extracted TLS trees. The resulting RMSE of model fit is 1.33% (compared to 1.44% when using the original8 parameters). As an example of how these measurements might be used for EO estimates of volume and AGB, an H-only allometry derived from TLS predicts volume with RMSE of ~20% (see Supplementary Fig. S1).
The other species-specific allometry we compare with is that of Kizha and Han9, the only one developed using destructive harvest and weighing. They worked in commercial logging sites, sampling smaller trees in the DBH range 2.54–84 cm. Trunk volume was estimated by section diameters up the trunk and mass was sampled via disks. Branch mass was sampled for various size classes, as well as foliage and live/dead fractions and empirical relationships with size developed for each. In this way the total wood volume and mass were estimated from each tree. The resulting model is the only species-specific allometry here that uses DBH only (along with a correction factor for bias in back-transformation to arithmetic units).
Generalised allometric models
We also compare TLS with two generalised (i.e. non-species specific) allometric models. These are the models of Jenkins et al.52 and the closely-related model of Chojnacky et al.53, which have been widely-used in the US to estimate regional AGB. Both models take the same form, and the model parameters are determined by species class. For Jenkins et al.52 Sequoia sempervirens is classified in the cedar/larch group. For Chojnacky et al.53 Sequoia sempervirens is classified in the Cupressaceae 0.30–0.39 spec. grav. group.
The Jenkins et al.52 model was developed from meta-analysis of more than 2000 published DBH-based allometric models for U.S. trees, in order to develop a set of national-scale AGB regression equations. This approach groups species into softwood and hardwood categories based on a combination of taxonomic relationships, wood specific gravity, and DBH-to-AGB relationships. An issue with this model is that in order to overcome the relatively small sample range of DBH, a form of bootstrapping was used to generate ‘pseudo data’ from the original samples. The resulting allometric model was then fitted to these pseudo data, which implies a fit to an existing fitted model. It is not clear how the resulting uncertainty is dealt with in this case.
The Chojnacky et al.53 model is based on the same underlying data as Jenkins et al.52 but re-analysed at DBH intervals within the DBH ranges of the original equations, and considering the similarity (or not in some cases) of the specific gravity of tree species within genera and/or families.
References
Van Pelt, R., Sillett, S. C., Kruse, W. A., Freund, J. A. & Kramer, R. D. Emergent crowns and light-use complementarity lead to global maximum biomass and leaf area in Sequoia sempervirens forests. For. Ecol.Manag. 375, 279–308 (2016).
Fujimori, T. Stem biomass and structure of a mature sequoia sempervirens stand on the Pacific Coast of Northern California. J. Jpn. For. Soc. 59(12), 435–441 (1977).
Busing, R. T. & Fujimori, T. Biomass, production and woody detritus in an old coast redwood (Sequoia sempervirens) forest. Plant Ecol. 177, 177–188 (2005).
Koch, G. W., Sillett, S. C., Jennings, G. M. & Davis, S. D. The limits to tree height. Nature 428(6985), 851 (2004).
Carder, A. C. Forest Giants of the World, Past and Present (Fitzhenry & Whiteside, Markham, 1995).
Harrison, J. G., Forister, M. L., Parchman, T. L. & Koch, G. W. Vertical stratification of the foliar fungal community in the world’s tallest trees. Am. J. Bot. 103(12), 2087–2095 (2016).
Sillett, S. C. et al. Increasing wood production through old age in tall trees. For. Ecol. Manag. 259, 976–994 (2010).
Sillett, S. C. et al. Allometric equations for Sequoia sempervirens in forests of different ages. For. Ecol. Manag. 433, 349–363 (2019).
Kizha, A. R. & Han, H.-S. Predicting aboveground biomass in second growth coast redwood: Comparing localized with generic allometric models. Forests 7, 96 (2016).
Parks, W.H. Redwood log characteristics: Sapwood thickness, bark thickness and log taper. Report number 1.20121. California Redwood Association, San Francisco (1952).
Keith, H., Mackey, B. G. & Lindenmayer, D. B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Nat. Acad. Sci. 106(28), 11635–11640 (2009).
Slik, J. F. et al. Large trees drive forest aboveground biomass variation in moist lowland forests across the tropics. Glob. Ecol. Biogeog. 22(12), 1261–1271 (2013).
Lindenmayer, D. B. & Laurance, W. F. The ecology, distribution, conservation and management of large old trees. Biol. Rev. 92(3), 1434–1458 (2016).
Rüger, N. et al. Demographic trade-offs predict tropical forest dynamics. Science 368(6487), 165–168 (2020).
Chave, J. et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145(1), 87–99 (2005).
Chave, J. et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 20(10), 3177–3190 (2014).
Burt, A. et al. Assessment of bias in pan-tropical biomass predictions. Front. For. Glob. Change Trop. For.https://doi.org/10.3389/ffgc.2020.00012 (2020).
Sillett, S. C., Van Pelt, R., Kramer, R. D., Caroll, A. L. & Koch, G. W. Biomass and growth potential of Eucalyptus regnans up to 100 m tall. For. Ecol. Manag. 348, 78–91 (2015).
Sillett, S. C. et al. How do tree structure and old age affect growth potential of California redwoods?. Ecol. Monog. 85(2), 181–212 (2015).
Kramer, R. D., Sillett, S. C. & Van Pelt, R. Quantifying aboveground components of Picea sitchensis for allometric comparisons among tall conifers in North American rainforests. For. Ecol. Manag. 430, 59–77 (2018).
Niklas, K. J. Influence of tissue density-specific mechanical properties on the scaling of plant height. Ann. Bot. 72, 173–179 (1993).
Chave, J. et al. Towards a worldwide wood economics spectrum. Ecol. Lett. 12, 351–366 (2009).
Luxford, R. F. & Markwardt, L. J. The strength and related properties of redwood. USDA Tech. Bull. 305, 20 (1932).
Wilson, P. L., Funck, W. J. & Avery, R. B. Fuelwood characteristics of northwestern conifers and hardwoods. Res. Bull. 60, 42 (1987).
Miles, P. D. & Smith, B. Specific gravity and other properties of wood and bark for 156 tree species found in North America. Res. Note NRS-38. Newtown Square, PA: U.S. (2009), Department of Agriculture, Forest Service, Northern Research Station, p. 35.
Clark, D. B. & Kellner, J. R. Tropical forest biomass estimation and the fallacy of misplaced concreteness. J. Veg. Sci. 23(6), 1191–1196 (2012).
Momo, S. T. et al. Using volume-weighted average wood specific gravity of trees reduces bias in aboveground biomass predictions from forest volume data. For. Ecol. Manag. 424, 519–528 (2018).
Réjou-Méchain, M., Tanguy, A., Piponiot, C., Chave, J. & Hérault, B. Biomass: An r package for estimating above-ground biomass and its uncertainty in tropical forests. Methods Ecol. Evol. 8(9), 1163–1167 (2017).
Chave, L. et al. Ground data are vital for remote sensing missions. In Surveys in Geophysics vol 71: Forest Biomass and Structure from Space (eds Scipal, K., Dubyah, R., Le Toan, T., Quegan, S., Cazenave, A., Lopez, T.) 40 (4), 863–880 (2019).
Duncanson, L. et al. The importance of global land product validation: Towards a standardized protocol for aboveground biomass. In Surveys in Geophysics vol 71: Forest Biomass and Structure from Space. (eds Scipal, K., Dubyah, R., Le Toan, T., Quegan, S., Cazenave, A., Lopez, T.) 40 (4), 979–999 (2019).
Disney, M. I. Terrestrial LiDAR: A 3D revolution in how we look at trees. New Phytol. 222(4), 1736–1741 (2018).
Disney, M. I. et al. Weighing trees with lasers: Advances, challenges and opportunities. R. Soc. Interface Focus 8, 2. https://doi.org/10.1098/rsfs.2017.0048 (2018).
Calders, K. et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 6(2), 198–208 (2015).
Gonzalez de Tanago, J. et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 9(2), 223–234 (2018).
Momo Takoudjou, S. et al. Using terrestrial laser scanning data to estimate large tropical trees biomass and calibrate allometric models: A comparison with traditional destructive approach. Methods Ecol. Evol. 9(4), 905–916 (2018).
Stovall, A. E., Anderson-Teixeira, K. J. & Shugart, H. H. Assessing terrestrial laser scanning for developing non-destructive biomass allometry. Forest Ecol. Manag. 427, 217–229 (2018).
Disney, M. I., Burt, A., Calders, K., Schaaf, C. & Stovall, A. Innovations in ground and airborne technologies as reference and for training and validation: Terrestrial laser scanning (TLS). In Surveys in Geophysics vol 71: Forest Biomass and Structure from Space. (eds Scipal, K., Dubyah, R., Le Toan, T., Quegan, S., Cazenave, A., Lopez, T.) 40 (4), 937–958 (2019).
Lau, A. et al. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 32, 1219–1231 (2018).
Shenkin, A. et al. The world’s tallest tropical tree in three dimensions. Front. For. Glob. Change.https://doi.org/10.3389/ffgc.2019.00032 (2019).
Verbeeck, H. et al. Time for a plant structural economics spectrum. Front. For. Glob. Change. 2, 43. https://doi.org/10.3389/ffgc.2019.00043 (2019).
Duncanson, L. et al. Implications of allometric model selection for county-level biomass mapping. Carbon Balance Manag. 12(1), 18 (2017).
Sileshi, G. W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 329, 237–254 (2014).
Enquist, B. J. Universal scaling in tree and vascular plant allometry: Toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 22, 1045–1064 (2002).
Niklas, K. J. A phyletic perspective on the allometry of plant biomass-partitioning patterns and functionally equivalent organ-categories. New Phytol. 171, 27–40 (2006).
Hunter, M. O., Keller, M., Victoria, D. & Morton, D. C. Tree height and tropical forest biomass estimation. Biogeosciences 10(12), 8385–8399 (2013).
Wilkes, P. et al. Data acquisition considerations for terrestrial laser scanning of forest plots. Rem. Sens. Environ. 196, 140–153 (2017).
Burt, A., Disney, M. I. & Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 10(3), 438–445 (2018).
Douhovnikoff, V. & Dodd, R. S. Clonal spread in second growth stands of coast redwood, sequoia sempervirens. In: Standiford, R. B. et al., technical editors. Proceedings of the Redwood Region Forest Science Symposium 2007: What Does the Future Hold? Gen. Tech. Rep. PSW-GTR-194. Albany, CA: Pacific Southwest Research Station, Forest Service, US Department of Agriculture. Vol 194, 65–72 (2007).
Raumonen, P. et al. Comprehensive quantitative tree models from terrestrial laser scanner data. Remote Sens. 5(2), 491–520. https://doi.org/10.3390/rs5020491 (2013).
Olofsson, K., Holmgren, J. & Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the RANSAC algorithm. Remote Sens. 6(5), 4323–4344 (2014).
Bellock, K. E. Alphashape Python toolbox, v 1.0.1. https://pypi.org/project/alphashape/ (2019).
Jenkins, J. C., Chojnacky, D. C., Heath, L. S. & Birdsey, R. A. National-scale biomass estimators for United States tree species. For. Sci. 49(1), 12–35 (2003).
Chojnacky, D. C., Heath, L. S. & Jenkins, J. C. Updated generalized biomass equations for North American tree species. Forestry 87(1), 129–151 (2014).
Acknowledgements
This research was supported by NASA CMS Grant NASA ROSES Carbon Monitoring System (CMS): Future Mission Fusion for High Biomass Forest Carbon Accounting, award 15-CMS15-0055. MD was funded in part by NERC Standard Grants NE/N00373X/1 and NE/P011780/1 and through capital equipment funding from UCL Geography and the NERC National Centre for Earth Observation (NCEO). We gratefully acknowledge the help of Aaron Arthur, Bill Keane, Karen Gaffney, Mark Tukman, Bill Maslach, Brendan O’Neil, Sonoma County Agricultural Preservation and Open Space District, and the State of California Department of Parks and Recreation for facilitating project coordination, and site access. We also thank Dave Lagomasino and Nathan Thomas (NASA) for assistance in data collection.
Author information
Authors and Affiliations
Contributions
Conceptualization, L.D., M.D.; data collection, A.B., M.D., L.D., J.A.; methodology and software, A.B., P.W.; formal analysis, M.D.; writing—original draft preparation, M.D.; writing—review and editing, A.L.L.; project administration and funding acquisition, L.D.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Disney, M., Burt, A., Wilkes, P. et al. New 3D measurements of large redwood trees for biomass and structure. Sci Rep 10, 16721 (2020). https://doi.org/10.1038/s41598-020-73733-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-73733-6
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.