Abstract
Patient-ventilator asynchronies can be detected by close monitoring of ventilator screens by clinicians or through automated algorithms. However, detecting complex patient-ventilator interactions (CP-VI), consisting of changes in the respiratory rate and/or clusters of asynchronies, is a challenge. Sample Entropy (SE) of airway flow (SE-Flow) and airway pressure (SE-Paw) waveforms obtained from 27 critically ill patients was used to develop and validate an automated algorithm for detecting CP-VI. The algorithm’s performance was compared versus the gold standard (the ventilator’s waveform recordings for CP-VI were scored visually by three experts; Fleiss’ kappa = 0.90 (0.87–0.93)). A repeated holdout cross-validation procedure using the Matthews correlation coefficient (MCC) as a measure of effectiveness was used for optimization of different combinations of SE settings (embedding dimension, m, and tolerance value, r), derived SE features (mean and maximum values), and the thresholds of change (Th) from patient’s own baseline SE value. The most accurate results were obtained using the maximum values of SE-Flow (m = 2, r = 0.2, Th = 25%) and SE-Paw (m = 4, r = 0.2, Th = 30%) which report MCCs of 0.85 (0.78–0.86) and 0.78 (0.78–0.85), and accuracies of 0.93 (0.89–0.93) and 0.89 (0.89–0.93), respectively. This approach promises an improvement in the accurate detection of CP-VI, and future study of their clinical implications.
Similar content being viewed by others
Introduction
Invasive mechanical ventilation (MV) is a life-support measure administered to patients who cannot breathe on their own. Patient-ventilator asynchronies occur when there is a mismatch between the ventilator’s setting and patient’s breathing pattern. Recent studies have emphasized the impact of asynchronies upon clinical outcomes1,2,3,4,5, focusing on the incidence of specific subtypes of asynchronies or on the asynchrony index, and also on their distribution over time given that they occur in clusters within prolonged uneventful periods1,2,3,4,5,6. Importantly, in most of these studies ventilator’s waveforms were analysed visually2,5,7,8; only a few analyses have been based on automated algorithms1,4,6,9,10 or, more recently, on machine learning algorithms incorporating not only ventilator waveforms but also clinical data11.
Asynchronies are difficult to define when supported only by visual assessment carried out by inexperienced personnel, since different types may develop in a short time period or may even overlap with each other. Furthermore, asynchronies, which are by nature time-limited and transient, lead to patient distress, impede the ventilator’s effectiveness in decreasing the work of breathing, increase the time on mechanical ventilation and have a negative impact on outcome1,2,4,7,12. Additionally, sometimes patient’s drive only becomes evident due to an increase in the respiratory rate itself13,14,15,16, which, given its irregular and complex behaviour, may be overestimated by visual observation or dedicated algorithms. Therefore, it would be extremely useful to have access to a method for assessing irregularity and complexity which could detect Complex Patient-Ventilator interactions (CP-VI), including not just asynchronies of any kind but also changes in the respiratory rate, in an automated, non-invasive and personalized fashion.
Normal physiological data are non-linear17. The complex behavior of a non-linear system cannot be characterized by the sum of its inputs, and the study of these systems requires methods that take into account the non-linear physiological response to a given stimulus. These methods could provide insights into organ-system interconnectivity, regulatory control, and complexity in time series during disease17,18,19.
Entropy is a non-linear method derived from the theory of complex systems which measures the randomness and predictability of stochastic processes. Various types of entropy have been used in clinical monitoring20,21,22. Sample Entropy (SE) is a measure of complexity and regularity, defined as the negative natural logarithm of the conditional probability that two sequences similar for m points will remain similar at the next point, where self-matching is not included23. Thus, a lower SE value indicates more self-similarity in a time series.
SE has proved to be an effective tool for investigating different types of time series data derived from various biological conditions in the human body. Examples of these conditions include the activation of inspiratory muscles in COPD patients24,25, the analysis of atrial fibrillation on electrocardiograms26, background electroencephalograms in Alzheimer’s patients27, heart rate variability28,29, human postural sway29 and seizure termination during electroconvulsive therapy30.
Interestingly, only a few entropy approaches have been applied in the respiratory system to study breath-to-breath variability and its components as predictors of successful separation from MV during spontaneous breathing trials (SBT)19,31,32,33,34. Breath-to-breath approaches suggest that increased irregularity of the respiratory system may be a marker of pulmonary health19 and may serve as a weaning predictor32,33,34,35, opening up the possibility that a certain degree of irregularity may be normal3,36. However, these studies rely on the detection of the appropriate respiratory cycle. Hence, the performance of automated algorithms in breathing cycle detection may be jeopardized when transient asynchronies occur during patient-ventilator interaction or even overlap with each other. In this respect, other authors have applied the SE to the entire signal, as is the case of Sá et al.37 who evaluated the respiratory changes by applying SE upon the entire airway flow signal providing an early and sensitive functional indicator of interstitial asbestosis.
We hypothesized that analyzing transient complexity of CP-VI may provide clinically relevant information during MV. Therefore, we sought to develop and validate a non-invasive method based on SE measurement using the entire airway pressure (Paw) and airway flow (Flow) waveforms to detect CP-VI, defined as the occurrence of asynchronies and changes in the respiratory rate.
Methods
Defining complex patient ventilator interactions
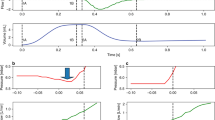
We defined CP-VI as a > 50% change in the respiratory rate13,35,38,39 and/or > 30% asynchronous breaths of any type (ineffective expiratory efforts, double cycling, premature cycling, prolonged cycling, or reverse triggering) over a 3-min period. A recent study found that 38% of mechanically ventilated patients had clusters of ≥ 30 ineffective expiratory efforts in a 3-min period (i.e., ≥ 50% of all breaths in a patient with a respiratory rate of 20 breaths per minute), and that the median duration of these clusters was 20 min4. Another study found that 59.7% of patients had clusters in which > 10% of all breaths in a 3-min period were double cycled, with a mean cluster duration of 15.5 min6. Figure 1 shows a representative example of different CP-VIs consisting of increased respiratory rate, asynchronies, or a combination of these phenomena.
Tracing of Flow and Paw from three different patients. (a) Continuous Positive Airway Pressure (CPAP) of 6 cmH2O. (b) Pressure assist-control ventilation (PCV) with pressure of 10 cmH2O, (c) PSV with a pressure support of 10 cmH2O and PEEP of 8 cmH2O. In (a1) and (a2), Complex Patient-Ventilator Interactions (CP-VI) consists of an increase in respiratory rate > 50%; in (b1) and (b2), it consists of > 30% asynchronies (ineffective expiratory effort, double cycling, premature cycling, prolonged cycling, and/or reverse triggering) in the 3-min period; and in (c1) and (c2) it consists of a combination of change in the respiratory rate and asynchronies.
Data acquisition and data analysis
The Better Care system (Better Care, Barcelona, Spain. US patent No. 12/538,940) continuously records Paw and Flow signals at a sample frequency of 200 Hz from intubation to liberation from MV9. Better Care uses drivers specifically designed to interact with output signals from mechanical ventilators and bedside monitors rather than directly with patients, synchronizing recorded signals and storing them for further analysis. We used MATLAB (The MathWorks, Inc., vR2018b, Natick, MA, USA) for signal processing, data analysis, and visual assessment. Signals were decimated at a sampling rate of 40 Hz before entropy calculation.
Study population
The findings presented in this paper represents an ancillary analysis on an ongoing clinical study (ENTROPY-ICU, ClincalTrials.gov NCT04128124) designed to assess the feasibility of using SE to identify CP-VI during MV. Data from 27 patients were obtained from an ongoing database at two centers in Spain. The database was constructed prospectively for the development of a connectivity platform (Better Care) to interoperate signals from different ventilators and monitors and subsequently compute algorithms for diagnosing patient-ventilator asynchronies (ClinicalTrial.gov, NCT03451461). The Comitè d’Ètica d’Investigació amb medicaments at the Corporació Sanitària Parc Taulí and the Clinical Research Ethics Committee of Fundació Unió Catalana d’Hospitals approved the database and the study protocol. The need for informed consent was waived because the current study was an ancillary analysis with anonymized data. The guidelines followed in this study were according to the applicable Spanish regulations (Biomedical Research Law 14/2007). This type of study must be evaluated and approved by at least one Institutional Review Board (IRB). Parc Taulí’s IRB approved this study to be carried out in all participating centers. The IRB approved the study allowing it to be carried out without the explicit request of informed consent from each participant given that it is a study with retrospective data. Spanish regulations allow studies to be carried out with this condition as long as they are approved by an IRB.
The SE analysis was performed on the complete set of Flow and Paw data collected during the two hours before self-extubation. Self-extubations, defined as extubations performed by the patient himself, are included in unplanned extubations but its mechanisms differ from accidental extubations40. Clinical and demographic data were obtained from medical charts (Table 1).
Visual validation of CP-VI
Experts’ visual assessment was considered the gold standard. Three critical care physicians with extensive experience in analyzing ventilator waveforms visually reviewed 92 15-min-long segments of Flow and Paw recordings from the two-hour period immediately before self-extubation. The 15-min window was selected based on two previous studies evaluating clusters of asynchronies, in which mean cluster duration was 15.5 and 20 min respectively6,10. An expert in MV selected the segments to ensure a balanced proportion of different ventilation modes (grouped into pressure support ventilation (PSV) or assist-control ventilation (ACV) modes, comprising volume assist-control and pressure assist-control ventilation) and of segments with and without CP-VIs. Every patient contributed both CP-VI and non-CP-VI segments with at least one 15-min segment of each type; however, some patients contributed more segments than others. In order to ensure that the most valuable CP-VI events were not missed, all the 15-min segments immediately preceding self-extubation were included. To ensure masking of the scorers, Flow and Paw tracings were randomly ordered in MATLAB prior to visual analysis. To standardize scoring criteria, scorers were provided with written descriptions of the characteristics of CP-VI before visual analysis. Scorers were asked to determine whether CP-VI were present in each segment. No time limitations were imposed.
Sample entropy
SE is a non-linear technique that measures the randomness of a series of data23. Compared to other approaches, SE’s main advantage is that it provides consistent results even in short and noisy medical time series19,23. To calculate SE, three parameters are necessary: the embedding dimension, m (a positive integer); the tolerance value or similarity criterion, r (a positive real number); and the total length of the series, N. Briefly, SE is defined as the negative logarithm of the conditional probability that two sequences of patterns of m consecutive samples that are similar to each other within a tolerance r will remain similar when one consecutive sample is added (\(m + 1\)), excluding self-matches. SE is calculated as follows23:
Given a time series of N samples \(\left\{ {x\left( n \right) = x\left( 1 \right),x\left( 2 \right), \ldots ,x\left( N \right)} \right\}\), a subset of \(N - m + 1\), overlapping vectors \(X_{m} \left( i \right)\) of length \(m\) are defined:
-
1.
Form m vectors defined by \(X_{m} \left( i \right) = \left[ {x\left( i \right),x\left( {i + 1} \right), \ldots ,x\left( {i + m - 1} \right)} \right],{ }i = 1,2, \ldots ,N - m + 1\). These represent \(m\) consecutive \(x\) values.
-
2.
Then, define Chebyshev distance between vectors \({ }X_{m} \left( i \right)\) and \(X_{m} \left( j \right)\), i.e., the maximum absolute difference between their scalar components:
$$d\left[ {X_{m} \left( i \right),X_{m} \left( j \right)} \right] = \begin{array}{*{20}c} {max} \\ {k = 0, \ldots ,m - 1} \\ \end{array} \left[ {\left| {x\left( {i + k} \right) - x\left( {j + k} \right)} \right|} \right].$$(1) -
3
For a given \(X_{m} \left( i \right)\), count the number of j \(\left( {1 \le j \ge N - m,i \ne j} \right)\), denoted as \(B_{i} \left( r \right)\), such that the distance between \(X_{m} \left( i \right)\) and \(X_{m} \left( j \right)\) is less than or equal to a threshold \(r\).
$$\begin{gathered} \hfill \\ B_{i}^{m} \left( r \right) = \frac{{B_{i} \left( r \right)}}{N - m - 1}, \\ \text{Then, for}\, 1 \le i \ge N - m, \hfill \\ \end{gathered}$$(2) -
4.
Defined \(B^{m} \left( r \right)\) as
$$B^{m} = \frac{1}{N - m}\mathop \sum \limits_{i = 1}^{N - m} B_{i}^{m} \left( r \right)$$(3) -
5.
This previous procedure is repeated, increasing the dimension to \(m + 1\) to calculate \(A_{i} \left( r \right)\) as the number of \(X_{m + 1} \left( i \right)\) within \(r\) of \(X_{m + 1} \left( j \right)\), where \(j\) ranges from 1 to \(N - m\left( {i \ne j} \right)\). Then,\({ }A_{i}^{m} \left( r \right)\) is defined as:
$$A_{i}^{m} \left( r \right) = \frac{{A_{i} \left( r \right)}}{N - m - 1}$$(4) -
6.
Set \(A^{m} \left( r \right)\) as
$$A^{m} = \frac{1}{N - m}\mathop \sum \limits_{i = 1}^{N - m} A_{i}^{m} \left( r \right)$$(5)
Thus, \(B^{m} \left( r \right)\) is the probability that two sequences will match for \(m\) samples, whereas \(A^{m} \left( r \right)\) is the probability that two sequences will match for \(m + 1\) samples. Finally, sample entropy is then defined as
which is estimated by the statistic:
The m parameter is generally taken as 2, while the r parameter normally ranges between 0.1 and 0.25 times the standard deviation (SD) of the segment analyzed of length N. In this study, SE was calculated over the Flow (SE-Flow) and Paw (SE-Paw) signals using a 30-s sliding window (N = 1,200 samples) with 50% overlap. SE was explored using m from 1 to 20 and with r values equal to 0.1, 0.2, 0.3, and 0.4 times the SD of each sliding window. To reduce noise and to increase the consistency of the results, we applied an 8-period-long exponential moving average filter to the SE series.
Automatic CP-VI detection
We devised an automated algorithm based on SE to detect CP-VI events (European patent application number EP19383116). Figure 2 summarizes the algorithm in a flowchart. Detection of a CP-VI depends on whether the percentage of change (PC) in SE with respect to the patient's own SE baseline value during the 15-min period is greater than a predefined threshold of change (Th). We calculated PC for SE-Flow and SE-Paw in each 15-min period in two ways, using the following derived features (the mean SE value [SE-Flowmean and SE-Pawmean], and the maximum SE value [SE-Flowmax and SE-Pawmax]), applying different values of Th (15%, 20%, 25%, 30%, 35%, 40%, 45%, and 50%). We hypothesized that SE values would be higher in periods with CP-VI than in periods with regular patient-ventilator interactions. Periods were considered to contain a CP-VI event when PC exceeded the Th. The optimal Th for CP-VI detection was selected during the SE setting optimization procedure (explained below).
Automatic CP-VI detection. Respiratory signals (Flow and Paw) are decimated at a sampling rate of 40 Hz. Sample entropy (SE) is calculated for different values of the embedding dimension (m) and tolerance (r). An 8-period-long exponential moving average is used to reduce noise and to increase the consistency of the SE results. Two SE features are determined for each 15-min period: the mean value and the maximum value. The percentage of change (PC) from the patient's own baseline value is calculated for each SE setting. When PC exceeds a determined threshold (Th), the period is considered to contain a CP-VI event. An optimization procedure is required to select the values of m, r, Th, respiratory signal, and SE feature that yield the most robust estimations of CP-VI.
Keim-Malpas41 recently proposed that alert thresholds derived from continuous analytic monitoring should be based on the degree of change from the patient’s own baseline, rather than on general cutoff thresholds. In our study there was no single baseline value common to all patients; each patient had their own baseline.
The baseline value of each SE feature was initialized with the value calculated in the first 15-min period. This value was updated with each new 15-min segment if the SE feature of the new one was lower than the current baseline.
Statistical analysis
Fleiss’ kappa coefficient was used to assess the reliability of agreement among scorers for visual assessment42. The automated CP-VI detection algorithm was applied over the SE series derived from the same Flow and Paw tracings previously used for visual assessment. To evaluate the performance of the automated algorithm with respect to the gold standard visual assessment, we calculated sensitivity, specificity, positive and negative predictive values (PPV and NPV respectively), accuracy, and the Matthews correlation coefficient (MCC)43. Widely used in biomedical research, the MCC is considered a balanced measure of the confusion matrix of true and false positives and negatives44,45,46. Calculation of the MCC is based on all four elements of the confusion matrix: true positive (TP), true negative (TN), false positive (FP), and false negative (FN) values, as follows:
MCC values can range from − 1 to + 1. An MCC value of − 1 suggests perfect disagreement between the predictions and the gold standard, and a value of 1 suggests perfect agreement between the predictions and the gold standard; a value of 0 indicates that the prediction is no better than random. The MCC index was used as the measure of effectiveness during the process to optimize SE settings so as to achieve the most robust CP-VI estimation.
Optimization procedure (selection of m, r, and Th)
In entropy studies, determining the optimal settings to robustly extract the randomness of a series of data is an important step47,48. To select the optimal settings for the SE parameters m and r and the optimal Th for estimating CP-VI, we used a repeated holdout cross-validation method with the MCC as a measure of effectiveness.
Figure 3 depicts the steps involved in the optimization and the validation procedure. Once the experts had visually validated the set of 92 observations, it was randomly divided into two subsets: 70% of the data for optimization and the remaining 30% of the data for validation. This optimization procedure was repeated a total of 15 times using different subsets (randomly selected each time) to capture as much relevant information as possible and to minimize the potential bias resulting from fitting the settings on a single partition. The MCC metric was computed for all combinations of m, r, and Th for each repetition. Finally, the maximum mean MCC value determined the optimal combination of SE settings and Th among all possible combinations. The optimization procedure was individually applied to the features derived from SE-Flow (SE-Flowmean, SE-Flowmax) and SE-Paw (SE-Pawmean, SE-Pawmax) in order to determine the respiratory signal and features that best reflect CP-VI.
Flowchart for the optimization procedure and validation. Procedure to select the optimal sample entropy (SE) settings (m and r) and the threshold of change (Th) for each SE airway flow (Flow) and airway pressure (Paw) features (SE-Flowmean, SE-Flowmax, SE-Pawmean, and SE-Pawmax). The dataset visually validated by the experts was randomly divided into two subsets: optimization (Opt.) and validation (Val.). The optimization procedure was repeated a total of 15 times using different subsets (randomly selected each time). The global maximum mean value of the Matthews correlation coefficient (MCC) determined the optimal values of m*, r*, and Th* among all possible combinations and all SE-derived features. Finally, the mean values of the measures of accuracy were computed for the optimal combination of parameters in both the optimization and the validation subsets.
In addition, a sensitivity analysis by using a small grid search of r values (step = 0.01) around the optimal value in the best features derived from SE-Flow and SE-Paw was performed to compare regions of confidence and to investigate whether the selected r value is a robust local maximum.
To assess the robustness of the optimization procedure, we computed the medians and interquartile ranges of all measures of performance (MCC, sensitivity, specificity, accuracy, PPV, and NPV) considering the optimal combination for both the optimization and validation subsets.
Results
Visual CP-VI analysis by experts
The experts visually assessed a total of 92 periods: 45 periods of PSV (22 with CP-VI and 23 without) and 47 periods of ACV (24 with CP-VI and 23 without). Fleiss’ kappa for inter-rater agreement was 0.90 (0.87–0.93), indicating almost perfect agreement.
Detecting CP-VI with SE
The exponential moving average filter reduced the noise in SE series and generated a smoothed SE version suitable for detecting CP-VI (see Supplementary Methods and Supplementary Fig. S1). Figure 4 shows representative examples of respiratory signal tracings with the corresponding SE-Flow (m = 2 and r = 0.2) and SE-Paw (m = 4 and r = 0.2) tracings. SE was highly sensitive to changes in the irregularity of the respiratory pattern occurring during ventilation.
Representative examples of ventilator signals for airway flow (Flow) (a1–a3) and airway pressure (Paw) (c1–c3) recorded over 15-min periods in the two hours prior to self-extubation, together with the sample entropy (SE) tracings derived from Flow (b1–b3) and Paw (d1–d3). Both, SE-Flow and SE-Paw were calculated with r = 0.2 × SD of each overlapping 30-s-long sliding window, by using different values of m equal to 2 and 4, respectively. Three 15-min periods are represented, corresponding to (1) no occurrence of CP-VI (left panel), (2) occurrence of CP-VI that returned to baseline values (middle panel), and (3) progressive increase in CP-VI leading to self-extubation. SE is highly sensitive to changes in irregularity during MV.
Optimization of SE settings, Th detection using a repeated holdout cross-validation procedure
Figure 5 shows the procedure used to optimize SE settings and Th for CP-VI detection. We calculated the mean MCC value for each combination of m, r, and Th for all derived features analyzed (SE-Flowmean, SE-Flowmax, SE-Pawmean, and SE-Pawmax). In general, SE-Paw features exhibit much less sensitivity to m parameter selection than SE-Flow features. SE-Flowmax and SE-Pawmax features yielded the highest mean MCC values. The highest MCC values for SE-Flowmax were found for values of m = 2, r equal to 0.2 and 0.3, and Th between 20 and 35%, whereas for SE-Pawmax were found for values of m equal to 3 and 4, r = 0.2, and Th between 25 and 30%. The optimal SE settings for SE-Flowmax were m = 2, r = 0.2, and Th = 25%, and for SE-Pawmax m = 4, r = 0.2, and Th = 30%. As regards the optimal SE settings, SE-Flowmax at Th = 25% (SE-Flowmax25) yielded the highest mean MCC value (0.84) and SE-Pawmax at Th = 30% (SE-Flowmax30) yielded the highest mean MCC value (0.86). Both SE-Flowmax25 and SE-Pawmax30 yielded their highest MCC values in 13 of the 15 repetitions. The sensitivity analysis conducted for the SE-Pawmax and SE-Flowmax features around the optimal value of r = 0.2 is shown in Supplementary Figure S3. Once we had determined the settings that best detected CP-VI, we evaluated the performance of the algorithm in the 15 repetitions of the cross-validation procedure. Figure 6 displays the algorithm’s performance statistics. The median values of all the parameters observed in the optimization subset were slightly higher than those observed in the validation subset (Supplementary Table S1); this is a common consequence of the repeated holdout cross-validation process. The performance of SE-Flowmax25 and SE-Pawmax30 stratified by ventilator modality (grouped into pressure support ventilation and assist-control ventilation modes) is shown in Supplementary Table S2.
Repeated holdout cross-validation process for optimization of sample entropy (SE) settings and threshold (Th) for the detection of complex patient-ventilator interactions. We calculated the mean Matthews correlation coefficient (MCC) for each derived feature analyzed and each combination of m (1 to 20), r (0.1, 0.2, 0.3, and 0.4 times the SD of each sliding window), and Th (15%, 20%, 25%, 30%, 35%, 40%, 45%, and 50%) a total of 15 times using different randomly selected subsets. The upper panels show the results of the optimization process for SE-airway flow (SE-Flow), and the lower panels show the results for SE-airway pressure (SE-Paw). The color bar in each subplot shows the mean MCC scale, where values near 1 indicate more robust and consistent results. The MCC was positive in all cases. The black dot in each subplot indicates the combination that yielded the maximum mean MCC.
Performance statistics for SE-Flowmax25 (m = 2 and r = 0.2) and SE-Pawmax30 (m = 4 and r = 0.2) for detecting CP-VI. Boxplots of (a) Matthews correlation coefficient (MCC), (b) sensitivity (Se), (c) specificity (Sp), (d) accuracy (Acc), (e) positive predictive value (PPV), and (f) negative predictive value (NPV) from 15 repetitions during optimization (white) and 15 repetitions during validation (gray). The red dot represents the mean value.
For comparative purposes, we also carried out the procedure for optimizing SE settings and Th over the unfiltered SE series. The Supplementary Methods and the Supplementary Figure S2 show the results obtained in this case.
Discussion
Our automatic algorithm for detecting CP-VI from ventilator signals proved highly sensitive and specific in individual patients. Using non-linear analysis of SE to measure irregularity and randomness in the entire set of physiological Flow and Paw signals, the algorithm compared data from different periods in each patient’s interaction with the ventilator to detect CP-VI. In our analyses the maximum changes of SE in both Flow and Paw signals yielded the most accurate results at different thresholds and settings. The most accurate results for SE-Flowmax were obtained with a threshold of change of 25% with m = 2, r = 0.2, and for SE-Pawmax with a threshold of change of 30% with m = 4 and r = 0.2.
The recognition of the hidden information contained in physiological time series draws attention to the extraordinary complexity of physiological systems49. Several non-linear techniques have been developed to study the irregularity and complexity of these physiomarkers18,23,50,51,52,53. Previous studies have used methods based on approximate entropy and sample entropy using breath-to-breath variability and derived indices19,23,32,33,34, which relies on the detection of the appropriate respiratory cycle.
The main advantage of our approach is that it does not require the detection of each single breathing cycle to measure irregularity in Flow and Paw waveforms and thus identify the development of a CP-VI. This approach makes a fundamentally different assumption about where complexity occurs in the physical signal, focusing on transient Flow and Paw complexity rather than breath-to-breath complexity in order to accurately identify changes in the respiratory rate and asynchronies which by their nature are transient and time-limited.
To our knowledge, no recommendations are currently available for the estimation of respiratory dynamics by applying an entropy approach to the entire dataset of Flow and Paw tracings during MV23,52. Recently, Sá et al.37, used SE estimation upon entire Flow signal without optimized parameters. Thus, one important contribution of our study is the description of a set of optimization and validation procedures based on a repeated holdout cross-validation method used in machine-learning models, which we used to obtain the optimal m, r and Th values. Ensuring the robustness of the validation procedure.
Our study also applied a personalized threshold to determine the occurrence of a CP-VI event based on a proportional change from the patient’s own baseline value, which is continuously updated. Continuous predictive analytics monitoring achieves early detection of changes in status over time in previously stable patients. Keim-Malpas et al.41 recently suggested that an absolute threshold of change from baseline values may not be clinically significant in real-world settings and could lead to a high rate of false-positives in patients with high baseline values54. In our study, thresholds of change of 25% and 30% from SE-Flowmax and SE-Pawmax respectively, proved to be the most accurate for CP-VI detection. The optimization procedure found that r = 0.2 is suitable for detecting CP-VI events using SE-Flowmax (m = 2, Th = 25%) or SE-Pawmax (m = 4, Th = 30%) features. Additionally, the sensitivity analysis indicates that r = 0.2 proved to be a more robust local maximum for SE-Flowmax feature. This might suggest that the algorithm predictions seems to be not influenced by small changes in underlying unknown parameters (i.e., different dataset, different measurement equipment or ventilator waveforms) when using SE-Flowmax (m = 2, r = 0.2, Th = 25%), and therefore, could be a more suitable feature than SE-Pawmax (m = 4, r = 0.2, Th = 30%).
Interestingly, both SE-Flowmax25 and SE-Pawmax30 performed well in detecting CP-VI in Assist-Control Ventilation, while SE-Flowmax25 performed slightly better than SE-Pawmax30 in Pressure Support Ventilation mode. The reason for the latter finding may be that during PSV the pressure is constant, and it is the flow waveform that exhibits more changes in accordance with patient’s demand and the mechanical properties of the diseased lung. However, due to the small sample size these sub-analysis results should be interpreted with care, and further research is needed.
Our study has several limitations. First, our algorithm responds to changes in the respiratory rate based on transient changes of Flow and Paw waveforms detected by SE, but not on inspiratory effort. This means that respiratory drive, the intensity of the neural output from the respiratory center that regulates the magnitude of inspiratory effort55, may not have been fully assessed15,56,57. Unfortunately, although many techniques have been proposed55,58,59,60 none have been implemented at the bedside to monitor drive and effort. Our proposed algorithm does not include measurements of effort; nevertheless, whenever a diaphragmatic contraction occurs unassisted by the ventilator, and an asynchrony develops our algorithm is able to detect it.
Second, although our method does not rely on the detection of breathing cycles to measure irregularity and is based on changes in SE of Flow and Paw waveforms, none of the features deriving from breath-to-breath variability were considered. Therefore, their potential importance in detecting CP-VI is yet to be assessed.
Third, while the dataset used for the repeated hold out cross-validation method was paired between segments with and without CP-VI, most of them were from tracings of patients who self-extubate, in whom the occurrence of events of poor patient-ventilator interactions is highly unpredictable. For that reason, the clinical meaning of CP-VI in critically ill patients is yet to be determined and requires more research. Additionally, in the current study we have only examined SE, and other promising measures of entropy may also provide adequate diagnostic tool. For instance, multiscale entropy analysis61,62, Fuzzy approximate entropy63, conditional entropy64 and distribution entropy65 could be others potentially useful entropy measures to be investigated.
Finally, we did not analyze data from proportional modes of MV. Thus, although it is tempting to speculate that ventilatory modes that adapt to patients’ efforts and variability might induce higher changes in SE, the performance of our algorithm in patients ventilated in these modes may differ substantially, and it should not be implemented in these modes until validated by future research.
Conclusion
Our non-invasive method based on SE measurement of Paw and Flow is able to detect CP-VI, defined as the occurrence of transient asynchronies and changes in the respiratory rate, with high accuracy. Clinical relevance and usefulness of identifying Complex Patient-Ventilator Interactions in different clinical scenarios deserves to be explored.
Data availability
The datasets generated and analyzed in the current study are available from the corresponding author on reasonable request.
Change history
09 November 2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Blanch, L. et al. Asynchronies during mechanical ventilation are associated with mortality. Intensive Care Med. 41, 633–641 (2015).
Thille, A. W., Rodriguez, P., Cabello, B., Lellouche, F. & Brochard, L. Patient-ventilator asynchrony during assisted mechanical ventilation. Intensive Care Med. 32, 1515–1522 (2006).
Rué, M. et al. Bayesian joint modeling of bivariate longitudinal and competing risks data: an application to study patient-ventilator asynchronies in critical care patients. Biom. J. 59, 1184–1203 (2017).
Vaporidi, K. et al. Clusters of ineffective efforts during mechanical ventilation: impact on outcome. Intensive Care Med. 43, 184–191 (2017).
Beitler, J. R. et al. Quantifying unintended exposure to high tidal volumes from breath stacking dyssynchrony in ARDS: the BREATHE criteria. Intensive Care Med. 42, 1427–1436 (2016).
de Haro, C. et al. Double cycling during mechanical ventilation: frequency, mechanisms, and physiological implications. Crit. Care Med. 46, 1385–1392 (2018).
De Wit, M. et al. Ineffective triggering predicts increased duration of mechanical ventilation. Crit. Care Med. 37, 2740–2745 (2009).
Wysocki, M. et al. Reduced breathing variability as a predictor of unsuccessful patient separation from mechanical ventilation. Crit Care Med 34, 2076–2083 (2006).
Blanch, L. et al. Validation of the Better Care® system to detect ineffective efforts during expiration in mechanically ventilated patients: a pilot study. Intensive Care Med. 38, 772–780 (2012).
Marchuk, Y. et al. Predicting patient-ventilator asynchronies with hidden Markov models. Sci. Rep. 8, 1–7 (2018).
Sottile, P. D., Albers, D., Higgins, C., Mckeehan, J. & Moss, M. M. The association between ventilator dyssynchrony, delivered tidal volume, and sedation using a novel automated ventilator dyssynchrony detection algorithm. Crit. Care Med. 46, e151–e157 (2018).
Tobin, M. J., Alex, C. G. & Fahey, P. J. Fighting the ventilator. in Principles and Practice of Mechanical Ventialtion (ed. Tobin, M. J.) 1121–1136 (2006).
Tobin, M. J. et al. The pattern of breathing during successful and unsuccessful trials of weaning from mechanical ventilation. Am. Rev. Respir. Dis. 134, 1111–1118 (1986).
Tobin, M. J., Perez, W., Guenther, S. M., D’Alonzo, G. & Dantzker, D. R. Breathing pattern and metabolic behavior during anticipation of exercise. J. Appl. Physiol. 60, 1306–1312 (1986).
Tobin, M. et al. Variability and timing of resting respiratory in healthy subjects drive. J. Appl. Physiol. 65, 309–317 (1988).
Benchetrit, G. Breathing pattern in humans: diversity and individuality. Respir. Physiol. 122, 123–129 (2000).
Godin, P. & Buchman, T. Uncoupling of biological oscillators: a complementary hypothesis concerning the pathogenesis of multiple organ dysfunction syndrome. Crit. Care Med. 24, 1107–1116 (1996).
Pincus, S. M. Greater signal regularity may indicate increased system isolation. Math. Biosci. 122, 161–181 (1994).
White, C. E. et al. Lower interbreath interval complexity is associated with extubation failure in mechanically ventilated patients during spontaneous breathing trials. J. Trauma 68, 1310–1316 (2010).
Dong, X. et al. An improved method of handling missing values in the analysis of sample entropy for continuous monitoring of physiological signals. Entropy 21, 274 (2019).
Martínez-Cagigal, V., Santamaría-Vázquez, E. & Hornero, R. Asynchronous control of P300-based brain–computer interfaces using sample entropy. Entropy 21, 230 (2019).
Su, C. et al. A comparison of multiscale permutation entropy measures in on-line depth of anesthesia monitoring. PLoS ONE 11, 1–22 (2016).
Richman, J. S. & Moorman, R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Hear. Circ. Physiol 278, 2039–2049 (2000).
Sarlabous, L. et al. Efficiency of mechanical activation of inspiratory muscles in COPD using sample entropy. Eur. Respir. J. 46, 1808–1811 (2015).
Sarlabous, L. et al. Electromyography-based respiratory onset detection in COPD patients on non-invasive mechanival ventilation. Entropy 21, 258 (2019).
Alcaraz, R. & Rieta, J. J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal. Process. Control 5, 1–14 (2010).
Abásolo, D., Hornero, R., Espino, P., Álvarez, D. & Poza, J. Entropy analysis of the EEG background activity in Alzheimer’s disease patients. Physiol. Meas. 27, 241–253 (2006).
Al-angari, H. M. & Sahakian, A. V. Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome. IEEE Trans. Biomed. Eng. 54, 1900–1904 (2007).
Lake, D. E. et al. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Regul. Integr. Comp. Physiol. 283, 789–797 (2002).
Yoo, C. S. et al. Automatic detection of seizure termination during electroconvulsive therapy using sample entropy of the electroencephalogram. Psychiatry Res. 195, 76–82 (2012).
El-Khatib, M., Jamaleddine, G., Soubra, R. & Muallem, M. Pattern of spontaneous breathing: potential marker for weaning outcome: Spontaneous breathing pattern and weaning from mechanical ventilation. Intensive Care Med. 27, 52–58 (2001).
Engoren, M. Approximate entropy of respiratory rate and tidal volume during weaning from mechanical ventilation. Crit. Care Med. 26, 1817–1823 (1998).
Papaioannou, V. E., Chouvarda, I. G., Maglaveras, N. K. & Pneumatikos, I. A. Study of multiparameter respiratory pattern complexity in surgical critically ill patients during weaning trials. BMC Physiol. 11, 2 (2011).
Papaioannou, V. E., Chouvarda, I., Maglaveras, N., Dragoumanis, C. & Pneumatikos, I. Changes of heart and respiratory rate dynamics during weaning from mechanical ventilation: a study of physiologic complexity in surgical critically ill patients. J. Crit. Care 26, 262–272 (2011).
Bien, M. Y. et al. Breathing pattern variability: a weaning predictor in postoperative patients recovering from systemic inflammatory response syndrome. Intensive Care Med. 30, 241–247 (2004).
Brochard, L. Breathing: does regular mean normal?. Crit. Care Med. 26, 1773–1774 (1998).
Sá, P. M., Castro, H. A., Lopes, A. J. & Melo, P. L. Entropy analysis for the evaluation of respiratory changes due to asbestos exposure and associated smoking. Entropy 21, 225 (2019).
Tobin, M. J. Advances in mechanical ventilation. N. Engl. J. Med. 344, 1986–1996 (2001).
Cohen, C. A., Zagelbaum, G., Gross, D. & Ph, D. Clinical manifestations of lnspiratory muscle fatigue. Am. J. Med. 73, 308–316 (1982).
Epstein, S. K., Nevins, M. L. & Chung, J. Effect of unplanned extubation on outcome of mechanical ventilation. Am. J. Respir. Crit. Care Med. 161, 1912–1916 (2000).
Keim-Malpass, J., Clark, M. T., Lake, D. E. & Moorman, J. R. Towards development of alert thresholds for clinical deterioration using continuous predictive analytics monitoring. J. Clin. Monit. Comput. (2019).
Fleiss, J. L., Cohen, J. & Everitt, B. Large sample standard errors of Kappa and weighted Kappa. Psychol. Bull. 72, 323–327 (1969).
Matthews, B. W. Comparison of the predicted and observed secondary struccture of T4 phagel lysozyme. Biochim. Biophys. Acta 405, 442–451 (1975).
Chaudhary, K., Nagpal, G., Dhanda, S. K. & Raghava, G. P. S. Prediction of Immunomodulatory potential of an RNA sequence for designing non-toxic siRNAs and RNA-based vaccine adjuvants. Sci. Rep. 6, 1–11 (2016).
Johnstone, D., Milward, E. A., Berretta, R. & Moscato, P. Multivariate protein signatures of pre-clinical Alzheimer’s disease in the Alzheimer’s disease neuroimaging initiative (ADNI) plasma proteome dataset. PLoS ONE 7, e34341 (2012).
Boughorbel, S., Jarray, F. & El-anbari, M. Optimal classifier for imbalanced data using Matthews correlation coefficient metric. PLoS ONE 12, 1–17 (2017).
Estrada, L., Torres, A., Sarlabous, L. & Jan, R. Improvement in neural respiratory drive estimation from diaphragm electromyographic signals using fixed sample entropy. IEEE J. Biomed. Heal. Informatics 20, 476–485 (2016).
Estrada, L., Torres, A., Sarlabous, L. & Jané, R. Influence of parameter selection in fixed sample entropy of surface diaphragm electromyography for estimating respiratory activity. Entropy 19, 460 (2017).
Buchman, T. G. The community of the self. Nature 420, 246–251 (2002).
Pincus, S. M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci U. S. A. 88, 2297–2301 (1991).
Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 5, 110–117 (1995).
Suki, B., Bates, J. H. T. & Frey, U. Complexity and emergent phenomena. Compr. Physiol. 1, 995–1029 (2011).
Seely, A. J. E. et al. Proceedings from the Montebello round table discussion. Second annual conference on complexity and variability discusses research that brings innovation to the bedside. J. Crit. Care 26, 325–327 (2011).
Sullivan, B. A. et al. Early heart rate characteristics predict death and morbidities in preterm infants. J. Pediatr. 174, 1–6 (2016).
Vaporidi, K. et al. Respiratory drive in critically Ill patients: pathophysiology and clinical implications. Am. J. Respir. Crit. Care Med. 201, 20–32 (2019).
Georgopoulos, D. & Roussos, C. Control of breathing in mechanically ventilated patients. Eur. Respir. J. 9, 2151–2160 (1996).
Georgopoulos, D. Effects of mechanical ventilation on control of breathing. in Principles and Practice of Mechanical Ventialtion (ed. Tobin, M. J.) 805–820 (2013).
Laghi, F. Assessment of respiratory output in mechanically ventilated patients. Respir. Care Clin. N. Am. 11, 173–199 (2005).
Tobin, M. J., Laghi, F. & Jubran, A. Ventilatory failure, ventilator support, and ventilator weaning. Compr. Physiol. 2, 2871–2921 (2012).
Bertoni, M. et al. A novel non-invasive method to detect excessively high respiratory effort and dynamic transpulmonary driving pressure during mechanical ventilation. Crit. Care 23, 1–10 (2019).
Raoufy, R. M., Ghafari, T. & Mani, A. R. Complexity analysis of respiratory dynamics Mohammad. Am. J. Respir. Crit. Care Med. 196, 247–248 (2017).
Costa, M. D. & Goldberger, A. L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 17, 1197–1203 (2015).
Chen, W., Zhuang, J., Yu, W. & Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 31, 61–68 (2009).
Porta, A. et al. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow. Biol. Cybern. 78, 71–78 (1998).
Li, P. et al. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 53, 77–87 (2015).
Acknowledgments
This work was funded by projects PI16/01606, integrated in the Plan Nacional de R+D+I and co-funded by the ISCIII- Subdirección General de Evaluación y el Fondo Europeo de Desarrollo Regional (FEDER). RTC-2017-6193-1 (AEI/FEDER UE). CIBER Enfermedades Respiratorias, and Fundació Parc Taulí.
Author information
Authors and Affiliations
Contributions
Study concept and design: L.S., J.A.E., R.M., C.d.H., and L.B. Data acquisition: L.S., J.A.E., C.d.H., C.S., M.B., G.G., A.O., and R.F. Data processing and interpretation: L.S., J.A.E., R.M., J.L.A., R.F., and L.B. Statistical analysis: L.S., R.M., and M.R. Figure preparation: L.S., J.A.E. and R.M. Drafting of the manuscript: L.S., J.A.E., and R.M. Revision of manuscript for important intellectual content: L.S., J.A.E., R.M., C.d.H., J.L.A., R.F., and L.B. Study supervision: L.S., J.A.E., R.M., C.d.H., A.O., R.F., and L.B. Data access and responsibility: L.B. had full access to all of the data in the study and takes full responsibility for the integrity of the data and the accuracy of the data analysis. L.S. and J.A.E. contributed equally to the study. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
L.S., J.A.E., R.M., C.d.H., J.L.A, and L.B. have been named in a provisional European patent application number EP19383116 owned by Corporació Sanitària Parc Taulí: “A device and method for respiratory monitoring in mechanically ventilated patients”. L.B. is inventor of a US patent owned by Corporació Sanitària Parc Taulí: “Method and system for managed related patient parameters provided by a monitoring device”, US Patent No. 12/538,940. L.B. own stock options of BetterCare S.L., a research and development spinoff of Corporació Sanitària Parc Taulí. The remaining authors have no conflicts of interest.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sarlabous, L., Aquino-Esperanza, J., Magrans, R. et al. Development and validation of a sample entropy-based method to identify complex patient-ventilator interactions during mechanical ventilation. Sci Rep 10, 13911 (2020). https://doi.org/10.1038/s41598-020-70814-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-70814-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.