Abstract
There is a heavy burden associated with influenza including all-cause hospitalization as well as severe cardiovascular and cardiorespiratory events. Influenza associated cardiac events have been linked to multiple biological pathways in a human host. To study the contribution of influenza virus infection to cardiovascular thrombotic events, we develop a dynamic model which incorporates some key elements of the host immune response, inflammatory response, and blood coagulation. We formulate these biological systems and integrate them into a cohesive modelling framework to show how blood clotting may be connected to influenza virus infection. With blood clot formation inside an artery resulting from influenza virus infection as the primary outcome of this integrated model, we demonstrate how blood clot severity may depend on circulating prothrombin levels. We also utilize our model to leverage clinical data to inform the threshold level of the inflammatory cytokine TNFα which initiates tissue factor induction and subsequent blood clotting. Our model provides a tool to explore how individual biological components contribute to blood clotting events in the presence of influenza infection, to identify individuals at risk of clotting based on their circulating prothrombin levels, and to guide the development of future vaccines to optimally interact with the immune system.
Similar content being viewed by others
Introduction
Influenza infection is associated with severe cardiovascular and cardiorespiratory events1,2,3,4,5. An increased risk of acute myocardial infarction has been observed within 7 days of influenza infection1. Several in vivo experiments in humans and animals found extensive and profound procoagulant effects due to influenza infection6. A positive association between influenza infection and stroke has also been observed7. Biological mechanisms explaining the various cardiovascular events associated with influenza have recently been proposed; however, a quantitative framework capturing these biological mechanisms to acute myocardial infarction (AMI) and stroke has not yet been established7. A model that can assist in predicting the risk of AMI and stroke arising from influenza infection is important to inform prevention and treatment strategies (such as vaccination) and enhance risk-assessment capabilities. This technical challenge offers an opportunity for mathematical modelling to play a role in filling this key knowledge gap.
Mathematical models describing the viral dynamics of influenza infection incorporate a variety of biological detail and data utilization, incorporating either in vitro or in vivo data sets (for a comprehensive recent review, see8). Similarly, extensive research has gone into the modelling, experimentation, and study of the dynamics of blood coagulation9,10,11,12,13,14,15 (for a review, see16). Despite the connectedness of the post-infection viral dynamics, immune response, and blood coagulation, no modeling study has been conducted to link these systems together. Here, we develop a comprehensive mathematical model capturing the major components of the probable biological mechanisms, with an objective of linking influenza infection to thrombotic cardiovascular events. This framework incorporates the modelling and synthesis of three key events; immune response to influenza infection, subsequent inflammation, and blood coagulation. We have identified tissue factor (TF) as the critical component linking inflammation to coagulation17,18. Hence, we model the induction of tissue factor arising from influenza virus infection. Our model incorporates this critical factor, TF, to establish a quantitative link between influenza infection and its effects triggering the blood coagulation cascade. As coagulation also plays a key role in arterial thrombosis, our integrated framework develops a model and analysis establishing linkage between influenza infection and arterial thrombosis19.
In light of the observed relationships between influenza infection and outcomes such as stroke and AMI1, we focus in this study on blood clots forming within arteries (arterial thrombosis). Although there are several pathways by which influenza may induce cardiovascular events, we focus on blood clot severity as a proxy for AMI or stroke risk19. Hence the outcome of our model is the size of arterial blockage which may form following influenza infection. Through the modelling of the crucial biological components arising from acute infection, such as IFN-I, CD8+ T Cells, TNF\(\alpha\), thrombin, and inflammatory cytokines8, we obtain several key qualitative and quantitative results. We estimate the threshold level of tissue factor (III) for which, if surpassed, a culprit atherosclerotic plaque will be disrupted and formation of a blood clot within an artery will occur. Furthermore, our model predicts that the resulting blood clot size following influenza infection is positively associated with circulating prothrombin ([II]) levels, which are affected by various genetic conditions and vary person-to-person20.
The rest of the paper is organized as follows: we present the key study results including an overview of the mathematical model structure, model simulations illustrating the key events leading to a blood clot, as well as the effects of circulating prothrombin levels on blood clot size. We also demonstrate how our model may provide an estimate for the threshold amount of inflammation (for which we use TNF\(\alpha\) as a proxy) required to initiate blood coagulation. Zooming out, we discuss several applications of our work as well as underlying assumptions and limitations of the mathematical model developed herein. In addition, we outline a number of opportune directions for future research.
Results
Formulation of model framework to model a linkage between influenza infection and blood clotting
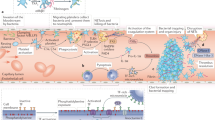
The backbone of our study is a mathematical model, which we leverage to study blood clotting within an artery as a consequence of influenza infection. We modelled the infection process using a system of ordinary differential equations (ODEs). In the model, we capture the viral infection process consisting of the dynamics of viral load, uninfected target epithelial cells, and infected target epithelial cells. Our model also describes the immune and inflammatory responses to infection. In particular, our model includes type I interferon (IFN-I), comprising a key portion of the innate immune response and CD8+ T cells, a key component of the adaptive immune system. We link inflammation to blood coagulation and subsequent clotting through the modelling of TF, a distinguishing feature of this study. Within this modelling framework, blood coagulation initiates the disruption of a culprit atherosclerotic plaque. The biological systems involved in key events leading to clotting are depicted in Fig. 1A. A schematic of the model structure illustrating the key model components and their relationships is shown in Fig. 1B.
Diagrams of Model (1): (A) Key events and systems involved in the possible disruption of a culprit atherosclerotic plaque and subsequent blood clot formation following influenza infection. Figure created using Microsoft PowerPoint, Version 2006 (https://www.microsoft.com/en-ca/microsoft-365/powerpoint). (B) Schematic diagram illustrating the model variables and primary relationships between them. Solid lines represent direct production or stimulation as assumed in model (1). Dotted lines represent enhanced production or synergism (i.e., the enhanced production of TNF \(\alpha\) in the presence of IL-10). See Methods for details of model development and its formulation. Figure created using BioRender (https://biorender.com/).
Model simulation results
Model consistency and time dynamics
Overall, the viral dynamics and resulting immune responses against influenza inflammation generated from our model are in agreement with existing models of similar scope21,22. The integrated model dynamics corresponding to a single influenza infection and the possible subsequent clotting events are displayed in Supplementary Figure S1 and S2 in the Supplementary Information (SI).
Estimation of threshold amount of TNF\(\alpha\) to induce tissue factor
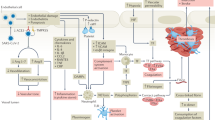
Using our mathematical model, we leverage recent clinical observations1 to estimate the threshold amount of the inflammatory cytokine TNFα required to initiate TF induction and subsequent clotting at the site of a vulnerable atherosclerotic plaque. In particular, we estimate this concentration of TNFα to be TIII = 27.36 pg/ml. This threshold TIII may provide a benchmark for determining a patient’s risk of cardiovascular event, which we elaborate on the potential clinical applications of TIII in the discussion. We also highlight its key role in Fig. 2; once TF is induced, the blood coagulation cascade occurs, and blood clot formation begins. For the details and strategy for estimating TIII see Supplementary Information (SI), section S1.2.
Figure illustrates key events leading to a blood clot: (A) TNF \(\alpha\) induced from influenza infection rises above the threshold level \({T}_{III}\), resulting in the induction of tissue factor (TF) expression at the site of a vulnerable atherosclerotic plaque (B). With TF present (C, D), the blood coagulation cascade begins and, simultaneously, prothrombin is consumed while thrombin is generated. TF exposure and thrombin presence allow for the formation of a blood clot (E1 and E2). This blood clotting event results in approximately 0.45% arterial blockage. (E2) The clot’s percentage obstruction over the course of 1,440 min (24 h) period. The two distinct growth phases of the blood clot are made apparent over this 24-h span (see “Estimation of threshold amount of TNFα to induce tissue factor” section for interpretation).
We also note that atherosclerotic plaque disruption and blood clotting may not necessarily occur following influenza infection. We capture this key fact with mathematical model (1); not all trajectories following infection result in blood clot formation. Many of the model parameters (representing rates of underlying biological mechanisms, cell counts, concentrations, and other biological properties) are implemented as ranges, rather than single values. Ranges are used to reflect estimated uncertainty in their true values. Therefore, each model run will produce different results (or trajectories).
Next, we illustrate the clotting event and the connecting links from inflammation to coagulation. When TNFα levels rise above the threshold TIII, TF expression is induced and the blood coagulation cascade begins, resulting in the disruption of a culprit atherosclerotic plaque and subsequent blood clot formation. We highlight this defining feature of model (1) in Fig. 2 and note that blood clots are formed rapidly following thrombin generation. The resulting clotting time is about 75 min (Fig. 2 (E1)), in agreement with prior in vitro experimental works10. We also depict blood clot size over the course of 1,440 min (24 h) to illustrate the long-term clotting behavior (Fig. 2 (E2)). Following initial blood clot formation there is a local accumulation of procoagulants such as TNFα and IL-17, platelets, and these factors contribute to the continued growth of the blood clot until the growth phase ends23. The model trajectories reflect this biphasic behavior as following blood clot formation, procoagulants TNFα and TF levels increase in time. The growth phase end is a result of thrombin depletion.
Effect of circulating prothrombin levels on the artery blockage
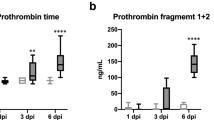
One prediction of model (1) is the positive association between blood clot severity and circulating prothrombin levels (illustrated in Fig. 3). High prothrombin levels have been correlated with a risk of arterial thrombosis and are also affected by genetic conditions, hence vary person-to-person20. We show how the blood clot severity, as predicted by model (1), depends on circulating prothrombin levels. However, the model-predicted likelihood of blood clotting formation following influenza infection remains constant. An influenza infection may not induce blood clot formation as TNF\(\alpha\) can remain below the threshold \({T}_{III}\) post-infection. In other words, the individual’s inflammatory state arising from infection may not be sufficient to disrupt an existing atherosclerotic plaque. We also note that a positive association between the magnitude of the thrombin peak and prothrombin levels have been observed20 and model (1) is in agreement, also capturing this association.
Effect of circulating prothrombin levels on clot size: For a brief description of the events leading to a blood clot in Panels (A–E), see Fig. 2. Panels (C, D) Initial values of prothrombin influence the size of the thrombin peak. This results in blood clot size dependence on the initial prothrombin level. Prothrombin levels in blood vary person-to-person and the risk of blood clot formation may depend accordingly20. Model (1) may provide the ability to quantify these differences in severity and subsequent risk. Panel (E) Resulting blood clot sizes due to varying circulating prothrombin levels. As initial prothrombin level increases, resultant blood clot size increases. As a result, model (1) may be used to quantify the role of prothrombin in determining blood clot severity.
Discussion
In this work, we present the development and simulation of a mathematical model that connects influenza virus infection to subsequent blood coagulation, blood clotting risk, and blood clotting severity. Our aim is to lay a foundation by modelling the risk of cardiovascular thrombotic events resulting from acute influenza infection, incorporating mechanistic details of the process. This foundational framework features modularity allowing for augmentation, expansion and future study.
Our primary contributions in terms of modelling are the connections linking the inflammatory response and blood coagulation. The model dynamics presented agree with several existing studies and the model produces biologically tractable viral trajectories21,22. Further, the blood clotting behavior generated from our integrated model captures many qualitative and quantitative features of in vitro experimentation by incorporating mechanistic biological detail10. Procoagulant effects observed in vivo in terms of their association with influenza infection are consistent with the model simulations6. This modelling framework is amenable to risk assessment and may be used to quantify the effects of influenza vaccination on subsequent blood clotting event risk and severity. This mathematical model may also be used to identify key parameters which contribute (positively or negatively) to blood clotting events (e.g. with sensitivity analysis). In other words, we may use the model to infer which particular biological actions/feedbacks are most crucial to blood clotting. One consequence of the model developed herein is that regulating TNFα also impacts the likelihood of developing a blood clot. As a result, we postulate that vaccine-induced TNFα regulation may reduce the chance of blood clot formation. Specifically, vaccines that aim to induce an immune response resulting in the production of antibodies that neutralize inflammatory cytokines (e.g. TNFα, IL-1β) may be weighed in terms of their impact on risk of cardiovascular events24,25,26. Currently, a phase I clinical trial of a vaccine targeting IL-1β has been completed as well as a phase IIa clinical trial for an anti-TNF vaccine25,26. In this light, our model may be used to quantify the effects of anti-cytokine therapy (e.g. anti-TNF therapeutics for rheumatoid arthritis) on the risk of cardiovascular events. Anti-inflammatory drugs exist; however, have several drawbacks making vaccines a potential attractive option in the future27. In addition, vaccines or adjuvants aiming to induce a T-cell response may be weighed in terms of the resulting cardiovascular event risk. Overall, this framework may prove to be useful for guiding ideal vaccine design and conducting scenario analyses. We also note that the model and parameter estimates may be implemented and made available in a user-friendly format (e.g. software package, web-based tool, etc.).
This model quantifies the size of a blood clot resulting from influenza infection. We restrict our study scope to arterial thrombosis arising from acute infection, as we are interested in quantifying AMI and stroke risk. We do note that our modelling framework is also amenable to the study of venous thrombosis. Whether the size of the blood clot translates to risk of thrombotic cardiovascular events (e.g. AMIs) is not clear at the present time. Similarly, the extent of these effects of blood clot size on thrombotic cardiovascular event risk has not yet been established to our best knowledge. Currently, the relationship between blood coagulation and blood clotting is informed using experimental in vitro data measuring clot size within a flow chamber and cannot exhibit cardiovascular events. On the other hand, humans can exhibit observable cardiovascular events; however, to our best knowledge we do not have the ability to dynamically and consistently measure clot size within a blood vessel or artery in a living patient. For these reasons, a quantitative link between blood clot size and thrombotic cardiovascular risk may not be tractable at the present time, although it is an important subject for future studies.
A key result of our work is the estimation of the threshold TNFα level required to initiate TF expression, TIII. We estimate TIII to be 27.36 pg/ml, which lies above the average clinical measurements of normal adult subjects with no significant illnesses (TNFα = 0.7 ± 0.2 pg/ml, n = 28 subjects)28. This threshold, TIII, also may distinguish TNFα levels between control adults with mild or moderate infection (TNFα = 14.80 ± 4.74 pg/ml) and patients with chronic liver failure (TNFα = 53 ± 74.4 pg/ml in surviving patients and TNFα = 87.76 ± 91.38 pg/ml among non-survivors)29. These clinical observations serve as a form of validation, as TIII may lie between TNFα levels of healthy individuals and those at-risk individuals with more severe complications (e.g., chronic liver failure). This threshold may be used in a clinical setting using patient's TNFα measurements taken over time as a proxy for risk. An observed increase or decrease in TNFα measurements may indicate cardiovascular distress and systemic inflammation, hence a change in risk of blood clotting may be inferred from this systemic measurement. In this sense, TNFα and threshold TIII may be used as a biomarker for cardiovascular risk. We also note that this threshold may depend on IFN-I levels, IL-1β, etc.
There are several simplifications made within this study to develop and illustrate our framework. The extrinsic blood coagulation system involves many additional interactions and components, which should be considered in future studies. Realistically blood clotting depends on spatial heterogeneity in blood plasma, blood flow velocity, fibrin, Factor IXa, Factor Xa, etc.20,28. We conducted our study for the case where atherosclerotic plaques are static elements, in fact they are complex and dynamic structures whose cellular and extracellular make-up may significantly affect the risk of cardiovascular atherosclerotic events30. In our study, TF is induced primarily by TNFα and IFN-I, with synergism from thrombin. TF induction is inhibited and regulated by many inflammatory cytokines, chemokines, and enzymes that should be considered in future studies31,32. In this study, we focus on cardiovascular outcomes immediately following acute influenza infection. As a result, we make a simplifying assumption that prothrombin is not replenished naturally and therefore, a host may exhibit a maximum of one clotting event. In the current work, we assumed that when sufficient concentration of TNF\(\alpha\) is present, which we take as proxy for inflammation, then TF is induced resulting in the disruption of an existing atherosclerotic plaque and subsequent blood clotting occurs. Lastly, we assume that a minimum amount of TNFα is required to induce TF. Once this amount of TNFα exceeds this threshold, TF is exposed. We expect the magnitude of such a threshold as TIII to vary based on the health status of individuals which may be verified clinically. We expect that this threshold is higher for young individuals compared to older individuals or those with underlying health conditions, who may be more susceptible to blood clotting. The alternative case is also possible; older adults and those with underlying health conditions may have a higher threshold. At-risk individuals likely have high resting TNFα levels, perhaps even higher than the 27.36 pg/ml threshold. Although this mechanistic study has neglected many components and interactions involved in the complex immune response, inflammatory response, and blood coagulation systems, we believe that we have established a flexible framework amenable to further augmentation and modification to account for further biological realism.
Future directions
The existing model (1) may be augmented to incorporate specific biomarkers for inflammation (e.g. IL-6), matrix metalloproteinases (MMPs), neutrophil activity, and platelet activity. The sensitivity of the primary biological actions and feedbacks impacting these markers on systemic inflammation and clot risk may be explored. Clinical measurements of these markers may also be used to assist with further study. Along these lines, we note that many model variables are proteins and cells which are routinely measured and there is a large amount of quantitative data for. In future studies, we shall use these cell and protein counts for model calibration, testing, and validation. We will add more physiological realism to the blood coagulation and blood clotting submodels, including feedbacks within the blood clot formation and inflammatory system13,33. Specifically, interleukins and TNFα may be induced as a result of blood clot formation. Also, this model and framework may be coupled to spatially heterogeneous coagulation and clotting models (e.g. 23,30,34,35,36). Future work may aim to estimate \({T}_{III}\) based on a groups of varying health status, such as high-risk groups. The impacts of pre-existing TNF\(\alpha\) on the timing and likelihood of blood clot formation may also be explored in follow-up works. Lastly, current influenza vaccines mainly aim at generating antibody responses to the virus, but a vaccine that yields flu-protective T cells, which would provide longer lasting memory responses, is lacking37,38. Therefore, this study may provide new insights that inform new strategies to develop more efficient vaccines that drive flu-protective T cell responses and novel antiviral therapies for influenza infections.
Methods
Model development
We develop the mathematical model linking viral infection to the immune and inflammatory response, blood coagulation, and subsequent blood clot formation using a system of ordinary differential equations. Based on biological evidence and prior modelling studies, we formulate a set of modelling assumptions to develop Model (1)10,12,15,18,21,22,23,27,31,32,33,34,39,40,41,42,43,44,45,46,47. The model is given below without detailed interpretation and development. The term-by-term mathematical formulation and detailed explanations of model assumptions are given in Section S1.1 in the Supplementary Information (SI). A list of the model variables, and units of measurement are also given in Supplementary Table S2. In this work, a model variable refers to the components of the biological system dynamically evolving over time. The model parameters broadly represent rates which characterize the evolution of the system.
Model (1): A mathematical model describing the influenza infection process and resulting immune response, inflammatory response, blood coagulation, and subsequent blood clotting:
where \(\Sigma_{1} = a_{11} X + a_{12} D\), \(\Sigma_{2} = a_{11} X + a_{12} D + \frac{{a_{21} V}}{{a_{22} + V}}\), and \(R_{F} = \frac{F}{{a_{RF} + F}}\).
Model variables: V = Virus (EID50/ml); T = Target epithelial cells (Cells); I = Infected epithelial cells (Cells); F = Type I interferon (dimensionless (We invite the reader to Supplementary Information (SI) S1.3 explaining the dimensions of IFN-I.)); R = Resistant target epithelial cells (Cells); C = CD8+ T cell (Cells); B = B cell (Cells); L = Interleukin-10 (pg/ml); D = Dead cell (Cells); X = TNF \(\alpha\) (pg/ml) ; M = Macrophage (Cells); K = Chemokines (Cells); [III] = Tissue factor (nM); [IIa] = Thrombin (nM); [II] = Prothrombin (nM); [AT] = Antithrombin (nM); Q = Blood clot size (% arterial blockage).
Data and model parameter estimation
We inform parameters for model (1) using data, existing models, and experimental findings from several sources1,12,21,22,23,27,46,48. We use model parameter values from existing influenza viral dynamics modeling studies21,22, blood coagulation modeling studies12,23. We determine remaining parameters by integrating several additional sources of experimental and clinical data. For the details of parameter estimation see the parameter estimation process in the Supplementary Information (SI) (section S1.2). The model parameters which inform the mathematical model (1) along with their respective ranges, units, and sources are in the Supplementary Information (SI) Supplementary Table S3.
Model simulation
To generate Figs. 2 and 3, Supplementary Figures S1 and S2, we first inform model (1) with parameters from their baseline values in Supplementary Table S3 and initial conditions in Supplementary Table S2. We then solve the corresponding system of ordinary differential equations numerically using Matlab’s ode45, an implementation of the Runge–Kutta method. We consider an uninfected individual at baseline and simulate the infection process numerically. In other words, we consider the system state initially at the disease free equilibrium of model (1) with an initial viral load, reflected in initial conditions shown in Supplementary Table S2 in the Supplementary Information (SI).
Data availability
No datasets were generated or analyzed during the current study.
References
Kwong, J. C. et al. Acute myocardial infarction after laboratory-confirmed influenza infection. N. Engl. J. Med. 378(4), 345–353 (2018).
DiazGranados, C. A. et al. Prevention of serious events in adults 65 years of age or older: A comparison between high-dose and standard-dose inactivated influenza vaccines. Vaccine 33(38), 4988–4993 (2015).
Pesonen, E. Acute myocardial infarction precipitated by infectious disease. Am. Heart J. 101, 512–513 (1981).
Tillett, H. E., Smith, J. W. G. & Gooch, C. D. Excess deaths attributable to influenza in England and Wales: Age at death and certified cause. Int. J. Epidemiol. 12(3), 344–352 (1983).
Blackburn, R., Zhao, H., Pebody, R., Hayward, A. & Warren-Gash, C. Laboratory-confirmed respiratory infections as predictors of hospital admission for myocardial infarction and stroke: Time-series analysis of English data for 2004–2015. Clin. Infect. Dis. 67(1), 8–17 (2018).
Madjid, M., Aboshady, I., Awan, I., Litovsky, S., & Casscells, S. W. Influenza and cardiovascular disease: is there a causal relationship? Texas Heart Inst. J. 31(1), 4–13 (2004), [Online]. Available: https://pubmed.ncbi.nlm.nih.gov/15061620.
Udell, J. A., Farkouh, M. E., Solomon, S. D. & Vardeny, O. Does influenza vaccination influence cardiovascular complications?. Expert Rev. Cardiovasc. Therapy 13(6), 593–596. https://doi.org/10.1586/14779072.2015.1044439 (2015).
Boianelli, A. et al. Modeling influenza virus infection: A roadmap for influenza research. Viruses 7(10), 5274–5304. https://doi.org/10.3390/v7102875 (2015).
Link, K. G. et al. A local and global sensitivity analysis of a mathematical model of coagulation and platelet deposition under flow. PLoS ONE 13(7), e0200917 (2018).
Shibeko, A. M. & Panteleev, M. A. Untangling the complexity of blood coagulation network: Use of computational modelling in pharmacology and diagnostics. Brief. Bioinform. 17(3), 429–439 (2015).
Hockin, M. F., Jones, K. C., Everse, S. J. & Mann, K. G. A model for the stoichiometric regulation of blood coagulation. J. Biol. Chem. 277(21), 18322–18333 (2002).
Arumugam, J. Simplified threshold phenomena in hypo-and hyper-coagulation. arXiv preprint arXiv:1706.00819, (2017).
Govindarajan, V. et al. Impact of tissue factor localization on blood clot structure and resistance under venous shear. Biophys. J. 114(4), 978–991 (2018).
Belyaev, A., Panteleev, M. A. & Ataullakhanov, F. I. Threshold of microvascular occlusion: Injury size defines the thrombosis scenario. Biophys. J. 109(2), 450–456 (2015).
Arumugam, J. & Srinivasa, A. A novel simplified model for blood coagulation: A piecewise dynamical model for thrombin with robust predictive capabilities. arXiv preprint arXiv:1705.07182, (2017).
Fogelson, A. L. & Neeves, K. B. Fluid mechanics of blood clot formation. Annu. Rev. Fluid Mech. 47, 377–403 (2015).
Foley, J. H. & Conway, E. M. Cross talk pathways between coagulation and inflammation. Circ. Res. 118(9), 1392–1408 (2016).
Witkowski, M., Landmesser, U. & Rauch, U. Tissue factor as a link between inflammation and coagulation. Trends Cardiovasc. Med. 26(4), 297–303 (2016).
Corrales-Medina, V. F., Musher, D. M., Shachkina, S. & Chirinos, J. A. Acute pneumonia and the cardiovascular system. Lancet 381(9865), 496–505 (2013).
Wolberg, A. S., Monroe, D. M., Roberts, H. R. & Hoffman, M. Elevated prothrombin results in clots with an altered fiber structure: A possible mechanism of the increased thrombotic risk. Blood 101(8), 3008–3013 (2003).
Price, I. et al. The inflammatory response to influenza A virus (H1N1): An experimental and mathematical study. J. Theor. Biol. 374, 83–93 (2015).
Cao, P. et al. On the role of CD8+ T cells in determining recovery time from influenza virus infection. Front. Immunol. 7, 611 (2016).
Bouchnita, A., Miossec, P., Tosenberger, A. & Volpert, V. Modeling of the effects of IL-17 and TNF-α on endothelial cells and thrombus growth. C.R. Biol. 340(11), 456–473 (2017).
Assier, E., Bessis, N., Zagury, J.-F. & Boissier, M.-C. IL-1 vaccination is suitable for treating inflammatory diseases. Front. Pharmacol. 8, 6 (2017).
Cavelti-Weder, C. et al. Development of an interleukin-1β vaccine in patients with type 2 diabetes. Mol. Ther. 24(5), 1003–1012 (2016).
Durez, P. et al. Therapeutic vaccination with TNF-Kinoid in TNF antagonist-resistant rheumatoid arthritis: A phase II randomized, controlled clinical trial. PLoS ONE 9(12), e113465 (2014).
Clauss, M. et al. Synergistic induction of endothelial tissue factor by tumor necrosis factor and vascular endothelial growth factor: Functional analysis of the tumor necrosis factor receptors. FEBS Lett. 390(3), 334–338 (1996).
Kapadia, S. R. et al. Elevated circulating levels of serum tumor necrosis factor-alpha in patients with hemodynamically significant pressure and volume overload. J. Am. Coll. Cardiol. 36(1), 208–212 (2000).
Page, M. J., Bester, J. & Pretorius, E. The inflammatory effects of TNF-α and complement component 3 on coagulation. Sci. Rep. 8(1), 1812. https://doi.org/10.1038/s41598-018-20220-8 (2018).
Finn, A., Nakano, M., Narula, J., Kolodgie, F. D. & Virmani, R. Concept of vulnerable/unstable plaque. Arterioscl. Thromb. Vasc. Biol. 30(7), 1282–1292 (2010).
Ruf, W. & Riewald, M. Regulation of tissue factor expression. In Madame Curie Bioscience Database [Internet] (Landes Bioscience, Austin, TX, 2000–2013) https://www.ncbi.nlm.nih.gov/books/NBK6620/.
van der Poll, T., de Jonge, E. & ten cate an, H., Cytokines as regulators of coagulation. In Madame Curie Bioscience Database [Internet] (Landes Bioscience, Austin, TX, 2000–2013). https://www.ncbi.nlm.nih.gov/books/NBK6207/.
Owens, A. P. III. & Mackman, N. Tissue factor and thrombosis: The clot starts here. Thromb. Haemost. 104(3), 432 (2010).
Bouchnita, A., Tosenberger, A. & Volpert, V. On the regimes of blood coagulation. Appl. Math. Lett. 51, 74–79 (2016).
Xu, Z., Chen, N., Kamocka, M. M., Rosen, E. D. & Alber, M. A multiscale model of thrombus development. J. R. Soc. Interface 5(24), 705–722 (2007).
Xu, S. et al. Model predictions of deformation, embolization and permeability of partially obstructive blood clots under variable shear flow. J. R. Soc. Interface 14(136), 441 (2017).
Krammer, F. & Palese, P. Advances in the development of influenza virus vaccines. Nat. Rev. Drug Discovery 14(3), 167 (2015).
Grebe, K. M., Yewdell, J. W. & Bennink, J. R. Heterosubtypic immunity to influenza A virus: Where do we stand?. Microbes Infect. 10(9), 1024–1029 (2008).
Pendurthi, U. R., Williams, J. T. & Rao, L. V. M. Inhibition of tissue factor gene activation in cultured endothelial cells by curcumin: Suppression of activation of transcription factors Egr-1, AP-1, and NF-κB. Arterioscler. Thromb. Vasc. Biol. 17(12), 3406–3413 (1997).
Almus, F. E., Rao, L. V. M. & Rapaport, S. I. Functional properties of factor VIIa/tissue factor formed with purified tissue factor and with tissue factor expressed on cultured endothelial cells. Thromb. Haemost. 62(04), 1067–1073 (1989).
Archipoff, G. et al. Heterogeneous regulation of constitutive thrombomodulin or inducible tissue-factor activities on the surface of human saphenous-vein endothelial cells in culture following stimulation by interleukin-1, tumour necrosis factor, thrombin or phorbol ester. Biochem. J. 273(3), 679–684 (1991).
Diamond, S. L. Systems analysis of thrombus formation. Circ. Res. 118, 1348–1362 (2016).
Bastarache, J. A., Sebag, S. C., Grove, B. S. & Ware, L. B. Interferon-γ and tumor necrosis factor-α act synergistically to up-regulate tissue factor in alveolar epithelial cells. Exp. Lung Res. 37(8), 509–517 (2011).
Chu, A. J. Tissue factor, blood coagulation, and beyond: An overview. Int. J. Inflamm. 201, 1 (2011).
Takeya, H., Gabazza, E. C., Aoki, S., Ueno, H. & Suzuki, K. Synergistic effect of sphingosine 1-phosphate on thrombin-induced tissue factor expression in endothelial cells. Blood 102(5), 1693–1700 (2003).
Liu, Y., Pelekanakis, K. & Woolkalis, M. J. Thrombin and tumor necrosis factor α synergistically stimulate tissue factor expression in human endothelial cells regulation through c-Fos and c-Jun. J. Biol. Chem. 279(34), 36142–36147 (2004).
Hamik, A., Setiadi, H., Bu, G., McEver, R. P. & Morrissey, J. H. Down-regulation of monocyte tissue factor mediated by tissue factor pathway inhibitor and the low density lipoprotein receptor-related protein. J. Biol. Chem. 274(8), 4962–4969 (1999).
Steffel, J., Akhmedov, A., Greutert, H., Lüscher, T. F. & Tanner, F. C. Histamine induces tissue factor expression: Implications for acute coronary syndromes. Circulation 112(3), 341–349 (2005).
Brox, J. H., Østerud, B., Bjørrlid, E. & Fenton, J. W. Production and availability of thromboplastin in endothelial cells: The effects of thrombin, endotoxin and platelets. Br. J. Haematol. 57(2), 239–246 (1984).
Deguchi, H. et al. Dilazep, an antiplatelet agent, inhibits tissue factor expression in endothelial cells and monocytes. Blood 90(6), 2345–2356 (1997).
Galdal, K. S., Lyberg, T., Evensen, S. A., Nilsen, E. & Prydz, H. Thrombin induces thromboplastin synthesis in cultured vascular endothelial cells. Thromb. Haemost. 53(02), 373–376 (1985).
Badimon, L. & Vilahur, G. Thrombosis formation on atherosclerotic lesions and plaque rupture. J. Intern. Med. 276(6), 618–632 (2014).
Marino, S., Hogue, I. B., Ray, C. J. & Kirschner, D. E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254(1), 178–196 (2008).
Acknowledgements
The authors would like to thank immunologists Bhargavi Duvvuri, Venkata Duvvuri, Gillian Wu, Chris Verschoor, and Ali Abdul-Sater for their invaluable feedback. Jianhong Wu is supported by the Natural Sciences and Engineering Research Council of Canada (Grant number: 105588-2011) and the Canada Research Chairs Program (Grant number: 230720). Jane Heffernan is supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grants Program, the Discovery Accelerator Supplements (DAS) Program, and the York Research Chairs Program. This project is also supported by the NSERC/Sanofi Industrial Research Chair Program in Vaccine Mathematics, Modelling and Manufacturing.
Author information
Authors and Affiliations
Contributions
Z.M., V.CM., S.X., and J.W. prepared the manuscript. Z.M., A.R., conducted numerical simulations. Z.M., A.R., and N.L.B. prepared the figures. Z.M., S.X., V.CM., A.R., J.L., B.S., E.T., J.H., J.W., A.C. and D.N. contributed to the research conceptualization.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
McCarthy, Z., Xu, S., Rahman, A. et al. Modelling the linkage between influenza infection and cardiovascular events via thrombosis. Sci Rep 10, 14264 (2020). https://doi.org/10.1038/s41598-020-70753-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-70753-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.