Abstract
Machine learning has the potential to facilitate the development of computational methods that improve the measurement of cognitive and mental functioning. In three populations (college students, patients with a substance use disorder, and Amazon Mechanical Turk workers), we evaluated one such method, Bayesian adaptive design optimization (ADO), in the area of delay discounting by comparing its test–retest reliability, precision, and efficiency with that of a conventional staircase method. In all three populations tested, the results showed that ADO led to 0.95 or higher test–retest reliability of the discounting rate within 10–20 trials (under 1–2 min of testing), captured approximately 10% more variance in test–retest reliability, was 3–5 times more precise, and was 3–8 times more efficient than the staircase method. The ADO methodology provides efficient and precise protocols for measuring individual differences in delay discounting.
Similar content being viewed by others
Introduction
Delay discounting, one dimension of impulsivity1, assesses how individuals make trade-offs between small but immediately available rewards versus large but delayed rewards. Delay discounting is broadly linked to normative cognitive and behavioral processes, such as financial decision making2, social decision making3, and personality4, among others. Also, individual differences in delay discounting are associated with several cognitive capacities, including working memory5, intelligence6, and top-down regulation of impulse control mediated by the prefrontal cortex7,8.
Delay discounting is a strong candidate endophenotype for a wide range of maladaptive behaviors, including addictive disorders9,10 and health risk behaviors for a review, see11. Studies of test–retest reliability of delay discounting demonstrate reliability both for adolescents12 and adults13, and genetics studies indicate that delay discounting may be a heritable trait9. As such, delay discounting has received attention in the developing field of precision medicine in mental health as a potentially rapid and reliable (bio)marker of individual differences relevant for treatment outcomes14,15,16. The construct validity of delay discounting has been demonstrated in numerous studies. For example, the delay discounting task is widely used to assess (altered) temporal impulsivity of various psychiatric disorders, including patients with substance use disorders e.g., 11, schizophrenia13,14, and bipolar disorder14. Therefore, improved assessment of delay discounting may be beneficial to many fields, including psychology, neuroscience, medicine15, and economics.
To link decision making tasks to mental functioning is a formidable challenge that requires simultaneously achieving multiple measurement goals. We focus on three aspects of measurement: reliability, precision, and efficiency. Reliable measurement of latent neurocognitive constructs or biological processes, such as impulsivity, reward sensitivity, or learning rate, is difficult. Recent advancements in neuroscience and computational psychiatry16,17 provide novel frameworks, cognitive tasks, and latent constructs that allow us to investigate the neurocognitive mechanisms underlying psychiatric conditions; however, their reliabilities have not been rigorously tested or are not yet acceptable18. A recent large-scale study suggests that the test–retest reliabilities of cognitive tasks are only modest19. Even if a test is reliable across time, confidence in the behavioral measure will depend on the precision of each measurement made. To our knowledge, few studies have rigorously tested the precision of measures from a neurocognitive test. Lastly, cognitive tasks developed in research laboratories are not always efficient, often taking 10–20 min or more to administer. With lengthy and relatively demanding tasks, participants (especially clinical populations) can easily fatigue or be distracted20, which can increase measurement error due to inconsistent responding. A by-product of low task efficiency is that the amount of data (e.g., number of participants) typically available for big data approaches to studying psychiatry is smaller than in other fields.
Several methods using fixed sets of choices currently exist to assess delay discounting, such as self-report questionnaires21 and computer-based tasks. The monetary choice questionnaire22 is an example, which contains 27 multiple choice questions and exhibits 5- and 57-week test–retest reliability of r’s within 0.7–0.8 in college students. Other delay discounting tasks use some form of an adjustment procedure in which individuals’ previous responses are used to determine subsequent trials based on heuristic rules for increasing or decreasing the values presented. Such methods often adjust the amount of the immediate reward22, with the goal of significantly reducing the number of trials required to identify discounting rates. However, many adjustment procedures still require dozens of trials to produce reliable results; a notable exception is the 5-trial delay discounting task, which uses an adjusting-amount method to produce meaningful measures of delay discounting in as few as five trials23. While it is difficult to imagine a more efficient task, its precision and test–retest reliability have not been rigorously evaluated. More generally, although the use of heuristic rules to inform stimulus selection can be an effective initial approach to improving experiment efficiency, such rules often lack a theoretical (quantitative) framework that can justify the rule.
Bayesian adaptive testing is a promising machine-learning method that can address the aforementioned challenges in efficiency, precision, and reliability to improve the study of individual difference in decision making using computer-based tasks24,25. It originates from optimal experimental design in statistics26 and from active learning in machine learning27. Adaptive design optimization (ADO; Fig. 1), an implementation of Bayesian adaptive testing, is a general-purpose computational algorithm for conducting adaptive experiments to achieve the experimental objective with the fewest possible number of observations. The ADO algorithm is formulated on the basis of Bayesian statistics and information theory, and works by using a formal cognitive model to guide stimulus selection in an optimal and efficient manner. Stimulus values in an ADO-based experiment are not predetermined or fixed, but instead are computed on the fly adaptively from trial to trial. That is, the stimulus to present on each trial is obtained by judiciously combining participant responses from earlier trials with the current knowledge about the model’s parameters so as to be the most informative with respect to the specific objective. The chosen stimulus is optimal in that it is expected to reduce the greatest amount of uncertainty about the unknown parameters in an information theoretic sense. Accordingly, there would be no “wasted”, uninformative trials; evidence can therefore accumulate rapidly, making the data collection highly efficient.
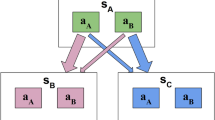
Schematic illustration of adaptive design optimization (ADO) in the area of delay discounting. Unlike the traditional experimental method, ADO aims to find the optimal design that extracts the maximum information about a participant’s model parameters on each trial. In other words, ADO identifies the most informative or optimal design (d*) using the participant’s previous choices (y), the mathematical model of choice behavior, and the participant’s model parameters (\(\theta\)). In our delay discounting experiment with ADO, y would be 0 (choosing smaller and sooner reward) or 1 (larger and later reward), the mathematical model would be the hyperbolic function (see “Methods”), \(\theta\) would be k (discounting rate) and \(\beta\) (inverse temperature), and d* would be the experimental design (a later delay and a sooner reward, which are underlined in the figure) that maximizes the integral of the local utility function, \(u(d,\theta ,y)\), which is based on the mutual information between model parameters (\(\theta\)) and outcome random variable conditional upon design (y|d). For more mathematical details of the ADO method, see24,25.
ADO and its variants have recently been applied across disciplines to improve the efficiency and informativeness of data collection (cognitive psychology28,29, vision30,31, psychiatry32, neuroscience33,34, clinical drug trials35, and systems biology36).
Here, we demonstrate the successful application of adaptive design optimization (ADO) to improving measurement in the delay discounting task. We show that in three populations (college students, patients with substance use disorders, and Amazon Mechanical Turk workers), ADO leads to rapid, precise, and reliable estimates of the delay discounting rate (k) with the hyperbolic function. Test–retest reliability of the discounting rate measured in the natural logarithmic scale (log(k)) reached up to 0.95 or higher within 10–20 trials (under 1–2 min of testing, including practice trials) with at least three times greater precision and efficiency than a staircase method that updates the immediate reward on each trial37. Although in the present study we used ADO for efficiently estimating model parameters with a single (hyperbolic) model, ADO can also be used to discriminate among a set of models for the purpose of model selection29,38,39,40.
Results
In Experiment 1, we recruited college students (N = 58) to evaluate test–retest reliability (TRR) of the ADO and staircase (SC) methods of the delay discounting task over a period of approximately one month, a span of time over which one might want to measure changes in impulsivity. Previous studies have typically used 1 week e.g., 41, 2 weeks42, or 3–6 months43 between test sessions to evaluate TRR. Students visited the lab twice. In each visit they completed two ADO and two SC sessions, allowing us to measure TRR within each visit and between the two visits. In each task (or session), students made 42 choices about hypothetical scenarios involving a larger but later reward versus a smaller but sooner reward. We examined TRR using concordance correlation coefficients44 within each visit and between the two visits, using the discounting rate log(k) of the hyperbolic function as the outcome measure (see “Methods”). Unless otherwise noted, all analyses involving the discounting rate were performed using log(k), with the natural logarithm base.
Past work customized the SC method to yield very good TRR11. Consistent with previous studies, in visits 1 and 2 of Experiment 1, within-visit TRR were 0.903 (visit 1) and 0.946 (visit 2), respectively. Nevertheless, ADO improved on this performance of SC, yielding values of 0.961 and 0.982, an increase of 10.8% (visit 1) and 6.9% (visit 2) in terms of the amount of variance accounted for (Figure S1; Figure S2–3 shows the results for all participants including the outliers with ADO and SC, respectively—see “Methods” for the criteria for outliers). We found that TRR was higher at visit 2 than at visit 1. This was true of ADO and SC, and thus is likely indicative of participants learning the task and better adapting themselves to it in the second session (a practice effect). Where ADO excels over the SC method is in efficiency and precision. We measured the efficiency of the method by calculating how many trials are required to achieve 0.9 TRR of the discounting rate, which was assessed cumulatively at each trial (Fig. 2). With respect to the efficiency, with ADO, while we should evaluate its performance with fewer than several trials rather cautiously, we achieved over 0.9 TRR within 7 trials at visit 1. At visit 2, TRR exceeded 0.9 within 6 trials. With the SC method, TRR failed to reach 0.9 even at the end of the experiment (42 trials) at visit 1, and reached 0.9 only after 39 trials at visit 2. Although 0.9 TRR is an arbitrary threshold, it was chosen because it is stringent. Conclusions do not change qualitatively even if a more conservative or liberal threshold is used. For example, with a threshold of 0.8, the TRR with ADO reached the threshold within 2 (visit 1) and 3 (visit 2) trials in Experiment 1. On the other hand, the TRR with SC reached the threshold within 24 (visit 1) and 33 (visit 2) trials. If we set the threshold to 0.95, the TRR with ADO reached the threshold within 24 (visit 1) and 8 (visit 2) trials. The SC failed to reach the threshold even after 42 trials. Regarding the precision, we measured it using within-subject variability, quantifying it as the standard deviation (SD) of an individual parameter posterior distribution. Specifically, ADO yielded approximately 3–5 times more precise estimates of discounting rate as measured by the smaller standard deviation of the posterior distribution of the discounting rate parameter (ADO visit 1: 0.122, visit 2: 0.098; SC visit 1: 0.413, visit 2: 0.537; Figure S4).
Comparison of ADO and Staircase (SC) within-visit test–retest reliability of temporal discounting rates when assessed cumulatively in each trial (ADO) or every third trial (SC) (Experiment 1, college students) at each of the two visits. Two visits were separated by approximately one month. In each visit, a participant completed two ADO sessions and two SC sessions (within-visit test–retest reliability). Test–retest reliability was assessed cumulatively in each trial (See “Methods” for the procedure). Shaded regions represent the 95% frequentist confidence interval of the concordance correlation coefficient (CCC).
ADO also showed superior performance when examined across visits separated by one month (Figure S5). All four TRR measures across the two visits converged at around 0.8 within 10 trials and were highly consistent with each other. In contrast, with the SC method, the trajectories of the four measures were much more variable and asymptote, if at all, below 0.8 towards the end of the experiment.
The parameter \(\beta\) is assumed to reflect consistency in task performance. We investigated if participants with low \(\beta\) at visit 1 showed greater discrepancies in discounting rates across visits 1 and 2. With ADO, we found small but significant negative correlations (all were weaker than − 0.270). This result suggests that participants who are less deterministic in their choices at visit 1 tend to show a larger discrepancy in discounting rates across the two visits. However, with the SC method, none of the correlations were statistically significant (p > 0.11). We believe this outcome is due to the fact that many participants’ inverse temperature rate with the SC method are less distributed and clustered near zero in comparison to those estimated with ADO (see Figure S2 for ADO estimates and Figure S3 for SC estimates). Overall, the results of Experiment 1 show that ADO leads to rapid, reliable, and precise measures of discounting rate.
In Experiment 2, we recruited 35 patients meeting the Diagnostic and Statistical Manual of Mental Disorders (5th ed. DSM-5) criteria for a substance use disorder (SUD) to assess the performance of ADO in a clinical population. The experimental design was the same as in Experiment 1 except that there was only a single visit. Figure 3A shows that even in this patient population, ADO still led to rapid, reliable, and precise estimates of discounting rates, again outperforming the SC method. With ADO, maximum TRR was 0.973 within approximately 15 trials. Consistent with the results of Experiment 1, the SC method led to a smaller maximum TRR (0.892) and it took approximately 25 trials to reach this maximum. Precision of the parameter estimate was five times higher when using ADO than the SC method (0.073 vs. 0.371). Figure S6 shows the results for all participants including the outliers in Experiment 2. Initially we set the upper bound of the discounting rate k to 0.1 assuming it would be sufficiently large for patients, but found that some patients’ discounting rate k reached ceiling. After recruiting 15 patients, we set the upper bound of the discounting rate k to 1 and no patient’s discounting rate k reached ceiling. Figure S7 suggests that the results largely remain the same whether we exclude those patients whose discounting rate reached ceiling or not.
Reliability and efficiency of the ADO method in Experiments 2 and 3 (A) Comparison of ADO and Staircase (SC) test–retest reliability of temporal discounting rates when assessed cumulatively in each trial (ADO) or every third trial (SC) (Experiment 2, patients with SUDs) (B) Test efficiency as measured by the cumulative test–retest reliability across trials (Experiment 3, Amazon MTurk workers). Dashed line = 0.9 test–retest reliability. Unlike Experiments 1 and 2, only ADO sessions were administered and each session consisted of 20 trials in Experiment 3. Shaded regions represent the 95% frequentist confidence interval of the concordance correlation coefficient (CCC).
In Experiment 3, we evaluated the durability of the ADO method, assessing it in a less controlled environment than the preceding experiments and with a larger and broader sample of the population, (808 Amazon Mechanical Turk workers). Each participant completed two ADO sessions, each of which consisted of 20 trials, which was estimated from Experiments 1 and 2 to be sufficient. In Experiment 3, ADO again led to an excellent maximum TRR (0.965), greater than 0.9 TRR within 11 trials as shown in Fig. 3B. Figure S8 shows the results for all participants, including outliers.
Table 1 summarizes all results across the three experiments. Comparison of the two methods clearly shows that ADO is (1) more reliable (capturing approximately 7–11% more variance in TRR), (2) approximately 3–5 times more precise (smaller SD of individual parameter estimates), and (3) approximately 3–8 times more efficient (fewer number of trials required to reach 0.9 TRR). As might be expected, when tested in a less controlled environment (Experiment 3), precision suffers (0.339), being only slightly less than that found with the SC method (0.371), while reliability and efficiency hardly change.
Lastly, we examined the correlation between the two model parameters (log(k): discounting rate and \(\beta\): inverse temperature rate) when we used ADO or SC. Typically a high correlation between model parameters is undesirable because these parameters may influence each other e.g., 45 and such a high correlation may lead to unstable parameter estimates. This was not the case for ADO; we found non-significant or weak (Pearson) correlation between the discounting rate and 1/β . Note that we separately calculated correlation coefficients in the two sessions within each visit. In Experiments 1 and 2, all but one correlation were non-significant and correlation coefficients never exceeded 0.25. In Experiment 3, with its very large sample, the correlation coefficients between the two parameters were 0.062 (p = 0.091) and 0.094 (p = 0.011), respectively, across the two sessions, further confirmation of parameter independence.
In contrast, with SC, the correlations between the two measures were much stronger45 in comparison to ADO. In Experiment 1, the correlation coefficients between the two parameters were at least 0.470 and all were highly significant (p < 0.0003). In Experiment 2, correlation coefficients were 0.340 (p = 0.066) and 0.229 (p = 0.223). Remember that only ADO was used in Experiment 3. These parameter correlation results further demonstrate the superiority of ADO over SC. Parameter estimates are most trustworthy for ADO.
Discussion
In three different populations, we have demonstrated that ADO led to highly reliable, precise, and rapid measures of discounting rate. ADO outperformed the SC method in college students (Experiment 1) and in patients meeting DSM-5 criteria for SUDs (Experiment 2). It held up very well in a less restrictive testing environment with a broader sample of the population (Experiment 3). The results of this study are consistent with previous studies employing ADO29,46, showing improved precision and efficiency. This is the first study demonstrating the advantages of ADO-driven delay discounting in healthy controls and psychiatric/online populations. In addition, this is one of the first studies that rigorously tested the precision of a latent measure (i.e., discounting rate) of a cognitive task. Such information is invaluable when evaluating methods and when making inferences from parameter estimates, as high precision can increase confidence. The SC method is an impressive heuristic method that delivers such good TRR (close to 0.90 in our study) that there is little room for improvement. Nevertheless, ADO is able to squeeze out additional information to increase reliability further. Where ADO excels most relative to the SC method is in precision and efficiency. The model-guided Bayesian inference that underlies ADO is responsible for this improvement. Unlike the SC method, which follows a simple rule of increasing or decreasing the value of a stimulus, ADO has no such constraint, choosing the stimulus that is expected to be most informative on the next trial. Trial after trial, this flexibility pays significant dividends in precision and efficiency, as the results of the three experiments show. Figures S9–10 illustrate how ADO and SC methods select upcoming designs (i.e., experimental parameters) in a representative participant (Figure S9 at visit 1 and Figure S10 at visit 2). In many cases, ADO quickly navigates to a small region of the design space. Interestingly, the selected region is often very consistent across multiple sessions and visits. SC shows a similar pattern but the stimulus-choice rule (the staircase algorithm) constrains choices to neighboring designs only, making it less flexible, and thus requiring more trials, than ADO.
In all fairness, the above benefits of ADO also come with costs. For example, trials that are most informative can be ones that are also difficult for the participant47. Repeated presentation of difficult trials can frustrate and fatigue participants. Another issue is that for participants who respond consistently, the algorithm will quickly narrow (fewer than 10 trials) to a small region of the design space and present the same trials repeatedly with the goal of increasing precision even further. It is therefore important to implement measures that mitigate such behavior. We did so in the present study by inserting easy trials among difficult ones once the design space narrowed to a small number of options, keeping the total number of trials fixed. Another approach is to implement stopping criteria, such as ending the experiment once parameter estimation stabilizes, which would result in participants receiving different numbers of trials.
Finally, ADO’s flexibility in design selection, discussed above, can result in greater trial-to-trial volatility in the early trials of the experiment, as the algorithm searches for the region in which the two reward-delay pairs are similarly attractive. Once found, volatility will be low. Although these seemingly random jumps in design might capture participants’ attention, we believe that a more salient feature of the experiment, present in both methods, is the similarity of choice pairs trial after trial in the latter half of the experiment, as the search hones in on a small region in the design space. In Experiments 1 and 2, participants completed both ADO-based and SC-based tasks. Potentially it may cause carryover effects in our within-subject design. We counterbalanced the order of task completion (ADO then SC versus the reverse) to neutralize any such impact on the results. Analyses comparing task order showed that test–retest reliability in ADO is barely affected by the order. For example, as seen in Figure S11, CCC was similar regardless of the order of task completion (ADO then SC versus the reverse).
Both ADO and SC methods led to different implementations of the same delay discounting task, and as such led to slightly different values of discounting rates: Correlations between the discounting rate from ADO and that from the SC method ranged from 0.733 to 0.903 in Experiment 1 (four comparisons). Of course no one truly knows the underlying discounting rate, but the fact that the association is not consistently high should not be surprising as it is true for any measures of human performance (e.g., measures of IQ, depression, or anxiety). Also, as mentioned above, ADO is more flexible than the SC method in the design choices selected from trial to trial. This difference in flexibility will impact the final parameter estimate, especially in a short experiment.
There are a few reasons why we prefer the ADO approach. First, the reason that the correlation between ADO and SC was not always high (> 0.9) is likely due to noise, not the tasks, which are indistinguishable except for the sequencing of experimental parameters (e.g., reward amount and delay pairs) across trials. The greater precision of ADO compared to SC (3–5 times greater) suggests that SC is the larger source of this noise (see Table 1 and Figure S4). Second, the reason for ADO's greater precision is known, and lies in the ADO algorithm, which seeks to maximize information gain on each trial. There is a theoretically-motivated objective being achieved in the ADO approach that justifies stimulus choices trial after trial, whereas the SC approach is not as principled. More specifically, in the large sample theory of Bayesian inference, the posterior distribution is asymptotically normal, thus unimodal and symmetric, and also importantly, the posterior mean is optimal (‘consistent’ in a statistical sense), meaning that it converges to the underlying ground truth as the sample size increases48. Additionally, as shown earlier, two model parameters were statistically uncorrelated with ADO, which was not the case with SC. Together, the transparency of how ADO works along with its high reliability, precision, and parameter stability are strong reasons to prefer ADO. In summary, while we cannot say whether estimates using ADO are closest to individuals’ true internal states, ADO’s high consistency within and especially across visits (Figure S5) demonstrates a degree of trustworthiness.
While we believe that ADO is an exciting, promising method that offers the potential to advance the current state of the art in experimental design in characterizing mental functioning, we should mention a few major challenges and limitations in its practical implementation. One is the requirement that a computational/mathematical model of the experimental task be available. Also, the model should provide a good account (fit) of choice behavior. We believe the success of ADO in the delay discounting task is partly due to the availability of a reasonably good and simple hyperbolic model with just two free parameters. However, while we demonstrate the promise of an ADO method only in the area of delay discounting in this work, our methodology can be easily extended to other cognitive tasks that are of interest to researchers in psychology, decision neuroscience, psychiatry, and related fields. For example, we are currently applying ADO to tasks involving value-based or social decision making, including choice under risk and ambiguity49 and social interactions e.g., 50. Preliminary results suggest that the superior performance of ADO observed here generalizes to other tasks. In addition, our recent work also demonstrates that ADO can be used to optimize the sequencing of stimuli and improve functional magnetic resonance imaging (fMRI) measurements51, which can reduce the cost of data acquisition and improve the quality of neuroimaging data.
Lastly, the mathematical details of ADO and its implementation in experimentation software can be a hurdle for researchers and clinicians. To reduce such barriers and allow even users with limited technical knowledge to use ADO in their research, we are developing user-friendly tools such as a Python-based package called ADOpy52 as well as web-based and smartphone platforms.
In conclusion, the results of the current study suggest that machine-learning based tools such as ADO can improve the measurement of latent neurocognitive processes including delay discounting, and thereby assist in the development of assays for characterizing mental functioning and more generally advance measurement in the behavioral sciences and precision medicine in mental health.
Methods
Reliability, precision, and efficiency were measured as follows: Reliability was measured using the concordance correlation coefficient (CCC), which assesses the agreement between two sets of measurements collected at two points in time44. It is superior to the Pearson correlation coefficient, which assesses only association but not agreement. We used the DescTools package in R to calculate CCC53. TRT across trials in an experiment was computed by calculating CCC on each trial. The number of estimated discounting rates that went into computing the correlation was always the number of participants (n = 58 in Experiment 1, n = 35 in Experiment 2, and n = 808 in Experiment 3), so this value remained fixed. What changes across trials was the number of observed choice responses that contribute to estimating each participant’s discounting rate (i.e., that contributed to the posterior distribution of the parameter estimate). Because the number of values that went into computing the correlation was fixed across trials, this method of assessing reliability brings out the improvement in TRT provided by each additional observation, starting from trial 2 and extending to the last trial of the experiment.
Precision was measured using within-subject variability, quantified as the standard deviation of an individual parameter posterior distribution. Efficiency was quantified as the number of trials required to reach 0.9 TRR. We used Bayesian statistics to estimate model parameters and frequentist statistics for most other analyses.
Experiment 1 (college students)
Participants
Fifty-eight adult students at The Ohio State University (25 males and 33 females; age range 18–37 years; mean 19.0, SD 2.9 years) were recruited and received course credit for their participation. For all studies reported in this work, we used the following exclusion criterion: a participant is excluded from further analysis if the participant’s standard deviation (SD) of a parameter value (individual parameter posterior distribution) is two SD greater than the group mean. In other words, we excluded participants who seemingly made highly inconsistent choices during the task.
Delay discounting task
Each participant completed two sessions at each of the two visits. The two visits were separated by approximately one month (mean = 28.3 days, SD = 5.3 days). In each visit, a participant completed four delay discounting tasks: two ADO-based tasks and two SC-based tasks. Each ADO-based or SC-based task included 42 trials. The order of task completion (ADO then SC versus the reverse) was counterbalanced across participants.
In the traditional SC method, a participant initially made a choice between $400 now and $800 at seven different delays: 1 week, 2 weeks, 1 month, 6 months, 1 year, 3 years, and 10 years. The order of the delays was randomized for each participant. By adjusting the immediate amount, the choices were designed to estimate the participant’s indifference point for each delay. Specifically, the immediate amount was updated after each choice in increments totaling 50% of the preceding increment (beginning with $200), in a direction to make the unchosen option more subjectively valuable. For example, when presented with $400 now or $800 in 1 year, selecting the immediate option will lead to a choice between $200 now or $800 in 1 year ($200 increment). Then, choosing the immediate option once more will lead to a choice between $100 now or $800 in 1 year ($100 increment). If the later amount is then chosen, the next choice will be between $150 now or $800 in 1 year ($50 increment). This adjusting procedure ends after receiving choices for the subsequent $25 and $12.5 increments. See11,14 for more examples of the procedure.
In the ADO method, the sooner delay and a later-larger reward were fixed as 0 day and $800. A later delay and a sooner reward were experimental parameters that were optimized on each trial. Based on the ADO framework and the participant’s choices so far, the most informative design (a later delay and a sooner reward) was selected on each trial. See prior publications24,25 and also Fig. 1 for technical details of the ADO framework.
Computational modeling
We applied ADO to the hyperbolic function, which has two parameters (k: discounting rate and \(\beta\): inverse temperature rate). The hyperbolic function has the form V = A/(1 + kD), where an objective reward amount A after delay D is discounted to a subjected reward value V for an individual whose discounting rate is k (k > 0). In a typical delay discounting task, two options are presented on each trial: a smaller-sooner (SS) reward and a later-lager (LL) reward. The subjective values of the two options are modeled by the hyperbolic function. We used softmax (Luce’s choice rule) to translate subjective values into the choice probability on trial t:
where \({V}_{ss}\) and \({V}_{LL}\) are subjective values of the SS and LL options. To estimate the two parameters of the hyperbolic model in the SC method, we used the hBayesDM package54. The hBayesDM package (https://github.com/CCS-Lab/hBayesDM) offers hierarchical and non-hierarchical Bayesian analysis of various computational models and tasks using Stan software55. The hBayesDM function of the hyperbolic model for estimating a single participant’s data is d_hyperbolic_single. Note that updating of our ADO framework is based on each participant’s data only. Thus, for fair comparisons between ADO and SC methods, we used an individual (non-hierarchical) Bayesian approach for analysis of data from the SC method. In ADO sessions, parameters (means and SDs of the parameter posterior distributions of the hyperbolic model) are automatically estimated on each trial. Note that estimation of the discounting rate was of primary interest in this project. We found that the TRR of the inverse temperature rate (\(\beta\)) of the softmax function is much lower than that of the discounting rate. We do not have a satisfying explanation and future studies are needed to investigate this issue. Estimates of the inverse temperature rate (a measure of response consistency or a degree of exploration/exploitation), \(\beta\), are provided in the Supplemental Figures.
Experiment 2 (patients meeting criteria for a substance use disorder)
Participants
Thirty-five individuals meeting DSM-5 criteria for a SUD and receiving treatment for addiction problems participated in the experiment (25 males and 10 females; age range 22–57 years; mean 35.8, SD 10.3 years). All participants were recruited through in-patient units at The Ohio State University Wexner Medical Center where they were receiving treatment for addiction. Trained graduate students and a study coordinator (Y.S.) used the Structured Clinical Interview for DSM-5 disorders (SCID-5) to assess diagnosis of a SUD. Final diagnostic determinations were made by W.-Y. A. on the basis of patients’ medical records and the SCID-5 interview. Exclusion criteria for all individuals included head trauma with loss of consciousness for over 5 minutes, a history of psychotic disorders, history of seizures or electroconvulsive therapy, and neurological disorders. Participants received gift cards for their participation (worth of $10/h).
Delay discounting task and computational modeling
The task and methods for computational modeling in Experiment 2 were identical to those in Experiment 1. For a subset of participants in Experiment 2 (15 out of 35), the upper bound for discounting rate (k) during ADO was set as 0.1 for computing efficiency and we noted that some participants’ k values reached ceiling (= 0.1). For the other participants (n = 20), the upper bound was set to 1. We report results that are based on all 35 patients (Fig. 3A) as well as results without participants whose k values reached the ceiling of 0.1 (Figure S7).
Experiment 3 (large online sample)
Participants
Eight hundred and eight individuals through Amazon Mechanical Turk (MTurk; 353 males and 418 females (37 individuals declined to report their sex); age mean 35.0, SD 10.8 years) were recruited. They were required to reside in the United States and be at least 18 years of age, and received $10/h for their participation. Out of 808 participants, 71 participants (8.78%) were excluded based on exclusion criteria (see Experiment 1).
Delay discounting task
Each participant completed two consecutive ADO-based tasks (sessions). The tasks were identical to the ADO version in Experiments 1 and 2 but consisted of just 20 trials per session (c.f., 42 trials per session in Experiments 1 and 2). There was no break between the two tasks, so participants experienced the experiment as a single session.
All participants received detailed information about the study protocol and gave written informed consent in accordance with the Institutional Review Board at The Ohio State University, OH, USA. All experiments were performed in accordance with relevant guidelines and regulations at The Ohio State University. All experimental protocols were approved by The Ohio State University Institutional Review Board.
References
Reynolds, B., Ortengren, A., Richards, J. B. & de Wit, H. Dimensions of impulsive behavior: Personality and behavioral measures. Behav. Process. 40, 305–315 (2006).
Meier, S. & Sprenger, C. Present-biased preferences and credit card borrowing. Am. Econ. J. Appl. Econ. 2, 193–210 (2010).
Harris, A. C. & Madden, G. J. Delay discounting and performance on the Prisoner’s dilemma game. Psychol. Rec. 52, 429–440 (2002).
Hirsh, J. B., Morisano, D. & Peterson, J. B. Delay discounting: Interactions between personality and cognitive ability. J. Res. Pers. 42, 1646–1650 (2008).
Bickel, W. K., Yi, R., Landes, R. D., Hill, P. F. & Baxter, C. Remember the future: Working memory training decreases delay discounting among stimulant addicts. Biol. Psychiatry 69, 260–265 (2011).
Shamosh, N. A. & Gray, J. R. Delay discounting and intelligence: A meta-analysis. Intelligence 36, 289–305 (2008).
Kable, J. W. & Glimcher, P. W. The neural correlates of subjective value during intertemporal choice. Nat. Neuro. 10, 1625–1633 (2007).
McClure, S. M., Laibson, D. I., Loewenstein, G. & Cohen, J. D. Separate neural systems value immediate and delayed monetary rewards. Sci. New Ser. 306, 503–507 (2004).
Anokhin, A. P., Grant, J. D., Mulligan, R. C. & Heath, A. C. The genetics of impulsivity: Evidence for the heritability of delay discounting. Biol. Psychiatry 77, 887–894 (2014).
Bickel, W. K. Discounting of delayed rewards as an endophenotype. Biol. Psychiatry 77, 846–847 (2015).
Green, L. & Myerson, J. A discounting framework for choice with delayed and probabilistic rewards. Psychol. Bull. 130, 769–792 (2004).
Anokhin, A. P., Golosheykin, S. & Mulligan, R. C. Long-term test–retest reliability of delayed reward discounting in adolescents. Behav. Process. 111, 55–59 (2020).
Heerey, E. A., Robinson, B. M., McMahon, R. P. & Gold, J. M. Delay discounting in schizophrenia. Cognit. Neuropsychiatry 12, 213–221 (2007).
Ahn, W.-Y. et al. Temporal discounting of rewards in patients with bipolar disorder and schizophrenia. J. Abnorm. Psychol. 120, 911–921 (2011).
Insel, T. R. The NIMH research domain criteria (RDoC) project: Precision medicine for psychiatry. Am. J. Psychiatry 171, 395–397 (2014).
Montague, P. R., Dolan, R. J., Friston, K. J. & Dayan, P. Computational psychiatry. Trends Cogn. Sci. 16, 72–80 (2012).
Stephan, K. E. & Mathys, C. Computational approaches to psychiatry. Curr. Opin. Neurobiol. 25, 85–92 (2014).
Hedge, C., Powell, G. & Sumner, P. The reliability paradox: Why robust cognitive tasks do not produce reliable individual differences. Behav. Res. 103, 1–21 (2017).
Enkavi, A. Z. et al. Large-scale analysis of test–retest reliabilities of self-regulation measures. Proc. Natl. Acad. Sci. 116, 5472–5477 (2019).
Sandry, J., Genova, H. M., Dobryakova, E., DeLuca, J. & Wylie, G. Subjective cognitive fatigue in multiple sclerosis depends on task length. Front. Neurol. 5, 24 (2014).
Kirby, K. N. & MarakoviĆ, N. N. Delay-discounting probabilistic rewards: Rates decrease as amounts increase. Psychon. Bull. Rev. 3, 100–104 (1996).
Kirby, K. N. One-year temporal stability of delay-discount rates. Psychon. Bull. Rev. 16, 457–462 (2009).
Koffarnus, M. N. & Bickel, W. K. A 5-trial adjusting delay discounting task: Accurate discount rates in less than one minute. Exp. Clin. Psychopharmacol. 22, 222–228 (2014).
Cavagnaro, D. R., Myung, J. I., Pitt, M. A. & Kujala, J. V. Adaptive design optimization: A mutual information-based approach to model discrimination in cognitive science. Neural Comput. 22, 887–905 (2010).
Myung, J. I., Cavagnaro, D. R. & Pitt, M. A. A tutorial on adaptive design optimization. J. Math. Psychol. 57, 53–67 (2013).
Atkinson, A. C. & Donev, A. N. Optimum experimental designs. El Observador de Estrellas Dobles 344, 2 (1992).
Cohn, D., Atlas, L. & Ladner, R. Improving generalization with active learning. Mach. Learn. 15, 201–221 (1994).
Myung, J. I. & Pitt, M. A. Optimal experimental design for model discrimination. Psych. Rev. 116, 499–518 (2009).
Cavagnaro, D. R. et al. On the functional form of temporal discounting: An optimized adaptive test. J. Risk Uncertain. 52, 233–254 (2016).
Lesmes, L. A., Jeon, S.-T., Lu, Z.-L. & Dosher, B. A. Bayesian adaptive estimation of threshold versus contrast external noise functions: The quick TvC method. Vis. Res. 46, 3160–3176 (2006).
Gu, H. et al. A hierarchical Bayesian approach to adaptive vision testing: A case study with the contrast sensitivity function. J. Vis. 16, 15–15 (2016).
Aranovich, G. J., Cavagnaro, D. R., Pitt, M. A., Myung, J. I. & Mathews, C. A. A model-based analysis of decision making under risk in obsessive-compulsive and hoarding disorders. J. Psychiatr. Res. 90, 126–132 (2017).
Lewi, J., Butera, R. & Paninski, L. Sequential optimal design of neurophysiology experiments. Neural Comput. 21, 619–687 (2009).
DiMattina, C. & Zhang, K. Active data collection for efficient estimation and comparison of nonlinear neural models. Neural Comput. 23, 2242–2288 (2011).
Wathen, J. K. & Thall, P. F. Bayesian adaptive model selection for optimizing group sequential clinical trials. Statist. Med. 27, 5586–5604 (2008).
Kreutz, C. & Timmer, J. Systems biology: Experimental design. FEBS J. 276, 923–942 (2009).
Mazur, J. E. An adjusting procedure for studying delayed reinforcement. Commons ML Mazur JE Nevin JA 6, 55–73 (1987).
Cavagnaro, D. R., Gonzalez, R., Myung, J. I. & Pitt, M. A. Optimal decision stimuli for risky choice experiments: an adaptive approach. Manag. Sci. 59, 358–375 (2013).
Cavagnaro, D. R., Pitt, M. A., Gonzalez, R. & Myung, J. I. Discriminating among probability weighting functions using adaptive design optimization. J. Risk Uncertain. 47, 255–289 (2013).
Cavagnaro, D. R., Pitt, M. A. & Myung, J. I. Model discrimination through adaptive experimentation. Psychon. Bull. Rev. 18, 204–210 (2011).
Matusiewicz, A. K., Carter, A. E., Landes, R. D. & Yi, R. Statistical equivalence and test–retest reliability of delay and probability discounting using real and hypothetical rewards. Behav. Proc. 100, 116–122 (2013).
Harrison, J. & McKay, R. Delay discounting rates are temporally stable in an equivalent present value procedure using theoretical and area under the curve analyses. Psychol. Rec. 62, 307–320 (2012).
Weatherly, J. N. & Derenne, A. Testing the reliability of paper-pencil versions of the fill-in-the-blank and multiple-choice methods of measuring probability discounting for seven different outcomes. Psychol. Rec. 63, 835–862 (2013).
Lin, L.I.-K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 45, 255 (1989).
Moutoussis, M., Dolan, R. J. & Dayan, P. How people use social information to find out what to want in the paradigmatic case of inter-temporal preferences. PLoS Comput. Biol. 12, e1004965 (2016).
Hou, F. et al. Evaluating the performance of the quick CSF method in detecting contrast sensitivity function changes. J. Vis. 16, 18–18 (2016).
Ahn, W.-Y. & Busemeyer, J. R. Challenges and promises for translating computational tools into clinical practice. Curr. Opin. Behav. Sci. 11, 1–7 (2016).
Gelman, A., Dunson, D. B. & Vehtari, A. Bayesian Data Analysis (CRC Press, Boca Raton, 2014).
Levy, I., Snell, J., Nelson, A. J., Rustichini, A. & Glimcher, P. W. Neural representation of subjective value under risk and ambiguity. J. Neurophysiol. 103, 1036–1047 (2010).
Xiang, T., Lohrenz, T. & Montague, P. R. Computational substrates of norms and their violations during social exchange. J. Neurosci. 33, 1099–1108 (2013).
Bahg, G. et al. Real-time Adaptive Design Optimization within Functional MRI Experiments. Computational Brain & Behavior https://doi.org/10.1007/s42113-020-00079-7 (2020).
Yang, J., Ahn, W.-Y., Pitt, M. A. & Myung, J. I. ADOpy: a Python package for optimizing data collection (in press). Behav. Res. Methods
Signorell A. et al. DescTools: Tools for Descriptive Statistics. R package version 0.99.34 (2020). https://cran.r-project.org/package=DescTools.
Ahn, W.-Y., Haines, N. & Zhang, L. Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hBayesDM package. Computat. Psychiatry 1, 24–57 (2017).
Carpenter, B. et al. Stan: A probabilistic programming language. J. Stat. Softw. 76, 25704 (2016).
Acknowledgements
The research was supported by National Institute of Health Grant R01-MH093838 to M.A.P. and J.I.M, the Basic Science Research Program through the National Research Foundation (NRF) of Korea funded by the Ministry of Science, ICT, & Future Planning (NRF-2018R1C1B3007313 and NRF-2018R1A4A1025891), the Institute for Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2019-0-01367, BabyMind), and the Creative-Pioneering Researchers Program through Seoul National University to W.-Y.A. We thank Andrew Rogers and Zoey Butka for their assistance in data collection.
Author information
Authors and Affiliations
Contributions
W.-Y.A., J.M., and M.P. conceived and designed the experiments. Y.S., N.H., and H. H. collected data. W.-Y.A. performed the data analysis and drafted the paper. J.M. and M.P. co-wrote subsequent drafts with W.-Y.A. H.G. performed the data analysis. All authors (W.-Y.A., H.G., Y.S., N.H., H.H., J.T., J.M., and M.P.) contributed to writing the manuscript and approved the final version of the paper for submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ahn, WY., Gu, H., Shen, Y. et al. Rapid, precise, and reliable measurement of delay discounting using a Bayesian learning algorithm. Sci Rep 10, 12091 (2020). https://doi.org/10.1038/s41598-020-68587-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-68587-x
This article is cited by
-
Seeking Pleasure, Finding Trouble: Functions and Dysfunctions of Trait Sensation Seeking
Current Addiction Reports (2023)
-
Real-time monitoring of sports performance based on ensemble learning algorithm and neural network
Soft Computing (2023)
-
The effect of individual-level adaptive stimulus selection on the group-level parameters for cognitive models
Behaviormetrika (2023)
-
Adaptive optimal stimulus selection in cognitive models using a model averaging approach
Behaviormetrika (2023)
-
Can Global Strategy Outperform Myopic Strategy in Bayesian Sequential Design?
Neural Processing Letters (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.