Abstract
Different polytypes of SiC are described and predicted in literature. Here, we report the first occurrence of an orthorhombic 6O-SiC polytype as rock-forming mineral in the nickel laterite mine of Tiebaghi (New Caledonia). This new class of SiC crystallizes in the space group Cmc21 with 12 atoms per unit cell [a = 3.0778(6) Å, b = 5.335(2) Å, c = 15.1219(6) Å, α = 90°, β = 90°, γ = 120°]. The density of 6O-SiC is about 3.22 g/cm3 and the calculated indirect bandgap at room temperature of 3.56 eV is identical to 6H-SiC. Our results suggest that 6O-SiC is the intermediate state in the wurtzite to rocksalt transformation of 6H-SiC.
Similar content being viewed by others
Introduction
SiC is a highly attractive material for fabrication of microelectronic and optoelectronic devices due to its outstanding physical properties, such as a wide bandgap, high thermal conductivity coupled with low thermal expansion. The wide bandgap makes SiC a very attractive semiconductor to make devices for applications in high power, high frequency and high temperature environment1,2,3,4,5,6. In addition, its high strength gives this material exceptional thermal shock resistant properties and an exceptional hardness4,5,6.
A large number of SiC polytypes are already described and predicted in literature. The most common polytypes include 3C, 2H, 4H, 6H, 8H, 9R, 10H, 14H, 15R, 19R, 20H, 21H, and 24R1,7,8, where C, H and R mean cubic, hexagonal and rhombohedral symmetries, respectively. Natural SiC, known as moissanite, is extremely rare. Natural occurrences can be divided into three categories: kimberlites9; metasomatic rocks10; peridotites, serpentinites and podiform chromitites11,12.
In this study, different grains of moissanite have been found and separated from the porosities of siliceous breccia originating from hydrofracturing of peridotites at Tiebaghi mine in New Caledonia (Fig. 1a). Moissanite occurs either as single grains or is associated with diamond in composite inclusions (Fig. 1c). These irregular fragments with a size of 10–75 μm exhibit various colors, including blue, green and yellow (Fig. 1b). Schmidt et al.13 have suggested that moissanite can be formed at very low temperatures during the alteration of ultramafic rocks, where hydrogen liberated by reactions involving serpentine would induce low oxygen fugacity, 6 to 8 log units below the Iron-Wustite buffer. However, SiC from peridotites and chromites in ophiolites are mainly subhedral to anhedral, and are similar to those observed in the siliceous breccia pores studied in this work. Rapid tectonic uplift would explain that these moissanite crystals are not decomposed to lower temperature phases. This finding suggests that these moissanite grains were liberated from the hostrocks and transported into the breccia pores13,14.
The structural, elastic and electronic properties of this new class of SiC were studied by single crystal X-rays diffraction, Raman spectroscopy and ab initio DFT calculation.
In this study, the optical microscopy analysis of the siliceous breccia porosities shows the presence of different crystals of moissanite. EDS analyzes confirm that all the moissanite crystals are mainly composed of C and Si (Fig. 1d).
Structural properties of SiC
An extracted grain with a dark blue color and largest dimensions smaller than 10 ×10 ×10 μm3 was selected for SCXRD experiments (Fig. 2). A full data collection has been performed on a Rigaku Synergy S single crystal diffractometer equipped with a Cu micro focus X-ray source and a Dectris Eiger 1M photon counting detector. A first analysis of the full diffraction pattern has been done using the 6H-SiC polytype with the cell parameters a ≈ 3.078 Å, b ≈ 3.078 Å, c ≈ 15.13 Å, α = 90°, β = 90° and γ = 120°15; unindexed reflections inducing a doubling of the a and b periodicities are observed. The data integration was performed using Crysalispro [CrysAlisPro Software System, Version 1.171.39.46. Rigaku] and the new unit cell is a = 6.165(4) Å, b = 6.169(4) Å, c = 15.129(10) Å° α = 89.95(5)° β = 89.97(5)° γ = 119.96(7)°. An internal reliability factor (Rint) showed from the intensities of symmetry equivalent reflections that the deviation from the Laue classes 6/mmm, 6/m, −3, −3 m1 or −31 m is always larger than 52%. This excludes unambiguously the hexagonal or trigonal symmetries. The reciprocal space was then interprated considering the orthorhombic unit cell a = 3.0778(6) Å, b = 5.335(2) Å, c = 15.1219(6) Å, α = 90°, β = 90° and γ = 90° and twin components related by a three-fold axis parallel to c. The new integration leads to a Rint value of about 12% for the mmm Laue class. This value far to be perfect suggests an imperfect data quality certainly related to the tiny dimension of the crystal. Nevertheless, the structure has been determined by charge – flipping method16 with Superflip17 in the Cmc21 space group and then refined using Jana200618. Cmc21 being non centrosymmetric, 3 additional twin domains have to be introduced. But only 3 twin domains related by a three fold axis have been found as significant from their respective intensities; the twin volume ratio are the following: 38(5)%, 36(5)% and 26(5)%.The final agreement factor is Rf = 0.0329(2) for 316 reflections with I ≥ 3σ(I) and 20 refinement parameters. A view of the structure is presented in Fig. 2c. The main structural characteristics of the 6H-SiC polytype are described as SiC4 tetrahedra sharing all their edges with their neighbours.
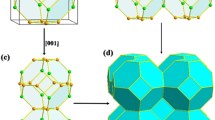
Single crystal diffraction experiment on 6O-SiC twinned single crystal. (a) one experimental frame exhibiting diffraction spots of SiC, (b) Part of the (0kl)* reciprocal plane of SiC assembled from the whole experimental frames. Reciprocal cell parameters and unit cell are drawn, (c) crystal structure refined in an orthorhombic 6O-SiC model and (d) stacking sequence of the 6O-SiC in the (1120) plane.
The crystal packing of 6O-SiC can be described by means of two alternating layers tilted with respect to one another by an angle close to 120°. However, slight differences can be noted compared to the hexagonal polytype. The 3 independent SiC4 groups are exhibiting distortions as evidenced by the Si-C bond lengths varying from 1.866(9) to 1.92(2) Å as well as by the Si-C-Si angles ranging from 107.8° to 111.2° which corresponds to deviations of nearly ±2° with respect to the values reported for cubic and hexagonal polyypes. This phenomenon is usually called planarization, a flattening of the tetrahedra correlated to an increase in bond angle. This leads to a non-centrosymmetric orthorhombic structure.
The structure can then be described by alternating a periodic stacking of blocks following the sequence …ABCACB… along the [0001] direction, illustrating the existence of six types of block boundaries (Fig. 2d). The atomic positions of the 6O-SiC polytype are given in Table 1.
In literature, 6H polytype is formed at very high temperatures (2300–2800 K) and at least at pressures of 3 GPa19. Because of the similarities between the polymorphism in SiC and ZnS, the transition models that have served as frameworks to study the wurtzite to rocksalt transition are the same for SiC. The high-pressure transition from the 6H wurtzite to the 3C rocksalt structure in SiC has been explored extensively with the help of computations20,21,22. It also has been observed in shock compression experiments at a pressure of 105 GPa22. It is found by ab initio calculations that 6H polytype under high temperature-pression undergoes a transition to the rocksalt structure through an orthorhombic intermediate state20. The space groups of the transition states are identified as Pmm2 and Imm220. Our results are particularly important because they suggest that the wurtzite to rock-salt phase transitions pass through the intermediate states with Cmc21 symmetry. It is interesting to note that an intermediate orthorhombic phase with Cmc21 symmetry has also been described in previous works for the same transition in different semiconductors such as GaN, InN, CdS and CdSe23. The finding of this new SiC structure being an intermediate phase between wurtzite and rock slat transition is in the line with the geodynamic context of the sample. Indeed, these SiC microcrystals occur together with diamond, and other reduced phases (Fe-Mn alloys, Al-rich chromite). These phases most likely crystallized in the lower mantle24. Second stage boninitic melts, described at Tiebaghi (New Caledonia)25,26, served as a natural elevator to transport these ultrahigh-pressure, reducing phases into the upper mantle. These resistant phases survived hydrothermal and supergene alteration.
Elastic properties of SiC
The elastic constant tensors of 3C-, 6H- and 6O-SiC crystals, determined by Brillouin scattering, are listed in Table 2 along with available computed and experimental elastic constants. Using the second order elastic constants, the bulk modulus B is computed.
In general, the intrinsic mechanical stability of a solid is determined by certain conditions concerning the Cij values related to the crystal symmetry. For an orthorhombic crystal, the independent elastic stiffness tensor reduces to nine components C11, C22, C33, C44, C55, C66, C12, C13 and C23 in the Voigt notation. The elastic components C11, C22 and C33 represent the elastic stiffness along the three-unit cell directions. The other constants are associated with either mixed behaviours (Cij’s with i ≠ j) or shears (C44, C55 and C66). The Born stability criteria27 for an orthorhombic system are:
The computed B1, B2, B3, and B4 values for the 6O-SiC are all positive with 1243, 824, 976, and 976 GPa, respectively. All the four conditions for mechanical stability are simultaneously satisfied and this clearly indicates that this orthorhombic polytype is a mechanically stable phase. C44 is an important parameter indirectly governing the indentation hardness of a material. The studied Cmc21 structure possesses a large C44 value of 175 GPa, meaning its relatively strong strength against shear deformation. The bulk modulus B of 3C, 6H and 6O structures are similar (B ≈ 215 GPa), which is the indication of high hardness of these semiconductor materials. The C33 value is superior to C11 and C22 values, showing the compressibility along the ab-plane to be more pronounced than along the c-axis, towards a more anisotropic phase compared to 3C and 6H. Elastic constants yield the compressibility of the c axis smaller than the a and b axis (0.0018 versus 0.0021 and 0.0021 GPa−1).
Vibrational properties of SiC
The Raman-active vibrational modes of our orthorhombic SiC were calculated through Density Functional Theory (DFT). For comparison, we also calculated the Raman spectra for cubic SiC and hexagonal 6H-SiC. 6H-SiC is among the most interesting SiC polytype for power electronic applications. Moreover, 6H-SiC exhibits high breakdown electric field, high thermal conductivity and a wide band gap of 3.1 eV at room temperature4. In addition, this polytype is the most abundant one occurring in terrestrial rocks.
The Raman spectra of SiC polytypes present in siliceous breccia pores are shown in Fig. 3a. We can detect three of the SiC polytypes: 3C, 6H and 6O.
References to standard transverse acoustic and optical phonons (TA and TO resp.), and longitudinal optical and acoustic phonons (LO and LA resp.) were obtained from literature for different polytypes28.
For 3C-SiC, only two strong Raman bands are observed at 972 cm−1 and 796 cm−1 assigned to the longitudinal E1(LO) and transverse A1(TO) optical phonon modes, respectively. For 6H-SiC, the experimental characteristic phonon modes are assigned as follows28: E2(TA) at 151 cm−1, E1(TA) at 240 cm−1, A1(LA) at 504 cm−1, E2(TO) at 762 and 783 cm−1, E1(TO) at 791 cm−1 and A1(LO) at 887 and 963 cm−1.
In the case of 6O-SiC, the main Raman modes were confirmed and matched with Raman-active vibrational modes in the orthorhombic Cmc21 structure. According to group theory, the orthorhombic Cmc21 structure with 12 atoms per unit cell gives rise to 33 Raman-active modes and factor group analysis gives irreducible mechanical representations for optical modes as Γoptic = 11A1 + 6A2 + 11B1 + 5B2, which are all Raman active. Table 3 shows the vibrational modes of 6O-SiC obtained by DFT calculations and observed experimentally by Raman spectroscopy.
We can notice that the Raman spectral features of the 6H- and 6O-SiC polytypes are close to each other. This similarity confirms the results obtained by SCXRD meaning that the structural properties of these two polytypes are very close.
The pressure dependence of the Raman vibration modes in 6H-SiC was measured up to 95 GPa29,30. In these studies29,30, the optical modes are all shifted to higher wavenumbers with pressure. Consequently, based on the comparison between the 6O and 6H vibrational modes, we can attribute the shift of the main intense modes to a variation of pressure. The strongest optical modes A1 for 6O-SiC are present at 786 cm−1, while for 6H-SiC the strongest band E2(TO) is present at 783 cm−1. Similar observation can be made for the 2 other optical transverse modes of 6H, E2(TO) and E1(TO) present at 762 cm−1 and at 791 cm−1, respectively, shifted by about 5 cm−1 towards high wavenumbers in 6O-SiC. Then, according to the pressure dependence of the vibration modes wavenumbers29,30, the observed shifts correspond to an increase in isostatic pressure close to 1 GPa. Accordingly, this suggests that the 6O polytype was formed at very high temperatures (2027–2527 °C) and at minimum pressures of 4 GPa.
Electronic properties of SiC
In Fig. 3b, we show the calculated bulk band structure of 6O-SiC using the Density Functional Theory. The results show that 6O-SiC is an indirect band gap semiconductor with the top valence band located at Γ of the Brillouin zone and the conduction band edge along the M-L symmetry line. The calculated indirect bandgaps for 3C, 6H and 6O-SiC are 2.90, 3.56 eV and 3.56 eV, respectively (Table 4). We notice that our calculations underestimate the experimental bandgap of the 3C and 6H SiC4 polytypes. However, since the calculated indirect bandgap value of the 6O-SiC is equal to that of 6H polytype, we can reasonably expect that the real indirect bandgap of the 6O polytype is around 3.10 eV.
In this study, we report the first occurrence of an orthorhombic 6O-SiC polytype as rock-forming mineral. 6O-SiC crystallizes in the space group Cmc21 with 12 atoms per unit cell. These findings establish a novel SiC mechanically stable phase with a density value close to that of 6H-SiC. The calculated indirect bandgap of 6H and 6O-SiC at room temperature are equals.
Among the SiC polytypes, 6H is the most easily synthetized and the best studied. For instance, 6H-SiC has been found to be very suitable substrates for GaN epitaxial layers for the deposition of laser diodes31.
The question that remains unresolved is if this new 6O-SiC structure can be also easily prepared, given its superior density? Most probably deposition as thin heteroepitaxial structures on single crystal substrates, known to stabilize films at large, GPa-like equivalent pressures, may allow future studies of this new phase.
Methods
Sample materials
Moissanite studied here naturally occurred in siliceous breccia rock (SB; SOLSA label: ER-NC00-0001) from Tiebaghi mine in New Caledonia. Tiebaghi is a mine and former village in Kaala-Gomen, New Caledonia, located on an ultramafic massif. The siliceous breccia samples are solid, porous beige rocks (pore size can reach cm scale). The breccia hosts lithoclasts of brownish-dark grey saprolite. Locally reddish spots occur, originating from weathering.
SEM/EDS measurements
Imaging and compositional analysis were performed using scanning electron microscope JEOL JSM-6400 equipped with an X-ray energy dispersive system (SEM/EDS) operating at 20 kV and sensitive to elements with atomic numbers from Na to U.
Micro-Raman measurements
The Raman spectra were recorded at room temperature using a DXR Raman microscope (Thermo Fisher Scientific, Inc., USA) equipped with a 900 lines/mm diffracting grating. The highest quality spectra (highest signal-to-noise) were obtained using green excitation (532 nm, Nd: YAG laser). Raman measurements were carried out at low laser power (approximately 1 mW at the sample surface) to avoid unintentionally heating alteration, structural modifications or phase transitions. A 100x magnification long working distance objective was used to focus the laser onto the sample and collect the scattered light in a backscattering geometry. Raw data was collected over a range of 80–2200 cm−1. The spectral region 3200–4000 cm−1 was investigated for some minerals species when OH stretching vibration modes were potentially expected. The spot diameter of the laser was estimated at 0.6 μm. Raman spectra were systematically recorded twice with an integration time of 60 s. For each mineral, 5 spectra were recorded and averaged. Peak deconvolution and integration were performed with the Origin software using the Gaussian-Lorentzian function.
SCXRD measurements
Single crystal X-ray diffraction. A Synergy S Rigaku 4-circles diffractometer equiped with Cu micro focus source and an Eiger 1M Dectric detector has been used to analyze the SiC grains. A full data collection was performed on the highest quality sample. The analysis of the reciprocal space is done using CrysalisPro software32. The structure has been solved using Superflip software17 and refined with Jana200618.
Computational details
The Raman-active vibrational modes of 60-SiC were calculated through Density Functional Theory (DFT) as implemented in the Crystal17 package33. The B3LYP approximation was used and the wave functions were expanded as a linear combination of Bloch functions using Gaussian-type atomic orbitals (6–31 G*)34. The Coulomb and exchange series were truncated with overlap thresholds of 10−8, 10−8, 10−8, 10−8 and 10−16, A Monkhorst-Pack sampling scheme of 16 × 16 × 16 for cubic SiC, 16 × 16 × 10 for hexagonal 6H-SiC and orthorhombic SiC were chosen after some tests. The convergence threshold on energy for the self-consistent-field procedure was fixed at 10−10 Hartree for structural optimizations and for vibration frequency calculations. Frequencies at the Gamma point were evaluated within the harmonic approximation as implemented in Crystal1735,36. The Raman intensities of the vibrational modes were calculated analytically by exploiting the scheme described by Maschio et al.37,38 at ambient temperature and an exciting wavelength of 532 nm. This scheme is based on the solutions of first and second-order coupled Perturbed–Hartree–Fock/Kohn–Sham (CPHF/KS) equations39,40. For the calculation of the elastic constants, we have used the default settings on size of lattice deformation (0.01 Å) and 3 points, including the central point with zero displacement for the numerical second derivatives calculations. We have used the default energy and force convergence criteria for vibrational frequency and elastic constants calculations as defined by Crystal17. These convergence criteria are typically tighter than separate. The band structure and DOS of the models were constructed along the appropriate high-symmetry directions of the corresponding irreducible Brillouin zone.
Data availability
The experimental and computational data that support the findings of this study are available from the corresponding author upon request.
References
Cheung, R. Silicon Carbide Microelectromechanical Systems for Harsh Environments. Imperial College Press, Сh.3, ISBN 1860946240 (2006).
Shiryaev, A. A., Griffin, W. L. Stoyanov, E. & Kagi, H. Natural silicon carbide from different geological settings: polytypes, trace elements, inclusions. 9th International Kimberlite Conference Extended, Abstract No. 9IKC-A-00075 (2008).
Zetterling, C. M. Process Technology for Silicon Carbide Devices. EMIS processing series, no. 2, INSPEC, IEE, UK (2002).
Yoshida, S. In Properties of Silicon Carbide (G. L. Harris (ed.), EMIS Data-review Series No. 13, INSPEC, London, (1995).
Ou, H. et al. Advances in wide bandgap SiC for optoelectronics. M. Eur. Phys. J. B. 87, 58 (2014).
Wellmann, P. J. Power Electronic Semiconductor Materials for Automotive and Energy Saving Applications – SiC, GaN, Ga2O3, and Diamond. Z. Anorg. Allg. Chem. 643, 1312–1322 (2017).
Kaiser, U., Chuvilin, A., Brown, P. D. & Richter, W. Origin of Threefold Periodicity in High-Resolution Transmission Electron Microscopy Images of Thin Film Cubic SiC. Microsc. Microanal. 5, 420–427 (1999).
Yaghoubi, A., Singh, R. & Melinon, P. Predicting the primitive form of rhombohedral silicon carbide (9R-SiC): A pathway toward polytypic heterojunctions. Cryst. Growth. Design 18, 7059–7064 (2018).
Shiryaev, A. A., Griffin, W. L. & Stoyanov, E. Moissanite (SiC) from kimberlites: Polytypes, trace elements, inclusions and speculations on origin. Lithos. 122, 152–164 (2011).
Di Pierro, S. et al. Rock-forming moissanite (natural silicon carbide). Am. Mineral. 88, 1817–1821 (2003).
Xu, S. et al. Moissanite in serpentinite from the Dabie Mountains in China. Mineral. Magazine. 72, 899–908 (2008).
Bai, W. et al. The PGE and base-metal alloys in the podiform chromitites of the Luobasa ophiolite, southern Tibet. Can. Mineral. 38, 585–598 (2000).
Schmidt, M. W., Gao, C., Golubkova, A., Rohrbach, A. & Connolly, J. A. Natural moissanite (SiC) - a low temperature mineral formed from highly fractionated ultra-reducing COH-fluids. Prog. Earth. Planet. Sci. 1, 27–30 (2014).
Mitchell, R. H. Kimberlites and lamproites: primary sources of diamond. Geosci. Can. 18, 1–16 (1991).
Capitani, G. C., Di Pierro, S. & Tempesta, G. The 6H-SiC structure model: Further refinement from SCXRD data from a terrestrial moissanite. Am. Mineral. 92, 403–407 (2015).
Oszlanyi, G. & Suto, A. Ab initio structure solution by charge flipping. Acta. Cryst. A60, 134–141 (2004).
Palatinus, L. & Chapuis, G. SUPERFLIP, a computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Cryst. 40, 786–790 (2007).
Petříček, V., Dušek, M. & Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 229, 345–352 (2014).
Daviau, K. & Lee, K. K. M. Decomposition of silicon carbide at high pressures and temperatures. Phys. Rev. B. 96, 174102 (2017).
Catti, M. Orthorhombic Intermediate State in the Zinc Blende to Rocksalt Transformation Pathof SiC at High pressure. Phys. Rev. Lett. 87, 035504 (2001).
Sekine, T. & Kobayashi. T. Shock compression of 6H polytype SiC to 160 GPa. Phys. Rev. B. 55, 8034 (1997). Pressure. Phys. Rev. Lett. 87, 035504 (2001).
Lu, Y. P., He, D. W., Zhu, J. & Yang, X. D. First-principles study of pressure-induced phase transition in silicon carbide. Phys. B. 403, 3543–3546 (2008).
Stokes, H. T. et al. Bilayer sliding mechanism for the wurtzite-to-rocksalt transition. Phys. Rev. B. 76, 012102 (2007).
Trumbull, R. B. et al. The carbon isotope composition of natural SiC (moissanite) from the Earth’s mantle: New discoveries from ophiolites. Lithos. 113, 612–620 (2009).
Campiglio, C., Marion, C. & Vannier, M. Etude d’une boninite à olivine de Nouvelle-Calédonie: pétrographie et chimisme des phases. Bull. Minéral. 109, 423–440 (1986).
Bailly, L. et al. Nickel-Typologie des minerai latéritiques de Nouvelle-Calédonie et facteurs de concentration de Co et Ni., Volume II, CNRT « Nickel et son environnement », p. 448 (2014).
Ravindran, P. et al. Density functional theory for calculation of elastic properties of orthorhombic crystals: application to TiSi2. J. Appl. Phys. 84, 4891–904 (1998).
Nakashima, S. & Harima, H. Raman Investigation of SiC Polytypes. Physica. Status. Solidi 162, 39–64 (1997).
Liu, J. & Vohra, Y. K. Raman modes of 6H polytype of silicon carbide to ultrahigh pressures: A comparison with silicon and diamond. Phys. Rev. Lett. 72, 4105 (1994).
Daviau, K. & Lee, K. K. M. High-Pressure, High-Temperature Behavior of Silicon Carbide: A Review. Crystals. 8, 217 (2018).
Zhang, L. et al. Influence of stress in GaN crystals grown by HVPE on MOCVD-GaN/6H-SiC substrate. Sci. Reports 4, 4179 (2014).
CrysAlisPro Software System, Version 1.171.38.41.Rigaku Oxford Diffraction, http://www.rigaku.com.
Dovesi, R. et al. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 114, 1287–1317 (2014).
Gatti, C., Saunders, V. R. & Roetti, C. Crystal field effects on the topological properties of the electron density in molecular crystals: The case of urea. J. Chem. Phys. 101, 10686–10696 (1994).
Pascale, F. et al. The calculation of the vibrational frequencies of crystalline compounds and its implementation in the CRYSTAL code. J. Comput. Chem. 25, 888–897 (2004).
Zicovich-Wilson, C. et al. Calculation of the vibration frequencies of α-quartz: The effect of Hamiltonian and basis set. J. Comput. Chem. 25, 1873–1881 (2004).
Maschio, L., Kirtman, B., Rerat, M., Orlando, R. & Dovesi, R. Ab initio analytical Raman intensities for periodic systems through a coupled perturbed Hartree-Fock/Kohn-Sham method in an atomic orbital basis. I. Theory. J. Chem. Phys. 139, 164101 (2013).
Maschio, L., Kirtman, B., Rerat, M., Orlando, R. & Dovesi, R. Ab initio analytical Raman intensities for periodic systems through a coupled perturbed Hartree-Fock/Kohn-Sham method in an atomic orbital basis. II. Validation and comparison with experiments. J. Chem. Phys. 139, 164102 (2013).
Ferrero, M., Rerat, M., Orlando, R. & Dovesi, R. The calculation of static polarizabilities of 1-3D periodic compounds. the implementation in the crystal code. J. Comput. Chem. 29, 1450–1459 (2008).
Ferrero, M., Rerat, M., Orlando, R. & Dovesi, R. Coupled perturbed Hartree-Fock for periodic systems: The role of symmetry and related computational aspects. J. Chem. Phys. 128, 014110 (2008).
Pizzagalli, L. Stability and mobility of screw dislocations in 4H, 2H and 3C silicon carbide. Acta. Materialia. 78, 236–244 (2014).
Stockmeier, M. et al. Thermal Expansion Coefficients of 6H Silicon Carbide. Mater. Sci. Forum. 600–603, 517–520 (2009).
Huang, H., Ghoniem, N. M., Wong, J. K. & Baskes, M. I. Molecular dynamics determination of defect energetics in β-SiC using three representative empirical potentials. Modell. Simul. Mater. Sci. Eng 3, 615–627 (1995).
Kamitani, K. et al. The elastic constants of siliconcarbide: a Brillouin-scattering study of 4H and 6H SiC single crystals. J. Appl. Phys. 82, 3152–3154 (1997).
Acknowledgements
We thank the European Commission for having sponsored this study in the frame of the SOLSA project (H2020 program): SC5-11d-689868. The DFT calculation work was done with the support of the French national computer center IDRIS under project no. 081842 and the regional computer center CRIANN under project no. 2007013.
Author information
Authors and Affiliations
Contributions
Y.E. performed the Raman measurements. Y.E., S.G. and D.C. carried out scanning electron microscopy studies. J.-F.B. performed additional Raman measurements and contributed to data analysis. S.P. performed the DFT calculations. F.K. contributed to elastic discussion. B.O. contributed to geological analysis and discussion on the SiC origin, O.P. performed the single crystal X-ray diffraction experiments and Y.E. wrote the manuscript with input from all authors. All authors discussed the results of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
El Mendili, Y., Orberger, B., Chateigner, D. et al. Insight into the structural, elastic and electronic properties of a new orthorhombic 6O-SiC polytype. Sci Rep 10, 7562 (2020). https://doi.org/10.1038/s41598-020-64415-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-64415-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.