Abstract
Achieving high mobility in SnO2, which is a typical wide gap oxide semiconductor, has been pursued extensively for device applications such as field effect transistors, gas sensors, and transparent electrodes. In this study, we investigated the transport properties of lightly Ta-doped SnO2 (Sn1−xTaxO2, TTO) thin films epitaxially grown on TiO2 (001) substrates by pulsed laser deposition. The carrier density (ne) of the TTO films was systematically controlled by x. Optimized TTO (x = 3 × 10−3) films with ne ~ 1 × 1020 cm−3 exhibited a very high Hall mobility (μH) of 130 cm2V−1s−1 at room temperature, which is the highest among SnO2 films thus far reported. The μH value coincided well with the intrinsic limit of μH calculated on the assumption that only phonon and ionized impurities contribute to the carrier scattering. The suppressed grain-boundary scattering might be explained by the reduced density of the {101} crystallographic shear planes.
Similar content being viewed by others
Introduction
Tin dioxide (SnO2) has been extensively studied as a practical transparent oxide semiconductor in various applications such as field-effect transistors1,2, gas sensors3,4,5, and transparent electrodes6,7,8. Hall mobility (μH) is a key parameter in determining the performance of such devices, and the μH values of bulk SnO2 single crystals are in the range of 70 to 260 cm2V−1s−1 at room temperature9,10,11. However, SnO2 thin films show a rather low μH of less than 100 cm2V−1s−1 even in well-optimized epitaxial films12,13, which limits the practical use of SnO2.
The lower μH in SnO2 epitaxial thin films is primarily attributable to the lack of lattice-matched substrates. Thus far, corundum Al2O3 and rutile TiO2 have been widely used as the substrates for the epitaxial growth14,15 of SnO2. Particularly, Al2O3, with a high thermal and chemical stability, is suitable for the growth of SnO2 thin films at high temperatures, but the SnO2 thin films deposited on Al2O3 suffer from lowered crystallinity owing to the difference between the crystal structures of the film and substrate. For example, very low μH values are frequently observed for epitaxial SnO2 films on Al2O3. TiO2 shares the same rutile structure as SnO2, but it has a relatively large lattice-mismatch with SnO2, which is 3.1% and 7.7% for the a-axis and c-axis, respectively. Indeed, it was reported that μH of the undoped SnO2 film with (001) orientation on TiO2 (001) was limited to a rather small value16, that is, ~40 cm2V−1s−1. To overcome the above-mentioned difficulty, very thick self-buffer layers12,13 have been employed to grow high-μH epitaxial SnO2 films on Al2O3.
Another important factor for achieving high μH is to control the carrier density (ne) because carriers play two competing roles in μH; an increase in ne enhances the screening of the Coulomb scattering potential and thus increases μH, whereas an increased amount of dopants suppresses μH owing to impurity scattering. To date, much effort has been made to grow undoped13,14,15,16,17,18 or heavily doped19,20,21,22 SnO2 films on a wide variety of substrates. Heavily doped SnO2 films, albeit practically important, show a low μH that is dominated by impurity scattering. Attempts to pursue high μH in undoped SnO2 thin films have been unsuccessful owing to the significant carrier scattering by the grain boundary18,23 and dislocation13,24 induced by lattice-mismatched substrates. There is a possibility to realize a high mobility in the intermediate ne region between undoped and heavily doped SnO2, but little attention has been paid to lightly doped12,23 SnO2 films.
In this study, we focus on lightly doped SnO2 thin films to achieve a high μH. We investigated the electrical transport properties of lightly Ta-doped SnO2 (Sn1−xTaxO2, TTO) films grown on TiO2 (001) substrates, which are isostructural to SnO2, with the smallest lattice mismatch. We found that the increase in ne by Ta-doping dramatically enhanced μH, probably owing to a screening of the carrier scattering by the grain boundaries and dislocations. The TTO films with ne ~ 1 × 1020 cm−3 exhibited μH of 130 cm2V−1s−1, which is the highest among SnO2 films thus far reported. Moreover, this value is close to the intrinsic limit of μH calculated by assuming that only phonon and ionized impurities contribute to the carrier scattering.
Results and Discussion
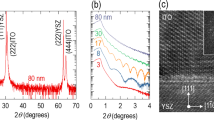
We first optimized the substrate temperature (Ts) for growth of the TTO film, where the Ta content x was fixed at 3 × 10−3. Figure 1(a) shows ω-2θ X-ray diffraction (XRD) patterns for the TTO films prepared at various Ts. Only 002 diffraction peaks from SnO2 and TiO2 were observed in all the films, which indicated epitaxial growth of (001)-oriented SnO2 films on TiO2 (001) without any impurity phases. Epitaxial growth of the SnO2 films were further confirmed by off-specular Φ-scan of 101 diffraction peaks from SnO2 and TiO2 substrates (see Supplementary Fig. S1 online). Figure 1(b) shows the reciprocal space map observed around the asymmetric 112 diffraction peak for the TTO film grown at Ts = 600 °C. The film was almost fully relaxed, as reported16 for undoped SnO2 films on TiO2 (001). Figure 1(c) plots the full width at half maximum of the rocking curve (ω scan, see Supplementary Fig. S2 online) of the 002 diffraction (FWHM002ω) as a function of Ts. Notably, FWHM002ω monotonically decreased with an increase of Ts and reached 0.07° at the highest Ts = 700 °C. This FWHM002ω value is much smaller than that reported for the SnO2 film on a thick self-buffer layer12, that is, 0.31°, which indicated very high crystallinity of the present TTO film. A similar trend, that is, improved crystallinity at high Ts, was reported in the previous research on SnO2 epitaxial films23,25,26. The TTO films grown at higher Ts tended to exhibit higher μH, as shown in Fig. 1(c). However, a slight decrease in μH was observed for the film grown at Ts = 700 °C in spite of the good crystallinity. We speculate that at such high Ts, interdiffusion of Sn and Ti atoms occurred at the film/substrate interface27, which might have caused impurity scattering and thus suppressed μH. Hereafter we fixed Ts at 600 °C.
(a) ω-2θ X-ray diffraction patterns for Sn1−xTaxO2 (TTO) films with x = 3 × 10−3 grown at various substrate temperatures (Ts). (b) A reciprocal space map around the asymmetric 112 diffraction peaks for a TTO film grown at Ts = 600 °C. A cross represents the peak position for bulk SnO2. (c) Ts dependence of Hall mobility (μH, circles) and full width at half maximum of rocking curve (ω scan) for 002 diffraction peak (FWHM002ω, diamonds) for the TTO (x = 3 × 10−3) films.
Next, we investigated the dependence of the transport properties of the TTO films on x. As shown in Fig. 2, the TTO film with the lowest x = 3 × 10−5 showed ne = 4 × 1017 cm−3 and μH = 36 cm2V−1s−1, which are close to those16 reported for undoped SnO2 films on TiO2 (001). Furthermore, ne was proportional to x and lay on the line representing a 100% doping efficiency, which indicated that each Ta5+ ion generated one carrier electron. This implied that the lightly-doped TTO films were free from unfavourable defects such as clustered dopants28 and accepter-like defects29. Remarkably, μH dramatically increased with increasing x at x ≤ 3 × 10−3. This behavior was rationalized by assuming an enhanced screening of dislocations13 and/or grain boundaries18,23 owing to the increased ne. The TTO films with x = 3 × 10−3 (ne ~ 1 × 1020 cm−3) exhibited the highest μH of 126–131 cm2V−1s−1, which is the highest among the μH values reported for undoped and doped SnO2 films so far. Further increase in x yielded a slight decrease in μH, possibly owing to the manifestation of ionized impurity scattering, as will be discussed later. The lowest resistivity, 2.5 × 10−4 Ωcm, and sheet resistance, 20.2 Ωsq.−1, were obtained for the TTO film with x = 1 × 10−2, as shown in Fig. 2(a).
Room temperature (a) resistivity, (b) carrier density (ne), and (c) μH for the TTO films as a function of x. The inset of (a) shows sheet resistance of the films. The broken line is the expected ne when all the doped Ta5+ ions substitute to the Sn4+ sites and generate one electron per Ta (100% doping efficiency).
We now discuss the transport properties of the TTO films in comparison with the literature data. Figure 3 plots μH against ne for thin films12,13,16,23, including ours, and bulk single crystals9,11 of SnO2. The previously reported μH values for thin films were generally lower than those of bulk single crystals with similar ne values. However, our TTO films with ne ~ 1 × 1020 cm−3 exhibited a record-high μH (130 cm2V−1s−1) for thin films, which is comparable to that for a bulk single crystal with a similar ne value. Such an extremely high μH value suggests that the film contained a negligibly small amount of extrinsic sources of carrier scattering, such as neutral impurities, grain boundaries, and dislocations. In other words, intrinsic sources of carrier scattering, such as phonons and ionized impurities, supposedly dominated μH.
Room temperature μH as a function of ne for SnO2 bulk single crystals (squares) and thin films [circles (present study) and triangles (literature data)]. The data for undoped single crystals in the a-direction (μa) and Sb-doped single crystals in the c-direction (μc) are from refs. 9,11, respectively. The data for Ta-doped (110)-, undoped (001)-, Sb-doped (101)-, and undoped (101)-films are from refs. 23,16,12,13, respectively. A solid line with diamond symbols (μcal) represents calculated μH assuming that only phonon (μlat, broken line) and ionized impurity (μiis, solid line) scattering contribute to μH (μcal−1 = μlat−1 + μiis−1).
To test the above-mentioned hypothesis, we calculated the Hall mobility (μcal) taking only phonon and ionized impurity scattering into account, as
where μlat is the lattice mobility associated with phonon scattering and μiis is the Hall mobility limited by ionized impurity scattering. For μlat, we used a fixed value (260 cm2V−1s−1) observed for undoped single crystals in the a-direction9. The μiis value was calculated by using the Brooks–Herring–Dingle (BHD) formula30, which has been successfully used to analyze μiis for Sn-doped In2O331, Al-doped ZnO28,29, and Nb-doped TiO232. The BHD formula is written as
where ε0 is the permittivity of free space, εr is the relative static dielectric constant, ħ is the reduced Planck’s constant, e is the elementary charge, and m* is the electron effective mass. Z and nI are the charge and the density of the ionized impurity, respectively. The screening function Fii is given by
with
Considering the high doping efficiency, all the doped Ta was supposed to behave as singly charged ions (Ta5+ substituting for Sn4+). Although it was difficult to determine the valence state of Ta in TTO experimentally33 (see Supplementary Fig. S3 online), theoretical calculations34,35 reported that Ta exists in the pentavalent state (Ta5+) in TTO. Thus, we assumed Z = 1 and nI = ne. Because the films in this study were (001)-oriented, we used εra = 13.5 for εr36. For m*, we used experimentally determined \({m}_{a}^{\ast }\) values as a function of ne and their linear interpolation37. As shown in Fig. 3, μcal was higher than most of the experimental data, which indicated that the suppression of μH arose from carrier scattering by extrinsic sources. Notably, however, the μH values at ne ≥ 9 × 1019 cm−3 (x = 3 × 10−3 and 1 × 10−2) in the present study agreed well with μcal. This proved that in these high μH films, carrier scattering by neutral impurities, dislocations, and grain-boundaries was negligibly small compared with that by ionized impurities and phonons, and that the reduced μH at ne = 2.4 × 1020 cm−3 (x = 1 × 10−2) was attributed to the increased ionized impurity scattering.
To discuss the carrier scattering mechanisms in more detail, we measured temperature dependences of ne and μH for in the TTO films with x = 3 × 10−4 – 1 × 10−2. As shown in Fig. 4(a), the ne values were independent of temperature, indicating that the TTO films in this study were in the degenerately-doped regime. Notably, the TTO films with x ≥ 1 × 10−3 showed negative temperature coefficients of μH (Fig. 4(b)) around room temperature, being the specific characteristic of phonon scattering. This implies that, at room temperature, the μH values are dominated by phonon scattering, in consistence with the arguments based on the room temperature data (Fig. 3). At low temperature, phonon scattering is suppressed9, and ionized impurities are supposed to be the intrinsic sources of carrier scattering. Remarkably, as shown in Fig. 4(c), μH at 10 K for the TTO film with x = 1 × 10−2 (ne = 2.4 × 1020 cm−3) agrees well with μiis, which is known to be temperature-independent in degenerately-doped regime. This result supports the conclusion that μH of the film is dominated by ionized impurity scattering and phonon scattering at room temperature (Fig. 3). As x and thus ne decreased, μH at 10 K started deviating downward from μiis. This behaviour indicates that the TTO films with x < 1 × 10−2 contain extrinsic sources of carrier scattering, pronounced especially at low temperature. Thermal-activation-type behaviour of μH was observed for the TTO film with x = 3 × 10−4 (Fig. 4(d)), demonstrating that μH is governed by grain boundary scattering38 in the film, although grain-boundary scattering in SnO2 epitaxial films has scarcely been studied so far. Dominguez et al. proposed that {101} crystallographic shear planes (CSPs) in SnO2 films, which are induced by misfit dislocations39, may act like grain boundaries18. Similarly, we speculated that the carrier scattering at {101} CSPs was responsible for the lower μH than μcal at ne < 9 × 1019 cm−3.
Temperature dependence of (a) ne and (b) μH for the TTO films with x = 3 × 10−4 – 1 × 10−2. (c) μH at 10 K (circles) as a function of ne, in comparsion with μiis (solid line). (d) μH for the TTO film with x = 3 × 10−4 plotted against the inverse of temperature (1/T). The dashed line represents the least-squares fit to the Arrhenius equation, yielding an activation energy value of 30.8 meV.
Judging from the complete screening by free carriers at ne ≥ 9 × 1019 cm−3, the CSP-based grain-boundary scattering in the TTO films was supposed to be weak. We considered that lattice matching and growth orientation play an essential role in the CSP-based grain-boundary scattering as follows. Owing to the good lattice-matching to SnO2, the TiO2 (001) substrate would induce lower densities of misfit dislocations and thus CSPs in the films than other substrates18,39. Furthermore, the angle between {101} CSPs and the basal plane of the SnO2 (001) film was approximately 34°, as shown in Fig. 5(a). The shallow angle would cause termination of the {101} CSPs at the crossing point with complementary {101} CSPs39 at the early stage of the film growth. Indeed, as shown in Fig. 5(b), cross-sectional transmission electron microscopy (TEM) observations revealed that the TTO films on the TiO2 substrate had lower densities of CSPs than those on other substrates18,39 and that the CSPs did not reach the film surface, which supported the above-mentioned scenario. These structural characteristics can account for the lower contribution of carrier scattering at the CSP-based grain boundaries to the carrier transport in the TTO films on TiO2 (001). However, SnO2 epitaxial films on other substrates than TiO2 (001) have reportedly shown highly populated {101} CSPs inclined steeply to the basal planes18,39, as schematically illustrated in Fig. 5(a). The CSPs in SnO2 epitaxial films are induced by misfit dislocations, and they are not energetically favorable in bulk crystal, unlike the CSPs induced by off-stoichiometry, as seen in oxygen-deficient rutile TiO2 crystals40. Therefore, the density of CSPs decreased as the film thickness increases18. Nevertheless, some of the CSPs in those films survived even near the surface of the films18. These results suggest that the CSP-based grain-boundary scattering is more significant in the SnO2 epitaxial films on other substrates than TiO2 (001), which can account for the lower μH than those for the TTO films on TiO2 (001), as depicted in Fig. 3.
(a) Schematics of {101} planes, at which crystallographic shear planes (CSPs) are formed, against SnO2 basal planes with (001), (101), (110), and (100) orientation using the VESTA program45. θ denotes the angle between {101} and each SnO2 basal plane. (b) Cross-sectional transmission electron microscopy image of a TTO film with x = 3 × 10−3. The incident electron beam was parallel to the [010] direction. The arrow in the film indicates {101} CSP.
To verify the proposed model, we investigated film thickness and growth orientation dependence of μH for TTO films with x = 3 × 10−3 grown on various substrates12,13,14,15,16,17,18,19,20,21,23,24,25,26,27,39,41,42, (001)-, (101)-, and (110)-planes of TiO2, and m-, r-, and c-planes of Al2O3 substrates (see Supplementary Fig. S4 online). Figure 6 plots room temperature ne and μH for the TTO films with various film orientations as a function of the film thickness. With increasing film thickness, the μH values increased probably owing to the synergistic effect of enlarged crystalline grains43,44 and reduced density of threading dislocations24 and {101} CSPs18,39. The highest μH was achieved for the (001)-oriented TTO films, followed in order by the (101)-, the (110)-, and the (100)-oriented ones. This behaviour can be explained by the CSP-based grain-boundary scattering because the angle between the CSP and the basal planes of the films becomes small in the same order (Fig. 5(a)). Notably, the TTO films with the same orientation showed similar μH values even though different kinds of substrates were used. The orientation dependence of μH cannot be explained by the anisotropy in electron effective mass of SnO2 (see Supplementary Fig. S5 online). It was suggested that {101} CSPs play a significant role in the carrier transport in the TTO epitaxial thin films.
Summary
We investigated the transport properties of Sn1−xTaxO2 (TTO) films with x = 3 × 10−5–1 × 10−2 epitaxially grown on TiO2 (001) substrates. The ne values for the TTO films were almost equal to the concentrations of Ta dopants, which demonstrated the very high doping efficiency of Ta. The μH values of the TTO films with ne ≥ 9 × 1019 cm−3 (x ≥ 3 × 10−3) agreed well with the intrinsic limit of μH assuming that only phonon and ionized impurities contributed to carrier scatterings. Negligible contribution of the grain-boundary scattering to μH might arise from a reduced density of CSPs. The TTO films with ne ~ 1 × 1020 cm−3 (x = 3 × 10−3) exhibited a very high μH of 130 cm2V−1s−1, which is the highest among SnO2 films thus far reported. The μH values for the TTO (x < 3 × 10−3) films rapidly decreased with a decrease of x, which suggested a weakened screening of dislocation and/or grain-boundary scatterings owing to the decreased ne.
Methods
TTO films with a thickness of 100–120 nm, with x = 3 × 10−5–1 × 10−2, were grown on TiO2 (001) substrates by pulsed laser deposition (PLD) with a KrF excimer laser. TTO films with x = 3 × 10−3 were grown (001)-, (101)-, and (110)-planes of TiO2, and m-, r-, and c-planes of Al2O3 substrates. The repetition rate and the fluence of the laser were set at 2 Hz and 1–2 J ∙ cm−2, respectively. The typical growth rate was 0.14–0.17 Å per shot. Sintered pellets of TTO with x = 3 × 10−4–1 × 10−2 were used as PLD targets. TTO films with x = 3 × 10−5 were fabricated by alternating ablation23 of a commercial undoped SnO2 (4 N purity, Toshima MFG) target and a TTO pellet with x = 3 × 10−4. In this study, nominal x values were used to represent the chemical compositions of the films because stoichiometric transfer of Ta from the targets to the films has been reported for TTO films grown under a similar condition23. The base pressure of the PLD chamber was maintained at 3 × 10−9 Torr. Oxygen partial pressure and Ts during film growth were 1 × 10−2 Torr and 400–700 °C, respectively. Crystal structure and crystallinity were evaluated by XRD measurements using a four-circle diffractometer (Bruker AXS, D8 DISCOVER). The cross-sectional microstructure of the films was observed by using a transmission electron micrscope (FEI, Titan Cubed G2 60-300) operated at 300 kV. Hall effect and resistivity were measured by using a standard six-terminal method. The Hall-bar width and the distance between voltage terminals for four-probe measurements were 1 mm and 2.4 mm, respectively. Ag or In electrodes were used for ohmic contacts. A laboratory constructed system equipped with a 2 T electromagnet was used for room temperature measurements. Current–voltage characteristics and Hall voltage-magnetic field characteristics were measured repeatedly (at least twice) to confirm the reliability and reproducibility of the measurements. Temperature dependence of the transport properties was measured with a commercially available system (Quantum design, physical properties measurement system (PPMS Model 6000)).
Data availability
The datasets during the current study are available from the corresponding author on reasonable request.
References
Yu, X., Marks, T. J. & Facchetti, A. Metal oxides for optoelectronic applications. Nat. Mater. 15, 383–396 (2016).
Wei Shih, C., Chin, A., Fu Lu, C. & Fang Su, W. Remarkably high mobility ultra-thin-film metal-oxide transistor with strongly overlapped orbitals. Sci. Rep. 6, 19023, https://doi.org/10.1038/srep19023 (2016).
Das, S. & Jayaraman, V. SnO2: A comprehensive review on structures and gas sensors. Prog. Mater. Sci. 66, 112–255 (2014).
Vallejos, S. et al. Aerosol assisted chemical vapour deposition of gas sensitive SnO2 and Au-functionalised SnO2 nanorods via a non-catalysed vapour solid (VS) mechanism. Sci. Rep. 6, 28464, https://doi.org/10.1038/srep28464 (2016).
Palla Papavlu, A. et al. Highly sensitive SnO2 sensor via reactive laser-induced transfer. Sci. Rep. 6, 25144, https://doi.org/10.1038/srep25144 (2016).
Ellmer, K. Past achievements and future challenges in the development of optically transparent electrodes. Nat. Photonics 6, 809–817 (2012).
Yang, J. K. et al. Reference of Temperature and Time during tempering process for non-stoichiometric FTO films. Sci. Rep. 5, 15001, https://doi.org/10.1038/srep15001 (2015).
Yu, S., Li, L., Lyu, X. & Zhang, W. Preparation and investigation of nano-thick FTO/Ag/FTO multilayer transparent electrodes with high figure of merit. Sci. Rep. 6, 20399, https://doi.org/10.1038/srep20399 (2016).
Fonstad, C. G. & Rediker, R. H. Electrical Properties of High-Quality Stannic Oxide Crystals. J. Appl. Phys. 42, 2911 (1971).
Galazka, Z. et al. Growth, characterization, and properties of bulk SnO2 single crystals. Phys. Status Solidi A 211, 66–73 (2014).
Morgan, D. F. & Wright, D. A. Electrical properties of single crystals of antimony-doped stannic oxide. Br. J. Appl. Phys. 17, 337–340 (1966).
White, M. E., Bierwagen, O., Tsai, M. Y. & Speck, J. S. Electron transport properties of antimony doped SnO2 single crystalline thin films grown by plasma-assisted molecular beam epitaxy. J. Appl. Phys. 106, 093704 (2009).
Mun, H., Yang, H., Park, J., Ju, C. & Char, K. High electron mobility in epitaxial SnO2−x in semiconducting regime. APL Mater. 3, 076107 (2015).
Semancik, S. & Cavicchi, R. E. The growth of thin, epitaxial SnO2 films for gas sensing applications. Thin Solid Films 206, 81–87 (1991).
Rachut, K., Körber, C., Brötz, J. & Klein, A. Growth and surface properties of epitaxial SnO2. Phys. status solidi A 211, 1997–2004 (2014).
Okude, M. et al. Effect of in situ annealed SnO2 buffer layer on structural and electrical properties of (001) SnO2/TiO2 heterostructures. J. Phys. D 41, 125309 (2008).
Zhen, Y. et al. Investigations of growth kinetics of pulsed laser deposition of tin oxide films by isotope tracer technique. J. Appl. Phys. 108, 1–7 (2010).
Dominguez, J. E., Fu, L. & Pan, X. Q. Effect of crystal defects on the electrical properties in epitaxial tin dioxide thin films. Appl. Phys. Lett. 81, 5168–5170 (2002).
Kim, Y., Lee, S. W. & Chen, H. Microstructural evolution and electrical property of Ta-doped SnO2 films grown on Al2O3 (0001) by metalorganic chemical vapor deposition. Thin Solid Films 405, 256–262 (2002).
Feng, X. et al. Highly thermal stable transparent conducting SnO2:Sb epitaxial films prepared on α-Al2O3 (0001) by MOCVD. Appl. Surf. Sci. 254, 6601–6604 (2008).
Luan, C., Zhu, Z., Mi, W. & Ma, J. Effect of Sb doping on structural, electrical and optical properties of epitaxial SnO2 films grown on r-cut sapphire. J. Alloys Compd. 586, 426–430 (2014).
Nakao, S. et al. High mobility exceeding 80 cm2V−1s−1 in polycrystalline Ta-Doped SnO2 thin films on glass using anatase TiO2 seed layers. Appl. Phys. Express 3, 031102 (2010).
Toyosaki, H., Kawasaki, M. & Tokura, Y. Electrical properties of Ta-doped SnO2 thin films epitaxially grown on TiO2 substrate. Appl. Phys. Lett. 93, 132109 (2008).
Vasheghani Farahani, S. K. et al. Influence of charged-dislocation density variations on carrier mobility in heteroepitaxial semiconductors: The case of SnO2 on sapphire. Phys. Rev. B 86, 245315 (2012).
Tsai, M. Y., White, M. E. & Speck, J. S. Plasma-assisted molecular beam epitaxy of SnO2 on TiO2. J. Cryst. Growth 310, 4256–4261 (2008).
White, M. E., Tsai, M. Y., Wu, F. & Speck, J. S. Plasma-assisted molecular beam epitaxy and characterization of SnO2 (101) on r-plane sapphire. J. Vac. Sci. Technol. A 26, 1300 (2008).
Palgrave, R. G., Bourlange, A., Payne, D. J., Foord, J. S. & Egdell, R. G. Interfacial diffusion during growth of SnO2 (110) on TiO2 (110) by Oxygen Plasma Assisted Molecular Beam Epitaxy. Cryst. Growth Des. 9, 1793–1797 (2009).
Ellmer, K. Resistivity of polycrystalline zinc oxide films: current status and physical limit. J. Phys. D 34, 3097–3108 (2001).
Jia, J., Oka, N., Kusayanagi, M., Nakatomi, S. & Shigesato, Y. Origin of carrier scattering in polycrystalline Al-doped ZnO films. Appl. Phys. Express 7, 105802 (2014).
Dingle, R. B. Scattering of electrons and holes by charged donors and acceptors in semiconductors. Philos. Mag. 46, 831–840 (1955).
Shigesato, Y. & Paine, D. C. Study of the effect of Sn doping on the electronic transport properties of thin film indium oxide. Appl. Phys. Lett. 62, 1268–1270 (1993).
Furubayashi, Y. et al. Transport properties of d-electron-based transparent conducting oxide: Anatase Ti1−xNbxO2. J. Appl. Phys. 101, 093705 (2007).
Weidner, M., Brötz, J. & Klein, A. Sputter-deposited polycrystalline tantalum-doped SnO2 layers. Thin Solid Films 555, 173–178 (2014).
Behtash, M., Joo, P. H., Nazir, S. & Yang, K. Electronic structures and formation energies of pentavalent-ion-doped SnO2: First-principles hybrid functional calculations. J. Appl. Phys. 117, 175101 (2015).
Williamson, B. et al. Resonant Ta Doping for Enhanced Mobility in Transparent Conducting SnO2. Chem. Mater. 32, 1964–1973 (2020).
Summitt, R. Infrared absorption in single-crystal stannic oxide: Optical lattice-vibration modes. J. Appl. Phys. 39, 3762–3767 (1968).
Feneberg, M. et al. Anisotropy of the electron effective mass in rutile SnO2 determined by infrared ellipsometry. Phys. Status Solidi A 211, 82–86 (2014).
Bruneaux, J., Cachet, H., Froment, M. & Messad, A. Correlation between structural and electrical properties of sprayed tin oxide films with and without fluorine doping. Thin Solid Films 197, 129–142 (1991).
Wakabayashi, H., Suzuki, T., Iwazaki, Y. & Fujimoto, M. Defect Structure of Heteroepitaxial SnO2 Thin Films Grown on TiO2 Substrates. Jpn. J. Appl. Phys. 40, 6081–6087 (2001).
Bursill, L. A. & Hyde, B. G. Crystallographic shear in the higher titanium oxides: structure, texture, mechanisms and thermodynamics. Prog. Solid State Chem. 7, 177–253 (1972).
Kim, D. H., Kim, W.-S., Lee, S. B. & Hong, S.-H. Gas sensing properties in epitaxial SnO2 films grown on TiO2 single crystals with various orientations. Sensors Actuators B Chem. 147, 653–659 (2010).
Kim, D. H., Kwon, J.-H., Kim, M. & Hong, S.-H. Structural characteristics of epitaxial SnO2 films deposited on a- and m-cut sapphire by ALD. J. Cryst. Growth 322, 33–37 (2011).
Agashe, C., Hüpkes, J., Schöpe, G. & Berginski, M. Physical properties of highly oriented spray-deposited fluorine-doped tin dioxide films as transparent conductor. Sol. Energy Mater. Sol. Cells 93, 1256–1262 (2009).
Isshiki, M. et al. Improving Mobility of F-Doped SnO2 Thin Films by Introducing Temperature Gradient during Low-Pressure Chemical Vapor Deposition. Jpn. J. Appl. Phys. 51, 095801 (2012).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 15K04687 and CREST, JST. S.N. gratefully acknowledges Ms. Reiko Nagashima of the University of Tokyo for her sincere encouragement. We thank Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.
Author information
Authors and Affiliations
Contributions
S.N. conceived the project. M.F. grew and characterized the films with the help of S.N., K.S. and Y.H. D.O. and K.M. performed the TEM observations. T.H. supervised the project. M.F., S.N., Y.H. and T.H. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fukumoto, M., Nakao, S., Shigematsu, K. et al. High mobility approaching the intrinsic limit in Ta-doped SnO2 films epitaxially grown on TiO2 (001) substrates. Sci Rep 10, 6844 (2020). https://doi.org/10.1038/s41598-020-63800-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-63800-3
This article is cited by
-
Spray pyrolyzed Al-doped SnO2 films with desirable type inversion and physical properties for use in transparent thin-film heater
Journal of Materials Science: Materials in Electronics (2024)
-
Transparent conductive SnO2 thin films via resonant Ta doping
Science China Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.