Introduction

Silicene, one of the two-dimensional group IV materials such as graphene, is a single layer of silicon atoms arranged in a honeycomb lattice and is similar to a buckled graphene lattice1,2,3,4. The low-energy physics of silicene can be described by the two-dimensional Dirac equation like graphene1,4,5. Silicene is a quantum spin Hall insulator with a spin-orbit coupling of 3.9 meV1,2,5, and various topological phases were predicted under an electric field and an exchange field4,6.

The layers in bilayer silicene can be bound together by covalent bonds unlike the layers in bilayer graphene bound by the van der Waals interaction. Due to a buckled structure, bilayer silicene can have various structures, which are semimetallic7,8. Multilayer silicene has been synthesized by several groups9,10,11, and effects of intercalation and hydrogenation on the (opto)electronic properties of bilayer silicene have been studied8,12. Most works on bilayer silicene have been done without considering electron-electron interactions. Under electron-electron interactions, bilayer silicene was predicted to be a topological superconductor13.

A planar AA-stacked bilayer silicene, where all the silicon atoms of a layer are covalently bonded to the silicon atom of the other layer, has the lowest energy7, but needs to overcome considerable energy barriers14. AB-stacked bilayer silicene, where the silicon atoms of a layer reside on top of a carbon atom (dimer sites) or a hollow center (nondimer sites) of the other layer, is known to be an antiferromagnetic insulator with an indirect band gap of 0.29 eV14. AB-stacked bilayer silicene has covalent interlayer bonds at the dimer sites, breaking the π-bond network of each layer, and the interactions of π-electrons localized on nondimer sites are responsible for the intralayer ferrimagnetic and interlayer antiferromagnetic order of AB-stacked bilayer silicene14.

On the other hand, the spin-valley degree of freedom characterized by the product of spin and valley indices is a new degree of freedom other than spin and valley, and can be employed for advanced electronics4,15,16. Inversion symmetry breaking together with spin-orbit coupling in monolayers of MoS2 was reported to lead to valley-contrasting spin splitting, which suppresses spin and valley relaxations and results in coexisting spin and valley Hall effects15. Antiferromagnetic order coupled to the valley degree of freedom was reported to result in the spin-valley degree of freedom, which leads to spin-valley-dependent optical selection rule and can lead to a renormalization of the valley gaps under a strong enough spin-orbit coupling16. In the π-band tight-binding models for monolayer and bilayer silicene, staggered exchange field was predicted to lead to a quantum spin-valley Hall insulator phase4,17,18.

The valley degree of freedom can be distinguished in systems where inversion symmetry is broken19,20,21,22,23. Under a small inversion symmetry-breaking potential, the Berry curvature is sharply peaked at each valley and the valley Chern number can be accurately defined20,23. If the inversion symmetry-breaking potential increases, the Berry curvature peak pertaining to each valley can be broadened and partially mixed with each other, and the valley Chern number obtained by integrating the the Berry curvature around a valley will deviate from the quantized value. In that case, it is not clear how the valley-related physics such as the bulk-edge correspondence would change. Actually, the inversion symmetry-breaking potential due to a spontaneous magnetic order may not be small enough to ensure the sharply peaked Berry curvature.

In this work, our density functional theory (DFT) calculations show that while the intralayer ferrimagnetic and interlayer antiferromagnetic order of AB-stacked bilayer silicene gives a non-quantized spin-valley Chern number, there exist backscattering-free gapless edge states corresponding to a quantum spin-valley Hall effect. Using a tight-binding (TB) model for a honeycomb bilayer, we found that the valley mixing occurs abruptly as the interlayer potential difference increases above a threshold, but occurs gradually as the staggered AB-sublattice potential increases. The interlayer potential difference induces an abrupt change of the valley Chern number from a quantized value to zero. The staggered AB-sublattice potential induces a gradual decrease of the valley Chern number from a quantized value, while maintaining backscattering-free gapless edge states corresponding to a quantum valley Hall effect. As a result, under an inversion symmetry-breaking potential in the form of the staggered AB-sublattice potential, such as an antiferromagnetic order and a hexagonal diatomic sheet, a finite but non-quantized (spin-)valley Chern number can correspond to a quantum (spin-)valley Hall insulator.

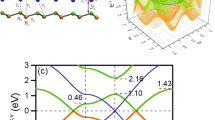
Figure 1(a) shows the spin density of AB-stacked bilayer silicene sheet. The spin density is mostly localized on the nondimer sites with intralayer ferrimagnetic and interlayer antiferromagnetic order as previously reported14. Figure 1(b) shows the band structure of AB-stacked bilayer silicene, where the energy bands with opposite spins were completely overlapped. The band structure indicates that the AB-stacked bilayer silicene is an antiferromagnetic insulator with an indirect band gap ~0.36 eV, consistently with a previous work14. Figure 1(c,d) show the Berry curvature maps for opposite spins. The Berry curvature shows opposite signs at opposite valleys and for opposite spins, indicating a possible spin-valley Hall effect. From the spin-valley-resolved Chern number \(C(s,\xi )\) ~sign(s\(\xi \))0.67, four types of the Chern number can be defined4,18. The Chern numbers were zero except for the spin-valley Chern number Csv ~ 2.68, which is not quantized but still indicates a spin-valley Hall effect.

Figure 1
figure 1

DFT calculations for bilayer silicene sheet. (a) Spin density. Green ball corresponds to silicon atom. The red and blue colors represent opposite spins. (b) Band structure. Energy bands with opposite spins were completely overlapped. (c,d) Show the Berry curvature maps for opposite spins. The bright and dark spots correspond to positive and negative Berry curvature, respectively. b1 and b2 represent reciprocal lattice vectors. K+ and K− correspond to the opposite valleys. (e,f) Show the band gap Eg and the spin-valley Chern number CSV as a function of \(\Delta d=(d-{d}_{0})/{d}_{0}\times 100\), where d (d0) is the strained (equilibrium) interlayer distance.

Full size image

The Berry curvature shows broad peaks of small height. The Berry curvature peak pertaining to each valley can be partially mixed, giving the non-quantized spin-valley Chern number. A small inversion-symmetry breaking potential ensures the sharply peaked Berry curvature20,23, and the staggered magnetization in the AB-stacked bilayer silicene decreases with increasing interlayer distance24. Figure 1(e,f) show the band gap and the spin-valley Chern number as a function of \(\Delta d=(d-{d}_{0})/{d}_{0}\times 100\), respectively, with a strained (equilibrium) interlayer distance d (d0).

The sublattice magnetization on the nondimer sites, obtained from the Mulliken population analysis, is 0.3 μB at equilibrium. As the interlayer distance increases, the sublattice magnetization gradually decreases to zero, becoming nonmagnetic when Δd~35%. As the interlayer distance increases, the antiferromagnetic band gap decreases due to the reduction of staggered magnetization, and the spin-valley Chern number gradually approaches Csv~4, confirming that the non-quantized spin-valley Chern number is due to a large staggered magnetization. Next, we have investigated AB-stacked bilayer silicene nanoribbons with zigzag edges in order to confirm the corresponding spin-valley Hall effect. The ribbon width is represented by the number N of the C-C pairs on a layer in the unit cell.

Figure 2 shows the band structures of the zigzag-edge nanoribbons with N = 16 near the Fermi level EF, where the energy bands with opposite spins were completely overlapped. As shown in Fig. 2(a), nanoribbons with bare edges have gapless edge states within the bulk gap, indicating that bilayer silicene can be a topologically nontrivial insulator while the spin-valley Chern number is not quantized. As can be seen in Fig. 2(b–d), there are gapless edge states when the dimer edge sites are terminated by hydrogen, but the gapless edge states disappear when the nondimer edge sites are terminated with hydrogen.

Figure 2
figure 2

DFT band structures of zigzag-edge nanoribbons with N = 16. The top of each panel shows the corresponding edge structure, where red dots correspond to hydrogen. (a) Bare edges. (b) Hydrogen termination at the dimer edge sites. (c) Hydrogen termination at the nondimer edge sites. (d) Hydrogen termination at both edge sites. Energy bands with opposite spins were completely overlapped.

Full size image

The gapless edge states in Fig. 2(a,b) are not connected with valence and conduction bands, which can be attributed to edge potentials. Nanoribbons inevitably have edge potentials, which can be induced by dangling σ-bonds, functional groups passivating the dangling bonds and edge-localized magnetic moments25,26,27. In a quantum valley Hall insulator, the dispersion of the edge state band is sensitive to edge potentials, varying from gapped flat-band to gapless chiral modes, because the edge potentials can introduce bearded-edge-like properties on the zigzag-edges20.

To check whether the gapless edge states correspond to any quantum Hall effect, we have investigated the square of the wavefunction \(|\Psi {|}^{2}\) near EF. Figure 3(a) shows \(|\Psi {|}^{2}\) at EF in the nanoribbons with bare edges, where the gapless edge states are confined on an edge, possibly indicating a quantum Hall effect. Figure 3(b) shows the schematics for the propagation of the gapless edge states constructed from \(|\Psi {|}^{2}\) at EF and the band velocity. Since each state contributes \(\tfrac{{e}^{2}}{h}\) to the conductivity, the Hall conductivity can be estimated in units of \(\tfrac{{e}^{2}}{h}\) by counting the number of states propagating in a given direction. In Fig. 3(b), we can obtain a spin-valley Hall conductivity σsv = 4 \(\tfrac{{e}^{2}}{h}\) and can confirm that backscattering of the gapless edge states requires inversion of the spin-valley index s\(\xi \). Time-reversal symmetry for a fixed valley and inter-valley separation for a fixed spin protects the gapless edge states from backscattering. As a result, the AB-stacked bilayer silicene is believed to be a quantum spin-valley Hall insulator, while the spin-valley Chern number is not quantized. In zigzag-edge nanoribbons with N = 32, we obtained the same results.

Figure 3
figure 3

Schematics for gapless edge states in the zigzag-edge nanoribbons with bare edges. (a) The square of the wavefunction \(|\Psi {|}^{2}\) at EF for N = 16. (b) Schematics for the propagating states at EF. The red and blue colors represent the opposite spins. The up and down arrows correspond to the opposite propagating directions. s, \(\xi \) and s\(\xi \) are spin, valley and spin-valley indices, respectively.

Full size image

The gapless edge states with σsv = 4 \(\tfrac{{e}^{2}}{h}\) correspond to Csv = 4, which is consistent with the spin-valley Chern number obtained at the limits of small staggered magnetization shown in Fig. 1(f). For a quantum spin-valley Hall insulator, the bulk-edge correspondence is known to be exactly established only at a topological domain wall4,18. At a vacuum interface, the number of gapless edge states depends on the edge condition and may not correspond to the spin-valley Chern number. Nevertheless, the gapless edge states in Figs. 2 and 3 show that the AB-stacked bilayer silicene is a quantum spin-valley Hall insulator while the spin-valley Chern number is not quantized.

The (spin-)valley Chern number and the bulk-edge correspondence are based on the assumption that opposite valleys are well separated19,20,21,22,23. At an armchair edge, where opposite valleys are completely mixed, the bulk-edge correspondence has no meaning. For a large inversion symmetry-breaking potential, the Berry curvature still centered on each valley may be broadened and partially mixed with each other, and thus the (spin-)valley Chern number obtained by integrating the Berry curvature around each valley may deviate from the quantized value. To clarify the effect of partial valley mixing, the TB model of Eq. (1) for the AB-stacked honeycomb bilayer was investigated (see the Methods section).

Figure 4(a) shows the absolute value of spin-valley-resolved Chern number \(|C(s,\xi )|\) as a function of the inversion symmetry-breaking potentials. We can consider two types of potential, interlayer potential difference 2V and staggered AB-sublattice potential Δ. For a small enough V and Δ, \(|C(s,\xi )|=1\). While \(|C(s,\xi )|\) abruptly changes from 1 to 0 as V increases to t0, \(|C(s,\xi )|\) gradually decreases as Δ increases. In the intralayer ferrimagnetic and the interlayer antiferromagnetic order, the staggered magnetization Mi corresponds to a combination of a interlayer potential difference and a staggered AB-sublattice potential, with opposite signs for opposite spins. As M increases, \(|C(s,\xi )|\) gradually decreases, too. The abrupt and gradual change of the spin-valley-resolved Chern number can be attributed to the Berry curvature.

Figure 4
figure 4

TB calculations for honeycomb bilayer sheet. (a) Absolute value of spin-valley-resolved Chern number \(|C(s,\xi )|\) as a function of inversion symmetry breaking potentials. (b,c) Show the Berry curvature maps for V = 0.9 and Δ = 0.9, respectively.

Full size image

Figure 4(b,c) show the Berry curvature maps for V = 0.9 and Δ = 0.9, respectively. For a small V and Δ, the Berry curvature is sharply peaked at each valley. The increase in V shifts the Berry curvature peak away from the valley while maintaining its sharp shape as shown in Fig. 4(b), and the mixing of the Berry curvature peak pertaining to each valley abruptly occurs when the Berry curvature peak reaches the Brillouin zone border. As shown in Fig. 4(c), the increase in Δ broadens and lowers the Berry curvature peak while maintaining its center at each valley, and the mixing of the tails of the Berry curvature peak pertaining to each valley gradually increases with Δ.

Under a staggered AB-sublattice potential Δ, the Berry curvature in a honeycomb monolayer was reported to be \(\Omega (q)=3\Delta \xi /2{({\Delta }^{2}+3{q}^{2})}^{3/2}\) for small q, where q is the wavevector measured from the K point in the Brillouin zone20. As Δ increases, the Berry curvature peak broadens while maintaining its center on each valley, consistently with our results. Under an interlayer potential difference 2V, the Berry curvature in a honeycomb bilayer was reported to be \(\Omega (q)=-\,2\xi {t}_{1}V{q}^{2}/{({q}^{4}+{t}_{1}^{2}{V}^{2})}^{3/2}\) for small q23. As V increases, the Berry curvature peak moves away from the valley, consistently with our results.

Regardless of the abrupt and gradual change of the spin-valley-resolved Chern number, the band gap increases as the inversion symmetry-breaking potential increases. It is clear that \(|C(s,\xi )|=1\) corresponds to a quantum (spin-)valley Hall insulator with gapless edge states at a topological domain wall, and \(|C(s,\xi )|=0\) corresponds to a topologically trivial insulator. To clarify whether a finite non-quantized \(|C(s,\xi )|\) due to the partial valley mixing corresponds to a quantum (spin-)valley Hall effect, we investigated N = 80 zigzag-edge honeycomb bilayer nanoribbons with a kink-type topological domain wall.

Figure 5(a,c,e) show the band structure, \(|\Psi |\) at E = 0 and a schematic for the propagating states at E = 0, respectively, for Δ = ±0.5 in each half of the nanoribbon. Figure 5(b,d,f) show the band structure, \(|\Psi |\) at E = 0 and a schematic for the propagating states at E = 0, respectively, for M = ±1 in each half of the nanoribbon. In both cases, \(C(s,\xi )\sim \pm \,0.5\) in each half of the nanoribbon. Within the bulk gap, we can see that there are gapless edge states which are well confined on the topological domain wall, and backscattering of the gapless edge states requires inversion of the (spin-)valley index.

Figure 5
figure 5

TB calculations for N = 80 zigzag-edge honeycomb bilayer nanoribbons with a kink-type topological domain wall. (a,c,e) Show the band structure, \(|\Psi |\) at E = 0 and a schematic for the propagating states at E = 0, respectively, for Δ = ±0.5 in each half of the nanoribbon. (b,d,f) show the band structure, \(|\Psi |\) at E = 0 and a schematic for the propagating states at E = 0, respectively, for M = ±1 in each half of the nanoribbon. The red and blue colors represent the opposite spins. The up and down arrows correspond to the opposite propagating directions. The solid and dashed arrows represent the opposite valleys.

Full size image

According to the bulk-edge correspondence4,21,22, the number of gapless edge state per valley per spin at the topological domain wall should be equal to the difference of the spin-valley-resolved Chern number between the two topological domains, \(C(s,\xi )-(\,-\,C(s,\xi ))=2C(s,\xi )\). In Fig. 5, the number of gapless edge state per valley per spin is 2, indicating that \(C(s,\xi )\) should be 1 according to the bulk-edge correspondence. While the (spin-)valley Chern number obtained by integrating the Berry curvature around each valley deviates from the quantized value due to the partial valley mixing, the gapless edge states still correspond to the quantized (spin-)valley Chern number obtained at the limits of well-separated valleys if the opposite valleys are not completely mixed and so if the (spin-)valley Chern number is not too close to zero.

As shown in Fig. 5(a), there are gapless edge states corresponding to the quantum valley Hall effect if \(\Delta \le 0.5{t}_{0}\). In the intralayer ferrimagnetic and interlayer antiferromagnetic order, the magnitude of the sublattice magnetization at the dimer sites (MD) is smaller than that at the nondimer sites (MND). When \({M}_{D}={M}_{ND}\), there are gapless edge states corresponding to the quantum spin-valley Hall effect if \({M}_{ND}\le {t}_{0}\). As MD decreases, the critical value of MND increases. When \({M}_{D}=0.1{M}_{ND}\), corresponding to Fig. 5(b), the gapless edge states survive if \({M}_{ND}\lesssim 3{t}_{0}\).

In the quantum (spin-)valley Hall effect with large staggered AB-sublattice potentials, the (spin-)valley Chern number is not well defined due to the valley mixing, but the gapless edge states still correspond to the (spin-)valley Chern number obtained at small potential limits. Even in the presence of spin mixing, the spin Chern number could be well defined by partitioning the occupied valence band into two spin sectors using the projected spin operator28,29. In a similar way, it is expected that the (spin-)valley Chern number can be well defined even in the presence of valley mixing, which requires further study.

To summarize, we have investigated AB-stacked bilayer silicene, known to be an antiferromagnetic insulator, by using the density functional theory calculations. While the spin-valley Chern number is not quantized, there exist backscattering-free gapless edge states within the bulk gap, indicating that the bilayer silicene is a quantum spin-valley Hall insulator. Using a tight-binding model for a honeycomb bilayer, we found that a non-quantized (spin-)valley Chern number may correspond to a quantum (spin-)valley Hall insulator under an inversion symmetry-breaking potential in the form of staggered AB-sublattice potential such as an antiferromagnetic order.

Methods

A SIESTA package30 using a localized linear combination of numerical atomic-orbital basis sets was employed for the DFT calculations. A generalized gradient approximation of Perdew-Burke-Ernzerhof (GGA-PBE) was used for the exchange and correlation potential31. A double-\(\zeta \) polarized basis set and norm-conserving Troullier-Martins pseudopotentials generated with a Perdew-Burke-Ernzerhof functional were used. The plane-wave cutoff energy of 350 Ry was used for the real-space grid, and k-points of 100 × 100 × 1 and 40 × 1 × 1 meshes in a Monkhorst-Pack scheme were used for bilayer silicene sheet and nanoribbons, respectively. The atomic coordinates were optimized by using the conjugated gradients method with a maximum force tolerance of 0.1 eV/nm. The equilibrium lattice constant a0 = 0.386 nm and the interlayer distance d0 = 0.251 nm between the covalently-bonded dimer sites were obtained from the total energy minimum, in agreement with a previous work14. Zigzag-edge nanoribbons were considered as a one-dimensional system periodic in a zigzag direction. The ribbon width is represented by the number N of the C-C pairs on a layer in the unit cell. The spin-orbit coupling, much smaller than the antiferromagnetic gap, was neglected.

Using the wavefunctions obtained from the DFT calculations on the bilayer silicene sheet, maximally localized Wannier functions were constructed within the Wannier90 code32. Berry curvatures were calculated based on the Wannier interpolation. Using the anomalous Hall conductivity calculation routine implemented in Wannier90 code, the spin-valley-resolved Chern number \(C(s,\xi )\) with spin s and valley \(\xi \) was calculated by integrating the Berry curvature over a half Brillouin zone. The spin-valley Chern number was defined as \({C}_{sv}=C(\,\uparrow ,{\rm{K}}\,+\,)-\) \({\rm{C}}(\,\downarrow \,,{\rm{K}}\,+\,)-{\rm{C}}(\,\uparrow \,,{\rm{K}}\,-\,)+{\rm{C}}(\downarrow \,,{\rm{K}}\,-\,)\) and the spin-valley Hall conductivity can be expressed as \({\sigma }_{sv}={C}_{sv}\) \(\tfrac{{e}^{2}}{h}\)33.

A π-band TB model Hamiltonian with nearest-neighbor hopping was introduced to model the AB-stacked honeycomb bilayer with broken inversion symmetry18,34:

$$H=-\,\sum _{\langle i,j\rangle s}\,{t}_{i,j}{c}_{is}^{\dagger }{c}_{js}+\sum _{is}\,({V}_{i}+{\Delta }_{i}+s{M}_{i}){c}_{is}^{\dagger }{c}_{is}.$$
(1)

The hopping amplitude \({t}_{i,j}={t}_{0}\) for in-plane hopping and \({t}_{i,j}={t}_{1}\) for interalyer hopping between the dimer sites. We set t0 = 1 and \({t}_{1}=0.1\). The second term corresponds to on-site potentials breaking inversion symmetry. The AB-stacked honeycomb bilayer has four sites A1, B1, A2 and B2 as shown in Fig. 2(a). On the basis of (A1,B1,A2,B2), Vi = (−1, −1, +1, +1)V corresponds to the interlayer potential difference. Δi = (−1, +1, −1, +1)Δ corresponds to the staggered AB-sublattice potential. Mi = (+1, −0.1, +0.1, −1)M models the intralayer ferrimagnetic and the interlayer antiferromagnetic order of AB-stacked bilayer silicene with a spin s = ±1.