Abstract
Long-distance quantum key distribution (QKD) has long time seriously relied on trusted relay or quantum repeater, which either has security threat or is far from practical implementation. Recently, a solution called twin-field (TF) QKD and its variants have been proposed to overcome this challenge. However, most security proofs are complicated, a majority of which could only ensure security against collective attacks. Until now, the full and simple security proof can only be provided with asymptotic resource assumption. Here, we provide a composable finite-key analysis for coherent-state-based TF-QKD with rigorous security proof against general attacks. Furthermore, we develop the optimal statistical fluctuation analysis method to significantly improve secret key rate in high-loss regime. The results show that coherent-state-based TF-QKD is practical and feasible, with the potential to apply over nearly one thousand kilometers.
Similar content being viewed by others
Introduction
Classical encryption communication plays a central role in network security, which, however, faces increasingly serious security threats with quantum computation1. Quantum key distribution (QKD)2,3 promises information-theoretically secure encryption communication with the laws of quantum mechanics. However, in practice, there are two important problems severely restrict QKD implementations. One is the rate-distance limit of QKD4, which means that the secret key rate is linear scaling with channel transmittance and bounded by the secret-key capacity of quantum channel4,5. It is believed that the limit of transmission distance is approximately 500 km ultralow-loss fibre6. The other is the quantum hacking attacks or, more precisely, the side-channel attacks on detection7. In the security proof of typical QKD, one requires that the detection probability of signal is basis-independent. However, it is very easy to be broken without being detected, for example, by the detector blinding attack8. The big gap between experimental realizations and theoretical models on the measurement devices is often exploited by eavesdroppers to successfully steal the key.
To circumvent the rate-distance limit, the trusted relay9 or quantum repeater10 schemes are proposed. However, the trusted relay significantly compromise the security while the quantum repeater techniques are far from practical implementation. To overcome the side-channel attacks on detection, the measurement-device-independent (MDI) QKD based on two-photon Bell state measurement11 has been proposed and experimentally demonstrated over 404 km ultralow-loss fibre12. Unfortunately, the secret key rate of MDI-QKD is far below typical QKD in realistic implementations12,13.
Recently, a novel protocol known as twin-field (TF) QKD14 has been introduced to simultaneously solve the above two problems by exploiting the single-photon interference in the untrusted relay, which provides a secret key rate proportional to the square-root of channel transmittance and is immune to any attack on measurement devices. Until now, several proof-of-principle experimental demonstration of TF-QKD have already been successfully performed15,16,17,18, indicating that the techniques of TF-QKD are realizable. The original TF-QKD is a remarkable breakthrough in the field of quantum communication even without unconditional security proof. To prove the security of TF-QKD, two types of variants are proposed19,20,21,22,23,24,25,26,27,28. One is the single-photon-based TF-QKD21,22,24 first proposed in ref.21 named as sending-or-not-sending protocol with a security proof against coherent attack. It is similar with the original TF-QKD using the single-photon component to extract secret key by implementing single-photon Bell state measurement22,24. Recently, we became aware that the single-photon based protocol and its key rate formula, Eq. (3) presented in ref.21 are actually same with the earlier protocol, sending-or-not-sending protocol proposed by Wang et al. We thank authors of ref.22 for pointing out this.The other is the coherent-state-based TF-QKD19,20,24,25,26,27,28, or called phase-matching QKD, which directly exploits the coherent state to extract secret key by implementing entangled coherent state measurement28. However, so far, taking into account all finite-size effects in TF-QKD with rigorously composable security proof is still missing, which severely influences TF-QKD to become as practical and feasible as typical QKD29,30 and MDI-QKD31 with composable security under realistic conditions.
In this work, we provide a composable finite-key analysis for coherent-state-based TF-QKD with rigorous security proof against general attacks. We make three contributions to obtain the optimal secret key rate and show that the transmission distance can surpass 800 km fibre with the realistic technology. First, we use the entropic uncertainty relation32 to prove the security of coherent-state-based TF-QKD in the finite-key regime. It is known to all that entropic uncertainty relation is well suited for the composable security proof against general attacks, which is rather direct and avoids various estimations29,30,31. Second, we develop the tight and rigorous multiplicative Chernoff bound and its variant to deal with the difference between the observed value and the expected value, which closes the gap between the large-deviation Chernoff bound method31 and the not-sufficiently-rigorous Gaussian analysis. Third, the tailored tail inequality for random sampling without replacement is the tightest, which further improves the secret key rate in the finite-key regime.
Results
Security definition
Before introducing our protocol, we follow the discussion of the so-called universally composable framework33. A general QKD protocol either outcomes a pair of key bit strings S and \(\hat{{\bf{S}}}\) for Alice and Bob or aborts denoted by S = S = ⊥. The length of bit strings S and S are both equal to \(\ell \). In general, the QKD protocol is called secure if the key bit strings satisfy two criteria, namely, the correctness and the secrecy criteria.
The correctness criterion is met if the key bit strings of Alice and Bob are identical, i.e., S = \(\hat{{\bf{S}}}\). However, the correctness criterion cannot be perfectly satisfied in experiment, which means that we may allow some negligible errors. Specifically, we say that a protocol is \({\varepsilon }_{{\rm{cor}}}\)-correct if \({\rm{\Pr }}[{\bf{S}}\ne \hat{{\bf{S}}}]\le {\varepsilon }_{{\rm{cor}}}\), i.e., the probability that Alice’s and Bob’s key bit strings are not identical does not exceed \({\varepsilon }_{{\rm{cor}}}\).
Let system E be the information of eavesdropper during the process of the QKD protocol, \({\{|s\rangle \}}_{s}\) be an orthonormal basis for Alice’s system and \({\rho }_{{\bf{E}}}^{s}\) be the state of the system E given any fixed value s of key bit string S. In order to define secrecy, we should introduce a description of the correlation between the key bit string of Alice S and eavesdropper, which can be given by the joint classical-quantum state \({\rho }_{{\bf{SE}}}=\sum _{s}\,{p}_{s}|s\rangle \langle s|\otimes {\rho }_{{\bf{E}}}^{s}\). The secrecy criterion is met if the system E completely has no correlation with the key bit string of Alice, i,e., ρSE = US⊗ρE, where \({U}_{{\rm{S}}}=\sum _{s}\,\frac{1}{|{\mathscr{S}}|}|s\rangle \langle s|\) is the uniform mixture of all possible values of the key bit string S. However, the secrecy criterion can still never be perfectly satisfied in experiment. We say that a protocol is \({\varepsilon }_{\text{sec}}\)-secret if the trace distance between the joint classical-quantum state ρSE and the ideal case described by US⊗ρE is no more than Δ, i.e.,
and \((1-{p}_{{\rm{about}}})\Delta \le {\varepsilon }_{\sec }\), where ∥·∥1 is the trace norm and pabort is the probability that the protocol aborts. Therefore, we say that a protocol is \(\varepsilon \)-secure if it is \({\varepsilon }_{{\rm{cor}}}\)-correct and \({\varepsilon }_{\text{sec}}\)-secret with \({\varepsilon }_{{\rm{cor}}}+{\varepsilon }_{\sec }\le \varepsilon \).
Protocol definition
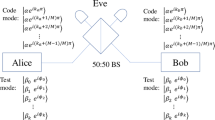
Here, we follow two protocols proposed in our very recent work28. One prepares cat state to bound the leaked information, called Protocol 1. The other exploits the phase-randomized coherent state (PRCS) to estimate the leaked information, called Protocol 2. For simplicity, we only consider the case of symmetric channel, while the case of the asymmetric channel can be directly generalized28. The schematic diagram of two protocols are illustrated in Fig. 1. Alice randomly chooses Z and X bases with probabilities pZ and 1 − pZ, respectively. Alice randomly prepares optical pulses with coherent states \(|\alpha \rangle \) and \(\langle -\alpha |\) in equal probabilities for the logic bits 0 and 1 if choosing the Z basis. For Protocol 1 (2), Alice randomly generates optical pulses with cat states \(|{\xi }^{+}(\alpha )\rangle =(|\alpha \rangle +|-\alpha \rangle )/\sqrt{2}\) and \(|{\xi }^{-}(\alpha )\rangle =(|\alpha \rangle -|-\alpha \rangle )/\sqrt{2}\) in equal probabilities for the logic bits 0 and 1 (PRCS) if choosing the X basis. Likewise, Bob does the same. The optical pulses are sent to the untrusted Charlie, who is assumed to perform the entangled coherent state measurement that projects them into an entangled coherent state. The decoy-state method34,35,36 will be used in Protocol 2 to estimate the leaked information.
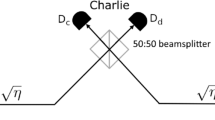
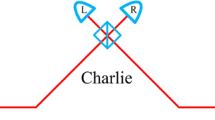
The setup of coherent-state-based TF-QKD. For Protocol 1 (2), Alice and Bob prepare coherent states \(|\pm \alpha \rangle \) if choosing Z basis and cat states \(|{\xi }^{\pm }(\alpha )\rangle \) (PRCS) if choosing X basis. They send the prepared quantum signals through insecure channel to the untrusted Charlie, who is supposed to perform an entangled coherent state measurement. As an example, Charlie let the two received optical pulses interfere at a symmetric beam splitter (BS), which has on each end a threshold single-photon detector. A click in the single-photon detector L implies a projection into the entangled coherent state \(|{\Phi }^{-}\rangle =1/\sqrt{{N}_{-}}(|\alpha \rangle |\alpha \rangle -|-\alpha \rangle |-\alpha \rangle )\), while a click in single-photon detector R indicates a projection into the entangled coherent state \(|{\Psi }^{-}\rangle =1/\sqrt{{N}_{-}}(|\alpha \rangle |-\alpha \rangle -|-\alpha \rangle |\alpha \rangle )\). Details can be found in main text.
Next, Charlie will disclose whether he has acquired a successful measurement result and which entangled coherent state is obtained. Alice and Bob only keep the data of successful measurement and discard the rest. They announce the basis and intensity information through the authenticated classical channel and only keep the events of the same basis. Finally, Bob flips a part of his key bit to correctly correlate with Alice’s (see Table 1). A detailed description of each step of Protocols 1 and 2 as follows.
State preaparation
The first four steps are repeated by Alice and Bob for i = 1, …, N until the conditions in the Sifting step are satisfied. In Protocol 1, Alice chooses a basis β ∈ {Z, X} and uniformly random bit r ∈ {0, 1} with probability pβ/2. Next, Alice prepares optical pulses with coherent state \(|{e}^{ir\pi }\alpha \rangle \) (cat state \((|\alpha \rangle +{e}^{ir\pi }|-\alpha \rangle )/\sqrt{2}\)) for Z (X) basis given by r. Likewise, Bob does the same thing. In Protocol 2, Alice chooses a basis β ∈ {Z, X} with probability pβ. Then, she chooses uniformly random bit r ∈ {0, 1} with probability 1/2 given by the Z basis and an intensity with probability pa given by the X basis. Next, Alice prepares optical pulses with coherent state \(|{e}^{ir\pi }\alpha \rangle \) for the Z basis given by r. She generates PRCS optical pulses of intensity a for X basis. Likewise, Bob does the same thing.
Distribution
Alice and Bob send their optical pulses to untrusted Charlie through the insecure quantum channel.
Measurement
Charlie let the two optical pulses interfere in the symmetric beam splitter and performs the entangled state measurement. For each i, he publicly informs Alice and Bob whether or not his measurement is successful and which entangled coherent state is obtained.
Sifting
Alice and Bob announce their basis choices and intensity settings over an authenticated classical channel when Charlie reports a successful event. Bob flips part of his key bits to correctly correlate with Alice’s (see Table 1). In Protocol 1, we define the set \({\mathscr{Z}}\) (\({\mathscr{X}}\)), which identifies signals when Alice and Bob select the same basis Z (X) and Charlie has a successful measurement. The protocol repeats these steps until \(|{\mathscr{Z}}|\ge n\) and \(|{\mathscr{X}}|\ge k\). In Protocol 2, we define two groups of sets \({\mathscr{Z}}\) and \({{\mathscr{X}}}_{a,b}\). The first (second) one identifies signals where Alice and Bob select the basis Z (X and the intensities a and b) and Charlie has a successful measurement. The protocol repeats these steps till \(|{\mathscr{Z}}|\ge n\) and \(|{{\mathscr{X}}}_{a,b}|\ge {k}_{a,b}\) ∀a, b.
Parameter estimation
Alice and Bob exploit the random bits from \({\mathscr{Z}}\) to form the raw key bit strings Z and Z′, respectively. In Protocol 1 (2), Alice and Bob use \({\mathscr{Z}}\) and \({\mathscr{X}}\) (\({{\mathscr{X}}}_{a,b}\)) to estimate the upper bound of phase error rate \({\varphi }_{{\rm{Z}}}\). If \({\varphi }_{{\rm{Z}}} > {\varphi }_{{\rm{t}}ol}\), Alice (Bob) assigns an empty string ⊥ to S (S) and aborts this protocol.
Error correction
Bob exploits an information reconciliation scheme to acquire an estimate \(\hat{{\bf{Z}}}\) of Z by revealing at most leakEC bits of error correction data. Then, Alice computes a hash of length \(\lceil {\log }_{2}(1/{\epsilon }_{{\rm{cor}}})\rceil \) by using a random universal2 hash function37 to Z. She sends the choice function and the hash to Bob. Bob uses the received hash function to compute the hash of \(\hat{{\bf{Z}}}\) and compares with Alice’s. If they are different, Alice (Bob) assigns an empty string to S (\(\hat{{\bf{S}}}\)) and aborts this protocol.
Privacy amplification
Alice exploits a random universal2 hash function37 to extract length \(\ell \) bits of secret key S from Z. Bob uses the same hash function (sent by Alice) to extract length \(\ell \) bits of secret key \(\hat{{\bf{S}}}\) from \(\hat{{\bf{Z}}}\).
Identifying any one of two entangled coherent states \(|{\Phi }^{-}\rangle =1/\sqrt{{N}_{-}}(|\alpha \rangle |\alpha \rangle -|-\alpha \rangle |-\alpha \rangle )\) and \(|{\Psi }^{-}\rangle =\)\(1/\sqrt{{N}_{-}}(|\alpha \rangle |-\alpha \rangle -|-\alpha \rangle |\alpha \rangle )\) can allow us to prove the security28, where N− = 2(1 − e−4μ) is the normalization factor, and μ = |α|2 is the intensity of coherent states \(|\pm \alpha \rangle \). Here, we consider that two entangled coherent states both can be identified. Indeed, the coherent-state-based TF-QKD is a prepare-and-measure protocol reduced from the entanglement-based QKD using heralded entanglement generation protocol (see Methods).
Security analysis
Here, we show the main result of our paper. One can make sure that Protocol 1 (2) introduced above is both \({\varepsilon }_{{\rm{cor}}}\)-correct and \({\varepsilon }_{\text{sec}}\)-secret if we choose an appropriate secret key of length \(\ell \). The required correctness criterion could be ensured by the error-verification step. Alice and Bob compare the random hash values of their corrected keys with failure probability \({\varepsilon }_{{\rm{hash}}}\), which means that identical probability of key bit strings S and \(\hat{{\bf{S}}}\) is more than \(1-{\varepsilon }_{{\rm{hash}}}\). Even if the protocol is aborted, resulting in S = \(\hat{{\bf{S}}}\) = ⊥, it is also correct. Thereby, the correctness of the protocol is \({\varepsilon }_{{\rm{cor}}}={\varepsilon }_{{\rm{hash}}}\).
For Protocol 1, the protocol is \({\varepsilon }_{\text{sec}}\)-secret if the secret key of length \(\ell \) satisfies
where h(x) = −xlog2x − (1 − x)log2(1 − x) is the binary Shannon entropy function. Recall that n and \({\varphi }_{{\rm{Z}}}\) are the number of bits and phase error rate in bit string Z. A sketch of the proof of Eq. (1) can be found in Methods. In the asymptotic limit, \({\varphi }_{{\rm{Z}}}={E}_{{\rm{X}}}\) since statistical fluctuations could be neglected, and thus \(\ell \) satisfies \(\ell \le n[1-h({E}_{{\rm{X}}})]-{{\rm{leak}}}_{{\rm{EC}}}\), as recently acquired in28. \(nh({\varphi }_{{\rm{Z}}})\) is the amount of information acquired by the eavesdropper in the quantum process, while leakEC is the information revealed by Alice in the error correction step.
For Protocol 2, the protocol is \({\varepsilon }_{\text{sec}}\)-secret if the secret key of length \(\ell \) satisfies (see Methods)
The other two main contributions of our work are the rigorous and tight statistical fluctuation analysis methods. One is the tightest multiplicative Chernoff bound and its variant to deal with the difference between the observed value and the expected value. The other is the tightest tail inequality for random sampling without replacement. In order to meet the composable security proof against general attacks in the finite-key regime, one can only assume the random variables are independent but not identically distributed. Traditionally, a large deviation theory with the Chernoff bound is proposed to deal with the parameter estimation in MDI-QKD with finite-key analysis31, which is a rigorous but not tight method, i.e., significant statistical fluctuations quickly decrease the expected secret key rate in the high-loss regime. Whereafter, another approach38 is proposed, attempting to close the gap between the rigorous large-deviation Chernoff bound method31 and the not-sufficiently-rigorous Gaussian analysis (independent and identically distributed). However, this approach offers a tighter estimation of the lower bound (given the small observed value) than the Gaussian analysis, which seems to be a counterfactual result as the method38 is superior to the Gaussian analysis. Our rigorously improved method are always inferior but comparable to the Gaussian analysis. Furthermore, we give two tailored tail inequalities (lower and upper tails) to deal with the random sampling without replacement issue, which directly utilizes hypergeometric function distribution and avoids any inequality scaling30,39. The rigorous proof and detailed analysis can be found in Supplementary Notes 1–3.
Discussion
Here, we perform the behaviour of the expected secret key rate provided in Eq. (1) of Protocol 1 and Eq. (2) of Protocol 2. In our simulation, we use the following parameters, a fibre-based channel with an ultralow-loss of 0.16 dB/km12. The efficiency and dark count rate of single-photon detector are 85% and 10−11 in the untrusted relay13. The security bounds of secrecy and correctness are fixed to \({\varepsilon }_{\text{sec}}={10}^{-10}\) and \({\varepsilon }_{{\rm{cor}}}={10}^{-15}\), the latter of which corresponds to a realistic hash tag size in practice37. For simplicity, we assume an error correction leakage that is a fixed fraction of the sifted key length n, i.e., leakEC = nζh(EZ), with the efficiency of error correction ζ = 1.1 and the quantum bit error rate EZ of the Z basis.
The results are shown in Figs. 2 and 3 where Alice and Bob exploit the three-intensity PRCS, one of which is a vacuum state. The detailed computational process of the phase error rate \({\varphi }_{{\rm{Z}}}\) can be found in Methods. The expected secret key rate (per pulse) \(\ell /N\) as a function of the transmission distance between Alice and Bob for different values of the total number of signals N sent by Alice and Bob given by overall misalignment 2% in the channel is shown in Fig. 2. For a given transmission distance, we optimize numerically \(\ell /N\) over all the free parameters of Protocols 1 and 2. For the case of symmetric channel, all parameters chosen by Alice and Bob are set to the same. Our simulation result shows clearly that coherent-state-based TF-QKD is the feasible scheme in the finite-key regime. Considering the case of 1 GHz repetition rate15, the secret key rate of Protocols 1 and 2 can break the repeaterless Pirandola-Laurenza-Ottaviani-Banchi (PLOB) bound5 even with a small finite size of data, say N = 108 (data collected in 0.1 s) for Protocol 1 and 1010 (data collected in 10 s) for Protocol 2. Moreover, the maximum transmission distance of Protocols 1 and 2 can be expanded up to 1000 km and 800 km with the realistic finite size of data N = 1013 (less than 2.8 h data). The secret key rate in Protocols 1 and 2 given by 470 km are both larger than 10−6 per pulse (1 kbps) under the finite size of data N = 1012. It means that the coherent-state-based TF-QKD has the potential to be actually used even when the communication distance is approximate to 500 km. This is impossible when using the traditional QKD or MDI-QKD, where the best results are 0.25 bps at 421 km of traditional QKD under the collective attacks assumption13 and 3.2 × 10−4 bps at 404 km of MDI-QKD under the coherent attacks assumption12.
Expected key rate as function of the distance. (a,b) Secret key rate \(\ell /N\) in logarithmic scale for Protocol 1 (2) as a function of the fibre distance. The colour lines correspond to different values for the total number of signals N sent by Alice and Bob. In comparison, the black line represents the repeaterless PLOB bound. For simulation, we consider the following parameters: the loss coefficient of the fibre channel is 0.16 dB/km, the detection efficiency and dark count rate are 85% and 10−11. The overall misalignment rate in the channel is set to 2%, and the security bound of secrecy is \({\varepsilon }_{\text{sec}}={10}^{-10}\). The results show clearly that the secret key rates of coherent-state-based TF-QKD in Protocols 1 and 2 can break the repeaterless PLOB bound even with a small finite size of data, say N = 108 for Protocol 1 and 1010 for Protocol 2. The maximum transmission distance of Protocols 1 and 2 are more than 1000 km and 800 km with the realistic finite size of data N = 1013.
Expected key rate as function of the block size. (a) Protocol 1. (b) Protocol 2. The plot shows the secret key rate \(\ell /N\) in logarithmic scale as a function of the total number of signals N sent by Alice and Bob in the transmission distance of 500 km. The security bound of secrecy \({\varepsilon }_{\text{sec}}={10}^{-10}\). The colour solid lines correspond to different values for the overall misalignment rate. The colour dotted lines show the corresponding asymptotic rates28. In comparison, the black line represents the PLOB bound given by the transmission distance of 500 km. The results show that the coherent-state-based TF-QKD is robust to the large misalignment rate even for a finite size of signals sent by Alice and Bob.
Figure 3 illustrates \(\ell /N\) as a function of N for different values of the misalignment in the transmission distance of 500 km. For comparison, this figure also includes the asymptotic secret key rate when Alice and Bob send an infinite number of signals28 and the repeaterless PLOB bound. For a given number of signals, we optimize numerically \(\ell /N\) over all the free parameters of Protocols 1 and 2. The fixed parameters are the ones described in the caption of Fig. 3. The simulation results show that the secret key rates of Protocols 1 and 2 are about 10−7 at the distance of 500 km with 1011 and 5 × 1013 signals, even given that the misalignment rate is up to 15%. The significant secret key rate of Protocols 1 and 2 at the distance of 500 km can be acquired only with 109 and 1011 signals when the misalignment rate is less than 5%.
In summary, we have proved the composable security of coherent-state-based TF-QKD in the finite-key regime against general attacks. The maximum transmission distance of Protocols 1 and 2 are more than 1000 km and 800 km with the realistic finite size of data, respectively. The coherent-state-based TF-QKD is the fully practical QKD protocol that offers an avenue to bridge the gap between trusted relay and quantum repeater in long-distance QKD implementations. In order to be immune to general attacks in the finite-key regime, the independent and identically distributed assumption of Gaussian analysis (the central-limit theorem) is no longer applicable. We have rigorously proved an improved Chernoff bound and its variant, which can close the gap between the large-deviation Chernoff bound method and the Gaussian analysis. Numerical simulations display that our improved method is always inferior but comparable to the Gaussian analysis. The rigorous and tight statistical fluctuation analysis methods of this work will be widely applied to quantum cryptography protocols with the finite-size effects, such as QKD, quantum digital signature, and quantum secret sharing. We remark that cat state has a certain distance from the actual application with current technique. Last but not least, the homodyne measurement may be exploited to identify the entangled coherent state in the coherent-state-based TF-QKD, which is worth considering in the future.
Methods
Entanglement-based protocol
In order to establish the secrecy of the protocols, we introduce an equivalently virtual entanglement-based protocol28, in which Alice and Bob prepare entangled states of a qubit and an optical mode \(|\psi \rangle =\frac{1}{\sqrt{2}}(|+z\rangle |\alpha \rangle +|-z\rangle |-\alpha \rangle )\), where qubit states \(|\pm z\rangle \) are the eigenstates of Pauli’s Z operator. They keep the qubit and send the optical mode to the untrusted Charlie, who performs the entangled coherent state measurement. The bipartite qubit entanglement states between Alice and Bob are thus generated via entanglement swapping. Indeed, the coherent states \(|\pm \alpha \rangle \) and the cat states \(|{\xi }^{\pm }(\alpha )\rangle \) will be sent to Charlie if they perform the Z- and X-basis measurement on the qubit system, respectively. Thereby, the coherent-state-based TF-QKD is a prepare-and-measure protocol reduced from the entanglement-based QKD using heralded entanglement generation protocol (we refer to the article28 for details).
Secrecy
Let us keep the entanglement-based QKD using heralded entanglement generation protocol in our mind. We exploit the entropic uncertainty relations29,32 to estimate bounds on the smooth min-entropy of the raw key conditioned on eavesdropper’s information. The Quantum Leftover Hash Lemma37 is exploited to give a direct operational meaning to the smooth min-entropy. Let E′ summarizes all information of eavesdropper learned about raw key of Alice Z, up to the error-correction step. By applying a random universal2 hash function to Z, one may extract a Δ-secret key of length \(\ell \) from Z,
where \({H}_{{\rm{\min }}}^{\varepsilon }({\bf{Z}}|{\bf{E}}{\boldsymbol{^{\prime} }})\) denotes the smooth min-entropy37, which quantifies the average probability that the eavesdropper guesses Z correctly by exploiting the optimal strategy with access to E′. Let \(\upsilon =\sqrt{{2}^{\ell -{H}_{{\rm{m}}in}^{\varepsilon }(Z|E\text{'})}}/2\), the secret key of length \(\ell \) is
The amount of bit information \({{\rm{leak}}}_{{\rm{EC}}}+{\log }_{2}(2/{\varepsilon }_{{\rm{cor}}})\) will be revealed to the adversary during the error-correction step. By using a chain-rule inequality for smooth entropies, we have \({H}_{{\rm{\min }}}^{\epsilon }({\bf{Z}}|{\bf{E}}{\boldsymbol{^{\prime} }})\ge {H}_{{\rm{\min }}}^{\epsilon }({\bf{Z}}|{\bf{E}})-{{\rm{leak}}}_{{\rm{EC}}}-{\log }_{2}(2/{\varepsilon }_{{\rm{cor}}})\), where E is the information of eavesdropper before the classical post-processing.
In order to bound the smooth min-entropy \({H}_{{\rm{\min }}}^{\epsilon }({\bf{Z}}|{\bf{E}}{\boldsymbol{^{\prime} }})\) by using the uncertainty relation for smooth entropies32, we consider a gedankenexperiment that Alice and Bob prepare the cat states instead of coherent states when they choose the Z basis. Alice and Bob need to use the bit strings X and X′ of length n to replace the raw key bit strings Z and Z′ in this hypothetical protocol, respectively. The smooth min-entropy can be given by
where the first inequality exploits the entropic uncertainty relation32. The smooth max-entropy \({H}_{{\rm{\max }}}^{\varepsilon }({\bf{X}}|{\bf{X}}^{\prime} )\) quantifies the required number of bits that Bob uses bit string X′ to reconstruct X, which leads to the second inequality29. \({\varphi }_{{\rm{Z}}}\) is the phase error rate of bit strings Z and Z′, i.e., the bit error rate of bit strings X and X′. In reality, \({\varphi }_{{\rm{Z}}}\) cannot be directly observed, which has to be estimated by using random-sampling (without replacement) theory.
Tight tail inequality
Here, we introduce three Lemmas to deal with the statistical fluctuation in the finite-key regime. Specifically, Lemma 1 is tailored for random sampling without replacement. Lemma 2 is the multiplicative Chernoff bound, which is used to bound the observed value, given the expected value. Lemma 3 is a variant of the multiplicative Chernoff bound, which is tailored to estimate the expected value, given the observed value. The rigorously proved tail inequalities in each lemma are the tightest due to avoiding excessive inequality scaling. See Supplementary Notes 1–3 for details.
Lemma 1:
Let \({{\mathscr{X}}}_{n+k}\,:\,=\{{x}_{1},{x}_{2},\cdots ,{x}_{n+k}\}\) be a string of binary bits with n + k size, in which the number of bit value 1 is unknown. Let \({{\mathscr{X}}}_{k}\) be a random sample (without replacement) bit string with k size from \({{\mathscr{X}}}_{n+k}\). Let λk be the probability of observed bit value 1 in \({{\mathscr{X}}}_{k}\). Let \({{\mathscr{X}}}_{n}\) be the remaining bit string, where the probability of observed bit value 1 in \({{\mathscr{X}}}_{n}\) is λn. Then, let \({C}_{i}^{j}=i!/[j!(i-j)!]\) be the binomial coefficient. For any \(\epsilon > 0\), we have the upper tail
where γ(a, b, c, d) is the positive root of the equation \(\mathrm{ln}\,{C}_{b}^{bc}+\,\mathrm{ln}\,{C}_{a}^{ac+a\gamma (a,b,c,d)}-\,\mathrm{ln}\,{C}_{a+b}^{(a+b)c+a\gamma (a,b,c,d)}-\,\mathrm{ln}\,d=0\). For any \(\hat{\epsilon } > 0\), we have the lower tail
where \(\hat{\gamma }(a,b,c,d)\) is the positive root of the equation \(\mathrm{ln}\,{C}_{b}^{bc}+\,\mathrm{ln}\,{C}_{a}^{ac-a\hat{\gamma }(a,b,c,d)}-\,\mathrm{ln}\,{C}_{a+b}^{(a+b)c-a\hat{\gamma }(a,b,c,d)}-\,\mathrm{ln}\,d=0\). If one does not find the positive root \(\hat{\gamma }(a,b,c,d)\), we let λn = 0.
Lemma 2:
Let X1, X2, ..., XN be a set of independent Bernoulli random variables that satisfy Pr(Xi = 1) = pi (not necessarily equal), and let \(X\,:\,=\mathop{\sum }\limits_{i=1}^{N}\,{X}_{i}\). The expected value of X is denoted as \({\mu }_{x}:\,=E[X]=\mathop{\sum }\limits_{i=1}^{N}\,{p}_{i}\). Then, let g(x, y) = [ey/(1 + y)1+y]x, for any δ > 0, we have the upper tail
where δ is the positive root of the equation \({\mu }_{x}[\delta -(1+\delta )\mathrm{ln}(1+\delta )]-\,\mathrm{ln}\,\varepsilon =0\). For any \(0 < \hat{\delta }\le 1\), we have the lower tail
where \(\hat{\delta }\) is the positive root of the equation \({\mu }_{x}[\hat{\delta }+(1-\hat{\delta })\mathrm{ln}(1-\hat{\delta })]+\,\mathrm{ln}\,\hat{\epsilon }=0\).
Lemma 3:
Let X1, X2 ..., XN be a set of independent Bernoulli random variables that satisfy Pr(Xi = 1) = pi (not necessarily equal), and let \(X\,:\,=\mathop{\sum }\limits_{i=1}^{N}\,{X}_{i}\). The expected value of X is denoted as \({\mu }_{x}\,:\,=E[X]=\mathop{\sum }\limits_{i=1}^{N}\,{p}_{i}\). An observed outcome of X is represented as x for a given trial. For any \(\epsilon > 0\), we have μx that satisfies
with failure probability \(\epsilon \), where \(\underline{{\mu }_{x}}\) is the lower bound of μx and Δ(z, y) is the positive root of the equation Δ(z, y) − [z + Δ(z, y)]ln[1 + Δ(z, y)/z] − lny = 0. For any \(\hat{\epsilon } > 0\), we have that μx satisfies
with failure probability \(\hat{\epsilon }\), where \(\overline{{\mu }_{x}}\) is the upper bound of μx and \(\hat{\Delta }(z,y)\) is the positive root of the equation \(\hat{\Delta }(z,y)+z\,\mathrm{ln}\,\{z/[z+\hat{\Delta }(z,y)]\}+\,\mathrm{ln}\,y=0\).
Statistical fluctuation of Protocol 1
In order to bound the phase error rate \({\varphi }_{{\rm{Z}}}\), we consider the gedankenexperiment picture. There are n + k bits corresponding to X basis. The observed error rate of k bits random sampled from n + k bits is \({E}_{{\rm{X}}}=\frac{1}{k}\mathop{\sum }\limits_{j=1}^{k}\,{r}_{x}\oplus {r^{\prime} }_{x}\), where rx and \(r{\text{'}}_{x}\) are Alice’s and Bob’s bits in set \({\mathscr{X}}\). By using the upper tail inequality for random sampling without replacement in Lemma 1, the remaining error rate of n bits, i.e., the phase error rate, can be given by
with failure probability \({\epsilon }_{1}\).
Finally, by composing the failure probability due to parameter estimation, we have a total secrecy of \({\varepsilon }_{\sec }=2\epsilon +\upsilon +{\epsilon }_{1}\), where we take \(\epsilon =\upsilon ={\epsilon }_{1}={\varepsilon }_{\sec }/4\).
Statistical fluctuation of Protocol 2
Since the cat states are replaced by PRCS for the X basis choice in Protocol 2, the bit error rate EX in the X basis cannot be directly observed. In order to bound the phase error rate \({\varphi }_{{\rm{Z}}}\), we need to use the following three steps.
First, let \({Q}_{a,b}^{\ast }\) be the expected gain when Alice and Bob send PRCS with intensities a and b, respectively, a, b ∈ {ν, ω, 0}. Therefore, we have the relations \({k}_{a,b}^{\ast }=N{p}_{{\rm{X}}}^{2}{p}_{a}{p}_{b}{Q}_{a,b}^{\ast }\), where f are the expected values corresponding to the observed values ka,b. In reality, we only know the observed values ka,b. By using a variant of the multiplicative Chernoff bound in Lemma 3, we can use the observed value for a given trial to estimate the upper (lower) bound of the expected value with a small failure probability \({\varepsilon }_{3}\). The PRCS can be seen as the mixed Fock states from the eavesdropper’s view. Let \({Y}_{n,m}^{\ast }\) be the expected yield when Alice sends n-photon and Bob sends m-photon. Thereby, the expected values \({\bar{Y}}_{n,m}^{\ast }\) can be estimated by using the decoy-state method with the three-intensity PRCS25,28,40. Once obtaining the upper bound of the expected yield \({\bar{Y}}_{n,m}^{\ast }\), one can calculate the upper bound of the observed yield \({\bar{Y}}_{n,m}\) by using the lower tail of the multiplicative Chernoff bound in Lemma 2. See Supplementary Note 4 for details. Note that for the case of n + m ≥ 5, we let the observed yield \({\bar{Y}}_{n,m}=1\).
Second, we consider the gedankenexperiment picture, in which Alice and Bob still send the cat states \(|{\xi }^{\pm }(\alpha )\rangle \) instead of PRCS when they choose the X basis in Protocol 2. Let QZ (QX) be the observed gain when Alice and Bob both prepare coherent states \(|\pm \alpha \rangle \) (cat states \(|{\xi }^{\pm }(\alpha )\rangle \)) for a given trial. By using the tail inequality for random sampling without replacement in Lemma 1, the observed value QX can be bounded by
with failure probability \({\varepsilon }_{1}\), where we have the relations n = NZQZ, NZ = NpZ2 and NX = NpX2. Thereby, the lower bound of the observed value is \(\underline{k}={N}_{{\rm{X}}}{\underline{Q}}_{{\rm{X}}}\).
Third, the upper bound of the observed value of the bit error rate \({\bar{E}}_{{\rm{X}}}\) can be estimated by28
where we have the error gain24,25,28
with \({P}_{n}^{\mu }={e}^{-\mu }{\mu }^{n}/n!\). By using the upper tail inequality for random sampling without replacement in Lemma 1, the phase error rate can be given by
with failure probability \({\varepsilon }_{1}\). We remark that the joint constraint method41 will further bound phase error rate in the finite-key regime.
Finally, by composing the failure probability due to parameter estimation, we have a total secrecy of \({\varepsilon }_{\sec }=2\varepsilon +\upsilon +2{\varepsilon }_{1}+9{\varepsilon }_{2}+17{\varepsilon }_{3}\), where we take \(\varepsilon =\upsilon ={\varepsilon }_{1}={\varepsilon }_{2}={\varepsilon }_{3}={\varepsilon }_{\sec }/31\).
Change history
16 July 2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Fedorov, A. K., Kiktenko, E. O. & Lvovsky, A. I. Quantum computers put blockchain security at risk. Nature 563, 465–467 (2018).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In Proceedings of the Conference on Computers, Systems and Signal Processing, 175–179 (IEEE Press, New York, 1984).
Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nature Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nature Commun. 8, 15043 (2017).
Gisin, N. How far can one send a photon? Frontiers of Physics 10, 100307 (2015).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nature Photonics 8, 595 (2014).
Lydersen, L. et al. Hacking commercial quantum cryptography systems by tailored bright illumination. Nature Photonics 4, 686 (2010).
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Lo, H.-K., Curty, M. & Qi, B. Measurement-deviceindependent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501 (2016).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Lucamarini, M., Yuan, Z., Dynes, J. F. & Shields, A. J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 557, 400 (2018).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nature Photonics 13, 334–338 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 123, 100505 (2019).
Zhong, X., Hu, J., Curty, M., Qian, L. & Lo, H.-K. Proof-of-principle experimental demonstration of twinfield type quantum key distribution. Phys. Rev. Lett. 123, 100506 (2019).
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. arXiv:1805.05511 (2018).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98, 062323 (2018).
Yin, H.-L. & Fu, Y. Measurement-device-independent twin-field quantum key distribution. Sci. Rep. 9, 3045 (2019).
Yu, Z.-W., Hu, X.-L., Jiang, C., Xu, H. & Wang, X.-B. Sending-or-not-sending twin-field quantum key distribution in practice. Sci. Rep. 9, 3080 (2019).
Curty, M., Azuma, K. & Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Information 5, 6 (2019).
Cui, C. et al. Twin-field quantum key distribution without phase postselection. Phys. Rev. Applied 11, 034053 (2019).
Lin, J. & Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 98, 042332 (2018).
Primaatmaja, I. W., Lavie, E., Goh, K. T., Wang, C. & Lim, C. C. W. Versatile security analysis of measurement-device-independent quantum key distribution. Phys. Rev. A 99, 062332 (2019).
Yin, H.-L. & Chen, Z.-B. Coherent-state-based twin-field quantum key distribution. Sci. Rep. 9, 14918 (2019).
Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. Nature Commun. 3, 634 (2012).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoystate quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Curty, M. et al. Finite-key analysis for measurementdevice-independent quantum key distribution. Nature Commun. 5, 3732 (2014).
Tomamichel, M. & Renner, R. Uncertainty relation for smooth entropies. Phys. Rev. Lett. 106, 110506 (2011).
Müller-Quade, J. & Renner, R. Composability in quantum cryptography. New J. Phys. 11, 085006 (2009).
Hwang, W.-Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Renner, R. Security of quantum key distribution. Int. J. Quantum Inf. 6, 1–127 (2008).
Zhang, Z., Zhao, Q., Razavi, M. & Ma, X. Improved key-rate bounds for practical decoy-state quantum-keydistribution systems. Phys. Rev. A 95, 012333 (2017).
Fung, C.-H. F., Ma, X. & Chau, H. F. Practical issues in quantum-key-distribution postprocessing. Phys. Rev. A 81, 012318 (2010).
Grasselli, F. & Curty, M. Practical decoy-state method for twin-field quantum key distribution. New J. Phys. 21, 073001 (2019).
Zhou, Y.-H., Yu, Z.-W. & Wang, X.-B. Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 93, 042324 (2016).
Acknowledgements
We thank Y. Fu, P. Liu and W. Zhu for their valuable discussions. This work was supported by the National Natural Science Foundation of China under Grant No. 61801420 and the Nanjing University.
Author information
Authors and Affiliations
Contributions
H.-L.Y. and Z.-B.C. conceived and designed the study. H.-L.Y. performed the numerical simulation. All authors contributed extensively to the work presented in this paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yin, HL., Chen, ZB. Finite-key analysis for twin-field quantum key distribution with composable security. Sci Rep 9, 17113 (2019). https://doi.org/10.1038/s41598-019-53435-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-53435-4
This article is cited by
-
High-dimensional quantum key distribution implemented with biphotons
Scientific Reports (2023)
-
Coherent phase transfer for real-world twin-field quantum key distribution
Nature Communications (2022)
-
More optimal relativistic quantum key distribution
Scientific Reports (2022)
-
Practical long-distance twin-field quantum digital signatures
Quantum Information Processing (2022)
-
Numerical finite-key analysis of quantum key distribution
npj Quantum Information (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.