Tight finite-key security for twin-field quantum key distribution

Abstract

Quantum key distribution (QKD) offers a reliable solution to communication problems that require long-term data security. For its widespread use, however, the rate and reach of QKD systems must be improved. Twin-field (TF) QKD is a step forward toward this direction, with early demonstrations suggesting it can beat the current rate-versus-distance records. A recently introduced variant of TF-QKD is particularly suited for experimental implementation, and has been shown to offer a higher key rate than other variants in the asymptotic regime, where users exchange an infinite number of signals. Here, we extend the security of this protocol to the finite-key regime, showing that it can overcome the fundamental bounds on point-to-point QKD with ~10¹⁰ transmitted signals. In many practical regimes of interest, our analysis offers higher key rates than those of alternative variants. Moreover, some of the techniques we develop are applicable to the finite-key analysis of other QKD protocols.

Introduction

Quantum key distribution (QKD) enables two remote parties, Alice and Bob, to generate a shared secret key in the presence of an eavesdropper, Eve, who may have unbounded computational power at her disposal^1,2,3. While, ideally, the two parties can be at any distance, in practice, due to the loss and noise in the channel, point-to-point QKD is limited to a certain maximum distance at which secret-key bits can securely be exchanged. In fact, the longest distance achieved to date in a terrestrial QKD experiment is ~400 km^4,5. The main limitation is the exponential decrease of the transmittance, η, with the channel length in optical fibres. Even with a high repetition rate of 10 GHz, it would take an average of ~2 min to send a single photon over a distance of 600 km of standard optical fibres, and ~300 years to send it over 1000 km⁶. Indeed, fundamental bounds^7,8,9,10,11 on the private capacity of repeaterless point-to-point QKD protocols show that their secret-key rate scales at best approximately linearly with η. A protocol that aims to overcome this linear scaling must then include at least one middle node. Interestingly, this is not a sufficient condition. A well-known counterexample is the so-called measurement-device-independent QKD (MDI-QKD)¹², which uses the middle node for an untrusted Bell-state measurement operation. There are, however, extensions of MDI-QKD that can improve its rate scaling from η to $\sqrt{\eta }$ by either using quantum memories^13,14 or quantum non-demolition measurements¹⁵. Such setups can, in fact, be considered to be the simplest examples of quantum repeaters^6,16, which are the ultimate solution to trust-free long-distance quantum communications¹⁷. However, even these simple versions may need more time to be efficiently implemented in practice^18,19.

Remarkably, the recently proposed twin-field QKD (TF-QKD)²⁰ can also overcome this linear scaling while using a relatively simple setup. TF-QKD is related to MDI-QKD, and it inherits its immunity to detector side channels. However, it relies on single-photon, rather than two-photon, interference for its entanglement swapping operation. The secret-key rate of this protocol was first conjectured²⁰ and then proven^21,22 to scale with $\sqrt{\eta }$ too, making this approach a strong candidate to beat the current QKD records^23,24,25,26 with today’s technology. The main experimental challenge is that single-photon interference needs very precise phase stability, which makes it more demanding than two-photon interference. Also, some of its current security proofs^21,22 need Alice and Bob to randomly choose a global phase, and then post-select only those rounds in which their choices match, which causes a drop in the secret-key rate. Since the original proposal, several variants of TF-QKD have been developed^27,28,29,30, sharing the single-photon interference idea and its consequent $\sqrt{\eta }$ scaling, but differing in their experimental setups and security proofs. Moreover, some of these variants have been shown to be robust against phase reference mismatch^28,29,30, which simplifies their experimental implementation.

In this paper, we focus on the TF-QKD variant introduced in ref. ²⁸, which has two key features: (i) it does not need phase post-selection, which results in a higher secret-key rate; and (ii) it is a convenient option for experimental implementation. Indeed, many of the current TF-QKD experiments use this variant^23,24,26. One of its defining characteristics is its unconventional security proof; specifically, its estimation of the phase-error rate, a parameter needed to bound the amount of key information that may have leaked to an eavesdropper. In many QKD protocols, the phase-error rate of the single-photon emissions in one basis can be directly estimated by bounding the bit-error rate of the single-photon emissions in the other basis. In the above TF-QKD variant, however, the encoding bases are not mutually unbiased. To estimate the phase-error rate, the authors in ref. ²⁸ use the complementarity³¹ between the “phase” and the “photon number” of a bosonic mode. In this case, the security of a bit encoded in the relative phase of two coherent pulses can be related to the detection statistics of photon-number states. More specifically, in the asymptotic regime, the phase-error rate can be bounded by a non-linear function of infinitely many yield probabilities for even photon-number states²⁸, which can be estimated via the decoy-state method^32,33,34.

While, in the asymptotic regime, the protocol in ref. ²⁸ can offer a higher key rate than its counterparts, it is not obvious if this advantage will still hold in a practical setting, where only a finite number of pulses is sent. In the finite-key regime, one should account for possible statistical fluctuations between the true phase-error rate and the measurement data used to estimate it. There are, however, two challenges in doing so. The first challenge is that the phase-error rate of the protocol is related to the measurement statistics of infinitely many combinations of photon-number states; in practice, one can only obtain bounds for a finite number of them, and dealing with the unbounded components is not as straightforward as in the asymptotic regime. The second challenge is that, unlike in many other QKD protocols, the encoding bases are not mutually unbiased. This opens the possibility that, under a coherent attack by Eve, the detection statistics of a particular round may depend on the basis choices made in previous rounds. Accounting for these correlations makes the analysis quite cumbersome.

In this work, we provide a rigorous security proof for the protocol in ref. ²⁸ that accounts for these two issues in the finite-key setting. Our security proof provides a tight bound on the key rate against general coherent attacks. To overcome the two main challenges mentioned above, we borrow ideas from the finite-key analysis of MDI-QKD³⁵ and the loss-tolerant protocol^36,37, as well as introduce several methods of our own. To obtain a tighter result, we employ a recent technique to bound the deviation between a sum of correlated random variables and its expected value³⁸ which can be much tighter than the widely employed Azuma’s inequality³⁹ when the success probability is low. Importantly, our numerical simulations show that the protocol can overcome the repeaterless bounds^8,9,10 for a block size of ~10¹⁰ transmitted signals in nominal working conditions.

During the preparation of this manuscript, an alternative finite-key security analysis for an identical protocol setup has been reported in ref. ⁴⁰, using an interesting, but different, approach. We would like to highlight that our analysis imposes fewer conditions on the setup parameters than that of ref. ⁴⁰, and results in a higher key rate in most practical regimes. In the “Discussion” section, we compare both approaches. We also compare our results with those of the sending-or-not-sending TF-QKD protocol introduced in ref. ³⁰, whose security has recently been extended to the finite-key regime⁴¹. We find that for reasonably large block sizes, and sufficiently low phase reference mismatch errors, the asymptotic key rate advantage of the scheme in ref. ²⁸ is maintained in the finite-key regime, for most practical ranges of distance.

Results

Protocol description

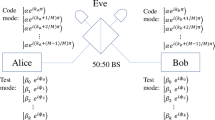
The setup of the TF-QKD protocol in ref. ²⁸ is illustrated in Fig. 1 and its step-by-step description is given below. Alice and Bob generate quantum signals and send them to a middle node, Charlie, who would ideally couple them at a balanced 50:50 beamsplitter and perform a photodetection measurement. For simplicity, we assume the symmetric scenario in which the Alice–Charlie and Bob–Charlie quantum channels are identical. We note, however, that our analysis can be straightforwardly extended to the asymmetric scenario recently considered in refs. ^42,43. The emitted quantum signals belong to two bases, selected at random. In the X basis, Alice and Bob send phase-locked coherent states $\left|\pm \alpha \right\rangle$ with a random phase of either 0 or π with respect to a pre-agreed reference. In the Z basis, Alice and Bob generate phase-randomised coherent states (PRCSs), which are diagonal in the Fock basis. The X-basis states are used to generate the key, while the Z-basis data is used to estimate the detection statistics of Fock states, in combination with the decoy-state method. This is a crucial step in estimating the phase-error rate of the key, thus bounding the information that could have been leaked to a potential eavesdropper. The detailed steps of the protocol are:

• (1) Preparation

  Alice (Bob) chooses the key-generation basis X with probability p_X or the parameter estimation basis Z with probability p_Z = 1 − p_X, and

  • (1.1) If she (he) chooses the X basis, she (he) generates a random bit b_A (b_B), prepares an optical pulse in the coherent state $|{(-1)}^{{b}_{A}}\alpha \rangle$ ($|{(-1)}^{{b}_{B}}\alpha \rangle$), and sends it to Charlie.

  • (1.2) If she (he) chooses the Z basis, she (he) sends an optical pulse in a PRCS of intensity μ, selected from the set $\underline{{\boldsymbol{\mu }}}=\{{\mu }_{0},{\mu }_{1},\ldots ,{\mu }_{d-1}\}$ with probability p_μ, where d is the number of decoy intensities used.

They repeat step (1) for N rounds.

• (2) Detection

  An honest Charlie measures each round separately by interfering Alice and Bob’s signals at a 50:50 beamsplitter, followed by threshold detectors D_c and D_d placed at the output ports corresponding to constructive and destructive interference, respectively. After the measurement, Charlie reports the pair (k_c, k_d), where k_c = 1 (k_d = 1) if detector D_c (D_d) clicks and k_c = 0 (k_d = 0) otherwise. If he is dishonest, Charlie can measure all rounds coherently using an arbitrary quantum measurement, and report N pairs (k_c, k_d) depending on the result. A round is considered successful (unsuccessful) if k_c ≠ k_d (k_c = k_d).

• (3) Sifting

  For all successful rounds, Alice and Bob disclose their basis choices, keeping only those in which they have used the same basis. Let ${{\mathcal{M}}}_{X}$ (${{\mathcal{M}}}_{Z}$) be the set of successful rounds in which both users employed the X (Z) basis, and let ${M}_{X}=\left|{{\mathcal{M}}}_{X}\right|$ (${M}_{Z}=\left|{{\mathcal{M}}}_{Z}\right|$) be the size of this set. Alice and Bob disclose their intensity choices for the rounds in ${{\mathcal{M}}}_{Z}$ and learn the number of rounds M^μν in ${{\mathcal{M}}}_{Z}$ in which they selected intensities $\mu \in \underline{{\boldsymbol{\mu }}}$ and $\nu \in \underline{{\boldsymbol{\mu }}}$, respectively. Also, they generate their sifted keys from the values of b_A and b_B corresponding to the rounds in ${{\mathcal{M}}}_{X}$. For those rounds in which k_c = 0 and k_d = 1, Bob flips his sifted key bit.

• (4) Parameter estimation

  Alice and Bob apply the decoy-state method to M^μν, for $\mu ,\nu \in \underline{{\boldsymbol{\mu }}}$, obtaining upper bounds ${M}_{nm}^{\,\text{U}\,}$ on the number of rounds M_nm in ${{\mathcal{M}}}_{Z}$ in which they sent n and m photons, respectively. They do this for all n, m ≥ 0 such that n + m is even and n + m ≤ S_cut for a prefixed parameter S_cut. Then, they use this data to obtain an upper bound ${N}_{{\rm{ph}}}^{\,\text{U}\,}$ on the number of phase errors, N_ph, in their sifted keys.

• (5) Postprocessing

  • (5.1) Error correction: Alice sends Bob a prefixed amount λ_EC of syndrome information bits through an authenticated public channel, which Bob uses to correct errors in his sifted key.

  • (5.2) Error verification: Alice and Bob compute a hash of their error-corrected keys using a random universal hash function, and check whether they are equal. If so, they continue to the next step; otherwise, they abort the protocol.

  • (5.3) Privacy amplification: Alice and Bob extract a secret-key pair (S_A, S_B) of length $\left|{S}_{A}\right|=\left|{S}_{B}\right|=\ell$ from their error-corrected keys using a random two-universal hash function.

Fig. 1: Setup of the simple TF-QKD protocol²⁸ considered in this work.

Alice and Bob generate their sifted key from the rounds in which they both select the X basis and Charlie declares that a single detector has clicked. The key bit is encoded in the phase of their coherent state. When the users select the same (a different) bit, the constructive (destructive) interference at Charlie’s 50:50 beamsplitter should cause a click in detector D_c (D_d). The Z-basis PRCSs are only used to estimate the phase-error rate of the X-basis emissions.

Parameter estimation and secret-key rate analysis

The main contribution of this work—see “Methods” section for the details—is a procedure to obtain a tight upper bound ${N}_{{\rm{ph}}}^{\,\text{U}\,}$ on the total number of phase errors N_ph in the finite-key regime for the protocol described above. Namely, we find that, except for an arbitrarily small failure probability ε, it holds that

$$\begin{array}{l}{N}_{{\rm{ph}}}\le {N}_{{\rm{ph}}}^{\,\text{U}\,}:=\frac{{p}_{X}^{2}}{{p}_{Z}^{2}}\mathop{\sum }\limits_{j=0}^{1}\left[\sum \limits_{\begin{array}{c}n,m\in {{\mathbb{N}}}_{j}\\ n+m\le S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\sqrt{{M}_{nm}^{\,\text{U}\,}+{{{\Delta }}}_{nm}}+\sqrt{{M}_{Z}+{{\Delta }}}\sum \limits_{\begin{array}{c}n,m\in {{\mathbb{N}}}_{j}\\ n+m> S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\,\right]^{2}+{{\Delta }},\end{array}$$

(1)

where p_nm∣X (p_nm∣Z) is the probability that Alice and Bob’s joint X (Z) basis pulses contain n and m photons, respectively, given by

$${p}_{nm| X}={\left|\langle \alpha |n \rangle\right|}^{2}{\left|\langle \alpha |m\rangle\right|}^{2},$$

(2)

$${p}_{nm| Z}=\sum _{\mu ,\nu \in \underline{\boldsymbol{\mu}}}{p}_{\mu }{p}_{\nu }{p}_{n| \mu }{p}_{m| \nu },$$

(3)

with ${p}_{n| \mu }={\mu }^{n}\exp (-\mu )/n!$ being the Poisson probability that a PRCS pulse of intensity μ will contain n photons; ${{\mathbb{N}}}_{0}$ (${{\mathbb{N}}}_{1}$) is the set of non-negative even (odd) integers; and Δ and Δ_nm are statistical fluctuation terms defined in step (4) of subsection “Instructions for experimentalists”, where we provide a step-by-step instruction list to apply our results to the measurement data obtained in an experimental setup. The rest of the parameters have been introduced in the protocol description.

When it comes to finite-key analysis, there is one key difference between the protocol considered in this work and several other protocols, such as, for example, decoy-state BB84⁴⁴, decoy-state MDI-QKD³⁵, and sending-or-not-sending TF-QKD⁴¹. In all the latter setups, when there are no state preparation flaws, the single-photon components of the two encoding bases are mutually unbiased; in other words, they look identical to Eve once averaged by the bit selection probabilities. This implies that such states could have been generated from a maximally entangled bipartite state, where one of its components is measured in one of the two orthogonal bases, and the other half represents an encoded key bit. In fact, the user(s) could even wait until they learn which rounds have been successfully detected to decide their measurement basis, effectively delaying their choice of encoding basis. This possibility allows the application of a random sampling argument: since the choice of the encoding basis is independent of Eve’s attack, the bit-error rate of the successful X-basis emissions provides a random sample of the phase-error rate of the successful Z-basis emissions, and vice versa. Then, one can apply tight statistical results, such as the Serfling inequality⁴⁵, to bound the phase-error rate in one basis, using the measured bit-error rate in the other basis. This approach, however, is not directly applicable to the protocol considered here, in which the secret key is extracted from all successfully detected X-basis signals, not just from their single-photon components. Moreover, the encoding bases are not mutually unbiased: the Z-basis states are diagonal in the Fock basis, while the X-basis states are not. This will require a different, perhaps more cumbersome, analysis as we highlight below.

To estimate the X-basis phase-error rate from the Z-basis measurement data, we construct a virtual protocol in which the users learn their basis choice by measuring a quantum coin after Charlie/Eve reveals which rounds were successful. Note that, because of the biased basis feature of the protocol, the statistics of the quantum coins associated to the successful rounds could depend on Eve’s attack. This means that the users cannot delay their choice of basis, which prevents us from applying the random sampling argument. Still, it turns out that the quantum coin technique now allows us to upper bound the average number of successful rounds in which the users had selected the X basis and obtained a phase error. This bound is a non-linear function of the average number of successful rounds in which they had selected the Z basis and respectively sent n and m photons, with n + m even. More details can be found in the “Methods” section; see Eq. (19).

The main tool we use to relate each of the above average terms to their actual occurrences, N_ph and M_nm, is Azuma’s inequality³⁹, which is widely used in security analyses of QKD to bound sums of observables over a set of rounds of the protocol (in our case, the set of successful rounds after sifting) when the independence between the observables corresponding to different rounds cannot be guaranteed. When using Azuma’s inequality, the deviation term Δ scales with the square root of the number of terms in the sum. In our case, Δ scales with $\sqrt{{M}_{{\rm{s}}}}$, where M_s is the number of successful rounds after sifting. For parameters of comparable magnitude to M_s, this provides us with a reasonably tight bound. Whenever the parameter of interest is small, however, the provided bound could instead be loose. This is the case for the crucial term ${M}_{00}^{{\rm{U}}}$ in Eq. (1), as vacuum states are unlikely to result in successful detection events, and thus the bound obtained with Azuma’s inequality can be loose. This is important because, in Eq. (1), the coefficient associated to the vacuum term is typically the largest. To obtain a better bound for this term, we employ a remarkable recent technique to bound the deviation between a sum of dependent random variables and its expected value³⁸. This technique provides a much tighter bound than Azuma’s inequality when the value of the sum is much lower than the number of terms in the sum. In particular, it provides a tight upper bound for the vacuum component M₀₀. In “Methods” section, we provide a statement of the result and we explain how we apply it to our protocol.

Having obtained the upper bound ${e}_{{\rm{ph}}}^{\,\text{U}\,}:={N}_{{\rm{ph}}}^{\,\text{U}\,}/{M}_{X}$ on the phase-error rate, we show in Supplementary Note A that, if the length of the secret key obtained after the privacy amplification step satisfies

$$\ell \le {M}_{X}\left[1-h({e}_{{\rm{ph}}}^{\,\text{U}\,})\right]-{\lambda }_{{\rm{EC}}}-{\mathrm{log}\,}_{2}\frac{2}{{\epsilon }_{{\rm{c}}}}-{\mathrm{log}\,}_{2}\frac{1}{4{\epsilon }_{{\rm{PA}}}^{2}},$$

(4)

the protocol is guaranteed to be ϵ_c-correct and ϵ_s-secret, with ${\epsilon }_{{\rm{s}}}=\sqrt{\varepsilon }+{\epsilon }_{{\rm{PA}}}$; where ε is the failure probability associated to the estimation of the phase-error rate, $h(x)=-x\,{\log}_{2}x-(1-x){\mathrm{log}\,}_{2}(1-x)$ is the Shannon binary entropy function, and λ_EC is number of bits that are spent in the error correction procedure. Here, our security analysis follows the universal composable security framework^46,47, according to which a protocol is ${\epsilon }_{\sec }$-secure if it is both ϵ_c-correct and ϵ_s-secret, with ${\epsilon }_{\mathrm{sec} }\le {\epsilon }_{{\rm{c}}}+{\epsilon }_{{\rm{s}}}$.

Instructions for experimentalists

Here, we provide a step-by-step instruction list to apply our security analysis to a real-life experiment:

• (1) Set the security parameters ϵ_c and ϵ_PA, as well as the failure probabilities ε_c and ε_a for the inverse multiplicative Chernoff bound and the concentration bound for sums of dependent random variables, respectively. Set S_cut. Calculate the overall failure probability ε of the parameter estimation process, which depends on the number of times that the previous two inequalities are applied. In general, $\varepsilon ={d}^{2}{\varepsilon }_{{\rm{c}}}+{\left(\lfloor \frac{S_{\rm{cut}}}{2}\rfloor +1\right)}^{2}{\varepsilon }_{{\rm{a}}}+{\varepsilon }_{{\rm{a}}}$, where d is the number of decoy intensities employed by each user. For S_cut = 4 and three decoy intensities, we have that ε = 9ε_c + 10ε_a.

• (2) Use prior information about the channel to obtain a prediction ${\tilde{M}}_{00}^{{\rm{U}}}$ on ${M}_{00}^{{\rm{U}}}$, the upper bound on the number of Z-basis vacuum events that will be obtained after applying the decoy-state method.

• (3) Run steps (1)–(3) of the protocol, obtaining a sifted key of length M_X, and Z-basis measurement counts M^μν for $\mu ,\nu \in \underline{{\boldsymbol{\mu }}}$. Let M_s = M_X + M_Z be the number of successful rounds after sifting.

• (4) Use the analytical decoy-state method included in the Supplementary Note B and the measured values of M^μν to obtain upper bounds ${M}_{nm}^{\,\text{U}\,}$, for all n, m such that n + m is even and n + m ≤ S_cut. Alternatively, use the numerical estimation method introduced in the Supplementary Notes of ref. ³⁵.

• (5) Set ${{\Delta }}=\sqrt{\frac{1}{2}{M}_{{\rm{s}}}\mathrm{ln}\,{\varepsilon }_{{\rm{a}}}^{-1}}$ and Δ_nm = Δ for all n, m except for m = n = 0. Substitute ${\tilde{{{\Lambda }}}}_{n}\to {\tilde{M}}_{00}^{{\rm{U}}}$ in Eq. (32) to find parameters a and b. Set

  $${{{\Delta }}}_{00}=\left[b+a\left(\frac{2{M}_{00}^{{\rm{U}}}}{{M}_{{\rm{s}}}}-1\right)\right]\sqrt{{M}_{{\rm{s}}}},$$

  (5)

• (6) Use Eq. (1) to find ${N}_{{\rm{ph}}}^{\,\text{U}\,}$ and set ${e}_{{\rm{ph}}}^{\,\text{U}\,}={N}_{{\rm{ph}}}^{\,\text{U}\,}/{M}_{X}$.

• (7) Use Eq. (4) to specify the required amount of privacy amplification and to find the corresponding length of the secret key that can be extracted. The key obtained is ${\epsilon }_{\sec }$-secure, with ${\epsilon }_{\mathrm{sec} }={\epsilon }_{{\rm{c}}}+{\epsilon }_{{\rm{s}}}$ and ${\epsilon }_{{\rm{s}}}=\sqrt{\varepsilon }+{\epsilon }_{{\rm{PA}}}$.

Discussion

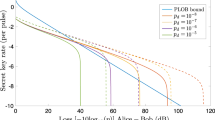
In this section, we analyse the behaviour of the secret-key rate as a function of the total loss. We simulate the nominal scenario in which there is no Eve and Charlie is honest. In this case, the total Alice–Bob loss includes the loss in the quantum channels, as well as the inefficiency of Charlie’s detectors. We compare the key rate for the protocol in Fig. 1, using the finite-key security analysis introduced in the previous section, with that of the sending-or-not-sending TF-QKD protocol^30,41, as well as with the finite-key analysis presented in ref. ⁴⁰. We also include the asymptotic secret-key capacity for repeaterless QKD systems over lossy channels, known as the PLOB bound⁹, for comparison. It is given by $-{\mathrm{log}\,}_{2}(1-\eta )$, where η is the transmittance of the Alice–Bob quantum channel, which includes the efficiency of Charlie’s detectors. While specific bounds for the finite-key setting have recently been studied^10,48, in the practical regimes of interest to this work, they numerically offer a negligible difference to the PLOB bound. The latter has then been used in all relevant graphs for consistency. To simulate the data that would be obtained in all protocols, we use the simple channel model described in Supplementary Note C, which accounts for phase reference mismatch and polarisation misalignment. Also, we assume that both users employ three decoy-state intensities μ₀ > μ₁ > μ₂. Since the optimal value μ₂ = 0 is typically difficult to achieve in practice, we set μ₂ = 10⁻⁴ and optimise the secret-key rate over the value of μ₀ and μ₁. We also optimise it over the selection probabilities, as well as over p_X and α.

In our simulations, we model the phase reference mismatch between Alice and Bob’s pulses by shifting Bob’s signals by an angle ϕ = δ_phπ, where δ_ph = 9.1%. This corresponds to a QBER of ~2% for most attenuations, matching the experimental results in ref. ²³. For brevity, we do not consider the effect of polarisation misalignment in our numerical results, but one can use the provided analytical model to study different scenarios of interest. In principle, even if the mechanism used for polarisation stability is not perfect, one can use polarisation filters to ensure that the same polarisation modes are being coupled at the 50:50 beamsplitter, at the cost of introducing additional loss. We assume a per-pulse dark count probability p_d = 10⁻⁸ for each detector. We assume an error correction leakage of λ_EC = fM_Xh(e_X), where e_X is the bit-error rate of the sifted key, and f is the error correction inefficiency, which we assume to be f = 1.16. For the security bounds, we set ϵ_c = ϵ_s = 10⁻¹⁰, and for simplicity we set ε = ϵ_PA = ϵ_s/3.

In Fig. 2, we display the secret-key rate per pulse achievable for different values of the block size, N, of transmitted signals. It can be seen that the protocol could outperform the repeaterless bound for a block size of ~10¹⁰ transmitted signals per user, at an approximate total loss of 50 dB. For standard optical fibres, this corresponds to a total distance of 250 km, if we neglect the loss in the photodetectors. At a 1 GHz clock rate, it takes only ~10 s to collect the required data. For a block size of 10¹¹ transmitted signals, the protocol can already outperform the repeaterless bound for a total loss ranging from 45 to over 80 dB. By increasing N, we approach the asymptotic performance of the protocol. We note that our choice of dark count probability, p_d = 10⁻⁸, may be conservative, since a dark count rate of 1 c.p.s., corresponding to p_d = 10⁻⁹ with a repetition rate of 1 GHz, may be achievable with state-of-the-art SSPD⁴⁹. In Supplementary Note D, we show an additional graph for p_d = 10⁻⁹. We find that, for sufficiently large block sizes, the maximum distance increases when the dark count probability decreases. Interestingly, however, this is not the case for N = 10¹⁰, for which the two curves are almost identical.

Fig. 2: Secret-key rate obtainable as a function of the channel loss.

We consider different values of the block size N, which represents the total number of rounds in the protocol. The overall Alice–Bob loss includes the loss in both quantum channels and in Charlie’s detectors. The simulation parameters are stated in the main text.

The dependence of the secret-key rate on the block size N has been shown in Fig. 3, at a fixed total loss of 50 dB and for several values of the phase reference mismatch δ_ph. In all cases, there is a minimum required block size to obtain a positive key rate. This minimum block size can be even <10⁹ in the ideal case of no phase reference mismatch, and it goes up to ~10¹⁰ at δ_ph = 20%. There is a sharp increase in the secret-key rate once one goes over this minimum required block size, after which one slowly approaches the key rate in the asymptotic limit. The latter behaviour is likely due to the use of Azuma’s inequality. One can, nevertheless, overcome the repeaterless bound at a reasonable block size in a practical regime where δ_ph ≤ 15%. At higher values of total loss this crossover happens at even larger values of δ_ph.

Fig. 3: Secret-key rate obtainable as a function of the block size N.

We assume a total loss of 50 dB and consider several values of the phase reference mismatch δ_ph. All other simulation parameters are stated in the main text.

In Fig. 4, we compare the performance of our protocol with that of the sending-or-not-sending TF-QKD protocol presented in refs. ^30,41. To compute the results of the sending-or-not-sending protocol, we have used the analysis in ref. ⁴¹, after correcting a mistake present in Appendix A of that work. Namely, according to Eqs. (S14)–(S19) of ref. ⁵⁰, if the failure probability of the phase-error rate estimation is $\bar{\varepsilon }$, then the smooth max entropy term in the left-hand side of Eq. (A5) should be ${H}_{\max }^{\sqrt{\bar{\varepsilon }}}$ instead of ${H}_{\max }^{\bar{\varepsilon }}$. In the asymptotic regime, the protocol considered in this work outperforms the sending-or-not-sending protocol at all values of total loss. For a block size of 10¹² transmitted signals, this is still the case up to 80 dB of total loss, after which the key rate is already <10⁻⁶ bits per pulse for both protocols. For a block size of 10¹⁰ transmitted signals, however, the curves for the two protocols cross at ~55 dB, after which the sending-or-not-sending protocol offers a better performance. This behaviour is due to the different statistical fluctuation analyses applied to the two protocols. As explained in the “Results” section, the single-photon components in the sending-or-not-sending protocol are mutually unbiased, allowing for a simpler and tighter estimation of the phase-error rate. This is not the case for our TF-QKD protocol, for which this estimation involves the application of somewhat looser bounds for several terms in Eq. (1). We conclude that for sufficiently large block sizes, and a sufficiently low phase reference mismatch, the protocol considered in this work maintains its better key rate performance over the sending-or-not-sending variant. We note that for smaller block sizes and higher values of phase reference mismatch, this comparative advantage is reduced, or even inverted in some regimes. For completeness, in Supplementary Note D, we provide additional simulation results for a broader range of parameter values.

Fig. 4: Comparison between this work (solid) and sending-or-not-sending TF-QKD^30,41 (dashed).

We consider different values for the block size N of transmitted signals. All other simulation parameters are stated in the main text.

Finally, in Fig. 5, we compare our results with those of the alternative analysis in ref. ⁴⁰. To compute the secret-key rate of the latter, we use the code provided by the authors, except for the adjustments needed to match it to the channel model described in Supplementary Note C. It can be seen that, in most regimes, the analysis introduced in this paper provides a higher key rate than that of ref. ⁴⁰. Moreover, we remark that the security proof presented in ref. ⁴⁰, in its current form, is only applicable when the state generated by the weakest decoy intensity μ₂ is a perfect vacuum state of intensity μ₂ = 0. The security analysis presented in this work, however, can be applied to any experimental value of μ₂, and we assume a value of μ₂ = 10⁻⁴, which may be easier to achieve in practice. That said, the security proof in ref. ⁴⁰ adopts an interesting approach that results in a somehow simpler statistical analysis. In particular, unlike in the analysis presented in this paper, the authors in ref. ⁴⁰ do not estimate the detection statistics of photon-number states as an intermediate step to bounding the phase-error rate. Instead, they show that the operator corresponding to a phase error can be bounded by a linear combination of the Z-basis decoy states. While this linear bound is asymptotically looser than the non-linear formula in Eq. (1), it allows the application of a simpler statistical analysis based on a double use of Bernoulli sampling. Given that the finite-key analysis of a protocol could be part of the software package of a product, we believe that the additional key rate achievable by our analysis in many regimes justifies its slightly more complex approach.

Fig. 5: Comparison between this work (solid) and the alternative analysis in ref. ⁴⁰ (dashed).

We consider different values for the block size N of transmitted signals. All other simulation parameters are stated in the main text.

In conclusion, we have proven the security of the protocol proposed in ref. ²⁸, in the finite-key regime and against coherent attacks. Our results show that, under nominal working conditions experimentally achievable by today’s technology, this scheme could outperform the repeaterless secret-key rate bound in a key exchange run of ~10 s, assuming a 1 GHz clock rate. In terms of key rate, it would also outperform other TF-QKD variants, as well as alternative security proofs, in many practical regimes of interest.

Methods

In this section, we introduce the procedure that we use to prove the security of the protocol, referring to the Supplementary Notes when appropriate. For notation clarity, we assume the symmetric scenario in which Alice and Bob employ the same X-basis amplitude α and the same set of Z-basis intensities $\underline{{\boldsymbol{\mu }}}$, which is optimal when the Alice–Charlie and Bob–Charlie channels are identical. However, the analysis can be applied as well to the asymmetric scenario^42,43 by appropriately redefining the parameters p_nm∣X and p_nm∣Z.

Virtual protocol

To bound the information leakage to Eve, we construct an entanglement-based virtual protocol that is equivalent to the actual protocol. In this virtual protocol, Alice and Bob measure their local ancilla systems in a basis that is conjugate to that used to generate the key. We refer to the error rate of the virtual protocol as the phase-error rate e_ph. The objective of the security analysis is to find an upper bound ${e}_{{\rm{ph}}}^{{\rm{U}}}$ such that $\Pr \left(\right.{e}_{{\rm{ph}}}>{e}_{{\rm{ph}}}^{{\rm{U}}}\left)\right.\le \varepsilon$. In Supplementary Note A, we show how this can be used to prove the security of the key obtained in the actual protocol.

In the virtual protocol, Alice replaces her X-basis emissions by the preparation of the state

$${\left|{\psi }_{X}\right\rangle }_{Aa}=\frac{1}{\sqrt{2}}({\left|+\right\rangle }_{A}{\left|\alpha \right\rangle }_{a}+{\left|-\right\rangle }_{A}{\left|-\alpha \right\rangle }_{a}),$$

(6)

where A is an ancilla system at Alice’s lab, a is the photonic system sent to Eve, and $\left|\pm \right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle \pm \left|1\right\rangle )$; while Bob replaces his X-basis emissions by a similarly defined ${\left|{\psi }_{X}\right\rangle }_{Bb}$. After Eve’s attack, Alice and Bob measure systems A and B in the Z-basis $\{\left|0\right\rangle ,\left|1\right\rangle \}$, which is conjugate to the X basis $\{\left|+\right\rangle ,\left|-\right\rangle \}$ that they would use to generate the key. It is useful to write the state in Eq. (6) as

$${\left|{\psi }_{X}\right\rangle }_{Aa}={\left|0\right\rangle }_{A}{\left|{C}_{0}\right\rangle }_{a}+{\left|1\right\rangle }_{A}{\left|{C}_{1}\right\rangle }_{a},$$

(7)

where $\left|{C}_{0}\right\rangle$ and $\left|{C}_{1}\right\rangle$ are the (unnormalised) cat states

$$\left|{C}_{0}\right\rangle =\frac{1}{2}(\left|\alpha \right\rangle +\left|-\alpha \right\rangle ),\qquad \quad \left|{C}_{1}\right\rangle =\frac{1}{2}(\left|\alpha \right\rangle -\left|-\alpha \right\rangle ).$$

(8)

Alice’s Z-basis emissions are diagonal in the Fock basis, and the virtual protocol replaces them by their purification

$${\left|{\psi }_{Z}\right\rangle }_{Aa}=\mathop{\sum }\limits_{n=0}^{\infty }\sqrt{{p}_{n| Z}}{\left|n\right\rangle }_{A}{\left|n\right\rangle }_{a},$$

(9)

where ${p}_{n| Z}={\sum }_{\mu \in \underline{{\boldsymbol{\mu }}}}{p}_{\mu }{p}_{n| \mu }$ is the probability that Alice’s Z-basis pulse contains n photons, averaged over the selection of μ. Unlike in the actual protocol, in the virtual protocol Alice and Bob learn the photon number of their signals by measuring systems A and B after Eve’s attack.

Lastly, Alice’s emission of ${\left|{\psi }_{X}\right\rangle }_{Aa}$ with probability p_X and ${\left|{\psi }_{Z}\right\rangle }_{Aa}$ with probability p_Z is replaced by the generation of the state

$${\left|\psi \right\rangle }_{{A}_{{\rm{c}}}Aa}=\sqrt{{p}_{X}}{\left|0\right\rangle }_{{A}_{{\rm{c}}}}{\left|{\psi }_{X}\right\rangle }_{Aa}+\sqrt{{p}_{Z}}{\left|1\right\rangle }_{{A}_{{\rm{c}}}}{\left|{\psi }_{Z}\right\rangle }_{Aa},$$

(10)

where A_c is a quantum coin ancilla at Alice’s lab; while Bob’s is replaced by an equally defined ${\left|\psi \right\rangle }_{{B}_{\mathrm{c}}Bb}$. Alice and Bob measure systems A_c and B_c after Eve’s attack, delaying the reveal of their basis choice. The full description of the virtual protocol is the following:

• (1) Preparation

  Alice and Bob prepare N copies of the state $\left|\phi \right\rangle ={\left|\psi \right\rangle }_{{A}_{{\rm{c}}}Aa}\otimes {\left|\psi \right\rangle }_{{B}_{\rm{c}}Bb}$ and send all systems a and b to Eve over the quantum channel.

• (2) Detection

  Eve performs an arbitrary general measurement on all the subsystems a and b of ${\left|\phi \right\rangle }^{\otimes N}$ and publicly announces N bit pairs (k_c, k_d). Without loss of generality, we assume that there is a one-to-one correspondence between her measurement outcome and her set of announcements. A round is considered successful (unsuccessful) if k_c ≠ k_d (k_c = k_d). Let ${\mathcal{M}}$ ($\bar{{\mathcal{M}}}$) represent the set of successful (unsuccessful) rounds.

• (3) Virtual sifting

  For all rounds, Alice and Bob jointly measure the systems A_c and B_c, learning whether they used the same or different bases, but not the specific basis they used. Let ${{\mathcal{M}}}_{{\rm{s}}}$ (${{\mathcal{M}}}_{{\rm{d}}}$) denote the set of successful rounds in which they used the same (different) bases.

• (4) Ancilla measurement

  • (4.1) For all rounds in ${{\mathcal{M}}}_{{\rm{s}}}$, Alice (Bob) first measures the system A_c (B_c) in $\{\left|0\right\rangle ,\left|1\right\rangle \}$, learning her (his) choice of basis. If the result is ${\left|0\right\rangle }_{{A}_{{\rm{c}}}}$ (${\left|0\right\rangle }_{{B}_{\rm{c}}}$), she (he) measures system A (B) in $\{\left|0\right\rangle ,\left|1\right\rangle \}$; if the result is ${\left|1\right\rangle }_{{A}_{{\rm{c}}}}$ (${\left|1\right\rangle }_{{B}_{\rm{c}}}$), she (he) measures system A (B) in the Fock basis.

  • (4.2) For all rounds in ${{\mathcal{M}}}_{{\rm{d}}}$, Alice (Bob) measures the systems A_c (B_c) and A (B), using the same strategy as in step (4.1).

• (5) Intensity assignment

  For all rounds in ${\mathcal{M}}$ in which Alice (Bob) obtained ${\left|1\right\rangle }_{{A}_{{\rm{c}}}}$ (${\left|1\right\rangle }_{{B}_{\rm{c}}}$), she (he) assigns each n-photon state to intensity μ with probability p_μ∣n.

• (6) Classical communication

  For all rounds in ${\mathcal{M}}$, Alice and Bob announce their basis and intensity choices over an authenticated public channel.

• (7) Estimation of the number of phase errors

  Alice and Bob calculate an upper bound on N_ph using their Z-basis measurement data.

Two points from the virtual protocol above require further explanation. The first is that, in the real protocol, Bob flips his key bit when Eve reports k_c = 0 and k_d = 1. This step is omitted from the virtual protocol, since the X-basis bit flip gate σ_z has no effect on Bob’s Z-basis measurement result. The second point concerns step (5), which may appear to serve no purpose, but is needed to ensure that the classical information exchanged between Alice and Bob is equivalent to that of the real protocol. The term p_μ∣n is the probability that Alice’s (Bob’s) Z-basis n-photon pulse originated from intensity μ, and it is given by

$${p}_{\mu | n}=\frac{{p}_{\mu }{p}_{n| \mu }}{{\sum }_{\mu \in \underline{\boldsymbol{\mu}}}{p}_{\mu }{p}_{n| \mu }}.$$

(11)

Phase-error rate estimation

We now turn our attention to Alice and Bob’s measurements in step (4.1) of the virtual protocol. Let u ∈ {1, 2, ..., M_s} index the rounds in ${{\mathcal{M}}}_{{\rm{s}}}$, and let ξ_u denote the measurement outcome of the uth round. The possible outcomes are ξ_u = X_ij, corresponding to ${\left|00\right\rangle }_{{A}_{{\rm{c}}}{B}_{\rm{c}}}{\left|ij\right\rangle }_{AB}$, where i, j ∈ {0, 1}; and ξ_u = Z_nm, corresponding to ${\left|11\right\rangle }_{{A}_{{\rm{c}}}{B}_{\rm{c}}}{\left|n,m\right\rangle }_{AB}$, where n and m are any non-negative integers. Note that the outcomes ${\left|10\right\rangle }_{{A}_{{\rm{c}}}{B}_{\rm{c}}}$ and ${\left|01\right\rangle }_{{A}_{{\rm{c}}}{B}_{\rm{c}}}$ are not possible due to the previous virtual sifting step. A phase error occurs when ξ_u ∈ {X₀₀, X₁₁}. In Supplementary Note E, we prove that the probability to obtain a phase error in the uth round, conditioned on all previous measurement outcomes in the protocol, is upper bounded by

$$\Pr \left({\xi }_{u}\in \{{X}_{00},{X}_{11}\}| {{\mathcal{F}}}_{u-1}\right)\le \frac{p_X^2}{p_Z^2}{\sum \limits_{j=0}^{1}}\left[\,{\sum \limits_{n,m\in {{\mathbb{N}}}_{j}}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}\Pr \left({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1}\right)}\,\right]^{2},$$

(12)

where ${{\mathcal{F}}}_{u-1}$ is the σ-algebra generated by the random variables ξ₁, ..., ξ_u−1, ${{\mathbb{N}}}_{0}$ (${{\mathbb{N}}}_{1}$) is the set of non-negative even (odd) numbers, and the probability terms p_nm∣X and p_nm∣Z have been defined in Eqs. (2) and (3). In Eq. (12), for notation clarity, we have omitted the dependence of all probability terms on the outcomes of the measurements performed in steps (2) and (3) of the virtual protocol.

Applying the concentration bound in Eq. (30), we have that, except with probability ε_a,

$$N_{\rm{ph}}\le \mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}\in \{{X}_{00},{X}_{11}\}| {{\mathcal{F}}}_{u-1}\right)+{{\Delta }},$$

(13)

where N_ph is the number of events of the form ξ_u ∈ {X₀₀, X₁₁} in ${{\mathcal{M}}}_{{\rm{s}}}$, and ${{\Delta }}=\sqrt{\frac{1}{2}{M}_{{\rm{s}}}\mathrm{ln}\,{\varepsilon }_{{\rm{a}}}^{-1}}$ is a deviation term. Similarly, from Eq. (30), we have that, except with probability ε_a,

$$\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1}\right)\le {M}_{nm}+{{\Delta }},$$

(14)

where M_nm is the number of events of the form ξ_u = Z_nm in ${{\mathcal{M}}}_{{\rm{s}}}$. As we will explain later, this bound is not tight when applied to the vacuum counts M₀₀. For this term, we use the alternative bound in Eq. (33), according to which, except with probability ε_a,

$$\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}={Z}_{00}| {{\mathcal{F}}}_{u-1}\right)\le {M}_{00}+{{{\Delta }}}_{00}.$$

(15)

In this case, the deviation term is given by

$${{{\Delta }}}_{00}=\left[b+a\left(\frac{2{M}_{00}}{{M}_{{\rm{s}}}}-1\right)\right]\sqrt{{M}_{{\rm{s}}}},$$

(16)

where a and b can be found by substituting ${\tilde{{{\Lambda }}}}_{n}$ by ${\tilde{M}}_{00}^{{\rm{U}}}$ in Eq. (31).

Now, we will transform Eq. (12) to apply Eqs. (13)–(15). Let us denote the right-hand side of Eq. (12) as $f({\overrightarrow{p}}_{u})$, where ${\overrightarrow{p}}_{u}$ is a vector of probabilities composed of $\Pr ({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1})$ ∀ n, m. If we expand the square in $f({\overrightarrow{p}}_{u})$, we can see that all addends are positive and proportional to $\sqrt{{p}_{1}{p}_{2}}$, where p₁ and p₂ are elements of ${\overrightarrow{p}}_{u}$, implying that $f({\overrightarrow{p}}_{u})$ is a concave function. Thus, by Jensen’s inequality⁵¹, we have

$$\frac{1}{{M}_{{\rm{s}}}}\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}f({\overrightarrow{p}}_{u})\le f \left(\frac{1}{{M}_{{\rm{s}}}}\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}{\overrightarrow{p}}_{u}\right).$$

(17)

After taking the average over all rounds M_s on both sides of Eq. (12), applying Eq. (17) on the right-hand side, and cancelling out the term 1/M_s on both sides of the inequality, we have that

$$\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}\in \{{X}_{00},{X}_{11}\}| {{\mathcal{F}}}_{u-1}\right)\le \frac{p_X^2}{p_Z^2}\mathop{\sum }\limits_{j=0}^{1}\left[{\sum \limits_{n,m\in {{\mathbb{N}}}_{j}}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1}\right)}\,\right]^{2}.$$

(18)

We are now ready to apply Eqs. (13)–(15) to substitute the sums of probabilities in Eq. (18) by N_ph and M_nm. However, note that, in their application of the decoy-state method, Alice and Bob only estimate the value of M_nm for terms of the form n + m ≤ S_cut, so it is only useful to substitute Eq. (14) for these terms. With this in mind, we obtain

$$\begin{array}{l}N_{\rm{ph}}-{{\Delta }}\le \frac{{p}_{X}^{2}}{{p}_{Z}^{2}}\mathop{\sum }\limits_{j=0}^{1}\left[\sum\limits _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m\le S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\sqrt{{M}_{nm}+{{{\Delta }}}_{nm}}+\sum\limits _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m> S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1}\right)}\,\right]^{2},\end{array}$$

(19)

where Δ_nm = Δ except for Δ₀₀.

We still need to deal with the sum over the infinitely many remaining terms of the form n + m > S_cut. For them, we apply the following upper bound

$$\mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}={Z}_{nm}| {{\mathcal{F}}}_{u-1}\right)\le \mathop{\sum }\limits_{u=1}^{{M}_{{\rm{s}}}}\Pr \left({\xi }_{u}=Z| {{\mathcal{F}}}_{u-1}\right)\le {M}_{Z}+{{\Delta }},$$

(20)

where ξ_u = Z denotes that Alice and Bob learn that they have used the Z basis in the uth round in ${{\mathcal{M}}}_{{\rm{s}}}$; and M_Z is the number of events of the form ξ_u = Z obtained by Alice and Bob. In the last step, we have used Eq. (30), using an identical argument as in Eq. (13). When we apply Eq. (20) to Eq. (19), we end up with the term

$$\sum _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m> S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\sqrt{{M}_{Z}+{{\Delta }}}=\sqrt{{M}_{Z}+{{\Delta }}}\sum _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m> S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}.$$

(21)

It can be shown that the infinite sum in Eq. (21) converges to a finite value if

$$\max \{\underline{{\boldsymbol{\mu }}}\}>{\alpha }^{2}.$$

(22)

Substituting Eq. (20) into Eq. (19), and isolating N_ph, we obtain

$${N}_{{\rm{ph}}}\le \frac{{p}_{X}^{2}}{{p}_{Z}^{2}}\mathop{\sum }\limits_{j=0}^{1}\left[\sum _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m\le S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\sqrt{{M}_{nm}+{{{\Delta }}}_{nm}}+\sqrt{{M}_{Z}+{{\Delta }}}\sum _{\begin{array}{c}n,m\in {{\Bbb{N}}}_{j}\\ n+m> S_{\rm{cut}}\end{array}}\sqrt{\frac{{p}_{nm| X}}{{p}_{nm| Z}}}\,\right]^{2}+{{\Delta }}.$$

(23)

Note that the right-hand side of Eq. (23) is a function of the measurement counts M_nm, which cannot be directly observed. They must be substituted by the upper bounds ${M}_{nm}^{{\rm{U}}}$ obtained via the decoy-state analysis, as explained below. After doing so, we obtain Eq. (1). The failure probability ε associated to the estimation of N_ph is upper bounded by summing the failure probabilities of all concentration inequalities used. That includes each application of Eqs. (30) and (33), which fail with probability ε_a; and each application of the multiplicative Chernoff bound in the decoy-state analysis, which fails with probability ε_c. In the case of three decoy intensities and S_cut = 4, we have ε = 9ε_c + 10ε_a. In our simulations, we set ε_c = ε_a for simplicity.

Decoy-state analysis

Since Alice and Bob’s Z-basis emissions are a mixture of Fock states, the measurement counts M_nm have a fixed value, which is nevertheless unknown to them. Instead, the users have access to the measurement counts M^μν, the number of rounds in ${{\mathcal{M}}}_{Z}$ in which they selected intensities μ and ν, respectively. To bound M_nm, we use the decoy-state method^32,33,34. This technique exploits the fact that Alice and Bob could have run an equivalent virtual scenario in which they directly send Fock states $\left|n,m\right\rangle$ with probability p_nm∣Z, and then randomly assign each of them to intensities μ and ν with probability

$${p}_{\mu \nu | nm}=\frac{{p}_{\mu \nu }{p}_{nm| \mu \nu }}{{p}_{nm| Z}},$$

(24)

where p_μν = p_μp_ν and p_nm∣μν = p_n∣μp_m∣ν. In particular, each of the instances in which Alice and Bob chose the Z basis, sent n and m photons, and Eve announced a detection is assigned to intensities μ and ν with a fixed probability p_μν∣nm, even if Eve employs a coherent attack. This implies that these assignments can be regarded as an independent Bernoulli trial, and M^μν can be regarded as a sum of independent Bernoulli trials. The average value of M^μν is

$${\Bbb{E}}[{M}^{\mu \nu }]=\mathop{\sum }\limits_{n,m=0}^{\infty }{p}_{\mu \nu | nm}{M}_{nm}.$$

(25)

In the actual protocol, Alice and Bob know the realisations M^μν of these random variables. By using the inverse multiplicative Chernoff bound^52,53, stated in Supplementary Note F, they can compute lower and upper bounds ${{\mathbb{E}}}^{\rm{L}}[{M}^{\mu \nu }]$ and ${{\mathbb{E}}}^{\text{U}}[{M}^{\mu \nu }]$ for ${\mathbb{E}}[{M}^{\mu \nu }]$. These will set constraints on the possible value of the terms M_nm. We are interested in the indices (i, j) such that i + j ≤ S_cut and i + j is even, and an upper bound on each M_ij can be found by solving the following linear optimisation problem

$$\begin{array}{l}\max {M}_{ij}\\ {\rm{s.t.}}\;\forall \mu ,\nu \ {{\mathbb{E}}}^{\text{U}}[{M}^{\mu \nu }]\ge \mathop{\sum }\limits_{n,m=0}^{\infty }{p}_{\mu \nu | nm}{M}_{nm},\\ \qquad\qquad\;{{\mathbb{E}}}^{\rm{L}}[{M}^{\mu \nu }]\le \mathop{\sum }\limits_{n,m=0}^{\infty }{p}_{\mu \nu | nm}{M}_{nm}.\end{array}$$

(26)

This problem can be solved numerically using linear programming techniques, as described in the Supplementary Note 2 of ref. ³⁵. While accurate, this method can be computationally demanding. For this reason, we have instead adapted the asymptotic analytical bounds of refs. ^42,54 to the finite-key scenario and used them in our simulations. The results obtained using these analytical bounds are very close to those achieved by numerically solving Eq. (26). This analytical method is described in Supplementary Note B.

Concentration inequality for sums of dependent random variables

A crucial step in our analysis is the substitution of the sums of probabilities in Eq. (18) by their corresponding observables in the protocol. Typically, this is done by applying the well-known Azuma’s inequality³⁹. Instead, we use the following recent result³⁸:

Let ξ₁, ..., ξ_n be a sequence of random variables satisfying 0 ≤ ξ_l ≤ 1, and let ${{{\Lambda }}}_{l}=\mathop{\sum }\nolimits_{u = 1}^{l}{\xi }_{u}$. Let ${{\mathcal{F}}}_{l}$ be its natural filtration, i.e. the σ-algebra generated by {ξ₁, ..., ξ_l}. For any n, and any a, b such that $b\ge \left|a\right|$,

$$\Pr \left[\mathop{\sum }\limits_{u=1}^{n}E({\xi }_{u}| {{\mathcal{F}}}_{u-1})-{{{\Lambda }}}_{n}\ge \left[b+a\left(\frac{2{{{\Lambda }}}_{n}}{n}-1\right)\right]\sqrt{n}\right]\le \exp \left[\frac{-2({b}^{2}-{a}^{2})}{{(1+\frac{4a}{3\sqrt{n}})}^{2}}\right].$$

(27)

By replacing ξ_l → 1 − ξ_l and a → −a, we also derive

$$\Pr \left[{{{\Lambda }}}_{n}-\mathop{\sum }\limits_{u=1}^{n}E({\xi }_{u}| {{\mathcal{F}}}_{u-1})\ge \left[b+a\left(\frac{2{{{\Lambda }}}_{n}}{n}-1\right)\right]\sqrt{n}\right]\le \exp \left[\frac{-2({b}^{2}-{a}^{2})}{{(1-\frac{4a}{3\sqrt{n}})}^{2}}\right].$$

(28)

In our analysis, we apply Eqs. (27) and (28) to sequences ξ₁, ..., ξ_n of Bernoulli random variables, for which $E({\xi }_{u}| {{\mathcal{F}}}_{u-1})=\Pr ({\xi }_{u}=1| {{\mathcal{F}}}_{u-1})$.

Now, if we set a = 0 on Eqs. (27) and (28), we obtain

$$\begin{array}{l}\Pr \left[{{{\Lambda }}}_{n}-\mathop{\sum }\limits_{u=1}^{n}\Pr ({\xi }_{u}=1| {{\mathcal{F}}}_{u-1})\ge b\sqrt{n}\right]\le \exp \left[-2{b}^{2}\right],\\ \Pr \left[\mathop{\sum }\limits_{u=1}^{n}\Pr ({\xi }_{u}=1| {{\mathcal{F}}}_{u-1})-{{{\Lambda }}}_{n}\ge b\sqrt{n}\right]\le \exp \left[-2{b}^{2}\right]\end{array}.$$

(29)

This is a slightly improved version of the original Azuma’s inequality, whose right-hand side is $\exp \left[-\frac{1}{2}{b}^{2}\right]$. Equating the right-hand sides of Eq. (29) to ε_a, and solving for b, we have that

$$\begin{array}{l}\mathop{\sum }\limits_{u=1}^{n}\Pr \left({\xi }_{u}=1| {\xi }_{1},...,{\xi }_{u-1}\right)\le {{{\Lambda }}}_{n}+{{\Delta }},\\ {{{\Lambda }}}_{n}\le \mathop{\sum }\limits_{u=1}^{n}\Pr \left({\xi }_{u}=1| {\xi }_{1},...,{\xi }_{u-1}\right)+{{\Delta }},\end{array}$$

(30)

with ${{\Delta }}=\sqrt{\frac{1}{2}n\,{\mathrm{ln}}\,{\varepsilon }_{{\rm{a}}}^{-1}}$, and where each of the bounds in Eq. (30) fail with probability at most ε_a.

The bound in Eq. (30) scales with $\sqrt{n}$, and it is only tight when Λ_n is of comparable magnitude to n. When Λ_n ≪ n, one can set a and b in Eq. (27) appropriately to obtain a much tighter bound. To do so, one can use previous knowledge about the channel to come up with a prediction ${\tilde{{{\Lambda }}}}_{n}$ of Λ_n before running the experiment. Then, one obtains the values of a and b that would minimise the deviation term if the realisation of Λ_n equalled ${\tilde{{{\Lambda }}}}_{n}$, by solving the optimisation problem

$$\begin{array}{lll}&{\mathop {\min }\limits_{a,b}} &\left[b+a\left(\frac{2{\tilde{{{\Lambda }}}}_{n}}{n}-1\right)\right]\sqrt{n}\\ &{\rm{s.t.}}&\exp \left[\frac{-2({b}^{2}-{a}^{2})}{{(1+\frac{4a}{3\sqrt{n}})}^{2}}\right]={\varepsilon }_{{\rm{a}}},\\ &&b\ge \left|a\right|.\end{array}$$

(31)

The solution to Eq. (31) is

$$\begin{array}{l}a=\frac{3\left(72\sqrt{n}{\tilde{{{\Lambda }}}}_{n}(n-{\tilde{{{\Lambda }}}}_{n}){\mathrm{ln}}\,{\varepsilon }_{a}-16{n}^{3/2}{\mathrm{ln}}^{2}{\varepsilon }_{a}+9\sqrt{2}(n-2{\tilde{{{\Lambda }}}}_{n})\sqrt{-{n}^{2}{\mathrm{ln}}\,{\varepsilon }_{a}(9{\tilde{{{\Lambda }}}}_{n}(n-{\tilde{{{\Lambda }}}}_{n})-2n{\mathrm{ln}}\,{\varepsilon }_{a})}\right)}{4(9n-8{\mathrm{ln}}\,{\varepsilon }_{a})(9{\tilde{{{\Lambda }}}}_{n}(n-{\tilde{{{\Lambda }}}}_{n})-2n{\mathrm{ln}}\,{\varepsilon }_{a})},\\ b=\frac{\sqrt{18{a}^{2}n-\left(16{a}^{2}+24a\sqrt{n}+9n\right){\mathrm{ln}}\,{\varepsilon }_{a}}}{3\sqrt{2n}}.\end{array}$$

(32)

After fixing a and b, we have that

$$\mathop{\sum }\limits_{u=1}^{n}\Pr \left({\xi }_{u}=1| {\xi }_{1},...,{\xi }_{u-1}\right)\le {{{\Lambda }}}_{n}+{{\Delta }}^{\prime} ,$$

(33)

except with probability ε_a, where

$${{\Delta }}^{\prime} =\left[b+a\left(\frac{2{{{\Lambda }}}_{n}}{n}-1\right)\right]\sqrt{n}.$$

(34)

In our numerical simulations, we have found the simple bound in Eq. (30) to be sufficiently tight for all components except the vacuum contribution M₀₀. For this latter component, we use Eq. (33) instead. However, note that the users do not know the true value of M₀₀, even after running the experiment. Instead, they will obtain an upper bound ${M}_{00}^{{\rm{U}}}$ on M₀₀ via the decoy-state method, and they will apply Eq. (33) to this upper bound. Therefore, to optimise the bound, the users should come up with a prediction ${\tilde{M}}_{00}^{{\rm{U}}}$ on the value of ${M}_{00}^{{\rm{U}}}$ that they expect to obtain after running the experiment and performing the decoy-state analysis, and then substitute ${\tilde{{{\Lambda }}}}_{n}\to {\tilde{M}}_{00}^{{\rm{U}}}$ in Eq. (31) to obtain the optimal values of a and b. To find ${\tilde{M}}_{00}^{{\rm{U}}}$, one can simply use their previous knowledge of the channel to come up with predictions ${\tilde{M}}^{\mu \nu }$ of M^μν, and run the decoy-state analysis using these values to obtain ${\tilde{M}}_{00}^{{\rm{U}}}$.