Abstract
The intrinsic functional architecture of the brain supports moment-to-moment maintenance of an internal model of the world. We hypothesized and found three interdependent architectural gradients underlying the organization of intrinsic functional connectivity within the human cerebral cortex. We used resting state fMRI data from two samples of healthy young adults (N’s = 280 and 270) to generate functional connectivity maps of 109 seeds culled from published research, estimated their pairwise similarities, and multidimensionally scaled the resulting similarity matrix. We discovered an optimal three-dimensional solution, accounting for 98% of the variance within the similarity matrix. The three dimensions corresponded to three gradients, which spatially correlate with two functional features (external vs. internal sources of information; content representation vs. attentional modulation) and one structural feature (anatomically central vs. peripheral) of the brain. Remapping the three dimensions into coordinate space revealed that the connectivity maps were organized in a circumplex structure, indicating that the organization of intrinsic connectivity is jointly guided by graded changes along all three dimensions. Our findings emphasize coordination between multiple, continuous functional and anatomical gradients, and are consistent with the emerging predictive coding perspective.
Similar content being viewed by others
Introduction
The brain has been described as an internal model of the world, dynamically constructing simulations from generative combinations of prior experience1,2,3. Intrinsic connectivity networks – ensembles of widely distributed brain regions with statistically dependent fluctuations in activity over time4,5,6 – are hypothesized to play a pivotal role in implementing and adjusting this model7,8,9,10,11,12,13,14,15. A parcellation approach to intrinsic connectivity networks assumes they are spatially discrete (i.e., modules) within the brain, such that each region belongs to one and only one network (e.g.16,17,18,19,20,21,22,23,24,25,26). Yet brain regions often show fluid coupling with different networks27,28,29, sometimes conceptualized as affiliating with multiple intersecting networks (e.g.30,31,32), and some networks play a more central role in the brain’s internal model than do others (e.g.10). A connectomics approach treats neural ensembles as overlapping sub-networks (e.g.33,34) that implement and update the internal model by communicating via densely connected “rich club” hub regions35,36. Connectomics does not, by itself, identify organizational features reflecting the brain’s ongoing activity (but see37 for a recent example of a connectomics approach that makes functional inferences). A cytoarchitecture approach provides additional computational insights by positing that the relative differences in cortical lamination in two connected cortical regions strongly predicts the type of information flow between those regions (e.g.38,39). When integrated with the principles of predictive processing1,2,40, this approach suggests specific hypotheses for the role that intrinsic connectivity networks play in maintaining and updating the brain’s internal model, the key hypothesis being that the internal model (called predictions) and learning signals (called prediction errors) propagate across neurons arranged in a loose hierarchy (see also41), with internal representations originating in limbic cortices, including agranular cortices that lack a well-defined layer IV and have sparser layers II and III, as well as dysgranular cortices with a rudimentary layer IV, such as the cingulate cortex, anterior insula and medial orbitofrontal cortex38. Moreover, via their projections to subcortical regions that regulate the autonomic nervous system and other systems of the internal milieu of the body (e.g., the hypothalamus, amygdala, ventral striatum, periaqueductal gray, parabrachial nucleus, nucleus of the solitary tract), limbic cortices are anatomically well-positioned to integrate information in the service of generating more efficient and accurate internal representations11,32. A crucial biological insight from the cytoarchitecture approach is that information flow in the cortex proceeds across continuous hierarchies. Notably, gradient-based approaches have also been successfully used to investigate cortical cell content42, thickness43, myelin content44, and genetic expression45,46,47. Therefore, across multiple levels of analysis, gradient-based approaches have facilitated investigations into the organizational patterns of brain structure and function.
In the current study, we integrated insights from the parcellation, connectomics, and cytoarchitectural approaches to develop a unified framework for describing the organizational features of intrinsic connectivity across the cerebral cortex. Specifically, we tested the hypothesis that intrinsic connectivity within the cortex is organized as interdependent gradients by which connectivity patterns show continuous similarity rather than discrete differences. Our approach emphasizes region-to-region affiliations in intrinsic connectivity (i.e., forming similarity gradients), which are largely ignored by the parcellation approach that focuses primarily on defining unique region-to-network affiliations. Our gradient-based analysis discovers how the connectivity of cortical regions shifts with changes in their location along several cortical hierarchies. Most importantly, our demonstration that intrinsic connectivity is organized on interdependent gradients is particularly novel, given that previous studies examining gradient-based cortical organization tended to treat connectivity gradients as statistically independent properties of the brain (e.g.48,49,50,51,52,53,54,55).
To sample intrinsic connectivity across the cortical sheet, we selected 109 seed regions across five intrinsic connectivity network motifs (recurring topographical patterns) most commonly identified in literature (Fig. S1 and Table S1) and estimated their intrinsic connectivity maps. This was done for two samples of participants (discovery sample N = 280, replication sample N = 270). For each seed, a group-level intrinsic connectivity map was computed and was used to generate a 109 × 109 similarity matrix with η2 56 as an index summarizing pairwise similarity between intrinsic connectivity maps (Fig. S2). We discovered the organizing properties within this similarity matrix using multidimensional scaling (MDS)57. Briefly, MDS produces a quantitative dimensional description of the underlying structure of the data and maps it to a Euclidean coordinate space while preserving the pairwise similarities between data points; closer proximity in the remapped space indicates higher similarity. MDS confers several advantages over other techniques, such as principal component analysis (PCA), in understanding intrinsic connectivity organization: (1) MDS does not assume but can discover whether intrinsic connectivity neatly decomposes into non-overlapping components and (2) MDS tends to yield fewer, more interpretable dimensions than PCA58.
MDS allows a geometric depiction of the similarity matrix, which was important because we predicted that similarities between intrinsic connectivity maps would be represented as a circular array referred to as a circumplex59 (Fig. S3A). A circumplex pattern would indicate that network similarities exist in a continuous rather than a discrete fashion, the latter of which involves connectivity maps clustering in certain parts of the N-dimensional space but not in others (Fig. S3B; e.g., a strict discrete parcellation scheme with high within-cluster similarity and between-cluster difference). A circumplex would also suggest that similarity among maps can be described using more than one feature (i.e., the similarity is heterogeneous – that is, two intrinsic connectivity maps compared using a single gradient would be incomplete because their similarities are simultaneously described by multiple, interdependent gradients reflecting multiple descriptive features60 rather than by uncorrelated, additive gradients (Fig. S3C; e.g., each gradient uniquely explains a functional domain, and knowing the affiliation of a brain region with one domain would reveal nothing about how the same region’s affiliation with another domain). These two non-circumplex alternative cases are referred to as simple structures61.
Results
Goodness-of-Fit
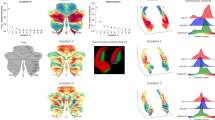
Stress and explained variance indicated that a three-dimensional solution was optimal to describe the similarities among the intrinsic connectivity maps in both discovery and replication samples (Fig. 1). A three-dimensional solution brought normalized stress below 0.0557 and captured over 98% of the variance58. All reported findings in the following sections were obtained using the discovery sample; similar results identified with the replication sample are reported in the SI (Figs S4–6). The three-dimensional solution remained optimal when we removed global signal regression from preprocessing, and also when we uniformly sampled 264 seeds across the cortex per17 (Fig. S7), indicating that the three-dimensional solution was robust to variations in preprocessing and seed definition.
Both goodness-of-fit estimates were highly replicable across the discovery and replication groups and suggested that a three-dimensional solution was optimal. Stress was plotted as a function of the number of estimated dimensions. Lower stress indicates better fit. The scree plot of normalized stress had an “elbow” when dimensionality was at 3, since further addition of dimensions did not substantially reduce normalized stress. Dashed line indicates normalized stress of 0.05. DAF was plotted as a function of the number of estimated dimensions. Higher DAF indicates better fit. Dashed line indicates DAF of 0.98.
Circumplexity
We plotted the dimension loadings (ranging between −1 and 1) associated with all 109 intrinsic connectivity maps in Fig. 2. As predicted, the similarity between connectivity maps displayed circumplex behavior, i.e., the maps arrayed in a circular formation rather than clustering in particular parts of the Euclidean space. In other words, the literature-based motifs were not distinct modules and instead showed graded similarity in a three-dimensional Euclidean space. According to definitions of a circumplex, (1) there should be no preferred rotation of the dimensions that anchor the structure62,63 and (2) all variables should have a constant radius from the center of the circle59,64,65. Statistics based on these two criteria suggest that the solution derived from our data can be described as a circumplex. First, there was no preferred rotational solution for the results, consistent with what would be observed in a true circumplex structure per66,67 (Rotation Test: RT = 0.01, p < 0.01; Variance Test: VT2 = 0.12, p < 0.01). Second, the maps had a mean distance of 0.69 from the center, with a standard deviation of 0.09. The Fisher Test FT66,67; computed as coefficient of variation (the ratio of the standard deviation to the mean), was 12.79%, indicating that the maps varied within 6.5% on each side of the 0.69-radius circle. This variation was within the range reported for circumplex structures in previous literature64. As expected, we obtained similar circumplex structure when sampling 264 seeds (RT = 0.06, p < 0.01; VT2 = 0.03, p < 0.01; FT = 11.45%), suggesting that the circumplex solution was robust to variations in seed definition (Fig. S8). Taken together, these findings, along with visual inspection of the solution, suggest that our solution indeed reveals circumplex features.
MDS results revealed that intrinsic connectivity patterns followed a circumplex structure of similarity. We calculated intrinsic connectivity maps based on 109 seeds across five most frequently identified network motifs in the published literature: attention (red), default mode (yellow), executive (green), exteroceptive (light blue), and salience (dark blue). Each point in the scatterplot represents a connectivity map. We plotted (A) Dimension 1 vs. Dimension 2, (B) Dimension 1 vs. Dimension 3, and (C) Dimension 2 vs Dimension 3 to facilitate interpretation.
Within this circumplex organization, connectivity maps seeded in the same motif were closer together in Euclidean space (Fig. 2) and showed graded degrees of similarity with connectivity maps belonging to other motifs. For example, in Fig. 2A, maps that were seeded in the salience motif (dark blue; e.g., anterior insula, anterior cingulate cortex and supramarginal gyrus) overlapped with those seeded in the executive (green; e.g., middle frontal gyrus and inferior parietal lobule) and attention motifs (red; e.g., frontal eye field and superior parietal lobule). In fact, all neighboring motifs shared some overlap except the maps seeded in the default mode motif (yellow; e.g., medial prefrontal cortex, posterior cingulate cortex, dorsolateral prefrontal cortex, angular gyrus, temporal pole, and lateral temporal cortex). In Fig. 2B,C, the lack of motif boundaries was even more prominent; default mode (yellow) and executive (green) motifs completely overlapped in Fig. 2B. Interestingly, connectivity maps within attention (red), exteroceptive (light blue) and salience (dark blue) motifs also showed large variability along Dimension 3. For instance, some regions of the salience motif (e.g., cingulo-opercular regions) had high loadings on Dimension 3, whereas others regions of the same motif (e.g., frontoparietal regions) had low loadings on Dimension 3 (Fig. 2B,C).
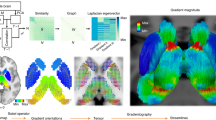
Gradient maps visualized on the brain surfaces. For each dimension, we created a gradient map by weighting every connectivity map by its dimension loading and summing across all weighted maps to create a composite (i.e., a weighted sum akin to factor scores). Gradient 1 (external vs. internal) captured a functional contrast between processing information from the external environment and the internal milieu. Gradient 2 (modulation vs. representation) captured a functional contrast between attentional modulation and content representation. Gradient 3 (anatomical centrality) captured a structural contrast between spatially central nodes and peripheral nodes. We visualized the gradient maps on inflated brain surfaces using Caret154.
As befits a circumplex, variation along one dimension was accompanied by variation along the others, indicating the interdependence of the features represented by those dimensions60. For example, in Fig. 2A, as loadings for connectivity maps seeded in the executive (green) and salience (dark blue) motifs decreased on Dimension 2, the former transitioned from zero to positive loadings on Dimension 1 while the latter transitioned from zero to negative loadings on Dimension 1. Therefore network motifs can be compared and contrasted based on how their loadings differently co-varied on all three dimensions. For example, when comparing between regions belonging to the default (yellow) vs. executive (green) motifs, we observe that both exhibit similar graded changes in Dimension 1 and Dimension 3 (Fig. 2B,C), however they exhibit remarkable differences in their involvement in Dimension 2 (Fig. 2A,C).
Dimension interpretation
To determine the architectural gradients associated with the MDS dimensions, we created three “gradient maps” (these maps included subcortical components, which are not discussed here because they are not directly relevant to the predictive processing framework). For each dimension, we first multiplied every connectivity map by its corresponding dimension loading to create weighted maps and then summed across all weighted maps to create a final composite gradient map (i.e., a weighted sum akin to factor scores). In this way, each map’s contribution to a gradient map depended on how strongly it related to the MDS dimension. The summary gradient maps in Fig. 3 provide complementary interpretational value to the scatterplots in Fig. 2 because we can directly examine the relationship between regions and gradients, bypassing the literature-based motif categories (to avoid confusion, we refer to values on MDS dimensions as dimension ‘loadings’ and values on gradient maps as gradient ‘scores’). The brain gradients captured three features of cortical architecture (Fig. 3).
Gradient 1 corresponded to an external vs. internal gradient, replicating51. Regions with lower scores on Gradient 1 belonged with motifs that are relatively important for representing signals that are external to the brain, such as the exteroceptive sensory motif (e.g., visual, auditory or sensorimotor networks; e.g.68), as well as motifs that are important for modulating the representations of those signals - e.g., the dorsal attention network69 and the salience motif consisting of the cingulo-opercular70, multimodal71, salience72 or ventral attention69 networks. Regions with higher scores on Gradient 1 belonged with motifs that are relatively important for constructing and maintaining the representations that constitute the brain’s internal model, such as the default mode73 and mentalizing74 networks, and motifs that are important for modulating those representations - e.g., executive control72 or multiple-demand75 networks.
Gradient 2 corresponded to a representation vs. modulation gradient. Regions with lower scores on Gradient 2 belonged with motifs that are important for representing mental content, such as sensory information in the primary sensory cortices and multimodal summaries of brain states in the default mode network68. Regions with higher scores on Gradient 2 belonged with modulation-related motifs (any process that operates on sensory or motor representations, such as attention regulation, goal maintenance, strategy selection, performance monitoring), such as the executive control76 and salience77 motifs.
Gradient 3 corresponded to anatomical centrality (geometric term describing lack of Euclidean distance from center of the brain78). Regions with lower scores on Gradient 3 were more peripheral in the cortex, including the primary visual cortex, lateral frontal and lateral parietal regions. Regions with higher scores on Gradient 3 occupied anatomically more central positions in the cortex. We empirically tested this gradient by correlating Dimension 3 loadings of the connectivity maps with anatomical centrality values of corresponding seeds (computed as normalized proximity to anterior commissure; Fig. S9, see detailed description in SI). We found a strong, positive association (Fig. 4A; r = 0.676, p < 0.001), suggesting that seeds located closer to the anatomical center of the brain tended to anchor intrinsic connectivity maps with higher loadings on Dimension 3. Anatomical centrality (Fig. 4B) can be considered a proxy for laminar differentiation78 since cortices become progressively laminated as one moves from the central limbic cortices (forming a ring around the corpus callosum and defining the limits of each hemisphere, including anterior to midcingulate cortex, anterior insula, and temporal pole) towards the periphery of the cortex (see38,79;).
Gradient 3 corresponded to anatomical centrality. (A) Dimension 3 loadings correlated positively with anatomical centrality (N = 109; r(107) = 0.676, p < 0.001). (B) Anatomical centrality for each seed was computed as (maximal distance – node distance)/maximal distance, where maximal distance is the distance for the node with maximal distance from the anterior commissure, with 0 indicating minimum anatomical centrality (at maximum distance from the anterior commissure) and 1 indicating maximum centrality (at the anterior commissure). The anterior commissure was used as a proxy for the center of the brain since it is approximately equidistant from the most distal points of the cerebrum. We visualized anatomical centrality values on inflated brain surfaces using Caret154.
Predictive processing framework. Starting with initial conditions in the body and in the world (T0), the brain is thought to continually predict forward in time (T1), preparing changes in the body’s internal systems to support upcoming motor actions. Efferent copies of these motor and visceromotor preparations function as their predicted sensory consequences, cascading to sensory systems to modulate the firing of sensory neurons in advance of incoming sensory inputs. Sensory inputs from the body and the world are continuously compared to prediction signals. If different, prediction errors are sent to update the brain’s internal model for future occasions. This framework is based on a structural model of cortico-cortical connections whereby predictions flow from less to more laminated (i.e., layered) cortices (‘feedback connections’), whereas prediction errors flow in the opposite direction (‘feedforward connections’)155,156. This structural model is consistent with a gradient- but not module-based organization scheme for intrinsic connectivity. This is because the whole brain is thought to participate in predictive processing, not by separating into mental modules, but by operating on a continuous two-way hierarchy. In the feedback direction, abstract predictions are unpacked into particular sensory simulations; at the same time in the feedforward direction, sensory information is compressed to be integrated with the brain’s internal model (see review in7). Figure adapted from104.
Discussion
Intrinsic functional connectivity within the cerebral cortex can be described by three interdependent architectural gradients, which spatially correlate with two functional features (external vs. internal and representation vs. modulation) and one structural feature (anatomically central vs. peripheral) of the brain. When projected into geometric space, the similarities between connectivity maps were represented by a circumplex structure. This finding suggests that the organization of intrinsic functional connectivity shows continuous similarity across multiple, interdependent gradients rather than discrete differences. Overall, our findings highlight the importance of simultaneously considering functional and anatomical hierarchies in the brain, integrating parcellation, connectomics, and architectural approaches to understanding cortical function.
Our results are consistent with available evidence that intrinsic connectivity can be described with continuous local48,53,55,80 and global51,54,81,82 gradients, suggesting that intrinsic connectivity motifs do not constitute discrete networks. Prior research using the parcellation approach identified spatially discrete intrinsic connectivity networks by: (1) using methods that force independence (e.g., cluster analysis16,17,18,19,20), (2) setting arbitrary thresholds that dissociate networks (e.g.69,83,84), or (3) emphasizing independence rather than correlation between networks when using methods such as ICA (e.g.85,86,87,88). Although these techniques may be useful for certain purposes (e.g., to create heuristic parcellation schemes), their emphasis on assigning a unique network membership to each cortical region does not allow a fully realized interpretation of the organizing principles underlying intrinsic functional connectivity, which are actually based on continuous similarity gradients. This is an important limitation of the parcellation approach, because recent evidence shows that network motifs are, in fact, connected, and overlapping in rich club hubs32, which has functional implications (e.g.8,89,90,91). Allowing coupling across networks, for instance, helps identify functional connections that are crucial for task-dependent global integration15,92.
More importantly, we observed that the similarities between functional connectivity patterns were not just graded, but their variations were also interdependent across the different gradients, as suggested by the circumplex ordering of similarities. The MDS solution satisfied two circumplex criteria: no preferred rotation and constant radius. In an ideal circumplex, elements are arrayed in a circular fashion, so mathematically, there is not one rotational solution that best describes the data structure59. Note that while it is important to establish a lack of preferred rotation for quantifying circumplexity, it is also important to determine one set of dimensions that best represents the features underlying functional connectivity organization for interpretational purposes60,93. The set of three dimensions reported herein are consistent with other findings on structural and functional organization of the brain (detailed below), indicating that the observed three dimensions are valid and useful in characterizing the organization of intrinsic functional connectivity. Our discovery aligned with the hypothesized interdependency scenario (Fig. S3A). In contrast, if a discrete simple structure (Fig. S3B) were found, it would mean that intrinsic connectivity was organized in a fully modular fashion, where each domain was its own dimension and was unrelated to the other dimensions, as reflected by concentrated loadings on one end of the dimension only. If a non-discrete simple structure (Fig. S3C) were found, it would mean that dimensions were independent from each other, e.g., Gradient 1 (internal vs. external) and Gradient 2 (modulation vs. representation) do not covary. In other words, knowing that default mode regions scored high on internal-processing would tell us nothing about how they scored on the representation vs. modulation gradient.
Notably, our results are also robust across methodological variations. To test the optimal dimensionality and stability of the circumplex structure observed in our data, we varied preprocessing (global signal regression) and analytical (seed definition) parameters to see if they would disrupt ordinal orderings in the similarity matrix, which could lead to changes in the MDS solution58. We performed global signal regression because it is considered an effective means to reduce artifacts in resting state data94, and deviation scoring in general (removing mean signal in raw data) enhances statistical power in circumplexity tests by removing any potential general factor66,67. This technique is also known to artificially inflate negative correlations95,96,97,98 because it shifts the entire distribution of correlations in the negative direction94. We anticipated the ordering of pairwise similarities to be retained with or without the shift. In addition, we selected 109 canonical network seeds from published papers because they should yield maximal between-network differences and uncover simple structures in the data (Fig. S3B,C) if they did exist. Since these literature-based seeds did not identify simple structures, we expected that a more comprehensive sampling of 264 seeds would likely fill out the space within the circumplex structure. As expected, the optimal dimensionality and general circular ordering of similarities were not affected by changes in the preprocessing and analytical parameters, and global signal regression improved the detection of circumplexity. These additional analyses demonstrate the robustness of the circumplex organization across methodological variations and provide strong support to our hypothesis of multiple interdependent gradients.
To interpret these gradients, we turned to a novel predictive processing framework that depends on cytoarchitecture to understand the intrinsic organization of the cerebral cortex. This predictive processing framework has been used to study topics as wide-ranging as sensory and motor systems99,100,101, individual neuron dynamics102, brain energetics103, and consciousness (e.g.7,9,11,100). This framework is anchored by the hypothesis (outlined in7,104) that an animal’s cerebral cortex, the cerebellum (e.g.105) and the hippocampus (e.g.106) create an internal model of the animal’s body in the world, constantly using past experiences to anticipate the needs of the body in relation to predicted sensory inputs and preparations for motor action, and attempting to meet those needs before they arise, through a process called allostasis107,108 (see Fig. 5 for a schematic diagram of this framework).
The three gradients describing cortical intrinsic connectivity can be interpreted as capturing different components of the predictive processing framework. Gradient 1 describes a gradient that runs, at one end, from the motifs that are important for processing the sensory input that continually confirms or refines the internal model (low gradient scores) to, at the other end, the motifs that are important for generating the prediction signals that constitute the brain’s internal model (high gradient scores). Regions low on this gradient belonged with primary sensory, attention, and salience motifs, which are more associated with externally oriented processes such as sensory perception, goal-directed selection for stimuli109, processing relevance of personally salient sensory information72, and the integration of multisensory information from the periphery71. Regions high on this gradient belonged with default mode and executive control motifs, which are more associated with internally oriented processes such as mind-wandering, introspection, and autobiographical planning110,111. This functional contrast is also sometimes called ‘external’ versus ‘internal’ modes of cognition112,113, or ‘bottom-up’ versus ‘top-down’ processing114. It is similar to the ‘principal sensorimotor-to-transmodal gradient’ obtained using a different dimension reduction technique on resting state fMRI data50,51, which was also anchored on one end by primary sensorimotor regions and on the other end by the default mode network. This gradient has been identified in tract-tracing studies of non-human primates (macaque51, and marmoset115) and is consistent with cortical myelin gradient49 as well as with genetic transcription gradient45,46,47,116, suggesting that the brain’s microstructural integrity and genetic profile are implicated in the brain’s functional wiring. Our interpretation is also consistent with evidence from the connectomics literature showing that default mode regions (high gradient scores) are capable of steering the brain into different states with little input of energy – i.e., using information available from the internal model (average controllability37), whereas salience regions (low gradient scores) drive the brain into states that require more input of energy – i.e., learning or encoding (modal controllability37).
Gradient 2 distinguishes voxels that belong to regions that predominantly represent prediction and prediction error signals from those voxels that belong to regions that predominantly implement attentional modulation, or precision117,118. Regions low on this gradient belonged with motifs that are more associated with content representation. More specifically, the default mode regions represent multimodal summaries of brain states68,119 or supramodal conceptual knowledge120, and are hypothesized to represent the brain’s internal model, whereas the primary sensory regions represent sensory input from the external environment68 and from the body7,121. Regions high on this gradient belonged with executive control and salience motifs, which are thought to be involved in top-down modulation of the default mode and executive networks (e.g.122,123), and are hypothesized to tune the precision of predictions and prediction errors, respectively7,121. It is not surprising that regions with high scores on this gradient replicate the task positive network124 or multiple demand network75, because fMRI experimental tasks are typically designed to require attention modulation (e.g., randomized trials and jittered inter-trial intervals elicit more deliberate, controlled and effortful processing104). The attention motif occupied the middle portion of the gradient, consistent with its role in linking sensory information to motor responses125. This gradient appears similar to the third principal gradient reported in51,126, although the authors provided no interpretation of this dimension.
Gradient 3, like the previous two gradients, was computed based on functional connectivity. However, this third gradient appeared to represent anatomical centrality, which is a structural feature related to the systematic variation in the degree of cortical laminar differentiation. Specifically, limbic cortices form the spatial core of each hemisphere. Multimodal association regions (granular cortices, eulaminate I), followed by primary sensory regions (granular or koniocortices, eulaminate II), spatially irradiate from the core limbic areas and exhibit increasingly developed laminar structure (reviewed in38,41,79,127,128,129). Consistent with this pattern, limbic cortices scored highly on Gradient 3, whereas multimodal association regions, followed by primary sensory areas scored progressively lower on Gradient 3. To our knowledge, no published empirical study has identified this third gradient in describing the organization of intrinsic functional connectivity. Within the predictive processing framework, the spatial position of the limbic core is important for several reasons. Developmentally, limbic cortices form first and generate widespread feedback projections to other regions in the brain38,130,131. They are hypothesized to easily modify neural activity in eulaminate areas and promote functional flexibility via its diverse feedback connections38. Therefore, limbic cortices have been hypothesized to create a highly connected, dynamic functional ensemble for information integration and accessibility in the brain11. Adding to this literature, our current finding shows that the spatially central position of limbic cortices also has implications for the organization of intrinsic functional connectivity. Integrating information about the cytoarchitecture of the brain (i.e., laminar differentiation) into functional connectivity organization can help us understand known fractionation schemes of the default mode and salience motifs in the literature. The default mode motif has been found to fractionate into a relatively central subsystem (including medial limbic nodes such as the subgenual anterior cingulate cortex, retrosplenial cortex, parahippocampal gyrus, and the hippocampal formation) and a relatively peripheral subsystem (including more lateral nodes such as the temporal parietal junction, lateral temporal cortex, and temporal pole)110. Similarly, the salience motif has been found to consist of a more central subsystem (including limbic nodes such as the amygdala, ventral anterior insula, and pregenual anterior cingulate cortex) and a more peripheral subsystem (including more lateral nodes such as medial frontal gyrus and supramarginal gyrus)84.
The novel evidence reported here encourages future research on several aspects related to the organization of intrinsic functional connectivity based on multiple interdependent gradients. First, following prior work revealing task-related modulation of intrinsic connectivity132, it would be important for future research to investigate whether the same gradients emerge during task states. Such work would clarify whether the three interdependent gradients found in the current study are stable features of functional cortical architecture regardless of situational demands. Second, our analyses involved correlation of blood-oxygen-level dependent (BOLD) activation time courses during a whole resting state scan, but recent research on dynamic functional connectivity shows that the amount of coherence between regions could vary in a short time period133,134 and in longer-term development135, prompting the question of whether the three-gradient architecture withstands dynamic reconfigurations in functional coupling observed over time. Third, we calculated the connectivity similarity matrix on a group level and did not probe individual differences. Recent research revealed finer details of network fractionation that were only observable at the individual level136, suggesting that the distribution of regions on the similarity gradients may slightly shift from person to person, as individual differences in functional coupling may arise given distinct past experiences. Examination of individual variations in the gradient-based organization of intrinsic connectivity, therefore, would be a promising avenue for future research in identifying its role in complex behaviors and psychological phenomena. To this end, high resolution fMRI acquisition and voxelwise analysis technique may facilitate a more nuanced understanding of individual-specific variations in similarity gradients. Fourth, our measure of anatomical centrality, based on distance to the anterior commissure, is one proxy for the laminar differentiation gradient; other measures (e.g., neuronal density or myelin) have been proposed as well, although they contain important limitations in capturing laminar differentiation (see detailed discussion in127). Future studies might consider the advantages of other estimates of laminar differentiation. Finally, a few previous studies43,51 have examined distance in the brain using geodesic distance along the curvatures of the cortical mantle instead of Euclidean distance. Future investigations should systematically compare the similarities and differences in their abilities to predict connectivity and other brain characteristics.
Materials and Methods
Participants
Participants in this study were 660 healthy young adults (55% female, 18–30 years), previously described in16,32,137,138. All were native English-speakers with normal or corrected-to-normal vision and reported no history of neurological or psychiatric conditions. Experimental protocol was approved by the institutional review boards of Harvard University and Partners Healthcare. All research was performed in accordance with relevant guidelines and written informed consent was obtained from all participants. We removed 79 participants (11%) due to head motion and outlying voxel intensities, and 31 participants (4.7%) due to a lack of signal in superior and lateral parts of the brain (outside of acquisition field). Our final dataset of 550 participants was randomly divided into a discovery sample of N = 280 (62% female, 19.3 ± 1.4 years) and a replication sample of N = 270 (53% female, 22.3 ± 2.1 years).
MRI and fMRI
Participants completed structural and resting-state MRI scans, as well as other tasks unrelated to the current analysis. MRI data were acquired at Harvard and the Massachusetts General Hospital across a series of matched 3T Tim Trio scanners (Siemens, Erlangen, Germany) using a 12-channel phased-array head coil. Structural data included a high-resolution multi-echo T1-weighted magnetization-prepared gradient-echo image (multi-echo MPRAGE). Parameters for the structural scan were as follows: repetition time (TR) = 2,200 ms, inversion time (TI) = 1,100 ms, echo time (TE) = 1.54 ms for image 1 to 7.01 ms for image 4, flip angle (FA) = 7°, voxel size 1.2 × 1.2 × 1.2 mm and field of view (FOV) = 230 mm. The resting state scan lasted 6.2 min (124 time points) and participants were instructed to remain still, stay awake, and keep their eyes open. The echo planar imaging (EPI) parameters for functional connectivity analyses were as follows: TR = 3,000 ms, TE = 30 ms, FA = 85°, voxel size 3 × 3 × 3 mm, FOV = 216 mm and 47 axial slices collected with interleaved acquisition and no gap between slices. To preprocess the resting state data, we removed first 4 volumes, corrected slice timing, corrected head motion, normalized to the MNI152 template, resampled to 2 mm cubic voxels, removed frequencies higher than 0.08 Hz, smoothed with a 6 mm FWHM kernel and did nuisance regression (six motion parameters, average global signal, average ventricular and white matter signals)139,140,141. We also preprocessed the same dataset without global signal regression (GSR) and obtained similar results (‘109 seeds, GSR−’; Figs S7 and S8).
Selection of network seed regions
From the network-parcellation literature, we selected 109 seed regions across five intrinsic connectivity network motifs most commonly identified in the literature. The rationale for choosing these canonical network anchors was to derive the most distinctive connectivity patterns possible and maximize the possibility of finding simple structures in functional organization if they existed. The attention motif consisted of visual attention regions, also collectively referred to as dorsal attention network16,69,83. For the default mode motif, we sampled seeds from amygdala affiliation142, default mode16,110, language143,144, and mentalizing74 networks. For the executive control motif, we sampled seeds from executive16,72,83 and multiple-demand75 networks. For the exteroceptive motif, we sampled seeds from amygdala perception142, auditory145,146,147, sensorimotor16,146,147,148, and visual16,145,146 networks. For the salience motif, we sampled seeds from amygdala aversion142, cingulo-opercular70, multimodal71, salience72,84 and ventral attention16,149 networks. See seed locations in Fig. S1 and MNI coordinates in Table S1. Homogeneity of each seed was calculated as the average temporal correlation between all unique pairs of within-seed voxels following previous reports18,81,150,151. The mean (M) and standard deviation (SD) of seed homogeneity for each network motif was identified as follows: Attention (M = 0.800, SD = 0.019), default (M = 0.822, SD = 0.016), executive (M = 0.810, SD = 0.016), exteroceptive (M = 0.795, SD = 0.023), and salience (M = 0.797, SD = 0.016). Overall, these values are comparable to or even higher than those reported in previous studies of functional connectivity parcellations, suggesting that seed homogeneity in the present study was sufficiently high on average. Seed homogeneity varied between the network motifs (F(4,1116) = 169.41, p < 0.001, ηp2 = 0.378), as previously shown (e.g.81). However, the observed seed heterogeneity was not relevant for testing our hypotheses because we focused on gradients examining all network motifs along a continuum rather than analyzing discrete, modular networks. Therefore, no further analyses were performed on this metric. We also sampled an alternative set of 264 seeds across the cortex17 and obtained similar results (‘264 seeds, GSR+’; Figs S7 and S8).
Functional connectivity and similarity matrix calculation
We calculated group-level whole-brain intrinsic connectivity maps following established seed-based procedure83,84. For each seed, we created a 4 mm spherical region of interest (ROIs) and extracted the average time course of BOLD activity within the ROI. We computed Pearson’s product moment correlations, r, between the seed time course and all voxels across the brain, converted those r values to z values using Fisher’s r-to-z transformation, and averaged the resulting z map across all subjects within each sample to obtain two group intrinsic connectivity maps per seed (one for each sample). To determine which connectivity values were meaningful in a group map, we relied on replication, as guided by classical measurement theory152, instead of imposing an arbitrary z threshold. This prevents type I and type II errors, which are enhanced with the use of stringent statistical thresholds153. It was uniquely important for us to consider all meaningful connectivity, including weaker but replicable connectivity, because its inclusion reveals more accurate degrees of similarity between intrinsic connectivity maps, while its exclusion means stronger connectivity is given more weight in comparisons and therefore enhances differences between network motifs. We binarized both group intrinsic connectivity maps at z = 0 since the interpretation of negative correlations can be ambiguous95,141 and took the conjunction between the two samples. We then masked the original non-binarized group intrinsic connectivity maps using this conjunction map to retain strengths of all positive correlations that are reliable across both samples. This procedure was repeated for all 109 seeds. Finally, for each sample, we calculated a 109 × 109 similarity matrix (η2 56) between all masked intrinsic connectivity maps. Functional connectivity and similarity matrix calculation is illustrated in Fig. S2. Note that we used the ‘replication sample’ both for determining which connectivity was meaningful and for showing replicable MDS results. To demonstrate that the high replicability observed in our results was not solely driven by the method of thresholding, we also thresholded functional connectivity at z = 0.284,142 instead of using replication. As expected, these analyses yielded similar three-dimensional (Fig. S10) circumplex solutions (Fig. S11). Additionally, given that some anticorrelations may be meaningful98, we tested the effect of including negative connectivity below z = −0.2 as well. This analysis yielded replicable three-dimensional (Fig. S12) circumplex solutions (Fig. S13).
MDS analysis
To model similarities in maps, we used the PROXCAL algorithm in SPSS 23 (www.ibm.com/DataStatistics/SPSS). For each sample, we used the 109 × 109 similarity matrix as input and tested model fit for dimensionalities between 1 and 10. We determined the optimal dimensionality using two goodness-of-fit estimates: stress and explained variance. Stress is the square root of a normalized ‘residual sum of squared’. Higher stress indicates worse fit. Optimal dimensionality often manifests as the elbow of the stress plot and brings stress below 0.0557. The measure we used for explained variance is dispersion accounted for (DAF), which is equivalent to squared Tucker’s coefficient of congruence. Both goodness-of-fit estimates across the two samples indicated 3 was the optimal dimensionality (Fig. 1). Therefore, as output of the MDS analysis, we obtained 3 sets of 109 dimension loadings for each sample.
Circumplexity evaluation
According to definitions of a circumplex, (1) there should be no preferred rotation of the dimensions that anchor the structure62,63 and (2) all variables should have a constant radius from the center of the circle59,64,65. We quantified the degree of circumplexity in the three-dimensional MDS solution using these two criteria, employing the Rotation or Variance Test, and the Fisher Test respectively66,67. The Rotation Test assesses the degree to which different rotations of the dimensions affects the solution. In addition, we also used the Variance Test (VT266 to assess the impact of rotation by measuring the coefficient of variation in the amount of variables that fall in between any orthogonal pair of axes. We compared the test statistics of the Rotation and Variance Tests to the critical values reported in66,67 to determine the likelihood that our solution achieved the formal criteria for circumplexity. The Fisher Test assesses the degree to which the elements array in constant radius by measuring the coefficient of variation (i.e., the ratio of the standard deviation to the mean) in vector length64. When testing the circumplexity in the published literature in personality and affect data, the data are first deviation scored (i.e., each raw score is subtracted from the subject’s mean score66,67). Since global signal regression at the individual subject level is comparable to deviation scoring, we only tested circumplexity of MDS results using data on which global signal regression was performed during preprocessing.
Anatomical centrality estimation
To estimate anatomical centrality, we used the anterior commissure as a proxy for the center point of the brain, since it is approximately equidistant from the most distal points of the cerebrum on the x, y, and z axes, and approximately occupies the middle point along the y axis of the medial limbic ring consisting of the cingulate cortex and medial orbitofrontal cortex (Fig. S9). We calculated the Euclidean distance between each seed (MNI x, y, z) and the anterior commissure (MNI 0, 0, 0) (\(\sqrt{({x}^{2}+{y}^{2}+{z}^{2})}\)) and computed a normalized measure of anatomical centrality for each seed defined as (maximal distance – node distance)/maximal distance, where maximal distance is the maximal distance from the anterior commissure to a seed, so that the anterior commissure would have an anatomical centrality of 1 and the most distant seed would have an anatomical centrality of 0. Anatomical centrality has been shown to be related to the degree of laminar differentiation and predictive of topological organization in the cortex78.
Data availability
The data that support the findings of this study are available as part of the Brain Genomics Superstruct Project (https://www.neuroinfo.org/gsp138). Gradients maps are available at: https://neurovault.org/collections/5449/.
References
Rao, R. P. N. & Ballard, D. H. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience 2, 79, https://doi.org/10.1038/4580 (1999).
Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav Brain Sci 36, 181–204, https://doi.org/10.1017/S0140525X12000477 (2013).
Spratling, M. W. A review of predictive coding algorithms. Brain Cogn 112, 92–97, https://doi.org/10.1016/j.bandc.2015.11.003 (2017).
Buckner, R. L. Human functional connectivity: new tools, unresolved questions. Proc Natl Acad Sci USA 107, 10769–10770, https://doi.org/10.1073/pnas.1005987107 (2010).
Deco, G., Jirsa, V. K. & McIntosh, A. R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat Rev Neurosci 12, 43–56, https://doi.org/10.1038/nrn2961 (2011).
Fox, M. D. & Raichle, M. E. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci 8, 700–711, https://doi.org/10.1038/nrn2201 (2007).
Barrett, L. F. The theory of constructed emotion: an active inference account of interoception and categorization. Soc Cogn Affect Neurosci 12, 1–23, https://doi.org/10.1093/scan/nsw154 (2017).
Barrett, L. F. & Satpute, A. B. Large-scale brain networks in affective and social neuroscience: towards an integrative functional architecture of the brain. Curr Opin Neurobiol 23, 361–372, https://doi.org/10.1016/j.conb.2012.12.012 (2013).
Barrett, L. F. & Simmons, W. K. Interoceptive predictions in the brain. Nat Rev Neurosci 16, 419–429, https://doi.org/10.1038/nrn3950 (2015).
Bressler, S. L. & Menon, V. Large-scale brain networks in cognition: emerging methods and principles. Trends in Cognitive Sciences 14, 277–290, https://doi.org/10.1016/j.tics.2010.04.004 (2010).
Chanes, L. & Barrett, L. F. Redefining the Role of Limbic Areas in Cortical Processing. Trends Cogn Sci 20, 96–106, https://doi.org/10.1016/j.tics.2015.11.005 (2016).
Goldman-Rakic, P. S. Topography of cognition: parallel distributed networks in primate association cortex. Annu Rev Neurosci 11, 137–156, https://doi.org/10.1146/annurev.ne.11.030188.001033 (1988).
McIntosh, A. R. Mapping cognition to the brain through neural interactions. Memory 7, 523–548, https://doi.org/10.1080/096582199387733 (1999).
Mesulam, M. The human frontal lobes: Transcending the default mode through contingent encoding. Principles of frontal lobe function, 8–30 (2002).
Shine, J. M. et al. Human cognition involves the dynamic integration of neural activity and neuromodulatory systems. Nature Neuroscience 22, 289–296, https://doi.org/10.1038/s41593-018-0312-0 (2019).
Yeo, B. T. et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol 106, 1125–1165, https://doi.org/10.1152/jn.00338.2011 (2011).
Power, J. D. et al. Functional network organization of the human brain. Neuron 72, 665–678, https://doi.org/10.1016/j.neuron.2011.09.006 (2011).
Craddock, R. C., James, G. A., Holtzheimer, P. E. 3rd, Hu, X. P. & Mayberg, H. S. A whole brain fMRI atlas generated via spatially constrained spectral clustering. Hum Brain Mapp 33, 1914–1928, https://doi.org/10.1002/hbm.21333 (2012).
Bellec, P., Rosa-Neto, P., Lyttelton, O. C., Benali, H. & Evans, A. C. Multi-level bootstrap analysis of stable clusters in resting-state fMRI. Neuroimage 51, 1126–1139, https://doi.org/10.1016/j.neuroimage.2010.02.082 (2010).
Wang, D. et al. Parcellating cortical functional networks in individuals. Nat Neurosci 18, 1853–1860, https://doi.org/10.1038/nn.4164 (2015).
Eickhoff, S. B., Yeo, B. T. T. & Genon, S. Imaging-based parcellations of the human brain. Nat Rev Neurosci 19, 672–686, https://doi.org/10.1038/s41583-018-0071-7 (2018).
Nelson, S. M. et al. A parcellation scheme for human left lateral parietal cortex. Neuron 67, 156–170, https://doi.org/10.1016/j.neuron.2010.05.025 (2010).
Hirose, S. et al. Functional relevance of micromodules in the human association cortex delineated with high-resolution FMRI. Cereb Cortex 23, 2863–2871, https://doi.org/10.1093/cercor/bhs268 (2013).
Wig, G. S., Laumann, T. O. & Petersen, S. E. An approach for parcellating human cortical areas using resting-state correlations. Neuroimage 93(Pt 2), 276–291, https://doi.org/10.1016/j.neuroimage.2013.07.035 (2014).
Laumann, T. O. et al. Functional System and Areal Organization of a Highly Sampled Individual Human Brain. Neuron 87, 657–670, https://doi.org/10.1016/j.neuron.2015.06.037 (2015).
Gordon, E. M. et al. Individual-specific features of brain systems identified with resting state functional correlations. Neuroimage 146, 918–939, https://doi.org/10.1016/j.neuroimage.2016.08.032 (2017).
Spreng, R. N., Sepulcre, J., Turner, G. R., Stevens, W. D. & Schacter, D. L. Intrinsic architecture underlying the relations among the default, dorsal attention, and frontoparietal control networks of the human brain. J Cogn Neurosci 25, 74–86, https://doi.org/10.1162/jocn_a_00281 (2013).
Krienen, F. M., Yeo, B. T. & Buckner, R. L. Reconfigurable task-dependent functional coupling modes cluster around a core functional architecture. Philos Trans R Soc Lond B Biol Sci 369, https://doi.org/10.1098/rstb.2013.0526 (2014).
Dixon, M. L. et al. Heterogeneity within the frontoparietal control network and its relationship to the default and dorsal attention networks. Proc Natl Acad Sci USA 115, E1598–E1607, https://doi.org/10.1073/pnas.1715766115 (2018).
Najafi, M., McMenamin, B. W., Simon, J. Z. & Pessoa, L. Overlapping communities reveal rich structure in large-scale brain networks during rest and task conditions. Neuroimage 135, 92–106, https://doi.org/10.1016/j.neuroimage.2016.04.054 (2016).
Yeo, B. T., Krienen, F. M., Chee, M. W. & Buckner, R. L. Estimates of segregation and overlap of functional connectivity networks in the human cerebral cortex. Neuroimage 88, 212–227, https://doi.org/10.1016/j.neuroimage.2013.10.046 (2014).
Kleckner, I. R. et al. Evidence for a large-scale brain system supporting allostasis and interoception in humans. Nature Human Behavior 1 (2017).
Sporns, O., Tononi, G. & Kotter, R. The human connectome: A structural description of the human brain. Plos Computational Biology 1, 245–251, https://doi.org/10.1371/journal.pcbi.0010042 (2005).
Fornito, A. & Bullmore, E. T. Connectomics: A new paradigm for understanding brain disease. Eur Neuropsychopharm 25, 733–748, https://doi.org/10.1016/j.euroneuro.2014.02.011 (2015).
van den Heuvel, M. P. & Sporns, O. Rich-club organization of the human connectome. J Neurosci 31, 15775–15786, https://doi.org/10.1523/JNEUROSCI.3539-11.2011 (2011).
van den Heuvel, M. P. & Sporns, O. An anatomical substrate for integration among functional networks in human cortex. J Neurosci 33, 14489–14500, https://doi.org/10.1523/JNEUROSCI.2128-13.2013 (2013).
Gu, S. et al. Controllability of structural brain networks. Nature Communications 6, https://doi.org/10.1038/ncomms9414 (2015).
Barbas, H. General cortical and special prefrontal connections: principles from structure to function. Annu Rev Neurosci 38, 269–289, https://doi.org/10.1146/annurev-neuro-071714-033936 (2015).
Hilgetag, C. C., Medalla, M., Beul, S. F. & Barbas, H. The primate connectome in context: Principles of connections of the cortical visual system. Neuroimage 134, 685–702, https://doi.org/10.1016/j.neuroimage.2016.04.017 (2016).
Friston, K. The free-energy principle: a unified brain theory? Nat Rev Neurosci 11, 127–138, https://doi.org/10.1038/nrn2787 (2010).
Mesulam, M. From sensation to cognition. Brain 121(Pt 6), 1013–1052 (1998).
Wei, Y., Scholtens, L. H., Turk, E. & van den Heuvel, M. P. Multiscale examination of cytoarchitectonic similarity and human brain connectivity. Netw Neurosci 3, 124–137, https://doi.org/10.1162/netn_a_00057 (2019).
Wagstyl, K., Ronan, L., Goodyer, I. M. & Fletcher, P. C. Cortical thickness gradients in structural hierarchies. Neuroimage 111, 241–250, https://doi.org/10.1016/j.neuroimage.2015.02.036 (2015).
Glasser, M. F. & Van Essen, D. C. Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. J Neurosci 31, 11597–11616, https://doi.org/10.1523/JNEUROSCI.2180-11.2011 (2011).
Krienen, F. M., Yeo, B. T., Ge, T., Buckner, R. L. & Sherwood, C. C. Transcriptional profiles of supragranular-enriched genes associate with corticocortical network architecture in the human brain. Proc Natl Acad Sci USA 113, E469–478, https://doi.org/10.1073/pnas.1510903113 (2016).
Anderson, K. M. et al. Gene expression links functional networks across cortex and striatum. Nat Commun 9, 1428, https://doi.org/10.1038/s41467-018-03811-x (2018).
Goulas, A., Margulies, D. S., Bezgin, G. & Hilgetag, C. C. The architecture of mammalian cortical connectomes in light of the theory of the dual origin of the cerebral cortex. Cortex. https://doi.org/10.1016/j.cortex.2019.03.002 (2019).
Anderson, J. S., Ferguson, M. A., Lopez-Larson, M. & Yurgelun-Todd, D. Connectivity gradients between the default mode and attention control networks. Brain Connect 1, 147–157, https://doi.org/10.1089/brain.2011.0007 (2011).
Huntenburg, J. M. et al. A Systematic Relationship Between Functional Connectivity and Intracortical Myelin in the Human Cerebral Cortex. Cereb Cortex 27, 981–997, https://doi.org/10.1093/cercor/bhx030 (2017).
Huntenburg, J. M., Bazin, P. L. & Margulies, D. S. Large-Scale Gradients in Human Cortical Organization. Trends Cogn Sci 22, 21–31, https://doi.org/10.1016/j.tics.2017.11.002 (2018).
Margulies, D. S. et al. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc Natl Acad Sci USA 113, 12574–12579, https://doi.org/10.1073/pnas.1608282113 (2016).
Oligschlager, S. et al. Gradients of connectivity distance are anchored in primary cortex. Brain Struct Funct 222, 2173–2182, https://doi.org/10.1007/s00429-016-1333-7 (2017).
O’Rawe, J. F., Ide, J. S. & Leung, H. C. Model testing for distinctive functional connectivity gradients with resting-state fMRI data. Neuroimage 185, 102–110, https://doi.org/10.1016/j.neuroimage.2018.10.022 (2018).
Guell, X., Schmahmann, J. D., Gabrieli, J. & Ghosh, S. S. Functional gradients of the cerebellum. Elife 7, https://doi.org/10.7554/eLife.36652 (2018).
Qin, S. et al. Large-scale intrinsic functional network organization along the long axis of the human medial temporal lobe. Brain Struct Funct 221, 3237–3258, https://doi.org/10.1007/s00429-015-1098-4 (2016).
Cohen, A. L. et al. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage 41, 45–57, https://doi.org/10.1016/j.neuroimage.2008.01.066 (2008).
Kruskal, J. B. & Wish, M. Multidimensional Scaling. (Sage Publications, 1978).
Davison, M. L. Multidimensional Scaling. (John Wiley & Sons Inc, 1983).
Guttman, L. In Mathematical thinking in the social sciences (ed Lazarsfeld, P. F.) 258–348 (Columbia University Press, 1957).
Barrett, L. F. & Bliss-Moreau, E. Affect as a Psychological Primitive. Adv Exp Soc Psychol 41, 167–218, https://doi.org/10.1016/S0065-2601(08)00404-8 (2009).
Thurstone, L. L. Multiple-factor analysis. (University of Chicago Press, 1947).
Conte, H. R. & Plutchik, R. A circumplex model for interpersonal personality traits. Journal of Personality and Social Psychology 40, 701–711 (1981).
Larsen, R. J. & Diener, E. Promises and problems with the circumplex model of emotion., Vol. 13 25–59 (Sage, 1992).
Fisher, G. A. Theoretical and methodological elaborations of the circumplex model of personality traits and emotions., 245–269 (American Psychological Association, 1997).
Gurtman, M. B. The circumplex as a tool for studying normal and abnormal personality: A methodological primer., 243–263 (Springer, 1994).
Acton, G. S. & Revelle, W. Interpersonal personality measures show circumplex structure based on new psychometric criteria. J Pers Assess 79, 446–471, https://doi.org/10.1207/S15327752JPA7903_04 (2002).
Acton, G. S. & Revelle, W. Evaluation of ten psychometric criteria for circumplex structure. Methods of Psychological Research Online 9 (2004).
Fernandino, L. et al. Concept Representation Reflects Multimodal Abstraction: A Framework for Embodied Semantics. Cereb Cortex 26, 2018–2034, https://doi.org/10.1093/cercor/bhv020 (2016).
Fox, M. D., Corbetta, M., Snyder, A. Z., Vincent, J. L. & Raichle, M. E. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc Natl Acad Sci USA 103, 10046–10051, https://doi.org/10.1073/pnas.0604187103 (2006).
Dosenbach, N. U. et al. Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci USA 104, 11073–11078, https://doi.org/10.1073/pnas.0704320104 (2007).
Sepulcre, J., Sabuncu, M. R., Yeo, T. B., Liu, H. & Johnson, K. A. Stepwise connectivity of the modal cortex reveals the multimodal organization of the human brain. J Neurosci 32, 10649–10661, https://doi.org/10.1523/JNEUROSCI.0759-12.2012 (2012).
Seeley, W. W. et al. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci 27, 2349–2356, https://doi.org/10.1523/JNEUROSCI.5587-06.2007 (2007).
Greicius, M. D., Krasnow, B., Reiss, A. L. & Menon, V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci USA 100, 253–258, https://doi.org/10.1073/pnas.0135058100 (2003).
Baetens, K., Ma, N., Steen, J. & Van Overwalle, F. Involvement of the mentalizing network in social and non-social high construal. Soc Cogn Affect Neurosci 9, 817–824, https://doi.org/10.1093/scan/nst048 (2014).
Fedorenko, E., Duncan, J. & Kanwisher, N. Broad domain generality in focal regions of frontal and parietal cortex. Proc Natl Acad Sci USA 110, 16616–16621, https://doi.org/10.1073/pnas.1315235110 (2013).
Miller, E. K. & Cohen, J. D. An integrative theory of prefrontal cortex function. Annu Rev Neurosci 24, 167–202, https://doi.org/10.1146/annurev.neuro.24.1.167 (2001).
Menon, V. & Uddin, L. Q. Saliency, switching, attention and control: a network model of insula function. Brain Struct Funct 214, 655–667, https://doi.org/10.1007/s00429-010-0262-0 (2010).
Zhang, J. et al. Topography impacts topology: anatomically central areas exhibit a “high-level connector’ profile in the human cortex. Cereb Cortex, https://doi.org/10.1093/cercor/bhz171 (2019).
Pandya, D. N., Petrides, M., Seltzer, B. & Cipolloni, P. B. Cerebral cortex: architecture, connections, and the dual origin concept. (Oxford University Press, 2015).
Tian, Y. & Zalesky, A. Characterizing the functional connectivity diversity of the insula cortex: Subregions, diversity curves and behavior. Neuroimage 183, 716–733, https://doi.org/10.1016/j.neuroimage.2018.08.055 (2018).
Schaefer, A. et al. Local-Global Parcellation of the Human Cerebral Cortex from Intrinsic Functional Connectivity MRI. Cereb Cortex 28, 3095–3114, https://doi.org/10.1093/cercor/bhx179 (2018).
Xu, T. et al. Assessing Variations in Areal Organization for the Intrinsic Brain: From Fingerprints to Reliability. Cereb Cortex, https://doi.org/10.1093/cercor/bhw241 (2016).
Vincent, J. L., Kahn, I., Snyder, A. Z., Raichle, M. E. & Buckner, R. L. Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. J Neurophysiol 100, 3328–3342, https://doi.org/10.1152/jn.90355.2008 (2008).
Touroutoglou, A., Hollenbeck, M., Dickerson, B. C. & Barrett, L. F. Dissociable large-scale networks anchored in the right anterior insula subserve affective experience and attention. Neuroimage 60, 1947–1958, https://doi.org/10.1016/j.neuroimage.2012.02.012 (2012).
Smith, S. M. et al. Correspondence of the brain’s functional architecture during activation and rest. Proc Natl Acad Sci USA 106, 13040–13045, https://doi.org/10.1073/pnas.0905267106 (2009).
Beckmann, C. F., DeLuca, M., Devlin, J. T. & Smith, S. M. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci 360, 1001–1013, https://doi.org/10.1098/rstb.2005.1634 (2005).
Damoiseaux, J. S. et al. Consistent resting-state networks across healthy subjects. Proc Natl Acad Sci USA 103, 13848–13853, https://doi.org/10.1073/pnas.0601417103 (2006).
Doucet, G. et al. Brain activity at rest: a multiscale hierarchical functional organization. J Neurophysiol 105, 2753–2763, https://doi.org/10.1152/jn.00895.2010 (2011).
Raz, G. et al. Functional connectivity dynamics during film viewing reveal common networks for different emotional experiences. Cogn Affect Behav Neurosci 16, 709–723, https://doi.org/10.3758/s13415-016-0425-4 (2016).
Yeo, B. T. et al. Functional Specialization and Flexibility in Human Association Cortex. Cereb Cortex 25, 3654–3672, https://doi.org/10.1093/cercor/bhu217 (2015).
Mars, R. B., Passingham, R. E. & Jbabdi, S. Connectivity Fingerprints: From Areal Descriptions to Abstract Spaces. Trends Cogn Sci 22, 1026–1037, https://doi.org/10.1016/j.tics.2018.08.009 (2018).
Hermundstad, A. M. et al. Structural foundations of resting-state and task-based functional connectivity in the human brain. Proc Natl Acad Sci USA 110, 6169–6174, https://doi.org/10.1073/pnas.1219562110 (2013).
Shepard, R. N. The mental image. American Psychologist 33, 125–137 (1978).
Murphy, K. & Fox, M. D. Towards a consensus regarding global signal regression for resting state functional connectivity MRI. Neuroimage 154, 169–173, https://doi.org/10.1016/j.neuroimage.2016.11.052 (2017).
Murphy, K., Birn, R. M., Handwerker, D. A., Jones, T. B. & Bandettini, P. A. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage 44, 893–905, https://doi.org/10.1016/j.neuroimage.2008.09.036 (2009).
Saad, Z. S. et al. Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain Connect 2, 25–32, https://doi.org/10.1089/brain.2012.0080 (2012).
Anderson, J. S. et al. Network anticorrelations, global regression, and phase-shifted soft tissue correction. Hum Brain Mapp 32, 919–934, https://doi.org/10.1002/hbm.21079 (2011).
Chai, X. J., Castañón, A. N., Ongür, D. & Whitfield-Gabrieli, S. Anticorrelations in resting state networks without global signal regression. NeuroImage 59, 1420–1428, https://doi.org/10.1016/j.neuroimage.2011.08.048 (2012).
Adams, R. A., Shipp, S. & Friston, K. J. Predictions not commands: active inference in the motor system. Brain Structure and Function 218, 611–643, https://doi.org/10.1007/s00429-012-0475-5 (2013).
Keller, G. B. & Mrsic-Flogel, T. D. Predictive Processing: A Canonical Cortical Computation. Neuron 100, 424–435, https://doi.org/10.1016/j.neuron.2018.10.003 (2018).
Shadmehr, R., Smith, M. A. & Krakauer, J. W. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci 33, 89–108, https://doi.org/10.1146/annurev-neuro-060909-153135 (2010).
Koren, V. & Deneve, S. Computational Account of Spontaneous Activity as a Signature of Predictive Coding. Plos Computational Biology 13, https://doi.org/10.1371/journal.pcbi.1005355 (2017).
Sengupta, B., Stemmler, M. B. & Friston, K. J. Information and Efficiency in the Nervous System-A Synthesis. Plos Computational Biology 9, https://doi.org/10.1371/journal.pcbi.1003157 (2013).
Hutchinson, J. B. & Barrett, L. F. The power of predictions: an emerging paradigm for psychological research. Current directions in psychological science 28, 280–291, https://doi.org/10.1177/0963721419831992 (2019).
Schlerf, J., Ivry, R. B. & Diedrichsen, J. Encoding of Sensory Prediction Errors in the Human Cerebellum. Journal of Neuroscience 32, 4913–4922, https://doi.org/10.1523/Jneurosci.4504-11.2012 (2012).
Gravina, M. T. & Sederberg, P. B. The neural architecture of prediction over a continuum of spatiotemporal scales. Curr Opin Behav Sci 17, 194–202, https://doi.org/10.1016/j.cobeha.2017.09.001 (2017).
Sterling, P. A. A model of predictive regulation. Physiol Behav 106, 5–15, https://doi.org/10.1016/j.physbeh.2011.06.004 (2012).
Sterling, P. & Laughlin, S. Principles of Neural Design. (MIT Press, 2015).
Corbetta, M. & Shulman, G. L. Control of goal-directed and stimulus-driven attention in the brain. Nat Rev Neurosci 3, 201–215, https://doi.org/10.1038/nrn755 (2002).
Andrews-Hanna, J. R., Reidler, J. S., Sepulcre, J., Poulin, R. & Buckner, R. L. Functional-anatomic fractionation of the brain’s default network. Neuron 65, 550–562, https://doi.org/10.1016/j.neuron.2010.02.005 (2010).
Christoff, K., Irving, Z. C., Fox, K. C., Spreng, R. N. & Andrews-Hanna, J. R. Mind-wandering as spontaneous thought: a dynamic framework. Nat Rev Neurosci 17, 718–731, https://doi.org/10.1038/nrn.2016.113 (2016).
Dixon, M. L., Fox, K. C. & Christoff, K. A framework for understanding the relationship between externally and internally directed cognition. Neuropsychologia 62, 321–330, https://doi.org/10.1016/j.neuropsychologia.2014.05.024 (2014).
Honey, C. J., Newman, E. L. & Schapiro, A. C. Switching between internal and external modes: A multiscale learning principle. Netw Neurosci 1, 339–356, https://doi.org/10.1162/NETN_a_00024 (2018).
Bar, M. The proactive brain: using analogies and associations to generate predictions. Trends in Cognitive Sciences 11, 280–289, https://doi.org/10.1016/j.tics.2007.05.005 (2007).
Buckner, R. L. & Margulies, D. S. Macroscale cortical organization and a default-like apex transmodal network in the marmoset monkey. Nat Commun 10, 1976, https://doi.org/10.1038/s41467-019-09812-8 (2019).
Diez, I. & Sepulcre, J. Neurogenetic profiles delineate large-scale connectivity dynamics of the human brain. Nat Commun 9, 3876, https://doi.org/10.1038/s41467-018-06346-3 (2018).
Feldman, H. & Friston, K. J. Attention, uncertainty, and free-energy. Front Hum Neurosci 4, 215, https://doi.org/10.3389/fnhum.2010.00215 (2010).
Moran, R. J. et al. Free energy, precision and learning: the role of cholinergic neuromodulation. J Neurosci 33, 8227–8236, https://doi.org/10.1523/JNEUROSCI.4255-12.2013 (2013).
Skerry, A. E. & Saxe, R. Neural representations of emotion are organized around abstract event features. Curr Biol 25, 1945–1954, https://doi.org/10.1016/j.cub.2015.06.009 (2015).
Binder, J. R. In defense of abstract conceptual representations. Psychon Bull Rev 23, 1096–1108, https://doi.org/10.3758/s13423-015-0909-1 (2016).
Barrett, L. F., Quigley, K. S. & Hamilton, P. An active inference theory of allostasis and interoception in depression. Philos Trans R Soc Lond B Biol Sci 371, https://doi.org/10.1098/rstb.2016.0011 (2016).
Sridharan, D., Levitin, D. J. & Menon, V. A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proc Natl Acad Sci USA 105, 12569–12574, https://doi.org/10.1073/pnas.0800005105 (2008).
Chen, A. C. et al. Causal interactions between fronto-parietal central executive and default-mode networks in humans. Proc Natl Acad Sci USA 110, 19944–19949 (2013).
Fox, M. D. et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America 102, 9673–9678, https://doi.org/10.1073/pnas.0504136102 (2005).
Corbetta, M., Patel, G. & Shulman, G. L. The reorienting system of the human brain: from environment to theory of mind. Neuron 58, 306–324, https://doi.org/10.1016/j.neuron.2008.04.017 (2008).
Guell, X., Schmahmann, J. D. & Gabrieli, J. D. E. Functional specialization is independent of microstructural variation in cerebellum but not in cerebral cortex. bioRxiv, https://doi.org/10.1101/424176 (2018).
Garcia-Cabezas, M. A., Zikopoulos, B. & Barbas, H. The Structural Model: a theory linking connections, plasticity, pathology, development and evolution of the cerebral cortex. Brain Struct Funct 224, 985–1008, https://doi.org/10.1007/s00429-019-01841-9 (2019).
Mesulam, M. M. Patterns in behavioral neuroanatomy. Association area, the limbic system, and hemispheric specialization., 1–70 (Oxford University Press, 1985).
Sanides, F. Functional architecture of motor and sensory cortices in primates in the light of a new concept of neocortex evolution. 137–208 (Appleton-Century-Crofts, 1970).
Caviness, V. S. Jr., Takahashi, T. & Nowakowski, R. S. Numbers, time and neocortical neuronogenesis: a general developmental and evolutionary model. Trends Neurosci 18, 379–383 (1995).
Dombrowski, S. M., Hilgetag, C. C. & Barbas, H. Quantitative architecture distinguishes prefrontal cortical systems in the rhesus monkey. Cereb Cortex 11, 975–988 (2001).
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S. & Petersen, S. E. Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251, https://doi.org/10.1016/j.neuron.2014.05.014 (2014).
Hutchison, R. M. et al. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage 80, 360–378, https://doi.org/10.1016/j.neuroimage.2013.05.079 (2013).
Lindquist, M. A., Xu, Y., Nebel, M. B. & Caffo, B. S. Evaluating dynamic bivariate correlations in resting-state fMRI: a comparison study and a new approach. Neuroimage 101, 531–546, https://doi.org/10.1016/j.neuroimage.2014.06.052 (2014).
Zhang, H., Shen, D. & Lin, W. Resting-state functional MRI studies on infant brains: A decade of gap-filling efforts. Neuroimage. https://doi.org/10.1016/j.neuroimage.2018.07.004 (2018).
Braga, R. M. & Buckner, R. L. Parallel Interdigitated Distributed Networks within the Individual Estimated by Intrinsic Functional Connectivity. Neuron 95, 457–471 e455, https://doi.org/10.1016/j.neuron.2017.06.038 (2017).
Buckner, R. L., Krienen, F. M., Castellanos, A., Diaz, J. C. & Yeo, B. T. The organization of the human cerebellum estimated by intrinsic functional connectivity. J Neurophysiol 106, 2322–2345, https://doi.org/10.1152/jn.00339.2011 (2011).
Holmes, A. J. et al. Brain Genomics Superstruct Project initial data release with structural, functional, and behavioral measures. Sci Data 2, 150031, https://doi.org/10.1038/sdata.2015.31 (2015).
Vincent, J. L. et al. Intrinsic functional architecture in the anaesthetized monkey brain. Nature 447, 83–86, https://doi.org/10.1038/nature05758 (2007).
Biswal, B., Yetkin, F. Z., Haughton, V. M. & Hyde, J. S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med 34, 537–541 (1995).
van Dijk, K. R. et al. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. Journal of Neurophysiology 103, 297–321, https://doi.org/10.1152/jn.00783.2009 (2010).
Bickart, K. C., Hollenbeck, M. C., Barrett, L. F. & Dickerson, B. C. Intrinsic amygdala-cortical functional connectivity predicts social network size in humans. J Neurosci 32, 14729–14741, https://doi.org/10.1523/JNEUROSCI.1599-12.2012 (2012).
Turken, A. U. & Dronkers, N. F. The neural architecture of the language comprehension network: converging evidence from lesion and connectivity analyses. Front Syst Neurosci 5, 1, https://doi.org/10.3389/fnsys.2011.00001 (2011).
Tomasi, D. & Volkow, N. D. Language network: segregation, laterality and connectivity. Mol Psychiatry 17, 759, https://doi.org/10.1038/mp.2012.99 (2012).
De Luca, M., Beckmann, C. F., De Stefano, N., Matthews, P. M. & Smith, S. M. fMRI resting state networks define distinct modes of long-distance interactions in the human brain. Neuroimage 29, 1359–1367, https://doi.org/10.1016/j.neuroimage.2005.08.035 (2006).
Krienen, F. M. & Buckner, R. L. Segregated fronto-cerebellar circuits revealed by intrinsic functional connectivity. Cereb Cortex 19, 2485–2497, https://doi.org/10.1093/cercor/bhp135 (2009).
Andoh, J., Matsushita, R. & Zatorre, R. J. Asymmetric Interhemispheric Transfer in the Auditory Network: Evidence from TMS, Resting-State fMRI, and Diffusion Imaging. The Journal of neuroscience: the official journal of the Society for Neuroscience 35, 14602–14611, https://doi.org/10.1523/JNEUROSCI.2333-15.2015 (2015).
Vahdat, S., Darainy, M., Milner, T. E. & Ostry, D. J. Functionally specific changes in resting-state sensorimotor networks after motor learning. J Neurosci 31, 16907–16915, https://doi.org/10.1523/JNEUROSCI.2737-11.2011 (2011).
Corbetta, M., Kincade, J. M., Ollinger, J. M., McAvoy, M. P. & Shulman, G. L. Voluntary orienting is dissociated from target detection in human posterior parietal cortex. Nat Neurosci 3, 292–297, https://doi.org/10.1038/73009 (2000).
Chong, M. et al. Individual parcellation of resting fMRI with a group functional connectivity prior. NeuroImage 156, 87–100, https://doi.org/10.1016/j.neuroimage.2017.04.054 (2017).
Ren, Y., Guo, L. & Guo, C. C. A connectivity-based parcellation improved functional representation of the human cerebellum. Sci Rep-Uk 9, 9115, https://doi.org/10.1038/s41598-019-45670-6 (2019).
Cronbach, L. J., Rajaratnam, N. & Gleser, G. C. Theory of generalizability: a liberalization of reliability theory. Br. J. Stat. Psychol. 16, 137–163 (1963).
Yarkoni, T. Big Correlations in Little Studies: Inflated fMRI Correlations Reflect Low Statistical Power-Commentary on Vul et al. Perspect Psychol Sci 4, 294–298, https://doi.org/10.1111/j.1745-6924.2009.01127.x (2009).
Van Essen, D. C. et al. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc 8, 443–459 (2001).
Barbas, H. Pattern in the laminar origin of corticocortical connections. J Comp Neurol 252, 415–422, https://doi.org/10.1002/cne.902520310 (1986).
Barbas, H. & Rempel-Clower, N. Cortical structure predicts the pattern of corticocortical connections. Cereb Cortex 7, 635–646 (1997).
Acknowledgements
B.C.D. was funded by the National Institute of Mental Health (R01 MH113234). L.F.B. was funded by the National Institute of Mental Health (R01 MH113234, R01 MH109464) and the National Cancer Institute (U01 CA193632).
Author information
Authors and Affiliations
Contributions
J.Z., O.A., A.T., B.C.D. and L.F.B. designed research; J.Z., O.A., B.C.D. and L.F.B. analyzed data; J.Z., Y.K. and L.F.B. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Abiose, O., Katsumi, Y. et al. Intrinsic Functional Connectivity is Organized as Three Interdependent Gradients. Sci Rep 9, 15976 (2019). https://doi.org/10.1038/s41598-019-51793-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-51793-7
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.