Abstract
Three new polymorphs of aluminosilicate paracelsian, BaAl2Si2O8, have been discovered using synchrotron-based in situ high-pressure single crystal X-ray diffraction. The first isosymmetric phase transition (from paracelsian-I to paracelsian-II) occurs between 3 and 6 GPa. The phase transition is associated with the formation of pentacoordinated Al3+ and Si4+ ions, which occurs in a stepwise fashion by sequential formation of Al-O and Si-O bonds additional to those in AlO4 and SiO4 tetrahedra, respectively. The next phase transition occurs between 25 and 28 GPa and is accompanied by the symmetry change from monoclinic (P21/c) to orthorhombic (Pna21). The structure of paracelsian-III consists of SiO6 octahedra, AlO6 octahedra and distorted AlO4 tetrahedra, i.e. the transition is reconstructive and associated with the changes of Si4+ and Al3+ coordination, which show rather complex behaviour with the general tendency towards increasing coordination numbers. The third phase transition is observed between 28 and 32 GPa and results in the symmetry decreasing from Pna21 to Pn. The transition has a displacive character. In the course of the phase transformation pathway up to 32 GPa, the structure of polymorphs becomes denser: paracelsian-II is based upon elements of cubic and hexagonal close-packing arrangements of large O2− and Ba2+ ions, whereas, in the crystal structure of paracelsian-III and IV, this arrangement corresponds to 9-layer closest-packing with the layer sequence ABACACBCB.
Similar content being viewed by others
Introduction
Local coordination of atoms in crystalline compounds is an important characteristic that determines their physical properties and behaviour under changing thermodynamic conditions. Being ‘useful fiction’, the parameters of coordination polyhedra can be used to estimate the physical properties of minerals by summation of properties of separate polyhedra1,2. Indeed, individual coordination polyhedra have the same properties invariant from structure to structure (such as shape, size, heat capacity, thermal expansivity, compressibility, etc.)3,4. Thus, the phase transitions accompanied by the changes in the coordination of chemical elements are associated with drastic changes of their chemical and physical properties. Silicates are probably the most important materials in human history, due to their leading role in geology, mineralogy, construction industry, pottery, material science, etc. The crystal chemistry of silicates is traditionally based upon the idea of nearly exclusive four- (under ambient conditions)5 or sixfold (under high pressure)6,7 coordination of silicon. Over the last few years there have been several reports on the high-pressure phase transitions of crystalline silicates, that were accompanied by the formation of new coordination environments around Si atoms and, in particular, SiO5 square pyramids or trigonal bipyramids. The first observation of this kind was made by Angel et al.8, who described a high-pressure modification of CaSi2O5 featuring Si atoms in five- and sixfold coordinations. This study initiated considerable theoretical work on the diversity of hypothetic phases with pentacoordinated silicon9,10,11,12,13, but very few experimental confirmations have been reported till recently, when a number of experimental results have appeared in the literature14,15,16,17,18.
Similarly to silicon, aluminum occurs predominantly in tetrahedral or octahedral coordination, though fivefold trigonal-bipyramidal polyhedra are much more common compared to silicon in silicates19. The well-known example is andalusite, Al2SiO520, which contains Al in octahedral and trigonal-bipyramidal coordinations. The AlO5 trigonal bipyramids are also present in the crystal structures of different compounds, including PbCa2Al8O1521, Ba8Al10B12O4122, LiAl7B4O1723, NaAl2(AlSi3)O10(OH)224, Tl3Al2P3O1225, Al6Ti2O1326, KAl2(PO4)2(OH)·nH2O27,28, Al2(OH)3(VO4)29, Al4B2O930, Al5BO931 (note that the last two compounds contain Al in all three coordination).
In our recent high-pressure studies on feldspar-related minerals such as danburite, CaB2Si2O815, and hurlbutite, CaBe2P2O832, we have discovered polymorphs of these materials, featuring TO5 trigonal bipyramids and TO6 octahedra (T = Si, Be, P). Observations of these exotic structural units has motivated us to investigate high-pressure behavior of closely related mineral paracelsian, BaAl2Si2O833, in order to illuminate correlations between transformation pathways and chemical and topological properties. Paracelsian and its monoclinic modification celsian34 possess aluminosilicate framework structures and belong to the feldspar group. Despite this fact, the framework topology of paracelsian is different from the feldspar topology. Paracelsian has a pseudo-orthorhombic crystal structure with the P21/a symmetry33,35,36. Its overall topology is identical to those observed in danburite, CaB2Si2O8, and hurlbutite, CaBe2P2O832, but the ordering scheme of tetrahedral cations is different. In paracelsian and hurlbutite, chemically distinct tetrahedral cations are in perfect alternation, whereas, in danburite, there are double Si2O7 and B2O7 tetrahedral groups15. The high-pressure behavior of celsian was studied recently by Curetti et al.37, who discovered a new P21/c high-pressure modification existing above 5.7 GPa.
In general, crystalline materials with the BaAl2Si2O8 composition attract considerable attention due to their various technological applications. They are widely used in glass and ceramic industries, including the production of low temperature co-fired ceramic (LTCC) materials38,39, due to the low dielectric constants and good microwave dielectric properties40,41,42,43,44. As BaAl2Si2O8 has low thermal expansion coefficients, high melting point and corrosion resistance, it is used as a refractory material40,45,46,47,48. In addition, celsian-based compounds (see below) are used as environmental barrier coating and matrix material in fibre-reinforced composites49,50. The BaAl2Si2O8 materials are also of importance as phosphors. For instance, BaAl2Si2O8 doped by Eu2+, Eu3+, Sm2+, Sm3+, Dy3+, Li+, Tb3+, Ce3+ demonstrate promising luminescent properties51,52,53,54,55,56.
From the mineralogical point of view, compounds with the BaAl2Si2O8 stoichiometry belong to the feldspar group, members of which are important rock-forming minerals found in all types of rocks and constituting over 50% of the Earth’s crust. They are essential constituents of most igneous rocks, but also found in association with metamorphic and sedimentary rocks. Feldspar-group minerals are very important for petrogenetic processes and any model used to describe phase equilibria and the structural changes of minerals in the Earth’s crust requires knowledge of their thermoelastic properties (such as the volume dependence upon pressure (the bulk modulus) and the volume thermal expansion, as well as their evolution with temperature and pressure). For instance, paracelsian, which is the subject of the current study, is associated with exhalative hydrothermal processes, low-and medium-grade metamorphism, and have been found in sedimentary and meta-sedimentary rocks.
Due to their high geological relevance and various technological applications, numerous X-ray diffraction studies at non-ambient conditions (high temperature (HT) and/or pressure (HP)) have been performed with detailed studies focused on orthoclase, sanidine, microcline, albite, and anorthite57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72. In feldspar-related minerals and inorganic compounds with divalent cations such as celsian, BaAl2Si2O837, PbAl2Si2O864, SrAl2Si2O873,74, and solid solutions between these compounds75,76,77, several phase transitions were found upon compression. However, all the reported phase transitions occur with a symmetry change but without reconstructive transformations in the aluminosilicate frameworks. Herein we report on the results of a high-pressure single-crystal X-ray diffraction study of paracelsian, BaAl2Si2O8, the compound showing step-wise pressure-induced transitions with the formation of phases with Si and Al changing their coordinations from tetrahedral to octahedral through a pentacoordinated form.
Experimental Section
In our experiments, we have used the samples of natural paracelsian from the Benallt Mine, Gwynedd, Wales, UK, obtained from a private systematic collection of Anatoly V. Kasatkin.
The high-pressure in situ single-crystal diffraction experiments were performed at the Extreme Conditions Beamline (ECB) at Petra III, DESY (Hamburg, Germany) using the procedures described previously15,17,32. For the pressure generation, the Mao-type symmetric diamond anvil cell (DAC) produced at ECB was used. Diamond anvils of Bühler-Almax type (X-ray opening 56 degree) with culet diameters of 300 μm were glued on tungsten backing seats and aligned. Rhenium gaskets were indented to about 30 μm and subsequently drilled to obtain sample chambers with approximate diameters of 150 μm. Two crystals with the approximate sizes of 10 × 10 × 5 μm3 were placed inside the sample chambers along with ruby sphere and tungsten crystals of about the same size. To achieve quasi-hydrostatic conditions, the DAC was loaded with a neon pressure-transmitting medium using the high-pressure gas loading systems of ECB. The pressures (Table 1) were determined using ruby fluorescence78.
Monochromatic X-ray diffraction experiments were performed at ECB using X-rays with a wavelength of 0.2905 Å. Diffraction patterns were collected using a Perkin Elmer 1621 detector. Before the experiment, the detector-to-sample distance was calibrated with CeO2 standard using the procedure implemented in the program Dioptas79. At each pressure, both a wide-scan and a stepped ω-scan were collected for each crystal. Wide-scans consisted of 40 s exposure during rotations of ±20° of the DAC. Step scans in the range ±28 degree were performed with individual exposures taken over 0.5° intervals to constrain the ω angle of maximum intensity of each peak. Collected diffraction images were analyzed using the program CrysAlis Pro©80. The SHELXL program package81 was used for all structural determinations.
The crystal structures of paracelsian were solved and refined at eleven pressure points (see Table S1), including ambient pressure. The crystal structures of paracelsian-I and II were refined with anisotropic displacement parameters at all pressures (0–21 GPa), except for the last pressure point (25 GPa). The crystal structure of paracelsian-III (28 GPa) was refined with anisotropic displacement parameters for all cations (Ba, Si, Al) and isotropic parameters for O, whereas the crystal structure of paracelsian-IV (32 GPa) was refined with anisotropic displacement parameters for Ba and some Si and Al atoms only.
The equation-of-state fits were performed with the EoSFit7c program82. The CRYSTAL14 software package was used to perform the solid-state DFT calculations83. The Peintinger−Oliveira−Bredow split-valence triple-ζ (pob-TZVP) basis sets84 were used for all atoms along with the hybrid Becke-3−Lee−Yang−Parr (B3LYP) functional. The electron-density distribution functions were calculated using experimentally observed geometries for each pressure point and analyzed using the TOPOND14 software85,86 with respect to the properties of (3,−1) bond critical points86.
Results
Crystal structure of paracelsian under ambient conditions
At ambient conditions the crystal structure of paracelsian was first determined by Smith35 as monoclinic but very nearly orthorhombic (Pnam). Later structure refinements33,36 confirmed the monoclinic character of the structure with the β angle in the range from 90.01° to 90.21°. The asymmetric unit contains four tetrahedrally coordinated cations T (two Si and two Al) atoms and eight O atoms. Polymerization of TO4 tetrahedra by corner sharing results in the formation of a tetrahedral framework, with channels outlined by four- and eight-membered rings along the a axis (Fig. 1). The channels with eight-membered rings are occupied by Ba atoms in either seven- (for Ba–O bonds shorter than 3 Å) or ninefold (taking into account two Ba–O bonds of 3.317(2) and 3.324(2) Å) coordination. The eight-membered rings are elliptically elongated with the ratio between the longest and shortest diagonals equal to 2.67.
As it was mentioned above, paracelsian is considered as a member of the feldspar group, though the topology of its tetrahedral framework is different from that in feldspars35,87. According to Smith and Brown87, the particular feature of the feldspar framework is the occurrence of double crankshaft chains cross-linked to form elliptical 8-membered rings. Such a description permits a simple explanation of the anisotropy of the physical properties of the material. The topological differences between feldspar and paracelsian structures87 could be described, using an algebraic code developed by Smith and Rinaldi88 in which a tetrahedron pointing up is denoted as U and one pointing down is denoted as D. According to this approach, eight-membered rings in the feldspar topology possess two types of configurations (UUUUDDDD and DUUDUDDU), whereas, in paracelsian, there is one type of eight-membered ring (DUUDUDDU) only.
High-pressure phase transitions of paracelsian
The high-pressure behaviour of paracelsian was investigated up to 32 GPa by single-crystal synchrotron X-ray diffraction. Up to 3 GPa, a continuous contraction of the unit cell (Fig. 2, Table S1) and a shortening of interatomic distances (Table S2) are observed. The compression is anisotropic, with the c and a axes showing the highest and the lowest compressibility, respectively.
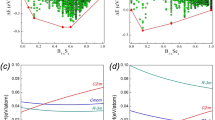
Above 6 GPa, paracelsian-I (ambient-pressure modification) transforms into paracelsian-II, the first high-pressure phase that has the same monoclinic space group (P21/c) as paracelsian-I. The phase transition is first-order, which is indicated by the abrupt change of the unit-cell parameters (Fig. 2, Table S1). The anomalous behaviour is observed for certain bond lengths (Table S2): the average 〈T–O〉 bond lengths in all TO4 tetrahedra increase between 3 and 7 GPa, which is an indication of increasing coordination number. The phase transition is induced by the rapid approach of additional oxygen atoms towards the coordination sphere of T atoms (Fig. 3a). The structural changes are displacive and are induced by shifts of the T (T = Si, Al) atoms along the c axis in such a way that across the eight-membered rings extra O2, O3 and O8 atoms approach coordination spheres of Si2, Al1 and Al2 atoms, respectively, (Fig. 4), leading to increase of their coordination numbers to fivefold. Between 3 and 7 GPa, the fifth Si–O distance decrease by more than 1.1 Å and the fifth Al–O distances decrease by more than 1.4 Å (Fig. 3a). At 7 GPa, the TO4 tetrahedra can be tentatively considered as TO4+1 configurations with the additional Si1–O and Si2–O contacts at distances of 2.755(3) and 2.634(3) Å, respectively, and the additional Al1–O and Al2–O contacts at distances of 2.279(3) and 2.410(3) Å, respectively. Upon further compression above 7 GPa length of the “fifth” contact in each TO4+1 polyhedron continuously decreases (Fig. 5). While the Al1–O8, Al2–O3 and Si2–O2 contacts undergo pronounced shortening and at 25 GPa their length become equal to 1.972(5), 1.927(5) and 1.993(5) Å, respectively, the Si1–O4 contact is more rigid and is longer than 2.4 Å at the same pressure (Fig. 5). At ~25 GPa, the geometry of three TO5 (where T is Si2, Al1 and Al2) polyhedra is trigonal-bipyramidal (Fig. 3b) with two long and three short equatorial T–O bonds (Fig. 3b, Table S2). The O–T–O apical bond angles are 7–12° away from the 180° angle required for a regular trigonal bipyramid. The formation of additional bonds results in the formation of dimers of edge-sharing TO5 polyhedra across the rings. However, the resulting structural units are different. The Si2O5 and Al2O5 groups share common vertices to form chains along the c axis (Fig. 6a), as it was observed for SiO5 polyhedra in danburite-II15, whereas Al1O5 bipyramids share the O–O edge to form a Al2O8 dimer (Fig. 6b), as found for datolite-II17. The coordination number of Ba atoms increases to 11 with the average bond lengths 2.71–2.85 Å depending upon the pressure. The BaO11 polyhedra link to each other by sharing faces to form chains extended along the c axis.
The TOn (T = Si, Al; n = 4, 5) polyhedra at 7 (a) and 25 (b) GPa. The distances for other bonds at 7 GPa in silicon polyhedra are in the range 1.608(3)–1.642(3) Å, in aluminum polyhedra 1.702(3)–1.834(3) Å, at 25 GPa in silicon polyhedra 1.597(5)–1.706(6) Å and in aluminum polyhedra 1.712(5)–1.896(6) Å.
Fragments of crystal structures of paracelsian-II (a,b) at 25 GPa and paracelsian-III (c–e) at 28 GPa. Blue and white polyhedra represent SiOn and AlOn (n = 4, 5, 6), respectively. (a) chains of Al2O5 and Si2O5 trigonal-bipyramids; (b) Al2O8 dimer with Al1 central atom; (c) layer of SiO6 octahedra; (d) chain of Al1O6 octahedra and Al2O4 distorted tetrahedra; (e) coordination of Al2 atom.
The DFT calculations and the analysis of theoretical electron-density distributions at different pressures indicate the existence of the Al1–O3 bond (2.279(3) Å) at pressures above 7 GPa, the Al2–O8 bond (2.095(4) Å) at pressures above 11 GPa and the Si2–O2 bond (2.077(5) Å) at pressures above 21 GPa (Fig. 7, Table S3), which is manifested by the appearance of the (3,–1) bond critical point (BCP) for the respective atom pairs. If one accepts that the formation of a new bond indicates a phase transition, paracelsian-II can be separated into three phases, paracelsian-IIa, paracelsian-IIb and paracelsian-IIc, which differ from each other by the presence of respective additional (fifth) T–O bonds. The transition between these polymorphs is continuous and isosymmetric, with paracelsian-IIa and paracelsian-IIb being intermediate phases between paracelsian-I and paracelsian-IIc.
Upon compression above 28 GPa, another first-order phase transition is detected by abrupt change of unit cell parameters (Fig. 2). The new phase, paracelsian-III, has the Pna21 space group (Table S1). Similarly to paracelsian-I and II, the crystal structure of paracelsian-III contains two Si, two Al, one Ba, and eight O sites. The P21/c → Pna21 transition is reconstructive and involves breaking of chemical bonds. As a result of the transition, the chains of Si2O5 trigonal bipyramids and isolated Si1O4 tetrahedra transform into sheets of SiO6 octahedra running parallel to the ab plane (Fig. 6c). In these layers, Si2O6 octahedra share edges to form chains parallel to the a axis that are connected to each other via zigzag chains of corner-sharing Si1O6 octahedra. The chains and dimers of AlO5 polyhedra present at 25 GPa transform into chains (Fig. 6d) of edge-sharing Al1O6 octahedra incrustated by strongly distorted Al2O4 tetrahedra (Fig. 6e). The coordination number of Ba increases from 11 to 12 with the average 〈Ba-O〉 bond length of 2.688 Å (Table S2). The presence of chemical bonds inside all polyhedra in paracelsian-III is in agreement with DFT and AiM calculations (Fig. 7, Table S3).
At the last pressure point of about 32 GPa, another phase, paracelsian-IV, is observed. It has the space group Pn and can be described as a distorted version of paracelsian-III. Due to the symmetry lowering (from orthorhombic to monoclinic), the number of crystallographic sites is doubled (Table S2), but no coordination changes are observed, which indicates a displacive character of the phase transition.
Equation of state and compressibility of paracelsian-II
The obtained P-V data between 6 and 25 GPa were used to determine an equation of state of paracelsian-II. The initial volume V0 and the room-temperature isothermal bulk modulus KT0 were determined to 621(3) Å3 and 81(4) GPa, respectively, by fitting Birch-Murnaghan second-order equation of state. For paracelsian, paracelsian-III and -IV, the available pressure points were insufficient to constrain an equation of state.
Discussion
High-pressure phases featuring SiO5 polyhedra are very rare in inorganic crystal chemistry and the mechanism of their formation is currently unclear. According to rules of thumb formulated by Prewitt and Downs89 and further generalized rules by Grochala et al.90, the increasing pressure leads to the increasing coordination numbers and the atomic arrangements in high-pressure structures show strong tendency to form close-packed arrays. According to Pakhomova et al.15, high-pressure crystal structures with pentacoordinated silicon may form as intermediate (transitional) configurations between relatively open ambient-pressure structure and ideal or distorted close-packed high-pressure structure.
Indeed, the arrangement of large ions (O2− anions and M2+ cations (M = Ca, Ba) in the crystal structures of transitional phases (containing pentacoordinated Al, Si and P) of danburite, hurlbutite and paracelsian (i.e. danburite-II, hurlbutite-II, hurlbutite-III and paracelsian-II) are similar and can be described as having elements of distorted cubic and hexagonal close packings with a square-like contact15. However, the polymorphs of the three compounds at higher pressures possess geometrically different close-packed arrangements. The crystal structure of danburite, CaB2Si2O8 (danburite-III)15, is based upon the cubic (ABC) close packing of O2− and Ca2+ ions with smaller cations in octahedral and tetrahedral interstices, whereas the crystal structures of hurlbutite-IV32 and paracelsian-III and IV are based upon more complex closest packing: 12-layer closest packing of Ca2+ and O2− ions with the layer sequence ABCACABCBCAB and 9-layer closest packing of Ba2+ and O2− ions with the layer sequence ABACACBCB (Fig. 8), respectively. The paracelsian III → paracelsian-IV phase transition is associated with small shifts of the packing ions, which results in more perfect close-packed arrangement. The same 9-layer closest packing was previously found for elemental Sm91,92 and 9R-modification of Li stable at low temperatures93 as well as for more chemically complex compounds such as ε-Hf3N294. This Sm-type layer consequence had been considered as a combination of face-centered cubic and hexagonal close-packed structures with the ratio 1:295.
In the course of high-pressure phase transitions in paracelsian, Al3+ ions adopt fivefold coordination first, before Si4+ cations do, which can be explained by the ionic radii (rion) of Al3+ and Si4+, which are equal to 0.39 and 0.26 Å for tetrahedral coordination, respectively96. This prompts Al3+ ions to form additional bonds more easily than Si4+ ions. It is noteworthy that small B3+ cations in danburite (tetrrion = 0.11 Å) do not change their coordination at all and remain tetrahedrally coordinated under all observed high-pressure interval.
The previous high-pressure (up to 5 GPa) and high-temperature (up to 1100 °C) single crystal X-ray diffraction studies of feldspars revealed phase transitions governed by the changes in the values of bridging T–O–T angles between the rigid TO4 units, whereas the latter do not undergo significant distortion and compression/expansion. The phase transitions are therefore of displacive character, owing to the considerable flexibility of tetrahedral frameworks accompanied by the cooperative motions of tetrahedral groups, such as tilting and rotating97,98. Paracelsian, BaAl2Si2O8, demonstrates a contrasting behaviour: upon the compression the TO4 units undergo strong distortions with subsequent formation of TO5 trigonal bipyramids (for both Si and Al).
The information-based structural complexity of paracelsian have been calculated using the TOPOS program package99 following the procedure outlined by Krivovichev100,101,102. The isosymmetric paracelsian-I → paracelsian-II phase transition does not result in any changes of structural complexities (the information content per atom and per unit cell, IG and IG,total, remain the same, 3.700 and 192.423 bits, respectively). The similar trend is observed for the paracelsian-II → paracelsian-III phase transition, whereas the formation of paracelsian-IV in the course of displacive phase transition (i.e. without changes in cation coordination) is associated with the increase in both IG and IG,total parameters (4.700 and 244.423 bits, respectively). This agrees well with the general empirical rule that high-pressure-induced reconstructive phase transitions (with coordination changes) do not result in the increase of structural complexity (not taking into account chemical bonds), whereas high-pressure-induced displacive transitions usually lead to the formation of structurally more complex phases.
Conclusions
In conclusion, the high-pressure study of paracelsian, BaAl2Si2O8, revealed three new phase transitions with the formation of three previously unknown high-pressure polymorphs, paracelsian-II, paracelsian-III and paracelsian-IV. The I → II phase transition is associated with the formation of pentacoordinated Al3+ and Si4+ ions, which remarkably occurs in a stepwise fashion by formation of additional Al–O and Si–O bonds, so that, technically speaking, paracelsian-II can be separated into three other polymorphs, IIa, IIb and IIc, with different number of additional bonds. The II → III phase transition is reconstructive and associated with the changes of Si4+ and Al3+ coordination, which show rather complex behaviour with the general tendency towards increasing coordination numbers. Finally, the III → IV transition has a displacive character. In the course of I → II → III → IV transformation pathway, the structure becomes denser: paracelsian-II is based upon elements of cubic and hexagonal close-packing arrangements of large O2− and Ba2+ ions, whereas, in the crystal structure of paracelsian-III and IV, this arrangement corresponds to 9-layer closest-packing with the layer sequence ABACACBCB.
Data Availability
All data generated or analysed during this study are included in this published article (and its Supplementary Information files).
References
Hazen, R. M. Comparative crystal chemistry and the polyhedral approach. Rev. Mineral. 14, 317–345 (1985).
Hazen, R. M. A useful fiction: polyhedral modeling of mineral properties. Amer. J. Sci. 288A, 248–269 (1988).
Chen, F., Ewing, R. C. & Clark, S. B. The Gibbs free energies and enthalpies of formation of U6+ phases: an empirical method of prediction. Amer. Mineral. 84, 650–664 (1999).
Chermak, J. A. & Rimstidt, J. D. Estimating the thermodynamic properties (ΔG 0 f and ΔH 0 f) of silicate minerals at 298K from the sum of polyhedral contributions. Amer. Mineral. 74, 1023–1031 (1989).
Liebau, F. Structural Chemistry of Silicates, p. 354. (Heidelberg: Springer-Verlag, 1985).
Finger, L. W. & Hazen, R. M. Crystal chemistry of six-coordinated silicon: a key to understanding the Earth’s deep interior. Acta Crystallogr. B47, 561–580 (1991).
Finger, L. W. & Hazen, R. M. Systematics of high-pressure silicate structures. Rev. Mineral. Geochem. 41, 123–155 (2000).
Angel, R. J., Ross, N. L., Seifert, F. & Fliervoet, T. F. Structural characterization of pentacoordinate silicon in a calcium silicate. Nature. 384, 441–443 (1996).
Warren, M. C., Redfern, A. T. & Angel, R. Change from sixfold to fivefold coordination of silicate polyhedra: Insights from first-principles calculations of CaSi2O5. Phys. Rev. B. 59, 9149–9154 (1999).
Hu, Q. Y. et al. Polymorphic phase transition mechanism of compressed coesite. Nature Comm. 6, 6630 (2015).
Martonák, R., Donadio, D., Oganov, A. R. & Parrinello, M. From four- to six-coordinated silica: Transformation pathways from metadynamics. Phys. Rev. B 76, 014120 (2007).
Martonák, R., Donadio, D., Oganov, A. R. & Parrinello, M. Crystal structure transformations in SiO2 from classical and ab initio metadynamics. Nat. Mater. 5, 623–626 (2006).
Badro, J. et al. Theoretical study of a five-coordinated silica polymorph. Phys. Rev. B. 56, 5797–5806 (1997).
Finkelstein, G. J., Dera, P. K. & Duffy, T. S. Phase transitions in orthopyroxene (En90) to 49 GPa from single-crystal X-ray diffraction. Phys. Earth Planet. Inter. 244, 78–86 (2015).
Pakhomova, A. S. et al. Closer look into close packing: pentacoordinated silicon in the high-pressure polymorph of danburite. IUCrJ. 4, 671–677 (2017).
Hu, Y., Kiefer, B., Bina, C. R., Zhang, D. & Dera, P. K. High-pressure γ-CaMgSi2O6: does penta-coordinated silicon exist in the Earth’s Mantle? Geophys. Res. Lett. 44, 11340–11348 (2017).
Gorelova, L. A., Pakhomova, A. S., Aprillis, G., Dubrovinsky, L. S. & Krivovichev, S. V. Pentacoordinated silicon in the high-pressure modification of datolite, CaBSiO4(OH). Inorg. Chem. Front. 5, 1653–1660 (2018).
Bykova, E. et al. Metastable silica high pressure polymorphs as structural proxies of deep Earth silicate melts. Nat. Comm. 9, 4789 (2018).
Santamaria-Perez, D. & Vegas, A. The Zintl-Klemm concept applied to cations in oxides. I. The structures of ternary aluminates. Acta Cryst. B59, 305–323 (2003).
Burnham, C. W. & Buerger, M. J. Refinement of the crystal structure of andalusite. Z. Kristallogr. 115, 269–290 (1961).
Artner, C. & Weil, M. PbCa2[Al8O15] with a novel three-dimensional aluminate anion. Acta Cryst. 68C, i1–i3 (2012).
Chen, X., Chu, Z., Chang, X., Zang, H. & Xiao, W. Synthesis, crystal structure, spectrum properties, and electronic structure of a new barium aluminoborate, Ba8[(Al6 IV)(Al2 IV)(Al2 V)B12 IIIO41]∞. J. Alloys Compd. 511, 74–80 (2012).
Ahman, J., Svensson, G. & Grins, J. Lithium aluminium borate, LiAl7B4O17. Acta Chem. Scand. 51, 1045–1050 (1997).
Comodi, P. & Zanazzi, P. F. Structural thermal behavior of paragonite and its dehydroxylate: a high-temperature single-crystal study. Phys. Chem. Minerals. 27, 377–385 (2000).
Devi, R. N. & Vidyasagar, K. Solid-state synthesis and characterization of novel aluminophosphates, A3Al2P3O12 (A = Na, K, Rb, Tl): influence of A+ ions on the coordination of aluminum. Inorg. Chem. 39, 2391–2396 (2000).
Norberg, S. T., Hoffmann, S., Yoshimura, M. & Ishizawa, N. Al6TiO13, a new phase in the Al2O3–TiO2 system. Acta Cryst. C61, i35–i38 (2005).
Dick, S., Gossner, U., Grossmann, G., Ohms, G. & Zeiske, T. Aluminiumphosphate mit azentrischen Schicht- und Raumnetzstrukturen aus topologisch verwandten Motiven: 1. KAl2(PO4)2(OH)·4(H2O). Z. Naturforsch., B: Chem. Sci. 52, 1439–1446 (1997).
Dick, S., Grossmann, G., Ohms, G. & Mueller, M. Aluminiumphosphate mit azentrischen Schicht- und Raumnetzstrukturen aus topologisch verwandten Motiven: 1. KAl2(PO4)2(OH)·2(H2O). Z. Naturforsch., B: Chem. Sci. 52, 1447–1455 (1997).
Pecquenard, B., Zavalij, P. Y. & Whittingham, M. S. Hydrothermal synthesis and characterization of a new aluminium vanadium oxide hydroxide Al2(OH)3(VO4). J. Mater. Chem. 8, 1255–1258 (1998).
Fischer, R. X. et al. Crystal structure of synthetic Al4B2O9: a member of the mullite family closely related to boralsilite. Am. Mineral. 93, 918–927 (2008).
Rothkirch, A. et al. Single-crystal diffraction at the Extreme Conditions beamline P02.2: procedure for collecting and analyzing high-pressure single-crystal data. J. Synchrotron Rad. 20, 711–720 (2013).
Pakhomova, A. et al. Penta- and hexa-coordinated beryllium and phosphorus in high-pressure modifications of CaBe2P2O8. Nat. Comm. 10, 2800 (2019).
Bakakin, V. V. & Belov, N. V. Crystal structure of paracelsian. Soviet Physics, Crystallography. 5, 826–829 (1960).
Newnham, R. E. & Megaw, H. D. The crystal structure of celsian (barium feldspar). Acta Cryst. 13, 303–312 (1960).
Smith, J. V. The crystal structure of paracelsian, BaAl2Si2O8. Acta Cryst. 6, 613–620 (1953).
Chiari, G., Gazzoni, G., Craig, J. R., Gibbs, G. V. & Louisnathan, S. J. Two independent refinements of the structure of paracelsian. Am. Mineral. 70, 969–974 (1985).
Curetti, N., Benna, P. & Bruno, E. High-pressure structural configuration and phase transition in celsian, BaAl2Si2O8. Phys. Chem. Minerals. 44, 181–192 (2017).
Song, X.-Q. et al. Temperature-stable BaAl2Si2O8–Ba5Si8O21–based low-permittivity microwave dielectric ceramics for LTCC applications. Ceram. Int. 43, 14453–14456 (2017).
Chen, S., Sun, Z. & Zhu, D.-G. Mineral-phase evolution and sintering behavior of MO–SiO2–Al2O3–B2O3 (M = Ca, Ba) glass-ceramics by low-temperature liquid phase sintering. Int. J. Miner. Metall. Mater. 25, 1042–1054 (2018).
McCauley, R. A. Polymorphism and dielectric electric properties of Ba- and Sr-containing feldspars. J. Mater. Sci. 35, 3939–3942 (2000).
Krzmanc, M. M., Valant, M. & Suvorov, D. The synthesis and microwave dielectric properties of SrxBa1-xAl2Si2O8 and CayBa1-yAl2Si2O8 ceramics. J. Eur. Ceram. Soc. 27, 1181–1185 (2007).
Lei, W., Ang, R., Wang, X. C. & Lu, W. Z. Phase evolution and near-zero shrinkage in BaAl2Si2O8 low-premittivity microwave dielectric ceramics. Mater. Res. Bull. 50, 235–239 (2014).
Song, X.-Q. et al. Sintering behavior and microwave properties of BaAl2-2x(ZnSi)xSi2O8 ceramics. J. Eur. Ceram. Soc. 38, 1529–1534 (2018).
Han, L.-C. et al. ZBAS on the structure and dielectric property of BaAl2Si2O8. J. Inorg. Mat. 33, 883–888 (2018).
Allameh, S. M. & Sandhege, K. H. Synthesis of celsian (BaAl2Si2O8) from solid Ba–Al2O3–SiO2 precursors: I, XRD and SEM/EDX analyses of phase evolution. J. Am. Ceram. Soc. 80, 3109–3126 (1997).
Fu, Y.-P., Chang, C.-C., Lin, C.-H. & Chin, T.-S. Solid-state synthesis of ceramics in the BaO–SrO–Al2O3–SiO2 system. Ceram. Int. 30, 41–45 (2004).
Viers, D. S. & Sandhage, K. H. Near-net-Shaped (Ba,Sr)Al2Si2O8 bodies by oxidation of machinable metal-bearing precursors. J. Am. Ceram. Soc. 82, 249–252 (1999).
Ibarra, M. N., Almanza, J. M., Cortes, D. A., Escobedo, J. C. & Martinez-Lopez, R. Chemical interaction between Ba-celsian (BaAl2Si2O8) and molten aluminium. Ceram. Int. 42, 3491–3496 (2016).
Lee, K. N. et al. Upper temperature limit of environmental barrier coating based on mullite and BSAS. J. Am. Ceram. Soc. 86, 1299–1306 (2003).
Bansal, N. P. & Setlock, J. A. Fabrication of fiber-reinforced celsian matrix composites. Compos. Part A – Appl. Sci. Manuf. 32, 1021–1029 (2001).
Im, W. B., Kim, Y. & Jeon, D. Y. Thermal stability study of BaAl2Si2O8: Eu2+ phosphor using its polymorphism for plasma display panel application. Chem. Mater. 18, 1190–1195 (2006).
Li, L. et al. Spontaneous Sm3+ → Sm2+ reduction ability of MAl2Si2O8 (M = Sr, Ba): Sm. J. Alloy Compd. 723, 527–535 (2017).
Ma, M. et al. Effect of sintering temperature on phase transformation and luminescence property of BaAl2Si2O8:Eu2+ phosphor. Micro Nano Lett. 13, (1390–1393 (2018).
Wan, Y. et al. Synthesis and luminescence properties of a new type of green fluorescent powder BaAl2Si2O8: Tb3+, Ce3+. Spectrosc. Spect. Anal. 37, 1595–1600 (2017).
Wang, F., Chen, H.-H., Tian, Y.-G. & Zhang, Q. Preparation and luminescenct properties of red phosphor BaAl2Si2O8:Eu3+, Li+. Chinese Rare Earth. 38, 80–86 (2017).
Sahu, I. P. Luminescence properties of dysprosium doped barium alumino-silicate phosphors prepared by the solid state reaction method. J. Mater. Sci. Mater. Electron. 27, 13134–13147 (2016).
Angel, R. J., Hazen, R. M., McCormick, T. C., Prewitt, C. T. & Smyth, J. R. Comparative compressibility of end-member feldspars. Phys. Chem. Minerals. 15, 313–318 (1988).
Angel, R. J. High-pressure structure of anorthite. Am. Mineral. 73, 1114–1119 (1988).
Angel, R. J. Order-disorder and the high-pressure P–1–I–1 transition in anorthite. Am. Mineral. 77, 923–929 (1992).
Daniel, I., Gillet, P. & Ghose, S. A new high pressure phase transition in anorthite (CaAl2Si2O8) revealed by Raman spectroscopy. Am. Mineral. 80, 645–648 (1995).
Daniel, I., Gillet, P., McMillan, P. F. & Richet, P. An in situ high-temperature structural study of stable and metastable CaAl2Si2O8 polymorphs. Mineral. Mag. 59, 25–33 (1995).
Daniel, I., Gillet, P., Poe, T. B. & McMillan, P. F. In situ high-temperature Raman spectroscopic studies of aluminosilicate liquids. Phys. Chem. Minerals. 22, 74–86 (1995).
Daniel, I., Gillet, P., McMillan, P. F., Wolf, G. & Verhelst, M. A. High-pressure behavior of anorthite: compression and amorphization. J. Geophys. Res. 102, 10313–10325 (1997).
Tribaudino, M., Benna, P., Bruno, E. & Hanfland, M. High pressure behavior of lead feldspar (PbAl2Si2O8). Phys. Chem. Minerals. 26, 367–374 (1999).
Liu, L.-G. & Gorsey, A. E. High-pressure phase transitions of the feldspars, and further characterization of lingunite. Int. Geol. Rev. 49, 854–860 (2007).
Hovis, G. L. et al. A simple predictive model for the thermal expansion of AlSi3 feldspars. Am. Mineral. 93, 1568–1573 (2008).
Hovis, G. L., Medford, A., Conlon, M., Tether, A. & Romanosli, A. Principles of thermal expansion in the feldspar system. Am. Mineral. 95, 1060–1068 (2010).
Tribaudino, M. et al. Thermal expansion of plagioclase feldspars. Contrib. Mineral. Petrol. 160, 899–908 (2010).
Tribaudino, M., Bruno, M., Nestola, F., Pasqual, D. & Angel, R. J. Thermoelastic and thermodynamic properties of plagioclase feldspars from thermal expansion measurements. Am. Mineral. 96, 992–1002 (2011).
Angel, R. J. et al. Structural controls on the anisotropy of tetrahedral frameworks: the example of monoclinic feldspars. Eur. J. Mineral. 25, 597–614 (2013).
Mookherjee, M. et al. Pressure induced elastic softening in framework aluminosilicate-albite (NaAlSi3O8). Sci. Rep. 6, 34815 (2016).
Sims, M. et al. Pressure-induced amorphization in plagioclase feldspars: a time-resolved powder diffraction study during rapid compression. Earth Planet. Sci. Lett. 507, 166–174 (2019).
McGuinn, M. D. & Redfern, S. A. T. Ferroelastic phase transition in SrAl2Si2O8 feldspar at elevated pressure. Min. Mag. 58, 21–26 (1994).
Pandoflo, F. et al. High-pressure I2/c–P21/c phase transformation in SrAl2Si2O8 feldspar. Am. Mineral. 96, 1182–1185 (2011).
McGuinn, M. D. & Redfern, S. A. T. Ferroelastic phase transition along the join CaAl2Si2O8–SrAl2Si2O8. Am. Mineral. 79, 24–30 (1994).
Nestola, F., Ballaran, T. B., Tribaudino, M. & Bruno, E. High-pressure phase transitions in Ca0.2Sr0.8Al2Si2O8 feldspar. Am. Mineral. 89, 1474–1479 (2004).
Benna, P. et al. The high-pressure structural configurations of Ca0.2Sr0.8Al2Si2O8 feldspar: the I–1–I2/c and I2/c–P21/c phase transitions. Am. Mineral. 92, 1190–1199 (2007).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 9, 4673–4676 (1986).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 35, 223–230 (2015).
Agilent. CrysAlis PRO. Agilent Technologies: Yarnton, Oxfordshire, England, 2012.
Sheldrick, G. M. A short history of SHELX. Acta Crystallogr. A64, 112 (2008).
Angel, R. J., Gonzalez-Platas, J. & Alvaro, M. EosFit-7c and a Fortran module (library) for equation of state calculations. Z. Kristallogr. 229, 405–419 (2014).
Dovesi, R. et al. CRYSTAL14: a program for ab initio investigation of crystalline solids. Int. J. Quantum Chem. 114, 1287–1317 (2014).
Peintinger, M. F., Oliveira, D. V. & Bredow, T. Consistent Gaussian basis sets of triple-zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 34, 451–459 (2013).
Gatti, C. & Casassa, S. TOPOND14. User’s Manual. CNR-ISTM of Milano: Milano, 2013.
Gatti, C., Saunders, V. R. & Roetti, C. Crystal field effects on the topological properties of the electron density in molecular crystals. The case of urea. J. Chem. Phys. 101, 10686–10696 (1994).
Smith, J. V. & Brown, W. L. Feldspar minerals. Berlin Heidelberg: Springer-Verlag. 828 p, (1988).
Smith, J. V. & Rinaldi, F. Framework structures formed from parallel four- and eight-membered rings. MM. 33, 202–212 (1962).
Prewitt, C. T. & Downs, R. T. High pressure crystal chemistry. Rev. Mineral. Geochem. 37, 283–317 (1998).
Grochala, W., Hoffmann, R., Feng, J. & Ashcroft, N. W. The chemical imagination at work in very tight places. Angew. Chem. 46, 3620–3642 (2007).
Ellinger, F. H. & Zachariasen, W. H. The crystal structure of samarium metal and samarium monoxide. J. Am. Chem. Soc. 75, 5650–5652 (1953).
Daane, A. H., Rundle, R. E., Smith, H. G. & Spedding, F. H. The crystal structure of samarium. Acta Cryst. A. 7, 532–535 (1954).
Overhauser, A. W. Crystal structure of lithium at 4.2 K. Phys. Rew. Let. 53, 64–65 (1984).
Rudy, E. The crystal structures of Hf3N2 and Hf4N3. Metallurgical Transactions. 1, 1249–1525 (1970).
Barrett S. D., Dhesi S. S. The structure of rare-earth metal surfaces. London, Imperial College Press. 2001.
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A32, 751–767 (1976).
Hazen, R. M. & Finger, L. W. Polyhedral tilting: a common type of pure displacive phase transition and its relationship to analcite at high pressure. Phase Transitions. 1, 1–22 (1979).
Hazen, R. M. & Finger, L. W. Comparative crystal chemistry: temperature, pressure, compositic and variation of the crystal structure. 231 p. (London, 1982).
Blatov, V. A., Shevchenko, A. P. & Proserpio, D. M. Applied topological analysis of crystal structures with the program package Topospro. Cryst. Growth Des. 14, 3576–3586 (2014).
Krivovichev, S. V. Topological complexity of crystal structures: quantitative approach. Acta Cryst. A68, 393–398 (2012).
Krivovichev, S. V. Structural complexity of minerals: information storage and processing in the mineral world. Mineral Mag. 77, 275–326 (2013).
Krivovichev, S. V. Which inorganic structures are the most complex? Angew. Chem. Int. Ed. 53, 654–661 (2014).
Acknowledgements
X-ray measurements high-pressure measurements were carried out at the PETRA III light source at DESY, a member of the Helmholtz Association (HGF). This research was supported by the Russian Science Foundation (grant 19-17-00038 to LAG and SVK).
Author information
Authors and Affiliations
Contributions
L.A.G. and A.S.P. performed high-pressure X-ray experiment and analysis; DFT calculations were performed by S.V.K. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gorelova, L.A., Pakhomova, A.S., Krivovichev, S.V. et al. High pressure phase transitions of paracelsian BaAl2Si2O8. Sci Rep 9, 12652 (2019). https://doi.org/10.1038/s41598-019-49112-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-49112-1
This article is cited by
-
Surface layer effect on high pressure phase growth in a bicrystal: phase field model and simulations
Continuum Mechanics and Thermodynamics (2024)
-
Compressibility of hingganite-(Y): high-pressure single crystal X-ray diffraction study
Physics and Chemistry of Minerals (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.