Abstract
Biological entities are key elements of biomedical research. Their definition and their relationships are important in areas such as phylogenetic reconstruction, developmental processes or tumor evolution. Hypotheses about relationships like phenotype order are often postulated based on prior knowledge or belief. Evidence on a molecular level is typically unknown and whether total orders are reflected in the molecular measurements is unclear or not assessed. In this work we propose a method that allows a fast and exhaustive screening for total orders in large datasets. We utilise ordinal classifier cascades to identify discriminable molecular representations of the phenotypes. These classifiers are constrained by an order hypothesis and are highly sensitive to incorrect assumptions. Two new error bounds, which are introduced and theoretically proven, lead to a substantial speed-up and allow the application to large collections of many phenotypes. In our experiments we show that by exhaustively evaluating all possible candidate orders, we are able to identify phenotype orders that best coincide with the high-dimensional molecular profiles.
Similar content being viewed by others
Introduction
Assessing the correspondence between observable phenotypes and their underlying molecular background is a challenging task in molecular biology. Even for pairwise comparisons it is not straight forward to confirm hypothesised relations in high-dimensional marker representations.
This becomes even more evident for higher order relations among multiple phenotypes. In this case, local events and global processes might be confused as they both can lead to the same pattern of observable phenotypes. While local - pairwise - events might be reflected by any type of pairwise differences, an overall connecting pattern is required for global processes. An example, for such higher level relations are ordinal phenotypes of type \(phenotyp{e}_{1}\,\prec \,phenotyp{e}_{2}\,\prec \,phenotyp{e}_{3}\) as they might occur in developmental processes1,2,3,4, like embryogenesis5, phylogenetic reconstruction6,7,8 or diagnostic stagings or gradings9,10,11,12. Their observable representations suggest an order of the phenotypes (\(\prec \)), which might lead to hypotheses on a connecting “ordinal” relation or process on a molecular level (Fig. 1B). Providing evidence for these hypotheses is quite challenging due to the high dimensionality of molecular profiles. Being defined for univariate categorical variables, the concept of ordinality can be embedded in many different ways in a multivariate real-valued feature representation. There might also be several ordinal relations that coexist in parallel.
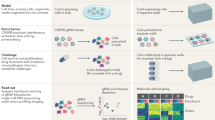
Assessment of phenotype order in molecular data (four phenotype/class example). (A) (Data): The data consists of a set of molecular measurements labelled with their phenotype names. (B) (Hypothesis): Is an ordinal relation on the phenotypes reflected in feature space? A trend in observable characteristics of phenotypes often induces hypotheses about ordinality on their molecular background. Its confirmation requires a reflection in the corresponding feature representation. (C) (Analysis): The analysis incorporates four different steps and evaluates which hypotheses are reflected in the specific feature representation. First, for all pairwise combinations binary base classifiers are trained in a pairwise manner. Second, for each possible order a cascade is built using the previously trained base classifiers. Third, the performance of these ensemble classifiers is analysed. The cascade classifier analyses each sample in a stepwise manner. For each base classifier it holds that if the sample belongs to its first class it is labelled and if not it is transferred to the next classifier. By doing so, regions of the feature space are defined and labelled dependent on the order of the base classifiers’ first class. Finally, a set of possible candidate cascades that show a good performance measured by the class-wise minimal sensitivity is returned.
In the research field of ordinal classification usually, a known order is used to improve classification performance. The assumption is that the given order between the classes (phenotypes) can be mapped to the given representation and hence also holds in the feature space. In this work, we instead propose a method that can check whether the reflection is provided, by elaborating a performance-based criterion for detecting and comparing ordinal structures in multivariate feature representations. We present an algorithm (CASCADES) that allows for systematic and exhaustive screens through the search space of all phenotype orders. It is applicable for extracting a small set of candidate orders from a feature representation that fulfils a minimal generalisation ability of a predictive model. Based on supervised classification, our method uses the canonical paradigm for learning relationships between raw uninterpreted feature representations and semantically meaningful phenotypes (classes, categories, concepts, etc.)13,14,15. Utilising feature representations and class memberships these techniques allow the extraction of phenotype-specific patterns and the construction of phenotype separating boundaries. In this way, classifiers identify characteristics of phenotypes or even learn the key attributes of their concepts. Mainly designed for discrimination the learning processes of classification algorithms often neglect the semantic relationships among classes. Standard training algorithms would neither request nor reconstruct such dependencies explicitly16,17,18.
For this reason, we focus on ordinal classifier cascades19 of binary base classifiers. They are a specialisation of general decision lists20,21,22. A predefined order of phenotypes constrains the learning algorithm of an ordinal classifier cascade. Initially designed for guiding the learning process, we showed that wrong assumptions on the class order can lead to severely decreased detection rates of an ordinal classifier cascade23.
In our approach (Fig. 1), we separate the training and evaluation of binary base classifiers from the construction of the classifier cascade. For the training, no order information is used, and each base classifier is trained independently. But the assumed phenotype order defines the evaluation sequence of these pairwise base classifiers. In each step of the evaluation a feature space region is labelled as decision region for a specific class, and the remaining space stays unlabelled. If the order is wrong, then samples of classes that are later in the order already lie within this region, whereas if it reflects the order they lie within the unlabelled region. Although trained only pairwise, the base classifiers show good performance when used to distinguish between a class and all following classes in the order.
Here, we utilise this susceptibility as a clear cut criterion for discriminating between class orders that allow a high generalisation ability or not. We provide theoretical upper bounds on the class-wise sensitivities of ordinal classifier cascades, which would enable the proposed algorithm to scale up to large collections of phenotypes. The combination of the pairwise training scheme and these bounds lead to a complexity reduction, as the number of base classifier trainings, in a single train-test experiment, for n classes is reduced from (n − 1)n! to (n − 1)n, and the number of cascade constructions and trainings is in the worst case n! but decreases by the number of cascades that do not pass this bound. We could show the utility of our method to identify reflected orderings in experimental evaluations on artificial data and gene expression profiles of developmental and ageing phenotypes.
Results
We evaluated the ability of the CASCADES algorithm to detect reflected orders in feature space based on artificial and existing gene expression datasets (see Methods). For our analysis a linear support vector machine (SVM)18 was chosen as a base classifier for the ordinal cascades due to its superior performance23. The SVM was imported from the LIBSVM library24. Its cost parameter was fixed to a value of one.
The performance of the ordinal cascades as well as their base classifiers were evaluated in 10 × 10 cross-validation (CV) experiments25. The 10 × 10 CV experiments were repeated for all class orders (\(|{\mathscr{Y}}|!\) experiments) and the performance was measured in terms of minimal class-wise sensitivity. All classification experiments were performed with help of the TunePareto software26.
Artificial datasets
We performed experiments on three different kinds of artificial datasets, two of them reflect an ordered sequence of sample clouds in the feature space (d1 and d2) and one does not (d3) (Supplementary Fig. S1). Each dataset comprises \(|{\mathscr{Y}}|=10\) classes (i = 1, …, 10) of 100 samples. The instances of class y are drawn independent and identically distributed from a normal distribution \({\bf{x}} \sim {\mathscr{N}}({{\bf{x}}}_{y},sd)\) in dependence of a class specific centroid my ∈ ℝ2. The standard deviation sd was identical for all classes. Experiments were performed for standard deviations sd ∈ {0.1, 0.2, …, 1.0}.
The analysis on the simple artificial datasets show that our method can distinguish between phenotype orders that are reflected and are not reflected in the two dimensional data. The ordinal assumption is imposed by a common increase in both features. The results for sd = 0.2 are given in Table 1. It can be seen that for d1 and d2 the correct order and its inverse are returned. All other possible orders show a minimal class-wise sensitivity lower than 50%. For d3 (non-ordinal) no order passed the threshold of 50%.
We additionally analysed the performance in dependency of the standard deviation of the artificial data clouds. For the dataset d1 (linear) and d2 (curved) the sensitivities under the correct assumption decline with increasing standard deviations (Supplementary Fig. S2). The corresponding bounds lie above the real sensitivities. For the wrong order, the sensitivity of at least one class drops. In the given example the sensitivities of classes y1 to y5 and the corresponding bounds are mainly identical to those of the correct class order but largest changes can be observed for classes y6 and y7. For the non-ordinal dataset d3 the minimal class-wise sensitivity is zero independent of the standard deviation (Supplementary Fig. S2).
For each dataset and each setting, all 10! ≈ 3.6⋅106 possible class orders are screened and the number of remaining class orders is reported (Supplementary Fig. S3). Datasets d1 and d2 show comparable results. Our method returned at most four candidate cascades for each experiment. With increasing standard deviation the distinction of classes became harder. Candidate cascades could only fulfil lower sensitivity thresholds t. The bounds of all rejected cascades predicted minimal sensitivities below 0.5. With lower thresholds the chance of finding more than two candidate cascades increased. As expected, no candidates were proposed for dataset d3 (non-ordinal). Evaluating the real minimal class-wise sensitivities of the remaining cascades revealed that additional candidates were rejected.
Gene expression datasets
Furthermore, experiments on existing gene expression data were performed (see Methods). We chose ordinal multi-class expression data for which the classes correspond to specific points in time of a process. In three datasets (d4, d5, d7) the classes correspond to developmental stages of Drosophila melanogaster1, Danio rerio2, and Caenorhabditis elegans4. Additionally, d7 was used with a different labelling. This further labelling was not based on stages but based on the point in time at which the sample was taken. The further dataset in our analysis d6 comprises transcriptome samples of human muscles3. The data was categorised into four classes according to the age (in years) of the participants. For all these datasets it is expected that the assumed order based on the order of points in time is reflected within the expression profiles. To test our method (CASCADES algorithm) on real data for which no order is assumed, we included gene expression profiles from cell lines that are derived from 9 different cancer tissue types27.
The results of the real datasets are shown in Table 1. As the performance of the cascade depends on a sensitivity bound which depends only on the performance of the independent base classifiers, first those candidate cascades are reported that pass a sensitivity bound t ≤ 0.5. For the temporal ordinal datasets d4–d8, the CASCADES algorithm rejected at least 83.3% of all candidate cascades. No candidate passed the CASCADES algorithm for the non-ordinal dataset d9. The number of candidates is further depleted by analysing the minimal class-wise sensitivity of the full cascades. For dataset d4, the highest minimal class-wise sensitivity (89.4%) was achieved by the correct class order. It was followed by the correct inverse class order (72.3%) and an incorrect class order (71.0%).
Three candidates passed the CASCADES algorithm for dataset d5. The highest minimal class-wise sensitivity was achieved by two candidate cascades (85.0%). Both reflect the inverse class order. The first one corresponds to the correct inverse class order. The second one assumes an incorrect class order \(embry{o}_{3}\,\prec \,embry{o}_{1}\,\prec \,embry{o}_{2}\). The third candidate achieved a minimal class-wise sensitivity of 54.7%. A general division between the adult and embryo samples can be observed. The order might be explained by the duration between the different states. Whereas all three embryonic samples cover a range of 10 days after birth, the first adult class comprises samples taken at month 3 and the adult2 class is 1–2 years after birth. As a result the order assumption \(embry{o}_{1}\,\prec \,embry{o}_{2}\,\prec \,embry{o}_{3}\) might only be reflected ambiguously.
Four class orders passed the CASCADES algorithm on dataset d6. Two of these candidates dropped out due to a minimal class-wise sensitivity lower than 50.0%. The remaining two achieved minimal class-wise sensitivities of 62.5%. One of these class orders corresponds to the correct class order. The second one proposes a partially consistent class order (\(ag{e}_{4}\prec ag{e}_{3}\)). As age3 and age4 comprise 10 years each and age1 and age2 20 years it can be argued, similar to the cascades of d5. The two classes age3 and age4 might be too similar under the order assumption leading to comparable results.
For dataset d7, the minimal class-wise sensitivity of the correct class order outperformed the performance of other candidate cascades (91.7%). All other candidate cascades achieved a minimal class-wise sensitivity of at most 66.7%. Only one candidate cascade passed the CASCADES algorithm when analysed on the level of points in time (d8). The correct class order gained a minimal class-wise sensitivity of 66.7%, which was achieved for class t2. All other classes achieved class-wise sensitivities of at least 80.0%. Especially this dataset shows that our analysis does not aim at improving the classification performance as much as possible, but rather finding the order that outperforms other orders and this independent of a specific performance, as long as the performance is better than 50%.
Discussion
Ordinal relations between phenotypes are often defined on a semantic level. These relations are assumed to be reflected in a given feature representation without evaluating whether these assumptions hold. It might be the case that independent causes lead to ordinal phenotype characteristics or that the order is not reflected in the chosen feature space because the measured features are not responsible for the observed order.
In this work, we present ordinal classification as an example of a supervised learning task that incorporates semantic relations in the training process of classification models. By constraining the learning process, ordinal classification results in a restricted model class, which is no longer able to separate an arbitrary landscape of classes. This property is used to falsify wrong assumptions on the dependencies of the classes and the chosen feature space.
We provide two theoretical upper bounds on the minimal class-wise sensitivity, which are utilised for accelerating the training of ordinal classifier cascades and allow an exhaustive evaluation of all possible class orders. In this way, ordinal classifier cascades are used as an explorative tool to screen for unknown ordinal dependencies. In our experiments, we give examples for up to 10 different classes resulting in the evaluation of over 3.6 million class orders. Although our algorithm requires pairwise training of the ensemble members, both the bounds and the algorithm are independent of the chosen type of base classifier, the binary training type and might be transferred to alternative ensembles.
Our experiments on the artificial data showed that only if any ordinality is reflected in the feature space possible sets of candidate orders are returned. If there is no ordinal sequence reflected no cascade passes the bound of 0.5. No order was detected for non-ordinal datasets. Always the correct order and its reverse were found as dominant order if cascades were returned for the artificial ordinal datasets.
For all datasets independent of the chosen standard deviation, at least 80% of all candidate cascades could be rejected due to minimal class-wise sensitivities lower than 50%. However, although the procedure can reconstruct the correct class order for all datasets, alternative ordinal class structures might be detected. In our experiments, these alternatives differ from the assumed class order in the position of the last two classes. A reason might be the lower number of constraints for these classes.
For biological applications, we evaluated our method on observable ordinal phenotypes for which a reflection in gene expression levels can be assumed. For three different model organisms we analysed developmental stages characterised by their morphology (D. melanogaster)1, age (Danio rerio)2 and number of C-lineage cells (C. elegans)4. For C. elegans also the sampling time points were used in the analysis.
Our screening procedure allowed to reveal ordinal structures within the gene expression profiles of all three model organisms. The hypothesised time relation or its inverse is always included in the set of best-performing cascades. In three out of those four datasets the hypothesised relation dominates with a performance gap towards all other cascades. This strongly indicates a reflection of these orderings in the profiles.
For the Danio rerio dataset (d5) two cascades rank first before a performance gap. There is a swap observed between the two youngest embryo phenotypes. This might be caused either by a data intrinsic reason that those classes are not distinct enough, as staging by days post fertilization has been shown to exhibit high variation in growth rate28, or by the technical aspect of the lower number of constraints for later classes.
In contrast to the developmental processes, of which the order of stages is tightly regulated by a genetic program5,29, ageing is influenced by multiple factors30. Nevertheless we resulted in comparable results for the dataset that measures age related gene expression changes. On the human muscle adaptation dataset 91.7% of all candidate orders were rejected. Among the remaining two candidates the expected order and only one false positive can be found. For non-ordinal phenotypes, as given by the collection of distinct cancer cell lines, no candidate cascades were observed. This indicates that ordinal relations are not a common phenomenon among multiple phenotypes.
Our method can, however, not only be used to confirm proposed hypotheses but also to explore the feature space for potential ordinal structures. This might become relevant if the relation is not easily accessible due to sampling. In surgery, for example, histologically distinguishable tissue regions can be defined in the same biopsy or in single-cell experiments various cell types are extracted from one sample. Within these feature spaces our procedure allows for screening of total ordinal cascades and additionally of ordinal sub-cascades embedded in a larger set of non-ordinal classes. It can hence be used to screen for intrinsic molecular ordinal structures and hypothesis relational axes, which might not be detected in a standard multi-class analysis.
Methods
We will use following notation throughout the description of the methodology behind the algorithm. An object is represented by a vector of real-valued measurements x = (x(1), …, x(n))T ∈ ℝn. Each object is assumed to be categorisable in one out of \(|{\mathscr{Y}}|\ge 2\) predefined classes \(y\in {\mathscr{Y}}\), where \({\mathscr{Y}}={\{{y}_{i}\}}_{i=1}^{|{\mathscr{Y}}|}\) denotes the space of all class labels. The general classification task will be to identify a function mapping c, a classifier, that allows the accurate prediction of the class labels of new unseen objects \(c\,:\,{{\mathbb{R}}}^{n}\to {\mathscr{Y}}=\{{y}_{1},\ldots ,{y}_{|{\mathscr{Y}}|}\}.\)
As quality measures, we utilise the conditional prediction rates of c. These estimate the probability of classifier c to predict the class label yj for samples of class yi based on a set of test samples \({{\mathscr{X}}}_{i}\). In its basic version, a conditional prediction rate can be calculated as
where \({\mathbb{I}}\)[⋅] denotes the indicator function. Other (re-) sampling strategies might be used for determining conditional prediction rates. However, they will not alter the theoretical characteristics discussed in this work. We distinguish between three types of conditional prediction rates: 1. sensitivities if yi = yj and \({y}_{i},{y}_{j}\in {\mathscr{Y}}\), 2. confusions if yi ≠ yj and \({y}_{i},{y}_{j}\in {\mathscr{Y}}\), 3. external rates if \({y}_{i}\notin {\mathscr{Y}}\) and \({y}_{j}\in {\mathscr{Y}}\).
While (class-wise) sensitivities and confusions build the standard quality measures of a confusion matrix31, the external rates describe the classifiers behaviour on foreign classes. They will especially be of interest when dealing with different label spaces.
In the basic multi-class classification scenario, a classifier is typically adapted in a data-driven training procedure based on a set of training samples \({{\mathscr{S}}}_{tr}={\{({{\bf{x}}}_{i},{y}_{i})\}}_{i=1}^{|{{\mathscr{S}}}_{tr}|}\). The basic assumption of this scenario are pairwise distinct classes \({y}_{1}\ne \ldots \ne {y}_{|{\mathscr{Y}}|},\) which can be separated in the chosen feature space. In the ordinal classification scenario it is additionally assumed that the labels in \({\mathscr{Y}}\) are totally ordered \({y}_{(1)}\prec \,\ldots \,\prec {y}_{(|{\mathscr{Y}}|)}.\) In this context, the symbol \({y}_{(i)}\) denotes the \(i\)th class of the order. We utilise the symbol \(\prec \) to indicate that the order relationship is only known for the label space. It is unclear, if this relationship is reflected by the chosen measurements. Nevertheless, ordinal classifiers rely on this assumption. The order of the classes is utilised for guiding the construction of the decision regions. It is provided as additional information to the training algorithm.
Ordinal classifier cascades
In the following, we will discuss ordinal classifier cascades of type
The cascade hi,j can be seen as a late-aggregation multi-classifier system32, where indices \(1\le i\le j < |{\mathscr{Y}}|\) indicate the base classifiers of the corresponding ensemble \( {\mathcal E} =\{{c}_{(i)},\ldots ,{c}_{(j)}\}\). The members of the ensemble are designed for separating two neighboured classes c(i):ℝn → {y(i),y(i+1)}.
An ordinal cascade will be called a full cascade if it is designed for predicting all labels of the label space \({\mathscr{Y}}\). Full cascades will be denoted by \(h={h}_{1,|{\mathscr{Y}}|-1}\). Other ordinal cascades will be called partial cascades.
The fusion strategy of an ordinal cascade can be interpreted as a sequence of logical conjunctions of its base classifiers
A scheme of this architecture can be found in Fig. 2. For classifying a sample x, the ensemble members c(k)(x) are evaluated sequentially according to the assumed order of classes. If a base classifier c(k)(x) predicts its first class label y(k), the procedure stops and hi,j(x) = y(k). If it predicts class label y(k+1) the sample is passed to the subsequent base classifier c(k+1). This fusion scheme implies following three characteristics on hi,j:
-
1.
Each class y(k), i < k < j + 1 can be predicted by two base classifiers.
-
2.
The lowest class y(i) can only be predicted by the first classifier c(i)(x). The highest classes y(j+1) can only be predicted by the last classifier c(j)(x).
-
3.
A sample x will only be passed to a base classifier c(k)(x), 1 < k ≤ j, if all its predecessors c(l)(x), l < k, decide for their second class y(l+1).
Structure of a full ordinal classifier cascade h. The cascade consists of a fixed order of base classifiers c(i), \(1\le i < |{\mathscr{Y}}|\). A sample x is passed sequentially from one base classifier to another. If a base classifier c(i)(x) predicts class label y(i), the procedure stops and the ensemble h predicts y(i). Otherwise the ensemble h predicts \({y}_{(|{\mathscr{Y}}|)}\).
Training algorithms for ordinal classifier cascades mainly focus on the training of the base classifiers. In the following, we utilise a pairwise inductive training, in which the training set \({{\mathscr{S}}}_{(k)}\) of a base classifier c(k) consists of the samples of classes y(k) and y(k+1)
In a previous study, this type of training showed to induce the highest susceptibility to incorrect assumptions on the class order23.
Upper bounds on class-wise sensitivities
The structural properties of the ordinal classifier cascade allow for the construction of upper limits on their empirical class-wise sensitivities. These bounds are based on the training of the cascade’s base classifiers and postulated in Theorem 1. Although this theorem is formulated for full cascades, the corresponding bounds can directly be applied for partial cascades.
Theorem 1 Let h denote an ordinal classifier cascade \(h:{{\mathbb{R}}}^{n}\to {\mathscr{Y}}=\{{y}_{(1)},\ldots ,{y}_{(|{\mathscr{Y}}|)}\}\) with base classifiers \( {\mathcal E} =\{{c}_{(1)},\ldots ,{c}_{(|{\mathscr{Y}}|-1)}\}\). Let furthermore \({{\mathscr{X}}}_{(i)}\) be a non-empty set of samples of class y(i). Then the sensitivity of h for y(i) is limited by
Proof. The theorem is a direct consequence of Lemmata 1 and 2 (see Supplementary).
Theorem 1 states that the sensitivities of an ordinal classifier cascade h can be upper bounded by several conditional prediction rates of its base classifiers. For class y(i), the sensitivity of the cascade is limited by the corresponding sensitivity of its ith base classifier c(i) (Eq. 4). It is also bounded by the predictions of all previous base classifiers c(k), k < i (Eq. 5). A sample of class y(i) will not be classified correctly, if it is classified as y(k) by c(k). The sensitivity of the cascade for class y(i) is therefore also limited by the conditional prediction rate of c(k) for predicting class label y(k+1) for samples of class y(i). A detailed theoretical proof can be found in the Supplementary.
Detection of ordinal class structures
Ordinal classifier cascades can be used for detecting wrong assumptions about the ordinality of the real class structures. Due to their susceptibility, these classifiers will fail when the real feature structures reflect a different class order or no class order at all. In a screening process, ordinal classifier cascades can be used for revealing unknown ordinal class structures. We have proposed the minimal class-wise sensitivity p* of an ordinal classifier cascade as a measure of the correctness of the assumed class order \({p}^{\ast }={{\rm{\min }}}_{1\le i\le |{\mathscr{Y}}|}{p}_{h}({y}_{(i)}|{{\mathscr{X}}}_{(i)}).\) A sensitivity threshold t ≤ p* is used for determining whether an ordinal class structure can be assumed or not. The criterion can be evaluated for each order of the classes in \({\mathscr{Y}}\).
The findings of Theorem 1 allow an alternative evaluation of this criterion. As a direct consequence of Theorem 1, the value of p* can again be upper bounded by conditional prediction rates of the base classifiers
Ordinal classifier cascades that are based on wrong assumptions about the ordinality of the classes can therefore be sorted out by the training of the corresponding base classifiers. A graphical illustration describing this sorting out based on a four class example and dependent on Eqs 6 and 7 can be found in Supplementary Fig. S4.
Coupled to a pairwise inductive training of the base classifiers (Eq. 3) the bounds of Theorem 1 can reduce complexity of screens for ordinal structures. As the training of a base classifier c(i) is only based on the samples of classes y(i) and y(i+1), it is no longer dependent on the position of the base classifiers within the cascade h. Cascades trained on different orders of \({\mathscr{Y}}\) will therefore consist of common building blocks. The exhaustive training of all \(|{\mathscr{Y}}|!\) cascades, each consisting of \(|{\mathscr{Y}}|-1\) base classifiers, can therefore be accelerated by precalculating and evaluating all possible \((|{\mathscr{Y}}|-1)|{\mathscr{Y}}|\) base classifiers ci,j:ℝn → {yi, yj}. Note that symbols yi, yj and ci,j no longer rely on an assumed class order.
In any case, the complexity of the exhaustive evaluation is mainly determined by the training and evaluation complexity of the base classifiers. A comparison of the precalculation scheme and a de novo calculation of all cascades in dependency on the numbers of classes \(|{\mathscr{Y}}|\) can be found in Table 2. For the presented numbers we assume an evaluation via a single training-test split. For three classes, the de novo strategy already requires twice the number of base classifier trainings and evaluations than the precalculation strategy. For ten classes, the de novo strategy trains more than 3⋅107 base classifiers while the precalculation scheme only demands 90 base classifiers. The number of base classifier trainings and evaluations might be increased by a constant factor if resampling strategies are applied.
The following quality measures are needed for the application of Theorem 1:
Here, FCi,j denotes the class-wise sensitivity of ci,j for predicting its first class label yi. The term SCi,j(r) denotes the conditional prediction rates of ci,j for samples of class yr that are classified as yj. Both quantities can be precalculated and memorised for all binary base classifiers (Table 3).
The CASCADES algorithm
We propose the recursive enumeration scheme \({\rm{CASCADES}}({\mathscr{Y}},{\mathscr{C}},{y}_{i},t)\) for the exhaustive training of all orders of \({\mathscr{Y}}\) (Fig. 3). It can be seen as a filter routine that rejects ordinal cascades that will not achieve a minimal class-wise sensitivity t ≤ p* according to the bounds of Theorem 1. The remaining cascades will be returned as a set of candidates \({\mathscr{C}}\).
CASCADES algorithm for an exhaustive screening of all orders of class labels \(y\in {\mathscr{Y}}\). The function parameters are the set of class labels \({\mathscr{Y}}\), a set of candidate cascades \({\mathscr{C}}\), the threshold t and yi which specifies the class label that was selected in the previous recursion.
The CASCADES algorithm is based on the evaluation of an extended confusion table as shown in Table 3. It will replace the training procedure of each base classifier (training-test split or resampling strategy) by looking up \(|{\mathscr{Y}}|-k\) conditional prediction rates, where k is the base classifiers position within the cascade. As there exist \((\begin{array}{l}|{\mathscr{Y}}|\\ k+1\end{array})\) possibilities of constructing subcascades (prefixes) of k base classifiers, at most \(f(|{\mathscr{Y}}|):=\mathop{\sum }\limits_{k=2}^{|{\mathscr{Y}}|}\,k(\begin{array}{l}|{\mathscr{Y}}|\\ k+1\end{array})\) comparisons are required in a worst case scenario. Nevertheless, this number will rapidly break down by utilising early stopping criteria.
A single cascade is represented as an ordered vector of class labels \(({y}_{(1)},\ldots ,{y}_{(|{\mathscr{Y}}|)})\in {\mathscr{C}}.\) Each candidate cascade is constructed sequentially. It is extended by a new class label in each recursive call of the algorithm. The construction stops, if the performance measures of the current base classifier falls under the chosen threshold t. In this case the candidate cascade is rejected.
The sequential extension of a partial cascade h1,k−1 improves the runtime of the exhaustive search. If the kth (candidate) base classifier does not fulfil the minimal criteria, all full ordinal cascades that utilise h1,k as prefix can be withdrawn. This corresponds to \((|{\mathscr{Y}}|-k-1)!\) full ordinal cascades. A single early stopping will reduce the number of lookups by at least \(f(|{\mathscr{Y}}|-k)\).
The algorithm is initialised with the full set of labels \({\mathscr{Y}}\), an empty set of candidate cascades \({\mathscr{C}}=\varnothing \), the chosen threshold t and yi = ∅. The parameter yi will later on indicate the class label selected in the previous recursion. In each recursion, the class labels \({y}_{j}\in {\mathscr{Y}}\) are tested as possible extensions of the candidate cascades in \({\mathscr{C}}\). If FCi,j ≥ t and \(\forall \,{y}_{r}\in {\mathscr{Y}}:{{\rm{SC}}}_{i,j}(r)\ge t\) the current base classifier ci,j fulfils the bounds on p*. In this case, class label yj can be added to the current candidate cascade and can be removed from the set of remaining labels \({\mathscr{Y}}\). The next base classifier will be chosen by a recursive call CASCADES(\({\mathscr{Y}}\backslash \{{y}_{j}\}\), \({{\mathscr{C}}}_{r}\), yj, t). If the current base classifier does not fulfil the minimal criteria, the corresponding (partial) candidate cascades are erased and an empty set ∅ is returned. All suitable candidate cascades are collected at the end of the recursive call. Although the algorithm CASCADES rejects cascades with too low minimal class-wise sensitivities, the remaining candidates are not guaranteed to fulfil the minimal criterion t ≤ p*. Each of the final candidates must therefore be cross-checked by an evaluation of the full cascade. CASCADES can directly be applied for the evaluation of partial ordinal cascades. By replacing the initial set of class labels \({\mathscr{Y}}\) by a subset \({\mathscr{Y}}\text{'}\subset {\mathscr{Y}}\), the algorithm will evaluate all orders of the class labels in \({\mathscr{Y}}\text{'}\).
Datasets
An overview of the characteristics of all datasets can be found in Supplementary Table S1. The datasets d5–d9 were collected from the gene expression omnibus repository33 (GSE13371, GSE47881, GSE2180, GSE32474) and processed using the robust multi-array average (rma) normalisation as implemented in the affy package34. For d4 the processed data was downloaded.
Linear dataset (d 1)
For a first series of experiments, the centroid of the ith class yi is chosen as \({{\bf{m}}}_{{y}_{i}}={(i,i)}^{T}\). In this way, the class centroids lie on a line.
Curved dataset (d 2)
For the second dataset, the class centroids were chosen depending on their predecessors. \({{\bf{m}}}_{{y}_{i}}={({m}_{{y}_{i}}^{(1)},{m}_{{y}_{i}}^{(2)})}^{T}={({m}_{{y}_{i-1}}^{(1)}+{u}_{i}^{(1)},{m}_{{y}_{i-1}}^{(2)}+{u}_{i}^{(2)})}^{T}\), where \({u}_{i}^{(1)},{u}_{i}^{(2)} \sim {\mathscr{U}}(0.5,2)\). As a starting point \({{\bf{m}}}_{{y}_{0}}={(0,0)}^{T}\) was chosen. This dataset has a curved shape.
Non-ordinal dataset (d 3)
The third artificial dataset is designed to be non-ordinal. The centers of the classes are arranged on a predefined two dimensional grid in the range [1, 4]2 (Supplementary Table S2).
Drosophila melanogaster (d 4)
The drosophila dataset generated by Arbeitman et al.1 consists of gene expression profiles of the fruit fly Drosophila melanogaster. These profiles consist of 4028 measurements and were collected at different points in time during the life cycle of the model organism. They can be categorised according to the developmental stages of Drosophila melanogaster: \(embryo\prec larva\prec pupa\prec adult.\) Overall the dataset contains profiles for 31 embryos, 10 larvae, 18 pupae and 8 adults. We use the natural order of the developmental stages as ordinal class labels for our experiment.
Danio rerio (d 5)
The dataset collected by Toyama et al.2 consists of gene expression profiles of the pineal glands of zebrafish (Danio rerio). The expression profiles were collected at five different time points: \(embry{o}_{1}\prec embry{o}_{2}\prec embry{o}_{3}\)\(\prec adul{t}_{1}\prec adul{t}_{2},\) where embryo1-embryo3 were collected 3, 5 and 10 days after birth and adult1 and adult2 were collected at an age of 3 months and 1–2 years. The dataset comprises 12–15 samples for each class. The age of the samples will be used as class order.
Human muscle adaptation (d 6)
Philips et al.3 have compared the transcriptome of human muscle cells before and after 20 weeks of supervised resistance-exercise training (RET). The corresponding dataset consists of paired gene expression profiles. For our experiments, the data was categorised into four classes according to the age (in years) of the participants: \(ag{e}_{1}\prec ag{e}_{2}\prec ag{e}_{3}\prec ag{e}_{4}.\) The class labels denote age intervals of \([20;40)\) years (18 samples), \([40;60)\) years (38 samples), \([60;70)\) years (16 samples) and \([70;80)\) years (16 samples). In order to avoid overoptimistic results, we ensured that the profiles of a subject are not used for training and testing the classifier simultaneously.
Caenorhabditis elegans (d 7 and d 8)
Baugh et al.4 analysed the influence of the homeodomain protein PAL-1 of the C-lineage-specific gene regulatory network in the model organism C. elegans. They gathered gene expression data of samples of wild-type embryos and mutant embryos with additional C blastomeres, as well as on samples of mutants without any C blastomeres. For our experiments we used data of the C-cell-free organisms, taken at 10 points in time after the 4-cell-stage of the embryo. We labelled these samples in two different ways. In the first experiment (d7) the samples were labelled according to the developmental stages proposed in the original publication: \(stag{e}_{1}\prec stag{e}_{2}\prec stag{e}_{3}\prec stag{e}_{4}\prec stag{e}_{5},\) where 0 and 23 minutes samples were merged in the stage1 class, 41 and 53 minutes samples in stage2, and samples taken at 66, 83 and 101 minutes after the 4-cell stage in the class stage3. stage4 only consists of samples taken at 122 minutes, and stage5 contains time points 143 and 186 minutes. In the second experiment (d8), the points in time were analysed solely: \({t}_{1}\,\prec \,{t}_{2}\,\prec \,{t}_{3}\,\prec {t}_{4}\,\prec \,{t}_{5}\,\prec \,{t}_{6}\,\prec {t}_{7}\,\prec \,{t}_{8}\,\prec \,{t}_{9}\,\prec \,{t}_{10}.\)
Various cancer cell lines (d 9)
Pfister et al.27 collected gene expression profiles from cell lines that derived from 9 different cancer tissue types (breast (15 samples), central nervous system (18 samples), colon (21 samples), leukemia (18 samples), melanoma (26 samples), non-small cell lung (26 samples), ovarian (21 samples), prostate (6 samples), renal (23 samples)). In contrast to d1–d8, the classes of this dataset are not assumed to fulfil an ordinal relationship as each group originates from a different tissue type: line1 ≠ line2 ≠ line3 ≠ line4 ≠ line5 ≠ line6 ≠ line7 ≠ line8 ≠ line9.
Data Availability
The drosophila dataset is available from http://flygenome.yale.edu/Lifecycle/. The other datasets are available from the GEO repository https://www.ncbi.nlm.nih.gov/gds: GSE13371, GSE47881, GSE2180, GSE32474.
References
Arbeitman, M. N. et al. Gene expression during the life cycle of Drosophila melanogaster. Sci. 297, 2270–2275, https://doi.org/10.1126/science.1072152 (2002).
Toyama, R. et al. Transcriptome analysis of the zebrafish pineal gland. Dev. Dyn. 238, 1813–1826, https://doi.org/10.1002/dvdy.21988 (2009).
Phillips, B. E. et al. Molecular networks of human muscle adaptation to exercise and age. PLOS Genet. 9, 1–15, https://doi.org/10.1371/journal.pgen.1003389 (2013).
Baugh, L. R. et al. The homeodomain protein PAL-1 specifies a lineage-specific regulatory network in the C. elegans embryo. Dev. 132, 1843–1854, https://doi.org/10.1242/dev.01782 (2005).
Long, C., Li, W., Liang, P., Liu, S. & Zuo, Y. Transcriptome comparisons of multi-species identify differential genome activation of mammals embryogenesis. IEEE Access 99, 1–1, https://doi.org/10.1109/ACCESS.2018.2889809 (2018).
Kearney, P. E., Hayward, R. B. & Meijer, H. Evolutionary trees and ordinal assertions. Algorithmica 25, 196–221, https://doi.org/10.1007/PL00008274 (1999).
Guénoche, A. Ordinal properties of tree distances. Discret. Math. 192, 103–117, https://doi.org/10.1016/S0012-365X(98)00068-5 (1998).
Kannan, S. & Warnow, T. Tree Reconstruction from Partial Orders. SIAM J. on Comput. 24, 511–519, https://doi.org/10.1137/S0097539793252195 (1995).
Buchholz, M. et al. Transcriptome analysis of microdissected pancreatic intraepithelial neoplastic lesions. Oncogene 24, 6626–6636, https://doi.org/10.1038/sj.onc.1208804 (2005).
Feldmann, U. & Steudel, I. Methods of ordinal classification applied to medical scoring systems. Stat. Medicine 19, 575–586, doi:10.1002/(SICI)1097-0258(20000229)19:4<575::AID-SIM357>3.0.CO;2-A (2000).
Bender, R. & Grouven, U. Ordinal logistic regression in medical research. J. Royal Coll. Physicians Lond. 31, 546–51 (1997).
Cardoso, J. S., da Costa, J. F. P. & Cardoso, M. J. Modelling ordinal relations with svms: An application to objective aesthetic evaluation of breast cancer conservative treatment. Neural Networks 18, 808–817, https://doi.org/10.1016/j.neunet.2005.06.023 (2005).
Bishop, C. Pattern Recognition and Machine Learning (Springer, New York, 2006).
Hastie, T., Tibshirani, R. & Friedman, J. H. The Elements of Statistical Learning (Springer, New York, 2001).
Webb, A. R. Statistical Pattern Recognition, 2nd edn (John Wiley & Sons Ltd., Chichester, 2002).
Fix, E. & Hodges, J. L. Discriminatory analysis: Nonparametric discrimination: Consistency properties. Tech. Rep. Project 21-49-004, Report Number 4, USAF School of Aviation Medicine, Randolf Field, Texas (1951).
Breiman, L., Friedman, J. H., Olshen, R. A. & Stone, C. J. Classification and Regression Trees. The Wadsworth statistics/probability series (Chapman and Hall/CRC, Boca Raton, 1984).
Vapnik, V. N. Statistical Learning Theory (John Wiley & Sons Ltd., New York, 1998).
Frank, E. & Hall, M. A simple approach to ordinal classification. In Raedt, L. D. & Flach, P. (eds) Machine Learning: ECML 2001 - 12th European Conference on Machine Learning. Proceedings, vol. 2167, 145–156, https://doi.org/10.1007/3-540-44795-413 (Springer, Berlin, 2001).
Rivest, R. L. Learning decision lists. Mach. Learn. 2, 229–246, https://doi.org/10.1007/BF00058680 (1987).
Kestler, H. A., Lausser, L., Lindner, W. & Palm, G. On the fusion of threshold classifiers for categorization and dimensionality reduction. Comput. Stat. 26, 321–340, https://doi.org/10.1007/s00180-011-0243-7 (2011).
Meyer, L. H. et al. Early Relapse in ALL Is Identified by Time to Leukemia in NOD/SCID Mice and Is Characterized by a Gene Signature Involving Survival Pathways. Cancer Cell 19, 206–217, https://doi.org/10.1016/j.ccr.2010.11.014 (2011).
Lattke, R., Lausser, L., Müssel, C. & Kestler, H. A. Detecting ordinal class structures. In Schwenker, F., Roli, F. & Kittler, J. (eds) Multiple Classifier Systems (MCS 2015), vol. 9132, 100–111, https://doi.org/10.1007/978-3-319-20248-89: (Springer International Publishing, Cham, 2015).
Chang, C.-C. & Lin, C.-J. LIBSVM: A library for support vector machines. ACM Transactions on Intell. Syst. Technol. 2, 27:1–27:27, https://doi.org/10.1145/1961189.1961199 (2011).
Japkowicz, N. & Shah, M. Evaluating Learning Algorithms: A Classification Perspective (Cambridge University Press, New York, 2011).
Müssel, C., Lausser, L., Maucher, M. & Kestler, H. A. Multi-objective parameter selection for classifiers. J. Stat. Softw. 46, 1–27, https://doi.org/10.1007/1179085329 (2012).
Pfister, T. D. et al. Topoisomerase I levels in the NCI-60 cancer cell line panel determined by validated ELISA and microarray analysis and correlation with indenoisoquinoline sensitivity. Mol. Cancer Ther. 8, 1878–1884, https://doi.org/10.1158/1535-7163.MCT-09-0016 (2009).
Parichy, D. M., Elizondo, M. R., Mills, M. G., Gordon, T. N. & Engeszer, R. E. Normal table of postembryonic zebrafish development: Staging by externally visible anatomy of the living fish. Dev. Dyn. 238, 2975–3015, https://doi.org/10.1002/dvdy.22113 (2009).
Dong, P. & Liu, Z. Shaping development by stochasticity and dynamics in gene regulation. Open Biol. 7, 170030, https://doi.org/10.1098/rsob.170030 (2017).
Rodríguez-Rodero, S. et al. Aging Genetics and Aging. Aging Dis. 2, 186–195, http://www.aginganddisease.org/EN/abstract/article_147277.shtml (2011).
Zuo, Y.-C. et al. Predicting peroxidase subcellular location by hybridizing different descriptors of Chou’ pseudo amino acid patterns. Anal. Biochem. 458, 14–19, https://doi.org/10.1016/j.ab.2014.04.032 (2014).
Lorena, A. C., de Carvalho, A. C. P. L. F. & Gama, J. M. P. A review on the combination of binary classifiers in multiclass problems. Artif. Intell. Rev. 30, 19–37, https://doi.org/10.1007/s10462-009-9114-9 (2009).
Edgar, R., Domrachev, M. & Lash, A. E. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 30, 207–210, https://doi.org/10.1093/nar/30.1.207 (2002).
Gautier, L., Cope, L., Bolstad, B. M. & Irizarry, R. A. affy–analysis of Affymetrix GeneChip data at the probe level. Bioinforma. 20, 307–315, https://doi.org/10.1093/bioinformatics/btg405 (2004).
Acknowledgements
The research leading to these results has received funding from the German Research Foundation (DFG, SFB 1074 project Z1, and GRK 2254 HEIST), and the Federal Ministry of Education and Research (BMBF, Gerontosys II, Forschungskern SyStaR, id 0315894 A; e:Med, SYMBOL-HF, id 01ZX1407A; conFirm, id 01ZX1708C) all to H.A.K.
Author information
Authors and Affiliations
Contributions
L.L. designed the algorithm and conceived the experiments, L.M.S. and L.-R.S. performed data acquisition and conducted the experiments, L.L., L.M.S. and L.-R.S. analysed the results, L.L., R.S. and F.S. implemented the algorithm, L.L. and F.S. drafted the manuscript, H.A.K. supervised and guided the study. L.L., L.M.S., L.-R.S. and H.A.K. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lausser, L., Schäfer, L.M., Schirra, LR. et al. Assessing phenotype order in molecular data. Sci Rep 9, 11746 (2019). https://doi.org/10.1038/s41598-019-48150-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48150-z
This article is cited by
-
Permutation-invariant linear classifiers
Machine Learning (2024)
-
Detecting Ordinal Subcascades
Neural Processing Letters (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.