Abstract
Ultrasonication is widely used to exfoliate two dimensional (2D) van der Waals layered materials such as graphene. Its fundamental mechanism, inertial cavitation, is poorly understood and often ignored in ultrasonication strategies resulting in low exfoliation rates, low material yields and wide flake size distributions, making the graphene dispersions produced by ultrasonication less economically viable. Here we report that few-layer graphene yields of up to 18% in three hours can be achieved by optimising inertial cavitation dose during ultrasonication. We demonstrate that inertial cavitation preferentially exfoliates larger flakes and that the graphene exfoliation rate and flake dimensions are strongly correlated with, and therefore can be controlled by, inertial cavitation dose. Furthermore, inertial cavitation is shown to preferentially exfoliate larger graphene flakes which causes the exfoliation rate to decrease as a function of sonication time. This study demonstrates that measurement and control of inertial cavitation is critical in optimising the high yield sonication-assisted aqueous liquid phase exfoliation of size-selected nanomaterials. Future development of this method should lead to the development of high volume flow cell production of 2D van der Waals layered nanomaterials.
Similar content being viewed by others
Introduction
Since the discovery of graphene1 and the characterisation of its properties1,2,3, it has shown huge potential in applications ranging from energy storage4, solar cells5, printed electronics6, composite fillers7, and water filtration membranes8. The discovery of graphene has also generated significant research interest into other 2D van der Waals layered nanomaterials, such as the family of metallic and semiconducting transition metal dichalcogenides9. One of the main challenges limiting the further applications and commercialisation of graphene and other 2D layered materials is that it remains difficult to produce large quantities of high-quality flakes with application specific size distributions. Many of the useful properties of graphene are indeed dependent on the lateral size and thickness of individual flakes3,5; for example, graphene flakes with large lateral dimensions (>1 μm) are used in polymer composites10 and conductive graphene inks6, flakes with smaller lateral dimensions (<1 μm) are employed in ceramic composites11, and graphene quantum dots (<100 nm) are found in photovoltaics, fuel cells, and catalysis applications12.
One of the most scalable graphene production routes is to exfoliate it from graphite in the liquid phase using ultrasonication13,14, shear mixing15, wet-jet milling16, or microfluidisation17. Although some liquid phase exfoliation methods report graphene yields as high as 100%16,17, a recent study demonstrated that the majority of commercially available graphene had less than 10% graphene content. This was due to the flakes containing more than 10 layers, which makes them nano graphite rather than multilayer graphene according to the ISO standard on graphene nomenclature18. Due to the wide flake size distributions (nm-μm) that are characteristic of liquid phase exfoliation techniques extensive centrifugation is often required to both narrow the size distribution and remove large graphitic flakes. Although cascade centrifugation has been shown to be effective in isolating narrow size distributions, it is time intensive, lowers the bulk concentration of the dispersed graphene and can inadvertently remove thinner graphene flakes with larger lateral dimensions as it separates flakes by their length19. As liquid phase exfoliation techniques typically produce dispersions with low intrinsic graphene concentrations (~0.1 mg ml−1), centrifugation and re-dispersion is often required to produce graphene dispersions with industrially viable concentrations (≥1 mg ml−1). As such, the removal of large graphene flakes can be unavoidable when producing graphene dispersions.
Despite microfluidisation, shear mixing and wet jet milling demonstrating superior exfoliation rates of pristine graphene flakes15,16,17, ultrasonication is one of the most widely used standalone methods to produce high-quality graphene dispersions, as well as being a complementary processing technique in other graphene production methods. The main limitations of using ultrasonication are its wide flake size distributions, low exfoliation rates, and comparatively low graphene yields. This is due to a poor understanding of the fundamental mechanisms driving graphene exfoliation, and a reliance upon purely empirical parameters such as sonication time13, temperature control20 and nominal electrical input power21 to monitor and develop ultrasonication strategies. Although acoustic cavitation is often suggested as the primary mechanism driving graphene exfoliation during sonication22,23, this has not been experimentally validated, and there have been no efforts to directly control and optimise acoustic cavitation during sonication. Using advanced cavitation metrology tools, we demonstrate that inertial cavitation drives graphene exfoliation during sonication for the first time. Furthermore, a controlled application of inertial cavitation is critical for optimising the sonication-assisted liquid phase exfoliation of graphene, resulting in improved graphene exfoliation rates, as well as a route towards in-situ size control of the graphene flakes. These findings will be instrumental in developing advanced ultrasonication strategies that will increase the large volume production and commercialisation of a wide range of 2D nanomaterials.
Acoustic Cavitation
Acoustic cavitation is the stimulated expansion and collapse of microbubbles in response to an applied acoustic field (Fig. 1a). Sonic baths and sonic horns generate acoustic cavitation by exciting a fluid with continuous or pulsed pressure waves at kHz frequencies. A regime with cavitating bubbles that have long lifetimes is referred to as non-inertial or stable cavitation, whereas inertial cavitation is characterized by short-lived cavitating bubbles which undergo violent and chaotic collapse24. Both types of cavitation exhibit physicochemical effects which are strongly dependent on the properties of the liquid being sonicated (density, viscosity and boiling point) as well as the acoustic field frequency, amplitude and geometry25. Stable cavitation generates short range vortices known as microstreaming, whereas inertial cavitation collapses radiate spherical shockwaves with velocities of up to 4,000 m s−1 with peak pressures of up to 6 GPa26. Intense liquid jets (jetting) with pressures of up to 1 GPa can also be generated during inertial collapse27. In a typical sonication environment, such as a sonic bath or sonotrode, both types of cavitation can exist simultaneously.
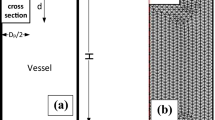
(a) Schematic of the growth and collapse of cavitating bubbles in response to an applied acoustic field and the associated pressure wave. (b) Photograph of the National Physical Laboratory’s 17-litre multi-frequency reference cavitating vessel with transducers around the circumference. (c) The frequency spectrum of cavitation signals arising from stable and inertial cavitation. The presence of harmonic activity is indicative of stable cavitation activity, and the rise in the background noise is indicative of inertial cavitation activity. (d) Ecav and the graphene yield as a function of the pre-amp voltage (the output voltage of a signal generator that was used to drive the reference vessels top row of 21.06 kHz transducers via a 400 W power amplifier). The hashed rectangle represents the pre-amp voltage range over which graphene was produced in this study. The uncertainty in Ecav is associated with the standard deviation of five independent measurements.
In this work, acoustic cavitation was generated by a multi-frequency reference cavitating vessel (Fig. 1b) that can produce stable and reproducible cavitation fields with a well-defined acoustic field distribution28. The acoustic signals that cavitating bubbles emit (Fig. 1c) were measured using a calibrated needle hydrophone. Inertial cavitation was delineated from stable cavitation by quantifying the broadband noise, over a MHz frequency range in which harmonic activity is indistinguishable from the background noise29. This was carried out by measuring the high frequency broadband energy30 (Equation 1), parametrised as \({E}_{cav}\).
where \({V}_{c}(f)\) are the spectral magnitudes measured from the frequency domain cavitation spectra (Fig. 1c) and f1 and f2 are 1.5 MHz and 2.5 MHz, respectively. The inertial cavitation threshold was determined by measuring \({E}_{cav}\) as a function of the nominal input power of the vessel; the measurement protocol is described in the Supplementary Information 1. As shown in Fig. 1d, the inertial cavitation threshold is characterised by a systematic rise in \({E}_{cav}\)29. This occurs above a pre-amp voltage of ~60 mVRMS, which corresponds to a nominal input electrical power of 5 Watts (corresponding to a vessel power density of around 0.3 W L−1).
To study graphene exfoliation arising from the physiochemical effects of acoustic cavitation, samples were produced by sonicating graphite in 28 ml low density polyethylene vials positioned in a region where inertial cavitation activity is intense and localised (Fig. S1.2a). Preliminary experiments found that graphene is first produced only after the onset of the inertial cavitation (Fig. 1d), which demonstrates that the physiochemical effects of inertial cavitation drive graphene exfoliation during ultrasonication. At high pre-amp voltages (high acoustic powers) \({E}_{cav}\) saturates due to cavitation shielding31, where a significant volume fraction of cavitating bubbles dynamically scatter and absorb the acoustic field. As there is a significant drop in the graphene exfoliation rate at high pre-amp voltages, Fig. 1d also suggests that cavitation shielding adversely affects the graphene exfoliation rate, however more work will need to be carried out to experimentally validate this. The highly non-linear nature of inertial cavitation combined with the significant perturbation of the graphene exfoliation rate at high acoustic powers (Fig. 1d) suggests that measurement and control of inertial cavitation is essential when developing sonication methodologies.
Results and Discussion
To explore the role of inertial cavitation on the liquid phase exfoliation of graphene, graphite with a narrow 45–75 μm size distribution (Supplementary Information 2.3), was exfoliated over a range of both pre-amp voltages (shown in Fig. 1c) and sonication times. A low initial graphite concentration (0.2 mg ml−1) was chosen to increase the dispersed graphene yield and minimise the population of the larger graphitic flakes post sonication, ensuring that the graphene size distributions are representative of the acoustic cavitation mechanisms which exfoliated them. As \({E}_{cav}\) is a direct and real time measurement of the inertial cavitation activity, which is the stimulus driving the liquid phase exfoliation of graphene, multiplying \({E}_{cav}\) by the total sonication time, t, quantifies the accumulated dose of inertial cavitation (ICD) experienced by the graphite and graphene flakes during sonication. This method for characterising the accumulated inertial cavitation activity has also featured in medical ultrasound studies employing analogous measurement protocols32,33,34. As the value of \(\,{E}_{cav}\), and therefore ICD is dependent on the waveform capture settings (vertical resolution, timebase and sampling rate), the MHz frequency band over which it is calculated, the frequency response of the hydrophone, and the hardware filtering and amplification in the signal chain (Fig. S1.1), absolute values obtained are arbitrary, though the units of ICD can be considered as volts squared. However, as the \({E}_{cav}\) measurements in this work were carried out using the same measurement protocol, the resultant ICD measurements are directly comparable.
Figure 2a shows that the graphene yield exhibits a power law relationship with ICD, such that there is a linear relationship between the graphene yield and the square root of the ICD (Fig. 2a, inset). As the ICD is a product of \(\,{E}_{cav}\) and sonication time, this square root relationship explains the observation of the graphene yield increasing as a function of the square root of sonication time13. As such, the graphene exfoliation rate can be increased for a given sonication time by increasing the intensity of the inertial cavitation activity, as measured by the square root of ICD (Fig. 2b). However due to cavitation shielding affects the inertial cavitation activity cannot be indefinitely increased by increasing the input power (Fig. 1d). Although the highest graphene yield (~18%) was amongst the highest in the sonication literature, the low initial graphite concentration results in an exfoliation rate which is less optimal for volume production. As such, Fig. 2a demonstrates inertial cavitation activity drives graphene exfoliation during sonication, and the graphene exfoliation rate is dependent on inertial cavitation dose rather than alternative cavitation metrics (Supplementary Information 3).
(a) The graphene yield (after centrifugation) as a function of the ICD and (inset) the square root of the ICD. (b) The graphene exfoliation rate as a function of the square root of the ICD. The symbols in (a) and (b) delineate the data as a function of sonication time, measured in minutes. Representative log-normal plots of (c) graphene length and (d) thickness distributions, measured from a dispersion which was sonicated for 150 minutes at a pre-amp voltage of 140 mVRMS, using SEM and AFM respectively. The uncertainty in the graphene yield is associated with the standard deviation of three graphene yield measurements at each sonication time and the uncertainty in ICD is associated with the standard deviation of five independent high frequency broadband energy measurements.
During exfoliation trials, it was found that sonication times beyond 120 minutes resulted in anomalously high graphene yields that appeared to deviate from the power law relationship with ICD (Fig. S2.5a). This was subsequently found to occur due to the temperature of the water in the LDPE vials increasing during long periods of sonication (Fig. S2.5b), resulting in faster bubble growth rates and therefore a greater frequency of inertial cavitation collapses35. Stable temperatures were maintained over long (150 and 180 minutes) sonication times by using an array of cooling fans to actively cool the vessel. As such, cooling strategies should be carefully considered when developing large volume sonication methodologies to ensure consistent exfoliation. Shorter sonication times, as well as pulsed ultrasonication, may help mitigate temperature increase during sonication.
To quantitatively investigate the evolution of the graphene size distribution as a function of ICD, the length and thickness of the graphene flakes were measured using scanning electron microscopy (SEM) and atomic force microscopy (AFM). The graphene length (Fig. 2c) and thickness (Fig. 2d) distributions were log-normal in shape, implying a multiplicative stochastic fracturing mechanism, whereas a bimodal distribution would be indicative of an erosion process36. Accordingly, it can be concluded that inertial cavitation, which is characterised by stochastic and energetic bubble collapse, fractures graphite/graphene during sonication in a multiplicative stochastic process. Figure 3a,b show that the mean length and thickness of graphene flakes decreases linearly as a function of the square root of the ICD. As the <0.5 μm lateral dimensions of the flakes in the post-sonication precipitate (Fig. S2.4) are significantly smaller than the dimensions of the initial graphite population (45–75 μm), this indicates that the entire initial graphite population has been fractured by the accumulated inertial cavitation activity during sonication. Therefore, during sonication the mean flake size will progressively decrease until the flakes are small enough to be suspended in the solution by the electrostatic repulsion of the adsorbed sodium cholate surfactant molecules. This is demonstrated in Fig. 3c,d, which show that the mean graphene length and thickness are both linearly correlated (Pearson’s R ~0.9) with the graphene yield.
The mean graphene (a) length and (b) thickness as a function of the ICD. The mean graphene (c) length and (d) thickness as a function of the graphene yield. The symbols in (a–d) delineate the data as a function of sonication time, measured in minutes. The graphene exfoliation rate (\({c}_{g}\,{t}^{-1}\)) as function of (e) the mean graphene length and (f) thickness for graphene samples produced with the highest and lowest pre-amp voltages (acoustic powers) used in this work. The uncertainty in the graphene yield and exfoliation rate is associated with the standard deviation of three graphene yield measurements at each sonication time, and the uncertainty in graphene length and thickness is associated with the standard error of ~300 and ~100 measurements, respectively.
The linear relationships between the graphene exfoliation rate and the flake size measurements in Fig. 3e,f indicate that the physical size of the graphite/graphene flakes limits the rate at which it is exfoliated during ultrasonication. This finding demonstrates that inertial cavitation preferentially exfoliates larger flakes during ultrasonication. Such a size preference likely arises from the increased size and/or surface area of larger flakes, which absorb a greater fraction of the shockwave energy generated by nearby inertially cavitating bubbles. Larger graphite flakes will also have an increased probability of containing structural defects such as holes or tears, resulting in a greater fracturing potential. Conversely, there may be a critical size below which graphite cannot be further exfoliated by continued sonication. This has been observed for graphene oxide37 and carbon nanotubes38 and is demonstrated by the saturation in the graphene yield as a function of ICD despite there being an abundance of ~0.5 μm size graphite flakes in the precipitate (Fig. S2.4). As such, inertial cavitation preferentially exfoliates larger ~0.5 μm size graphite flakes, whereas small dispersed flakes are indirectly exfoliated by the physiochemical effects of nearby inertial cavitation activity.
Graphene exfoliation is likely to be driven by a combination jetting, microstreaming and shockwaves during sonication. As jetting is facilitated by nearby extended surfaces, and the maximum size of the graphite used (sieved to 45–75 μm) is much smaller than the resonant size of the cavitating bubbles present in this work (~160 μm at 21.06 kHz), jetting events within the graphene dispersion will significantly decrease in frequency as the mean flake size decreases during sonication. However, jetting may also exfoliate any graphite/graphene flakes in the vicinity of the LDPE vials’ walls. The local shear stresses generated by collapsing bubbles, known as microstreaming, are also unlikely to drive exfoliation as graphene was not observed below the inertial cavitation threshold where microstreaming still occurs. Furthermore, as the speed of microstreaming vortices is proportional to the squared frequency of cavitating bubbles39, the shear forces they generate will be more effective at megasonic frequencies40. Consequently, shockwave exfoliation, which is facilitated by a combination of fracturing41 and the high velocity interparticle collisions42,43, is the most probable exfoliation mechanism during sonication. However, as shockwaves lose more than 50% of their initial energy over the first 25 μm of propagation due to absorption26, and will be attenuated by dispersed graphene flakes (which will increase in density during sonication), graphene exfoliation is most likely facilitated by the shockwaves generated by immediately adjacent inertial cavitation collapse events.
Raman characterisation for material quality and flake size quantification
Spectroscopic trends in the graphene samples were explored using visible Raman spectroscopy. To ensure that the measurements were representative of the graphene dispersions, 120 spectra were collected and averaged across 20 × 20 μm areas of re-stacked graphene films. These films, which were produced using vacuum filtration, contain dense ordered networks (~50% free volume) of nanosheets such that the laser beam (532 nm excitation wavelength) interrogates 100 s of flakes per measurement44. The Raman spectrum of graphene, shown in Fig. 4a, consists of the characteristic G, D, and 2D peaks, which are indicative of many properties including functionalisation, strain, defects, and size distribution44,45,46,47,48. Specifically it has been established that the ratio of the intensity of the D peak (~1320 cm−1) to that of the G peak (~1580 cm−1) is indicative of graphene nanosheet size, and the shape and intensity of the 2D peak (~2700 cm−1) changes as function of graphene nanosheet thickness44,47.
(a) Normalised Raman spectra of graphene dispersions produced at the maxima and minima of the ICD range. (b) The ID/IG ratio as a function of the square root of the ICD. The uncertainty in the ID/IG ratio and the ICD is associated with the standard deviation of three Raman measurements and five broadband energy measurements per sample, respectively.
Figure 4a shows that the ratio of the G peak to the D peak intensity, ID/IG, increases between the minima and maxima of the ICD range. As the inverse of the ID/IG ratio is proportional to the length of graphene flakes44, Fig. 4b shows that the graphene length is decreasing over the ICD range. Although this trend mirrors the quantitative SEM length distributions in Fig. 3a, it is less strongly correlated due to the intentionally low centrifugation speeds used in this work (1000 rpm, 120 g) which were chosen to minimise the effects of centrifugation on the dispersed graphene population. The resulting wide size distributions are evidenced by the large variances in the ID/IG ratio that were observed across each two-dimensional Raman map (Fig. S4.2a). This is likely the cause of the large uncertainties and anomalies in the ID/IG ratio (Fig. 4b) measured from graphene samples produced at a high ICD.
The I2D/IG intensity ratio was ~0.45 across the entire ICD range, suggesting a mean graphene thickness of ~5 layers44, whereas the AFM data suggested a decreasing thickness as a function of ICD (Fig. 3b). This inconsistency is likely due to the large variances in the I2D/IG ratio that were observed across each two-dimensional Raman map (Fig. S4.2b) and suggests that is challenging to get representative Raman data from restacked graphene films containing wide flake size distributions. Alongside graphene size distribution analysis, Raman spectroscopy can also be used to quantify the defects in graphene. Eckmann et al.48 reported that the ratio of the D peak to the D’ peak was dependant on the defect type, such that an ID/ID’ ratio of ~13, ~7, and ~3 indicates the presence of sp3 defects, vacancy defects and, edge defects respectively. As ID/ID’ was found to be ~3 for all graphene samples in this work, this shows that inertial cavitation causes flake scission without introducing a significant number of basal plane defects in graphene during sonication.
Conclusion
In conclusion, by optimising the inertial cavitation dose higher graphene exfoliation rates can be achieved over shorter sonication times, with minimal temperature increases and low nominal input powers. We demonstrate that inertial cavitation preferentially exfoliates larger flakes and that the graphene exfoliation rate and flake dimensions are strongly correlated with, and therefore can be controlled by, inertial cavitation dose; which is a direct measurement of the violent collapses that are indicative of inertial cavitation. During sonication graphite is fractured in a multiplicative process by the shockwaves generated by immediately adjacent inertial cavitation activity; few basal plane defects are incorporated. We also show that temperature increase during sonication can result in inconsistent exfoliation, and therefore temperature control strategies should be employed to ensure consistent ultrasonication. More generally, we show that careful measurement and control of acoustic cavitation is critical when developing efficient ultrasonication methodologies and which by extension can ultimately lead to high volume flow cell production of 2D van der Waals layered nanomaterials.
Methods
Pre-treated and sieved Asbury Carbons fine flake graphite (0.2 mg ml−1) was sonicated in LDPE Nalgene vials (28 ml, Fisher Scientific) with sodium cholate surfactant (3 mg ml−1, Sigma Aldrich). The LDPE vials were sonicated continuously at 21.06 kHz for up to 3 hours in NPL’s multi-frequency reference vessel. After sonication, the graphene dispersions were left to sediment overnight before being centrifuged at 1000 rpm (120 rcf) for 2 hours before being characterised with UV-Vis, AFM, SEM and Raman spectroscopy. The graphene yield is given by \((({c}_{g}/{c}_{gi})\ast 100)\), where \({c}_{g}\) is the graphene concentration that is calculated from UV-Vis spectra, and \({c}_{gi}\) is the concentration of the pre-treated and sieved graphite. Acoustic cavitation measurement details, experimental methodology development, and the graphene characterisation methods are described in detail in the supplementary information.
Data availability
Details of the data and how to request access are available from the University of Surrey Publications Repository.
References
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Lee, C., Wei, X., Kysar, J. W. & Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008).
Balandin, A. A. Thermal properties of graphene and nanostructured carbon materials. Nature Materials 10, 569 (2011).
Raccichini, R., Varzi, A., Passerini, S. & Scrosati, B. The role of graphene for electrochemical energy storage. Nature Materials 14, 271 (2015).
Yin, Z. et al. Graphene‐based materials for solar cell applications. Advanced Energy Materials 4, 1300574 (2014).
Torrisi, F. et al. Inkjet-printed graphene electronics. ACS Nano 6, 2992–3006 (2012).
Stankovich, S. et al. Graphene-based composite materials. Nature 442, 282–286 (2006).
Cohen-Tanugi, D. & Grossman, J. C. Water desalination across nanoporous graphene. Nano letters 12, 3602–3608 (2012).
Nicolosi, N., Chhowalla, M., Kanatzidis, M. G., Strano, M. S. & Coleman, J. N. Liquid exfoliation of layered materials. Science 340, 1226419 (2013).
May, P., Khan, U., O’Neill, A. & Coleman, J. N. Approaching the theoretical limit for reinforcing polymers with graphene. Journal of Materials Chemistry 22, 1278–1282 (2012).
Porwal, H. et al. Effect of lateral size of graphene nano-sheets on the mechanical properties and machinability of alumina nano-composites. Ceram. Int. 42, 7533–7542 (2016).
Zhang, Z., Zhang, J., Chen, N. & Qu, L. Graphene quantum dots: an emerging material for energy-related applications and beyond. Energy & Environmental Science 5, 8869–8890 (2012).
Lotya, M., King, P. J., Khan, U., De, S. & Coleman, J. N. High-concentration, surfactant-stabilized graphene dispersions. ACS Nano 4, 3155–3162 (2010).
Khan, U., O’Neill, A., Lotya, M., De, S. & Coleman, J. N. High‐concentration solvent exfoliation of graphene. Small 6, 864–871 (2010).
Paton, K. R. et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nature Materials 13, 624 (2014).
Castillo, A. E. D. R. et al. High-yield production of 2D crystals by wet-jet milling. arXiv preprint arXiv:1804.10688 (2018).
Karagiannidis, P. G. et al. Microfluidization of graphite and formulation of graphene-based conductive inks. ACS Nano 11, 2742–2755 (2017).
International Organization for Standardization (ISO). Nanotechnologies–Vocabulary–Part 13: Graphene and related two-dimensional (2D) materials. ISO/TS 80004-13:2017 (2017).
Backes, C. et al. Production of highly monolayer enriched dispersions of liquid-exfoliated nanosheets by liquid cascade centrifugation. ACS Nano 10, 1589–1601 (2016).
Kim, J. et al. Direct exfoliation and dispersion of two-dimensional materials in pure water via temperature control. Nature communications 6, 8294 (2015).
Buzaglo, M. et al. Critical parameters in exfoliating graphite into graphene. Physical Chemistry Chemical Physics 15, 4428–4435 (2013).
Ciesielski, A. & Samorì, P. Graphene via sonication assisted liquid-phase exfoliation. Chem.Soc.Rev. 43, 381–398 (2014).
Muthoosamy, K. & Manickam, S. State of the art and recent advances in the ultrasound-assisted synthesis, exfoliation and functionalization of graphene derivatives. Ultrason.Sonochem. 39, 478–493 (2017).
Lauterborn, W., Kurz, T., Geisler, R., Schanz, D. & Lindau, O. Acoustic cavitation, bubble dynamics and sonoluminescence. Ultrason. Sonochem. 14, 484–491 (2007).
Leighton, T. The Acoustic Bubble, Chapter 4. (Academic Press, London, 2012).
Pecha, R. & Gompf, B. Microimplosions: Cavitation collapse and shock wave emission on a nanosecond time scale. Phys. Rev. Lett. 84, 1328 (2000).
Dular, M., Bachert, B., Stoffel, B. & Širok, B. Relationship between cavitation structures and cavitation damage. Wear 257, 1176–1184 (2004).
Wang, L. et al. Towards a reference cavitating vessel Part III—design and acoustic pressure characterization of a multi-frequency sonoreactor. Metrologia 52, 575 (2015).
Hodnett, M. & Zeqiri, B. Toward a reference ultrasonic cavitation vessel: Part 2-Investigating the spatial variation and acoustic pressure threshold of inertial cavitation in a 25 kHz ultrasound field. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on 55, 1809–1822 (2008).
Hodnett, M., Chow, R. & Zeqiri, B. High-frequency acoustic emissions generated by a 20 kHz sonochemical horn processor detected using a novel broadband acoustic sensor: a preliminary study. Ultrason. Sonochem. 11, 441–454 (2004).
Hodnett, M., Choi, M. J. & Zeqiri, B. Towards a reference ultrasonic cavitation vessel. Part 1: Preliminary investigation of the acoustic field distribution in a 25 kHz cylindrical cell. Ultrason. Sonochem. 14, 29–40 (2007).
Robertson, J. & Becker, S. Influence of acoustic reflection on the inertial cavitation dose in a Franz diffusion cell. Ultrasound Med. Biol. 44, 1100–1109 (2018).
Chen, W., Matula, T. J., Brayman, A. A. & Crum, L. A. A comparison of the fragmentation thresholds and inertial cavitation doses of different ultrasound contrast agents. J. Acoust. Soc. Am. 113, 643–651 (2003).
Hwang, J. H., Tu, J., Brayman, A. A., Matula, T. J. & Crum, L. A. Correlation between inertial cavitation dose and endothelial cell damage in vivo. Ultrasound Med. Biol. 32, 1611–1619 (2006).
Plesset, M. S. Temperature effects in cavitation damage. Journal of Basic Engineering 94, 559–563 (1972).
Kouroupis-Agalou, K. et al. Fragmentation and exfoliation of 2-dimensional materials: a statistical approach. Nanoscale 6, 5926–5933 (2014).
Liscio, A. et al. Evolution of the size and shape of 2D nanosheets during ultrasonic fragmentation. 2D Materials 4, 025017 (2017).
Hennrich, F. et al. The mechanism of cavitation-induced scission of single-walled carbon nanotubes. The Journal of Physical Chemistry B 111, 1932–1937 (2007).
Grieser, F. et al. Sonochemistry and the Acoustic Bubble, Chapter 3 (Elsevier, 2015).
Brems, S. et al. Nanoparticle removal with megasonics: a review. ECS Journal of Solid State Science and Technology 3, N3010–N3015 (2014).
Krasyuk, I. et al. Investigation of the spall strength of graphite using nano-and picosecond laser pulses. 653, 012002
Doktycz, S. J. & Suslick, K. S. Interparticle collisions driven by ultrasound. Science 247, 1067–1069 (1990).
Prozorov, T., Prozorov, R. & Suslick, K. S. High velocity interparticle collisions driven by ultrasound. J. Am. Chem. Soc. 126, 13890–13891 (2004).
Backes, C. et al. Spectroscopic metrics allow in situ measurement of mean size and thickness of liquid-exfoliated few-layer graphene nanosheets. Nanoscale 8, 4311–4323 (2016).
Malard, L., Pimenta, M., Dresselhaus, G. & Dresselhaus, M. Raman spectroscopy in graphene. Physics Reports 473, 51–87 (2009).
Pimenta, M. et al. Studying disorder in graphite-based systems by Raman spectroscopy. Physical Chemistry Chemical Physics 9, 1276–1290 (2007).
Ferrari, A. C. & Basko, D. M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nature Nanotechnology 8, 235–246 (2013).
Eckmann, A. et al. Probing the nature of defects in graphene by Raman spectroscopy. Nano Letters 12, 3925–3930 (2012).
Acknowledgements
This work was supported by the U.K. National Measurement System (NMS) under the innovation R&D programme and by the U.K. Engineering and Physical Sciences Research Council (EPSRC) via the Centre for Doctoral Training in Micro and Nano Materials and Technology at the University of Surrey. The authors would like to thank Dr. B. Zeqiri, Dr. A. Pollard, Dr. K. Paton, Dr A. Wain, Dr. A. Sesis and Ms. E. Legge for useful discussions and technical assistance in sample preparation, characterisation and data analysis.
Author information
Authors and Affiliations
Contributions
P.T. carried out the graphene production and analysis work. M.H., R.D. and J.D.C. supervised the project. M.H. advised on the use of NPL’s multi-frequency reference cavitation vessel and assisted in interpreting acoustic cavitation measurement data. All authors contributed to the interpretation of the results and the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
Aspects of the work presented here have been included on a pending patent application GB1812056.8 which has been filed by NPL Management Limited. The Authors declare no other financial or non-financial competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Turner, P., Hodnett, M., Dorey, R. et al. Controlled Sonication as a Route to in-situ Graphene Flake Size Control. Sci Rep 9, 8710 (2019). https://doi.org/10.1038/s41598-019-45059-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-45059-5
This article is cited by
-
Experimental comparison of the effects of the two designed probes for exfoliation of graphene by sonication
Scientific Reports (2024)
-
Microfluidization technique for graphene exfoliation: An overview and recent progress
Journal of Nanoparticle Research (2024)
-
A high-yield and size-controlled production of graphene by optimizing fluid forces
Journal of Materials Science (2023)
-
A review of low-cost approaches to synthesize graphene and its functional composites
Journal of Materials Science (2023)
-
Recent advances of the graphite exfoliation processes and structural modification of graphene: a review
Journal of Nanoparticle Research (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.