Abstract
The interaction of light with nanometer-sized solids provides the means of focusing optical radiation to sub-wavelength spatial scales with associated electric field enhancements offering new opportunities for multifaceted applications. We utilize collective effects in nanoplasmas with sub-two-cycle light pulses of extreme intensity to extend the waveform-dependent electron acceleration regime into the relativistic realm, by using 106 times higher intensity than previous works to date. Through irradiation of nanometric tungsten needles, we obtain multi-MeV energy electron bunches, whose energy and direction can be steered by the combined effect of the induced near-field and the laser field. We identified a two-step mechanism for the electron acceleration: (i) ejection within a sub-half-optical-cycle into the near-field from the target at >TVm−1 acceleration fields, and (ii) subsequent acceleration in vacuum by the intense laser field. Our observations raise the prospect of isolating and controlling relativistic attosecond electron bunches, and pave the way for next generation electron and photon sources.
Similar content being viewed by others
Introduction
The collective response of electrons in a nanomaterial to intense few-cycle (<5 fs) laser pulses1 enables unprecedented spatio-temporal control over electron dynamics2,3 and electron emission4. Sub-cycle control becomes feasible by manipulating the waveform of the incident field, e.g. by changing the carrier-envelope phase (CEP)5. At laser intensities below the damage threshold of the nanomaterial, the nanoscale localization of electromagnetic fields has become a versatile tool for fundamental research6 as well as applications7,8, including nanoscale electron accelerators, where the accelerating near-field reaches a few-GVm−1 resulting in electron kinetic energies in the keV level9,10,11,12 for intensities below 1014 Wcm−2. When driven by a waveform-controlled few-cycle laser13, the near-field acceleration can lead to isolated electron bunches14. While the incident laser radiation is characterized by its maximum amplitude \({E}_{L,0}\), angular frequency \({\omega }_{L}\) or wavelength \({\lambda }_{L}\) and CEP \({\phi }_{CEP}\), the evanescent near-field can be characterized by a decay length \({l}_{d}\) describing its exponential fall-off away from the surface – see Supplementary Materials (SM). For wavelength-sized particles, the scattering of light can be understood by the Mie theory, where the near-field distribution for spherical and cylindrical nanostructures is size-dependent, and its maximum amplitude follows the classical Mie angular dependence. These angles are about 90° off-axis for small targets (≪λL) in the dipole regime, and tilt towards the laser propagation direction for wavelength-sized objects4. The motion of a free electron born under these conditions in a linearly polarized laser field is described by a “quivering” amplitude of \({l}_{q}=e{E}_{L,0}/({m}_{e}{\omega }_{L}^{2})\) and an average energy corresponding to the ponderomotive energy \({U}_{p}={m}_{e}{c}^{2}\sqrt{1+{a}_{0}^{2}/2}-1\), where e and me are the electron charge and mass, c is the speed of light in vacuum and \({a}_{0}=|e{E}_{L,0}/({m}_{e}{\omega }_{L}c)|={[{I}_{L}({{\rm{W}}{\rm{c}}{\rm{m}}}^{-2}){\lambda }_{L}^{2}({\mu {\rm{m}}}^{2})/1.37\times {10}^{18}]}^{1/2}\) is the normalized vector potential of the laser with intensity IL. Recently, sub-cycle electron emission has been reported6,15 in the low intensity regime (a0 ≪ 1), when the emitted electron leaves the accelerating near-field within a half oscillation, i.e. ld/lq ≪ 1. Here, the traditional quivering picture breaks down and the energy scaling differs substantially from the ponderomotive prediction.
On the other hand, highly intense pulses (a0 > 1, i.e. IL > 1018 Wcm−2) from TW-PW lasers generate MeV-GeV femtosecond electron bunches16,17,18,19,20 in gas targets or keV-MeV electrons21,22,23,24 from solid or overdense plasma targets. Furthermore, direct vacuum laser acceleration (VLA)25,26,27,28,29,30 utilizing these lasers has also been proposed due to its accelerating field, >1 TVm−1, significantly exceeding that of low-density plasma accelerators (≈0.1 TVm−1). Only the sub-cycle confinement of these relativistic interactions31, where the electron oscillatory velocities are comparable to the speed of light, would generate sub-fs electron pulses32,33, providing even isolated bunches with quasi-single-cycle lasers34,35. However, energy limitation of the necessary few-cycle laser technology has so far restricted the attosecond control to non-relativistic interactions36. Nanostructure-assisted interaction37,38,39 and electron acceleration40,41 has been hardly accessible to high-intensity TW and not to PW lasers due to their long duration (>20 fs) and poor high-dynamic-range temporal contrast in the ps to ns range that modifies or even destroys the target before the peak of the pulse. Former experiments generating relativistic electrons40,41 utilized surface plasmon (SP) polaritons on gratings and thus prohibiting the generation of electron bunches in the attosecond regime. On the other hand, predictions for localized SPs1 in nanoplasmas are very promising35 for a0 ≫ 1 including novel features such as intensity dominance over the final electron directionality, appearance of attosecond MeV electron bunches, or enlargement of the skin depth \(({\delta }_{p}^{\ast })\). Since in relativistic plasmas \({l}_{d}/{l}_{q}\propto {a}_{0}^{-3/2}\), the sub-cycle emission is expected at a larger extent (see SM). In this work, we gain new insight on the sub-cycle nature as well as electric field dependence on the nanoscale electron acceleration. The experimental findings are supported by 3D particle-in-cell (PIC) simulations. We find a two-step mechanism, where high-charge electron pulses are emitted and pre-accelerated in the sub-cycle near-field of a sub-wavelength-sized plasma formed originally from a tungsten nanotip, and subsequently further accelerated in vacuum by the laser field.
Results
Relativistic nanoplasmas
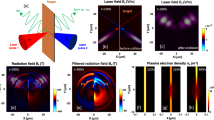
In our experiments electron emission was studied by tightly focusing a laser pulse [full-width-at-half-maximum (FWHM) spot diameter \({\sigma }_{{\rm{FWHM}}}=1.22\) µm] with an estimated temporal contrast of 1017 from the 16 TW, sub-5 fs Light Wave Synthesizer 20 system (see SM) with p-polarization on the tip of a nano-needle (electric field is perpendicular to the needle as shown in Supplementary Fig. S1), which was replaced for each laser shot (see Fig. 1a). Most of the electron emission took place perpendicularly to the needle in the laser polarization plane and was measured by two scintillating screens (see SM), SL and SR (see Fig. 1b), covering an angle of almost ±90° off the laser propagation direction and a third screen ST along the needle axis. Figure 1c shows an average of the angular distributions at an ultra-relativistic peak intensity of I0 ≈ 6 × 1019 Wcm−2, consisting of multi-10 pC divergent electron bunches propagating about \({\theta }_{\mathrm{Left},\mathrm{Right}}\approx \pm \,25^\circ \) off the laser axis and Fig. 1d presents peaked electron spectra with careful background subtraction (background is plotted with dashed gray line) extending up to 7–9 MeV measured in 40° with a dipole magnet. It is expected that electrons with even higher energy are propagating in 25° direction. Similarly, divergent lower-charged beams were measured on ST, and furthermore, the emission was highly sensitive to polarization as shown in Supplementary Fig. S1.
Experimental setup and basic electron beam properties. (a) Magnified image of a nano-needle (AFM probes, ©Bruker). (b) The laser pulse is tightly focused onto a tungsten nano-needle and the generated electron beams are detected by scintillating screens SL and SR. (c) Electron angular distribution averaged over 46 shots at of I0 ≈ 6 × 1019 Wcm−2 showing two highly divergent electron lobes. The black dashed lines mark the maximum of the emission on both screens. Due to spatial limitation of SR the electron emission angle is referenced to SL, peaking on average about \({\theta }_{{\rm{Left}}}\approx -\,25^\circ \). (d) Two typical single-shot electron spectra (after subtracting the background, which is plotted with dashed gray line), reaching energies beyond the ponderomotive energy, \({U}_{p}\approx 1.2\) MeV. The two black horizontal bars indicate the resolution at the given electron energies.
Intensity-dominated interaction
The detected electron charge \({N}_{{\rm{Left}}}\) and emission direction \({\theta }_{{\rm{Left}}}\) were studied as a function of target radius R and laser intensity IL by changing the pulse duration. During the scans, the angular divergence of the electron beams remained similar to that in Fig. 1c. \(|{\theta }_{{\rm{Left}}}|=|{\theta }_{{\rm{Left}}}|({I}_{L},\,R)\) and \({N}_{{\rm{Left}}}={N}_{{\rm{Left}}}({I}_{L})\) are shown in Fig. 2a,b, respectively. The classical Mie regime is recovered when shooting at \({I}_{L}\approx {10}^{17}\) Wcm−2, after chirping the pulses. At lower intensities the emission angle \({\theta }_{{\rm{Left}}}\) shifts towards 90°, reaching a maximum deviation of ≈70°, which matches the theoretical Mie angle of a 100 nm < Reff < 200 nm radius target (see SM). The target size was scanned in two different ways: (i) shifting the target out of focus (Z-scan), so that the spatially expanded laser beam interacts with a larger portion of the target (green star in Fig. 2a, where \(R\approx 6{R}_{{\rm{tip}}}\)) at a lower intensity \({I}_{L}\approx {10}^{18}\) Wcm−2 determined by the laser divergence; and (ii) focusing to a thicker part of the needle (blue triangle in Fig. 2a, where \(R\approx 10{R}_{{\rm{tip}}}\)). In both cases, the interaction with a larger target resulted in a more forward-directed electron emission: \(|{\theta }_{{\rm{Left}}}({R}_{1})| > |{\theta }_{{\rm{Left}}}({R}_{2})|\), for \({R}_{1} < {R}_{2}\), regardless of the laser intensity as observed in Fig. 2a. These findings clearly indicate that some characteristic Mie features, i.e. that a larger target results in an electron emission towards the laser propagation direction, are still valid at relativistic intensities32 and the target size is still nanometric during the interaction. Furthermore, Fig. 2b shows charges up to 90 pC, which scale with intensity as \(N\propto {I}_{L}^{0.66\pm 0.21}\), similar to previous theoretical studies42. It also puts our results in perspective with respect to other reported experiments using few-cycle lasers at 6 orders-of-magnitude lower intensity on isolated nanoparticles4.
Intensity and target-size dependent electron beams. (a) Emission angle of electrons \(|{\theta }_{{\rm{Left}}}|\) as a function of intensity, which is controlled by changing the pulse duration, i.e. chirping the laser pulses (full red square: unchirped, full black squares: chirped pulses). Emission angle dependence on target size by aiming at a thicker part of the needle (blue triangle) as well as on target size and intensity by shifting the target out of focus (Z-scan, green star). Simulated emission angles35 (open gray circles) by changing the laser energy (see Methods). Dashed lines correspond to Mie angles at the given radii. (b) Emitted charge measured on SL (full squares) as a function of the peak laser intensity in the chirp scan. It follows a scaling of \({I}_{L}^{0.66\pm 0.21}\) (fit: red line), similar to previous results using nano-spheres at 1–3 × 1013 Wcm−2 (full triangles)4, i.e. at \({10}^{-6}{I}_{0}\) with a scaling of \({I}_{L}^{0.85}\) (fit: green line). Emitted charge from 3D PIC simulations (open circles), following a similar growth of \({I}_{L}^{0.73}\) (fit: gray line).
Waveform-dependent relativistic electron emission
The waveform of the few-cycle driving laser pulses determines the asymmetry between the observables such as N or θ. The electron yield asymmetry parameter is defined as \({A}_{N}({\phi }_{CEP})=[{\tilde{N}}_{{\rm{Left}}}({\phi }_{CEP})-{N}_{{\rm{Right}}}({\phi }_{CEP})]/[{\tilde{N}}_{{\rm{Left}}}({\phi }_{CEP})+{N}_{{\rm{Right}}}({\phi }_{CEP})]\) (see SM) and Fig. 3a presents the measured \({A}_{N}({\phi }_{CEP})\) with simultaneously observed CEP values for each of the laser shots (46 in total). The electron yield as well as the direction of the electron beam as a function of the CEP oscillated in an anti-correlated (within error bars, see SM) and sinusoidal way in the polarization plane reaching a maximum asymmetry amplitude of 0.18 and 7°, respectively, with a period of 2π. These results clearly demonstrate an unprecedented waveform dependence of the entire electron bunch properties in the relativistic interaction, even without any energy filtering.
Waveform controlled electron emission. (a) Measured (full squares) and simulated (open circles) charge asymmetry parameter with fits as a function of the incoming laser CEP. (b) Measured emission angle \({\theta }_{{\rm{Left}}}\) and (c) simulated emission angles θ with fits as a function of the CEP.
Discussion
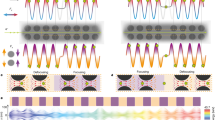
3D particle-in-cell (PIC) simulations (see SM) were performed to gain a deeper understanding of the electron emission physics. The overall mechanism relies on a 2-step process, somewhat similar to that in ref.21: (1) relativistic electron emission by the enhanced near-field and (2) VLA-type acceleration of these electrons by the high intensity laser pulse in vacuum. Well before the laser pulse reaches the nanotip, the increasing laser intensity turns it into plasma. Although free electrons would quiver with lq ≈ 1 μm amplitude at the peak of the laser field, the space-charge force of the ions suppresses this oscillation. When the incident laser light couples with the plasmonic field at a later time instant T = t1, the localized enhanced near-field component directed into the target reaches its maximum value of ≈1.3E0 as depicted in Fig. 4a. This net field pulls a slab of plasma electrons of thickness \({\delta }_{p}^{\ast }\) strongly outwards at about 90° with respect to the laser propagation direction. The charge of the extracted bunch scales42 as \(N\propto {E}_{L}{\delta }_{p}^{\ast }\propto {I}_{L}^{0.75}\), in agreement with the observations in Fig. 2b. The emission interval is limited to 300 as due to the temporally varying localized SP field and mirrored on the y > 0 half-plane after each laser half-cycle32. The amplitude of the outward scattering near-field is reduced due to the screening effect of the density gradient from the newly born outward-propagating electron bunch itself.
Simulation and analysis of the two-step interaction process. (a) First step: Normalized electron density of the nanotarget (grayscale) and normalized electric field (color arrows) during the extraction of an isolated electron bunch (marked with black ellipse) from the target by the near-field at 90° off the laser axis at time T = t1; and its oblique acceleration in the near-field at \(T={t}_{1}+1.3\,{\rm{f}}{\rm{s}}\). (b) Second step: Normalized electron density (grayscale) and electric field (color arrows) during the vacuum laser acceleration of the tracked isolated bunch at \(T={t}_{1}+3.3\,{\rm{f}}{\rm{s}}\). (c) Electron energy and propagation angle evolution as a function of the bunch distance to the target surface \({s}_{{\rm{bunch}}}\) and as a function of time. (d) Electron energy after approximately one Rayleigh length of propagation at \(T={t}_{1}+14.4\) fs. Inset: energy spectra of the individual electron pulses.
After surpassing the target’s electrostatic potential (≈3 MeV at \({s}_{{\rm{bunch}}}=100\) nm distance from the target surface), the directly-emitted bunch will not return to the surface43 and experiences the near-field (on average 10 TVm−1) up to ≈500 nm (a few ld) and gains a maximum energy of 5 MeV. In this region the propagation direction of electrons, plotted in Fig. 4c, is oblique to the laser axis (see Fig. 4a at \(T={t}_{1}+1.3\,{\rm{f}}{\rm{s}}\)) and resembles that of the near-fields (see Supplementary Fig. S2). Around \({s}_{{\rm{bunch}}}=500\) nm, the first step comes to an end. Hence, the near-field “passes the baton” to the laser for subsequent acceleration in a second phase as indicated for \({s}_{{\rm{bunch}}} > 500\) nm in Fig. 4c. The whole emission is naturally in the sub-half-cycle regime6, i.e. the electrons are not rescattered after their emission, because the strong plasmon field (as shown in Supplementary Fig. S3) boosts their energy to relativistic values within a few ld (see Supplementary Fig. S2).
One optical cycle later, as shown in Fig. 4b, the dense electron bunch is slightly delayed with respect to the laser electric field and sits between two transverse laser field extrema21,23. It is then synchronized to and accelerated further by the laser, which has a maximum accelerating field strength of \({E}_{VLA}\approx 3\,{{\rm{T}}{\rm{V}}{\rm{m}}}^{-1}\). The details of vacuum laser acceleration mechanism are beyond the scope of this paper and will be the subject of a future publication. The propagation angle strongly deviates from the original Mie angle (Fig. 2a) mainly due to the forward acceleration by “surfing” on the travelling laser wave35, as summarized in Fig. 4c. Although the synchronization prevails well beyond the ZR, i.e. the Rayleigh length, the maximum gained energy of an electron is \({\rm{\Delta }}E\approx 5\) MeV at \({s}_{{\rm{bunch}}}\approx {Z}_{R}\) as shown in Fig. 4d at \(T={t}_{1}+14.4\) fs. The final maximum energy is almost 10 MeV, in good agreement with Fig. 1d. Such a high accelerating field \({E}_{VLA}\), is a direct consequence of reaching the VLA regime through a sub-cycle relativistic injection. The magnitude of the overall acceleration field is experimentally supported by the total energy gain and the focusing conditions: \({\rm{\Delta }}E/{Z}_{R}\approx 9\,{\rm{M}}{\rm{e}}{\rm{V}}/4.8\,\mu {\rm{m}}\approx 2\) TVm−1. A longer simulation up to 30 μm from the target was performed to confirm the main observations, supporting that the maximum electron energy is unchanged and the attosecond bunch duration is retained even at this propagation distance.
Simulations confirmed that a significant pre-plasma with finite extension was not present in the experiment (see Supplementary Fig. S4). Further PIC simulations at different peak laser intensities support the simple considerations that the first step final energy scales as \({a}_{0}{l}_{d}\propto \sqrt{{a}_{0}}\) whereas the post acceleration step scales with \({a}_{0}\) (see SM), similar to previous studies29,42,44. The emission in the first step is intrinsically waveform dependent. As observed in Fig. 3a, about 15–20% of the total emitted charge oscillates periodically. Most importantly, this asymmetry allows the tracked bunch (labeled “2”) to be isolated via energy-filtering. The emitted bunches to left and right do not follow symmetric trajectories, as expected from ponderomotive scattering27,45, but the strongest half-cycle bends a bunch (2) the closest to the laser axis in agreement with the experimental observations in Fig. 3b. This bunch has the highest energy, but its charge is lower than the sum of the other two bunches (1, 3) at the other side, which explains the anti-correlation between Fig. 3a,b. An unprecedented degree of control is thus introduced by access to the CEP, which can be used to manipulate the angular distribution.
It should be noted that the acceleration gradients in the present work are an order of magnitude higher than in ref.21 thanks to the much tighter focusing and much shorter laser pulse duration which ensures an isolated bunch. Furthermore, using mass-limited nanotargets we have an extra degree of control over the experiment by selecting the size of these targets and thus the charge in electron bunch and indirectly also its energy spread.
In conclusion, we demonstrated relativistic electrons accelerated in the sub-cycle regime from nanoplasmas. Our targets preserve their nanometric scale due to unprecedented temporal structure of the intense pulses. Our experimental findings are consistent with a two-step acceleration process, where the nanoscale near-field and laser vacuum acceleration lead to attosecond MeV electron pulses. This technology provides record-breaking accelerating electric fields strengths beyond TVm−1 exceeding all other methods. Our proof-of-principle experiments pave the way to the next generation table-top electron sources and provide new high-energy photon sources. Potential applications by combining ultra-strong few-cycle laser pulses with isolated attosecond relativistic electron bunches could provide a source of energetic X-ray radiation with attosecond pulse durations via Thomson scattering with a counter-propagating laser pulse46 very near to the nanotip. Using mass-limited targets the short electron bunch duration can be longer preserved, which possibly allows X-ray generation via free-electron laser seeding or highest temporal and very high spatial resolution via electron diffraction.
Methods
Near-field description
The near-field around the nanotarget is described as \({E}_{NF}(r,t)=\alpha {E}_{L}(t)\,\exp \,(\,-\,r/{l}_{d})\), where α is the enhancement factor, ld is the decay length, r is the distance from the surface and \({E}_{L}(t)\) is the laser field. The latter is \({E}_{L}(t)={E}_{L,0}(t)\cos ({\omega }_{L}t+{\phi }_{CEP})\), where \({E}_{L,0}(t)\) is the field envelope with a maximum amplitude of \({E}_{L,0}\), \({\omega }_{L}=2\pi c/{\lambda }_{L}\) is the laser angular frequency, c is the speed of light, λL is the laser wavelength, and \({\phi }_{CEP}\) is the CEP.
Optical parametric synthesizer
Laser pulses from the 10 Hz repetition rate Light Wave Synthesizer 20 (LWS-20) optical parametric synthesizer system47 contain, from 70–75 mJ at the laser, after losses in the beam steering system 40 mJ energy on-target. Its spectrum spans from 580 up to 1020 nm with a central wavelength of 740 nm. It was focused on the tip of a new nano-needle for each shot. The tight focusing using an off-axis parabolic mirror with an f/1 resulted in a FWHM spot diameter of σFWHM = 1.22 μm and a short measured Rayleigh length of ZR ≈ 4.8 μm, see Supplementary Fig. S5. The compressed pulse duration is reaching sub-5 fs and the corresponding laser peak intensity is \({I}_{0}\approx 6\times {10}^{19}\) Wcm−2. The laser is equipped with a CEP phase meter for single-shot CEP tagging48. Moreover, nano-scale solid experiments require a very clean laser pulse (excellent high-dynamic-range temporal intensity contrast) of around 7–8 orders of magnitude to avoid early pre-plasma generation that significantly extends the effective target size due to the typical target damage thresholds of ~1013 Wcm−2 for few-cycle pulses49. The LWS-20 has ultrahigh contrast that is estimated to be 1017 outside the pump temporal window50, i.e. about 30 ps or more before and after the main pulse and 107 at 2 ps. This is sufficient to fulfill the previous requirement, which has been carefully proven not to alter the target at all in the experiments.
Setup for basic characterization of the relativistic electrons
The electron angular distribution was measured with two absolutely calibrated BIOMAX scintillating screens51, SL and SR, which were placed a few cm’s away from the target. SL covered an angle range of [−90°:5°] and a smaller circular screen SR, [15°:75°] as shown in Fig. 1b. Parameters such as electron directionality \({{\theta }}_{{\rm{Left}}}\) or full electron yield were only measured in SL due to spatial limitations of SR. For the sake of completeness, a third screen ST was placed on top of the target covering a solid angle of ≈2.5 sr. The electron spectrum was measured by placing a dipole magnet about 3 cm away from the target after removing SL about 40° off-axis due to spatial limitations in the setup. It had an entrance aperture of 5 × 10 mm2 corresponding to about 60 msr solid angle and its exit was covered with scintillating screens which were imaged to a CCD outside the chamber. The influence of X-rays on measured electron charge values by SL, SR and ST screens was excluded by comparing the charge obtained in the spectrometer, where the scintillating screen was parallel to the target direction, with the corresponding solid angle on SL.
CEP dependent charge asymmetry parameter
The asymmetry parameter AN is defined by the integrated electron angular distributions in an equal solid angle to the left and right sides. Thus, integration spans from −75°(75°) to −15°(15°) on SL (SR). This corresponds to the whole measured charge on the right side \({N}_{{\rm{Right}}}\), but only a fraction of \({N}_{{\rm{Left}}}\), i.e. \({\tilde{N}}_{{\rm{Left}}}\), due to the reduced solid angle.
PIC simulations
The 3D PIC simulations were performed with the code EPOCH52. The target was a hemisphere with a diameter of 400 nm placed on top of a truncated cone whose upper circular base surface had the same diameter. The density of the target was 100 times overdense (\({n}_{e}=100{n}_{c}\)). It was irradiated by a Gaussian 4.5 fs (FWHM) laser pulse with polarization perpendicular to the target and a FWHM focal spot diameter of 1.22 µm, reaching a peak intensity of 5 × 1019 Wcm−2 and a0 = 4.5 at 740 nm wavelength. The results of Fig. 4, Supplementary Figs S2, S4, 6–7 were obtained with a cosine pulse (\({\phi }_{CEP}=0\)), while Supplementary Fig. S3 with a sine pulse (\({\phi }_{CEP}=-\,\pi /2\)). The simulation box was 12 × 12 × 8 µm−3 divided in ΔX = 15.63 nm, ΔY = 11.78 nm, ΔZ = 15.63 nm. A full simulation time of 40 fs and a total pseudoparticle number of 2.7 × 108 were used. Further simulations at different peak laser intensities were also performed while typically keeping the other parameters unchanged. A longer simulation, lasting 160 fs and involving a larger box of 12 × 12 × 18 µm−3 divided in ΔX = 15.63 nm, ΔY = 11.78 nm, ΔZ = 15.63 nm, was performed to follow the accelerated bunches in vacuum up to 35 µm distance from the target. The scaling of the electron bunch charge with intensity was simulated by varying laser energy instead of pulse duration as in the experiments due to limited computational resources. A comparison of the two intensity control methods was tested with 45 fs pulse duration and 5 × 1019 Wcm−2 intensity delivering similar angular distribution and charge. Only the CEP triggered asymmetry was not present, see Supplementary Fig. S8.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Stockman, M. I. Nanoplasmonics: past, present, and glimpse into future. Opt. Express 19, 22029–22106 (2011).
Krüger, M., Schenk, M. & Hommelhoff, P. Attosecond control of electrons emitted from a nanoscale metal tip. Nature 475, 78–81 (2011).
Zherebtsov, S. et al. Controlled near-field enhanced electron acceleration from dielectric nanospheres with intense few-cycle laser fields. Nat. Phys. 7, 656–662 (2011).
Süßmann, F. et al. Field propagation-induced directionality of carrier-envelope phase controlled photoemission from nanospheres. Nat. Commun. 6, 7944, https://doi.org/10.1038/ncomms8944 (2015).
Krausz, F. & Ivanov, M. Attosecond Physics. Rev. Mod. Phys. 81, 163, https://doi.org/10.1103/RevModPhys.81.163 (2009).
Herink, G., Solli, D. R., Gulde, M. & Ropers, C. Field-driven photoemission from nanostructures quenches the quiver motion. Nature 483, 190–193 (2012).
Zhang, R. et al. Chemical mapping of a single molecule by plasmon-enhanced raman scattering. Nature 498, 82–86 (2013).
Tang, L. et al. Nanometre-scale germanium photodetector enhanced by a near-infrared dipole antenna. Nat. Photonics 2, 226–229 (2008).
Hoffrogge, J. et al. Tip-based source of femtosecond electron pulses at 30 keV. J. Appl. Phys. 115, 094506, https://doi.org/10.1063/1.4867185 (2014).
Fennel, T. et al. Plasmon-enhanced electron acceleration in intense laser metal-cluster interactions. Phys. Rev. Lett. 98, 143401, https://doi.org/10.1103/PhysRevLett.98.143401 (2007).
Dombi, P.- et al. Observation of few-cycle, strong-field phenomena in surface plasmon fields. Opt. Express 18, 24206, https://doi.org/10.1364/OE.18.024206 (2010).
Li, S. & Jones, R. R. High-energy electron emission from metallic nano-tips driven by intense single-cycle terahertz pulses. Nat. Commun. 7, 13405, https://doi.org/10.1038/ncomms13405 (2016).
Baltuška, A. et al. Attosecond control of electronic processes by intense light fields. Nature 421, 611–615 (2003).
Ciappina, M. F. et al. Attosecond physics at the nanoscale. Rep. Prog. Phys. 80, 054401, https://doi.org/10.1088/1361-6633/aa574e (2017).
Park, D. J. et al. Strong field acceleration and steering of ultrafast electron pulses from a sharp metallic nanotip. Phys. Rev. Lett. 109, 244803, https://doi.org/10.1103/PhysRevLett.109.244803 (2012).
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267–270 (1979).
Buck, A. et al. Real-time observation of laser-driven electron acceleration. Nat. Phys. 7, 543–548 (2011).
Lundh, O. et al. Few femtosecond, few kiloampere electron bunch produced by a laser-plasma accelerator. Nat. Phys. 7, 219–222 (2011).
Leemans, W. et al. Multi-GeV electron beams from capillary-discharge-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 113, 245002, https://doi.org/10.1103/PhysRevLett.113.245002 (2014).
Xu, J. et al. Dynamics of electron injection in a laser-wakefield accelerator. Phys. Plasmas 24, 083106, https://doi.org/10.1063/1.4996906 (2017).
Thévenet, M. et al. Vacuum laser acceleration of relativistic electrons using plasma mirror injectors. Nat. Phys. 12, 355–360 (2016).
Mordovanakis, A. G. et al. Quasimonoenergetic electron beams with relativistic energies and ultrashort duration from laser-solid interactions at 0.5 kHz. Phys. Rev. Lett. 103, 235001, https://doi.org/10.1103/PhysRevLett.103.235001 (2009).
Tian, Y. et al. Electron emission at locked phases from the laser-driven surface plasma wave. Phys. Rev. Lett. 109, 115002, https://doi.org/10.1103/PhysRevLett.109.115002 (2012).
Brandl, F. et al. Directed acceleration of electrons from a solid surface by sub-10-fs laser pulses. Phys. Rev. Lett. 102, 195001, https://doi.org/10.1103/PhysRevLett.102.195001 (2009).
Esarey, E., Sprangle, P. & Krall, J. Laser acceleration of electrons in vacuum. Phys. Rev. E 52, 5443–5453 (1995).
Varin, C. & Piché, M. Relativistic attosecond electron pulses from a free space laser-acceleration scheme. Phys. Rev. E 74, 045602(R), https://doi.org/10.1103/PhysRevE.74.045602 (2006).
Hartemann, F. V. et al. Nonlinear ponderomotive scattering of relativistic electrons by an intense laser field at focus. Phys. Rev. E 51, 4833–4843 (1995).
Popov, K., Bychenkov, V. Y., Rozmus, W. & Sydora, R. Electron vacuum acceleration by a tightly focused laser pulse. Phys. Plasmas 15, 013108, https://doi.org/10.1063/1.2830651 (2008).
Pang, J. et al. Subluminous phase velocity of a focused laser beam and vacuum laser acceleration. Phys. Rev. E 66, 066501, https://doi.org/10.1103/PhysRevE.66.066501 (2002).
Wong, L. J. et al. Laser-induced linear-field particle acceleration in free space. Sci. Rep. 7, 11159, https://doi.org/10.1038/s41598-017-11547-9 (2017).
Mourou, G., Tajima, T. & Bulanov, S. Optics in the relativistic regime. Rev. Mod. Phys. 78, 309–371 (2006).
Liseykina, T. V., Pirner, S. & Bauer, D. Relativistic attosecond electron bunches from laser illuminated droplets. Phys. Rev. Lett. 104, 095002, https://doi.org/10.1103/PhysRevLett.104.095002 (2010).
Popov, K. I., Bychenkov, V. Y., Rozmus, W., Sydora, R. D. & Bulanov, S. S. Vacuum electron acceleration by tightly focused laser pulses with nanoscale targets. Phys. Plasmas 16, 053106, https://doi.org/10.1063/1.3139255 (2009).
Naumova, N. et al. Attosecond electron bunches. Phys. Rev. Lett. 93, 195003, https://doi.org/10.1103/PhysRevLett.93.195003 (2004).
Di Lucchio, L. & Gibbon, P. Relativistic attosecond electron bunch emission from few-cycle laser irradiated nanoscale droplets. Phys. Rev. ST Accel. Beams 18, 023402, https://doi.org/10.1103/PhysRevSTAB.18.023402 (2015).
Borot, A. et al. Attosecond control of collective electron motion in plasmas. Nat. Phys. 8, 416–421 (2012).
Purvis, M. A. et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nat. Photon. 7, 796–800 (2013).
Cerchez, M. et al. Generation of laser-driven higher harmonics from grating targets. Phys. Rev. Lett. 110, 065003, https://doi.org/10.1103/PhysRevLett.110.065003 (2013).
Ceccotti, T. et al. Evidence of resonant surface-wave excitation in the relativistic regime through measurements of proton acceleration from grating targets. Phys. Rev. Lett. 111, 185001, https://doi.org/10.1103/PhysRevLett.111.185001 (2013).
Fedeli, L. et al. Electron acceleration by relativistic surface plasmons in laser-grating interaction. Phys. Rev. Lett. 116, 015001, https://doi.org/10.1103/PhysRevLett.116.015001 (2016).
Sgattoni, A., Fedeli, L., Cantono, G., Ceccotti, T. & Macchi, A. High field plasmonics and laser-plasma acceleration in solid targets. Plasma Phys. Control. Fusion 58, 014004, https://doi.org/10.1088/0741-3335/58/1/014004 (2016).
Andreev, A. A. & Platonov, K. Y. Generation of electron nanobunches and short-wavelength radiation upon reflection of a relativistic-intensity laser pulse from a finite-size target. Opt. Spectrosc. 114, 788–797 (2013).
Paulus, G. G., Becker, W., Nicklich, W. & Walther, H. Rescattering effects in above-threshold ionization: a classical model. J. Phys. B: At. Mol. Opt. Phys. 27, L703, https://doi.org/10.1088/0953-4075/27/21/003 (1994).
Kozák, M., Eckstein, T., Schönenberger, N. & Hommelhoff, P. Inelastic ponderomotive scattering of electrons at a high-intensity optical travelling wave in vacuum. Nat. Phys. 14, 121–125 (2018).
Malka, G. & Miquel, J. L. Experimental confirmation of ponderomotive-force electrons produced by an ultrarelativistic laser pulse on a solid target. Phys. Rev. Lett. 77, 75–78 (1996).
Khrenikov, K. et al. Tunable All-Optical Quasimonochromatic Thomson X-Ray Source in the Nonlinear Regime. Phys. Rev. Lett. 114, 195003, https://doi.org/10.1103/PhysRevLett.114.195003 (2015).
Rivas, D. E. et al. Next generation driver of intense attosecond sources. Sci. Rep. 7, 5224, https://doi.org/10.1038/s41598-017-05082-w (2017).
Wittmann, T. et al. Single-shot carrier-envelope phase measurement of few-cycle laser pulses. Nat. Phys. 5, 357–362 (2009).
Summers, A. M. et al. Optical damage threshold of Au nanowires in strong femtosecond laser fields. Opt. Express 22, 4235–4246 (2014).
Mikhailova, J. M. et al. Ultrahigh-contrast few-cycle pulses for multipetawatt-class laser technology. Opt. Lett. 36, 3145–3147 (2011).
Buck, A. et al. Absolute charge calibration of scintillating screens for relativistic electron detection. Rev. Sci. Instrum. 81, 033301, https://doi.org/10.1063/1.3310275 (2010).
Extendable PIC Open Collaboration project UK and http://ccpforge.cse.rl.ac.uk/gf/project/epoch/.
Acknowledgements
The authors acknowledge the support of Ferenc Krausz. This work is supported by DFG Project Transregio TR18, The Munich Centre for Advanced Photonics (MAP) and by the Euratom research, training programme 2014–2018 under grant agreement No. 633053 within the framework of the EUROfusion Consortium. L.V. acknowledges the support by a grant from the Swedish Research Council (2016-05409). M.F.K. is grateful for support by the European Union via the ERC grant ATTOCO (no. 307203).
Author information
Authors and Affiliations
Contributions
D.E.C. built the experimental setup with help from L.H. and together with T.M.O. conducted the experiments; L.V. and J.S. planned the experiments and L.V. supervised the project; L.d.L and P.G. performed the simulations and helped D.E.C., T.M.O., M.F.K. and L.V. to interpret the experimental data and the simulations; D.E.C. and L.V. wrote the manuscript with input from other coauthors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cardenas, D.E., Ostermayr, T.M., Di Lucchio, L. et al. Sub-cycle dynamics in relativistic nanoplasma acceleration. Sci Rep 9, 7321 (2019). https://doi.org/10.1038/s41598-019-43635-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-43635-3
This article is cited by
-
Attosecond and nano-Coulomb electron bunches via the Zero Vector Potential mechanism
Scientific Reports (2024)
-
Unforeseen advantage of looser focusing in vacuum laser acceleration
Communications Physics (2024)
-
Intense laser interaction with micro-bars
Scientific Reports (2023)
-
Vacuum laser acceleration of super-ponderomotive electrons using relativistic transparency injection
Nature Communications (2022)
-
Towards isolated attosecond electron bunches using ultrashort-pulse laser-solid interactions
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.