Abstract
Identifying potential protein-ligand interactions is central to the field of drug discovery as it facilitates the identification of potential novel drug leads, contributes to advancement from hits to leads, predicts potential off-target explanations for side effects of approved drugs or candidates, as well as de-orphans phenotypic hits. For the rapid identification of protein-ligand interactions, we here present a novel chemogenomics algorithm for the prediction of protein-ligand interactions using a new machine learning approach and novel class of descriptor. The algorithm applies Bayesian Additive Regression Trees (BART) on a newly proposed proteochemical space, termed the bow-pharmacological space. The space spans three distinctive sub-spaces that cover the protein space, the ligand space, and the interaction space. Thereby, the model extends the scope of classical target prediction or chemogenomic modelling that relies on one or two of these subspaces. Our model demonstrated excellent prediction power, reaching accuracies of up to 94.5–98.4% when evaluated on four human target datasets constituting enzymes, nuclear receptors, ion channels, and G-protein-coupled receptors . BART provided a reliable probabilistic description of the likelihood of interaction between proteins and ligands, which can be used in the prioritization of assays to be performed in both discovery and vigilance phases of small molecule development.
Similar content being viewed by others
Introduction
Exploring protein-ligand interactions is essential to drug discovery and chemical biology in navigating the space of small molecules and their perturbations on biological networks. Such interactions are essential to developing novel drug leads, predicting side-effects of approved drugs and candidates, and de-orphaning phenotypic hits. Therefore, the accurate and extensive validation of protein-ligand interactions is central to drug development and disease treatment. Experimentally determining and analysing protein-ligand interactions can be challenging1,2, often involving complex pull-down experiments and orthogonal validation assays. Therefore, multiple efforts have been dedicated to developing rapid computational strategies to predict protein-ligand interactions for prioritizing experiments and streamlining the experimental deconvolution of the interaction space. For example, docking simulations, in which the 3D-structure of the target is used to evaluate how well individual candidate ligands bind to a structure, have been productively applied to identify novel interactions between clinically relevant targets and small molecules3,4. Appreciably, docking simulations are unfeasible when 3D structures of targets (e.g., those derived from crystallization and X-ray diffraction experiments) are not available, as exemplified by many G protein-coupled receptors (GPCRs), which are membrane-spanning proteins that are inherently difficult to crystallize. Conversely, ligand-based methods (e.g., fingerprint similarity searching, pharmacophore models, and machine learning approaches) are increasingly applied in research and development for the prediction of on- and off-target interactions, but often require large amounts of available ligand data to achieve the desired predictive accuracy. Another widely used computational strategy is text mining, which uses databases of scientific literature such as PubMed5. Text mining relies on keyword searching and is limited in its capability to detect novel bindings. The process can be further complicated by the redundancy of compound or protein names in the literature6.
Recently, to circumvent the shortcomings of the ligand- and target-based methods and to benefit from all available information, computational chemogenomics (or proteochemometric modelling) has emerged as an active field of predictive modelling. Here, the study of protein-ligand interactions simultaneously combines the protein target and ligand information with machine learning approaches to provide valuable insights into the interaction space. For example, several methods exist that are capable of predicting target protein families and binding sites based on the known structures of a set of ligands7,8,9,10. However, with scant information about the actual proteins, predicted interactions are, at best, only between the known ligands and different protein families. Some approaches, which are target-centric, make full use of the protein features, but fail to predict interactions of orphan ligands as the latter have no known links to any proteins11. Several methods have been proposed to consider both the protein sequences and ligand chemical structures simultaneously in prediction12,13,42.
We hypothesised that chemogenomic modelling could profit from including not only information on the ligand and protein similarity but also explicitly on the pharmacological interaction space and hence the relationship between the ligands and the proteins (Fig. 1a). The combined information is composed of three sub-spaces, the shape of which resembles a bow tie, hence the name bow-pharmacological space. It covers a protein space that encodes protein sequence features, a ligand space that contains the fingerprints of chemical compounds, and an interaction space, coded by known interactions that connect the protein and ligand. Furthermore, we describe a novel prediction model by applying Bayesian Additive Regression Trees (BART) and other machine learning methods on these combined features from protein, ligand, and interaction information. Feature selection as well as subsampling experiments highlighted the utility of all the available descriptor subspaces and hence of the bow-pharmacological space (BOW space) newly developed here. Compared to other classical machine learning algorithms, the BART algorithm outperformed all tested methods and demonstrated good prediction power (94–99% accuracy on different datasets). Furthermore, BART can provide a quantitative description of the likelihood of predicted interactions and thereby provide an important measure of predictive uncertainty. In addition to retrospective analysis, we also highlight one exemplary prediction for a novel ligand of the KIF11 protein that was successfully validated using a docking simulation and subsequently confirmed by a crystallography study executed by an independent research group.
Bow-pharmacological space. (a) The bow-pharmacological space spans three subspaces: protein space in blue, ligand space in green, and interaction space in pink. Filled circles represent proteins and triangles represent ligands. Protein–ligand pairs of known interactions from published databases are denoted as “known” whereas those not curated in the databases are denoted as “new.” Solid lines indicate known interactions in the interaction space while dashed lines illustrate three kinds of unknown interactions (① unknown protein with known ligand, ② known protein with unknown ligand, ③ unknown protein with unknown ligand). (b) Features in bow-pharmacological space.
Results
Prediction based on bow-pharmacological space and BART
To predict the likelihood of protein-ligand interactions, information of both the known interactions and the non-interactions (positive and negative data) are required to build the training and testing datasets. For each protein-ligand pair (interaction or non-interaction), we coded 439 features in the bow-pharmacological space (Fig. 1). Based on these features, a statistical model was built to predict whether there was an interaction between a protein and a ligand. Due to the complexity of multiple possible interactions between proteins and ligands, we applied the Bayesian Additive Regression Trees (BART) to build the prediction model. BART is a Bayesian “sum-of-trees” model in which each tree is constrained by a regularized prior to be a weak learner, and fitting and inference are accomplished via an iterative Bayesian backfitting MCMC algorithm that generates samples from a posterior. BART enables full posterior inference including point and interval estimates of the unknown regression function as well as the marginal effects of potential predictors14 (see Methods).
To benchmark our approach against work by other researchers, we constructed our prediction models on published datasets by Yamanishi et al.12, Bleakley et al.13, Cao et al.15, Jacob et al.16 and He et al.17. When these datasets were combined, the numbers of enzymes, ion channels, GPCRs, and nuclear receptors were 664, 204, 95, and 26, respectively; the numbers of known drugs were 445, 210, 223, and 54, respectively; and the numbers of known interactions were 2926, 1476, 635, and 90, respectively.
The robustness of our model was assessed by a ten-fold cross-validation. We evaluated our model performances for sensitivity, specificity, accuracy, average receiver operating characteristic (ROC) curve, and the area under the curve (AUC) (see Methods). The accuracy of our model was 94.5%, 96.7%, 98.4%, and 95.6% for all four groups of proteins (enzymes, ion channels, GPCRs, and nuclear receptors). On the same dataset, our method performed better than other existing prediction methods that are based on chemical and genomic spaces12, protein sequence and drug topological structures15, a chemogenomics approach16, as well as functional group and biological features17 (Fig. 2).
Comparison with other four prediction methods on the same dataset. (a) The prediction performance in enzymes, ion channels, GPCRs, and nuclear receptors were compared. Grey bars represent the performance (accuracy) of other methods, and black bars represent the performance of our method. (b) The performance values of our model and the other four methods.
To directly compare the performance of BART with other established machine learning models, we used our training data (see Methods) to perform cross-validation experiments using random forest, support-vector machines (SVM), decision trees, and logistic regression. All models showed good performance (AUC > 0.9) when provided with the BOW space, while BART still showed superior performance (Fig. 3). Not surprisingly, the random forest–with arguably the most similar prediction architecture–showed the most similar performance, being outperformed by BART only in sensitivity. Simpler models such as decision trees showed lower performance on all applied measures. Interestingly, the well-established SVM showed the lowest accuracy, which was due to its low sensitivity but high specificity. Random forest, on the other hand, showed high sensitivity and low specificity. BART excelled in both measures and highlights the ability of the method to correctly classify both positive and negative data.
Features in bow-pharmacological space
It is unknown whether all 439 features in our bow-pharmacological space contribute to the prediction and which features are more predictive than the others. Hence, we performed feature selection on the training data of the entire dataset (enzyme, ion channel, GPCR, and nuclear receptor) using Boruta, an algorithm that determines the relevance by using a wrapper approach built around a random forest classifier that compares real features to random probes18. Boruta divides features into three categories: “important”, “tentative”, and “unimportant.” First, we collected “important” features to form a feature dataset called “strictly selected features.” Next, we selected the “important” and “tentative” features to make up the “selected features.” The numbers of feature sets for individual models were summarized in Fig. 4. In general, “strictly selected features” contained almost half of all of the features, and “selected features” were close to two-thirds of all features. Importantly, we noted that every subspace (ligand, protein, and bow-interaction space) had conserved features, which highlights that the predictive accuracy depends on all descriptor subspaces. Moreover, this implies that all subspaces of the bow-pharmacological space contained relevant and non-redundant information (Fig. 4c). To test for the validity of the selected features through this approach, we tested the accuracy of all machine learning models here described when trained exclusively on the selected features, and saw only minor losses in performance. This highlights that the selected features are indeed able to decipher the interaction space using various different classification algorithms, and further increases the confidence in the novel descriptors proposed.
Prediction models before and after feature selection on the entire dataset (Enzyme, Ion channel, GPCR and Nuclear receptor). (a) The prediction accuracy of models with different feature sizes. (b) The number of features and prediction performance. (c) The number of selected features in each part of bow-pharmacological space.
As a direct test of the utility of the bow-pharmacological interaction space, we decided to train all our machine learning models on all ligand and protein descriptors except the bow-interaction space. We observed a drop in all investigated performance measures, most notably a drop of around 10% of the AUC, highlighting the importance of the bow space to achieve the performance here reported. Interestingly, sensitivity seemed most affected, suggesting that the bow space is most useful to increasing the true positive rate.
We built prediction models with either “strictly selected features” or “selected features” for the three datasets in section 3 and compared the model performances. As shown in Fig. 4a,b, models with fewer features did not predict considerably better. Based on the increasing number in the feature sets (234, 280 and 439), the prediction accuracy was raised to 92.5%, 93.1% and 95.2%, respectively.
Index-based physicochemical features (IPC) facilitates prediction and interpretation
Effective representation of proteins and ligands is essential for identifying drug-target interactions and it has previously been discussed that an optimal descriptor needs to be identified for a chemogenomic project19. In addition to our novel interaction space that extends the chemogenomic capabilities, we have also devised a new feature to represent proteins, called the index-based physicochemical feature (IPC). Previous protein representations fall into two general categories: structure-based and sequence-based. The structure-based representations rely on the knowledge of protein structure, which is not always available for most proteins; sequence-based representations only require information about the protein sequence, which is readily available. Typically, a sequence-based method uses the information of the amino acid composition of a protein, but neglects the sequence order of the amino acids in the polypeptide chain. To represent proteins with both the amino acid composition and sequence order information, we put forward IPC, a new feature that considers the effects from neighbouring amino acids. The effect of flanking amino acids to center amino acids declines as the distance of two amino acids increases along the protein sequence (see Methods).
To evaluate the impact of IPC protein representation on model performance, we built one model with basic physicochemical features (BPC), which are classic sequence-based features for protein-related predictions and a second model with index-based physicochemical features (IPC). The model built with IPC features performed better than the model built with BPC in predicting protein-ligand interactions (Fig. 5). The IPC model achieved a prediction accuracy of 74.8% in comparison with the BPC model’s achieved 64.4%. This suggests that the proposed distance-aware IPC features were more informative than BPC for encoding protein sequence in protein-ligand prediction problems.
Comparison of the predictions based on basic physicochemical features (BPC) or index-based physicochemical features (IPC). (a) Sensitivity, specificity, accuracy, and AUC are plotted from left to right. Green bars represent the performance of prediction based on basic physicochemical features (BPC), red bars on index-based physicochemical features (IPC). (b) The performance values of BPC and IPC.
Case studies
To test whether our prediction algorithm would identify any useful ligand-target interactions, we specifically investigated some of the most confident predictions. For example, based on our model, gamma-aminobutyric acid (CID000000119) was predicted with a high probability to interact with three proteins, but olfactory receptor 7G2 (ENSP00000303822) was put forward as the most likely interaction candidate protein (a segment of results generated by our model is tabulated in Supplement Table S1). The interaction between CID000000119 and 7G2 was revealed in the literature20 but had not been collected in the database yet.
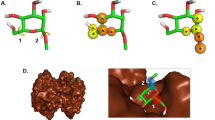
To illustrate that our model is able to search for new ligands of important target proteins, we present a case study to predict new interacting ligands for kinesin-like protein, KIF11. KIF11 is a cytoskeletal protein that belongs to the kinesin-like protein family and plays a role in chromosome positioning, centrosome separation, and bipolar spindle establishment during cell mitosis. KIF11 is inhibited by certain small molecules such as Monastrol, a prototype anti-cancer drug that selectively inhibits a mitotic kinesin Eg5, several derivatives of which are currently under clinical trials and being investigated in the field of malignant tumour study21. Based on our model’s prediction, KIF11 interacts with ispinesib mesilate (G7X) with a probability of 0.92. To verify the prediction, we performed a docking simulation and literature search. In the docking result, G7X was obviously bound to KIF11 (Fig. 6). The binding affinity calculated by AutoDock Vina (1.1.2) is −9.5 kcal/mol, which falls within the conventional binding energy interval of −9 to −12 kcal/mol. The prediction and simulation results were further validated recently by an independent group using a crystallography method. Their results showed the same pose as the docked pose22, attesting to the predictive accuracy of our model.
Discussion
Protein-ligand interactions are fundamental for myriad processes occurring in living organisms. Our investigation into these interactions is therefore promising for our understanding of the biochemical underpinning of cellular systems and of perturbations into these systems, and constitutes a major step in drug discovery research. With the development of sophisticated computer algorithms, protein-ligand interactions have been increasingly deconvoluted by in silico approaches. Our study described the development of a machine learning approach based on a new class of descriptors as well as a novel algorithm to accurately predict protein-ligand (drug-target) interactions.
For the first time, we applied the Bayesian additive regression trees (BART) algorithm on a uniform space that encodes feature information from proteins and ligands, a classical chemogenomic approach, but here for the first time also include an interaction space that encodes for known protein-ligand interactions. This space was constructed by relying on average fingerprints—a concept that has been underexplored in the computational drug design community and has most notably been applied as median molecules in de novo design23,24,25 as well as implicitly when using clustering approaches26,27. This information space was coined the bow-pharmacological space. It encapsulates essentially non-redundant and relevant information for predicting interaction between proteins and potential ligands or vice versa and we showed a significant increase in performance over various established machine learning algorithms when supplied with the novel descriptor, highlighting its utility (Fig. 1). Furthermore, we also developed novel protein target descriptors that included predicted tertiary structure and showed an improved performance over two-dimensional protein descriptors. We foresee an increased interest in using such types of descriptors by other researchers in pharmaceutical and chemical biology research.
In our model, BART, a non-parametric Bayesian regression approach, is applied. It provides a reliable posterior mean and interval estimates of the true regression function as well as the marginal effects of potential predictors14, while many other binary classification tools (e.g., KNN, SVM)28,29 simply produce a binary yes-or-no result. For the interaction within a protein-ligand pair, BART generates a probabilistic scoring of the likelihood of the interaction. An in silico probabilistic evaluation of the likelihood of interactions could serve as an initial filtering step to select the most probable candidates out of a pool of hundreds or even thousands, thus lowering the experimental cost and time.
Our approach extends our knowledge of potential ligands for a specific protein, and proteins that interact with a specific ligand are useful in drug discovery efforts to identify yet undiscovered protein-ligand interactions. In addition, the probability index of protein-ligand pairs can be used for filtering and stratifying multiple drug candidates, as well as for evaluating the off-target effects of specific drugs and other protein-ligand interactions. With the high predictive accuracy and high-throughput performance of our prediction algorithm, we envision that more drugs will be able to be evaluated and developed more rapidly, and a deeper understanding of drug effects and drug targets will be achieved.
Models and Methods
Construction of bow-pharmacological space
All features in the bow-pharmacological space are summarized in Fig. 1b. In the protein space, we considered three main feature types for comprehensively representing a protein. These feature types include the amino acid composition, physicochemical features of the protein, and property groups in the polypeptide sequence. Further, these types were subdivided into ten feature sets designated F1, F2, …, F10. The composition vector (CV, as F1) contains information about the amino acid composition of the primary protein sequence, but not its relative position. To describe both the composition and the relative position of amino acids in the protein sequence, we used the composition moment vector (CMV, as F2).
In addition, we included three different types of physicochemical features: first, basic physicochemical features (BPC, as F3) such as hydrophobicity, charge, and polarity serve as a classic description of protein sequence, which has performed well for many protein-related prediction problems30,31,32; second, the neighbourhood-based physicochemical feature (NPC, as F4) complemented the BPC by combining the target amino acid site and its two neighbours; and third and most importantly, the index-based physicochemical feature (IPC, as F5) was constructed with the assumptions that each site on the protein sequence had an effect on others and that the effects were related to the protein composition (see Methods). Regarding amino acid positions, amino acids that were close to the primary sequence could be part of flexible loops and therefore not close in 3D space. Conversely, amino acids that were far apart might form a pocket. IPC is the descriptor that incorporated the secondary/tertiary structure (prediction). Additionally, we incorporated five feature sets for the protein property groups, including the R groups (RG, as F6), the electronic groups (EleG, as F7), the exchange groups (ExG, as F8), the hydrophobic groups (HG, as F9) and the side chain groups (SCG, as F10).
In the ligand space, we adopted the MACCS fingerprint, one of the most widely used “structural fingerprints” based on pre-defined chemical substructures33. MACCS has 166-bit structural key descriptors, each of which is associated with a SMARTS pattern that represents a functional group or test of a combination of substructure34.
In the protein-ligand interaction space, the links that represented the known interactions between proteins and their ligands were quantified. As shown in Fig. 7, known ligands of each protein were coded by the MACCS keys; these keys were averaged to generate a unique fingerprint that represented the known links between each protein and the ligands. We named this feature MACCSP.
Gold standard dataset
The interactions between ligands and target proteins were retrieved from the KEGG BRITE35 and DrugBank databases36. The number of known interactions are 5,125 in total; 2926, 1476, 635, and 90 for enzymes, ion channels, GPCRs and nuclear receptors, respectively. The number of known proteins/drug targets in each category was 664, 204, 95, and 26, respectively. Chemical structures of the drugs and ligands were obtained from the DRUG and COMPOUND Sections in the KEGG LIGAND database35. Amino acid sequences of the target proteins were obtained from the NCBI database. Taken together, 5,125 interactions were treated as the positive dataset.
The negative dataset (non-interactions) was composed of the proteins and ligands which were not in the 5,125 interactions. The protein pool was generated by eliminating 1,051 proteins in the positive dataset from the 16,267 human-origin proteins in Swiss-Prot (2012). The ligand pool was generated by eliminating the ligands in the positive dataset from the 525,766,279 ligands in the STITCH database (2012). After mixing the positive and negative datasets, a randomly selected 70% of the data was used for training and the other 30% was used for testing. In our study, both 10-fold cross-validation and independent testing were used to assess model performance.
Coding features in bow-pharmacological space
Protein space
Feature 1: Composition vector (CV, 20 dimensions).
CVi denotes the percentage composition of amino acid (AA) i in the protein sequence:
CVi = (number of amino acid i in the sequence)/(total number of AA’s in the sequence).
20 amino acids were coded in alphabetical order: A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y, and were denoted AA1, AA2, …, AA20, respectively.
Feature 2: First and second order composition moment vector (CMV, 40 dimensions).
The composition moment vector of a protein was defined as follows:
For k = 1, \({x}_{i}^{(1)}\) is the i-th entry of the first-order composition moment vector,
and for k = 2, \({x}_{i}^{(1)}\) is the i-th entry of the second-order composition moment vector,
where CMV is the composition of the i-th AA in the sequence, N is the length of the AA sequence, nij is the j-th position of AAi and k is the order of the composition moment vector.
The first and second orders of CMV were used, while the zeroth order reduces to the composition vector (CV, feature 1).
Feature 3: Basic physicochemical features (BPC, 7 dimensions).
In this study, seven physicochemical properties were chosen from AA index. They include hydrophobicity, charge, polarity, volume, flexibility, isoelectric point, and refractivity. For each of these properties, the basic physicochemical feature is calculated by \(BPC=\sum _{i=1}^{N}{P}_{i}\), where Pi is the relevant physicochemical property of the i-th amino acid in the sequence.
Feature 4: Neighbourhood-based physicochemical features (NPC, 7 dimensions).
The seven physicochemical properties in the NPC are the same as those in the BPC. For each property, the NPC feature considers the effect of the properties of its neighbouring AA and is calculated by \(NPC=\sum _{i=1}^{N}|{({P}_{i})}^{2}-{P}_{i-1}\times {P}_{i+1}|\), where N is the length of the protein sequence, and Pi is the concerned physicochemical property of the i-th amino acid in the sequence.
Feature 5: Index based physicochemical features (IPC, 7 dimensions).
The seven physicochemical properties used in IPC are the same as those in the BPC and the NPC. For each property, the IPC feature is calculated in three steps.
Step 1:
where P1(Ri) is the original value of physicochemical feature 1 (seven in total, first is hydrophobicity). \({P}_{1}^{0}\) is the average of the basic physicochemical feature 1 over the 20 AAs, and \(SD({P}_{1}^{0})\) is the corresponding standard deviation. Pi is also calculated for i in 2, …, 7 (six other physicochemical features: charge, polarity, volume, flexibility, isoelectric point and refractivity).
Step 2:
where k is the interval between two amino acids, k ∈ [1, N − 1]; N is the number of amino acids in the sequence. δk is the k-th correlation factor that reflects the sequence order correlation between all the k-th most contiguous residues.
For example, with k = 1, we have
and with k = 2, we have
Accordingly, all the J and δ values can be calculated.
Step 3:
After calculating all the J and δk, calculate the IPC,
Feature 6: R group features (RG, 5 dimensions).
There are five types of protein R groups. RGi is the percentage of all amino acids in the sequence that have R groups of type i, where i = 1, 2, …, 5. The case of i = 1 corresponds to non-polar aliphatic AAs (A, G, I, L, M, V), i = 2 to polar uncharged AAs (C, N, P, Q, S, T), i = 3 to positively charged AAs (H, K, R), i = 4 to negative AAs (D, E), and i = 5 to aromatic AAs (F, W, Y).
Feature 7: Electronic group features (EleG, 5 dimensions).
EleGi is the percentage composition of electronic group i in the sequence, where i = 1, 2, …, 5. The case in which i = 1 corresponds to electron donor AAs (A, D, E, P), i = 2 to weak electron donor AAs (I, L, V), i = 3 to electron acceptor AAs (K, N, R), i = 4 to weak electron acceptor AAs (F, M, Q, T, Y), and i = 5 to neutral AAs (G, H, S, W).
Feature 8: Exchange group features (ExG, 6 dimensions).
Exchange groups were clustered by the conservative replacements of amino acids during evolution. ExG1 corresponds to the amino acid C; ExG2 to A, G, P, S, T; ExG3 to D, E, N, Q; ExG4 to H, K, R; ExG5 to I, L, M, V; and ExG6 to F, W, Y.
Feature 9: Hydrophobicity group features (HG, 4 dimensions).
Hydrophobicity groups were formed according to the water-soluble side chains of amino acids. HGi is the percentage composition of hydrophobicity group i in the sequence. The case i = 1 corresponds to hydrophobic AAs (A, C, F, G, I, L, M, P, V, W, Y), i = 2 to hydrophobic basic AAs (H, K, R), i = 3 to hydrophobic acidic AAs (D, E), and i = 4 to hydrophobic polar with uncharged side chain AAs (N, Q, S, T).
Feature 10: Side chain group features (SCG, 6 dimensions).
Side chain groups were based on the attributes of side chains including molecular weight, polarity, aromaticity, and charge. SCGi is the percentage composition of side chain group i in the sequence. The case in which i = 1 corresponds to tiny side chain AAs (A, G), i = 2 to bulky side chain AAs (F, H, R, W, Y), i = 3 to polar-uncharged AAs (D, E), i = 4 to charged side chain AAs (D, E, H, I, K, L, R, V), i = 5 to polar side chain AAs (D, E, K, N, Q, R, S, T, W, Y), and i = 6 to aromatic side chain AAs (F, H, W, Y). Although this feature and Feature 6 were both based on the R groups of amino acids, they are different in division criteria and biological meaning.
Ligand space
Feature 11: MACCS for ligands (MACCSL, 166 dimensions).
Each ligand was represented with a MACCS key fingerprint, which was calculated with molecular operating environment (MOE). MACCS encoded the molecular structure in 166 bits (binary digits). Each bit in a structural fingerprint corresponds to the presence (1) or absence (0) of a specific substructure in the molecule.
Protein-ligand interaction space
Feature 12: MACCS for proteins (MACCSP, 166 dimensions).
To encode the information of known protein-ligand interactions, we first collected all the known ligands for each specific protein and then added up the MACCSL values of these interacted ligands. Finally, the sum was divided by the total number of connected ligands.
Feature selection by Boruta
The Boruta algorithm is a wrapper method built around the random forest classification algorithm18. Random forest is a category of ensemble methods in which classification is performed by voting of multiple unbiased weak classifiers (decision trees). These decision trees are independently developed on different samples drawn independently and randomly from the training set. A random permutation of each feature was performed, and the resultant loss of accuracy of the classification was measured for each tree to infer the importance of the feature.
BART and other machine learning models
Bayesian Additive Regression Trees (BART) is a Bayesian tree ensemble method for non-parametric learning. The unique characteristic of BART is a regularization prior that encourages the decision trees in the Bayesian tree ensemble to be small in size. The sum of the resultant trees, each of which is a weak learner, combines to be a non-parametric model that explains and predicts the relation between the predictors and responses. The trees and the corresponding weights are developed with the boosting algorithm implemented through Markov chain Monte Carlo (MCMC).
We used the R package Bart to implement this method. BART was defined by a statistical model: a prior and a likelihood. The features proposed above are used as input into the BART algorithm. Essentially, BART first constructed a simple weak learner by a prior and then built a Bayesian “sum-of-trees” model. To fit the model, BART employed a tailored version of Bayesian backfitting Markov chain Monte Carlo (MCMC) method that interactively constructed and fitted successive residuals37. The probability values above 0.5 generated by BART were classified to “interaction” group, and the values equal/below 0.5 were classified to “non-interaction” group.
Besides BART, other machine learning methods were applied as well, including logistic regression38, support vector machine (SVM)39, decision tree, and random forest. Logistic regression is a statistical method for analyzing a dataset in which there are one or more independent variables that determine an outcome, and is used for estimating the probability of an event38. Support vector machine (SVM) efficiently performs a non-linear classification using what is called the kernel trick, implicitly mapping inputs into high-dimensional feature spaces to build a maximum margin hyperplane. A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences. Random forest is a meta-estimator that fits a number of decision tree classifiers. Each tree gives a classification, and we say the tree “votes” for that class. The forest selects the classification having the most votes in the forest. We used Python along with a machine learning package, scikit-learn (specifically linear_model.LogisticRegression with parameter C = 1e5) to implement logistic regression. The SVM models were built based on the libsvm package from Sklearn (svm.SVC), where gamma was set at 0.0001 and C was set at 100. We implemented decision trees with the function tree. DecisionTreeClassifier from the sklearn package. We used the RandomForestClassifier class in Sklearn.ensemble along with the number of jobs equal to six for algorithm implementation.
Performance measurements
We conducted a 10-fold cross-validation and independent testing to evaluate the predictive performance of the models. A confusion matrix was applied to calculate sensitivity, specificity, and overall accuracy of our classifiers. Accuracy = (TP + TN)/(TP + FP + TN + FN), Sensitivity = TP/(TP + FN), and Specificity = TN/(TN + FP), where TP is the number of true positives, TN is true negatives, FP is false positives, and FN is false negatives. Furthermore, Receiver Operator Characteristic (ROC) curves were plotted to depict relative trade-offs between accuracy and coverage with TP on the y-axis and FP on the x-axis40. The area under the ROC curve (AUC) was also calculated as a measurement of performance41.
References
Kuruvilla, F. G., Shamji, A. F., Sternson, S. M., Hergenrother, P. J. & Schreiber, S. L. Dissecting glucose signalling with diversity-oriented synthesis and small-molecule microarrays. Nature 416, 653–657, https://doi.org/10.1038/416653a (2002).
Haggarty, S. J., Koeller, K. M., Wong, J. C., Butcher, R. A. & Schreiber, S. L. Multidimensional chemical genetic analysis of diversity-oriented synthesis-derived deacetylase inhibitors using cell-based assays. Chem Biol 10, 383–396, doi:S1074552103000954 (2003).
Halperin, I., Ma, B., Wolfson, H. & Nussinov, R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 47, 409–443, https://doi.org/10.1002/prot.10115 (2002).
Cheng, A. C. et al. Structure-based maximal affinity model predicts small-molecule druggability. Nature biotechnology 25, 71–75, https://doi.org/10.1038/nbt1273 (2007).
Altman, R. B. et al. Text mining for biology–the way forward: opinions from leading scientists. Genome biology 9(Suppl 2), S7, https://doi.org/10.1186/gb-2008-9-s2-s7 (2008).
Zhu, S., Okuno, Y., Tsujimoto, G. & Mamitsuka, H. A probabilistic model for mining implicit ‘chemical compound-gene’ relations from literature. Bioinformatics 21(Suppl 2), ii245–251, https://doi.org/10.1093/bioinformatics/bti1141 (2005).
Balakin, K. V. et al. Property-based design of GPCR-targeted library. J Chem Inf Comput Sci 42, 1332–1342, doi:ci025538y (2002).
Singh, N., Cheve, G., Ferguson, D. M. & McCurdy, C. R. A combined ligand-based and target-based drug design approach for G-protein coupled receptors: application to salvinorin A, a selective kappa opioid receptor agonist. J Comput Aided Mol Des 20, 471–493, https://doi.org/10.1007/s10822-006-9067-x (2006).
Gruber, C. W., Muttenthaler, M. & Freissmuth, M. Ligand-based peptide design and combinatorial peptide libraries to target G protein-coupled receptors. Curr Pharm Des 16, 3071–3088, doi:BSP/CPD/E-Pub/000182 (2010).
Bartoschek, S. et al. Drug design for G-protein-coupled receptors by a ligand-based NMR method. Angew Chem Int Ed Engl 49, 1426–1429, https://doi.org/10.1002/anie.200905102 (2010).
Rognan, D. Chemogenomic approaches to rational drug design. British journal of pharmacology 152, 38–52, https://doi.org/10.1038/sj.bjp.0707307 (2007).
Yamanishi, Y., Araki, M., Gutteridge, A., Honda, W. & Kanehisa, M. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 24, i232–240, https://doi.org/10.1093/bioinformatics/btn162 (2008).
Bleakley, K. & Yamanishi, Y. Supervised prediction of drug-target interactions using bipartite local models. Bioinformatics 25, 2397–2403, https://doi.org/10.1093/bioinformatics/btp433 (2009).
Chipman, H. A., George, E. I. & McCulloch, R. E. BART: Bayesian additive regression trees. The Annals of Applied Statistics 4, 266–298 (2010).
Cao, D. S. et al. Large-scale prediction of drug-target interactions using protein sequences and drug topological structures. Anal Chim Acta 752, 1–10, https://doi.org/10.1016/j.aca.2012.09.021 (2012).
Jacob, L. & Vert, J. P. Protein-ligand interaction prediction: an improved chemogenomics approach. Bioinformatics 24, 2149–2156, https://doi.org/10.1093/bioinformatics/btn409 (2008).
He, Z. et al. Predicting drug-target interaction networks based on functional groups and biological features. PLoS One 5, e9603, https://doi.org/10.1371/journal.pone.0009603 (2010).
Miron, B. & Kursa, W. R. R. Feature Selection with the Boruta Package. Journal of Statistical Software 36, 1–13 (2010).
Brown J. B., Niijima, S., Shiraishi, A., Nakatsui, M. & Okuno, Y. Chemogenomic approach to comprehensive predictions of ligand-target interactions: A comparative study. 2012 IEEE International Conference on Bioinformatics and Biomedicine Workshops 2012, 136–142 (2012).
Priest, C. A. & Puche, A. C. GABAB receptor expression and function in olfactory receptor neuron axon growth. Journal of neurobiology 60, 154–165, https://doi.org/10.1002/neu.20011 (2004).
Valensin, S. et al. KIF11 inhibition for glioblastoma treatment: reason to hope or a struggle with the brain? BMC Cancer 9, 196, https://doi.org/10.1186/1471-2407-9-196 (2009).
Talapatra, S. K., Schuttelkopf, A. W. & Kozielski, F. The structure of the ternary Eg5-ADP-ispinesib complex. Acta Crystallogr D Biol Crystallogr 68, 1311–1319, https://doi.org/10.1107/S0907444912027965 (2012).
Brown, N., McKay, B. & Gasteiger, J. The de novo design of median molecules within a property range of interest. Journal of Computer-Aided Molecular Design 18(12), 761–771 (2004).
Brown, N., McKay, B., Gilardoni, F. & Gasteiger, J. A Graph-Based Genetic Algorithm and Its Application to the Multiobjective Evolution of Median Molecules. Journal of Chemical Information and Computer Sciences 44(3), 1079–1087 (2004).
Schneider, G. & Fechner, U. Computer-based de novo design of drug-like molecules. Nature Reviews Drug Discovery 4(8), 649–663 (2005).
Reker, D., Rodrigues, T., Schneider, P. & Schneider, G. Identifying the macromolecular targets of de novo-designed chemical entities through self-organizing map consensus. Proceedings of the National Academy of Sciences 111(11), 4067–4072 (2014).
Engels, M. F. M. et al. A Cluster-Based Strategy for Assessing the Overlap between Large Chemical Libraries and Its Application to a Recent Acquisition. Journal of Chemical Information and Modeling 46(6), 2651–2660 (2006).
Li, S., Harner, E. J. & Adjeroh, D. A. Random KNN feature selection - a fast and stable alternative to Random Forests. BMC Bioinformatics 12, 450, https://doi.org/10.1186/1471-2105-12-450 (2011).
Louis, B., Agrawal, V. K. & Khadikar, P. V. Prediction of intrinsic solubility of generic drugs using MLR, ANN and SVM analyses. Eur J Med Chem 45, 4018–4025, https://doi.org/10.1016/j.ejmech.2010.05.059 (2010).
Yan, C. et al. Predicting DNA-binding sites of proteins from amino acid sequence. BMC Bioinformatics 7, 262, https://doi.org/10.1186/1471-2105-7-262 (2006).
Bianchi, V., Gherardini, P. F., Helmer-Citterich, M. & Ausiello, G. Identification of binding pockets in protein structures using a knowledge-based potential derived from local structural similarities. BMC Bioinformatics 13(Suppl 4), S17, https://doi.org/10.1186/1471-2105-13-S4-S17 (2012).
Madera, M., Calmus, R., Thiltgen, G., Karplus, K. & Gough, J. Improving protein secondary structure prediction using a simple k-mer model. Bioinformatics 26, 596–602, https://doi.org/10.1093/bioinformatics/btq020 (2010).
Yongye, A. B. et al. Consensus models of activity landscapes with multiple chemical, conformer, and property representations. J Chem Inf Model 51, 1259–1270, https://doi.org/10.1021/ci200081k (2011).
SMARTS Theory Manual. Daylight Chemical Information Systems, Santa Fe, New Mexico.
Kanehisa, M. et al. From genomics to chemical genomics: new developments in KEGG. Nucleic acids research 34, D354–357, https://doi.org/10.1093/nar/gkj102 (2006).
Wishart, D. S. et al. DrugBank: a knowledgebase for drugs, drug actions and drug targets. Nucleic acids research 36, D901–906, https://doi.org/10.1093/nar/gkm958 (2008).
Chen, R. et al. Prediction of conversion from mild cognitive impairment to Alzheimer disease based on bayesian data mining with ensemble learning. The neuroradiology journal 25, 5–16, https://doi.org/10.1177/197140091202500101 (2012).
Hosmer, D. W., Hosmer, T., Le Cessie, S. & Lemeshow, S. A comparison of goodness-of-fit tests for the logistic regression model. Statistics in medicine 16, 965–980 (1997).
Van Gestel, T. et al. Bayesian framework for least-squares support vector machine classifiers, gaussian processes, and kernel Fisher discriminant analysis. Neural computation 14, 1115–1147, https://doi.org/10.1162/089976602753633411 (2002).
Linden, A. Measuring diagnostic and predictive accuracy in disease management: an introduction to receiver operating characteristic (ROC) analysis. Journal of evaluation in clinical practice 12, 132–139, https://doi.org/10.1111/j.1365-2753.2005.00598.x (2006).
Streiner, D. L. & Cairney, J. What’s under the ROC? An introduction to receiver operating characteristics curves. Canadian journal of psychiatry. Revue canadienne de psychiatrie 52, 121–128 (2007).
Reker, D., Schneider, P., Schneider, G. & Brown, J. B. Active learning for computational chemogenomics. Future Medicinal Chemistry 9(4), 381–402 (2017).
Acknowledgements
This work is supported by the grants from the Key Research Area Grant 2016YFA0501703 and 2017YFA0505500 of the Ministry of Science and Technology of China, the National Natural Science Foundation of China (Nos. 61832019, 61503244, 31771476), the Natural Science Foundation of Henan Province (162300410060) and Joint Research Funds for Medical and Engineering and Scientific Research at Shanghai Jiao Tong University (YG2017ZD14). Daniel Reker is a Swiss National Science Foundation Fellow (P2EZP3_168827 and P300P2_177833). We thank Michael Brent from the Center for Genome Sciences and Systems Biology, Washington University in St. Louis for supporting this work and providing services from the computational cluster. We thank Zeke Maier, Brian Haynes, Holly Brown and other members in the Michael Brent Lab for helpful discussion and technical assistance. We thank Etienne Caron and Lorenz Blum for reading the manuscript drafts and providing comments.
Author information
Authors and Affiliations
Contributions
L.L. and C.C.K. wrote the manuscript. L.L. and D.Q.W. conceived the study design. D.R., J.B., N.K.L., H.S.W. and L.N.C. supported manuscript preparation and experimental design. L.L., H.L., H.D., C.C.K. and H.M.F. wrote code, ran the model, and analysed the data.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, L., Koh, C., Reker, D. et al. Predicting protein-ligand interactions based on bow-pharmacological space and Bayesian additive regression trees. Sci Rep 9, 7703 (2019). https://doi.org/10.1038/s41598-019-43125-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-43125-6
This article is cited by
-
Anesthetic drug discovery with computer-aided drug design and machine learning
Anesthesiology and Perioperative Science (2024)
-
Pathogenomic in silico approach identifies NSP-A and Fe-IIISBP as possible drug targets in Neisseria Meningitidis MC58 and development of pharmacophores as novel therapeutic candidates
Molecular Diversity (2023)
-
In silico prediction suggests inhibitory effect of halogenated boroxine on human catalase and carbonic anhydrase
Journal of Genetic Engineering and Biotechnology (2022)
-
A machine learning model for classifying G-protein-coupled receptors as agonists or antagonists
BMC Bioinformatics (2022)
-
Hesperidin abrogates bisphenol A endocrine disruption through binding with fibroblast growth factor 21 (FGF-21), α-amylase and α-glucosidase: an in silico molecular study
Journal of Genetic Engineering and Biotechnology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.