Abstract
Traditional human societies use two of biology’s solutions to reduce free-riding: by collaborating with relatives, they rely on the mechanism of kin-selection, and by forming highly clustered social kin-networks, they can efficiently use reputation dynamics. Both of these solutions assume the presence of relatives. This paper shows how social networks change during demographic transition. With falling fertility, there are fewer children that could be relatives to one another. As the missing kin are replaced by non-kin friends, local clustering in the social network drops. This effect is compounded by increasing population size, characteristic of demographic transition. The paper also shows that the speed at which reputation spreads in the network slows down due to both falling fertility and increasing group size. Thus, demographic transition weakens both mechanisms for eliminating free-riders: there are fewer relatives around, and reputation spreads slower. This new link between falling fertility and the altered structure of the social network offers novel interpretations of the origins of legal institutions, the Small World phenomenon, the social impact of urbanisation, and the birds-of-a-feather friendship choice heuristic.
Similar content being viewed by others
Introduction
The ability and propensity to make friends, that is, lasting, non-kin, positive social affiliations, is a human universal1,2,3,4,5, with deep evolutionary roots6,7,8,9. Despite this, humans, like most animals10, prefer collective action with kin11,12,13,14,15,16, similar to elephants17, African wild dogs18, and bottle nose dolphins19. People prefer the majority of their social contacts to be kin rather than friends whenever it is possible20,21,22,23. For instance, in contemporary forager cultures (such as the Ache24, Ju/’hoansi24, Agta25, and Mbendjele25), the average member of an average band is connected to about three-quarters of the other band members either via direct biological or affinal, through-marriage, link24. This ratio increases further in traditional agriculturalist societies25. Most of the social world of traditional societies in general is dominated by direct or affinal kin, especially when it comes to organising collective action26,27,28,29.
Almost all modern societies have gone through demographic transition during the past two hundred years30,31,32, characterised by falling mortality followed by falling fertility, resulting in increased population size and permanently low fertility30,32,33,34. A trivial social consequence of decreasing fertility is that it reduces the number of relatives. For instance, if the average fertility per woman is 5, then an average individual will have 4 siblings, and 40 first-degree cousins (5 offsprings on average for each of the four siblings of the mother and the four siblings of the father). If, however, fertility falls to 2 per woman then the average individual will have 1 sibling, and only 4 cousins. Thus, a shift from total fertility rate (TFR) of 5 to TFR of 2, the typical start and end points during demographic transition, reduces the number of same-generation relatives with whom a grandmother is shared from 44 to 5. As the total number of relatives is dependent on the population’s fertility, the available set of kin is dramatically reduced during demographic transition. Even if people would prefer to include kin more than non-kin in their social network as much after the transition as before, in low-fertility societies there are just not enough kin to serve as social contacts35.
Although the effect of falling fertility on many aspects of the society has been much discussed36,37, the literature about the relationship between social networks and fertility has been in one causal direction so far: the focus has been on the way social networks mitigate attitudes towards child bearing38,39,40,41. In fact, part of the much-contested literature34 concerning the origins and mechanism of demographic transition suggested that falling fertility is a network phenomenon42,43, supported at least in part by culture-specific empirical evidence44,45. The empirical literature has established that a fall in the number of children can impact the structure of the social networks by showing that kin contacts decline with demographic transition and industrialisation46,47,48. If and how replacing kin with friends in societies characterised by falling fertility affects the structure of social networks is a question that has been so far unexplored.
Given that independent of culture, humans tend to prefer ego group sizes with relatively small individual variation49,50,51,52, people living in low fertility societies find themselves in a deficit of social contacts when the number of possible relatives falls with demographic transition35. This problem is solved by replacing the missing kin with non-kin friends. This is helped by the fact that the method of bonding, that is, making and maintaining friends, is via frequent meaningful meetings and interactions, similar to maintaining relationships among biological relatives53,54.
Having non-kin friends solves the problem of how to achieve the desired number of social contacts, but raises a completely different issue. As a simple thought experiment shows, the structure of the social network around an individual who is surrounded by relatives is likely to be different from one surrounded by friends. The reason is that an ego’s relatives are more likely to be relatives to one another than the ego’s friends are to be friends themselves. For instance, if an individual has two full siblings, i.e., sharing both parents, then, by definition, they themselves will be siblings to each other. However, if an individual has two good friends, although it is possible that these friends will be friends with each other, this is far from certain. This phenomenon is likely to have an impact on the structure of the social network people live in (Fig. 1).
Illustration for how the clustering coefficient can change even when the degree, i.e., the number of connections, is unchanged. Panel (a) is a stylised representation of a high-fertility society in which five agents are depicted, who are all connected to one another and, in addition, to one further person each. Panel (b) also depicts five agents; these are, however, only connected to two other agents within this circle, and an additional three others outside the circle and not connected to each other. This panel is the stylised representation of a low-fertility and/or urbanised society. Note that the network degree of each agent is five on both panels, i.e., each agent in the circle has five social connections. Yet, the clustering coefficients of all agents, i.e., the number of closed triangles out of all the possible triangles in their individual social network, is 50% in Panel (a) and 0% in Panel (b).
This paper investigates how the social network structure changes when individuals replace kin with friends as a consequence of falling fertility.
Network Structure – Methods
Let us create a population of many generations, in which the biological relatedness is tracked. For this, each individual is defined by the following record:
where i is the index number of the agent, \({g}_{i}\in \{0,1\}\) is the gender of the agent, \({F}_{i}=\{{p}_{i,1},{p}_{i,2},{p}_{i,3},{p}_{i,4},{m}_{i},{f}_{i}\}\) is the set of the index numbers of the agent’s four grandparents, mother and father.
Let Is denote the set of agents belonging to generation s. Let us assume that the agents form heterosexual pairs among unrelated individuals:
where Ps is thus the set of pairs formed in generation s. (Notice that the above pair-formation rule implies that if the number of females and males is not even, some of the more numerous gender do not find a partner. The model also assumes that the pairings last a life-time, and are monogamous).
Let k denote the fertility of any single pair, and assume that it is a Poisson-distributed random variable:
where κ denotes the expected value of fertility, and thus the average fertility in the population.
Let Bx,y denote the set of children born to the pair formed by x and y:
where the gender of a child is random, uniformly distributed.
Let Bs denote all the births to a generation:
Notice that the expected size of this set is as follows:
where ns denotes the population size in generation s, and E is the expectations operator. (The expected size is only approximate, as a small fraction of the population does not pair up due to the random number of the two sexes, and the assumption that the pairings are monogamous).
Thus, if the fertility of the population is larger than replacement, the size of the population increases generation by generation.
Using equations (1) to (6) and starting with an initial population of 50–100, I simulated, using Wolfram Mathematica, the population dynamics in successive generations, varying the fertility, κ, between 2.5 and 5.0. (The upper limit of this range is given by the average fertility in traditional hunter-gatherer societies55, while the lower end reflects a computational reason: at 2.5 the populations do not collapse during simulation).
I ran each simulation until the total population size exceeded a target number (500 or 2000). In most cases the final generation’s population size exceeded the target number. When this was the case, I eliminated randomly chosen agents so that the final population size was exactly in line with the target number. This way I had built a library of simulated populations, each being a list of agents’ records containing the index numbers of their parents and grandparents as defined in equation (4).
Next, I built a binominal adjacency matrix, a, for each population in the library, assuming that the agents regard each others as kin if they share at least one grandparent:
Notice that in most hunter-gatherer societies, relatives are recognised and tracked on average up to second cousin56. For computational reasons, I assumed kin recognition up to first cousin only. (Otherwise the target group sizes would have had to be unrealistically large: and would take too long to compute all the steps). There is no reason why the theoretical observations of this paper would be different with the cut-off being at first-degree as opposed to second-degree cousins.
Trivially, the adjacency matrix a is diagonally symmetric, for if i is related to j, then by definition j is also related to i:
Thus the adjacency matrix, a, defines a graph in which each edge is undirected, and corresponds to a mutually recognised kin relationship:
Let d(g) denote the average degree of the graph g:
Notice that the average number of relatives is dependent on the fertility parameter, κ. If there are more children born, there are more relatives.
(See Fig. S1a for the relationship between d(g) and κ).
Let us assume that each agent has a uniform need for and capacity to maintain a certain number of social contacts. This assumption is in line with empirical evidence suggesting that, due to the limited social time budget57, the number of meaningful social contacts of an average human lies within a relatively narrow range58,59,60, and is a standard assumption of the behavioural synchrony model family61,62,63. Let ν denote this parameter. I assume that this social capacity parameter is set arbitrarily at ν = 60. (I chose this level as it is just a little higher than the average number of relatives in the upper end of the fertility range in the simulations. Ethnographic demography suggests that in hunter-gatherer societies most social contacts are recognised as either close or distant biological kin, or affinal kin through marriage24,25,26,27,28,29, and there is only a relatively small space for non-kin friends. This suggests that a limit just above the number of recognised kin in the highest fertility case is, albeit arbitrary, qualitatively correct). For agents that had a higher number of relatives than the limit, ν, I eliminated a random set of relatives up to the limit. (See Fig. S1b for the relationship between d(g) and κ after this truncation).
Because ν is chosen so that the number of recognised relatives is just under this limit in the case of the high-fertility population, depending on the simulation fertility parameter, κ, the agents are almost always short of social contacts, to a varying extent. To fill the gap, the agents were assigned random “friends”. To do this, I added random edges between unrelated agents to the adjacency matrix (and as a consequence, to the social network graph), until each agent’s number of social contacts was at the capacity, ν.
Let b denote the adjacency matrix of all connections between social contacts, and h the corresponding social network graph. Due to the graph-generation method, the degree of each agent in the h graph is uniform:
In this way I created a library of pairs of a and b adjacency matrices and corresponding pairs of g and h social network graphs. Notice that because g is the network of relatives, and h is the entire social network which includes all relatives, g is a subgraph of h.
Let δi,j denote the shortest path between nodes i and j in the graph h. Let χi denote the local clustering coefficient of agent i:
that is, the number of triadic closures around agent i in proportion to all possible such triads.
Using this definition, let χ denote the average local clustering coefficient of graph h:
And let δ denote the average graph distance among the vertices of graph h:
Network Structure – Results
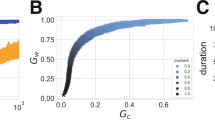
Falling fertility changes the structure of the social network in two ways: as the average degree of the kin-only graph, d(g) falls, both the average local clustering, χ, and the average graph distance, δ, decreases (Fig. 2). In other words, the lack of relatives results in fewer closed triads, i.e., social contacts are less likely to be linked to each other, but also there are fewer steps between unconnected agents.
When friends replace relatives, local clustering falls, and the graph distances become shorter. In both panels, the x-axis is the average number of relatives an average individual has. (At the upper limit of 60, all the social contacts of the individuals are relatives). Panel (a) y-axis: the average local clustering coefficient, i.e., the average number of closed social triads around individuals. Panel (b) y-axis: the graph distance, i.e., the average length of shortest routes between nodes in the network. Blue: group size at 500. Red: group size at 2000. (Each colour on each panel represents 400 independently simulated repeats).
Notice that group size plays an important role in both the fertility-clustering and the fertility-graph distance relationships. First, local clustering is lower in larger groups, due to the fact that friends are chosen from a larger population, and hence are less likely to be social contacts to one another (Fig. 2a). With falling fertility, local clustering decreases faster in larger groups (Fig. S2a). Second, while larger groups have higher graph distances (Fig. 2b), falling fertility decreases graph distances faster in larger groups (Fig. S2b).
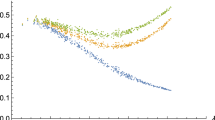
A different way to illustrate the changing graph distance phenomenon is via assessing how many others agents can reach in a given number of steps. Trivially, there is only one agent at a zero-step distance: the ego herself. At a one-step distance is her set of social connections, fixed at ν = 60 due to the assumption that the number of social contacts does not vary as a function of fertility. As fertility falls, the number of agents that are two steps away from the ego increases in both group sizes (Fig. 3). At the same time, those that are three steps away reduce in number. In other words, many agents that would be three steps away before falling fertility, become only two steps away. The set of friends of friends enlarges.
The number of contacts in two- and three-step distances. Panel (a) group size at 500; panel (b) group size at 2000. Green: the number of contacts of an average ego which are two steps away in the social network of the ego. Brown: the number of contacts three steps away. (Each colour on each graph represents 400 independently simulated repeats).
For instance, in the case of the 2000-sized groups (Fig. 3b), the number of two-step away agents triples from the highest fertility societies to the lowest fertility ones. At the same time, the number of three-step away agents falls to one-third of the original.
Reputation Dynamics – Methods
During demographic transition, fertility falls and population size increases, which, as shown above, changes the structure of the social network. Although the network degree, i.e., the number of social partners of the agents, is unchanged, the local clustering coefficient decreases both as fertility falls and as group size increases. To see how this alteration in the network structure changes the speed at which social information spreads in the network, let us consider the following reputation regime.
Let the n × n size matrix r denote a reputation matrix, where ri,j ∈ {0, 1} is agent i’s belief of agent j’s type. Let us assume that in round 0, all agents have a reputation of being type 0 in the eyes of all others:
In round 1 a randomly selected agent, denoted by xi, is observed by one randomly selected social contact of his, denoted by xj, as type 1. (For instance, xi cheats on xj in a game and thus reveals himself to her as untrustworthy). Formally:
where
and
In each successive round, the agents “gossip” with their contacts about shared acquaintances (either friends or relatives). They update their beliefs such that, if either of them thinks that the acquaintance is a cheater then they both update their belief to cheater. Let α denote the probability that such gossip takes place among a pair of contacts.
Formally, for agent i let βi denote the number of agents that are at the same time (i) connected to agent i, and (ii) connected to agent xi, and (iii) and have a reputation of xi as 1:
Then let agent i update her belief about xi in the following way:
Notice that in this reputation dynamics 0 can only turn to 1, not the other way around. In this version, there is no forgiving.
The interpretation of the reputation mechanics is that in a group of co-operators a defector emerges, whose true nature is observed by one contact. The question that this model answers is how fast and how far the news travels in the network. The role of α can be interpreted as either transmission probability, or the likelihood that an agent adopts the belief of a social contact. In the latter case, β can be interpreted as a propensity for the agent to follow the wisdom of the crowd.
Reputation Dynamics – Results
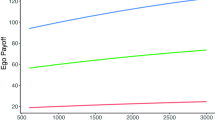
Both fertility and population size affect the speed and extent of reputational dispersion (Fig. 4a). First, independent of population size, reputation travels faster in high-fertility compared to low-fertility societies. Second, independent of fertility, reputation travels slower in larger populations.
Reputation dynamics on mixed friend-kin social networks. Panel (a): reputation dynamics without forgiving. Panel (b): reputation dynamics with forgiving. Low fertility is defined as the number of relatives being less than one-third of total social contacts: d(g) < 1/3 ν. High fertility is defined as the number of relatives being higher than one-third of all social contacts: d(g) > 1/3 ν. (α = 0.1, π = 0.50. Number of graphs in the library: 400 for both n = 500 and n = 2000).
Thus, if demographic transition is characterized by falling fertility and increasing population size, then the compound effect is a weakening of the reputation effect. If this reputation is about the stance to cooperate or free ride in a costly collective action (i.e., 0 for cooperative stance and 1 for free riding stance), and if the reputation effect is what maintains the cooperative stance, then both falling fertility and increasing population size should lead to an increase in free riding.
In the above reputation mechanics I assumed that once a reputation belief turns from 0 to 1, there is no change back. It is interesting to consider an alternative mechanism characterised by forgiving (or forgetting). Let us assume that in each round, after the updating of equations (19)-(20), each belief 1 can be turned, independently, into 0 at probability π.
Given that the forgiving possibility is independent among individual contacts, it is not surprising that forgiving is likely to take place only when a small number of agents have turned their beliefs to 1 (Fig. 4b). As a consequence, high-fertility populations never really forgive, while low-fertility populations forgive (or forget) fast.
This reinforces the qualitative results of the version of reputation mechanics that does not include forgetting: falling fertility during demographic transition is likely to undermine the reputation-based punishment of free riding.
Discussion
During the past two centuries, most contemporary societies have gone through demographic transition30,31,32,33,34. Before the change, mortality was high, and so was fertility: many children were born, many died, and the two variables more or less balanced out. When the transition began, first mortality fell, which, usually a generation or more later was followed by a drop in fertility. As a consequence, by the end of the transition, the society had a larger population, while family size shrank.
The first model presented in this paper shows that these two outcomes of demographic transition, i.e., a large population made up of small families, restructures the social network in two key ways. First, both the increased population size, and the decreased fertility result in a drastic fall of the local clustering coefficient. In traditional societies, characterised by high fertility and small group size, the majority of social contacts of an average individual are likely to be relatives and thus also likely to be connected to each other. With demographic transition, this changes: an individual’s social contacts are less likely to be social contacts with each other. Second, the falling clustering probability also results in decreasing graph distance among members of the society. After demographic transition, the number of others that can be reached in two steps increases sharply. These structural changes in the social network altered the world of the societies that underwent demographic transition.
By describing the ego-scale change in the texture of the social network resulting from fertility transition, the model spans out a framework in which some social phenomena that have not previously been regarded as related to demographic processes may be re-examined. In particular, it is possible that it was the falling graph distance that led to the rise of the Small World phenomenon; and that falling clustering weakened the reputation-based social norm enforcement typical of small-scale, high-fertility societies. I discuss these two phenomena below.
Small World
In the decade between the mid-1990s and the mid-2000s, a new research field emerged: the statistical analysis of the social network among millions of people64, based on the rise of social networking sites and the emergence of network analysis as an academic discipline65,66. One key early finding was that the Small World phenomenon holds for large societies, and maybe the entire global population67.
This paper shows that the Small World phenomenon could have been caused by the pattern of falling fertility that first characterised Western Europe starting 200–300 years ago, which from the middle of the 20th century became a global phenomenon. The global population’s average fertility fell from 5.2 children per woman to 2.5 children between 1960 and 201068. A secondary effect, if any, comes from any method that allows an increase in social contacts, which social networking sites probably do, although the size of this effect is much debated69,70,71. In other words, the Small World phenomenon can be attributed to demographic transition rather than to internet-based social networking sites. The latter, together with the new science of social network analysis, merely allowed the recognition of the phenomenon.
Social norm enforcement
All social species have a problem of organising collective action. Sometimes the solution is dependent only on the ability to coordinate movement, e.g., a flock of fish or a herd of ungulates balancing predator avoidance or moving between patches of resources. Many species, however, rely on the costly contribution of individuals, and thus face the problem of how to ensure that group members pull their weight. Unless some solution emerges to deter free-riding, collective action collapses. Two main solutions have been invented by evolution: inclusive fitness72,73,74 and reputation dynamics75,76. The former relies on the presence of biological relatives, while the latter requires a stable social network with high local clustering. Traditional small-scale, high-fertility societies use both of these tricks when they organise collective action via kinship networks35. This paper shows that falling fertility in demographic transition affects both pathways: fewer children mean that families are smaller, and thus the individuals’ social networks are necessarily filled with friends more than with family; and at the same time, falling local clustering slows the spread of social information within the network.
In other words, demographic transition weakens the traditional methods of norm enforcement. One solution to this problem has been the emergence of the modern legal system, that is, an institutional framework that changes the incentives by altering individuals’ payoffs via standardised third-party punishers. In particular, the model’s result suggests that rules guiding interactions in collective action are likely to emerge in parallel with the shift from kin-based to non-kin-based social networks.
Urbanisation and Law
This paper assumes that agents form social connections with others that they recognise as relatives before they fill any gap in social contact numbers with non-kin friends. This assumption is based on empirical literature showing that both non-human social animals as well as humans consistently prefer to form social connections with relatives over non-relatives10,13,16,17,18,22,77. However, although as a general approximation the assumption of strong preference of network edges for kin over non-kin friends is well founded, empirically the relationship is not absolute24,25,53,54. In fact, the frequency of meaningful interaction affects the emotional closeness with both kin and non-kin54, mediated at least in part by geographical distance21.
To recognise this effect, let the concept ‘effective fertility’ denote the level of virtual fertility that corresponds to the number of relatives that agents have in their actual social network. Note that in a traditional society, the effective fertility is the same as actual fertility. However, in non-traditional societies it may not be so. If, for instance, others than relatives live in between an individual and her kin, frequent meaningful interaction will facilitate the formation of social network ties with these non-kin. Thus, real relatives are crowded out by spatially in-between non-kin.
This phenomenon is likely to occur in urban spaces, as well as in displaced, migrant populations. In all of these examples, the individuals lose connections to their real relatives even if they exist. For instance, in an urban space, maintaining meaningful relationships with relatively distant kin is likely to be more costly. Similarly, displaced or migrant populations are likely to have left at least some of their kin behind. A similar impact can result from epidemics if they affect the population evenly and, following the same logic, also from warfare. As a consequence, the available number of kin with whom the individuals could populate their social networks, falls. The effect on the social network is equivalent to real fertility falling.
Thus, urbanisation triggers a change in the social network structure, similar to decreasing fertility, without an actual drop in the number of children born. In an urban space, effective fertility falls without actual fertility changing. If this is true, then with urbanisation the average graph distance in the social network decreases, creating a Small World effect, while the social network’s local clustering falls, weakening the social sanction for norm-breaking, free-riding. This may explain why ideas travel faster in cities78, innovation rates correlate with city density79, and that the first codification of laws has been associated with the rise of early cities80. Furthermore, the falling clustering coefficient might explain some of the social factors of why people living in cities are more likely to feel lonely, and suffer from depression81,82,83.
Birds of a feather
The second key assumption of the model is that while the agents’ relatives are determined by biological lineage, the friends who fill the gap in social connections are chosen at random. Indeed, people tend to be born into kin networks, and thus, the assumption that the agents’ set of relatives is pre-determined is plausible. However, in reality, friends tend not to be chosen as a random draw from the non-kin pool of the population. Humans prefer friends with whom they share cultural heritage, preferences, tastes20,84,85.
If at least some of these characteristics are passed on within families from one generation to the next, then non-kin friends chosen for their similarity are likely to be less distant in the social network than a person drawn entirely randomly. To the extent this is the case, associative friendship choice counteracts the structural effect of falling fertility on the social network. However, as long as there is at least some level of randomness in kin-replacing friendship formation, the birds of a feather effect merely moderates rather than eliminates the phenomena predicted in this paper.
As higher local clustering results in an increased incentive not to free-ride on each other, and thus strengthens the network reputation effect, it is the interest of individual agents to increase the local clustering around them. In fact, this is exactly what people tend to do when they act in a way that results in triadic closures around them86. “I have somebody you must meet. You two will hit it off mightily” is a line that sounds as if making the new acquaintance was the interest of the two friends previously unknown to each other. That may be; however, if triadic closure is achieved in this way, it might benefit the introducer more than those introduced. For, if the new social tie becomes active, the introducer’s local clustering coefficient is guaranteed to increase, while that of the two new acquaintances may not (if the price of the new friend is dropping an old one in a way that this breaks up a triad).
Humans regularly engage in social activities that are likely to increase the local clustering in their social network. It may be having a hobby, joining a club, playing a team sport87,88,89. In fact, maybe the ultimate motivation for choosing a friend that is similar in some key characteristics is that this results in triadic closure90,91.
It is also possible that people adapt to the falling clustering coefficient by focusing on a select few social contacts. This friendship formation heuristic goes to the core of two important further assumptions of the paper: (i) that the number of social contacts is fixed, and (i) that all social contact links are unweighted, i.e., an edge either exists or it does not, and thus they are homogenous across the graph. This is not necessarily the case.
Recent empirical evidence suggests that as social networking sites and apps reduced the cost of maintaining social relationships, the number of social contacts, of any form, has increased considerably92. If the new social contacts are loosely linked friends, the first model of this paper suggests that social networking sites would decrease the clustering coefficient, albeit not the number of closed triads.
At the same time, empirical evidence suggests that the number of social contacts with whom the connection is strong, i.e., the core social network of individuals, has decreased in size both in offline networks of increasingly urban populations93, as well as on social networking sites94. This paper’s results suggest that such an increasing focus on the close network could be hypothesized as an adaptive response to falling fertility and increasing rate of urbanisation. The modelling consequences of this dual process are for future work.
In summary, the models of this paper introduce a new, causal link from demographic processes such as fertility transition, urbanisation, epidemics, warfare, and migration to social trust, and the emergence of legal institutions. The shared characteristic of all these demographic phenomena is that kin are replaced by friends either because fewer relatives were born as in the case of falling fertility, or because the relatives that are alive are not available as in the case of urbanisation and population displacement, or they have died as in the case of epidemics and warfare. As the missing kin are replaced by friends, the social network’s clustering coefficient falls, weakening the traditional mechanisms for eliminating free-riders. It is this mechanism that links these phenomena to falling societal trust, social alienation, and ultimately, the rise of a new way of ensuring collective action among non-kin: institutionalised norm enforcement. Thus, it is demographic processes that led to the weakening inclusive fitness-based, and network reputation-based solutions to the costly collective action problem, resulting in the emergence of a third solution: legal institutions.
Data Availability
This is a theoretical paper, there is no data associated with this manuscript.
References
David-Barrett, T. et al. Communication with Family and Friends across the Life Course. PloS one 11, https://doi.org/10.1371/journal.pone.0165687 (2016).
Eagle, N., Pentland, A. & Lazer, D. Inferring friendship network structure by using mobile phone data. Proceedings of the National Academy of Sciences of the United States of America 106, 15274–15278, https://doi.org/10.1073/pnas.0900282106 (2009).
Hruschka, D. J. Friendship: development, ecology, and evolution of a relationship. (University of California Press, 2010).
Rotkirch, A., Lyons, M., David-Barrett, T. & Jokela, M. Gratitude for Help among Adult Friends and Siblings. Evol Psychol-Us 12, 673–686 (2014).
David-Barrett, T. et al. Women favour dyadic relationships, but men prefer clubs: cross-cultural evidence from social networking. PloS one 10, e0118329, https://doi.org/10.1371/journal.pone.0118329 (2015).
DeScioli, P. & Kurzban, R. The Alliance Hypothesis for Human Friendship. PloS one 4, https://doi.org/10.1371/journal.pone.0005802 (2009).
Hruschka, D. J. & Henrich, J. Friendship, cliquishness, and the emergence of cooperation. Journal of theoretical biology 239, 1–15, https://doi.org/10.1016/j.jtbi.2005.07.006 (2006).
Massen, J. J. M. & Koski, S. E. Chimps of a feather sit together: chimpanzee friendships are based on homophily in personality. Evolution and Human Behavior 35, 1–8, https://doi.org/10.1016/j.evolhumbehav.2013.08.008 (2014).
Seyfarth, R. M. & Cheney, D. L. The evolutionary origins of friendship. Annual review of psychology 63, 153–177, https://doi.org/10.1146/annurev-psych-120710-100337 (2012).
Clutton-Brock, T. Cooperation between non-kin in animal societies. Nature 462, 51–57, https://doi.org/10.1038/nature08366 (2009).
Shavit, Y., Fischer, C. S. & Koresh, Y. Kin and Nonkin under Collective Threat - Israeli Networks during the Gulf-War. Soc Forces 72, 1197–1215, https://doi.org/10.2307/2580298 (1994).
Johnson, S. B. & Johnson, R. C. Support and Conflict of Kinsmen in Norse Earldoms, Icelandic Families, and the English Royalty. Ethol Sociobiol 12, 211–220, https://doi.org/10.1016/0162-3095(91)90004-A (1991).
Sear, R. & Mace, R. Who keeps children alive? A review of the effects of kin on child survival. Evolution and Human Behavior 29, 1–18, https://doi.org/10.1016/j.evolhumbehav.2007.10.001 (2008).
Morgan, C. J. Eskimo hunting groups, social kinship and the possibility of kin selection in humans. Ethol Sociobiol 1, 83–86 (1979).
Essock-Vitale, S. M. & McGuire, M. T. Women’s lives viewed from an evolutionary perspective: II. Patterns of helping. Ethol Sociobiol 6, 155–173 (1985).
Betzig, L. & Turke, P. Food sharing on Ifaluk. Current Anthropology 27, 397–400 (1986).
Archie, E. A., Moss, C. J. & Alberts, S. C. In Amboseli Elephants: A long-term perspective on a long-lived mammal (eds Moss, C. J. & Croze, H.) (University of Chicago Press, 2011).
Creel, S. & Creel, N. M. The African wild dog: behavior, ecology, and conservation. (Princeton University Press, 2002).
Krutzen, M. et al. Contrasting relatedness patterns in bottlenose dolphins (Tursiops sp.) with different alliance strategies. P Roy Soc B-Biol Sci 270, 497–502, https://doi.org/10.1098/Rspb.2002.2229 (2003).
Curry, O. & Dunbar, R. I. Do birds of a feather flock together? The relationship between similarity and altruism in social networks. Human nature 24, 336–347, https://doi.org/10.1007/s12110-013-9174-z (2013).
Pollet, T. V., Roberts, S. G. & Dunbar, R. I. Going that extra mile: individuals travel further to maintain face-to-face contact with highly related kin than with less related kin. PloS one 8, e53929, https://doi.org/10.1371/journal.pone.0053929 (2013).
Hughes, A. L. Evolution and human kinship. (Oxford University Press, 1988).
Burton-Chellew, M. N. & Dunbar, R. I. M. Are Affines Treated as Biological Kin? A Test of Hughes’s Hypothesis. Current Anthropology 52, 741–746, https://doi.org/10.1086/661288 (2011).
Hill, K. R. et al. Co-residence patterns in hunter-gatherer societies show unique human social structure. Science 331, 1286–1289, https://doi.org/10.1126/science.1199071 (2011).
Dyble, M. et al. Sex equality can explain the unique social structure of hunter-gatherer bands. Science 348, 796–798, https://doi.org/10.1126/science.aaa5139 (2015).
Allen, N. J. The Evolution of Kinship Terminologies. Lingua 77, 173–185 (1989).
Panter-brick, C. Motherhood and subsistence work: the Tamang of rural Nepal. Human ecology 17, 205–228 (1989).
Berté, N. A. In Human reproductive behaviour (eds Betzig, L., Borgerhoff Mulder, M. & Turke, P.) 83–96 (Cambridge University Press., 1988).
Hames, R. Garden labor exchange among the Ye’Kwana. Ethology and Sociobiology 8, 259–284 (1987).
Caldwell, J. C. & Caldwell, B. Demographic transition theory. (Springer, 2006).
Canning, D. The causes and consequences of demographic transition. Population studies 65, 353–361, https://doi.org/10.1080/00324728.2011.611372 (2011).
Caldwell, J. C. Toward a Restatement of Demographic Transition Theory. Popul Dev Rev 2, 321–366, https://doi.org/10.2307/1971615 (1976).
Chesnais, J.-C., Kreager, P. & Kreager, E. The demographic transition: stages, patterns, and economic implications: a longitudinal study of sixty-seven countries covering the period 1720–1984. (Clarendon Press, 1992).
Galor, O. The demographic transition: causes and consequences. Cliometrica 6, 1–28, https://doi.org/10.1007/s11698-011-0062-7 (2012).
David-Barrett, T. & Dunbar, R. I. M. Fertility, kinship, and the evolution of mass ideologies. Journal of theoretical biology 417, 20–27, https://doi.org/10.1016/j.jtbi.2017.01.015 (2017).
Galor, O. The demographic transition and the emergence of sustained economic growth. J Eur Econ Assoc 3, 494–504, https://doi.org/10.1162/1542476054473170 (2005).
Myrskyla, M., Kohler, H. P. & Billari, F. C. Advances in development reverse fertility declines. Nature 460, 741–743, https://doi.org/10.1038/nature08230 (2009).
Bernardi, L. & Klarner, A. Social networks and fertility. Demographic Research 30, 641–669 (2014).
Keim, S., Klarner, A. & Bernardi, L. Qualifying Social Influence on Fertility Intentions Composition, Structure and Meaning of Fertility-relevant Social Networks in Western Germany. Curr Sociol 57, 888–907, https://doi.org/10.1177/0011392109342226 (2009).
Madhavan, S., Adams, A. & Simon, D. Women’s networks and the social world of fertility behavior. Int Fam Plan Perspec 29, 58–68, https://doi.org/10.2307/3181059 (2003).
Kohler, H. P., Behrman, J. R. & Watkins, S. C. The density of social networks and fertility decisions: Evidence from South Nyanza District, Kenya. Demography 38, 43–58, https://doi.org/10.1353/dem.2001.0005 (2001).
Newson, L., Postmes, T., Lea, S. E. G. & Webley, P. Why are modern families small? Toward an evolutionary and cultural explanation for the demographic transition. Personality and Social Psychology Review 9, 360–375, https://doi.org/10.1207/s15327957pspr0904_5 (2005).
Newson, L. et al. Influences on communication about reproduction: the cultural evolution of low fertility. Evolution and Human Behavior 28, 199–210, https://doi.org/10.1016/j.evolhumbehav.2007.01.003 (2007).
Mathews, P. & Sear, R. Does the kin orientation of a British woman’s social network influence her entry into motherhood? Demographic Research 28, 313–340, https://doi.org/10.4054/DemRes.2013.28.11 (2013).
Colleran, H. & Mace, R. Social network- and community-level influences on contraceptive use: evidence from rural Poland. P R Soc B 282, https://doi.org/10.1098/rspb.2015.0398 (2015).
Murphy, M. Variations in kinship networks across geographic and social space. Popul Dev Rev 34, 19-+, https://doi.org/10.1111/j.1728-4457.2008.00204.x (2008).
Murphy, M. Family and Kinship Networks in the Context of Ageing Societies. Int Stud Popul 8, 263–285, https://doi.org/10.1007/978-90-481-3553-0_11 (2010).
Murphy, M. Long-Term Effects of the Demographic Transition on Family and Kinship Networks in Britain. Popul Dev Rev 37, 55–80, https://doi.org/10.1111/j.1728-4457.2011.00378.x (2011).
Dunbar, R. I. M. & Spoors, M. Social Networks, Support Cliques, and Kinship. Hum Nature-Int Bios 6, 273–290 (1995).
Hill, R. A. & Dunbar, R. I. M. Social network size in humans. Hum Nature-Int Bios 14, 53–72 (2003).
Dunbar, R. I. & Shultz, S. Evolution in the social brain. Science 317, 1344–1347, https://doi.org/10.1126/science.1145463 (2007).
David-Barrett, T. & Dunbar, R. I. Processing power limits social group size: computational evidence for the cognitive costs of sociality. Proceedings. Biological sciences/The Royal Society 280, 20131151, https://doi.org/10.1098/rspb.2013.1151 (2013).
Roberts, S. G. B. & Dunbar, R. I. M. Communication in social networks: Effects of kinship, network size, and emotional closeness. Personal Relationships 18, 439–452, https://doi.org/10.1111/j.1475-6811.2010.01310.x (2011).
Roberts, S. G. B. & Dunbar, R. I. M. The costs of family and friends: an 18-month longitudinal study of relationship maintenance and decay. Evolution and Human Behavior 32, 186–197, https://doi.org/10.1016/j.evolhumbehav.2010.08.005 (2011).
Caldwell, J. C. & Caldwell, B. K. Pretransitional population control and equilibrium. Pop Stud-J Demog 57, 199–215, https://doi.org/10.1080/0032472032000097100 (2003).
Dunbar, R. I. M. In The Archaeology of Human Ancestry: Power, Sex and Tradition (eds Steele, J. & Shennan, S.) 380–396 (Routledge, 1997).
Lehmann, J., Korstjens, A. H. & Dunbar, R. I. M. Group size, grooming and social cohesion in primates. Anim Behav 74, 1617–1629, https://doi.org/10.1016/j.anbehav.2006.10.025 (2007).
Goncalves, B., Perra, N. & Vespignani, A. Modeling Users’ Activity on Twitter Networks: Validation of Dunbar’s Number. PloS one 6, https://doi.org/10.1371/journal.pone.0022656 (2011).
David, B., Huszti, E., Barna, I. & Fu, Y. C. Egocentric contact networks in comparison: Taiwan and Hungary. Social Networks 44, 253–265, https://doi.org/10.1016/j.socnet.2015.10.001 (2016).
Kardos, P., Leidner, B., Pleh, C., Soltesz, P. & Unoka, Z. Empathic people have more friends: Empathic abilities predict social network size and position in social network predicts empathic efforts. Social Networks 50, 1–5, https://doi.org/10.1016/j.socnet.2017.01.004 (2017).
David-Barrett, T. & Carney, J. The deification of historical figures and the emergence of priesthoods as a solution to a network coordination problem. Relig Brain Behav 6, 307–317, https://doi.org/10.1080/2153599x.2015.1063001 (2016).
David-Barrett, T. & Dunbar, R. I. M. Social elites can emerge naturally when interaction in networks is restricted. Behavioral Ecology 25, 58–68, https://doi.org/10.1093/beheco/art085 (2014).
David-Barrett, T. & Dunbar, R. I. M. Cooperation, behavioural synchrony and status in social networks. Journal of theoretical biology 308, 88–95, https://doi.org/10.1016/j.jtbi.2012.05.007 (2012).
Dodds, P. S., Muhamad, R. & Watts, D. J. An experimental study of search in global social networks. Science 301, 827–829, https://doi.org/10.1126/science.1081058 (2003).
Scott, J. & Carrington, P. J. 1 online resource (xvi, 622 pages) (SAGE, London; Thousand Oaks, Calif., 2011).
Freeman, L. C. The development of social network analysis: a study in the sociology of science. (Empirical Press, 2004).
Watts, D. J. Six degrees: the science of a connected age. (Norton, 2003).
WorldBank. World Bank Development Indicators. (2017).
Dunbar, R. I. M. Do online social media cut through the constraints that limit the size of offline social networks? Royal Society Open Science 3, https://doi.org/10.1098/rsos.150292 (2016).
Pollet, T. V., Roberts, S. G. B. & Dunbar, R. I. M. Use of Social Network Sites and Instant Messaging Does Not Lead to Increased Offline Social Network Size, or to Emotionally Closer Relationships with Offline Network Members. Cyberpsych Beh Soc N 14, 253–258, https://doi.org/10.1089/cyber.2010.0161 (2011).
Johnson, R., Kovacs, B. & Vicsek, A. A comparison of email networks and off-line social networks: A study of a medium-sized bank. Social Networks 34, 462–469, https://doi.org/10.1016/j.socnet.2012.02.004 (2012).
Hamilton, W. D. Evolution of Altruistic Behavior. Am Nat 97, 354-&, https://doi.org/10.1086/497114 (1963).
Hamilton, W. D. Genetical Evolution of Social Behaviour 2. Journal of theoretical biology 7, 17-&, https://doi.org/10.1016/0022-5193(64)90039-6 (1964).
Hamilton, W. D. Genetical Evolution of Social Behaviour I. Journal of theoretical biology 7, 1-&, https://doi.org/10.1016/0022-5193(64)90038-4 (1964).
Axelrod, R. & Dion, D. The Further Evolution of Cooperation. Science 242, 1385–1390, https://doi.org/10.1126/science.242.4884.1385 (1988).
Axelrod, R. & Hamilton, W. D. The Evolution of Cooperation. Science 211, 1390–1396, https://doi.org/10.1126/science.7466396 (1981).
Krutzen, M. et al. Contrasting relatedness patterns in bottlenose dolphins (Tursiops sp.) with different alliance strategies. Proceedings. Biological sciences/The Royal Society 270, 497–502, https://doi.org/10.1098/rspb.2002.2229 (2003).
Bettencourt, L. & West, G. A unified theory of urban living. Nature 467, 912–913, https://doi.org/10.1038/467912a (2010).
Pan, W., Ghoshal, G., Krumme, C., Cebrian, M. & Pentland, A. Urban characteristics attributable to density-driven tie formation. Nature communications 4, https://doi.org/10.1038/ncomms2961 (2013).
Katz, S. N. The Oxford international encyclopedia of legal history. (Oxford University Press, 2009).
Romans, S., Cohen, M. & Forte, T. Rates of depression and anxiety in urban and rural Canada. Soc Psych Psych Epid 46, 567–575, https://doi.org/10.1007/s00127-010-0222-2 (2011).
Marsella, A. J. Urbanization, mental health, and social deviancy. A review of issues and research. Am Psychol 53, 624–634 (1998).
Cyril, S., Oldroyd, J. C. & Renzaho, A. Urbanisation, urbanicity, and health: a systematic review of the reliability and validity of urbanicity scales. Bmc Public Health 13, https://doi.org/10.1186/1471-2458-13-513 (2013).
McPherson, M., Smith-Lovin, L. & Cook, J. M. Birds of a feather: Homophily in social networks. Annual Review of Sociology 27, 415–444, https://doi.org/10.1146/Annurev.Soc.27.1.415 (2001).
David-Barrett, T. et al. Life Course Similarities on Social Network Sites. Adv Life Course Res (2016).
Kossinets, G. & Watts, D. J. Empirical analysis of an evolving social network. Science 311, 88–90, https://doi.org/10.1126/science.1116869 (2006).
Schaefer, D. R., Simpkins, S. D., Vest, A. E. & Price, C. D. The Contribution of Extracurricular Activities to Adolescent Friendships: New Insights Through Social Network Analysis. Dev Psychol 47, 1141–1152, https://doi.org/10.1037/a0024091 (2011).
Heidler, R., Gamper, M., Herz, A. & Esser, F. Relationship patterns in the 19th century: The friendship network in a German boys’ school class from 1880 to 1881 revisited. Social Networks 37, 1–13, https://doi.org/10.1016/j.socnet.2013.11.001 (2014).
Cheadle, J. E. & Schwadel, P. The ‘friendship dynamics of religion,’ or the ‘religious dynamics of friendship’? A social network analysis of adolescents who attend small schools. Soc Sci Res 41, 1198–1212, https://doi.org/10.1016/j.ssresearch.2012.03.014 (2012).
Wimmer, A. & Lewis, K. Beyond and Below Racial Homophily: ERG Models of a Friendship Network Documented on Facebook. Am J Sociol 116, 583–642, https://doi.org/10.1086/653658 (2010).
Lewis, K., Gonzalez, M. & Kaufman, J. Social selection and peer influence in an online social network. Proceedings of the National Academy of Sciences of the United States of America 109, 68–72, https://doi.org/10.1073/pnas.1109739109 (2012).
Croom, C., Gross, B., Rosen, L. D. & Rosen, B. What’s Her Face(book)? How many of their Facebook “friends” can college students actually identify? Computers in Human Behavior 56, 135–141, https://doi.org/10.1016/j.chb.2015.11.015 (2016).
McPherson, M., Smith-Lovin, L. & Brashears, M. E. Social isolation in America: Changes in core discussion networks over two decades. Am Sociol Rev 71, 353–375, https://doi.org/10.1177/000312240607100301 (2006).
Yau, J. C., Reich, S. M., Wang, Y., Niiya, M. & Mark, G. More friends, more interactions? The association between network size and interactions on Facebook. First Monday 23 (2018).
Author information
Authors and Affiliations
Contributions
I am the sole author, and hence all contributions are mine.
Corresponding author
Ethics declarations
Competing Interests
The author declares no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
David-Barrett, T. Network Effects of Demographic Transition. Sci Rep 9, 2361 (2019). https://doi.org/10.1038/s41598-019-39025-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39025-4
This article is cited by
-
The anatomy of a population-scale social network
Scientific Reports (2023)
-
Herding Friends in Similarity-Based Architecture of Social Networks
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.