Abstract
Microbubble contrast agents are widely used in ultrasound imaging and therapy, typically with transmission center frequencies in the MHz range. Currently, an ultrasound center frequency near 250 kHz is proposed for clinical trials in which ultrasound combined with microbubble contrast agents is applied to open the blood brain barrier, since at this low frequency focusing through the human skull to a predetermined location can be performed with reduced distortion and attenuation compared to higher frequencies. However, the microbubble vibrational response has not yet been carefully evaluated at this low frequency (an order of magnitude below the resonance frequency of these contrast agents). In the past, it was assumed that encapsulated microbubble expansion is maximized near the resonance frequency and monotonically decreases with decreasing frequency. Our results indicated that microbubble expansion was enhanced for 250 kHz transmission as compared with the 1 MHz center frequency. Following 250 kHz insonation, microbubble expansion increased nonlinearly with increasing ultrasonic pressure, and was accurately predicted by either the modified Rayleigh–Plesset equation for a clean bubble or the Marmottant model of a lipid-shelled microbubble. The expansion ratio reached 30-fold with 250 kHz at a peak negative pressure of 400 kPa, as compared to a measured expansion ratio of 1.6 fold for 1 MHz transmission at a similar peak negative pressure. Further, the range of peak negative pressure yielding stable cavitation in vitro was narrow (~100 kPa) for the 250 kHz transmission frequency. Blood brain barrier opening using in vivo transcranial ultrasound in mice followed the same trend as the in vitro experiments, and the pressure range for safe and effective treatment was 75–150 kPa. For pressures above 150 kPa, inertial cavitation and hemorrhage occurred. Therefore, we conclude that (1) at this low frequency, and for the large oscillations, lipid-shelled microbubbles can be approximately modeled as clean gas microbubbles and (2) the development of safe and successful protocols for therapeutic delivery to the brain utilizing 250 kHz or a similar center frequency requires consideration of the narrow pressure window between stable and inertial cavitation.
Similar content being viewed by others
Introduction
Microbubbles (MBs) composed of a gas core with a stabilizing shell serve as contrast agents for ultrasound imaging. Each MB is a few microns in diameter, and hence can be safely injected intravenously. At frequencies that match the range of clinical ultrasound, MBs are highly echogenic due to the impedance mismatch between the MB and the surrounding tissue and their near resonant oscillation. This oscillation yields a strong returned echo from an incident ultrasound pulse, with single MBs detected within vessels in vivo. Therefore, MBs are extensively used for ultrasound imaging1, and more recently, for super resolution imaging2,3. In addition to imaging, MBs are also used for therapeutic applications including drug delivery4, gene-based therapy5,6, and blood brain barrier (BBB) opening7,8,9. Upon ultrasound excitation, MBs cavitate and pulsate volumetrically. Among other parameters, the oscillation dynamics depend on the acoustic peak negative pressure (PNP), frequency, and MB diameter. Optical observations of MBs have been used to study their radial oscillations10, translation11, and fragmentation12,13,14,15 for both free and adherent MBs16,17.
The safety of MB-based treatments is assessed by monitoring MB cavitation. MBs under stable and inertial cavitation have distinct acoustical signatures that are detected by real-time feedback provided by MBs echoes9,18,19. At a low acoustic pressure, the MB gas is compressed and expanded repeatedly, a process known as stable cavitation. During long-lasting stable cavitation oscillations, adjacent cell membranes are temporarily altered, facilitating therapeutic delivery20. This process is associated with microstreaming surrounding the MBs that can reversibly modify the permeability of the cell membranes21. At a high acoustic pressure, inertial cavitation occurs. The MBs rapidly collapse and will be destroyed via fragmentation into smaller MBs or gas diffusion. MB collapse can produce liquid jets that release high levels of energy and may cause severe mechanical damage to the surrounding tissues because of its associated high internal temperature, pressure, and velocity jets22,23,24,25. Inertial cavitation may result in thermal and/or mechanical injury to normal brain adjacent to the clinical target and may result in devastating and potentially fatal intracranial hemorrhage.
MB excitation is typically performed in the frequency range of commercial ultrasound imaging (1–5 MHz). A lower transmission center frequency is desirable to enhance the penetration depth and enlarge the focal zone. Clinical therapeutic ultrasound systems typically operate with a center frequency between 650 kHz and 1.5 MHz26,27,28. Yet, systems using a center frequency of ~220 kHz are now entering clinical and human use29,30. For brain therapy applications, the lower frequency aids in focusing through the human skull to a predetermined location with minimal distortion and attenuation, as compared to higher frequencies31 and eliminates the need for extensive patient-specific correction32. In addition, for the undersampled transducer arrays used in therapeutic ultrasound, the use of a lower frequency also facilitates beam steering by reducing grating lobes. However, the oscillation of MB contrast agents has not been fully assessed in this frequency range.
The mechanical index33 (PNP divided by the square root of the center frequency) and the cavitation index34 (PNP divided by the center frequency) are parameters that were derived to gauge the likelihood of adverse bioeffects from inertial cavitation and monitor the MB activity during stable cavitation. The inverse dependence of these parameters on the ultrasound center frequency predicts larger adverse bioeffects at lower frequencies. The resonant size of typical MBs is at frequencies between 2 and 10 MHz35. Therefore, for frequencies lower than 800 kHz, the MBs are significantly smaller than the resonance wavelength. In the past it was assumed that below 800 kHz, the mechanical and cavitation indices will not be valid, and that larger acoustic pressures will be required to initiate stable and inertial cavitation34,36,37. However, for a free gas bubble, the response to quasistatic pressure changes in the liquid (i.e. excitation well below the natural resonance frequency) shows that a rarefactional pressure threshold exists above which unstable equilibrium conditions arise. The pressure at which this growth occurs is known as the Blake threshold and is a consequence of the fact that an unshelled MB in liquid cannot withstand arbitrarily high static tension induced by rarefactional pressure38,39,40. In vivo BBB opening studies with a center frequency of ~250 kHz in rabbits7,41 and macaques42, suggest that the window in which increased BBB permeability can be safely achieved is narrow, and report tissue damage above a relatively low PNP of 300 kPa. Therefore, in order to use this low frequency safely, there is a need to characterize the oscillation of shelled MBs following transmission of an ultrasound pulse with a center frequency near 250 kHz.
Here, characterization of MB dynamics was performed through theoretical predictions, ultra high-speed optical imaging and passive cavitation detection of single oscillating MBs. Specifically, MB resting radii of ~0.75 and ~1.5 µm, were selected and investigated to approximate the radii of Definity and Optison (each commercially available) MBs. Finally, in vivo blood brain barrier opening was studied with transcranial ultrasound in mice.
Materials and Methods
Modeling of the MB oscillation at 250 kHz is of primary importance in predicting the stable cavitation range for treatment. The basis of MB oscillation models is the Rayleigh-Plesset Equation (RPE) for a clean (unencapsulated) MB43,44. Previous experimental results13,23,45 supported the validity of the RPE model for insonation at 1 MHz. More elaborate models incorporate nonlinearities in shell elasticity and viscosity46. Here, the numerical evaluations were performed using two models. The first is the modified RPE that estimates the MB radial oscillations while taking into account the effects of liquid compressibility, the shell and the surrounding tissue, as described previously47. The second is the Marmottant model, which accounts for buckling and rupture of the shell during oscillation48.
To provide a basis of comparison, we designate a lower limit on MB expansion ratio of 1.1 as a value where stable cavitation is established and that generates harmonic echoes (although other lower limits can also be considered). To further facilitate comparison, an expansion ratio upper limit of 3.5 was chosen as representing the regime resulting in crossover between stable and inertial cavitation (previous predictions ranged from 2.3 to 3.513,49).
Numerical evaluation parameters
At 250 kHz, a preliminary evaluation of the RPE indicates that the expansion ratio can exceed 35-fold at a PNP of 500 kPa. Since the surface area is proportional to the square value of the expansion ratio, at these large expansions, the resulting gas/water interface is exposed and the MBs can be modeled as clean gas (unshelled) MBs using the RPE46. In comparison, at 1 MHz, the oscillations at the same PNP range reach a maximal expansion ratio of 4, hence the shell effect is not negligible at this frequency.
All numerical evaluations were performed in MATLAB (Mathworks, Natick, MA). In the modified RPE47, a clean gas MB oscillating at a center frequency of 250 kHz was simulated by setting to zero the shell density, shear modulus, viscosity and thickness, as well as the surface tension of the inner radius. The surface tension of the MB outer radius set to that of saline (0.07 N/m). Using the same model, MB oscillations at a center frequency of 1 MHz were simulated according to previously described parameters47. Shell density was 1000 kg/m3, shell shear modulus was 122 MPa, shell viscosity was 2.5 Pa·s, shell thickness was 1.5 nm, surface tension of the inner radius was 0.04 N/m, and surface tension of the outer radius was 0.056 N/m.
In the Marmottant model, MBs were simulated according to48. The shell surface dilatational viscosity was 7.2 × 109 N, the elastic compression modulus was 0.55 N/m, and the initial surface tension of the MB outer radius was set to that of saline (0.07 N/m).
Experimental design considerations
In this analysis we focus on insonation using 250 kHz which is far below (more than a factor of 10) the resonance frequency (fc) for both clean gas and lipid-shelled MBs (Table 1)50. For 250 kHz insonation, the onset of high amplitude oscillation is therefore expected to be predicted by the Blake threshold at least for clean gas MBs, and we validate the applicability to lipid-shelled MBs here. Alternatively, a frequency of 1 MHz is less than a factor of ten from the resonance frequency for lipid-shelled MBs, thus the Blake threshold is not applicable for this frequency. The 1 MHz center frequency (closer to resonance) is therefore used as a basis for comparison to 250 kHz excitation (far from resonance).
We also consider the Blake threshold for the MB parameters and MBs studied here. The Blake pressure threshold for a clean gas MB in water at room temperature39 is given by
where PB is the Blake pressure threshold, r0 is the resting radius of the MB, σ is the surface tension, Pstat is the static pressure, and Pv is the vapor pressure. Here, we set σ to 0.07 N/m, Pstat to 100 kPa, Pv to 2.33 kPa.
Microbubble preparation
MBs composed of a gas core containing perfluorobutane (C4F10) encapsulated in a phospholipid shell, were prepared as reported in51 and briefly summarized here. The lipid shell is a combination of disteroylphosphatidylcholine (DSPC), and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] (ammonium salt) (DSPE-PEG2K) (Avanti Polar Lipids, Alabaster, AL) with a DSPC:DSPE-PEG2K ratio of 90:10 mol/mol. First, MB precursor solution was made using a thin-film hydration method and then was kept in 1 ml vials at 4 °C until use. Upon use, a single MB vial was activated by 45 seconds of shaking using a VIALMIX shaker (Lantheus Medical Imaging). Size selection was performed to separate the larger MBs (radii of above 1 µm), from the smaller MBs (radii of below 1 µm). The separation was performed by centrifuging the suspension at 16 relative centrifugal force for 1 minute, followed by 45 relative centrifugal force for 1 minute. After centrifuging, the turbid liquid at the bottom of the syringe contained the smaller MBs, whereas the MB cake contained the larger MBs. The smaller MB suspension underwent a second purification to remove MBs smaller than 0.5 µm in radii, by centrifuging at 300 relative centrifugal force for 3 minutes, 3 times, and collecting the MB cake. The size and concentration of the purified MBs were measured with a particle counter system (Accusizer 770 A, Particle Sizing Systems, Port Richey, FL). The MBs were used within three hours of their preparation. To confirm the MB stability over this period, the size and concentration was measured with the particle counter system immediately after preparation and at the end of the experiments. The size distribution and concentration changed by less than 5% between the measurements.
For the ultra high-speed imaging experiments, both larger (1.5 µm in radius), and smaller (0.75 µm in radius) MBs were independently studied. For the acoustical measurements and the in vivo experiments, the smaller sized MBs were used in order to narrow the distribution.
Ultra high-speed optical imaging setup
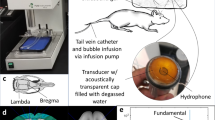
The experimental setup (illustrated in Fig. 1a) was composed of an inverted microscope (IX70, Olympus, Melville, NY), with a 100x objective and numerical aperture of 1 (Achroplan 100 × , Zeiss, Thornwood, NY). The in-house made lipid-shelled MBs were diluted in saline to approximately 5 × 104 MBs/µl. The diluted solution was pushed through a 200-μm cellulose tube with a manual microinjector (Narishige, Inc., East Meadow, NY). The cellulose tube was placed in a degassed water tank and positioned in the optical field of view of the microscope. The imaged MBs were located at the center of the cellulose fiber. Two transducers were used for insonation. First, a 250 kHz spherically-focused single-element transducer (H115, Sonic Concepts, Bothell, Washington) was placed in the degassed water tank, and aligned to focus on the cellulose fiber in the microscope’s field of view. This transducer has an aperture diameter of 64 mm, a focal distance of 51 mm, f-number of 0.79, lateral full width half maximum (FWHM) of 7 mm and axial FWHM of 50 mm.
The transducer’s pressure was calibrated with a wideband needle hydrophone (HNP-0400, Onda, Sunnyvale, CA, USA; 15% uncertainty in the hydrophone calibration at 250 kHz), and the received pressure signals were displayed on a digital oscilloscope (DPO4034, Tektronix, OR, USA). Here, the pressure corresponding to each predicted expansion was increased slightly (within the error of the hydrophone calibration, 30 kPa) to facilitate comparison between the theoretical and experimental results. Alternatively, the 250 kHz transducer was replaced by a 1 MHz spherically-focused transducer (ILO108HP, Valpey Fisher). This transducer has an aperture diameter of 25.4 mm, a focal distance of 50.8 mm, f-number of 2, lateral FWHM of 3.8 mm and axial FWHM of 46.8 mm. An arbitrary waveform generator (AWG 2021, Tektronix, Wilsonville, OR) was used to generate the desired radio frequency (RF) signal consisting of three to five-cycles of a sinusoid with a 250 kHz or 1 MHz center frequency. The signal was amplified with an RF power amplifier (325LA, ENI, Rochester, NY). Optical images were captured with an ultra high-speed camera (Imacon 468, DRS Hadland, Santa Cruz, CA). The high-speed camera triggered the arbitrary waveform generator, and after a delay equal to the sound propagation time from the transducer to the cellulose fiber, light from a xenon flash illuminated the microscope’s field of view via a 1 mm fiber-optic cable. The ultra high-speed camera captured a streak image (temporal resolution of 28 ns and spatial resolution of 120 nm) of the diameter of the MB as a function of time. Post processing of the images was performed in Matlab to yield the resting MB radius and expansion ratio.
Passive cavitation detection setup
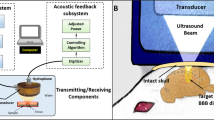
The spectra of the oscillating MBs echoes were recorded passively using a flat 1 MHz single element transducer (IMO102HP, Valpey Fisher) during interaction with a 250 kHz pulse. Four independent observations were made at each transmitted pressure for each of the frequencies of 250 kHz and 1 MHz. The transducer was positioned perpendicular to the 250 kHz transducer in the water tank and aligned azimuthally to focus at the cellulose fiber, as illustrated in Fig. 1b. The manual microinjector was used to introduce the MBs into the cellulose, at the same dilution of 5 × 104 MBs/µl used in the high-speed camera imaging experiments. The receive echoes were displayed using a digital oscilloscope (DPO4034, Tektronix, OR, USA), and saved for post processing in Matlab. Since therapeutic ultrasound typically uses long waveforms, the transmitted pulse consisted of a 100-cycle burst, representing the steady state excitation34 with PNP varied between 0 to 500 kPa. The transducer response was calibrated for each PNP prior to each experiment, by introducing degassed saline into the cellulose fiber, recording the spectra following insonation and subtracting this background signal from the echoes obtained throughout the experiments. Next, MBs were injected into the fiber and their corresponding response was recorded. The same process was repeated with a transmitted frequency of 1 MHz.
In vivo transcranial ultrasound parameters
All animal-related work performed by our laboratory was in accordance with the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health and all animal experiments were performed under a protocol approved by the Institutional Animal Care and Use Committee of the University of California, Davis. To determine the stable cavitation region where safe BBB disruption occurs with 250 kHz ultrasound, 7 groups of FVB mice (Charles River) were studied with the following protocols: (1) no treatment control (NTC) (n = 3), (2) ultrasound-only (no MBs) with a PNP of 500 kPa (twice the highest PNP used with MBs + ultrasound) (n = 3), (3) MBs + 75 kPa PNP (n = 3), (4) MBs + 100 kPa PNP (n = 6), (5) MBs + 150 kPa PNP (n = 6), 6) MBs + 190 kPa PNP (n = 3), and (6) MBs + 250 kPa PNP (n = 1). Contrast enhancement observed in the T1-weighted MR images was used to evaluate the BBB disruption. Prior to the experiment, fur around the treated area was shaved and then further removed using depilatory cream. Ultrasound gel was used as coupling agent. Anesthesia was induced with 2% isoflurane in oxygen (2 L/min). The mouse was positioned in the supine position at the focal depth of the transducer (z = 45 mm). Sonication was performed after injection of a 50 µL bolus of 4 × 107 in-house made MBs (average radius of 0.75 µm) into the tail vein of the animal. Sonication included ultrasound bursts of 10 ms, pulse repetition frequency of 0.2 Hz, and a total of 20 bursts.
At this low frequency, and for the thin skull of a mouse (thickness of ~0.4 mm), attenuation of the beam is negligible. To validate this assumption, a piece of ex vivo mouse skull was placed in the water tank between the transducer and the needle hydrophone. Pressure measurements with the skull positioned at the same orientation as in the in vivo experiments, showed no attenuation compared to water. Hence it can be concluded that the measured pressure behind the skull is attenuated only by the distance of the soft tissue that the beam propagates in (0.5 dB/cm/MHz), and not by the skull.
Magnetic resonance imaging
At 0 and 3 hours following ultrasound treatment, BBB opening was assessed using a Bruker Biospec 70/30 (7 T) small animal magnetic resonance imaging (MRI) scanner (Bruker BioSpin MRI, Ettlingen, Germany). The MRI system was equipped with a 72 mm internal diameter volume RF coil for signal transmission and a four-channel mouse brain phased array coil for signal reception. Animals were injected with gadoteridol (0.3 mmol/kg) intraperitoneally and imaged axially and coronally with a T1-weighted sequence (RARE: RARE factor = 2, TR = 300 ms, TE = 6 ms, NEX = 6; FOV = 19.2 × 19.2 mm2; MTX = 192 × 192, ST/SI = 1 mm/1 mm). Data were acquired and images were reconstructed using ParaVision 5.1 (Bruker BioSpin MRI). Assessment of contrast enhancement due to BBB opening was performed by calculating the contrast enhancement at the treated area relative to a non-treated area.
Histological evaluation
A subset of mice from each treated group (75, 100 and 150 kPa ultrasound and MBs) were monitored for 48 hours and were then euthanized. All other mice were euthanized at the end of the sonication day. Post euthanasia, the mouse brain was immediately harvested. The brains were maintained in 10% formalin solution for 7 days and underwent coronal sectioning in the area where the BBB was opened, according to the MRI assessment. Hematoxylin and eosin staining was used to investigate these paraffin-embedded, 4 μm thick brain sections.
Results
Numerical evaluation results
The Blake threshold predicts the growth of MB oscillations above a pressure threshold for excitation frequencies that are well below the resonance frequency of the MB (f0 ≪ fc,). From Equation 1, for a clean gas MB, PB is expected to be 175 and 140 kPa for MB radii of 0.75 and 1.5 µm, respectively. Therefore, for the 250 kHz center frequency (over an order of magnitude from MB resonance), MB oscillations were characterized below and above the Blake threshold pressure.
A range of PNP from 0 to 500 kPa was evaluated at center frequencies of 250 kHz and 1 MHz. We particularly focused on finding the PNP range that yields expansion ratios between 1.1 and 3.5 as approximate limits of stable and inertial cavitation, as previous literature has reported an upper limit of inertial cavitation between 2.3 and 3.513,49. The RPE predicts that in response to a 75 kPa, 250 kHz pulse, harmonic emissions are evident in the received echo spectrum from a 0.75 µm radius MB resulting in a 1.1-fold expansion ratio. Predicted echo bandwidth increased with an increase in the transmission pressure to 190 kPa and resulting 3.5-fold expansion ratio (Fig. 2a).
Theoretical predictions using the modified Rayleigh-Plesset Equation of MB oscillation at 250 kHz and 1 MHz with a three-cycle excitation. (a) Received spectrum for the transmitted pulse (Tx pulse) and echoes corresponding to 1.1-fold (75 kPa) and 3.5-fold (190 kPa) expansion following 250 kHz transmission, for 0.75 µm radius MBs. Maximal expansion as a function of MB radius and peak negative pressure (PNP) with an expansion of 1.1 and 3.5 fold indicated by the green and red lines, respectively, and the Blake threshold by the blue line (b) for a center frequency of 250 kHz. (c) for a center frequency of 1 MHz.
The RPE predicts a faster increase in expansion ratio at 250 kHz compared to 1 MHz (Fig. 2b,c). With 250 kHz transmission, MB expansion increases rapidly with a small increase in the transmitted pressure. For smaller MBs (~0.75 μm radius) and the 250 kHz transmission frequency, the MB expansion ratio increases nonlinearly and reaches 35-fold at 500 kPa (Fig. 2b), compared to 3.5-fold at 1 MHz for the same PNP. For larger MBs (~1.5 μm radius), the expansion ratio is smaller and reaches 20-fold and 4.5-fold for 250 kHz and 1 MHz, respectively, at a PNP 500 kPa.
Based on the distance between the green and red lines in Fig. 2b,c, we observe that the stable cavitation pressure range is narrower for the 250 kHz center frequency than for the 1 MHz center frequency (~a factor of 2). The onset of inertial cavitation for 250 kHz occurs at pressures below 200 kPa, and in close proximity to the Blake threshold. For example, for the 250 kHz center frequency, the range of pressures for which the MB expansion ratio remains between 1.1 and 3.5-fold is 75 to 190 kPa for 0.75 µm radius MBs and 55 to 165 kPa for 1.5 µm radius MBs, compared to 245 to 500 kPa and 125 to 400 kPa for the same MB size at 1 MHz.
Ultra high speed imaging results
We experimentally validated these predictions by observing single MBs insonified at a center frequency of 250 kHz using an ultra high-speed camera to capture the streak image of the diameter of the MB as a function of time. Images of ~250 single oscillating MBs were captured and processed. Representative streak images at four PNP values are presented in Fig. 3, where the red tick marks indicate the 4 µs period of the three-cycle excitation waveform. At a PNP of 100 kPa, stable cavitation was observed for both 0.75 and 1.5 µm radii (Fig. 3a,b). The crossover from stable to inertial cavitation occurred below a PNP of 165 kPa and 190 kPa for the 1.5 µm and 0.75 µm MBs, respectively. As a result, the smaller 0.75 µm MBs remained intact following insonation at 165 kPa (Fig. 3c), while the larger MB fragmented (Fig. 3d). A pressure of 190 kPa resulted in fragmentation of the 0.75 µm MB, hence at this pressure both MBs were observed to oscillate and fragment (Fig. 3e,f). At 300 kPa, expansion to a diameter greater than 45 µm was followed by fragmentation (Fig. 3g,h).
Increasing the PNP to 400 kPa resulted in a maximal expansion ratio of 1.6 for 1 MHz insonation (Fig. 4a), in agreement with the theoretical predictions. In comparison, for a center frequency of 250 kHz, an expansion ratio of 30 fold was observed with the same PNP (Fig. 4b).
Image post-processing determined the resting MB diameter and expansion ratio for experimental measurements (n = 4 each parameter set). With the 250 kHz center frequency, experimental observations of the expansion ratio as a function of PNP were similar to the RPE and the Marmottant model predictions for MBs with radii of 0.75 μm (Fig. 5a) and 1.5 μm (Fig. 5b). The expansion ratio increases rapidly as a function of pressure and reaches 35 and 17-fold at 500 kPa for the 0.75 and 1.5 μm resting radii, respectively.
Ultra high-speed camera experimental observations and theoretical predictions for MB expansion ratio using the modified Rayleigh-Plesset Equation (RPE) and the Marmottant model, as a function of peak negative pressure (PNP) for a transmission center frequency of 250 kHz and 1 MHz. (a) for MBs with radii of 0.75 μm. (b) for MBs with radii of 1.5 μm.
Passive cavitation detection results
The cavitation activity excited by a 250 kHz or 1 MHz burst for each PNP was then estimated using the second harmonic amplitude52 recorded passively using a 1-MHz transducer (Fig. 6a). The acoustical results follow the same trend of the theoretical predictions and the optical observations. For a center frequency of 250 kHz (black line, Fig. 6a), the signal increases linearly until ~175 kPa, followed by a non-linear increase in signal that is associated with inertial cavitation. The threshold for a rapid increase in the echo is similar to the optical and acoustical measurements; however, the slope of the increase differs, as expected, since the MB echo varies with the second derivative of the radial fluctuations. For a center frequency of 1 MHz (red line, Fig. 6a), the increase in expansion ratio begins at a higher PNP (400 kPa). The amplitude of the second harmonic at 500 kPa is reduced by 25 dB compared to a frequency of 250 kHz.
Passive cavitation detection. (a) RF amplitude of the second harmonic as a function of the peak negative pressure (PNP). Ultraharmonic components at 250 kHz insonation are indicated by the green arrows (b) Magnitude of the received echo spectrum following excitation of the MBs as a function of normalized frequency using 400 kPa and a center frequency of 250 kHz (black), and 1 MHz (red).
The spectral components further indicate inertial cavitation is associated with ultraharmonic components and increased broadband energy. At 400 kPa, the expansion ratio of MBs with the 1 MHz insonation is 1.6 (shown earlier in Fig. 4a). In this stable cavitation range, harmonic emission is expected (red line, Fig. 6b). Alternatively, at 250 kHz, for the same PNP of 400 kPa, the expansion ratio is 30 (shown earlier in Fig. 4b). Thus, strong inertial cavitation, with ultraharmonic amplitude similar to the harmonic components, and wideband signals are evident (black line, Fig. 6b).
In vivo transcranial ultrasound results
To complement the in vitro MB characterization, we sought to evaluate the range of pressure resulting in safe and effective BBB opening in vivo over a PNP range of 75 to 250 kPa. Contrast enhancement observed in the T1-weighted MR images was used to evaluate the BBB disruption. For the control groups of NTC and ultrasound-only (Fig. 7a), no contrast enhancement was observed. The group treated with 75 kPa PNP ultrasound and MBs (Fig. 7b), showed no contrast enhancement. In all groups treated with ultrasound and MBs, at a PNP of above 75 kPa, successful BBB opening in the sonicated area was observed (Fig. 7c–h). Mice treated with a PNP above 150 kPa (e.g. 190 kPa (Fig. 7g) and 250 kPa (Fig. 7h)) showed signs of acute neurological damage and were euthanized post treatment. For all other mice, contrast enhancement was additionally evaluated 3 hours post treatment. Contrast agent accumulation was not enhanced in the NTC, the ultrasound-only cohorts, and the mice treated with 75 kPa PNP ultrasound and MBs compared to the 0-hour time point. Contrast agent accumulation was enhanced in mice insonified with the 100 and 150 kPa PNPs at 3 hours post treatment compared to the 0-hour time point (Fig. 7d,f compared to Fig. 7c,e and Fig. 8a). Comparing the results of histology and the contrast enhancement, we find that a contrast enhancement of above 80% is associated with acute damage in the corresponding treated mice. Further, we find that there is a significant difference between the groups that were treated with different PNPs (Fig. 8b).
Coronal T1-weighted MR images. The contrast enhancement area is indicated by the red dashed circles. (a) US (ultrasound)-only with 500 kPa peak negative pressure (PNP), 3 hours post treatment. (b) ultrasound + MBs with 75 kPa PNP, 3 hours post treatment. (c,d) Ultrasound + MBs with 100 kPa PNP, at 0 and 3 hours post treatment respectively. (e,f) Ultrasound + MBs with 150 kPa PNP, at 0 and 3 hours post treatment respectively. (g) Ultrasound + MBs with 190 kPa PNP, at 0 hours post treatment. (h) Ultrasound + MBs with 250 kPa PNP, at 0 hours post treatment.
Contrast enhancement observed using magnetic resonance imaging (MRI). (a) Contrast enhancement as a function of ultrasound peak negative pressure (PNP) at 0 and 3 hours post treatment. (b) Contrast enhancement increases with the PNP of the therapeutic ultrasound pulse at 0 hours post treatment. *Indicates p < 0.05, and **indicates p < 0.01.
No changes were observed on histological evaluation for the NTC (Fig. 9a,b), ultrasound-only, and ultrasound + MBs 75, 100 and 150 kPa cohorts. No changes in five veterinary health measures (activity, weight, food intake, posture and hydration) were observed, and no pathological changes were detected in mice that were monitored for 48 hours post treatment. In the histological images associated with the higher PNPs of 190 (Fig. 9c,d) and 250 kPa (Fig. 9e,f), lesions were evident. Edema and acute micro vessel hemorrhage were observed through the presence of extravascular red blood cells, in addition to perivascular infiltration and vascular congestion.
Histological photomicrographs obtained 1 hour post treatment. (a) No treatment control (NTC). (b) 20x magnification of the dashed black square area in a. (c) MBs + 190 kPa peak negative pressure (PNP) ultrasound. (d) 20x magnification of the dashed black square area in c. (e) MBs + 250 kPa PNP ultrasound. (f) 20x magnification of the dashed black square area in e.
Discussion and Conclusions
Opening of the blood brain barrier to deliver therapeutics is an important goal. When commercial MB contrast agents oscillate in stable cavitation, transport to the brain can be safely accomplished. However, large oscillations and transient cavitation can damage delicate brain tissue and must be avoided18,19. Currently, an ultrasound center frequency near 250 kHz is proposed for therapeutic clinical human studies to open the blood brain barrier, rather than the intensively-studied MHz insonation frequency range18. The use of such a low ultrasound transmission center frequency is desirable to enhance penetration depth, enlarge the focal zone to reduce treatment time for larger clinically-important targets, minimize distortion and attenuation, and to facilitate beam steering throughout the brain using typical undersampled 2D therapeutic transducer arrays. This 250 kHz frequency is an order of magnitude below the resonance frequency of ultrasound contrast agents. While many previous studies have focused on resonant MB oscillation and assumed that oscillation is maximized at resonance, here we demonstrated that high amplitude oscillations can occur far from resonance, even for encapsulated MBs.
Our results indicate that MB expansion is enhanced for 250 kHz transmission as compared with the 1 MHz center frequency. In fact, predicted and measured expansion ratios reached 30-fold with 250 kHz at a PNP of 400 kPa, as compared to a measured expansion ratio of 1.6-fold for 1 MHz transmission at a similar PNP. Both in vitro and in vivo, we found that the oscillation of lipid-shelled MBs was similar to that of clean gas bubbles at this low frequency, and the effect of the MB shell was negligible due to the exposed gas/water interface resulting from the large expansion. The Marmottant model accounts for the surface tension modifications of the MB shell and its rupture for large oscillations. Under these assumptions, the MB behaves as a clean gas MB once the expansion extends beyond the rupture radius53—an inherent result of the Marmottant model for large expansion ratios which allows this model to predict the expansion ratio at 250 kHz. Similarly, numerical results obtained with the RPE, parameterized for a clean gas MB, were also consistent with the experimental observations.
The in vitro experiments were performed with MBs housed within a 200 µm cellulose tube. It was previously reported that when the distance between a MB and the tube wall is larger than 25 times the MB resting diameter, the MB behaves as if it is in an infinite fluid54. Here, since the MB diameters were less than 3 µm, the tube diameter was 200 µm, and the MBs imaged with the ultra high-speed camera were located at the center of the tube, their distance from the tube wall fulfills the above condition. Additionally, regardless of the vessel rigidity index, the natural frequency of a 3 µm MB oscillating in a 200 µm vessel is not significantly altered as described in Figs 3 and 5 in35. The assumption that the oscillation is similar to that of MBs within an infinite fluid is further validated by the similarity between the theoretical predictions of MBs oscillations assuming infinite space and the experimental results.
The Blake threshold has previously been applied to predict high amplitude oscillations of clean gas bubbles in the quasi static state (i.e. when they are insonified well below their resonance frequency) and predicts infinite growth beyond a static tension threshold. Since the resonance frequency for such clean gas MBs is 2.5 and 6 MHz for MB radii of 0.75 and 1.5 µm, the Blake threshold can be applied for 250 kHz insonation but not for 1 MHz insonation. The resulting Blake pressure threshold for low frequency insonation of MB radii of 0.75 and 1.5 µm is 175 and 140 kPa, respectively. These pressures are in agreement with the onset of inertial cavitation for encapsulated MBs as detected with the ultra high-speed camera imaging. We found that the Blake threshold can be accurately applied to predict the expansion of lipid-shelled MBs in the 250 kHz frequency range.
We emphasize that our study is limited to lipid-shelled MBs. However, the pressure threshold for the onset of inertial cavitation with shell materials such as albumin or polymer is expected to be different. Further study is needed to quantify the 250 kHz PNP range transitioning from stable cavitation to inertial cavitation for such materials.
In vivo results validated enhanced BBB opening with parameters similar to in vitro work
In vivo transcranial ultrasound at a center frequency of 250 kHz combined with MB injection in mice showed localized uptake of an MR contrast agent and confirmed BBB disruption at a PNP of 100–250 kPa. However, at PNPs above 150 kPa, inertial cavitation-induced mechanical lesions were evident. This indicates that the in vivo transition to inertial cavitation occurs near a PNP of 190 kPa and follows the same trend as MB oscillations in 200-µm cellulose fibers. Our previous work showed that (1) smaller vessels have a constraining effect on MB oscillations45, and also that (2) MB-mediated permeability changes can occur in vessels as large as 50 µm where the largest oscillations will occur55. Given that the microvasculature is composed of vessels with a range of diameters, we chose to study oscillation in larger vessels recognizing that the oscillation in the tubing used here will be similar to that in 40 µm or larger vessels, that this will be the largest oscillation that will occur, and that vascular changes do occur in vessels in this size range.
Results from our study confirm that the contrast enhancement estimation may hold a predictive value in assessing the safety of the treatment. When the ultrasound PNP is such that the MBs are in inertial cavitation, the treatment effect moves beyond a transient change in permeability and can potentially induce damage to brain tissue. The relationship between contrast enhancement and the duration of BBB permeability enhancement has been previously reported56, as well as the relationship between contrast enhancement, the magnitude of inflammatory response57 and changes in gene expression58. In this study, contrast enhancement below 80% did not result in a detectable injury. This correlation may help guide the safety standards for our particular experimental setup. However, the exact relationship between contrast enhancement and the safety of the treatment depends on the specific experimental setup, the ultrasound parameters, the species, the region of brain sonicated, the concentration of MRI contrast agent in circulation, the type of MRI contrast agent administered, etc. Therefore, the exact relationship should be established per experimental configuration.
Study considerations
The numerical evaluations assume that the MBs remain spherical during stable and inertial cavitation. Indeed, during inertial cavitation, MBs can fragment asymmetrically. Here, only streak images that exhibited radial symmetry oscillations were selected and analyzed. The ultra high-speed camera captures images with a temporal resolution of 28 ns, and an acquisition period of 16 µs (corresponding to 4 cycles of the 250 kHz transducer). Hence, we chose a three-cycle excitation for acquisitions with the ultra-high speed camera in order to visualize the entire oscillation. Since the maximal expansion ratio for inertial cavitation is achieved during the second cycle, the acquisition of three cycles was sufficient for the analysis of the expansion ratio that was performed here; Further, the maximal expansion analysis is also valid for longer transmissions that are used for therapeutic applications. Therapeutic ultrasound typically uses long waveforms, therefore for the cavitation detection and the in vivo study, we used 100-cycle bursts. The steady-state response that was characterized using passive cavitation detection and followed a similar trend as the results obtained with the ultra high-speed imaging.
In summary, the development of safe and successful protocols for therapeutic delivery to the brain, utilizing 250 kHz or a similar center frequency requires consideration of the narrow pressure window between stable and inertial cavitation. As a result, passive monitoring of the MB cavitation activity during an ultrasound treatment is particularly important in this low frequency range.
Data Availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Cosgrove, D. & Lassau, N. Imaging of perfusion using ultrasound. Eur. J. Nucl. Med. Mol. Imaging 37, 65–85 (2010).
Errico, C. et al. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 527, 499–502 (2015).
Foiret, J. et al. Ultrasound localization microscopy to image and assess microvasculature in a rat kidney. Sci. Rep. 7, 1–12 (2017).
Lai, C.-Y., Fite, B. Z. & Ferrara, K. W. Ultrasonic enhancement of drug penetration in solid tumors. Front. Oncol. 3, 204 (2013).
Chen, S. et al. Efficient gene delivery to pancreatic islets with ultrasonic microbubble destruction technology. Proc. Natl. Acad. Sci. USA 103, 8469–8474 (2006).
Chen, R., Chiba, M., Mori, S., Fukumoto, M. & Kodama, T. Periodontal gene transfer by ultrasound and nano/microbubbles. J. Dent. Res. 88, 1008–1013 (2009).
Hynynen, K. et al. Focal disruption of the blood–brain barrier due to 260-kHz ultrasound bursts: a method for molecular imaging and targeted drug delivery. J. Neurosurg. 105, 445–454 (2006).
Marquet, F. et al. Real-Time, Transcranial Monitoring of Safe Blood-Brain Barrier Opening in Non-Human Primates. PLoS One 9, e84310 (2014).
Sun, T. et al. Closed-loop control of targeted ultrasound drug delivery across the blood–brain/tumor barriers in a rat glioma model. Proc. Natl. Acad. Sci. 114, E10281–E10290 (2017).
De Jong, N. et al. Optical imaging of contrast agent microbubbles in an ultrasound field with a 100-MHz camera. Ultrasound Med. Biol. 26, 487–492 (2000).
Dayton, P. A., Allen, J. S. & Ferrara, K. W. The magnitude of radiation force on ultrasound contrast agents. J. Acoust. Soc. Am. 112, 2183–2192 (2002).
Chomas, J. E. et al. Optical observation of contrast agent destruction. Appl. Phys. Lett. 77, 1056–1058 (2000).
Chomas, J. E., Dayton, P., May, D. & Ferrara, K. Threshold of fragmentation for ultrasonic contrast agents. J. Biomed. Opt. 6, 141–150 (2001).
Sun, Y., Kruse, D. E., Dayton, P. A. & Ferrara, K. W. High-frequency dynamics of ultrasound contrast agents. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 1981–1991 (2005).
Caskey, C. F., Qin, S., Dayton, P. A. & Ferrara, K. W. Microbubble tunneling in gel phantoms. J. Acoust. Soc. Am. 125, EL183–EL189 (2009).
Borden, M. A. et al. Influence of lipid shell physicochemical properties on ultrasound-induced microbubble destruction. Ieee Trans. Ultrason. Ferroelectr. Freq. Control 52, 1992–2002 (2005).
Zhao, S., Kruse, D. E., Ferrara, K. W. & Dayton, P. A. Acoustic response from adherent targeted contrast agents. J. Acoust. Soc. Am. 120, EL63–EL69 (2006).
Tung, Y. S. et al. In vivo transcranial cavitation threshold detection during ultrasound-induced blood-brain barrier opening in mice. Phys. Med. Biol. 55, 6141–6155 (2010).
O’Reilly, M. A. & Hynynen, K. Blood-Brain Barrier: Real-time Feedback-controlled Focused Ultrasound Disruption by Using an Acoustic Emissions–based Controller. Radiology 263, 96–106 (2012).
Ferrara, K., Pollard, R. & Borden, M. Ultrasound microbubble contrast agents: fundamentals and application to gene and drug delivery. Annu. Rev. Biomed. Eng. 9, 415–447 (2007).
Wu, J., Ross, J. P. & Chiu, J. Reparable sonoporation generated by microstreaming. J Acoust Soc Am 111, 1460–1464 (2002).
Sheikov, N., McDannold, N., Vykhodtseva, N., Jolesz, F. & Hynynen, K. Cellular mechanisms of the blood-brain barrier opening induced by ultrasound in presence of microbubbles. Ultrasound Med Biol 30, 979–989 (2004).
Caskey, C. F., Stieger, S. M., Qin, S., Dayton, P. A. & Ferrara, K. W. Direct observations of ultrasound microbubble contrast agent interaction with the microvessel wall. J Acoust Soc Am 122, 1191–1200 (2007).
Freund, J. B., Colonius, T. & Evan, A. P. A Cumulative Shear Mechanism for Tissue Damage Initiation in Shock-Wave Lithotripsy. Ultrasound Med. Biol. 33, 1495–1503 (2007).
Miller, D. L. & Quddus, J. Diagnostic ultrasound activation of contrast agent gas bodies induces capillary rupture in mice. Proc. Natl. Acad. Sci. 97, 10179–10184 (2000).
Martin, E., Jeanmonod, D., Morel, A., Zadicario, E. & Werner, B. High-Intensity Focused Ultrasound for Noninvasive Functional Neurosurgery. Ann. Neurol. 66, 858–861 (2009).
Elias, W. J. et al. A Pilot Study of Focused Ultrasound Thalamotomy for Essential Tremor. new Engl. J. o f Med. 369, 640–648 (2013).
Iacopino, D. G. et al. Preliminary experience with a transcranial magnetic resonance–guided focused ultrasound surgery system integrated with a 1.5-T MRI unit in a series of patients with essential tremor and Parkinson’s disease. Neurosurg Focus 44, 1–10 (2018).
Krishna, V., Sammartino, F. & Rezai, A. A Review of the Current Therapies, Challenges, and Future Directions of Transcranial Focused Ultrasound Technology Advances in Diagnosis and Treatment. JAMA Neurol. 75, 246–254 (2018).
Lipsman, N. et al. Blood–brain barrier opening in Alzheimer’s disease using MR-guided focused ultrasound. Nat. Commun. 9, 1–8 (2018).
Hynynen, K. & Jolesz, F. A. Demonstration of potential noninvasive ultrasound brain therapy through an intact skull. Ultrasound Med. Biol. 24, 275–283 (1998).
Yin, X. & Hynynen, K. A numerical study of transcranial focused ultrasound beam propagation at low frequency. Phys. Med. Biol. 50, 1821–1836 (2005).
Apfel, R. E. & Holland, C. K. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound Med. Biol. 17, 179–185 (1991).
Bader, K. B. & Holland, C. K. Gauging the likelihood of stable cavitation from ultrasound contrast agents. Phys Med Biol 58, 127–144 (2013).
Qin, S. & Ferrara, K. W. The natural frequency of nonlinear oscillation of ultrasound contrast agents in microvessels. Ultrasound Med. Biol. 33, 1140–1148 (2007).
Neppiras, E. A. & Noltingk, B. E. Cavitation produced by ultrasonics: Theoretical conditions for the onset of cavitation. Proc. Phys. Soc. Sect. B 64, 1032–1038 (1951).
Leal, L. G. Bubble dynamics in time-periodic straining flows. J. Fluid Mech. 218, 41–69 (1990).
Blake, F. G. The onset of cavitation in liquids: I. (Harvard University, 1949. Tech. Memo, 1949).
Lauterborn, W. Numerical investigation of nonlinear oscillations of gas bubbles in liquids. J. Acoust. Soc. Am. 59, 283–293 (1976).
Harkin, A., Nadim, A. & Kaper, T. J. On acoustic cavitation of slightly subcritical bubbles. Phys. Fluids 11, 274–287 (1999).
Jones, R. M. et al. Three-dimensional transcranial microbubble imaging for guiding volumetric ultrasound-mediated blood-brain barrier opening. Theranostics 8, 2909–2926 (2018).
McDannold, N., Arvanitis, C. D., Vykhodtseva, N. & Livingstone, M. S. Temporary disruption of the blood-brain barrier by use of ultrasound and microbubbles: Safety and efficacy evaluation in rhesus macaques. Cancer Res. 72, 3652–3663 (2012).
Rayleigh, L. On the pressure developed in a liquid during the collapse. Philos. Mag. 34, 94–98 (1917).
Plesset, M. S. The Dynamics of Cavitation Bubbles. J. Appl. Mech. 16, 277–282 (1949).
Caskey, C. F., Kruse, D. E., Dayton, P. A., Kitano, T. K. & Ferrara, K. W. Microbubble oscillation in tubes with diameters of 12, 25, and 195 microns. Appl. Phys. Lett. 88, 0339021–0339023 (2006).
Doinikov, A. A. & Bouakaz, A. Review of shell models for contrast agent microbubbles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58, 981–993 (2011).
Qin, S. & Ferrara, K. W. A model for the dynamics of ultrasound contrast agents in vivo. J. Acoust. Soc. Am. 128, 1511–1521 (2010).
Marmottant, P. et al. A model for large amplitude oscillations of coated bubbles accounting for buckling and rupture. J. Acoust. Soc. Am. 118, 3499–3505 (2005).
Flynn, H. G. Cavitation dynamics: II. Free pulsations and models for cavitation bubbles. J. Acoust. Soc. Am. 58, 1160–1170 (1975).
Doinikov, A. A., Haac, J. F. & Dayton, P. A. Resonance frequencies of lipid-shelled microbubbles in the regime of nonlinear oscillations. Ultrasonics 49, 263–268 (2009).
Zhang, H. et al. Ultrasound Molecular Imaging of Tumor Angiogenesis with a Neuropilin-1-Targeted Microbubble. Biomaterials 1, 104–113 (2016).
Sboros, V. et al. Absolute measurement of ultrasonic backscatter from single microbubbles. Ultrasound Med. Biol. 31, 1063–1072 (2005).
Postema, M., Van Wamel, A., Lancée, C. T. & De Jong, N. Ultrasound-induced encapsulated microbubble phenomena. Ultrasound Med. Biol. 30, 827–840 (2004).
Thomas, D. H., Sboros, V., Emmer, M., Vos, H. & Jong, N. Microbubble oscillations in capillary tubes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60, 105–114 (2013).
Stieger, S. M. et al. Enhancement of Vascular Permeability with Low-Frequency Contrast-enhanced Ultrasound in the Chorioallantoic Membrane Model. Radiology 243, 112–121 (2007).
Marty, B. et al. Dynamic study of blood-brain barrier closure after its disruption using ultrasound: A quantitative analysis. J. Cereb. Blood Flow Metab. 32, 1948–1958 (2012).
McMahon, D. & Hynynen, K. Acute inflammatory response following increased blood-brain barrier permeability induced by focused ultrasound is dependent on microbubble dose. Theranostics 7, 3989–4000 (2017).
Kovacs, Z. I. et al. Disrupting the blood–brain barrier by focused ultrasound induces sterile inflammation. Proc. Natl. Acad. Sci. 114, E75–E84 (2017).
Acknowledgements
This work was supported by the National Institutes of Health (NIHR01CA112356, NIHR01CA199658, NIHR01CA211602, NIHR01CA210553, NIHR01CA134659, NIHR01CA227687, and NIHR01EB026094).
Author information
Authors and Affiliations
Contributions
T.I. performed the numerical evaluations and the experiments, analyzed the experiments results, and drafted the manuscript. A.I. fabricated the experimental setups and helped in performing the experiments. J.F. assisted with the numerical evaluations and contributed to the manuscript preparation. C.F.C. and J.K. assisted with the passive cavitation detection experiments. C.F.C. helped in drafting the manuscript. B.Z.F. contributed to the MRI experiment. H.Z. assisted with MB preparation. L.M.M. and S.T. contributed to the in vivo experiments. K.B.P. helped to draft the manuscript. S.Q. and K.W.F. advised the work and contributed to the experimental design and to the manuscript preparation. All authors have approved the final article.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ilovitsh, T., Ilovitsh, A., Foiret, J. et al. Enhanced microbubble contrast agent oscillation following 250 kHz insonation. Sci Rep 8, 16347 (2018). https://doi.org/10.1038/s41598-018-34494-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-34494-5
Keywords
This article is cited by
-
Deep laser microscopy using optical clearing by ultrasound-induced gas bubbles
Nature Photonics (2022)
-
Development of an ultrasound guided focused ultrasound system for 3D volumetric low energy nanodroplet-mediated histotripsy
Scientific Reports (2022)
-
Design method and machine learning application of acoustic holographic computational metamaterials
Science China Technological Sciences (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.