Abstract
In environments where orientation is ambiguous, the visual system uses prior knowledge about lighting coming from above to recognize objects, determine which way is up, and reorient the body. Here we investigated the extent with which assumed light from above preferences are affected by body orientation and the orientation of the retina relative to gravity. We tested the ability to extract shape-from-shading with seven human male observers positioned in multiple orientations relative to gravity using a modified KUKA anthropomorphic robot arm. Observers made convex-concave judgments of a central monocularly viewed stimulus with orientations of a shading gradient consistent with being lit from one of 24 simulated illumination directions. By positioning observers in different roll-tilt orientations relative to gravity and when supine, we were able to monitor change in the light-from-above prior (the orientation at which a shaded disk appears maximally convex). The results confirm previous findings that the light-from-above prior changes with body orientation relative to gravity. Interestingly, the results varied also with retinal orientation as well as an additional component that was approximately twice the frequency of retinal orientation. We use a modelling approach to show that the data are well predicted by summing retinal orientation with cross-multiplied utricle and saccule signals of the vestibular system, yielding gravity-dependent biases in the ability to extract shape-from-shading. We conclude that priors such as light coming from above appear to be constantly updated by neural processes that monitor self-orientation to achieve optimal object recognition over moderate deviations from upright posture at the cost of poor recognition when extremely tilted relative to gravity.
Similar content being viewed by others
Introduction
To reconstruct the three-dimensional structure of the world, humans use multiple sources of sensory information to estimate environmental properties in addition to relying on prior knowledge to optimally interpret sensory signals1. The Bayesian framework has been successful in explaining perceptual phenomena, because it is a statistical framework in which environmental statistics can naturally be incorporated using prior expectations about the world. In this framework, the ambiguities in the sensory information are represented in the likelihood functions, while the prior probability distribution represents pre-existing experience about the statistical regularities derived from the surrounding environment. The posterior probability distribution is proportional to the product of the prior and the likelihood function and is thought to form the basis for the percept. It remains unclear, however, what statistics priors exactly represent or in what reference frames they are coded. One extreme approach would be that environmental statistics are coded in allocentric (world-centred) coordinates such that the priors represent the statistics of the external world irrespective of the sensory receptors with which they are experienced. The other extreme approach may be that environmental statistics are coded in egocentric (receptor-centred) coordinates. In this case the priors would represent the statistics of retinal input (i.e., the statistics of the world convolved with retinal orientation). Alternatively, they may be a mixture of both that might even be flexibly adapted.
Consider for example the light from above prior2,3,4,5,6,7,8,9,10,11: if this prior represents the light source direction relative to gravity in the world (i.e., the statistics of the external world), the brain would need to discount the orientation of the head, the eyes and the body relative to gravity while learning this prior (world-centred coordinates). On the other hand, the brain may simply encode the statistics of the light source direction as determined on the receptor (here the retina), in which case the statistics are convolved with the eye, body, and head orientations while learning this prior (eye-centred coordinates).
From the literature, we know that in environments where orientation is ambiguous, the visual system uses prior knowledge about lighting coming from above to recognize objects, determine which way is up, and reorient the body2,3. The prior assumption that light comes from above can be measured using a shape-from-shading task4,5,6,7,8,9,10,11 where assumed lighting direction in the ability to extract shape from shading is predominantly predicted by orientation of the stimulus on the retina (i.e., predominantly eye-centred coordinates). This can be shown using the following demonstration. With one eye closed, the central patch in Fig. 1a (left) appears convex because it and three flankers (which enhance the effect) are brighter (i.e., shaded least) at the top. In Fig. 1a (right), the convex-concavity of the central patch is ambiguous as lighting now comes from the side but when observed by tilting the head to the left, then followed by tilting the head to the right, the central patch appears convex and then concave, consistent with the hypothesis that ‘above’ as regards the ‘light-from-above prior’ does not strictly refer to gravitational above5,6,7,8,9,10. Whether the light-from-above prior is fixed within a particular frame of reference or some combination has been previously explored5,6,7,8,9,10 where it has been shown that the head, the eye, gravity and vision all provide important frames of reference in determining how the light prior (LP) interacts with the stimulus to affect perception. Our objective with this experiment is to better understand the underlying integration process. To do so, we measure the change of the LP when observers are positioned in multiple orientations relative to gravity. As the eyes will counter-rotate to be oriented between gravity and the head across a range of body orientations when tilted in the roll plane, this allows us to assess the relative contribution of each of these frames of reference in determining the LP. Further, using this data set we can assess the underlying integration process using a modeling approach with a transfer function description of how known retinal orientation and the response properties of the utricle and saccule signals of the vestibular system may be integrated to resolve shape-from-shading across reference frames.
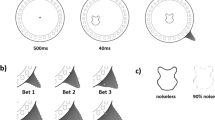
(a) Shape-from-shading stimuli. Central patch (3.03° visual angle), consistent with light-from-above (left) flanked by six peripheral patches (11.95° from centre). Another central patch (right) is ambiguous when viewed upright, convex when left-tilted, concave when right-tilted. (b) The Max Planck CyberMotion Simulator9 positioned observers (upright, supine, and upside-down shown). (c) Participant seated with neck brace, harness, and game pad observing stimuli through circular aperture tube in a room that would be dark during testing.
Methods
We investigated the relative contributions of head-on-body and retinal orientation relative to gravity in change of the light-from-above prior. We tested the ability to extract shape-from-shading with observers positioned in multiple orientations relative to gravity using a modified KUKA anthropomorphic robot arm12 (Fig. 1b,c). Seven 21–30 y male observers with normal vision monocularly viewed stimuli (Fig. 1a, left side) from 50 cm through a circular aperture (29.5 cm) in 12 roll postures (0:30:330°) relative to gravity (0°) and when supine (Fig. 1b). Posture order was randomized. Observers made convex-concave judgments of a central stimulus whose shading gradient orientation was consistent with illumination from one of 24 directions (0:15:345°). Each orientation was randomly presented 6 times. Each participant completed 1,728 trials (12 × 24 × 6) that took approximately 2 hours to complete. Trials began with a central green fixation circle (0.53° of visual arc; 1 s), followed by test stimuli (1.5 s), a uniform monochromatic random noise mask stimulus (1 s), and a gray background screen until observer response. Observers gave their informed and written consent prior to their inclusion in the study that the ethics review board of the Max Planck Institute for Biological Cybernetics approved in accordance with the Declaration of Helsinki. Data available from the authors.
The peak of the LP (LPp) for each participant in each posture was inferred from the data fit (Fig. 2). Here, the percentage of presentations that participants identified the central stimulus as ‘convex’ was plotted as a function of the lighting direction that the central stimulus was lit from. Two sigmoidal functions (Equation 1) were fitted to the participants’ response rate using Sigmaplot v12, which uses a residual sum of squares curve fitting approach to determine each of the convex-to-concave and concave-to-convex transitions for each body orientation. Here one sigmoid function was fit to the descending data points (convex to concave) and the other was fit to the ascending data points (concave to convex), with the two sets of data points divided by hand.
where: x0 corresponds to the 50% point and σ is the standard deviation. The average of the orientations at which these two transitions occurred was taken as the LPp.
(a) Supine LP data (symbolized by head symbol at the top) averaged across all participants. Stimuli lit from above (top of the head) correspond with 0° with values between 0:180° indicating being lit rightward and 180:360° indicating being lit leftward. Here the proportion of stimuli perceived as convex (dots) is fit by two sigmoidal functions (curved lines) each centred at a concave-convex transition whose average gives the peak of the LP (LPp radial line). Note supine data not included in model. (b) LP data averaged across participants with the body tilted (symbolized by separate head symbols for each orientation) in gravity coordinates and (c) the same data shown relative to head coordinates (right side; mean: 333.5°; range: 328° to 340°).
Results
When supine, where the influence of gravity and torsional eye movement are nulled, the LPp averaged across participants was up and significantly to the left of the head by −31.9° (s.e.: 8.7; one-sample t-test: t(6) = 3.5, p = 0.012, β = 0.839; Normality (Shaprio-Wilk): passed, p = 0.832; see Fig. 2a). Figure 2b shows the LPp averaged across participants for each body orientation in gravitational coordinates, whereas Fig. 2c shows these same data in body coordinates. As the purpose of our experiment was to assess gravity-dependent change in the LPp, we measured the LPp in each body orientation and subtracted this from the LPp that was measured with the observer upright relative to gravity so to express the LPp in head-centered coordinates (Fig. 3). This was done not only to look at change in the LPp relative to a baseline upright posture, but also to account for the large individual differences in the LPp leftward bias. Within this head-centered reference frame, the utricle would give zero response (sin(0) = 0) and the saccule would be maximal (cos(0) = 1) when the observer is upright. This is the 0 point on the abscissa where all observers are truly upright and change of the LPp relative to the LPp when upright collapses to zero (i.e., no change). Thus, if the LPp has a tilt of 10° to the left relative to gravitational ‘above’ when upright then any change of the LP will be made relative to this offset bias (i.e., 0 change when upright).
Change in the LPp averaged across participants (black symbols) relative to upright posture (0° on abscissa; red head symbol) for roll tilt of the observer. Prediction for change in the LPp from head orientation (i.e., no change; green horizontal prediction line), retinal orientation (blue prediction line; from13), otoliths (red prediction line; see Fig. 4), or the retinal + otolith model (black prediction line; see Fig. 4). Error bars, +/−1 s.e.m.
Significant change of the LP with posture rules out that the LPp is fixed to the head (RMANOVA: F(12,72) = 3.2, p = 0.001, β = 0.925; Normality (Shapiro-Wilk): passed, p = 0.825; Equal variance: passed, p = 0.091; Fig. 2b radial lines). When the head tilts relative to gravity, the eyes partially counter-rotate in order to maintain perceptual stability. Thus, if the LP were fixed to the retina, data in Figure 3 would vary sinusoidally by Equation 213 (blue line, R2 = 0.28, p = 0.06). We find however that change of the LPp is best fitted by the near equally weighted sum of the product of utricle (i.e., sin(head tilt)) and saccule (i.e., cos(head tilt)) responses to tilt of the head relative to gravity14,15 (red line) added to retinal orientation13 (Fig. 4; black line in Fig. 3; R2 = 0.94, p < 0.001; Equation 3).
where: y is change of the LPp, ø is head tilt relative to gravity, k is a gain, and wo and we are weights attributed to the otolith and retinal orientation relative to gravity components, respectively.
Theoretical model (Equation 3) showing how the inverse (−Ø) product (x symbol) of utricle (sin(head tilt)) and saccule (cos(head tilt)) signals with a gain of 14.7 are summed with retinal orientation (5.4° * −sin(ø)) with near equal weights (0.52 and 0.48, respectively) to predict change in the change in LPp for roll tilt of the observer. Retinal orientation prediction from13. The amplitude of multiplied otolith signals and weighting relative to retinal orientation are free parameters.
A Bayesian Information Criterion (MATLAB® 2013; aicbic function) was then calculated comparing our model with two free parameters (constant gain, relative weights; Equation 3, Fig. 3 black line, Fig. 4) with the simple parameter-free eye in head model (Equation 2, Fig. 3 blue line) which yielded a ΔBIC score of 132.154 in favour of Equation 3 over Equation 2, which is considered to be a “very strong” difference16. This suggests that participants’ estimates of shape from shading are better predicted with a retinal orientation model plus the inclusion of an additional component, which we attribute to cross multiplied otolith signals as depicted in Fig. 4.
Discussion
That the LP represents a bias of light coming from above and to the left of the head both when supine and when positioned in various roll-tilt body orientations relative to gravity is consistent with previous psychophysical6,8,9,11,17 and neuroimaging reports18. Although the supine data suggest that the leftward bias is largely within the head-on-body frame of reference, our results also confirm previous work that this prior is not invariant when the body tilts relative to gravity (i.e., it does not reside solely in a unique frame of reference)5,6,7,8,9,10. Rather the likelihood function that represents sensory information about light coming from above and to the left changes with incoming orthogonal vestibular responses to tilt of the head relative to gravity. One distinguishing feature of our results is that while we confirm the results of others that gravity can change the LP5,6,7,8,9, our methods and modelling approach are able to distinguish gravity’s differential influence on ocular torsion of the eye versus change in central processing of visual shape from shading information.
It has been previously found that LP data are consistent with a combination of both retinal and gravitational frameworks, where the LP is largely predicted from retinal orientation plus an additional gravitational component9. It is important to note that the retinal model for predicting change of the LP with tilt of the body relative to gravity fit to data in the present experiment is quite robust for small changes in orientation (i.e., 0–60° such as in9), where retina-based and head-based predictions are more similar than at extreme tilt angles. What distinguishes our results is the large range of observer tilt angles used to test shape from shading perception with the body extremely tilted to better understand deviations from the retinal prediction. Here, when nearly upside-down (e.g, 150°) predictions for head and retina-based frames of reference fail to predict change in the LP from an initial upright posture. Consequently, because the light-from-above prior is updated when extremely tilted relative to gravity and not aligned with gravity anymore, errors in object recognition may increase as the light is still likely to come from the gravity upright direction.
One interpretation of our results put forward in our model is that otolith signals are multiplied and added to visual information in a retinotopic reference frame. There is, however, an alternative explanation for our results. Our model works on the assumption that the direction of the light-from-above prior can be represented as a weighted sum of sin(theta) * cos(theta) and sin(theta) terms. As the first term is equivalent to sin(2 * theta), an alternative equation of the data can be represented by the first two sinusoidal harmonics. As both equations are possible, future work will be required to determine the underlying neurophysiological determinants. Given that the data has to go through the point (0,0) and is antisymmetric (i.e., has opposite signs on either side of theta = 0), the alternative explanation of the data being represented by the first two sinusoidal harmonics is entirely plausible and accordingly tell us little about the underlying physiology on its own. We are in favour of interpreting the results of our experiment as likely being the sum of cross-multiplied utricle and saccule signals added to the retinal component based largely from supportive literature for such a mechanism. Multiplication has been suggested to play a role in many aspects of neural computation14,19. Response properties consistent with multiplication have been observed in auditory neurons of the barn owl where multiplication of separate postsynaptic potentials tuned to interaural time and level differences form a coherent representation of auditory space20. Neural recordings that support cross-multiplication of vestibular signals at the level of the vestibular nucleus have also been reported21. Neurons in monkey posterior parietal cortex exhibit gain field properties that can be explained by a multiplication of retinal and eye or head position signals22 and functional magnetic resonance imaging experiments in humans have revealed that neurons in this region also decode shape-from-shading18 and respond to vestibular stimulation23. Finally, not only is there a physiological basis for suggesting that cross multiplication of otolith signals is biologically plausible, there is reasonable cause for the central nervous system to perform these transformations. To wit, as perceptual measures of verticality also suggest these multiplicative response properties14,24, we suggest that cross-multiplication of otolith signals may be used to update the representation of 3D space in parietal cortex. Future neurophysiological work is thus required to assess whether cross multiplication of otolith signals are added to visual information in a retinotopic reference frame or alternatively whether the added component is derived from the first two sinusoidal harmonics of otolith signals.
In conclusion, priors such as light coming from above appear to be constantly updated by neural processes that monitor self-orientation to achieve optimal object recognition over moderate deviations from upright posture at the cost of poor recognition when extremely tilted relative to gravity. This interpretation is consistent with numerous other studies, which indicate that the brain constructs an internal representation of the body with a prior assumption that the head is upright14,17,25,26,27,28,29,30. Previously it was suggested that the gravitational frame of reference might become insignificant when an observer is upside-down7. Within this framework, robust cue-combination can be found for small conflicts between stimuli, but when larger conflicts appear (such as when observers are upside–down) then one frame of reference is expected to dominate. Our results support this approach but also provide additional insight into the possible source for the gravitational cue being cross-multiplied utricle and saccule signals of the vestibular system, yielding gravity-dependent biases in the ability to extract shape-from-shading.
References
Ernst, M. O. & Bülthoff, H. H. Merging the senses into a robust percept. Trends Cog. Sci. 8, 162–169 (2004).
Howard, I.P. & Templeton, W.B. Human spatial orientation. (John Wiley and Sons Ltd. London 1966).
Howard, I.P. Human visual orientation. (John Wiley and Sons Ltd. New York 1982).
Brewster, D. Edinburgh J. Sci. 4, 99−108 (1826).
Yonas, A., Kuskowski, M. & Sternfels, S. The role of frames of reference in the development of responsiveness to shading information. Child Dev. 50, 495–500 (1979).
Sun, J. & Perona, P. Where is the sun? Nat. Neurosci. 1, 183–184 (1998).
Howard, I. P., Bergstrom, S. S. & Ohmi, M. Shape from shading in different frames of reference. Perception 19, 523–530 (1990).
Jenkin, H. L., Jenkin, M. R., Dyde, R. T. & Harris, L. R. Shape-from-shading depends on visual, gravitational, and body-orientation cues. Perception 33, 1453–1461 (2004).
Adams, W. J. Frames of reference for the light-from-above prior in visual search and shape judgements. Cognition 107, 137–150 (2008).
Kleffner, D. A. & Ramachandran, V. S. On the perception of shape from shading. Percept. Psychophys. 52, 18–36 (1992).
Mamassian, P., Jentzsch, I., Bacon, B. A. & Schweinberger, S. R. Neural correlates of shape from shading. Neuroreport 14, 971–975 (2003).
Barnett-Cowan, M., Meilinger, T., Vidal, M., Teufel, H. & Bülthoff, H. H. MPI CyberMotion Simulator: Implementation of a novel motion simulator to investigate multisensory path integration in three dimensions. J. Vis. Exp. 63, e3436 (2012).
Bockisch, C. J. & Haslwanter, T. Three-dimensional eye position during static roll and pitch in humans. Vis. Res. 41, 2127–2137 (2001).
Mittelstaedt, H. The subjective vertical as a function of visual and extraretinal cues. Acta. Psychol. (Amst) 63, 63–85 (1986).
Fernandez, C. & Goldberg, J. M. Physiology of peripheral neurons innervating otolith organs of the squirrel monkey. I. Response to static tilts and to long-duration centrifugal force. J. Neurophysiol. 39, 970–984 (1976).
Kass, R. E. & Raftery, A. E. Bayes factors. J. Am. Stat. Assoc. 90, 773–795 (1995).
Barnett-Cowan, M., Jenkin, H. L., Dyde, R. T., Jenkin, M. R. & Harris, L. R. Asymmetrical representation of body orientation. J Vis. 13(2), 3, 1–9 (2013).
Gerardin, P., Kourtzi, Z. & Mamassian, P. Prior knowledge of illumination for 3D perception in the human brain. Proc. Acad. Nat. Sci. 107, 16309–16314 (2010).
Koch C. Biophysics of computation: information processing in single neurons. (Oxford Univ. Press, Oxford 1998).
Peña, J. L. & Konishi, M. Auditory spatial receptive fields created by multiplication. Science 292, 249–252 (2001).
Wei, M., Luan, H., Carney, L. H. & Newlands, S. Interaction of Horizontal Translation and Yaw Rotation Signals on Convergent Neurons in the Vestibular Nuclei. Assoc. Res. Otolaryngol. Abs: 287 (2012).
Anderson, R. A., Snyder, L. H., Bradley, D. C. & Xing, J. Multimodal representation of space in the posterior parietal cortex and its use in planning movements. Annu. Rev. Neurosci. 20, 303–330 (1997).
Bense, S., Stephan, T., Yousry, T. A., Brandt, T. & Dieterich, M. Multisensory cortical signal increases and decreases during vestibular galvanic stimulation (fMRI). J Neurophysiol. 85, 886–899 (2001).
Van Beuzekom, A. D. & Van Gisbergen, J. A. M. Properties of the internal representation of gravity inferred from spatial-direction and body-tilt estimates. J. Neurophysiol. 84, 11–27 (2000).
Mittelstaedt, H. A new solution to the problem of the subjective vertical. Naturwissenschaften 70, 272–81 (1983).
Barnett-Cowan, M., Dyde, R. T. & Harris, L. R. Is an internal model of head orientation necessary for oculomotor control? Ann. NY Acad. Sci. 1039, 314–324 (2005).
Dyde, R. T., Jenkin, M. R. & Harris, L. R. The subjective visual vertical and the perceptual upright. Exp. Brain Res. 173, 612–622 (2006).
MacNeilage, P. R., Banks, M. S., Berger, D. R. & Bülthoff, H. H. A Bayesian model of the disambiguation of gravitoinertial force by visual cues. Exp. Brain Res. 179, 263–290 (2007).
Schwabe, L. & Blanke, O. The vestibular component in out-of-body experiences: A computational approach. Frontiers Hum. Neurosci. 2, 17 (2008).
Barnett-Cowan, M. & Bülthoff, H. H. Human path navigation in a three-dimensional world. Behav. Brain Sci 36, 544–545 (2012).
Acknowledgements
We gratefully thank K. Beykirch, M. Kerger, H.J. Teufel & J. Tesch for technical assistance and scientific discussion, and to Ksander de Winkle and Séamas Weech for reviewing an earlier version of this manuscript. Max Planck Society postdoctoral stipend to M.B-C.; M.O.E. funded by EU grant 248587 ‘THE’; H.H.B. by WCU (World Class University) program funded by the Ministry of Education, Science and Technology through the National Research Foundation of Korea (R31-10008).
Author information
Authors and Affiliations
Contributions
M.B.-C., M.O.E. and H.H.B. designed the experiment. M.B.-C. prepared and ran the experiment, and analysed the data. M.B.-C. and M.O.E. interpreted the data and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barnett-Cowan, M., Ernst, M.O. & Bülthoff, H.H. Gravity-dependent change in the ‘light-from-above’ prior. Sci Rep 8, 15131 (2018). https://doi.org/10.1038/s41598-018-33625-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-33625-2
Keywords
This article is cited by
-
Microgravity induces overconfidence in perceptual decision-making
Scientific Reports (2023)
-
Recognizing why vision is inferential
Synthese (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.