Abstract
The atom-photon entanglement using the Laguerre-Gaussian (LG) beams is studied in the closed-loop three-level V-type quantum systems. We consider two schemes with near-degenerate and non-degenerate upper levels: in the first, the effect of the quantum interference due to the spontaneous emission is taken into account and in the second, a microwave plane wave is applied to the upper levels transition. It is shown that the atom-photon entanglement in both schemes depends on the intensity profile as well as the orbital angular momentum (OAM) of the applied fields so that the various spatially dependent entanglement patterns can be generated by Laguerre-Gaussian beams with different OAMs. However, due to the zero intensity,no entanglement appears in the center of the optical vortex beams. As a result, the entanglement between dressed atom and its spontaneous emissions in different points of the atomic vapor cell can be controlled by the OAM of the applied fields. Moreover, our numerical results show that the number of the local maximum degree of entanglement (DEM) peaks depends on the OAM of the applied fields. The degrees of freedom for OAM play a crucial role in spatially dependent atom-photon entanglement in such a way that it may possess broad applications in high-dimensional quantum information processing and data storage.
Similar content being viewed by others
Introduction
Entanglement is generally a quantum mechanical phenomenon without any classical analogous which makes a correlation between the parts of a multi-partite system1,2. A quantum state of a bipartite entangled system cannot be described by a simple tensor product of quantum states of two subsystems3. Not only does atom-photon entanglement play an outstanding role in quantum mechanics such as early measurement of Bell inequality violations4, but it has also high potential applications in teleportation5, cryptography6, error correction7 and other quantum computation processes8.
Generally speaking, the angular momentum carried by light can be distinguished by the spin angular momentum associated with circular polarization9 and the orbital angular momentum (OAM) associated with the spatial distribution of the wavefront. In 1992, Allen et al. showed that the Laguerre-Gaussian (LG) laser mode has a well-defined OAM, as \(l\hslash \) per photon, and proposed an experiment to observe the torque on cylindrical lenses arising from the reversal of the helicity of a LG mode10. An additional motivation for recent studies of LG beams is as a route to obtain narrower electromagnetically induced transparency (EIT) spectrum than the conventional Gaussian one11,12,13. The transmission of structured light has been measured using the phase profile in cold rubidium atoms and been shown that the EIT is spatially dependent for vortex light beams14. Recently, Mahmoudi et al. has investigated the effect of LG intensity profile on the optical spectrum of multi-photon resonance phenomena. It has been found that the linewidth of the optical spectrum due to the multi-photon transition becomes narrower in the presence of a LG beam15. They have also studied trap split in an atomic system interacting with femtosecond LG laser pulses16. More recently, we have demonstrated that the LG beam can decrease the full width at the half maximum of the output probe intensity in the electromagnetically induced focusing17.
It is well known that a LG light beam with an azimuthal phase dependence of \({e}^{-il\varphi }\) carries quantized OAM18. Due to the fact that the optical properties of the closed-loop quantum systems, in multi-photon resonance condition, depend on the relative phase of applied fields19 the effect of the OAM of the LG beams can be seen in this system due to the azimuthal phase factor of LG beam via the multi-photon transitions.
Increasing the complexity of entangled systems is important in the various applications of the entanglement in quantum information tasks which can be essentially done by increasing the number of particles involved in the entanglement20 or the entanglement dimensionality of a system21. The alternative method to increase the entanglement dimensionality of a system is to use the LG modes. High-dimensional entanglement has recently attracted increasing attention in both fundamental and applied research in quantum mechanics. The use of these states can enhance quantum communication schemes by increasing their channel capacity and offering improved robustness against sophisticated eavesdropping attacks. However, one of the methods for generating higher order entangled states is using the OAM basis22. Recently, quantum logic gates also have been achieved experimentally23 and applied for generating high dimensional Bell States in this basis24. Although there are a lot of scientific reports on high dimensional photon states in OAM basis, it seems a deep fundamental research is necessary for atom-photon interaction in OAM basis, too. Moreover, we believe that the simulated atom-photon system can be a good source for high dimensional entangled states.
In this paper, we study the effect of intensity profile and OAM of light beams on the quantum entanglement in the three-level V-type quantum systems. In the first scheme, we consider V-type atomic system with two near-degenerate excited levels. In the presence of quantum coherence due to the spontaneous emission the transition of the electron between two excited states becomes possible and the V-type atomic system switches to the closed-loop configuration. In the second scheme, we consider two non-degenerate excited states and the quantum coherence between two upper levels is induced by applying a microwave field to the upper levels transition. Then, the optical properties of such systems depend on the OAM of the applied fields. We are interested in studying the entanglement of dressed atom and its spontaneous emission, using the LG fields with different OAMs. We use the von Neumann entropy as a measure of the degree of entanglement (DEM). It is shown that the DEM completely depends on the position of space points, so that the various points in the atomic vapor cell experience different DEM. Moreover, we find that the DEM is dependent on both magnitude and sign of the OAM of light beams. Then, the DEM can be controlled by the intensity profile, as well as the OAM of the applied fields. It is worth noting that the maximal value of DEM is obtained in the second scheme.
Theoretical Framework
In general, an entangled quantum system consisting of two subsystems, A and B, is described by the reduced density matrix. The state of the entangled system is not a simple tensor product of the subsystems reduced density matrices, \({\rho }_{AB}\ne {\rho }_{A}\otimes {\rho }_{B}\). In thermodynamics, entropy is a fundamental physical quantity describing the degree of randomness of the system. Thus, we can represent the entanglement adopting the reduced quantum entropy. Various measures such as the reduced entropy of entanglement25, the relative entropy of entanglement7, entanglement of formation26 and entanglement of distillation27 have been introduced for DEM. Here, we use the definition of the von Neumann reduced entropy of entanglement. The von Neumann entropy, as a helpful quantity for calculating the DEM between the subsystems, is given by
where \(\rho \) is the density matrix operator. It can be easily found that the von Neumann entropy vanishes for a bipartite system in pure state28. In 1970, Araki and Lieb demonstrated that the subsystems entropies satisfy in the triangle inequality29
at any time t. Here, \({S}_{AB}(t)\) is the total entropy of the composite system. Based on equation (2), for a atom-field system initially in a disentangled pure state, partial entropies of the field and the atom will be equal at all times after the interaction of two subsystems is switched on. Then, our information about any of the subsystems is an indication of the entanglement of the whole system. A decreasing partial entropy means that each subsystem evolves towards a pure quantum state, whereas in an initially pure system an increasing partial entropy drives the two components to lose their individuality and become entangled30. So the DEM for atom-field system would be
where λi is the reduced density matrix operator eigenvalues. The maximum value of DEM for a N-level quantum system is given by lnN, in which the population is uniformly distributed in the dressed states of the system31,32. Now, we are going to study the effect of applied LG fields on the atom-photon entanglement in two schemes of closed-loop three-level atomic systems.
Three-Level V-Type Atomic Systems
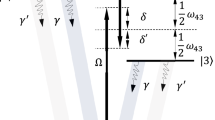
We assume an ensemble of three-level V-type atomic system with two near-degenerate excited states \(\mathrm{|2}\rangle \) and \(\mathrm{|3}\rangle \) and a ground state \(\mathrm{|1}\rangle \), as shown in Fig. 1. As a realistic example, we consider the sodium \({D}_{2}\) line (\({\mathrm{|3}}^{2}{S}_{\mathrm{1/2}},F=1\rangle \leftrightarrow {\mathrm{|3}}^{2}{P}_{\mathrm{3/2}}\rangle \)); \(\mathrm{|1}\rangle \), \(\mathrm{|2}\rangle \), and \(\mathrm{|3}\rangle \) correspond to sublevels \({\mathrm{|3}}^{2}{S}_{\mathrm{1/2}},F=1\rangle \), \({\mathrm{|3}}^{2}{P}_{\mathrm{3/2}},F^{\prime} =0\rangle \), and \({\mathrm{|3}}^{2}{P}_{\mathrm{3/2}},F^{\prime} =1\rangle \), respectively. Here, the upper levels are not exactly degenerated, however, if the energy difference of the upper levels is less than the natural line width, it can be considered as the near-degenerate levels and both transitions interact with a common vacuum state. Here the energy difference of upper levels is 15.8 MHz, which is less than the natural line width of the transition \((\,\sim \,61.35\,MHz)\). The spontaneous emission rates from two near-degenerate excited states \(\mathrm{|2}\rangle \) and \(\mathrm{|3}\rangle \) to the ground state is denoted by \(2{\gamma }_{1}\) and \(2{\gamma }_{2}\), respectively. In such a system, the spontaneous emission passing through the indistinguishable paths lead to the quantum interference called as spontaneously generated coherence (SGC). The transition \(\mathrm{|1}\rangle \leftrightarrow \mathrm{|2}\rangle \) is driven by the right LG field with frequency \({\omega }_{R}\) and Rabi frequency \({{\rm{\Omega }}}_{R}={\overrightarrow{\mu }}_{12}\mathrm{.}{\overrightarrow{E}}_{R}/\hslash \), while the transition \(\mathrm{|1}\rangle \leftrightarrow \mathrm{|3}\rangle \) is excited by the left LG field with frequency \({\omega }_{L}\) and Rabi frequency \({{\rm{\Omega }}}_{L}={\overrightarrow{\mu }}_{13}.{\overrightarrow{E}}_{L}/\hslash \). Here \({\overrightarrow{E}}_{R(L)}\) denotes the amplitude of right (left) LG field. The parameter \({\mu }_{ij}\) represents the induced dipole moment of the \(|i\rangle \leftrightarrow |j\rangle \) transition.
Schematics of the three-level \(V\)-type atomic system with two near-degenerate excited states \(\mathrm{|2}\rangle \) and \(\mathrm{|3}\rangle \) and a ground state \(\mathrm{|1}\rangle \). \(2{\gamma }_{1}\) and \(2{\gamma }_{2}\) are the spontaneous emission rates from upper levels to lower level which are in the order of MHz. Two applied LG fields, \({{\rm{\Omega }}}_{L}\) and \({{\rm{\Omega }}}_{R}\), and the SGC make the proposed system a closed-loop system.
The interaction Hamiltonian of the system under the electric-dipole and rotating-wave approximations can be written as
where \({{\rm{\Delta }}}_{R}={\omega }_{R}-{\omega }_{21}\) and \({{\rm{\Delta }}}_{L}={\omega }_{L}-{\omega }_{31}\) are the applied fields frequency detunings with respect to the atomic transition frequencies. The parameter \({\omega }_{ij}\) is the central frequency of \(|i\rangle \leftrightarrow |j\rangle \) transition. Both applied fields are chosen as the LG fields and are given by
where \({E}_{{0}_{L}}\)(\({E}_{{0}_{R}}\)) and \({l}_{L}\)(\({l}_{R}\)) are the left(right) field amplitude and Orbital angular momentum, respectively. Gaussian and LG beam waists are denoted by \({w}_{G}\) and \({w}_{LG}\), respectively. Note that the beam waists of left and right applied fields are considered to be equal for enhancement the effect of their interaction with atomic system on the DEM. Using the von Neumann equation, the Bloch equations for such a system takes the form
where \({\rm{\Delta }}={{\rm{\Delta }}}_{R}-{{\rm{\Delta }}}_{L}={\omega }_{R}-{\omega }_{L}\). The parameter \(\eta \) in equation (6) stands for the SGC strength.
We now introduce the dressed states generated by applied fields which are useful for understanding the optical properties of the system. The physics of the entanglement can be explained via the population distribution of the dressed states. For the proposed model, the dressed states in the absence of spontaneous emissions are given by
The dressed states population can be obtained as
Now, we are interested in studying the DEM for V-type atomic system by numerically solving equations (3) and (6). It is assumed that the multi-photon resonance condition is fulfilled. All frequency parameters are scaled by \({\gamma }_{1}\), which is in the order of MHz for the chosen atomic system. We consider different intensity profiles, i.e., Gaussian and LG modes for the applied fields and investigate steady-state behavior of the DEM in different points of atomic vapor cell. Figure 2 shows the DEM as a function of x for the applied Gaussian fields, (a) \({l}_{L}={l}_{R}=0\), first mode (b) \({l}_{L}={l}_{R}=1\) and second mode of applied LG fields (c) \({l}_{L}={l}_{R}=2\). Used parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \), \(\eta =0.99\), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({{\rm{\Omega }}}_{{0}_{R}}=9\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}=0\), multi-photon resonance condition. Red lines indicate the maximum of DEM positions in panels (a)–(c). In panel (a), it can be easily seen that the DEM changes from zero to a maximum value, for different values of x. The DEM vanishes where the beams’ intensity becomes zero. Panels (b) and (c) shows that the zero intensity in the center of LG profile implies a disentanglement in the center of LG modes. So, the spatially dependent behavior of DEM is related to the intensity profile of two applied fields. Note that the effect of OAMs’ sign on the DEM is not seen in one dimension calculation.
Steady-state behavior of the DEM versus \(x\) for (a) \({l}_{L}={l}_{R}=0\), (b) \({l}_{L}={l}_{R}=1\) and (c) \({l}_{L}={l}_{R}=2\). Used parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \), \(\eta =0.99\), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({\Omega }_{{0}_{R}}=9\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}=0\). Red lines indicate the maximum of DEM position in all panels.
A physical meaning of entanglement lies on the dressed states conception. For explanation of DEM behavior in the presence of spontaneous emissions, we calculate the density matrix operator eigenvalues which describe the dressed states population in the presence of spontaneous emmision. The uniform population distribution of the dressed states induce the maximal entanglement to the atomic system. By numerically solving equation (6) and diagonalizing the density matrix, the dressed states population can be obtained as a function of x. We would like to investigate the dressed states population in different points of the atomic vapor cell. In the following, Fig. 3 shows the dressed states population versus x corresponding to Fig. 2. As seen in all panels of Fig. 3, the population is distributed only in two states around \(x=0\) and the DEM value reaches to \(ln2\), while a part of population transfers to the third state at the maximum point of DEM and the population is nearly uniformly distributed in the three dressed states, with respect to the population distribution at \(x=0\).
Steady-state behavior of density matrix eigenstates versus \(x\) for (a) \({l}_{L}={l}_{R}=0\), (b) \({l}_{L}={l}_{R}=1\) and (c) \({l}_{L}={l}_{R}=2\). Solid, dashed and dash-dotted curves show the first, second and third eigenstates, respectively. The same parameters as in Fig. 2 are used in all panels. Red line, in each of panels, corresponds to the position of maximum of DEM.
Note that in one dimension calculation, the effect of the OAM of light beams on the atom-photon entanglement does not take into account, so, we have to continue our calculations in two dimensions to include the contribution of the OAM of applied LG fields. According to equation (5), the OAM of light appears as a phase term, \({e}^{il\phi }\). It is expected that the optical properties of the V-type atomic system depend on the OAM of light beam in closed-loop configuration. In Fig. 4, we depict the DEM density plots as a function of x and \(y\) for different modes of applied fields with \({l}_{L}=-\,3,\ldots ,3\) and \({l}_{R}=0,\ldots ,3\). Used parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \), \(\eta =0.99\), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({{\rm{\Omega }}}_{{0}_{R}}=9\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}=0\). There are \(28\) panels for different choices of LG modes of applied fields. For \({l}_{L}={l}_{R}=0\), the DEM changes from zero to its maximum value in a determined radius and decreases to nearly maximal value of DEM of two-level system, \(ln2\). However, for equal OAM modes of two applied LG fields, \({l}_{L}={l}_{R}=l\), the DEM value has a central symmetry with a disentanglement point at the origin coordinates due to the zero intensity of applied fields. These results in the \(x\) direction are in good agreement with one dimensional results of Fig. 2. Here, we show that the DEM behavior completely depends on the OAM of applied fields in two dimensions. The local maximum DEM ring switches to \(2l\) maximum DEM regions when the rotation direction of wavefront is turned to counter-clockwise, \({l}_{L}=-\,{l}_{R}=l\). The obtained results are in good agreement with the presented petal-like patterns in references33 and34 in which, it was shown that the superposition pattern of two LG beams with \(l\) of opposite sign has a symmetric structure with \(2l\) petals. The DEM profile is similar to the interference pattern of two applied LG fields. Moreover, we extend our calculations for different LG modes and it can be generally seen that the number of local maximum peaks equals \(|{l}_{L}-{l}_{R}|\) in all panels. So, the atom-photon entanglement pattern can be controlled by OAM of light beams.
DEM density plots as a function of \(x\) and \(y\) for different modes of applied fields with \({l}_{L}=-\,\mathrm{3,}\,\mathrm{...,}\,3\) and \({l}_{R}=\mathrm{0,}\,\mathrm{...,}\,3\). Size of each density plot is \(2\,mm\,\times \,2\,mm\) in which horizontal and vertical axes are \(x\) and \(y\) axes, respectively. Used parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \), \(\eta =0.99\), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({{\rm{\Omega }}}_{{0}_{R}}=9\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}=0\).
Now, we are going to investigate the DEM behavior of the system beyond multi-photon resonance condition, \({\rm{\Delta }}\ne 0\). However, we drop the explicit time dependent phase factors in equation (6). Then, our results are valid only near multi-photon resonance condition. The right (left) field is considered as a plane-wave (LG field). In Fig. 5, we display the DEM density plot as a function of \(x\) and \(y\) in different points of the cross-section of atomic vapor cell for a Gaussian left field, \({l}_{L}\mathrm{=0}\). Used parameters for the applied fields are assumed to be \({{\rm{\Omega }}}_{R}=9\gamma \), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({w}_{G}=1\,mm\) and \({\rm{\Delta }}=\gamma \), beyond multi-photon resonance condition. The atomic parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \) and \(\eta =0.99\). It is shown that the DEM tends to its maximal value, \(ln3\), in a special radius which depends on the characteristics of the Gaussian field. The DEM density plots for the different modes of LG field are plotted versus \(x\) and \(y\), as shown in Fig. 6. The applied fields parameters are \({{\rm{\Omega }}}_{R}=9\gamma \), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({w}_{LG}=270\,\mu m\) and \({\rm{\Delta }}=\gamma \). The atomic properties are chosen to be same as in Fig. 5. Figure 6(a) shows the DEM variations for the first mode of LG field, \({l}_{L}=1\). The DEM behavior, specially around maximal DEM regions, is very similar to spiral-shaped fringes due to the interference of first mode of LG light beam with a plane-wave18,34. In Fig. 6(b) it is clearly seen that the DEM behavior for the negative OAM of the first mode of LG field is in good agreement with the rotation direction of spiral arms of LG field and plane-wave interferogram. We repeat our numerical calculations for positive and negative OAMs of the second and third modes of LG left field, \({l}_{L}=\mathrm{2,}-\,\mathrm{2,}\,\mathrm{3,}-\,3\) in panels (c)–(f), respectively. An investigation on Fig. 6(c–f) shows that the DEM patterns are similar to the interference pattern of different modes of LG beam with the plane-wave. Therefore, the spatially dependent DEM can be controlled either magnitude or sign of the OAM of the applied LG field.
Density plot of the DEM versus \(x\) and \(y\), beyond multi-photon resonance condition, when two applied fields are considered as a plane-wave (right field) and a Gaussian (left field). Used parameters for the applied fields are \({{\rm{\Omega }}}_{R}=9\gamma \), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({w}_{G}=1\,mm\) and \({\rm{\Delta }}=\gamma \). The atomic parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \) and \(\eta =0.99\).
DEM density plots as a function of \(x\) and \(y\) for a plane-wave laser as the right field and a LG field as the left field with different modes, \({l}_{L}=1\) and \(-1\), (a,b), \({l}_{L}=2\) and \(-2\), (c,d), \({l}_{L}=3\) and \(-3\), (e,f), beyond multi-photon resonance condition. Size of each density plot is \(1.4\,mm\,\times \,1.4\,mm\) in which horizontal and vertical axes are \(x\) and \(y\) axes, respectively. The applied fields parameters are \({{\rm{\Omega }}}_{R}=9\gamma \), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({w}_{LG}=270\,\mu m\) and \({\rm{\Delta }}=\gamma \). The atomic properties are chosen to be same as in Fig. 5.
Closed-Loop Three-Level V-Type Atomic Systems
In this section, we propose an ensemble of three-level V-type atomic system with two non-degenerate excited states and apply a planar microwave field, \({{\rm{\Omega }}}_{m}\), to the \(\mathrm{|2}\rangle \leftrightarrow \mathrm{|3}\rangle \) transition and two other fields shown in Fig. 7, which can be prepared in the Rb Rydberg atoms35.
Schematics of the closed-loop three-level \(V\)-type atomic system with two non-degenerate excited states \(\mathrm{|2}\rangle \) and \(\mathrm{|3}\rangle \) and a ground state \(\mathrm{|1}\rangle \) which can be prepared in the Rb Rydberg atoms. The spontaneous emission rate related to \(\mathrm{|2}\rangle \leftrightarrow \mathrm{|3}\rangle \) transition is denoted by \(2{\gamma }_{3}\); \(2{\gamma }_{1}\) and \(2{\gamma }_{2}\) are the spontaneous emission rates from upper levels to lower level which are in the order of MHz. Two applied LG fields, \({{\rm{\Omega }}}_{L}\) and \({{\rm{\Omega }}}_{R}\) and one planar microwave field, \({{\rm{\Omega }}}_{m}\), establish a closed-loop atomic system.
Using the von Neumann equation and the interaction Hamiltonian of the system, the Bloch equations for the system are obtained by
where \({\rm{\Delta }}={{\rm{\Delta }}}_{L}-{{\rm{\Delta }}}_{R}-{{\rm{\Delta }}}_{m}\).
Here, we are going to show the behavior of the DEM in a closed-loop three-level \(V\)-type atomic system using equations (3) and (9). A planar microwave field is applied to the \(\mathrm{|2}\rangle \leftrightarrow \mathrm{|3}\rangle \) transition. It is assumed that the multi-photon resonance condition is fulfilled. Figure 8 presents the density plots of DEM versus \(x\) and \(y\) for different modes of applied fields with \({l}_{L}=-\,\mathrm{3,}\,\mathrm{...,}\,3\) and \({l}_{R}=\mathrm{0,}\,\mathrm{...,}\,3\). Size of each density plot is \(2\,mm\,\times \,2\,mm\) in which horizontal and vertical axes are \(x\) and \(y\) axes, respectively. The microwave Rabi frequency, relaxation rate between two excited states and detuning of the microwave field frequency are considered to be \({{\rm{\Omega }}}_{m}=7\gamma \), \({\gamma }_{3}=2\gamma \) and \({{\rm{\Delta }}}_{m}=0\), respectively. Other used parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \), \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({{\rm{\Omega }}}_{{0}_{R}}=9\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}=0\). It is shown that the maximal entanglement can be obtained in different regions of atomic vapor cell by applying a planar microwave field instead of the SGC effect. Two applied Gaussian fields, \({l}_{L}={l}_{R}=0\), create maximal value of DEM in a central circular region of atomic vapor cell. Now, let us refer to the DEM density plots in which two applied LG fields have equal OAMs, \({l}_{L}={l}_{R}=l\). A comparison between the related panels shows that the region of disentanglement has been grown for larger OAMs. It is worth to note that for LG modes with opposite sign OAMs, \({l}_{L}=-\,{l}_{R}=l\), the maximal DEM doughnut-like region splits to \(4l\) symmetric segments. Other \(21\) planes in Fig. 8 show the DEM behavior in different points of the atomic vapor cell for different choices of OAM of two applied fields. An investigation on all panels of Fig. 8 confirms that the DEM patterns follow a common model which are extremely dependent on OAM and have \(\mathrm{2|}{l}_{L}-{l}_{R}|\) maximal regions.
DEM density plots as a function of \(x\) and \(y\) for different modes of applied fields with \({l}_{L}=-\,\mathrm{3,}\,\mathrm{...,}\,3\) and \({l}_{R}=\mathrm{0,}\,\mathrm{...,}\,3\). Size of each density plot is \(2\,mm\,\times \,2\,mm\) in which horizontal and vertical axes are \(x\) and \(y\) axes, respectively. Three applied fields characteristics are chosen to be \({{\rm{\Omega }}}_{{0}_{L}}=7\gamma \), \({{\rm{\Omega }}}_{{0}_{R}}=9\gamma \), \({{\rm{\Omega }}}_{m}=7\gamma \), \({w}_{G}=1\,mm\), \({w}_{LG}=270\,\mu m\) and \({{\rm{\Delta }}}_{L}={{\rm{\Delta }}}_{R}={{\rm{\Delta }}}_{m}=0\). The atomic system parameters are \({\gamma }_{1}={\gamma }_{2}=\gamma \) and \({\gamma }_{3}=2\gamma \).
Conclusion
In conclusion, we studied quantum entanglement between an ensemble of three-level atomic system and its spontaneous emissions. In the first scheme, we investigated the steady-state behavior of the DEM in a three-level \(V\)-type atomic system with the SGC effect under the multi-photon resonance condition. We found an intriguing result which illustrates an explicit dependency between the DEM density plot and the OAM of LG light beams. Moreover, we showed that the DEM density plot pattern is corresponding to the interference pattern of the two applied fields. In the second scheme, a microwave plane field was applied to the non-degenerate upper levels transition which leads to the maximal DEM. It was demonstrated that the number of maximal entanglement peaks is determined by the OAM of the applied LG fields. Both disentanglement and maximal DEM were simultaneously obtained in the second scheme. The presented results can be used in optical communications and information storage via preparing high-dimensional Hilbert space.
References
Brassard, G., Chuang, I., Lloyd, S. & Monroe, C. Quantum computing. Proc. Natl. Acad. Sci. USA 95, 11032–11033 (1998).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Ficek, Z. & Swain, S. Quantum Coherence and Interference; Theory and Experiments (Springer, 2004).
Freedman, S. J. & Clauser, J. F. Experimental test of local hidden variables theories. Phys. Rev. Lett. 28, 938–941 (1972).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991).
Bennett, C. H., DiVincenzo, D. P., Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996).
Benenti, G., Casati, G. & Strini, G. Principles of Quantum Computation and Information; vol 1: Basic Concepts (World Scientific, 2004).
Beth, R. A. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 50, 115 (1936).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185 (1992).
Anupriya, J., Ram, N. & Pattabiraman, M. Hanle electromagnetically induced transparency and absorption resonances with a Laguerre Gaussian beam. Phys. Rev. A 81, 043804 (2010).
Chanu, S. R., Singh, A. K., Brun, B., Pandey, K. & Natarajan, V. Subnatural linewidth in a strongly-driven degenerate two-level system. Opt. Commun. 284, 4957–4960 (2011).
Akin, T. G., Krzyzewski, S. P., Marino, A. M. & Abraham, E. R. I. Electromagnetically induced transparency with Laguerre-Gaussian modes in ultracold rubidium. Opt. Commun. 339, 209–215 (2015).
Radwell, N., Clark, T. W., Piccirillo, B., Barnett, S. M. & Franke-Arnold, S. Spatially dependent electromagnetically induced transparency. Phys. Rev. Lett. 114, 123603 (2015).
Kazemi, S. H. & Mahmoudi, M. Multi-photon resonance phenomena using Laguerre-Gaussian beams. J. Phys. B: At. Mol. Opt. Phys. 49, 245401 (2016).
Kazemi, S. H., Ghanbari, S. & Mahmoudi, M. Trap split with Laguerre-Gaussian beams. J. Opt. 19, 085503 (2017).
Amini Sabegh, Z., Maleki, M. A. & Mahmoudi, M. Phase-controlled electromagnetically induced focusing in a closed-loop atomic system. J. Opt. Soc. Am. B 34, 2446–2451 (2017).
Padgett, M., Courtial, J. & Allen, L. Light’s orbital angular momentum. Phys. Today 57, 35–40 (2004).
Mahmoudi, M. & Evers, J. Light propagation through closed-loop atomic media beyond the multiphoton resonance condition. Phys. Rev. A 74, 063827 (2006).
Greenberger, D. M., Horne, M. A., Shimony, A. & Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Krenn, M. et al. Generation and confirmation of a (100 × 100)-dimensional entangled quantum system. Proc. Natl. Acad. Sci. USA 111, 6243–6247 (2014).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).
Babazadeh, A. et al. High-dimensional single-photon quantum gates: Concepts and experiments. Phys. Rev. Lett. 119, 180510 (2017).
Wang, F. et al. Generation of the complete four-dimensional Bell basis. Optica 4, 1462–1467 (2017).
Vedral, V., Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying entanglement. Phys. Rev. Lett. 78, 2275–2279 (1997).
Audenaert, K., Verstraete, F. & Moor, B. De Variational characterizations of separability and entanglement of formation. Phys. Rev. A 64, 052304 (2001).
Lo, H. K. & Popescu, S. Concentrating entanglement by local actions: Beyond mean values. Phys. Rev. A 63, 022301 (2001).
Phoenix, S. J. D. & Knight, P. L. Fluctuations and entropy in models of quantum optical resonance. Ann. Phys. 186, 381–407 (1988).
Araki, H. & Lieb, E. H. Entropy inequalities. Commun. Math. Phys. 18, 160–170 (1970).
Phoenix, S. J. D. & Knight, P. L. Establishment of an entangled atom-field state in the Jaynes-Cummings model. Phys. Rev. A 44, 6023 (1991).
Phoenix, S. J. D. & Knight, P. L. Comment on Collapse and revival of the state vector in the Jaynes-Cummings model: An example of state preparation by a quantum apparatus. Phys. Rev. Lett. 66, 2833 (1991).
Abazari, M., Mortezapour, A., Mahmoudi, M. & Sahrai, M. Phase-controlled atom-photon entanglement in a three-level V-type atomic system via spontaneously generated coherence. Entropy 13, 1541–1554 (2011).
Li, Y., Zhou, Z. Y., Ding, D. S. & Shi, B. S. Sum frequency generation with two orbital angular momentum carrying laser beams. J. Opt. Soc. Am. B 32, 407–411 (2015).
Vickers, J., Burch, M., Vyas, R. & Singh, S. Phase and interference properties of optical vortex beams. J. Opt. Soc. Am. A 25, 823–827 (2008).
Tate, D. A. & Gallagher, T. F. Microwave-optical two-photon excitation of Rydberg states. Phys. Rev. A 97, 033410 (2018).
Acknowledgements
We would like to thanks A. Babazadeh for helpful discussions and comments on this work.
Author information
Authors and Affiliations
Contributions
All authors developed the research conceptions, analysed, and discussed the obtained results. Z.A.S. and R.A. performed the calculations and wrote the paper with major input from M.M.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Amini Sabegh, Z., Amiri, R. & Mahmoudi, M. Spatially dependent atom-photon entanglement. Sci Rep 8, 13840 (2018). https://doi.org/10.1038/s41598-018-32051-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-32051-8
Keywords
This article is cited by
-
Spatial-dependent quantum dot-photon entanglement via tunneling effect
Scientific Reports (2022)
-
Quantum Control of Atom-Photon Entanglement via Structure Light in a Three-Level Medium
International Journal of Theoretical Physics (2022)
-
Microwave-induced orbital angular momentum transfer
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.