Abstract
This paper presents a new system for the detection of human respiration behind obstacles using impulse ultra-wideband (UWB) radar. In complex environments, low signal-to-noise ratios (SNRs) as they can result in significant errors in the respiration, heartbeat frequency, and range estimates. To improve the performance, the complex signal demodulation (CSD) technique is extended by employing the signal logarithm and derivative. A frequency accumulation (FA) method is proposed to suppress mixed products of the heartbeat and respiration signals and spurious respiration signal harmonics. The respiration frequency is estimated using the phase variations in the received signal, and a discrete short-time Fourier transform (DSFT) is used to estimate the range. The performance of the proposed system is evaluated along with that of several well-known techniques in the literature.
Similar content being viewed by others
Introduction
In recent years, the detection of living persons behind obstacles impulse ultra-wideband (UWB) radar has been investigated1,2,3,4,5. UWB radar has been used for the detection of humans6,7, moving subjects8,9, imaging in through-wall conditions10,11, search and rescue12,13, positioning indoors14,15, and public order and security16 because of its high range resolution and penetrability17,18,19,20. It can be used to detect human vital sign signals such as respiration and heart rates, but this can be difficult as thorax movement is usually only several millimeters, and the signal attenuation can be severe.
Previous researches on human vital sign detection have focused on suppressing stationary and/or nonstationary clutters, estimating the respiration frequency and heart rate, the analysis of signal characteristics, and other related problems21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42. The characteristics of human respiration signals were analyzed in both time and frequency domain24,25 using the Hilbert-Huang transform (HHT) and fast Fourier transform (FFT). In27, clutter similar to respiration signals was suppressed using adaptive clutter cancellation. In28, the arctangent demodulation (AD) technique was employed in a UWB pulse radar system to accurately extract vital sign signals over long distances and in and through-wall conditions. However, this technique is complex and decreases the computational efficiency. A maximum likelihood estimator was considered in29 to determine the period of vital sign signals under considering the additive-white-Gaussian-noise (AWGN). A post-processing algorithm was developed for respiration motion detection. The stationary and nonstationary clutters were removed by employing the singular-value-decomposition (SVD) algorithm when the signal-to-noise ratio (SNR) is low30. A tracing technique was considered to extract the respiration impulse response, but this approach is effective only when the SNR is high and over small distances35. LTS i.e. linear trend subtraction method was employed in30 to reduce the linear trend. In37, a higher order cumulants (HOC) technique was applied to extract vital sign signals considering that the fourth order cumulants of AWGN is zero. The classic EEMD i.e. ensemble empirical mode decomposition technique was used in38 to estimate the heart rate of a living person by improving the SNR and removing clutter. An improved arctangent demodulation (AD) algorithm was proposed to increase the accuracies of human heart rate estimate40. In42, a state-space method (SSM) was employed to extract vital sign signals including human respiration and heartbeat signals.
Most detection techniques are not effective over long distances and in through-wall conditions. To solve these problems, an algorithm based on UWB radar is developed here to calculate accurately vital sign signals in challenging environments. This is achieved by suppressing stationary, non-stationary and other clutter as well as the linear trend. The products of the vital sign signals and their harmonics are removed by employing a CSD-based frequency accumulation (FA) method. This is shown to perform better than several well-known techniques. The range information between human subject and radar is estimated considering the characteristics of vital sign signals and a discrete short-time Fourier transform (DSFT). Experimental results obtained using a UWB radar system at the Key Laboratory of Electromagnetic Radiation and Sensing Technology, Institute of Electronics, Chinese Academy of Sciences (IECAS), are used to evaluate the performance of the proposed technique.
The following parts of the paper are arranged as follows. The model of signal detection is given in Section 2, and the proposed method for vital sign detection is presented in Section 3. Section 4 provides performance results to evaluate the detection method, and the conclusions are presented in Section 5.
Signal Detection
Vital Sign Signal Model
Vital sign signals may be obtained due to the time delay changes of a transmitted UWB pulse. The distance between human chest and radar is32
where the range between the radar and the center of human chest is given by d030, fr and Ar are the frequency and amplitude of human respiratory movement, respectively. \({f}_{h}\) and \({A}_{h}\) are the heart rate and heartbeat amplitude, respectively32.
With only one human subject present in the detection environment and all other objects are considered as static, the impulse responses are
where \(\sum _{i}{a}_{i}\delta (\tau -{\tau }_{i})\) represent the responses from all these static objects with time delay τi and vibration amplitude ai30, and \({a}_{v}\delta (\tau -{\tau }_{v}(t))\) represents the impulse response of the vital signs with amplitude av and time delay \({\tau }_{v}(t)\)32. This delay is then
where \(v=3\times {10}^{8}\) m/s, \({\tau }_{0}=2{d}_{0}/v\),\({\tau }_{r}=2{A}_{r}/v\), and \({\tau }_{h}=2{A}_{h}/v\).
The signal received at the radar is then
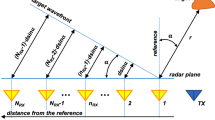
where \(s(\tau )\) represents the transmitted pulse. \(R(\tau ,t)\) for a respiration signal is shown in Fig. 1. Slow-time represents the received pulse number and fast-time represents the range. In the signal model, t is slow-time with frequency components denoted by f, and τ is fast-time with frequency components denoted by υ. The average human chest location is shown as a dashed line.
The discrete signal corresponding to (4) is
where \(1/{T}_{s}\) represents the pulse repetition frequency (PRF), \(t=n{T}_{s}\), \(n=0,\ldots ,\,N-1\) denote t samples, δT represents the sampling time in τ, \({\delta }_{R}=v{\delta }_{T}/2\) \(m=0,\ldots ,\,M-1\) denote τ samples, \(h[m,n]\) represent vital signs, and \(c[m]\) represent static clutters. To avoid ambiguities in range and frequency aliasing, Ts should satisfy
In a real environment, (5) becomes
where \({a}_{M\times N}\) represents linear trend term, \({w}_{M\times N}\) represents AWGN, \({q}_{M\times N}\) represents non-stationary clutters, \({g}_{M\times N}\) represents unknown clutters, and \({z}_{M\times N}\) represents the clutters introduced by moving objects. A reflected pulse must be acquired within one pulse duration so that
where Tw is the −6 dB pulse width.
Vital Sign Signal Detection
In static environments, the received pulses are shown in (4). Usually, the pulses without \(c[m]\) are
The frequencies of the vital sign signals are obtained by performing FT on \(\tilde{R}({\rm{m}}{\delta }_{T},t)\) in t given by
This can be acquired using the two-dimension FT of \(Y(\upsilon ,f)\) given by
where
and \(S(\upsilon )\) is the FT of the transmitted UWB pulse. This can be represented using Bessel functions as
where \({\beta }_{r}=2\pi {A}_{r}\) and \({\beta }_{h}=2\pi {A}_{h}\).
Then, (10) is rewritten as
where
The maximum value of (17) can be obtained as
and setting \(l=0\) in
gives the respiration signal
setting k = 0 in (19), we can acquire the heartbeat signals as
UWB Radar
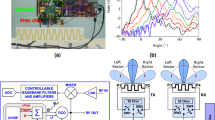
The experimental data was obtained using a UWB radar with parameters given in32. The radar center frequency is 400 MHz and the PRF is 600 kHz. The UWB pulses were acquired form six segments simultaneously with a time window of 124 ns, Ms = 682 samples per segment, and M = 4092 fast-time samples. NA samples are averaged to improve the SNR. Thus, a set of data is obtained every MsNA/PRF = 34.1 ms, and it takes 17.6 s to receive N = 512 pulses in slow-time. A combination of equivalent-time and real-time sampling34 is employed as it provides better performance than equivalent-time sampling only35.
Figure 2 shows the matrix R obtained using the UWB radar with a human subject at a distance of 9 m from the receiver in an outdoor environment which is described in Section IV. The vital sign signals are not evident due to the significant signal attenuation caused by the through-wall and long distance conditions. Thus, obtaining these signals in real environments is challenging, which motivates the development of a new method for vital sign detection.
Detection Algorithm
The new method for detection of the vital sign is designed in this section. A flowchart of this algorithm is given in Fig. 3. Two volunteers participated in this research. They were informed of the risks associated with participating in the experiments. This research was approved by both Ocean University of China and the Chinese Academy of Sciences. All experiments were performed in accordance with the relevant international guidelines and regulations.
Clutter Suppression
Respiration signals are typically corrupted by strong static clutters which are approximately slow-time invariant30. The DC component can be estimated as
resulting in the matrix31
To further remove static clutter, range profile subtraction is employed which is32
and then adaptive background subtraction is applied using a weighting coefficient \(\lambda \) to obtain
which gives
where \(\lambda =0.9\) and \(p[m,1]={\rm{\Omega }}[m,1]\)43.
The LTS method estimates the linear trend \({a}_{M\times N}\) and removes it from the received pulses. A least-squares fit is used to eliminate \({a}_{M\times N}\) from the received pulses in slow-time by assuming that the starting point is a linear model for the received pulses. This can be expressed in matrix form as
where \(X=[\frac{k}{N}\,{1}_{N}]\), \(k=0,1,\ldots ,N-1,\) and \(\beta \) denotes the unknown coefficient matrix which can be obtained by multiplying (27) by \({X}^{{\rm{T}}}\)
Rearranging gives
Using (28) and (29), the linear trend can be calculated as
As a result, we can acquire the results given by
In high SNR conditions, vital signs can easily be obtained even under \({q}_{M\times N}\) conditions. However, this clutter can significantly degrade signal estimation. SVD divides \(W\) into complementary subspaces which represent independent features of the received signal. This can be used to reduce the static/non-static clutter and increase the SNR. This decomposition is given by
where \(S\) is a diagonal matrix, \(U\) is a \(M\times M\) unitary matrix and \(V\) is a \(N\times N\) unitary matrix. The elements of \(S\) are the singular values \({\sigma }_{i}\) which are ranked in descending order, i.e. \(\sigma 1\ge \sigma 2\ge \sigma 3\ge \cdot \cdot \cdot \ge {\sigma }_{r}\ge 0\). The columns of \(U\) are the left singular vectors and the columns of \(V\) are the right singular vectors. The eigenvectors of \(W{W}^{{\rm{T}}}\) are U and the eigenvectors of \({W}^{{\rm{T}}}W\) are V.
The SVD in (32) can be expressed as
where \({M}_{k}\) is the kth intrinsic image with the same dimensions as \(W\). The intrinsic images are arranged in descending order. M1 is the first intrinsic image and is considered as \({q}_{M\times N}\). The images M2, M3, …, Mk typically contain the majority of the vital sign signals, while Mk+1,…, MG mainly contain noise. Therefore, (33) can be rewritten as
where \({M}_{C}\) denotes \({q}_{M\times N}\), i.e. the first intrinsic image, \({M}_{T}\) is the images containing the vital sign signals and \({M}_{N}\) is the remaining images. SVD can be used to remove \({q}_{M\times N}\) which gives
Note that it is difficult to estimate k so it is not possible to suppress the noise using this technique.
SNR Improvement
The detection environment including the signal frequency can have a significant effect on the received signals37. As a result, the traditional matched filter maybe invalid for vital signs detection. Instead, a Butterworth bandpass filter (BPF) is employed which has transfer function44
where \({N}_{f}=5\) is the filter order and \({\omega }_{c}\) is the cutoff frequency. This filter is composed of a Butterworth low pass filter (LPF) and a Butterworth high pass filter (HPF). This filter is used on (35) in the fast-time which gives
where \({N}_{b}={N}_{a}=5\), \({\kappa }_{i}\) and \({\chi }_{i}\) are the filter coefficients.
An average extraction filter is now used to eliminate low- and high-frequency clutter. The output is
where \(k=1,\,\ldots ,\,\lfloor M/\beta \rfloor \), \(\beta =7\) is the number of filter coefficients, \(\lfloor M/\beta \rfloor \) is the maximum integer less than \(M/\beta \), and \({{\boldsymbol{\Lambda }}}_{M\times N}=0\) when \(M > \lfloor M/\beta \rfloor \). Equations (22–38) are used to suppress the components \(c[m]\), \({a}_{M\times N}\), \({q}_{M\times N}\), and \({g}_{M\times N}\). \({z}_{M\times N}\) can be removed when there are no motions in the detection area. The resulting ideal signal is then
Range Determination
The standard deviation (SD) of the received pulses is used for range estimation of human subject. The SD for fast-time index m is45
where \({\mu }_{m}\) is the mean. The data from a female volunteer at 9 m far from the radar were used for SD calculation in through-wall conditions, and Fig. 4 gives the results. This figure shows that the SD is large when a subject is present, which indicates that it can be used for the detection of vital sign signals. Figure 5 shows the corresponding spectrums obtained from the SD values in the target area using an FT, which indicates the SD is periodic, and thus can be used for range estimation.
The DSFT of (40) is used for analyzing signal characteristics in time-frequency domain46,47. Windowing is also employed, which gives
where p represents frequency and \({\rm{\Xi }}\) represents the used Hamming window which is expressed as
where α = 0.54 and β = 0.46. The DSFT window length must be chosen carefully. If it is too small, there will be excessive, and the result tends to zero length increases. A window of O = 512 was chosen based on extensive simulation results. The DSFT is shown in Fig. 6 and has a range error of only 0.104 m. Figure 7 shows the calculated SD values and the corresponding spectrums using DSFT without a human subject in the environment. Compared Figs 6 with 7(b), result indicates that the range information can be acquired by employing the DSFT technique, which is given by
where \(\widehat{\tau }\) denotes the time delay, i.e. the peak value from (39).
Frequency Estimation
The time index for the delay estimate \(\widehat{\tau }\) is
To estimate the vital sign signal frequencies, an FT is performed on (39), which gives
Using the time index in (44), (45) can be given by
and taking the logarithm gives4
where the term j2kπ represents the phase variation due to any non-static objects and k is an integer. The unwrapping method can be used to remove this term20, but differentiation provides a simpler solution16. The imaginary part of (47) includes the phase variation of the vital signs \(j2\pi \frac{\Im }{{\delta }_{{\rm{T}}}}{\tau }_{v}(t)\). Compared with the approach in Section II, the products of the vital signs and the harmonics are not as significant when only the phase is considered. Further, differentiating the logarithm term is simple and straightforward, making this method suitable for real-time vital sign detection16. Using (3), the result is
where \(\text{'}\) denotes differentiation, and the corresponding discrete form as
The respiration frequency is typically 0.2 Hz to 0.5 Hz with an amplitude of 5 to 15 mm, and the heart rate is 0.8 Hz to 2.5 Hz with an amplitude of 2 to 3 mm38. The SNCR can thus be improved using a window for these frequencies. A rectangular window with length \(\kappa \) in the frequency domain is employed for each slow-time dimension which gives
where \(\odot \) is the window operator and \({k}^{\ast }\) is the minimum index. The FA method proposed in48 is employed to suppress any remaining clutters existing in vital sign signals in the same frequency band. This gives
where
Performance Results
Compared with several well-known techniques, the detection capability of the presented algorithm is tested in this section. This is achieved using experimental results obtained in both indoor and outdoor environments.
Experimental Setup
Figure 8 shows the UWB radar experimental setup. The wall has a thickness of 100 cm and is composed of brick (30 cm), reinforced concrete (40 cm), and wood (30 cm). The four experiments described below were conducted to obtain data for performance evaluation.
-
1.
This experiment was carried out at IECAS outdoors as shown in Fig. 9(a). A female subject stood breathing normally and facing the radar. The subject stood at 11 m, 9 m, 6 m, and 3 m far from the radar successively. The radar was placed on a table at a height of 1.5 m.
-
2.
This experiment was conducted indoors at the China National Fire Equipment Quality Supervision Center (CNFEQSC) as shown in Fig. 9(b). A male subject stood 12 m, 10 m, 7 m, and 4 m far from the radar. The radar was placed on a table at a height of 1.3 m.
An actuator was used instead of a human subject in experiments 3 and 4. The actuator moves at a frequency of 0.3333 Hz with an amplitude of 3 mm.
-
3.
This experiment was carried out at IECAS outdoors as shown in Fig. 10(a). The actuator was placed on a table at a height of 1.3 m at a distance of 11 m from the radar.
-
4.
This experiment was conducted at CNFEQSC indoors as shown in Fig. 10(b). The actuator was placed 12 m, 10 m, 7 m, and 4 m far from the radar.
The performance of the proposed, FFT, constant false alarm ratio (CFAR)34, and MHOC37 methods as well as the advanced method (AM)36, the FA method with different times, and the CSD42 and logarithm CSD (LCSD) techniques are evaluated in the following sections using the experimental data.
Initial Detection Performance
In this subsection, based on the data from experiment 1, the performance of the clutter suppression steps is considered with the subject 9 m from the radar. The results after removing the DC component and static clutter are given in Fig. 11(a,b), respectively, and Fig. 11(c) presents the results after removing the linear trend. These figures show that human respiration signals are quite weak and as a consequence, the oscillations are challenging to determine. The results after SVD and fast-time filtering are given in Fig. 11(d,e), respectively. These show a further reduction in the clutter which improves the respiration signal. Figure 11(f) shows the results after slow-time filtering and indicates that the respiration signal is significantly improved compared to the received signal in Fig. 2.
Human Subject Detection Outdoors
In this subsection, the data from experiment 1 is used for evaluating the performance of the detection method. Usually, the SNR of vital signs increases with decreasing distance between the radar and human subject due to large-scale attenuation32. The improvement in SNR can thus be used to evaluate the performance, which can be obtained as
where \({\mu }_{r}\) is the frequency index corresponding to the target, and \({\gamma }_{1}\) and \({\gamma }_{2}\) are the boundaries of the frequency window.
The data sets acquired outdoors were used to evaluate four detection methods. Figure 12 gives the calculated SD results and the corresponding spectrums using the DSFT technique are shown in Fig. 13. The errors in the estimations of range information are 26 cm, 11 cm, 5 cm, and 5 cm at ranges of 11 m, 9 m, 6 m and 3 m, respectively.
Table 1 gives the estimations of human respiration frequency, range errors, and SNR values from (53) for four detection algorithms. This shows that the presented method supplies the most accurate range estimates and high SNR, particularly for long distances. At a distance of 11 m, the SNR with the proposed method is 3.25 dB while the SNR is only −15.3 dB with the CFAR method, a difference of 18.6 dB. The respiration frequency estimates using the proposed method are 0.26 Hz at 11 m, 0.29 Hz at 9 m, 0.26 Hz at 6 m, and 0.32 Hz at 3 m, respectively, which are considerably more accurate than with the other methods. Figure 14 gives the results acquired from the CFAR technique, which indicate that the range information cannot be estimated accurately with this method over long distances. Figure 14(b–d) show that there remains significant clutter at distances of 6 m or more.
To evaluate the heart rate estimation performance, the data with a male subject outdoors was used. A typical resting heart rate is 75 to 81 beats per minute, corresponding to frequencies of 1.25 to 1.35 Hz. Figure 15 shows that the heart rate estimates for the proposed method are 1.34 Hz, 1.34 Hz, and 1.45 Hz, respectively. It was not possible to obtain estimates using the CFAR method. The corresponding SNR values for the proposed and CFAR methods are given in Table 2. This shows that the proposed method provides a significant SNR improvement over the CFAR method as the smallest difference is 9.43 dB at a distance of 6 m. The very low SNR values for the CFAR method are the reason the heart rate could not be estimated.
Human Subject Detection Indoors
The data from experiment 2 is now used for evaluating the detection performance. Figure 16 shows the calculated SD values with the proposed method and the DSFT results are given in Fig. 17. The range estimates are 11.8 m, 9.89 m, 6.95 m, and 4.06 m for distances of 12 m, 10 m, 7 m and 4 m, respectively, and show that the range information can be estimated more accurately indoors. This is because it is a controlled environment which lacks factors such as wind. The respiration frequency estimation results are shown in Fig. 18. The estimates of for the four distances are 0.26 Hz, 0.29 Hz, 0.26 Hz, and 0.32 Hz.
Clutter Suppression
The capability of removing clutters was evaluated using the data from experiment 1 at 6 m. The harmonics and the products of the vital sign signals were suppressed using the FA method and the results are given in Figs 19 and 20. This shows that the four-FA method can supply a better SNR improvement than the FFT, two-FA, and one-FA methods. Table 3 gives the SNR values and shows that the additional improvement is minimal when the FA method is performed six times. The SNR for the FFT, CSD, logarithm CSD (LCSD) and differentiated LCSD (DLCSD) methods is also given in Table 4. The corresponding frequency domain results for the CSD, LCSD, and DLCSD methods are given in Fig. 21(b–d), respectively. The range estimation results in Fig. 14 show that these methods do not effectively suppress the clutter compared to the proposed method.
Actuator Experiment Results
The data from the conducted actuator experiments were used for testing the presented algorithm. The actuator was used to imitate human respiration with the amplitude of 3 mm and a frequency of 0.3333 Hz and. Figure 22 shows the SD values for the proposed method using the data from experiment 4 and the corresponding range and frequency estimation results are given in Figs 23 and 24, respectively. The frequency estimate from Fig. 24(a) is 0.353 Hz. The frequency estimate using the CSD method from Fig. 24(b) is 0.11 Hz and the estimate using the LCSD method from Fig. 24(c) is 0.56 Hz. The FFT method provides the worst performance as the frequency estimate from Fig. 24(d) is 0.12 Hz. Compared with the actual frequency of 0.3333 Hz, the proposed method provides the best estimate with an error of only 0.019 Hz. The frequency estimates using the outdoor data from experiment iii is shown in Fig. 25. The frequency estimates and corresponding deviations are given in Table 4 for three trials of the experiment. All these results indicate that the presented algorithm has the smallest deviation and significantly outperforms the other algorithms.
Conclusion
Vital sign detection was considered in this paper for applications such as after a natural disaster. The respiration and heartbeat frequencies were estimated using an impulse UWB radar. The CSD-based FA method was shown to be effective in suppressing signal products and harmonics. The discrete short-time Fourier transform (DSFT) of the calculated standard deviation (SD) values was used to estimate the range information of the volunteer. Experimental data obtained using a UWB radar were used to evaluate the performance of several techniques. The results obtained indicate that the proposed method can more effectively remove clutter and improve the SNR than the other methods. Further, it provides better range and frequency estimates49,50,51,52,53.
Availability of Data and Materials
All data analyzed during this study are included in this paper.
References
Liang, S. D. Sense-through-wall human detection based on UWB radar sensors. Signal Process. 126, 117–124 (2016).
Muqaibel, A. H., Abdalla, A. T., Alkhodary, M. T. & Alawsh, S. A. Through-the-wall radar imaging exploiting Pythagorean apertures with sparse reconstruction. Digit. Signal Process. 61, 86–96 (2017).
Stanciu, M. I., Azou, S., Rădoi, E. & Şerbănescu, A. A Statistical analysis of multipath interference for impulse radio UWB systems. J. Franklin. I. 352, 5952–5967 (2014).
Wang, J. et al. Noncontact distance and amplitude-independent vibration measurement based on an extended DACM algorithm. IEEE Trans. Instrum. Meas. 63, 145–153 (2014).
Singh, A., Gao, X., Yavari, E. & Zakrzewski, M. Data-based quadrature imbalance compensation for a CW Doppler radar system. IEEE Trans. Microw. Theory Techn. 61, 1718–1724 (2013).
Wang, G., Gu, C., Inoue, T. & Li, C. A hybrid FMCW-interferometry radar for indoor precise positioning and versatile life activity monitoring. IEEE Trans. Microw. Theory Techn. 62, 2812–2822 (2014).
Mercuri, M., Soh, P. J., Boccia, L. & Schreurs, D. Optimized SFCW radar sensor aiming at fall detection in a real room environment. in Proc. IEEE Biomed. Wireless Technol. Netw. Sens. Syst., Austin TX USA, 4–6 (2013).
Mercuri, M., Ping, J. S., Pandey, G. & Karsmakers, P. Analysis of an indoor biomedical radar-based system for health monitoring. IEEE Trans. Microw. Theory Techn. 61, 2061–2068 (2013).
Muqaibel, A. & Safaai-Jazi, A. Characterization of wall dispersive and attenuative effects on UWB radar signals. J. Franklin I. 345, 640–658 (2008).
Wang, Y., Liu, Q. & Fathy, A. E. Simultaneous localization and respiratory detection of multiple people using low cost UWB biometric pulse Doppler radar sensor. in IEEE MTT-S Int. Microw. Symp. Dig., Montreal QC Canada (2012).
Wang, Y., Liu, Q. & Fathy, A. E. CW and pulse–Doppler radar processing based on FPGA for human sensing applications. IEEE Trans. Geosci. Remote Sens. 51, 3097–3107 (2013).
Koo, Y. S., Ren, L., Wang, Y. & Fathy, A. E. UWB MicroDoppler radar for human gait analysis, tracking more than one person, and vital sign detection of moving persons. In IEEE MTT-S Int. Microw. Symp. Dig., Seattle WA USA, 1–4 (2013).
Nijsure, Y., Tay, W. P., Gunawan, E. & Wen, F. An impulse radio ultrawideband system for contactless noninvasive respiratory monitoring. IEEE Trans. Biomed. Eng. 60, 1509–1517 (2013).
Li, J., Liu, L. & Zeng, Z. Advanced signal processing for vital sign extraction with applications in UWB radar detection of trapped victims in complex environments. IEEE J. Sel. Topics Appl. Earth Observat. Remote Sens. 7, 783–791 (2014).
Li, Z., Li, W. & Lv, H. A novel method for respiration-like clutter cancellation in life detection by dual-frequency IR-UWB radar. IEEE Trans. Microw. Theory Techn. 61, 2086–2092 (2013).
Hu, W. et al. Noncontact accurate measurement of cardiopulmonary activity using a compact quadrature Doppler radar sensor. IEEE Trans. Biomed. Eng. 61, 725–735 (2014).
Gu, C. & Li, C. Assessment of human respiration patterns via noncontact sensing using doppler multi-radar system. Sensors 15, 6383–6398 (2015).
Lazaro, A., Girbau, D. & Villarino, R. Techniques for clutter suppression in the presence of body movements during the detection of respiratory activity through UWB radars. Sensors 14, 2595–2618 (2014).
Chuantao, L. et al. A method for remotely sensing vital signs of human subjects outdoors. Sensors 15, 14830–14844 (2015).
Ren, L., Kooet, Y., Wang, Y. & Fathy, A. Noncontact multiple heartbeats detection and subject localization using UWB impulse doppler radar. IEEE Microw. Wirel. Compon. Lett. 25, 690–692 (2015).
Vu, V. T., Sjogren, T. K., Pettersson, M. I. & Gustavsson, A. Detection of moving targets by focusing in UWB SAR theory and experimental results. IEEE Trans. Geosci. Remote Sens. 48, 3799–3815 (2010).
Zhuge, X. & Yarovoy, A. A sparse aperture MIMO-SAR based UWB imaging system for concealed weapon detection. IEEE Trans. Geosci. Remote Sens. 49, 509–518 (2011).
Ascione, M., Buonanno, A., D’Urso, M. & Angrisani, L. A new measurement method based on music algorithm for through-the-wall detection of life signs. IEEE Trans. Instrum. Meas. 62, 13–26 (2013).
Liu, L., Liu, Z. & Barrowes, B. Through-wall bio-radiolocation with UWB impulse radar-observation, simulation and signal extraction. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 4, 791–798 (2011).
Liu, L. et al. Numerical simulation of UWB impulse radar vital sign detection at an earthquake disaster site. Ad Hoc Netw. 13, 34–41 (2014).
Baldi, M. et al. Non-invasive UWB sensing of astronauts’ breathing activity. Sensors 15, 565–591 (2015).
Li, Z., Li, W., Lv, H. & Zhang, Y. A novel method for respiration-like clutter cancellation in life detection by dual-frequency IR-UWB radar. IEEE Trans. Microw. Theory Technol. 5, 2086–2092 (2013).
Liang, X. et al. An improved algorithm for through-wall target detection using ultra-wideband impulse radar. IEEE Access 5, 22101–22118 (2017).
Conte, E., Filippi, A. & Tomasin, S. ML period estimation with application to vital sign monitoring. IEEE Signal Process. Lett. 17, 905–908 (2010).
Nezirovíc, A., Yarovoy, A. & Ligthart, L. P. Signal processing for improved detection of trapped victims using UWB radar. IEEE Trans. Geosci. Remote Sens. 48, 2005–2014 (2010).
Liang, X. et al. Through-wall Human Being Detection Using UWB Impulse Radar. EURASIP J Wirel Comm 2018, 1–17 (2018).
Liang, X. et al. Improved denoising method for through-wall vital sign detection using UWB impulse radar. Digit. Signal Process 74, 72–93 (2018).
Zhang, Z. Human-target detection and surrounding structure estimation under a simulated rubble via UWB radar. IEEE Trans. Geosci. Remote Sens. 10, 328–331 (2013).
Xu, Y., Wu, S., Chen, C. & Chen, J. A novel method for automatic detection of trapped victims by ultrawideband radar. IEEE Trans. Geosci. Remote Sens. 50, 3132–3142 (2012).
Xie, Y. & Fang, G. Equi-amplitude tracing algorithm based on base-band pulse signal in vital sign detecting. Electron. Inf. Technol. 31, 1132–1135 (2009).
Liang, X. et al. Ultra-wide band impulse radar for life detection using wavelet packet decomposition. Phys Commun-Amst 29, 31–47 (2018).
Xu, Y., Dai, S., Wu, S. & Chen, J. Vital sign detection method based on multiple higher order cumulant for ultra-wideband radar. IEEE Trans. Geosci. Remote Sens. 50, 1254–1265 (2012).
Hu, X. & Jin, T. Short-range vital signs sensing based on EEMD and CWT using IR-UWB radar. Sensors 16, 2025, https://doi.org/10.3390/s16122025 (2016).
Li, C. & Lin, J. Random body movement cancellation in Doppler radar vital sign detection. IEEE Trans. Microw. Theory Techn. 56, 3143–3152 (2008).
Park, B. K., Boric-Lubecke, O. & Lubecke, V. M. Arctangent demodulation with DC offset compensation in quadrature Doppler radar receiver systems. IEEE Trans. Microw. Theory Techn. 55, 1073–1079 (2007).
Naishadham, K. & Piou, J. E. A robust state space model for the characterization of extended returns in radar target signatures. IEEE Trans. Antennas Propag. 56, 1742–1751 (2008).
Ren, L. et al. Phase-based methods for heart rate detection using UWB impulse Doppler radar. IEEE Trans. Microw. Theory 64, 3319–3331 (2016).
Hu, J., Zhu, G., Jin, T. & Zhou, Z. Adaptive Through-wall indication of human target with different motions. IEEE Geosci. Remote Sens. Lett. 11, 911–915 (2013).
Mak, J. C. C., Bois, A. & Poon, J. K. S. Programmable multiring Butterworth filters with automated resonance and coupling tuning. IEEE J. Sel. Top. Quant. 22, 1–9 (2016).
Liang, X., Zhang, H., Lv, T. & Gulliver, T. A. Energy detector based TOA estimation for MMW systems using machine learning. Telecommun. Syst. 64, 417–427 (2017).
Allen, B. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Trans. Audio Speech 25, 235–238 (1977).
Wojcicki, K., Milacic, M., Stark, A. & Lyons, J. Exploiting conjugate symmetry of the short-time Fourier spectrum for speech enhancement. IEEE Signal Process. Lett. 15, 461–464 (2008).
Marple, L. Computing the discrete-time “analytic” signal via FFT. IEEE Trans. Signal Process. 47, 2600–2603 (1999).
Huang, M. C. et al. A self-calibrating radar sensor system for measuring vital signs. IEEE Trans. Biomed. Circuits Syst. 10, 352–363 (2016).
JalaliBidgoli, F., Moghadami, S. & Ardalan, S. A compact portable microwave life-detection device for finding survivors. IEEE Embedded Syst. Lett. 8, 10–13 (2016).
Gennarelli, G., Ludeno, G. & Soldovieri, F. Real-time through-wall situation awareness using a microwave Doppler radar sensor. Remote Sens. 8, 621, https://doi.org/10.3390/rs8080621 (2016).
Le, C., Dogaru, T., Nguyen, L. & Ressler, M. A. Ultra-wideband radar imaging of building interior: Measurements and predictions. IEEE Trans. Geosci. Remote Sens. 47, 1409–1420 (2009).
Huang, Q., Qu, L. & Fang, G. UWB through-tall imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 48, 1408–1415 (2010).
Acknowledgements
This work was funded by the Science and Technology on Electronic Test & Measurement Laboratory (9140C120102150C12055 and 6142001010101), Nature Science Foundation of China (41527901, 61501424 and 61701462), and the Ao Shan Science and Technology Innovation Project of Qingdao National Laboratory for Marine Science and Technology (2017ASKJ01).
Author information
Authors and Affiliations
Contributions
All authors contributed to writing and editing this manuscript. X. Liang conceived and designed the experiments, performed the experiments, and analyzed the data. H. Zhang and T. Aaron Gulliver reviewed the results and revised the manuscript. J. Deng helped to update the resubmitted paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liang, X., Deng, J., Zhang, H. et al. Ultra-Wideband Impulse Radar Through-Wall Detection of Vital Signs. Sci Rep 8, 13367 (2018). https://doi.org/10.1038/s41598-018-31669-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-31669-y
This article is cited by
-
Automatic radar-based 2-D localization exploiting vital signs signatures
Scientific Reports (2022)
-
Contactless analysis of heart rate variability during cold pressor test using radar interferometry and bidirectional LSTM networks
Scientific Reports (2021)
-
A dataset of radar-recorded heart sounds and vital signs including synchronised reference sensor signals
Scientific Data (2020)
-
Preclinical Evaluation of a Noncontact Simultaneous Monitoring Method for Respiration and Carotid Pulsation Using Impulse-Radio Ultra-Wideband Radar
Scientific Reports (2019)
-
An improved signal processing algorithm for VSF extraction
Multidimensional Systems and Signal Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.