Abstract
It is widely known that the switching time is determined by the thermal stability parameters and external perturbations such as magnetic field and/or spin polarized current in magnetic nano-structures. Since the thermal stability parameter and switching time are crucial values in the design of spin-transfer torque magnetic random access memory, the measurement of the switching time is important in the study of the switching behavior of ferromagnetic nano-structures. In this study, we focus on the distribution of the switching time. Within the limit of a large energy barrier, a simple analytical expression between damping constant and anisotropy field with switching time distribution is obtained and confirmed by numerically solving the Fokker-Planck equation. We show that the damping constant and anisotropy field can be extracted by measuring the full width half maximum of the switching time distribution in the magnetic nano-structure devices. Furthermore, the present method can be applied to not only single nano-structure, but also inhomogeneous nano-structure arrays.
Similar content being viewed by others
Introduction
Statistical distributions of measurable physical quantities always have significant physical meanings. Extrinsically, statistical distribution causes measurement error and/or limitations of the accuracy of measurement instruments, in addition to inhomogeneity of samples. Without these extrinsic source ubiquitous finite distributions of the measurable physical quantities can be characterized by the line width, statistical deviation, or full width half maximum (FWHM), and they reveal information about important intrinsic physical quantities such as the atomic layer spacing or the grain size1. For example, the peak position (x0) and the FWHM (Δx) of the X-ray diffraction peak in a θ − 2θ measurement can give us the atomic layer spacing and information on the grain size1. And, the peak position and width of a low angle X-ray reflection gives us some information on the layer thickness and roughness. In magnetic measurements, the peak position and FWHM of ferromagnetic resonance (FMR) spectra are related with the magnetic energy (including anisotropy, exchange, and demagnetization energies) and the Gilbert damping constant2, More generally, in any kind of resonance experiment such as one using an RLC circuit or a damped harmonic oscillator, not only the peak position, but also the peak width always has important physical meanings.
Despite the importance of these distributions, most studies on the switching time in magnetic nano-structures, which is essential in modern nano-scale spintronic devices, have focused only on the switching time itself, experimentally3,4,5,6,7,8,9,10,11,12,13 and/or theoretically14,15,16,17,18,19,20,21. The thermally activated switching time of magnetic nano-structures is determined by the Néel-Arrhenius equation22 through the thermal stability parameter and the attempt frequency23. Since certain values of the thermal stability parameter ensure digital data storage firmness and write error rate (WER), these values must be carefully examined. Therefore, with/without an external perturbation such as an external magnetic field and/or spin-polarized current, the switching behaviors have been actively studied for decades. However, no studies so far have paid attention to the physical meaning of the switching time distribution.
The damping constant is an important physical property of magnetic materials; it reflects the energy dissipation paths of the given magnetic system. Especially, the critical current for switching in spin-transfer torque magnetic random access memory (STT-MRAM) is proportional to the damping constant24; therefore, the characterization of the damping constant of ultra-thin magnetic materials is a challenging issue in the development of STT-MRAM. The damping constant is influenced not only by the intrinsic material properties25, but also by many extrinsic sources26,27,28,29. Especially, ultra-thin magnetic multilayers in magnetic tunneling junctions (MTJ), and spin pumping30,31, from adjacent layers, can alter the damping constant significantly. Furthermore, edge effects of the nano-structure can be another source of discrepancy from the bulk values of the damping constant of nano-sized MTJ cells32. Therefore, determination of the exact damping constant of each nano-sized MTJ cell will be important in the study of STT-MRAM.
In this study, we find a useful analytic expression for the FWHM of switching time distribution and the damping constant. It is revealed that (i) the FWHM is inversely proportional to the external field, (ii) the damping constant can be extracted from the FWHM, and (iii) the effective anisotropy field can be obtained from the intercept of the relation between reduced external field and FWHM. We analytically solved the Fokker-Planck equation (FPE)14,32 to obtain the analytic expression and numerically confirmed the validity and limitations of the presented technique. We also found that our technique might be useful in the determination of the damping constant and the effective anisotropy energy, or of the thermal stability parameters of a nano-sized patterned ferromagnet. Furthermore, it can be applicable not only to single cells, but also to many cell arrays with finite inhomogeneous material parameters, the use of which is much easier and practical in experiments.
Results
Switching time for a nano-structure, solution of Fokker Planck equation
The magnetization switching dynamics for nano-structures is well understood and can be obtained by solving the Landau-Lifshitz-Gilbert (LLG) equation. Our concern is the probability of magnetization switching of a free layer of the STT-MRAM; however, solving the stochastic LLG equation requires large computational resources. In this case, it is very convenient to use the Fokker-Planck equation (FPE) because it can statistically describe the switching of the magnetization14,33. The FPE is a partial differential equation that describes the flow of the probability density function under certain circumstances. With the thermal fluctuation field, it was reported decades ago that the probability of magnetization switching can be obtained by solving the FPE33. Recently, Butler et al.14 extended the FPE using the spin transfer torque and magnetic field for more general cases. According to Butler’s work14, the FPE of the probability distribution of a polar angle as a function of time in the case of uniaxial anisotropy with the limit of single domain approximation can be expressed by
where ρ(θ, τ) is the probability that the magnetization is pointing in direction θ relative to the film normal (+z-axis) at time \(\tau =\frac{\alpha \gamma {H}_{k}}{1+{\alpha }^{2}}t\), the dimensionless time scale; Δ = Ku,effV/kBT is the thermal stability factor, where Ku,eff is the effective uniaxial anisotropy, V is the volume of the sample, kB is the Boltzmann constant; and T is the absolute temperature. Also, \(i=\frac{I}{{I}_{Co}}\) and \(h=\frac{{H}_{app}}{{H}_{k}}\) are the reduced current and the magnetic field, where I is applied current and ICo is the critical current with only the Slonczewski term, Happ is an applied field (it is always negative to switch the initial + z magnetization) and Hk = 2Ku,eff/μ0MS is an effective anisotropy field including the uniaxial anisotropy and demagnetization energies.
The cumulative switching probability function PS(τ) is given by ref.14
Here, v = i − h − 1, and v > 0 implies larger current (negative field) than the switching current (field); switching occurs very rapidly. v < 0 means the applied current (field) is smaller than the critical value, so the switching probability is extremely low and only thermally activated switching is possible with long switching time. Here, it must be mentioned that the sign of h is always negative to switch the initial +z magnetization. W(τ) is defined by the ansatz \(\rho (\theta ,\tau )=A(\tau )\exp (-{\theta }^{2}/W(\tau ))\), where A(τ) and W(τ) are related with the normalization condition of probability14. Therefore, the physical meaning of W(τ) is the width of the distribution of θ at the given time. When τν ≫ 1, and there is strong current (field) or long time, W is very large; then PS → 1, which implies that almost 100% switching occurs. It must be mentioned that Eqs (2) and (3) are approximations, such that numerical calculation of Eq. (1) is required to obtain solutions for general cases.
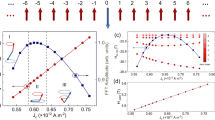
Figure 1(a) shows a typical example of a cumulative switching probability PS(τ) when h = −1.5 and i = 0 with α = 0.01; Δ = 68.25 at 300 K (corresponding to Hk = 8000 Oe). The corresponding v = 0.5 and τ = 1.41 × 109(Hz)⋅t(s). The time derivative \(\frac{d{P}_{S}(\tau )}{d\tau }\) is shown in Fig. 1(b); it follows the log-normal distribution. We depict it again in log-scale, \(\mathrm{log}(\tau )\), to obtain a normal distribution function, as shown in Fig. 1(c).
Let us find the peak position and FWHM of \(\frac{d{P}_{S}(\tau )}{d\tau }\). By taking τ derivative of Eq. (2),
In order to find the peak position, we have to find a value of τ0 that will satisfy the condition of \(\frac{{d}^{2}{P}_{S}({\tau }_{0})}{d{\tau }^{2}}=0\). After tedious algebra, we find
The FWHM can be determined by its definition
Due to the complex form of Eq. (6), FWHM cannot be easily obtained analytically, only a numerical solution is available. Let us assume a large barrier case (Δ > 40), and τν ≫ 1. We can make proper approximations of Eq. (4), and obtain
From Eq. (7), the peak position and height of the peak are
Equation (8) is not in exactly the same form as the results of Eqs (2.12) and (2.14) in ref.14; however, it has a similar dependence on v. If we ignore the logarithmic term, we can roughly say that \({{\tau }_{0}}^{-1}\) is proportional to Happ when only the magnetic field is applied. More details will be provided later.
The FWHM (=Δτ) of the peak is given by
Here, Wk is the k-th branch of the Lambert W function, and e is Euler’s number. Eq. (10) is the central result of our study. It implies that the dimensionless FWHM of the switching time distribution (Δτ) is inversely proportional to v, and we can rewrite Eq. (10) as
With the assumption of small α ≪ 1 and the magnetic field only case (I = 0, Happ < −Hk, h < −1), Eq. (11) can be simplified for Δt to give the FWHM in units of seconds,
This is the main finding in this study. If we measure Δt−1 as a function of Happ, we can obtain a linear line: the slope is \(\frac{-\alpha \gamma }{1.223}\) and the intercept of the y-axis is \(\frac{-\alpha \gamma }{1.223}{H}_{k}\). Therefore, we can determine the damping constant of the ferromagnetic nano-structure from the switching time distribution measurement. Furthermore, we can also determine Hk from the intercept.
Numerical solution of Fokker Planck equation
Determination of α and H k from the switching time distribution
We were able to depict the numerically calculated PS(τ) and dPs(τ)/dτ by numerically solving the FPE. The material parameters and dimensions of the sample were the following values: Δ = 60, α = 0.0134,35 and volume of the cell = π 30 × 30 × 1 nm3, Ms = 1.0 × 106 A/m; corresponding Hk is 1.4 × 105 A/m in Fig. 2(a,b) for various h (from −1.1 to −5.0). The stronger the magnetic field, the shorter the peak switching time, as can be clearly seen in Fig. 2(a,b). From the log-normal distribution of dPs/dτ, we can numerically obtain Δt−1 and plot it as a function of γHapp/1.223 to find the slope and intercept, as shown in Fig. 2(c), with linear fitting. The slope of the linear fit is −0.00958 (=−αfit), and Hk,fit = 1.264 × 105 A/m is obtained from the intercept of −0.2196 GHz (=−γHk,fit/1.223). The error from the input value is acceptable (αfit/αinput = 0.96 ~ 4% error and Hk,fit/Hk,input = 0.90 ~ 10% error). Despite the crude approximation of Eq. (13), the agreement is excellent. From Fig. 2(c), we can confirm that the analytic expression Eq. (13) is well matched with the full numerical results.
(a)PS, (b) dPS/dτ for various h (=−1.1 ~ −5.0) and (c) Δt−1 as a function of γHapp/1.223 with the linear fitting result of Eq. (13).
Equation (13) is somewhat similar to the well-known relation between the line width and the damping constant in FMR experiments, \({\rm{\Delta }}H={\rm{\Delta }}{H}_{ext}+\frac{4\pi }{\sqrt{3}}\frac{\alpha f}{\gamma }\), where ΔH, ΔHext, and f are the peak to peak line width, extrinsic line width from inhomogeneity of the samples, and measurement frequency, respectively36,37. Generally, in FMR measurement, α is determined from the slope of ΔH as a function of f. However, the FMR signal is proportional to the volume of the sample; it is extremely difficult to carry out FMR measurement for ultra-thin nano-sized samples.
Effect of various Δ, H k, and temperature
Figure 3(a) shows the numerically calculated Δt−1 as a function of γHapp/1.223 for various Δ (=30, 40, 50, 60) at 300 K. With the same α input values, Hk varies with Δ\((=\frac{{\mu }_{0}{M}_{s}{H}_{k}V}{2{k}_{B}T})\) for a constant temperature. From Eq. (13), it can be easily understood that the slopes are the same, and only the intercepts change with Δ or Hk. The error of α is only 4~5%, while the error of Hk is rather larger (10~16%). When Δ is larger, the error is smaller. Practically, the value of Δ required for STT-MRAM application is >60; the typical error in this method is about 5% for α and 10% for Hk.
We depicted Δt−1 again as a function of γHapp/1.223 for various temperatures (100, 200, and 300 K) with the same materials parameters, as shown in Fig. 3(b). Since we varied only the temperature with constant Hk (=1.59 × 105 A/m), all Δt−1 plots collapse to a single line. This is also well explained by Eq. (13), in which there is no dependence on temperature. However, physically, it sounds very strange. It seems that the switching time distribution is independent of the temperature. When we take a close look at the derivation process, the Δ dependence disappears during the approximation with the assumption of Δ ≫ 1. The truth however is that there is a very small temperature dependence in the numerical solutions; Δt−1 is almost insensitive to the temperature. Therefore, Eq. (13) works well with a wide range of temperature and is useful to determine the temperature dependent value α if the assumption of Δ ≫ 1 is valid. Experimentally, Eq. (13) requires only measurements of the switching time distribution as a function of the applied field; we do not need any other material parameters for the determination of α; this will be a very strong point of the presented technique.
Inhomogeneous nano-structure array
So far, we have considered only switching time distributions for a single nano-structure. The switching time distribution can be obtained by repeated switching measurement for a single cell. However, generally, nano-size single cell measurement is not experimentally easy. Practically, switching measurement of many cells is experimentally easier because of the larger signal; furthermore, many-cell measurements give us a statistical switching time distribution. However, when we consider many cells simultaneously, the inhomogeneity of each cell must be addressed. For many possible reasons, nano-size cell anisotropy and size will vary from cell to cell. Such inhomogeneity of individual cells will influence the measurement of Δt−1. The sample to sample variation of Hk or Δ is a serious problem in practical STT-MRAM production. The variation of each cell, δHk or δΔ, is the main source of switching voltage (current) distribution; it must be monitored and controlled to reduce write bit error in STT-MRAM.
We assumed a finite normal distribution of Δ values with a standard deviation of σΔ. Each dPs/dτ is plotted in Fig. 4(a) for σΔ = 10 and Δ = 60. The peak and FWHM of dPs/dτ are found to change with various Δ. After calculating dPs/dτ for each Δ, we obtained a weighted averaged dPs/dτ with an assumption of normal distribution. Since we assumed a normal distribution, the averaged dPs/dτ is identical to \({(d{P}_{s}/d\tau )}_{{\sigma }_{{\rm{\Delta }}}=60}\). Therefore, surprisingly enough, the ratios of Δt−1 to Happl are almost identical for cases of σΔ = 0, 5, and 10, as shown in Fig. 5(b), and the obtained values of α and Hk are the same as those of the single cell case. Here, σΔ = 0 is the single Δ value or single cell case. This result seems at a glance counterintuitive; however, it is physically correct. The presented measurement technique is solid for the inhomogeneity of Δ of each cell; this implies that the variations of Hk and volume of each cell do not affect the determination of the value of α in the presented technique. Since Eq. (13) is linear to α and Hk, we can always obtain the average values of α and Hk for the cell array.
Δt−1 as a function of h = Happ/Hk. The deviation from the linear dependence increases when |h| < 1. The symbols represent the full numerical solution of the FPE, and the red solid lines are the linear fitting results of Eq. (13).
Validity and limitations of Eq. (13)
We derived Eq. (13) with the assumption of τν ≫ 1. We were interested in a large enough case of Δ > 50, because the thermal stability must be guaranteed for STT-MRAM applications. Furthermore, the ν ≫ 1 condition implies a large enough STT current and/or magnetic field to ensure STT and/or field driven switching processes. We have to emphasize that Eq. (13) is not valid for thermally activated switching, where v ≤ 0. Figure 5 shows the limitations of the presented technique. For large |h|, the linearity of Δt−1 is excellent, while in the small |h| region, Δt−1 deviates from linear behavior. In our numerical calculations (for Δ = 60), |h| > 1.25 is required, and a larger |h| gives better fitting results. For experiments, the linearity of the curve of Δt−1 vs. h will be a criterion of the validity of the measurement. Figure 6 shows the difference between the exact solution of Eq. (6) and the approximated solution of Eq. (10), assuming a larger energy barrier. The difference between the exact and approximated solutions is smaller for larger thermal stability factors. The difference between Eqs (6) and (10) is sufficiently small (<1%) for large Δ and large h.
Discussion
We theoretically and numerically study the relation between damping constant and anisotropy field with the FWHM of the switching time distribution for the magnetic nano-structure. The physical meaning of the switching time distribution has so far not been considered in most studies, and so we reveal that the switching time distribution contains important physical information such as the line width of the FMR measurement. We derive approximate analytic expressions of the full-width half-maximum (FWHM, Δt) of the switching time distribution for the case of a high thermal barrier. We find that the measured Δt−1, as a function of the external field, shows linear dependence; the damping constant α and the effective anisotropy field can be extracted using the damping constant α and the intercept. The FWHM of the switching time distribution is in a range of nanoseconds; this is expected to be large enough to be resolved by state-of-the-art experimental techniques. Our prediction allows us to estimate the damping constant and the effective anisotropy field simultaneously from the switching time distribution of a nano-size patterned sample.
References
Scherrer, P. Bestimmung der Grosse und der Inneren Struktur von Kolloidteilchen Mittels Rontgenstrahlen. Gottinger Nachrichten Gesell. 2, 98–100 (1918).
Kittel, C. & Mitchell, A. H. Ferromagnetic relaxation and gyromagnetic anomalies in metals. Phys. Rev. 101, 1611 (1956).
Koch, R. H., Katine, J. A. & Sun, J. Z. Time-Resolved Reversal of Spin-Transfer Switching in a Nanomagnet. Phys. Rev. Lett. 92, 088302 (2004).
Nowak, J. J. Dependence of voltage and size on write error rates in spin-transfer torque magnetic random-access memory. IEEE Mag. Lett. 7, 3102604 (2016).
Lee, K., Kan, J. J., Fullerton, E. E. & Kang, S. H. Write error rate slopes of in-plane magnetic tunnel junctions. IEEE Mag. Lett. 3, 3000604 (2012).
Sharrock, M. P. Measurement and interpretation of magnetic time effects in recording media. IEEE Trans. MAG 35, 4414 (1999).
Sbiaa, R. et al. Reduction of switching current by spin transfer torque effect in perpendicular anisotropy magnetoresistive devices. J. Appl. Phys. 109, 07C707 (2011).
Thomas, L. et al. Perpendicular spin transfer torque magnetic random access memories with high spin torque efficiency and thermal stability for embedded applications. J. Appl. Phys. 115, 172615 (2014).
Pufall, M. R. et al. Large-angle, gigahertz-rate random telegraph switching induced by spin-momentum transfer. Phys. Rev. B 69, 214409 (2004).
Hahn, C. et al. Time-resolved studies of the spin-transfer reversal mechanism in perpendicularly magnetized magnetic tunnel junctions. Phys. Rev. B 94, 214432 (2016).
Bedau, D. et al. Spin-transfer pulse switching: From the dynamic to the thermally activated regime. Appl. Phys. Lett. 97, 262502 (2010).
Bedau, D. et al. Ultrafast spin-transfer switching in spin valve nanopillars with perpendicular anisotropy. Appl. Phys. Lett. 96, 022514 (2010).
Heindl, R., Rippard, W. H., Russek, S. E., Pufall, M. R. & Kos, A. B. Validity of the thermal activation model for spin-transfer torque switching in magnetic tunnel junctions. J. of App. Phys. 109, 073910 (2011).
Butler, W. H. et al. Switching Distributions for Perpendicular Spin-Torque Devices Within the Macrospin Approximation. IEEE Trans. MAG. 48, 4684–4700 (2012).
Bertram, H. N. & Peng, Q. Numerical simulations of the effect of record field pulse length on medium coercivity at finite temperatures. IEEE Trans. MAG 34, 1543–1545 (1998).
Bertram, H. N. & Richer, H. J. Arrhenius–Néel thermal decay in polycrystalline thin film media. J. Appl. Phys. 85, 4991 (1999).
Igarashi, M., Akagi, F., Yoshida, K. & Nakatani, Y. Effect of angle dependent attempt frequency on Arrhenius-Neel thermal decay in thin film media. IEEE Trans. MAG 36, 2459–2461 (2000).
Victora, R. H. Predicted time dependence of the switching field for magnetic materials. Phys. Rev. Lett. 63, 457 (1989).
Breth, L. et al. Thermal switching field distribution of a single domain particle for field-dependent attempt frequency. J. Appl. Phys. 112, 023903 (2012).
Lee, K.-S., Lee, S.-W., Min, B.-C. & Lee, K.-J. Thermally activated switching of perpendicular magnet by spin-orbit spin torque. Appl. Phys. Lett. 104, 072413 (2014).
He, J., Sun, J. Z. & Zhang, S. Switching speed distribution of spin-torque-induced magnetic reversal. J. Appl. Phys. 101, 09A501 (2007).
Néel, L. Théorie du traînage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites. Annales de Géophysique 5, 99–136 (1949).
Suh, H.-J. et al. Attempt frequency of magnetization in nanomagnets with thin-film geometry. Phy. Rev. B 78, 064430 (2008).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1 (1996).
Gilmore, K., Idzerda, Y. U. & Stiles, M. D. Identification of the Dominant Precession-Damping Mechanism in Fe, Co, and Ni by First-Principles Calculations. Phys. Rev. Lett. 99, 027204 (2007).
Song, H.-S. et al. Observation of the intrinsic Gilbert damping constant in Co/Ni multilayers independent of the stack number with perpendicular anisotropy. Appl. Phys. Lett. 102, 102401 (2013).
Kim, K.-W., Moon, J.-H., Lee, K.-J. & Lee, H.-W. Prediction of Giant Spin Motive Force due to Rashba Spin-Orbit Coupling. Phys. Rev. Lett. 108, 217202 (2012).
Moon, J.-H., Seo, S.-M. & Lee, K.-J. Effect of Enhanced Damping Due to Spin-Motive Force on Field-Driven Domain Wall Motion. IEEE Trans. MAG 46, 2167–2170 (2010).
Moon, J.-H. & Lee, K.-J. Effect of enhanced damping caused by spin-motive force on vortex dynamics. J. Appl. Phys. 111, 07D120 (2012).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced Gilbert Damping in Thin Ferromagnetic Films. Phys. Rev. Lett. 88, 117601 (2002).
Kim, D.-H., Kim, H.-H. & You, C.-Y. Suppression of the spin pumping in Pd/Ni81Fe19 bilayers with nano-oxide layer. Appl. Phys. Lett. 99, 072502 (2011).
Ozatay, O. et al. Sidewall oxide effects on spin-torque- and magnetic-field-induced reversal characteristics of thin-film nanomagnets. Nat. Mater. 7, 567–573 (2008).
Brown, W. F. Thermal Fluctuations of a Single-Domain Particle. Phys. Rev. 130, 1677 (1963).
Song, H.-S. et al. Intrinsic and extrinsic Gilbert damping in exchange-biased IrMn/Cu/CoFe trilayer films. Appl. Phys. Express 8, 053002 (2015).
Sohn, J.-W. et al. Gilbert damping in asymmetric MgO(Ta)/CoFeB/Ta(MgO) structures with perpendicular magnetic anisotropy. Curr. Appl. Phys. 16, 481–485 (2016).
Beaujour, J.-M. et al. Ferromagnetic resonance linewidth in ultrathin films with perpendicular magnetic anisotropy. Phy. Rev. B 80, 180415(R) (2009).
Cho, J. et al. Study of spin dynamics and damping on the magnetic nanowire arrays with various nanowire widths. J. Magn. Magn. Mater. 409, 99–103 (2016).
Acknowledgements
This research was supported by NRF-2016R1A6A3A11935187, NRF-2017R1A2B3002621, and NRF-2015M3D1A1070465 through the National Research Foundation of Korea, funded by the Ministry of Education, and by the DGIST R&D Program of the Ministry of Science and ICT(18-BT-02).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moon, JH., Lee, T.Y. & You, CY. Relation between switching time distribution and damping constant in magnetic nanostructure. Sci Rep 8, 13288 (2018). https://doi.org/10.1038/s41598-018-31299-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-31299-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.