Abstract
Rho GTPases play crucial roles in cell polarity and pattern formation. ROPs, Rho of plant GTPases, are widely involved in cell wall patterning in plants, yet the molecular mechanism underlying their action remains unknown. Arabidopsis ROP11 is locally activated to form plasma membrane domains, which direct formation of cell wall pits in metaxylem vessel cells through interaction with cortical microtubules. Here, we show that the pattern formation of cell wall pits is governed by ROP activation via a reaction-diffusion mechanism. Genetic analysis and reconstructive assays revealed that ROPGEF4/7 and ROPGAP3/4, which encode ROP activators and inactivators, respectively, regulated the formation of ROP-activated domains; these in turn determined the pattern of cell wall pits. Mathematical modelling showed that ROP-activation cycle generated ROP domains by reaction-diffusion mechanism. The model predicted that a positive feedback and slow diffusion of ROP11-ROPGEF4 complex were required to generate ROP-activated domains. ROPGEF4 formed a dimer that interacted with activated ROP11 in vivo, which could provide positive feedback for ROP activation. ROPGEF4 was highly stable on the plasma membrane and inhibited ROP11 diffusion. Our study indicated that ROP-based reaction-diffusion system self-organizes ROP-activated domains, thereby determines the pit pattern of metaxylem vessels.
Similar content being viewed by others
Introduction
Pattern formation during plant and animal development is a fundamental issue in biology. The mathematical principle underlying self-organizing pattern formation was first proposed and studied by Turing1. This theoretical work showed clearly that the dynamics of simple reactions including at least two chemical species and their diffusion could spontaneously generate periodic spatial distributions. The conditions for pattern formation in this system was initially given as “diffusion-induced instability” (or Turing instability). Later, this mechanism was re-formulated with more intuitive expression “activator-inhibitor system”, which highlighted the importance of local activation by lower diffusion of the activator and long-range inhibition by higher diffusion of the inhibitor2. There is increasing evidence that the reaction-diffusion system is involved in various tissue and organ development3,4,5,6,7. Several studies combining molecular biology and theoretical modelling have partially revealed the molecular background of reaction-diffusion systems in tissues and organ patterning8.
Spatial patterns are also formed in the subcellular space. Rho/Rac GTPases are conserved signalling enzymes that play central roles in directing subcellular patterns9,10,11,12,13. They are present in two states: a GTP-bound active form and a GDP-bound inactive form. GTP-bound GTPases interact with their effector proteins to induce downstream signalling, whereas GDP-bound GTPases do not interact with effectors. The switch between GTP/GDP-bound states is controlled by guanine nucleotide exchanging factors (GEFs) and GTP-activating proteins (GAPs). GEFs activate GTPases by exchanging GDP with GTP. Conversely, GAPs promote GTP hydrolysis of the GTPase to produce an inactive GDP-bound form14.
An example in which spatial pattern of Rho GTPase directs formation of subcellular patterns is cell wall patterning in plants. We previously demonstrated that pit pattern of secondary cell walls is prefigured by local activation of a Rho/Rac GTPase, ROP11, in differentiating tracheary elements of Arabidopsis metaxylem vessels (hereafter, metaxylem vessel cells). The locally activated ROP11 recruits MIDD1-Kinesin-13A complex, which in turn induces cortical microtubule disassembly, resulting in formation of pits in secondary cell walls15,16. Local activation of ROP11 is mediated by a GEF, ROPGEF4, and a GAP, ROPGAP3. Ectopic expression of ROP11, together with ROPGEF4 and ROPGAP3, is sufficient for localized activation of ROP11 and formation of plasma membrane domains17. Furthermore, we recently reported that cortical microtubules regulate the shape of ROP-activated plasma membrane domains through IQD13 and CORD1, which confines and releases ROP-activated domains, respectively18,19.
As it is still unclear how ROP-activated domains are generated and what determines the pattern of ROP-activated domains, we investigated the mechanism underlying secondary cell wall pit patterning using genetics, reconstructive techniques, and mathematical modelling. ROPGEF4/7 and ROPGAP3/4 dose-dependently determined the density of ROP-activated domains, which in turn determined the pattern of the pits formed in the secondary cell walls. Mathematical modelling demonstrated that ROP-activation/inactivation cycle generated ROP domains by reaction-diffusion mechanism. The model predicted that a positive feedback and slow diffusion of ROP-ROPGEF complex were required to generate ROP domains. We found that ROPGEF4 formed a dimer that interacted in vivo with activated ROP11, which could provide positive feedback for ROP activation. ROPGEF4 was highly stable on the plasma membrane and inhibited ROP11 diffusion. Our study indicated that ROP-activation/inactivation cycle self-organizes ROP-activated domains via a reaction-diffusion mechanism, thereby determines the pit pattern in secondary cell walls.
Results
ROPGEFs positively regulate the density and size of secondary cell wall pits
In Arabidopsis metaxylem vessels, ROPGEF4, which encodes a plant-specific GEF family protein, is partially required for secondary cell wall pit formation17, suggesting that other ROPGEF genes also function in metaxylem vessels. We focused on ROPGEF7, which is preferentially expressed in xylem vessels20. Although there are no T-DNA insertion lines for ROPGEF7, we identified an EMS mutant harbouring an AT-insertion between 260 T and 261 G in the second exon of ROPGEF7. This mutation caused a frame-shift of the coding sequence, resulting in a premature stop codon in the catalytic domain of ROPGEF7 (Figure S1A). We designated this mutant ropgef7-1.
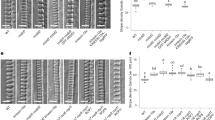
The secondary cell wall pits of ropgef4-1, ropgef7-1, and ropgef4-1 ropgef7-1 mutants were sparser and smaller than those of wild-type plants (Fig. 1A). The density and area of secondary cell wall pits in ropgef4-1 were about 70% (Fig. 1B) and 80% (Fig. 1C) of those of wild-type plants, respectively. The ropgef7-1 phenotype resembled ropgef4-1 but showed a greater reduction in both density and area of secondary cell wall pits (Fig. 1A–C). We also examined the effect of ROPGEF7 knock-down by introducing pLexA:ROPGEF7-RNAi to wild-type plants. The pits in the secondary cell walls of pLexA:ROPGEF7-RNAi plants were sparsely distributed and small, indistinguishable from the ropgef7-1 phenotype (Figures S1E–S1G). We concluded that ropgef7-1 was a loss-of-function mutant and ROPGEF7 was required for normal secondary cell wall pit formation. The ropgef4-1 ropgef7-1 double mutants displayed similar reductions in density and area of secondary cell wall pits to ropgef7-1 (Fig. 1A–C). The reduced pit phenotypes of ropgef4-1 and ropgef7-1 could be rescued by introducing pROPGEF4:GFP-ROPGEF4 and pROPGEF7:YFP-ROPGEF7, respectively. These results demonstrate that both ROPGEF4 and ROPGEF7 positively regulated the formation of secondary cell wall pits.
ROPGEFs and ROPGAPs regulate the secondary cell wall pit patterns. (A–C) Phenotype of metaxylem vessels in roots of wild-type (WT), ropgef4-1 (gef4-1), ropgef7-1 (gef7-1), and ropgef4-1 ropgef7-1 plants (C), of ropgef4-1 plants expressing GFP-ROPGEF4, and of ropgef7-1 plants expressing YFP-ROPGEF7 (A and B). (D–F) Phenotype of metaxylem vessels of WT, ropgap3-1, ropgap4-2, and ropgap3-1 ropgap4-2 plants (F), and ropgap3-1 ropgap4-2 plants harbouring pROPGAP4:GFP-ROPGAP4 (D and E). (G–I) Phenotype of metaxylem vessels of WT and ROPGAP3ox plants. (A,D and G) Differential interference contrast microscopy (DIC) of xylem vessels. Arrowheads indicate secondary cell wall pits. Scale bars = 10 (A and G) and 5 (D) µm. (B,E and H) Density of secondary cell wall pits in roots. Data are means ± SD (n = 10 (B) and 12 (E and H) plants). **P < 0.01; ***P < 0.001; ANOVA with Scheffe’s test (B and E) and Wilcoxon rank sum test (H). (C,F and I) Area of secondary cell wall pits in roots. Data are means ± SD (n = 10 (F) and 12 (C and I) plants). **P < 0.01; ***P < 0.001; ANOVA with Scheffe’s test (C and F) and student’s t test (I).
In addition to reductions in density and size, pits were distributed less evenly across the secondary cell walls of ropgef4-1 ropgef7-1 plants than of wild-type plants (Fig. 2A–C). This phenotype was more obvious in the omni-directional image showing 360° of the cell wall area (Fig. 2D). The distance between pits in wild-type plants was less than 10 µm, and usually between 2.5 and 7.5 µm (Fig. 2A); by contrast, there was a broad distribution of distances between the pits in ropgef4-1 ropgef7-1 mutants that ranged up to 42.5 µm (Fig. 2B), indicating that the pits were less evenly spaced. The distribution of distances between pits in ropgef4-1 ropgef7-1 double mutants was more highly skewed than in wild-type plants (Fig. 2C). These data suggested that ROPGEF4 and ROPGEF7 were required for periodic formation of secondary cell wall pits.
Distributions of secondary cell wall pits in ropgef and ropgap mutants. Distribution of secondary cell wall pits in WT and ropgef4-1 ropgef7-1 plants (A–D), ropgap3-1 ropgap4-2 plants (E–H), or GAP3ox plants (I–M). (A,B,E,F,I and J) Histograms showing distances between secondary cell wall pits in WT (A,E and I) and mutant plants (B,F and J). n = 108 (A), 64 (B), 69 (E), 63 (F), 90 (I), and 110 (J) pits. (C,G and K) Degree of skewness of distributions of distances between secondary cell wall pits. White rectangles represent means; black bars represent medians; black dots represent outliers; n = 12 (C and K) and 10 (G) plants; ***P < 0.001, **P < 0.01, *P < 0.05; student’s t test (C and K); Wilcoxon rank sum test (G). (D,H and M) Omni-directional images of metaxylem vessel cells. Scale bars = 5 µm. (L) Distances between secondary cell wall pits in wild type and GAP3ox plants. Data are the mean ± SD (n = 12 plants). ***P < 0.001; student’s t test.
ROPGAPs positively regulate the pit density, but negatively regulate pit size
ROPGAP3 is localized in the plasma membrane of the secondary cell wall pits, and is required for local activation of ROP1117. To investigate the roles of ROPGAP3 in pitted cell wall patterning, we studied the metaxylem vessels of ropgap3-1 plants, which have a T-DNA insertion in the first exon of ROPGAP3 (Figure S1A). ROPGAP3 mRNA levels in ropgap3-1 were about 10% of those in wild-type plants (Figure S1B); however, we could not find any differences between wild-type and ropgap3-1 plants in the density (Fig. 1E) or area (Fig. 1F) of secondary cell wall pits (Fig. 1D), probably due to redundancy between ROPGAP genes. We therefore focused on ROPGAP4, which is preferentially expressed in xylem vessels20, and studied rogap4-2 plants harbouring a T-DNA insertion at the exon of ROPGAP4 (Figure S1A). Expression of ROPGAP4 mRNA in ropgap4-2 mutants was about 15% that in wild-type plants (Figure S1C), and ropgap4-2 displayed a reduced density (Fig. 1E) and larger size (Fig. 1F) of pits than wild-type plants. The large pit phenotype of ropgap4-2 was enhanced in ropgap3-1 ropgap4-2 double mutants, while the sparse pit phenotype of ropgap4-2 was not affected in ropgap3-1 ropgap4-2 double mutants (Fig. 1F). Introduction of pROPGAP4:GFP-ROPGAP4 rescued the pit density phenotype of ropgap3-1 ropgap4-2 (Fig. 1E). These data indicated that ROPGAP3 and ROPGAP4 negatively regulated pit size and that ROPGAP4 positively regulated pit formation. ROPGAP3 may also regulated pit formation positively, but the contribution of ROPGAP3 was likely minor, thereby masked by the action of ROPGAP4.
To clarify the role of ROPGAP3, we next investigated the effect on secondary cell wall pit formation of ROPGAP3 over-expression. We fused the ROPGAP3 coding sequence with the promoter sequence of IRX3, which is strongly expressed in xylem vessels21, and introduced this construct (pIRX3:ROPGAP3) to wild-type plants (GAP3ox). Expression of ROPGAP3 mRNA was 14-fold higher in GAP3ox plants than in wild-type plants (Figure S1D). The secondary cell wall pits were denser and smaller in GAP3ox plants than in wild-type plants (Fig. 1G–I). These results suggested that, as with ROPGAP4, ROPGAP3 positively regulated pit formation, but negatively regulated pit size
As in the ropgef4-1 ropgef7-1 double mutant, pits were less evenly distributed in the secondary cell walls of ropgap3-1 ropgap4-2 than in wild-type plants (Fig. 2H). There was a wider range of distances between pits in ropgap3-1 ropgap4-2 double mutants than in wild-type plants (Fig. 2E–G). By contrast, the distances between pits in GAP3ox plants were smaller and more evenly distributed than in wild-type plants (Fig. 2I–M). These data imply that ROPGAP3 and ROPGAP4 were also required for periodic formation of secondary cell wall pits
ROPGEF and ROPGAP dose-dependently regulate the density of ROP domains
Our genetic analysis indicated that ROPGEFs and ROPGAPs regulated formation of the pits in secondary cell walls. Given that ROP-activated domains direct formation of secondary cell wall pits17, levels of ROPGEF and ROPGAP expression may determine the pit pattern through regulating the formation of ROP-activated domains. In the ropgef and ropgap mutants, ROP-activated domains were specifically associated with the altered pit patterns (Figure S2A), implicating that ROPGEF and ROPGAP expression levels affected the pattern of ROP-activated domains. To determine whether ROPGEFs and ROPGAPs regulated the pattern of ROP-activated domains, we examined the relationship between ROPGEF and ROPGAP expression and ROP domain patterns by using an ectopic reconstruction of ROP-activated domains; pLexA:ROP11, pLexA:ROPGEF4PRONE (the catalytic domain of ROPGEF4), and pLexA:ROPGAP3, were co-introduced into tobacco (Nicotiana benthamiana) leaves by the syringe-infiltration with R. radiobacter. Two days after infiltration, the leaf samples were harvested and inoculated with 2 µM estradiol to simultaneously express the introduced genes. This enables the formation of numerous plasma membrane domains marked with ROPGEF4PRONE and activated ROP11 in the tobacco leaf epidermal cells17. As full length ROPGEFs auto-inhibit their GEF activity22, ROPGEF4PRONE was used instead of full length ROPGEF4. ROPGEF4PRONE rescued the pit pattern phenotype of ropgef4-1 to the same extent as full length ROPGEF4 did (Figs 1B, S2B and S2C) and localized to secondary cell wall pits in roots (Figure S2D). ROPGEF4PRONE was therefore fully functional in pit patterning. ROP11 was locally activated just around ROPGEF4PRONE domains (Figure S2E)17, thus patterns of ROPGEF4 PRONE domains indicated those of ROP-activated domains.
Following induction of ROP11, tagRFP-ROPGEF4PRONE, and GFP-ROPGAP3, numerous ROPGEF4 domains formed on the plasma membrane (Fig. 3A). We recorded images from over 100 cells expressing various levels of tagRFP-ROPGEF4PRONE and GFP-ROPGAP3, and quantified the mean intensity of GFP-ROPGAP3 and tagRFP-ROPGEF4PRONE, as well as the density of ROPGEF4PRONE domains in each cell. There was a positive correlation between domain density and mean intensity of GFP-ROPGAP3 (Fig. 3B) and tagRFP-ROPGEF4PRONE (Fig. 3C). These correlations suggested that the density of ROPGEF4PRONE domains was coupled with the expression levels of ROPGEF4PRONE and ROPGAP3. This result was consistent with the pit pattern phenotypes of the ropgef4 and ropgef7 mutants, ropgap3 ropgap4 double mutants, and ROPGAP3-over-expressing plants. These data suggested that ROPGAP3 and ROPGEF4 determined the pit pattern of secondary cell walls by regulating the pattern of ROP-activated domains.
Effects of ROPGAP3 and ROPGEF4 levels on ROP domain patterning. (A) Formation of sparse (left) and dense (right) ROP domains (yellow arrowheads) in N. benthamiana leaf epidermal cells. pLexA:tagRFP-ROPGEF4PRONE and pLexA:GFP-ROPGAP3 were introduced together with pLexA:ROP11. Scale bars = 10 µm. (B and C) Plots of (B) GFP-ROPGAP3 intensity and ROP domain density; (C) tagRFP-ROPGEF4PRONE intensity and ROP domain density. n = 165 cells. rs: Spearman’s rank correlation coefficient.
We next tested whether ROPGEF7PRONE mediates formation of ROP-activated domains. Previously we reported that ectopic expression of ROPGEF7PRONE together with ROP11 and ROPGAP3 did not generate domains in leaf epidermal cells17. As ROPGEFs have different affinity to different ROPs, we assumed that ROPGEF7 activates ROPs other than ROP11. We therefore re-examined the ability of ROPGEF7PRONE to form domains by using ROP2, which is another ROP expressed in xylem vessels20. ROPGEF7PRONE formed domains on the plasma membrane when expressed with ROPGAP3 and ROP2 (Figure S2F). This suggested that ROPGEF7 also regulate patterns of ROP-activated domains to direct formation of secondary cell wall pits.
Mathematical Model and Analysis
Although our genetic analysis suggested that ROPGEF and ROPGAP determine the pit pattern through regulating the pattern of ROP domains, it is unclear how the ROP domains are formed. Considering that the density of ROP domains varied with the levels of ROPGEF and ROPGAP expression, it is plausible that ROP domains were self-organized through the action of ROPGEFs and ROPGAPs.
Reaction-diffusion system1 is a potential mechanism capable of self-organization of the ROP domains. To examine this hypothesis, we developed a mathematical model of pattern formation of ROP activities on the plasma membrane. In this model, we considered all the reactions involving ROP, binding of GAP or GEF molecules with ROPs, GDP/GTP exchange (GEF activity), and GTP hydrolysis (GAP activity), which constituted a circular state-transition network, illustrated in Fig. 3A (black arrows). The mobility of ROP molecules on the plasma membrane was modelled as diffusion in a two-dimensional space, and we have the following reaction-diffusion (RD) model for the dynamics of ROP (See also Fig. 4A):
Mathematical analysis of pattern formation of ROP activity. (A) Schematic representation of reaction network for dynamics of concentration of ROP states. ui(x, t)s are u1: GDP-ROP; u2: GDP-ROP ROPGEF complex; u3: GTP-ROP ROPGEF complex; u4: GTP-ROP; u5: GTP-ROP ROPGAP complex; and u6: GDP-ROP ROPGAP complex. ki are parameters associated to reaction rates, \({k}_{i}=\partial {r}_{i}/\partial {u}_{i} > 0\) (i = 1, …, 6). Parameters of regulation are given as k7 = ∂r1/∂u2, k8 = ∂r1/∂u3, \({p}_{1}=\partial {r}_{1}/\partial {F}_{G}\cdot \partial {F}_{G}/\partial {u}_{i}\) (i = 2, 3), and \({p}_{2}=\partial {r}_{4}/\partial {F}_{P}\cdot \partial {F}_{P}/\partial {u}_{i}\) (i = 5, 6). (B and C) Distribution of successful parameter sets: (B) Distribution of \({k}_{1} \sim {k}_{8}\); and (C) \({D}_{1} \sim {D}_{6}\). (D) Pearson’s product-moment correlation among parameter values in successful sets. (E) Numerical simulations of dynamics of pattern formation of ROP activities represented by u1, u2, u3, and u4.
In the RD equations, ui(x, t)s are time-variable spatial distribution of concentrations of u1: GDP-ROP; u2: GDP-ROP ROPGEF complex; u3: GTP-ROP ROPGEF complex; u4: GTP-ROP; u5: GTP-ROP ROPGAP complex; and u6: GDP-ROP ROPGAP complex. ri is reaction rate with Ki = ∂ri/∂ui > 0 (i = 1, …, 6); FG and FP are concentrations of free cytoplasmic GEF and GAP molecules, respectively. At a glance, the network structure of the RD model differs from that of typical system showing Turing instability, like activator-inhibitor system. In the following we examined the condition of the network structure for generating periodic spatial patterns.
As feedback regulation is considered to be important for pattern formation in RD systems23, we examined the effects of two mechanisms that may act as feedback in the ROP-activation/inactivation cycle. Firstly, due to conservation of the total amount of GEF, an increase in GEF-bound states in a cell will reduce the number of free GEF molecules in the cytoplasm, which will in turn reduce the GEF-binding reaction. This negative regulation of GEF-binding reaction by free GEF was incorporated into the model by setting \({p}_{1}\equiv \partial {r}_{1}/\partial {F}_{G}\cdot \partial {F}_{G}/\partial {u}_{i}\le 0\) (i = 2, 3). Similarly, negative regulation of the GAP-binding reaction by free GAP was modelled as \({p}_{2}\equiv \partial {r}_{4}/\partial {F}_{P}\cdot \partial {F}_{P}/\partial {u}_{i}\le 0\) (i = 5, 6) (blue curves in Fig. 4A). Secondly, we considered GEF dimerization. ROPGEFs form homo-dimer in vitro, in which each subunits interact and catalyse ROP molecules24. Once a subunit of ROPGEF dimer interacts with ROP, the other subunit of the dimer will activate another ROP nearby. This will enhance the reaction rate of ROP-GEF binding by producing a locally higher concentration of ROP-GEF complexes. This positive feedback from GEF-bound states to GEF-binding reaction was modelled by setting \({K}_{7}\equiv \partial {r}_{1}/\partial {u}_{2}\ge 0\), \({K}_{8}\equiv \partial {r}_{1}/\partial {u}_{3}\ge 0\) (red curves in Fig. 4A). Based on these arguments we developed three models: (A) Closed-circuit model without regulations (p1 = 0, p2 = 0; K7 = K8 = 0); (B) Inhibition from conserved quantities (\({p}_{1} < 0\), \({p}_{2} < 0\); K7 = K8 = 0); and (C) Positive feedback from dimerization (p1 = 0, p2 = 0; \({K}_{7} > 0\), \({K}_{8} > 0\)). We compared dynamical properties originated from difference in network structures.
We analysed the models using three methods: (i) mathematical analysis; (ii) numerical analysis; and (iii) numerical simulation. In the mathematical analysis, we adopt “structural analysis” where the structural conditions of the reaction network for pattern formation was determined based on Turing instability (see Methods). We obtained the following strong result: the closed-circuit model (A) and the inhibition model (B) never show Turing instability from their structures, while the positive feedback model (C) can represent the Turing instability. This result implies that the negative regulation by the conserved quantities, GEF and GAP, did not contribute to pattern formation. The presence (\({p}_{1} < 0\) or \({p}_{2} < 0\)) or absence (p1 = 0 or p2 = 0) of this regulation did not influence Turing instability. On the other hand, positive feedback from GEF-bound states (u2 and u3) on the GEF-binding reaction (r1) was necessary for pattern formation (Table S1). If we removed the positive feedback regulation (K7 = K8 = 0) from the model, the system never satisfied the condition of Turing instability, although the condition could be met in the original model with such regulation (\({K}_{7},{K}_{8} > 0\)).
Using the network including positive feedback, we performed exhaustive searches to examine the quantitative conditions of the parameter values for pattern formation. Parameter values were changed randomly, and the condition of Turing instability was examined numerically for each parameter set. By examining the statistical properties of successful parameter sets, we identified a quantitative condition of parameters. Figure 4B shows that the coefficient of reaction 1 was high, that of reaction 2 was low in the successful parameter sets, indicating the importance of the rates of ROP-GEF binding and GEF reaction. Figure 4C shows that the diffusion coefficient of u2 (and u3) were small, indicating that the diffusion rate of ROP-GEF complex must be slow to form ROP-activated domains.
This tendency can be understood by analogy with the activator-inhibitor system. The Turing instability condition requires a smaller diffusion of activator than other factors; thus u2 (or u3) with positive feedback (\({K}_{7},{K}_{8} > 0\)) plays the role of an activator in the reaction network while u4 − u6 are inhibitors. The correlations between parameters (Fig. 4D) enabled additional interpretations of the properties of the system. The negative correlation between K2 and D3 suggested that increasing K2 resulted in a lower total amount of u2, and required u3, rather than u2, to take the role of activator with smaller D3; the negative correlation between K3 and D2 could be interpreted inversely. These correlations implied that either u2 or u3 had to be the activator in this system.
Finally, we calculated the dynamical change in spatial patterns of active ROP using numerical simulation of the model including all feedback regulations (\({p}_{1} < 0\), \({p}_{2} < 0\); \({K}_{7} > 0\), \({K}_{8} > 0\)). Figure 4E and Movie S1 show an example of the periodic domains of activated ROPs obtained using one of the successful parameter sets. The obtained patterns resembled the observed distributions of active ROP in experiments (Figure S2E)17.
In vivo interaction between ROP11 and ROPGEFs/ROPGAPs
Our mathematical analysis demonstrated that the ROP-activation/inactivation cycle could generate ROP-activated domains by the reaction-diffusion mechanism. The model predicted positive feedback from GEFs and slower diffusion of GEF-ROP complex. To determine whether ROPGEF4 was involved in the feedback reaction, we tested the in vivo interactions of ROPGEF4PRONE with ROP11, ROP11G17V (a constitutive GTP-bound active form), ROP11T22N (a constitutive GDP-bound inactive form of ROP11), and ROPGEF4PRONE using a bimolecular fluorescence complementation (BiFC) assay and fluorescent resonance energy transfer (FRET) in tobacco leaf epidermal cells.
We first performed the BiFC assay. YFP signals were detected when nYFP (N-terminal half of YFP)-ROPGEF4PRONE was expressed together with cYFP (C-terminal half of YFP)-ROP11, cYFP-ROP11G17V, or cYFP-ROPGEF4PRONE, but YFP signals were not detected when nYFP-ROPGEF4PRONE was co-expressed with cYFP-ROP11T22N (Fig. 5A), suggesting that ROPGEF4 PRONE preferentially interacted with GTP-ROP11 and with ROPGEF4PRONE itself.
ROPGEF4PRONE interacts with GTP-ROP11 and inhibits the diffusion of ROP11 in tobacco leaf epidermal cells. (A) BiFC assay between nYFP-ROPGEF4PRONE and cYFP-ROP11, cYFP-ROP11G17V, cYFP-ROP11T22N, or cYFP-ROPGEF4PRONE. Scale bars = 20 µm. (B) FRET efficiency between CFP-ROPGEF4PRONE and YFP-ROP11 derivatives or YFP-ROPGEF4PRONE. Data are means ± SD (n = 12). *P < 0.05; ***P < 0.001; ANOVA with Scheffe’s test. (C and D) FRAP analysis of GFP-ROP11 and tagRFP-ROPGEF4PRONE. GFP-ROP11 was expressed alone (NONE) or together with tagRFP-ROPGEF4PRONE, tagRFP-ROPGEF4, or tagRFP-ROPGAP3 in tobacco leaf epidermal cells. Kymograph of photo-bleached area at the mid plane of leaf epidermal cells (C; top); intensity plots of photo-bleached area (C; bottom); and fluorescence recovery percentage 60 s after photo-bleaching (D) are shown. In (C), t indicates time after the onset of scan. x indicates position along the plasma membrane. Photo-bleach was executed at 6 s. Data are means ± SD (n = 12). Bar = 5 µm. ***P < 0.001; **P < 0.01; ANOVA with Scheffe’s test. Note that the recovery of GFP signals at the edges of photo-breached area is faster than that at the centre of the area in C (None and +tagRFP-GAP3). (E) FRAP analysis of tagRFP-ROPGEF4PRONE and GFP-ROPGAP3 in ROP11-activated domains. ROP11 was co-expressed with tagRFP-ROPGEF4PRONE and GFP-ROPGAP3. Kymograph of photo-bleached area (left top) and intensity of photo-bleached area (left bottom), and recovery of fluorescence at 60 s after photo-bleaching (right). Data are means ± SD (n = 15). Scale bar = 1 µm. ***P < 0.001; Welch’s t test. (F to I) Schematic model of secondary cell wall pit patterning. (F) The ROP-activation cycle generates periodic ROP-activated domains by reaction-diffusion mechanism. Positive feedback is provided by ROPGEF4 dimers interacting with GTP-ROP11. (G) ROPGEFs and ROPGAPs determine the density of ROP-activated domains. (H) The size and shape of ROP-activated domains are determined through the action of microtubule-associated proteins (MAPs). ROP-activated domains promote depletion of cortical microtubules. (I) Secondary cell walls are deposited on the area outside of the ROP11-activated domains, resulting in the formation of secondary cell wall pits.
We next carried out FRET analysis that could detect direct interaction between proteins in vivo. The mean FRET efficiency between CFP-ROPGEF4PRONE and YFP-ROP11 (15%), YFP-ROP11G17V (9%), or YFP-ROPGEF4PRONE (55%) was significantly higher than that between CFP-ROPGEF4PRONE and YFP-ROP11T22N (−2%) (Fig. 5B). Our data suggested that ROPGEF4PRONE forms dimer and directly bind to GTP-ROP11, besides the regular binding for GDP-GTP exchange. In this context, activated GTP-ROP11 could recruit a ROPGEF4PRONE dimer, which in turn activates another, nearby ROP11. This could result in a positive feedback of ROP activation.
ROPGEF4PRONE is highly stable on the plasma membrane
To investigate diffusion of ROP11 and ROPGEF4PRONE at the plasma membrane, we analysed fluorescence recovery after photo-bleaching (FRAP) of ROP11 and ROPGEF4PRONE. We introduced pLexA:GFP-ROP11 or pLexA:tagRFP-ROPGEF4PRONE into tobacco leaf epidermal cells, photo-bleached regions of the plasma membrane at the mid plane of the cells, and recorded the recovery of the fluorescence for 60 s (Fig. 5C). GFP-ROP11 fluorescence recovered to 40% of pre-bleaching intensity by 60 s after bleach (Fig. 5D). The dynamic recovery or GFP-ROP11 fluorescence could be due to lateral diffusion and/or cytoplasmic shuttling of ROP11. The faster recovery at the edges of photo-bleached region than at the central region (Fig. 5C) suggested that a significant amount of ROP11 molecules diffused laterally on the plasma membrane. By contrast, there was little recovery of tagRFP-ROPGEE4PRONE fluorescence, suggesting that ROPGEF4PRONE was stable on the plasma membrane.
As ROPGEF4PRONE interacted with ROP11 in vivo, we hypothesized that ROPGEF4PRONE influenced the dynamics of ROP11. We co-introduced GFP-ROP11 and tagRFP-ROPGEF4PRONE into tobacco leaf epidermal cells and analysed the recovery of GFP-ROP11 signals after photo-bleaching. Recovery of GFP-ROP11 was dramatically inhibited in the presence of ROPGEF4PRONE (Fig. 5C and D). As with ROPGEF4PRONE, tagRFP-ROPGEF4 (the full length version of ROPGEF4) also inhibited recovery of GFP-ROP11 fluorescence (Fig. 5C and D), suggesting that ROPGEF4 inhibited diffusion of ROP11. In contrast to ROPGEF4, tagRFP-ROPGAP3 slightly inhibited the recovery of GFP-ROP11, suggesting that ROPGAP3 also affected the diffusion of ROP11 but much more weakly than ROPGEF4. Consistent with this, ROPGAP3 was entirely cytoplasmic, thus the diffusion of ROPGAP3 could not be studied using FRAP analysis.
We next quantified the recovery of tagRFP-ROPGEF4PRONE in the ROP-activated domains. TagRFP-ROPGEF4PRONE was introduced, together with ROP11 and GFP-ROPGAP3, into tobacco leaf epidermal cells. GFP-ROPGAP3 was faintly localized to the plasma membrane; thus both tagRFP-ROPGEF4PRONE and GFP-ROPGAP3 were subjected to FRAP analysis. TagRFP-ROPGEF4PRONE did not recover but GFP-ROPGAP3 recovered to 30% of pre-bleaching intensity (Fig. 5E). These data suggested that ROPGEF4PRONE formed a stable domain in the plasma membrane, while ROPGAP3 was dynamic.
ROPGAP3 interacts with the active form of ROP11
Our model predicted feedback from ROPGEF4PRONE, and we subsequently showed that ROPGEF4PRONE could produce feedback for ROP activation. We next determined whether ROPGAPs were also involved in a feedback reaction. As ROPGAP promotes production of GDP-ROP, ROPGAP had to interact with GDP-ROP to provide positive feedback. We conducted a BiFC assay to test interactions between ROPGAP3 and ROP11 in tobacco leaf epidermis. YFP signals were detected when cYFP-ROPGAP3 was expressed with nYFP-ROP11G17V, but not when cYFP-ROPGAP3 was expressed with nYFP-ROP11 or nYFP-ROP11T22N (Figure S3A). The mean FRET efficiency between CFP-ROPGAP3 and YFP-ROP11 (18%) or YFP-ROP11G17V (39%) was significantly higher than that between CFP-ROPGAP3 and YFP-ROP11T22N (−0.2%) (Figure S3B). These data suggested that ROPGAP3 specifically interacted with GTP-ROP11 in vivo, a result consistent with previous reports that ROPGAPs interact through their Cdc42/Rac interactive binding motif (CRIB, an effector-binding domain) and GAP domain with the active form of ROPs to inactivate them25,26. We therefore concluded that ROPGAP3 was not part of the feedback reaction and acted simply as a GAP in vivo.
Discussion
In metaxylem vessel cells, domains of activated ROPs direct secondary cell wall pit formation17. Ectopic expression of ROP11 together with ROPGEF4 and ROPGAP3 induced formation of ROP-activated domains; this suggested that ROP11-activation/inactivation cycle could spontaneously generate ROP-activated domains17. Our mathematical model using reaction-diffusion equations showed that the ROP-activation/inactivation cycle can generate the ROP11-activated domains. Domain generation required feedback from GEF and slow diffusion of the GEF-ROP complex. We showed that ROP11 form a dimer and interacts directly with GTP-ROP11 in vivo. This could provide positive feedback to ROP activation, as the dimer would be recruited to GTP-ROP11 and subsequently activate another ROP11 nearby. We also showed that ROPGEF4PRONE was stable on the plasma membrane and inhibited diffusion of ROP11. Thus our results supported a model in which the ROP-activation/inactivation cycle generated ROP domains by the reaction-diffusion mechanism (Fig. 5F).
Although our observation indicated that ROPGEF4 provides positive feedback by direct binding of ROPGEF4 dimer to GTP-ROP11, it would be also possible that scaffold proteins mediate positive feedback of ROPGEF4. Several receptor-like kinases (RLKs) interact with ROPGEFs, including ROPGEF427,28,29,30. Cell walls affect the diffusion rate of membrane proteins, including RLKs31. ROPGEF4PRONE was stable at the plasma membrane. ROPGEF4 may interact with RLKs to form the slow-diffusive complex. In pollen tubes, a RLK, PRK2, phosphorylates ROPGEF1, which in turn activates ROP132. The activated GTP-ROP1 interacts with both ROPGEF1 and PRK2, which promotes ROPGEF-PRK2 interaction, resulting in a positive feedback for ROP activation32,33. Similarly, RLKs may also act as scaffolds to provide positive feedback from ROPGEF4 to ROP11 activation.
In contrast to ROPGEF4, ROPGAPs are not likely to provide positive feedback to ROP inactivation. Our mathematical model generated ROP-activated domains without setting positive feedback to ROP inactivation. In the model, ROPGAPs globally inactivated the diffusive ROP at the plasma membrane. In pollen tubes, ROPGAPs maintain the ROP-activated domain through global inactivation of diffusive ROP propagating from the apex to lateral region34. Similarly, in metaxylem vessel cells, ROPGAPs may maintain the ROP-activated domains through global inactivation of diffusive ROP propagating outward from the ROPGEF domains.
ROP-based reaction-diffusion system can explain not only formation of ROP11 domains but also pattern formation of the domains. We showed that secondary cell wall pits were formed in periodic patterns and that loss of ROPGEFs or ROPGAPs impaired the periodic pattern of the pits. Our mathematical model showed that ROP-reaction generated ROP-activated domains in a periodic pattern in the absence of prepattern, consistent with the nature of reaction-diffusion system. Thus, it is plausible that, in differentiating metaxylem vessel cells, ROP-activation/inactivation cycle self-organizes ROP-activated domains in a periodic pattern, then the domains function as the first positional cue to direct formation of periodic pits in secondary cell walls (Fig. 5F).
Our genetic analysis showed that ROPGEFs and ROPGAPs positively regulate the density of secondary cell wall pits. We also showed that the density of ROP-activated domains is determined by levels of ROPGEFs and ROPGAPs, suggesting that ROPGEFs and ROPGAPs determines the pattern of pits by regulating the pattern of ROP-activated domains (Fig. 5G). Given that ROP-activation/inactivation cycle self-organizes ROP domains by reaction-diffusion mechanism, it is plausible that the density of the domain is also determined through reaction-diffusion mechanism. In reaction-diffusion system, domain patterns of different density can be formed by varying the diffusion rate of the components35. The inhibitory effects on ROP diffusion rate of ROPGEFs and ROPGAPs may contribute to the density of ROP domains. Precise modelling of the behaviour of ROPGEFs and ROPGAPs should reveal the mechanism by which ROPGEF and ROPGAP levels determine the density of pits.
Our observation suggested that ROPGEFs and ROPGAPs positively and negatively regulate the pit size, respectively. We previously showed that the pit size is positively regulated by the microtubule-depolymerizer, Kinesin-13A. Kinesin-13A is recruited to the ROP-activated domains via MIDD115. Thus it is plausible that ROPGEFs and ROPGAPs indirectly determine the pit size by regulating the amount of active ROP11 to recruit Kinesin-13A. This notion is consistent with the pit size phenotype of ropgef and ropgap mutants, which could decrease and increase the amount of active ROP11, respectively. In addition to Kinesin-13A, IQD13 and CORD1 regulate the size and shape of ROP domains through cortical microtubules surrounding the ROP domains, which in turn determine the size and shape of secondary cell wall pits18,19 (Fig. 5H). Once the pattern and shape of ROP domains are determined, secondary cell walls would be deposited along the cortical microtubules lying at the outside of the ROP domains, resulting in the formation of secondary cell wall pits (Fig. 5I). Thus, the ROP-activation/inactivation reaction governs the formation of the pitted pattern of secondary cell walls.
In yeasts, Cdc42 GTPase directs polarity formation through reaction-diffusion mechanism36. Cdc42 GTPase is activated by a GEF, Cdc24, and then the activated Cdc42 recruits Cdc24 through the PAK-Bem1 scaffold, providing positive feedback37. In this system, the reaction components diffuse rapidly in the cytoplasm of tiny intracellular space, which causes competition between domains, resulting in formation of single domain for budding within the cell38. In contrast to yeast model, in metaxylem vessel cells, ROP-activation cycle generated co-existing multiple domains depending on the levels of ROPGEFs and ROPGAPs to direct pitted secondary cell wall pattern. Our study revealed that ROP/Rho GTPase-reaction cycle could not only generate polarity but self-organize periodic patterns of plasma membrane domains. The ROP/Rho-driven reaction-diffusion system may thus contribute to a broad range of subcellular pattern formation.
Methods
Plant materials and growth conditions
All Arabidopsis plants used in this study were in the Col-0 background. The T-DNA insertion lines, ropgap3-1 (SALK_056521) and ropgap4-2 (SALK_152535), were obtained from the Arabidopsis Biological Resource Center (ABRC). ropgef4-1 (SAIL_184_c08) has been reported previously17; ropgef7-1 was generated by EMS mutagenesis in this study.
Seedlings were grown on 0.5× MS agar medium containing 0.2% sucrose at 22 °C under constant light. For the observation of root metaxylem vessels, 7-day-old seedlings were used. DIC images of xylem vessels were acquired at the area that are 8 to 12 mm away from the tip of primary roots.
Quantitative RT-PCR
Total RNA was purified from the roots of Arabidopsis using the Favor Prep Plant total RNA purification Mini Kit (FAVORGEN, http://www.favorgen.com/). Purified RNA was reverse transcribed using oligo (dT) 20 primers and SuperScript IV reverse transcriptase (ThermoFisher Scientific, https://www.thermofisher.com/). Quantitative RT-PCR was performed using THUNDERBIRD SYBR qPCR Mix (Toyobo, http://www.toyobo-global.com/) and a LightCycler 96 (Roche Diagnostics, https://www.roche.com). Gene expression data were acquired and analysed using LightCycler software. Target gene expression levels were normalized against expression of an internal standard, UBQ10.
Plasmid construction
To generate pROPGEF4:GFP-ROPGEF4, pROPGEF7:YFP-ROPGEF7, and pROPGAP4:GEF-ROPGAP4, the genomic sequence of each gene, including the upstream promoter region, was amplified using PCR and cloned into the pENTR/D-TOPO vector. The GFP or YFP coding sequence was fused to the 5′ end of the coding sequence using Ligation High II (Toyobo). To generate pIRX3:ROPGAP3, 1.5 kbp of the promoter region of IRX3 was inserted into the NotI site of pENTR/D-TOPO containing the ROPGAP3 coding sequence. This clone was recombined with the pGWB501 vector. To generate pLexA:CFP-ROPGAP3, p LexA:cYFP-ROPGAP3, and their truncation derivatives, pENTR/D-TOPO carrying full length or truncated ROPGAP3 were recombined with pER-ECFP-X and pER-xYFP-X. To generate pLexA:nYFP-ROPGEF4PRONE and pLexA:cYFP-ROPGEF4PRONE, pENTR/D-TOPO carrying ROPGEF4PRONE was recombined with pER-nYFP-X and pER-cYFP-X39. All clones were verified by DNA sequencing. To generate ROPGEF7RNAi, the first 400 bp of ROPGEF7 coding sequence was recombinated with pER-RNAi gateway vector, in which two complementary gateway cassette with an intron spacer was inserted into the ApaI site of pER8 vector.
Microscopy
An inverted fluorescence microscope (IX83-ZDC, Olympus, https://www.olympus-lifescience.com/) fitted with a confocal unit (CSU-W1, Yokogawa), a cooled CCD camera (ORCA-R2, Hamamatsu Photonics) or an EM-CCD camera (iXon3-888, ANDOR), an UplanSAPO 60× water-immersion objective (NA = 1.2, Olympus), an UplanSAPO 10× objective (NA = 0.4, Olympus), and laser lines set at 458, 488, and 561 nm was used. Images were acquired with MetaMorph software (Molecular Devices). An EM-CCD camera was used for recoding tagRFP-ROPGEF4PRONE and GFP-ROPGAP3 in tobacco leaf epidermis.
To obtain omni-directional views of metaxylem vessels, an Olympus FV3000 inverted confocal microscope (Olympus) equipped with an UPLAN 60× water-immersion objective (NA = 1.2) and a laser line set to 514 nm was used.
Omni-directional imaging of secondary cell walls
Secondary cell walls of Arabidopsis root cells were stained with propidium iodide, and then z-stack images were acquired using a confocal microscope (FV3000, Olympus). The image stacks were processed and converted into 360° 2-dimensional images using a ImageJ (https://imagej.nih.gov/ij/) plug-in16.
FRET analysis
We calculated the FRET efficiency between CFP-ROPGEF4PRONE and YFP-ROP11 derivatives and between CFP-ROPGEF4PRONE and YFP-ROPGEF4PRONE using the acceptor photo-bleaching method. CFP- and YFP-tagged proteins were expressed in tobacco leaf epidermal cells by the transient gene expression method (see below). Mid plane of the epidermal cells were scanned under FV3000 confocal microscope equipped with an UplanSAPO 60× water-immersion objective (NA = 1.2). Narrow rectangular area of the plasma membrane were photo-bleached with a 514 nm laser at 100% power. Immediately after photo-bleaching, CFP emission was recorded three times with 5 s interval. FRET efficiency was calculated as E = 100 × (A-B)/B, where E indicates FRET efficiency, and B and A indicate the averaged intensity of three images before and after photo-bleaching, respectively. Before the calculation of FRET efficiency, the background intensity was subtracted from the intensity of CFP
FRAP analysis
FRAP analysis was performed with FV3000 confocal microscope equipped with an UplanSAPO 60× water-immersion objective (NA = 1.2). GFP- or tagRFP-tagged proteins were expressed in tobacco leaf epidermal cells by the transient gene expression method (see below). Mid plane of leaf epidermal cells were scanned, then narrow rectangular area of the plasma membrane at the mid plane were photo-bleached with a 488 nm laser or a 561 nm laser at 100% power for GFP or tagRFP, respectively. Immediately after photo-bleaching, images were scanned every 1 s for 60 s. Recovery rate (%) was calculated as R = 100 × (A-I)/(B-I), where R indicates recovery rate, I, A, and B indicate average intensity of the breached area immediately after bleaching, 60 s after photo-bleaching, and before photo-bleaching, respectively.
Transient gene expression in Nicotiana benthamiana
Transient gene expression in N. benthamiana was performed as described previously17. Rhizobium radiobacter strains GV3101 MP90 harbouring expression constructs were grown on LB media plates with appropriate antibiotics. R. radiobacter cells were resuspended in infiltration buffer (10 mM MES (pH 5.7), 10 mM MgCl2, 50 mg/L acetosyringone). Equal volumes of R. radiobacter suspensions carrying different expression constructs were combined for co-infiltration, and mixed with a suspension of R. radiobacter carrying the p19 silencing suppressor in a 1:1 ratio. Mixed suspensions were adjusted to an OD 600 of 1.0. The mixed suspensions were infiltrated into leaves of 3- to 4-week-old N. benthamiana plants. The leaf samples were harvested 2 days after infiltration and inoculated with 2 µM oestradiol for subsequent observation for 1 day.
Quantification of ROPGEF4PRONE domain in the reconstitution assay
To reconstitute ROPGEF4PRONE domains, pLexA:ROP11, pLexA:tag-RFP-ROPGEF4PRONE, and pLexA:ROPGAP3, were co-introduced into tobacco leaves by the syringe-infiltration with R. radiobacter. Two days after infiltration, the leaf samples were harvested and inoculated with 2 µM estradiol. ROPGEF4PRONE domains formed in leaf epidermal cells were observed and recorded using the CSU-W1 system (see above). All images were processed with maximum intensity projection. Subsequently, regions of the ROPGEF4PRONE domains and cell area were manually selected. The numbers of the ROPGEF4PRONE domains were manually counted.
Quantification of the area of secondary cell wall pits and the distance between pits
To quantify the area of and distance between secondary cell wall pits, the regions and positions of secondary cell wall pits in DIC images were manually selected and analysed using ImageJ. Pit density was calculated as the number of secondary cell wall pits divided by the area of metaxylem vessel cells.
Statistical analysis
The student’s t test, Welch’s t test, Wilcoxon rank sum test, and ANOVA with Scheffe test were used to analyse data. Sample sizes (n) and P-values are indicated in the figure legends. In scatter plot analyses, Spearman’s rank correlation coefficient was used.
Mathematical Model
Let us consider the following reaction-diffusion equations on a two-dimensional square space:
where ui(x, t)s are time-variable spatial distribution of concentrations of ROPs. The concentration of free GEF FG and free GAP FP is determined by the following conservation law of GEF and GAP:
where TG, TP, L and V (assumed to be L3) are constant parameters indicating the total amounts of GEF and GAP, the length of a side of the square space, and the cell volume respectively.
Fourier Transformation around a stationary state
Suppose that an ordinary differential equation (ODE) system obtained by removal of diffusion terms in (S1) has a positive stationary state \({u}_{i}^{\ast }(i=1,\cdots ,6)\), \({F}_{G}^{\ast }\) and \({F}_{P}^{\ast }\), that should satisfy the following equations:
The perturbations around the stationary state \({u}_{i}^{\ast }\), \({F}_{G}^{\ast }\) and \({F}_{P}^{\ast }\) are:
The differential equations for the perturbations are written as:
where the partial derivatives are evaluated at the stationary state \({u}_{i}^{\ast }\), \({F}_{G}^{\ast }\), \({F}_{P}^{\ast }\). From the conservation laws, the perturbations of FG and FP are given by
We take Fourier transformation:
where \({\boldsymbol{m}}=({m}_{x},{m}_{y})=(\frac{2\pi {n}_{x}}{L},\frac{2\pi {n}_{y}}{L}),({n}_{x},{n}_{y}\in {\mathbb{N}})\), \(m=\sqrt{{m}_{x}^{2}+{m}_{y}^{2}}\), and δi,j indicates Kronecker delta:
Then the following equations must be hold.
The linearized dynamics in the Fourier space is written separately for the mode m is 0 and positive. For the Fourier mode m = 0,
where the parameters K1 ~ K8,p1,p2 are defined as:
For the Fourier mode \(m > 0\),
The biological evidences require the positive values for the parameters \({K}_{i} > 0\), (i = 1, …, 6), non-negative values for \({K}_{i}\ge 0\) (i = 7, 8), and non-positive values for \(\,{p}_{1}\le 0\),\(\,{p}_{2}\le 0\).
Mathematical analysis
The condition of a reaction-diffusion system for periodic pattern formation was given as Turing’s instability, which consists of two parts: (i) equilibrium of the linearized ODE system (S9) is stable; and (ii) homogeneous distribution of the stationary state is unstable, i.e., the linearized PDE (S11) is unstable for some values of m. The stability of the linearized system is determined by the Routh-Hurwitz criterion (see below) from the linearized matrix J or its correspondence J−m2D (Murray, 2002). In a model with n variables, the condition of stability is given as intersections of n inequalities. We analysed the stability condition symbolically from the distribution of zero and nonzero entries in the Jacobian matrixes J and J − m2D40. We call such symbolic analysis “structural analysis”. By the structural analyses, we discuss conditions of structures of the reaction network to satisfy the Turing instability without depending on details of nonlinear functions of the systems.
Three different versions of the models were compared: (A) Closed-circuit model without regulations (p1 = 0, p2 = 0; K7 = K8 = 0); (B) Inhibition from conserved quantities (\({p}_{1} < 0\), \({p}_{2} < 0\); K7 = K8 = 0); and (C) Positive feedback from dimerization (p1 = 0, p2 = 0; \({K}_{7} > 0\), \({K}_{8} > 0\)). The symbolic formula of six inequalities for the Turing condition was determined and analysed based on Routh-Hurwitz criterion via Mathematica. The closed-circuit model (A) and the inhibition model (B) never show Turing instability from their structure. The positive feedback model (C) can represent the Turing instability. The results give the structural conditions of the reaction network required for Turing instability. Positive feedback is necessary while the conservation law does not contribute to the Turing instability.
Routh-Hurwitz criterion
The Routh-Hurwitz criterion, which gives a necessary and sufficient condition for the stability of a linear dynamical system, is described as follows. Given the characteristic polynomial, \(P(\lambda )={\lambda }^{n}+{a}_{1}{\lambda }^{n-1}+\cdots +{a}_{n-1}\lambda +{a}_{n}\) with all real coefficients ai, i = 1, …n, the n Hurwitz matrices are defined using the coefficients ai of the characteristic polynomial:
and
where aj = 0 for \(j > n\). Then, all of the roots of the polynomial equation P(λ) = 0 are negative or have negative real part, if and only if the determinants of all Hurwitz matrices are positive:
Numerical analysis
Using the positive feedback model (C), which can satisfy the Turing instability condition structurally, the qualitative condition of 14 parameters (\({K}_{1} \sim {K}_{8}\) and \({D}_{1} \sim {D}_{6}\)) was examined. We generated 108 sets of parameters randomly using uniform distributions of \({K}_{1} \sim {K}_{8}\in (0,10]\) and \({D}_{1} \sim {D}_{6}\in (0,{10}^{2}]\). Among them, 580,362 parameter sets satisfied the Turing condition qualitatively. The probability P(Ki)dKi for \(i=1 \sim 8\) and P(Di)dDi for \(i=1 \sim 6\) are shown in Fig. 3B and C. The obtained values of parameters K1 and K7 were biased larger and that of K2 was biased lower, respectively. The obtained values of D1 was biased larger, and that of D3 was lower. Especially, the obtained value of the parameter D2 was significantly small compared with the other diffusion coefficients.
Numerical simulation
To calculate the dynamics of the reaction-diffusion systems of the model including all feedback regulations (\({p}_{1} < 0\), \({p}_{2} < 0\); \({K}_{7} > 0\), \({K}_{8} > 0\)), we adopt the following nonlinear reaction system:
with the Hill coefficient n = 5. The following relations connects the general formulation shown in (S1) and the above specific choices of functions (S15):
The parameter values and initial states are selected from randomly determined sets, that satisfy the Turing instability condition quantitatively. The chosen parameters are: a = 57.113932, Km = 3.097872, c = 0.658876, k2 = 2.261496, k3 = 5.751476, k4 = 3.324223, k5 = 2.002325, k6 = 7.099055, D1 = 42.373001, D2 = 2.107038, D3 = 54.475096, D4 = 52.561383, D5 = 52.796738, and D6 = 71.697538. At the initial state, concentrations of uis were given homogeneously as \({\bar{u}}_{1}^{0}=0.18\), \({\bar{u}}_{2}^{0}=0.57\), \({\bar{u}}_{3}^{0}=0.22\), \({\bar{u}}_{4}^{0}=0.15\), \({\bar{u}}_{5}^{0}=0.65\), and \({\bar{u}}_{6}^{0}=0.18\). with small fluctuations. The other parameters are given as TG = 105L2, TP = 105L2.
Alternative Direction Implicit Method (ADI method) (W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery (2007). “Section 20.3.3. Operator Splitting Methods Generally”. Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press.) was used for numerical calculations with a small time-step (\({\rm{\Delta }}t=0.01\)). For numerical calculations, a square lattice including 100×100 sites with a periodic boundary condition was used. The time evolution of ui patterns in the numerical calculation is shown in Fig. 4E (times t = 0, 5 and 100).
References
Turing, A. M. The chemical basis of morphogenesis. Proc. R. Soc. Lond. B Biol. Sci. 237, 37–72 (1952).
Gierer, A. & Meinhardt, H. A theory of biological pattern formation. Kybernetik 12, 30–39 (1972).
Shiratori, H. & Hamada, H. The left-right axis in the mouse: from origin to morphology. Development 133, 2095–2104, https://doi.org/10.1242/dev.02384 (2006).
Raspopovic, J., Marcon, L., Russo, L. & Sharpe, J. Modeling digits. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science 345, 566–570, https://doi.org/10.1126/science.1252960 (2014).
Economou, A. D. et al. Periodic stripe formation by a Turing mechanism operating at growth zones in the mammalian palate. Nat. Genet. 44, 348–351, https://doi.org/10.1038/ng.1090 (2012).
Fujita, H., Toyokura, K., Okada, K. & Kawaguchi, M. Reaction-diffusion pattern in shoot apical meristem of plants. PloS one 6, e18243, https://doi.org/10.1371/journal.pone.0018243 (2011).
Nakamasu, A., Takahashi, G., Kanbe, A. & Kondo, S. Interactions between zebrafish pigment cells responsible for the generation of Turing patterns. Proc. Natl. Acad. Sci. USA 106, 8429–8434, https://doi.org/10.1073/pnas.0808622106 (2009).
Economou, A. D. & Green, J. B. Modelling from the experimental developmental biologists viewpoint. Semin. Cell Dev. Biol. 35, 58–65, https://doi.org/10.1016/j.semcdb.2014.07.006 (2014).
Yang, Z. & Lavagi, I. Spatial control of plasma membrane domains: ROP GTPase-based symmetry breaking. Curr. Opin. Plant Biol. 15, 601–607, https://doi.org/10.1016/j.pbi.2012.10.004 (2012).
Wu, C. F. & Lew, D. J. Beyond symmetry-breaking: competition and negative feedback in GTPase regulation. Trends Cell Biol. 23, 476–483, https://doi.org/10.1016/j.tcb.2013.05.003 (2013).
Chiou, J. G., Balasubramanian, M. K. & Lew, D. J. Cell Polarity in Yeast. Annu. Rev. Cell Dev. Biol., https://doi.org/10.1146/annurev-cellbio-100616-060856 (2017).
Simon, C. M., Vaughan, E. M., Bement, W. M. & Edelstein-Keshet, L. Pattern formation of Rho GTPases in single cell wound healing. Mol. Biol. Cell 24, 421–432, https://doi.org/10.1091/mbc.E12-08-0634 (2013).
Bement, W. M. et al. Activator-inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium. Nature cell biology 17, 1471–1483, https://doi.org/10.1038/ncb3251 (2015).
Hodge, R. G. & Ridley, A. J. Regulating Rho GTPases and their regulators. Nature reviews. Molecular cell biology 17, 496–510, https://doi.org/10.1038/nrm.2016.67 (2016).
Oda, Y. & Fukuda, H. Rho of plant GTPase signaling regulates the behavior of Arabidopsis kinesin-13A to establish secondary cell wall patterns. Plant Cell 25, 4439–4450, https://doi.org/10.1105/tpc.113.117853 (2013).
Oda, Y., Iida, Y., Kondo, Y. & Fukuda, H. Wood cell-wall structure requires local 2D-microtubule disassembly by a novel plasma membrane-anchored protein. Curr. Biol. 20, 1197–1202, https://doi.org/10.1016/j.cub.2010.05.038 (2010).
Oda, Y. & Fukuda, H. Initiation of cell wall pattern by a Rho- and microtubule-driven symmetry breaking. Science 337, 1333–1336, https://doi.org/10.1126/science.1222597 (2012).
Sugiyama, Y., Wakazaki, M., Toyooka, K., Fukuda, H. & Oda, Y. A Novel Plasma Membrane-Anchored Protein Regulates Xylem Cell-Wall Deposition through Microtubule-Dependent Lateral Inhibition of Rho GTPase Domains. Curr. Biol. 27, 2522–2528 e2524, https://doi.org/10.1016/j.cub.2017.06.059 (2017).
Sasaki, T., Fukuda, H. & Oda, Y. CORTICAL MICROTUBULE DISORDERING1 Is Required for Secondary Cell Wall Patterning in Xylem Vessels. Plant Cell 29, 3123–3139, https://doi.org/10.1105/tpc.17.00663 (2017).
Brady, S. M. et al. A high-resolution root spatiotemporal map reveals dominant expression patterns. Science 318, 801–806, https://doi.org/10.1126/science.1146265 (2007).
Gardiner, J. C., Taylor, N. G. & Turner, S. R. Control of cellulose synthase complex localization in developing xylem. Plant Cell 15, 1740–1748 (2003).
Berken, A., Thomas, C. & Wittinghofer, A. A new family of RhoGEFs activates the Rop molecular switch in plants. Nature 436, 1176–1180, https://doi.org/10.1038/nature03883 (2005).
Murray, J. D. Mathematical Biology. (Springer, 2002).
Thomas, C., Fricke, I., Scrima, A., Berken, A. & Wittinghofer, A. Structural evidence for a common intermediate in small G protein-GEF reactions. Mol. Cell 25, 141–149, https://doi.org/10.1016/j.molcel.2006.11.023 (2007).
Wu, G., Li, H. & Yang, Z. Arabidopsis RopGAPs are a novel family of rho GTPase-activating proteins that require the Cdc42/Rac-interactive binding motif for rop-specific GTPase stimulation. Plant Physiol. 124, 1625–1636 (2000).
Schaefer, A., Miertzschke, M., Berken, A. & Wittinghofer, A. Dimeric plant RhoGAPs are regulated by its CRIB effector motif to stimulate a sequential GTP hydrolysis. J. Mol. Biol. 411, 808–822, https://doi.org/10.1016/j.jmb.2011.06.033 (2011).
Kaothien, P. et al. Kinase partner protein interacts with the LePRK1 and LePRK2 receptor kinases and plays a role in polarized pollen tube growth. Plant J. 42, 492–503, https://doi.org/10.1111/j.1365-313X.2005.02388.x (2005).
Zhang, Y. & McCormick, S. A distinct mechanism regulating a pollen-specific guanine nucleotide exchange factor for the small GTPase Rop in Arabidopsis thaliana. Proc. Natl. Acad. Sci. USA 104, 18830–18835, https://doi.org/10.1073/pnas.0705874104 (2007).
Duan, Q., Kita, D., Li, C., Cheung, A. Y. & Wu, H. M. FERONIA receptor-like kinase regulates RHO GTPase signaling of root hair development. Proc. Natl. Acad. Sci. USA 107, 17821–17826, https://doi.org/10.1073/pnas.1005366107 (2010).
Huang, G. Q. et al. Arabidopsis RopGEF4 and RopGEF10 are important for FERONIA-mediated developmental but not environmental regulation of root hair growth. The New phytologist, https://doi.org/10.1111/nph.12432 (2013).
Martiniere, A. et al. Cell wall constrains lateral diffusion of plant plasma-membrane proteins. Proc. Natl. Acad. Sci. USA 109, 12805–12810, https://doi.org/10.1073/pnas.1202040109 (2012).
Chang, F., Gu, Y., Ma, H. & Yang, Z. AtPRK2 promotes ROP1 activation via RopGEFs in the control of polarized pollen tube growth. Molecular plant 6, 1187–1201, https://doi.org/10.1093/mp/sss103 (2013).
Gu, Y., Li, S., Lord, E. M. & Yang, Z. Members of a novel class of Arabidopsis Rho guanine nucleotide exchange factors control Rho GTPase-dependent polar growth. Plant Cell 18, 366–381, https://doi.org/10.1105/tpc.105.036434 (2006).
Hwang, J. U. et al. Pollen-tube tip growth requires a balance of lateral propagation and global inhibition of Rho-family GTPase activity. J. Cell Sci. 123, 340–350, https://doi.org/10.1242/jcs.039180 (2010).
Ouyang, Q., Li, R., Li, G. & Swinney, H. Dependence of Turing pattern wavelength on diffusion rate. J. Chem. Phys. 102, 5 (1995).
Goryachev, A. B. & Pokhilko, A. V. Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett. 582, 1437–1443, https://doi.org/10.1016/j.febslet.2008.03.029 (2008).
Kozubowski, L. et al. Symmetry-breaking polarization driven by a Cdc42p GEF-PAK complex. Curr. Biol. 18, 1719–1726, https://doi.org/10.1016/j.cub.2008.09.060 (2008).
Wu, C. F. et al. Role of competition between polarity sites in establishing a unique front. eLife 4, https://doi.org/10.7554/eLife.11611 (2015).
Oda, Y., Iida, Y., Nagashima, Y., Sugiyama, Y. & Fukuda, H. Novel coiled-coil proteins regulate exocyst association with cortical microtubules in xylem cells via the conserved oligomeric golgi-complex 2 protein. Plant Cell Physiol. 56, 277–286, https://doi.org/10.1093/pcp/pcu197 (2015).
Maybee, J. S., Olesky, D. D., Driessche, Pvd & Wiener, G. Matrices, digraphs, and determinants. SIAM J. Matrix Anal. Appl. 10, 20 (1989).
Acknowledgements
We thank N. Chua (Rockefeller University) for the pER8 vector, U. Grossniklaus (University of Zurich) for the pMDC7 vector, and T. Nakagawa (Shimane University) for the pGWB vectors. We also thank Y. Noguchi (National Institute of Genetics), F. Hasegawa (National Institute of Genetics), and Y. Tanaka (National Institute of Genetics) for technical assistance. We also thank Y. Hiromi (National Institute of Genetics) for discussion and critical reading of the manuscript. This work was supported by grants from MEXT KAKENHI (grant no. 16H01247 to YO and 15H05958 to HF), the JSPS KAKENHI (grant no. 16J03646 to YN, 16H06172 to YO and 16H06377 to HF), the Japan Science and Technology Agency (JST; Precursory Research for Embryonic Science and Technology project [PRESTO] to YO [grant no. JPMJPR11B3], and Core Research for Evolutional Science and Technology [CREST] to AM [grant no. JPMJCR13W6]), and the Mitsubishi Foundation to YO, the Naito Foundation to HF. Computations were partially performed on the NIG supercomputer at ROIS National Institute of Genetics. YN is a special joint researcher of the National Institute of Genetics and ST is a special postdoctoral researcher in RIKEN (Award number K1731017).
Author information
Authors and Affiliations
Contributions
Y.O., A.M., and H.F. designed the research. Y.N. and Y.O. performed experiments and data analysis. T.S. analysed genome sequences. S.T. and A.M. performed mathematical analysis. Y.N., Y.O., A.M., and H.F. wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nagashima, Y., Tsugawa, S., Mochizuki, A. et al. A Rho-based reaction-diffusion system governs cell wall patterning in metaxylem vessels. Sci Rep 8, 11542 (2018). https://doi.org/10.1038/s41598-018-29543-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-29543-y
This article is cited by
-
Microtubule-associated phase separation of MIDD1 tunes cell wall spacing in xylem vessels in Arabidopsis thaliana
Nature Plants (2024)
-
Two subtypes of GTPase-activating proteins coordinate tip growth and cell size regulation in Physcomitrium patens
Nature Communications (2023)
-
Confined-microtubule assembly shapes three-dimensional cell wall structures in xylem vessels
Nature Communications (2023)
-
Neue Methoden ermöglichen die Live-Beobachtung der Holzentstehung
BIOspektrum (2022)
-
Long-term single-cell imaging and simulations of microtubules reveal principles behind wall patterning during proto-xylem development
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.