Abstract
The AlGaN/GaN heterostructure field-effect transistors with different gate lengths were fabricated. Based on the chosen of the Hamiltonian of the system and the additional polarization charges, two methods to calculate PCF scattering by the scattering theory were presented. By comparing the measured and calculated source-drain resistances, the effect of the different gate lengths on the PCF scattering potential was confirmed.
Similar content being viewed by others
Introduction
AlGaN/GaN heterostructure field-effect transistors (HFETs) have emerged as excellent devices for high-frequency and high-power applications1,2,3,4,5,6,7,8,9,10,11,12,13,14, owing to their superior properties such as high electron mobility, high saturation electron velocity, and large critical breakdown field15,16,17,18,19,20,21,22,23,24,25. Polarization Coulomb field (PCF) scattering, stemming from the non-uniform distribution of the strain in the AlGaN barrier layer, can affect the electron mobility, parasitic source access resistance, transconductance, and device linearity in AlGaN/GaN HFETs26,27,28,29,30,31,32,33,34,35,36,37,38,39,40. Based on the perturbation theory, the theoretical model of PCF scattering has been established31, which makes it possible to quantitative study of PCF scattering35,36,37,38,39,40. The Hamiltonian of electrons in the source-drain channel can be split into two parts \(\hat{H}={\hat{H}}_{0}+\hat{H}^{\prime} \), where \({\hat{H}}_{0}\) is known as the Hamiltonian of the unperturbed system, and \(\hat{H}^{\prime} \) is called the perturbation. For PCF scattering, \(\hat{H}^{\prime} \) originates from the effect of additional polarization charges on the channel electrons, and is referred as the PCF scattering potential. The polarization charges underneath the gate region can be altered by the gate bias41, leading to the polarization charges at the AlGaN/GaN interface uneven. The non-uniform distribution of polarization charges can generate the PCF scattering potential. The gate length is relevant with the non-uniform distribution of polarization charges26,30,35,38. Hence, the different gate lengths can affect the PCF scattering potential. If the PCF scattering potential is large enough, the accuracy of the PCF scattering model based on the perturbation theory may be challenged. Therefore, exploring the effect of different gate lengths on PCF scattering potential is necessary.
In this paper, the AlGaN/GaN HFETs with different gate lengths were fabricated. By comparing the measured and calculated source-drain resistances, the influence of different gate lengths on PCF scattering potential was explored.
Results and Discussion
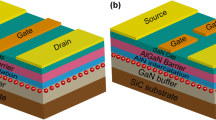
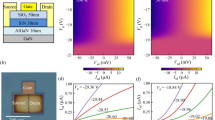
As shown in Fig. 1, the AlGaN/GaN HFETs with source-drain spacing (LSD) of 20 μm and the gate width (WG) of 100 μm were fabricated. The Schottky gate was symmetrically placed in the middle between the source and drain ohmic contacts. The gate lengths (LG) of Sample 1, 2, and 3 are 4, 10, and 16 μm, respectively. The DC I-V characteristics for the three samples were measured, as shown in Fig. 2(a). From the I-V characteristics, the total resistance R in the source-drain channel as a function of gate bias can be obtained by R = VDS/IDS − 2RC, as shown in Fig. 2(b). Here IDS refers to the source-drain current corresponding to the source-drain voltage VDS = 0.1 V. The C-V characteristics for the three samples were performed, as shown in Fig. 3(a). Integration of measured gate capacitance over gate bias yielded the two-dimensional electron gas (2DEG) electron density n2D under the gate region26,27,28,31, as shown in Fig. 3(b).
In AlGaN/GaN HFETs, the main scattering mechanisms include polarization Coulomb field (PCF), polar optical phonon (POP), acoustic phonon (AP), interface roughness (IFR), and dislocation (DIS) scatterings26,31,42,43,44,45,46,47,48,49,50. R can be determined by the scattering theories of the 2DEG electrons in AlGaN/GaN HFETs31,38,46,47,48,49,50.
In AlGaN/GaN HFETs, the 2DEG electrons can be written as Ψ(x, y, z) = A−1/2ψ(z)exp(ik x x + ik y y)31,38,46,48,50. Here A is the normalization constant, k x , k y refer to the components of k in the x-direction and y-direction, respectively. ψ(z) = (b3z2/2)1/2exp(−bz/2) refers to the quantized wave in z-direction and b = (33m*e2n2D/8ε0εsћ2)1/3 is the variational parameter. m* refers to the electron effective mass of GaN, ε0 is the dielectric permittivity, and εs refers to the static dielectric constant of GaN. The ψ(z) under different n2D can be calculated, as shown in Fig. 4. It is apparent ψ(z) is closely relevant with n2D. The larger n2D is, the closer the 2DEG electrons to the AlGaN/GaN interface is. Hence, Ψ(x, y, z) depends on n2D. We note that n2D under the gate region is increased with the gate bias, while n2D under the free-contact region (including the gate-source region and the gate-drain region) is constant. Therefore, it is different for Ψ(x, y, z) under the gate region and the free-contact region.
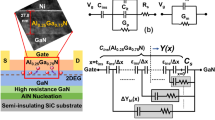
PCF scattering originates from the non-uniform distributed polarization charges at the AlGaN/GaN interface26,27,31. Before device processing, because of the spontaneous and piezoelectric polarization, there are uniform distributed polarization charges at the AlGaN/GaN interface, as shown in Fig. 5(a), which cannot scatter the channel electrons. The charge density of the uniform distributed polarization charges is named as ρ0. Due to the converse piezoelectric effect, the strain of the AlGaN barrier layer underneath the gate region can be altered by the gate bias, as shown in Fig. 5(b). The polarization charge density under the gate region, labeled as ρG, can be calculated as following36,37,38,41
where e33 and C33 are the piezoelectric coefficient and the elastic stiffness tensor of AlGaN, respectively, VGS is the gate-source voltage and dAlGaN is the thickness of the AlGaN barrier layer. The free-contact region cannot be affected by the gate bias, where the polarization charges is still equal to ρ0. The non-uniform distributed polarization charges between the gate region and the free-contact region can induce PCF scattering potential. The difference between the non-uniform distributed polarization charges and the uniform distributed polarization charges is defined as the additional polarization charges, labeled as Δσ. The PCF scattering potential originates from Δσ, and the determination of Δσ is based on the chosen of the Hamiltonian of electrons.
The perturbation theory is used in the PCF scattering calculation. The Hamiltonian of electrons in the source-drain channel can be split into two parts \(\hat{H}={\hat{H}}_{0}+\hat{H}^{\prime} \), where \({\hat{H}}_{0}\) is known as the Hamiltonian of the unperturbed system, and \(\hat{H}^{\prime} \) is very small compared to \({\hat{H}}_{0}\). As a result, \(\hat{H}^{\prime} \) is called the perturbation, for its effects on the energy spectrum and eigenfunctions will be small. Here \(\hat{H}^{\prime} \) originates from the effect of additional polarization charges on the channel electrons, and is referred as the PCF scattering potential. When the gate bias is applied to the AlGaN barrier layer, the electrons under the gate region can be modulated. Then in the source–drain channel electron system, there are two types of \({\hat{H}}_{0}\), which are the \({\hat{H}}_{0}\) for the electrons under the gate region, and the \({\hat{H}}_{0}\) for the electrons under the free contact region. Both can likely be treated as \({\hat{H}}_{0}\).
If the \({\hat{H}}_{0}\) for the electrons under the free-contact region is chosen, as shown in Fig. 5(c), Ψ(x, y, z) in the free-contact region is used. This is defined as the Method 1. Because the 2DEG electron density under the free-contact region is equal to n2D0 (here n2D0 refers to the 2DEG electron density under the gate region corresponding to VGS = 0 V), n2D = n2D0 is used in Ψ(x, y, z). The polarization charges under the free-contact region is ρ0, therefore the additional charges can be obtained by36,37,38,41
The additional polarization charges Δσ1 is under the gate region. Based on the obtained Δσ1, the PCF scattering potential can be written as31,37,38,50
If the \({\hat{H}}_{0}\) for the electrons under the gate region is chosen, as shown in Fig. 5(d), Ψ(x, y, z) under the gate region is used. This is defined as the Method 2. Here n2D under the gate region is used for Ψ(x, y, z). The additional polarization charges can be determined by
The additional polarization charges Δσ2 is under the gate-source region and the gate-drain region. Based on the obtained Δσ2, the PCF scattering potential can be expressed by31,37,38,50
Here LGS and LGD refer to the gate-source spacing and gate-drain spacing, respectively.
In the next calculation processing, as discussed above, the different wave functions Ψ(x, y, z) and the PCF scattering potential V(x, y, z) are adopted for two different methods. With the obtained Ψ(x, y, z) and V(x, y, z), the scattering matrix element is given by31,37,38,50
where q x , q y refer to the components of the wave vector q in the x-direction and y-direction, respectively. The change in q during a scattering process is related to the scattering angle θ between initial state k and final state k′ by q = |2(2m*ℏ−2E) 1/2sin (θ/2)|.
Then the energy dependent scattering rate for the PCF scattering can be obtained31,37,38,50
where ћ is the Planck constant. The screening function S (q, Te) is31,37,38,50
Here the form factor F (q) is31,37,38,50
The closer the 2DEG electrons to the additional polarization charges is, the stronger the Coulomb screening effect is. Therefore, the 2DEG channel electrons, which are the nearest to the additional polarization charges, are chosen in Eq. (9). That is, for Method 1, Δσ1 is under the gate region and the electron wave function under the gate region is used in Eq. (9). Conversely, for Method 2, Δσ2 is under the free-contact region and the electron wave function under the free-contact region is used in Eq. (9).
The polarizability function Π (q, Te, E) is31,37,38,50
In this equation, Θ(x) is the usual step function, kF = (2πn2D)1/2 is the Fermi wave vector, Te is the electron temperature, EF is the Fermi energy, and E is the energy.
At the end, the momentum relaxation time τPCF for PCF scattering can be got31,37,38,50
where f0, the Fermi function, is
Here kB is the Boltzmann constant.
The momentum relaxation times τPOP, τAP, τIFR, and τDIS for POP, AP, IFR, and DIS scatterings were obtained by the pre-existing calculation formulas31,37,38,50. Considering n2D between the gate region and the free-contact region is different, the R for three samples can be determined with the resistance RG under the gate region plus the resistance RF under the free-contact region31,37,38,50.
Here \({\tau }_{{\rm{POP}}}^{{\rm{G}}}\), \({\tau }_{{\rm{AP}}}^{{\rm{G}}}\), \({\tau }_{{\rm{IFR}}}^{{\rm{G}}}\), and \({\tau }_{{\rm{DIS}}}^{{\rm{G}}}\) refer to the momentum relaxation times for POP, AP, IFR, and DIS scatterings under the gate region, respectively. \({\tau }_{{\rm{POP}}}^{{\rm{F}}}\), \({\tau }_{{\rm{AP}}}^{{\rm{F}}}\), \({\tau }_{{\rm{IFR}}}^{{\rm{F}}}\), and \({\tau }_{{\rm{DIS}}}^{{\rm{F}}}\) refer to the momentum relaxation times for POP, AP, IFR, and DIS scatterings under the free-contact region, respectively. The calculated R for the three samples was shown in Fig. 6. Firstly, there is a distinct difference between the measured R and the calculated R excluding PCF scattering. This means PCF scattering is not ignorable in AlGaN/GaN HFETs. Then R, including the calculated PCF scattering by the two methods, was obtained. It is apparent that the calculated results by Method 1 has better accord with the measured values for Sample 1, and the calculated results by Method 2 agree well with the measured values for Sample 3. Different from the two samples, the calculated results by both Method 1 and Method 2 have a significant difference with the measured values for Sample 2. This phenomenon can be explained as following.
The measured source-drain channel resistance (Measured), and the calculated source-drain channel resistance calculated by Method 1 (Method 1), Method 2 (Method 2) as well as without PCF scattering (Without PCF), as a function of gate bias for (a) Sample 1, (b) Sample 2, and (c) Sample 3, respectively.
POP, AP, IFR, and DIS scatterings are consistent for the three samples, therefore the difference should come from the PCF scattering calculation with the two methods. PCF scattering is calculated by the scattering model based on the perturbation theory. The perturbation theory is most suitable when \(\hat{H}\) is very close to \({\hat{H}}_{0}\) and PCF scattering can be solved exactly. To this end, H′ should be far less than H0. The less H′ is, the more precise the calculated PCF scattering is. H′ is the PCF scattering potential V (x, y, z). Therefore, for a more clear presentation, the average value of V (x, y, z) can be expressed by36,37,38
Here, considering the 2DEG wave function distribution in z-direction, as shown in Fig. 4, z = 50 nm is adopted. The calculated \(\overline{V}\) with two methods for the three samples was shown in Fig. 7.
For sample 1, because LG = 4 μm and LSD = 20 μm, the free-contact region is larger than the gate region. With Method 2, Δσ2 and V2 (x, y, z) are used. Because of the large free-contact region, there are numerous additional polarization charges under the free-contact region, which will induce a large PCF scattering potential, namely a larger H′. The large H′ can affect the precision of the calculated PCF scattering. Conversely, with Method 1, Δσ1 and V1 (x, y, z) are adopted. Due to the small gate length, the additional polarization charges underneath the gate region is small for a large source-drain distance, leading to smaller V (x, y, z) or H′. As shown in Fig. 7(a), the \(\overline{V}\) obtained by Method 1 is smaller than that obtained by Method 2. The smaller \(\overline{V}\) means a less H′, which can improve the precision of the PCF scattering calculation. This means for a small gate length, it is appropriate that V1 (x, y, z) is treated as the PCF scattering potential.
For Sample 3, because LG = 16 μm and LSD = 20 μm, the gate region is larger than the free-contact region. As discussed above, in order to obtain a small H′, the additional polarization charges under the free-contact region should be chosen. This means Δσ2 and V2 (x, y, z) should be adopted. As shown in Fig. 7(c), the \(\overline{V}\) obtained by Method 2 is smaller than that obtained by Method 1. Hence Method 2 is more suitable for the PCF scattering calculation, which agrees well with the results as shown in Fig. 6(c). This indicates that for a large gate length, V2 (x, y, z) should be adopted as the PCF scattering potential.
For Sample 2, on account of LG = 10 μm and LSD = 20 μm, the gate region is equal to the free-contact region. H′ obtained by the two methods both cannot be small enough, as shown in Fig. 7(b), which affect the precision of the PCF scattering calculation. Therefore, the obtained R by two methods has a significant difference with the measured values.
In addition, as the gate bias is more negative, the number of additional polarization charges (Δσ1 and Δσ2) is increased. The increased Δσ can increase the V (x, y, z) and H′, as show in Fig. 7, which also can reduce the precision of the PCF scattering calculation. That is why as the gate bias is decreased, the deviation between the calculated R and the measured R is increased. This further indicated that the explanation for the effect of different gate lengths on PCF scattering potential is suitable.
Conclusions
In summary, with the measured and calculated source-drain channel resistances for the AlGaN/GaN HFETs with different gate lengths, the effect of different gate lengths on PCF scattering potential was analyzed. It is found that the gate length can influence the determination of the Hamiltonian of the system and the additional polarization charges, and then affect the PCF scattering potential. This study offers an effective way for improving the precision of the PCF scattering model.
Methods
Sample fabrication
The AlGaN/GaN heterostructure was grown by molecular beam epitaxy (MBE) on a sapphire substrate. The epitaxial structure consists of, from the bottom to the top, a 100-nm-thick AlN nucleation layer, a 1-μm-thick GaN buffer layer with carbon doped, a 1-μm-thick GaN channel layer, a 0.7-nm-thick AlN interlayer, a 25.5-nm-thick AlGaN barrier layer with 21% Al composition, and a 3-nm-thick GaN cap layer. A high sheet electron density (n2D) of 8.4 × 1012 cm−2 and a high electron mobility (μ) of 2340 cm2/V∙s were obtained by Hall measurement. Device isolation was achieved by inductively coupled plasma reactive ion etching (ICP-RIE) using BCl3/Cl2 gas mixture. Ti/Al/Ni/Au-based ohmic metal stack was then deposited and annealed in N2 ambient at 850 °C for 30 s. The ohmic contact resistance RC = 10 Ω was obtained by the transmission line method (TLM). Finally, a Ni/Au metal stack was deposited to form the gate electrode. The source-drain spacing (LSD) is 20 μm, and the gate width (WG) is 100 μm. The Schottky gate was symmetrically placed in the middle between the source and drain ohmic contacts. As shown in Fig. 1(b), the gate lengths (LG) of Sample 1, 2, and 3 were 4 μm, 10 μm and 16 μm, respectively.
Measurements
Current-voltage (I-V) measurements and capacitance-voltage (C-V) measurements were performed by using an Agilent B1500A and Agilent B1520A Semiconductor Parameter Analyzers, respectively.
References
Latorre-Rey, A. D., Sabatti, F. F. M., Albrecht, J. D. & Saraniti, M. Hot electron generation under large-signal radio frequency operation of GaN high-electron- mobility transistors. Appl. Phys. Lett. 111, 013506, https://doi.org/10.1063/1.4991665 (2017).
Ma, J. & Matioli, E. Slanted tri-gates for high-voltage GaN power devices. IEEE Electron Device Lett. 38, 1305–1308, https://doi.org/10.1109/LED.2017.2731799 (2017).
Tang, G. et al. Digital integrated circuits on an E-mode GaN power HEMT platform. IEEE Electron Device Lett. 38, 1282–1285, https://doi.org/10.1109/LED.2017.2725908 (2017).
Blaho, M. et al. Annealing, temperature, and bias-induced threshold voltage instabilities in integrated E/D-mode InAlN/GaN MOS HEMTs. Appl. Phys. Lett. 111, 033506, https://doi.org/10.1063/1.4995235 (2017).
Zhang, K. et al. High-Linearity AlGaN/GaN FinFETs for Microwave Power Applications. IEEE Electron Device Lett. 38, 615–618, https://doi.org/10.1109/LED.2017.2687440 (2017).
Chiu, H. et al. RF Performance of In Situ SiNx Gate Dielectric AlGaN/GaN MISHEMT on 6-in Silicon-on-Insulator Substrate. IEEE Trans. Electron Devices. 64, 4065–4070, https://doi.org/10.1109/TED.2017.2743229 (2017).
Sun, S. et al. AlGaN/GaN metal-insulator-semiconductor high electron mobility transistors with reduced leakage current and enhanced breakdown voltage using aluminum ion implantation. Appl. Phys. Lett. 108, 013507, https://doi.org/10.1063/1.4939508 (2016).
Brown, D. F. et al. Self-Aligned AlGaN/GaN FinFETs. IEEE Electron Device Lett. 38, 1445–1448, https://doi.org/10.1109/LED.2017.2747843 (2017).
Mi, M. et al. Millimeter-Wave Power AlGaN/GaN HEMT Using Surface Plasma Treatment of Access Region. IEEE Trans. Electron Devices. 64, 4875–4881, https://doi.org/10.1109/TED.2017.2761766 (2017).
Ostermaier, C. et al. Dynamics of carrier transport via AlGaN barrier in AlGaN/GaN MIS-HEMTs. Appl. Phys. Lett. 110, 173502, https://doi.org/10.1063/1.4982231 (2017).
Yang, L. et al. Enhanced gm and fT With High Johnson’s Figure-of-Merit in Thin Barrier AlGaN/GaN HEMTs by TiN-Based Source Contact Ledge. IEEE Electron Device Lett. 38, 1563–1566, https://doi.org/10.1109/LED.2017.2757523 (2017).
Suria, A. J. et al. Thickness engineering of atomic layer deposited Al2O3 films to suppress interfacial reaction and diffusion of Ni/Au gate metal in AlGaN/GaN HEMTs up to 600 °C in air. Appl. Phys. Lett. 110, 253505, https://doi.org/10.1063/1.4986910 (2017).
Zhang, Y. et al. High-Temperature-Recessed Millimeter-Wave AlGaN/GaN HEMTs With 42.8% Power-Added-Efficiency at 35 GHz. IEEE Electron Device Lett. 39, 727–730, https://doi.org/10.1109/LED.2018.2822259 (2018).
Mi, M. et al. 90 nm gate length enhancement-mode AlGaN/GaN HEMTs with plasma oxidation technology for high-frequency application. Appl. Phys. Lett. 111, 173502, https://doi.org/10.1063/1.5008731 (2017).
Ambacher, O. et al. Two dimensional electron gases induced by spontaneous and piezoelectric polarization in undoped and doped AlGaN/GaN heterostructures. J. Appl. Phys. 87, 334, https://doi.org/10.1063/1.371866 (2000).
Shinohara, K. et al. Scaling of GaN HEMTs and Schottky Diodes for Submillimeter-Wave MMIC Applications. IEEE Trans. Electron Devices. 60, 2982–2996, https://doi.org/10.1109/TED.2013.2268160 (2013).
Feng, Y. et al. Anisotropic strain relaxation and high quality AlGaN/GaN heterostructures on Si (110) substrates. Appl. Phys. Lett. 110, 192104, https://doi.org/10.1063/1.4983386 (2017).
Chen, J. et al. Room-temperature mobility above 2200 cm2/V·s of two-dimensional electron gas in a sharp-interface AlGaN/GaN heterostructure. Appl. Phys. Lett. 106, 251601, https://doi.org/10.1063/1.4922877 (2015).
Manfra, M. J. et al. Electron mobility exceeding 160000 cm2/V·s in heterostructures grown by molecular-beam epitaxy. Appl. Phys. Lett. 85, 5394, https://doi.org/10.1063/1.1824176 (2004).
Hao, R. et al. Breakdown Enhancement and Current Collapse Suppression by High-Resistivity GaN Cap Layer in Normally-Off AlGaN/GaN HEMTs. IEEE Electron Device Lett. 38, 1567–1570, https://doi.org/10.1109/LED.2017.2749678 (2017).
Jiang, Q. et al. 1.4-kV AlGaN/GaN HEMTs on a GaN-on-SOI Platform. IEEE Electron Device Lett. 34, 357–359, https://doi.org/10.1109/LED.2012.2236637 (2013).
Selvaraj, S. L. et al. 1.4-kV Breakdown Voltage for AlGaN/GaN High-Electron-Mobility Transistors on Silicon Substrate. IEEE Electron Device Lett. 33, 1357–1377, https://doi.org/10.1109/LED.2012.2207367 (2012).
Bouzid-Driad, S. et al. AlGaN/GaN HEMTs on Silicon Substrate With 206-GHz FMAX. IEEE Electron Device Lett. 34, 36–38, https://doi.org/10.1109/LED.2012.2224313 (2013).
Liu, X. et al. AlGaN/GaN Metal-Oxide-Semiconductor High-Electron-Mobility Transistor with Polarized P(VDF-TrFE) Ferroelectric Polymer Gating. Sci. Rep. 5, 14092, https://doi.org/10.1038/srep14092 (2015).
Pearton, S. J. & Ren, F. GaN Electronics, Adv. Mater. 12, 1571, 10.1002/1521-4095(200011)12:21<1571::AID-ADMA1571>3.0.CO;2-T (2000).
Zhao, J. et al. Electron mobility related to scattering caused by the strain variation of AlGaN barrier layer in strained AlGaN/GaN heterostructures. Appl. Phys. Lett. 91, 173507, https://doi.org/10.1063/1.2798500 (2007).
Lv, Y. et al. Polarization Coulomb field scattering in AlGaN/AlN/GaN heterostructure field-effect transistors. Appl. Phys. Lett. 98, 123512, https://doi.org/10.1063/1.3569138 (2011).
Luan, C. et al. Influence of the side-Ohmic contact processing on the polarization Coulomb field scattering in AlGaN/AlN/GaN heterostructure field-effect transistors. Appl. Phys. Lett. 101, 113501, https://doi.org/10.1063/1.4752232 (2012).
Luan, C. et al. Polarization Coulomb field scattering in In0.18Al0.82N/AlN/GaN heterostructure field-effect transistors. J. Appl. Phys. 112, 054513, https://doi.org/10.1063/1.4752254 (2012).
Lv, Y. et al. Influence of the ratio of gate length to drain-to-source distance on the electron mobility in AlGaN/AlN/GaN heterostructure field-effect transistors. Nanoscale Res. Lett. 7, 434, https://doi.org/10.1186/1556-276X-7-434 (2012).
Luan, C. et al. Theoretical model of the polarization Coulomb field scattering in strained AlGaN/AlN/GaN heterostructure field-effect transistors. J. Appl. Phys. 116, 044507, https://doi.org/10.1063/1.4891258 (2014).
Luan, C. et al. Influence of polarization coulomb field scattering on the subthreshold swing indepletion-mode AlGaN/AlN/GaN heterostructure field-effect transistors. Physica E. 62, 76–79, https://doi.org/10.1016/j.physe.2014.04.027 (2014).
Zhao, J. et al. Effects of rapid thermal annealing on the electrical properties of the AlGaN/AlN/GaN heterostructure field-effect transistors with Ti/Al/Ni/Au gate electrodes. Appl. Phys. Lett. 105, 083501, https://doi.org/10.1063/1.4894093 (2014).
Zhao, J. et al. A study of the impact of gate metals on the performance of AlGaN/AlN/GaN heterostructure field-effect transistors. Appl. Phys. Lett. 107, 113502, https://doi.org/10.1063/1.4931122 (2015).
Yang, M. et al. Study of source access resistance at direct current quiescent points for AlGaN/GaN heterostructure field-effect transistors. J. Appl. Phys. 119, 224501, https://doi.org/10.1063/1.4953645 (2016).
Yang, M. et al. Study of gate width influence on extrinsic transconductance in AlGaN/GaN heterostructure field-effect transistors with polarization Coulomb field scattering. IEEE Trans. Electron Devices. 63, 3908–3913, https://doi.org/10.1109/TED.2016.2597156 (2016).
Yang, M. et al. Effect of polarization Coulomb field scattering on parasitic source access resistance and extrinsic transconductance in AlGaN/GaN heterostructure FETs. IEEE Trans. Electron Devices. 63, 1471–1477, https://doi.org/10.1109/TED.2016.2532919 (2016).
Cui, P. et al. Influence of different gate biases and gate lengths on parasitic source access resistance in AlGaN/GaN heterostructure FETs. IEEE Trans. Electron Devices. 64, 1038–1044, https://doi.org/10.1109/TED.2017.2654262 (2017).
Cui, P. et al. Effect of polarization Coulomb field scattering on device linearity in AlGaN/GaN heterostructure field-effect transistors. J. Appl. Phys. 122, 124508, https://doi.org/10.1063/1.5005518 (2017).
Cui, P. et al. Improved Linearity with Polarization Coulomb Field Scattering in AlGaN/GaN Heterostructure Field-Effect Transistors. Sci. Rep. 8, 983, https://doi.org/10.1038/s41598-018-19510-y (2018).
Anwar, A. F. M., Webster, R. T. & Smith, K. V. Bias induced strain in AlGaN/GaN heterojunction field effect transistors and its implications. Appl. Phys. Lett. 88, 203510, https://doi.org/10.1063/1.2203739 (2006).
Fang, T. et al. Effect of Optical Phonon Scattering on the Performance of GaN Transistors. IEEE Electron Device Lett. 33, 709–711, https://doi.org/10.1109/LED.2012.2187169 (2012).
Li, T. et al. Monte Carlo evaluations of degeneracy and interface roughness effects on electron transport in AlGaN–GaN heterostructures. J. Appl. Phys. 88, 829, https://doi.org/10.1063/1.373744 (2000).
Jena, D., Gossard, A. C. & Mishra, U. K. Dislocation scattering in a two-dimensional electron gas. Appl. Phys. Lett. 76, 1707, https://doi.org/10.1063/1.126143 (2000).
Xu, X. et al. Dislocation scattering in Al x Ga1-xN/GaN heterostructures. Appl. Phys. Lett. 93, 182111, https://doi.org/10.1063/1.126143 (2008).
Ridley, B. K., Foutz, B. E. & Eastman, L. F. Mobility of electrons in bulk GaN and A l xGa1−xN/GaNheterostructures. Phys. Rev. B. 61, 16862, https://doi.org/10.1103/PhysRevB.61.16862 (2000).
Antoszewski, J. et al. Scattering mechanisms limiting two-dimensional electron gas mobility in Al0.25Ga0.75N/GaN modulation-doped field-effect transistors. J. Appl. Phys. 87, 3900, https://doi.org/10.1063/1.372432 (2000).
Hsu, L. & Walukiewicz, W. Electron mobility in Al x Ga1−xN/GaN heterostructures. Phys. Rev. B. 56, 1520, https://doi.org/10.1103/PhysRevB.56.1520 (1997).
Polyakov, V. M. et al. Intrinsically limited mobility of the two-dimensional electron gas in gated AlGaN/GaN and AlGaN/AlN/GaN heterostructures. J. Appl. Phys. 106, 023715, https://doi.org/10.1063/1.3174441 (2009).
Gurusinghe, M. N., Davidsson, S. K. & Andersson, T. G. Two-dimensional electron mobility limitation mechanisms in AlxGa1−xN/GaN heterostructures. Phys. Rev. B. 72, 045316, https://doi.org/10.1103/PhysRevB.72.045316 (2005).
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 11574182, Grant 11174182, Grant 61674130, Grant 11471194, Grant 11571115, and Grant 61504127, and in part by the Developing Foundation of CAEP under Grant 2014A05011.
Author information
Authors and Affiliations
Contributions
P.C. and Z.L. contributed to the research design, experiment measurements, data analysis, and manuscript preparation. J.M. and Y.L. fabricated the device. H.L. and A.C. carried out the mathematical calculation. C.F., C.L., Y.Z. and G.D. provided scientific advice. All authors reviewed this manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cui, P., Mo, J., Fu, C. et al. Effect of Different Gate Lengths on Polarization Coulomb Field Scattering Potential in AlGaN/GaN Heterostructure Field-Effect Transistors. Sci Rep 8, 9036 (2018). https://doi.org/10.1038/s41598-018-27357-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-27357-6
This article is cited by
-
A novel AlGaN/GaN heterostructure field-effect transistor based on open-gate technology
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.