Abstract
Dirhenium halide dianions received considerable attention in past decades due to the unusual metal–metal quadruple bond. The systematic structural evolution of dirhenium halide clusters has not been sufficiently studied and hence is not well-understood. In this work, we report an in-depth investigation on the structures and electronic properties of doubly charged dirhenium halide clusters Re2X82− (X = F, Cl, Br, I). Our computational efforts rely on the well-tested unbiased CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method combined with density functional theory calculations. We find that all ground-state Re2X82− clusters have cube-like structures of D4h symmetry with two Re atoms encapsulated in halogen framework. The reasonable agreement between the simulated and experimental photoelectron spectrum of the Re2Cl82− cluster supports strongly the reliability of our computational strategy. The chemical bonding analysis reveals that the δ bond is the pivotal factor for the ground-state Re2X82− (X = F, Cl, Br, I) clusters to maintain D4h symmetric cube-like structures, and the enhanced stability of Re2Cl82− is mainly attributed to the chemical bonding of 5d orbital of Re atoms and 3p orbital of Cl atoms.
Similar content being viewed by others
Introduction
The discovery1 of the metal–metal quadruple bond in dirhenium halide Re2Cl82−, which is recognized as an important milestone in the development of modern inorganic chemistry, has stimulated intensive research work in the field of transition metal chemistry2,3. Understanding the properties of the metal–metal multiple bond is significant to further elucidate the chemistry of transition metal complexes. As a prototypical metal–metal multiple bonded ion, Re2Cl82− has been studied extensively in the past decades2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. The experimental and theoretical investigations mainly focused on the preparation4,5,6, the molecular structure7,8, the metal–metal multiple bond2,9,10,11,12,13,14 and the electronic properties4,10,15,16,17,18,19,20,21,22 of Re2Cl82− in the octachlorodirhenate salts. Previous studies7,8,9,10,11,12,13 have determined the geometry structure of Re2Cl82− to be of D4h symmetry, and confirmed the formation of Re–Re quadruple bond is due to the σ2π4δ2 subset of the bonding orbitals. Due to the difficulty of preparing the Re2Cl82− dianion in the gas phase, Wang et al.21 first measured the photoelectron spectrum (PES) of gaseous Re2Cl82− several decades after the discovery of the metal−metal multiple bond, leading to a thorough understanding of the Re–Re quadruple bond and its electronic structure.
Compared to the extent of the investigations on Re2Cl82−, similar treatments of the heavier halogen derivative Re2Br82−, which contains the Re–Re quadruple bond as well, are limited4,17,23,24. To our knowledge, sparse studies have been reported on the lighter halogen derivative Re2F82−. Peters et al.25 initially synthesized (n-Bu4N)2[Re2F8]·4H2O, which contains Re2F82−, via Re2Cl82− and (n-Bu4N)F·3H2O reacting in CH2Cl2 solution. Conradson et al.26 later confirmed the presence of the Re–Re quadruple bond in Re2F82− using X-ray absorption fine structure and resonance Raman spectroscopy. The structure of Re2F82− was determined to be eclipsed D4h geometry by Henkel et al.27. Recently, Balasekaran et al.28 prepared the (NH4)2[Re2F8]·2H2O salt in nearly 90% yield by the reaction of (n-Bu4N)2[Re2Cl8] with molten NH4HF2. They also investigated the molecular and electronic structure along with the electronic absorption spectrum of Re2F82− relying on multiconfigurational quantum chemical calculations. Compared to Re2F82−, studies on Re2I82− are sparse as well. Glicksman et al.29 firstly reported a synthesis route of Re2I82− via the reaction of the dirhenium complex Re2(O2CC6H5)4Cl2 and HI with Bu4N+ in ethanol or methanol to produce the (Bu4N)2Re2I8 salt. Preetz et al.30 prepared (Bu4N)2Re2I8 successfully for the first time in a simple procedure by the reaction of (Bu4N)2Re2X8 with HI in dichloromethane. Preetz et al.31 also reported measurements of the resonance Raman spectrum of (Bu4N)2Re2I8, while Cotton et al.32 studied its crystal structure until a few years later. Extensive studies on Re2X82− have been reported, but almost all previous studies focused on Re2X82− dianions in crystals. There has been no systematic work on Re2X82− (X = F, Cl, Br and I) clusters until now, so the following questions attract our interests: (i) It is not clear whether Re2X82− clusters are characterized by the same molecular geometry as Re2X82− dianions in crystals. (ii) Does the chemical bonding in Re2X82− clusters differ from that of dianions in crystals? (iii) What is the relative stability of Re2X82− clusters? Consequently, we turn our attention to the systematic study of lowest-energy geometries and electronic structures of Re2X82− (X = F, Cl, Br, I) clusters.
As a first step of our study on the structural evolution of Re2X82− clusters, we perform a search for the the low-energy structures of Re2X82− (X = F, Cl, Br, I) by means of the CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) code combined with DFT (density functional theory) calculations. We get the ground-state structures of Re2X82− clusters from the above calculations and subsequently investigate their relative stabilities and chemical bonding. This paper is organized as follows. The obtained results and a pertinent discussion are in the following. Then we summarize our conclusions. Last, a detailed presentation of the computational method is described.
Results and Discussion
Geometric Structure
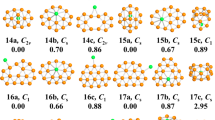
The lowest-energy structures of the Re2X82− (X = F, Cl, Br, I) clusters, together with other three typical low-lying isomers are shown in Fig. 1. The optimized vibrational frequencies and atomic coordinates of ground-state Re2X82− (X = F, Cl, Br, I) clusters are all collected in Table S1 and Table S2 of the supplementary information. According to their energies from low to high, all isomers are denoted by na, nb, nc and nd (n = 1, 2, 3,4), in which a, b, c and d stand for Re2F82−, Re2Cl82−, Re2Br82− and Re2I82−, respectively. The electronic states, point group symmetries, average binding energies, HOMO−LUMO (the highest occupied molecular orbitals and the lowest unoccupied molecular orbitals) energy gaps, together with charge on Re atoms and halogen atoms of the ground-state Re2X82− clusters are summarized in Table 1. In addition, the electronic states, point group symmetries, relative energies, HOMO−LUMO energy gaps of all isomers are given in Table S3.
It can be seen in Fig. 1 that the ground state 1a, 1b, 1c and 1d of Re2X82− (X = F, Cl, Br, I) all possess cube-like geometric structures with D4h symmetry. The geometric structures of ground-state Re2X82− (X = F, Cl, Br, I) clusters favor low-spin 1A1g state and have the same symmetry with those in crystals2,7,11,23,27,32. With the increase of the halogen atom size, the Re–Re bond length in Re2X82− varies from Re2F82− to Re2I82− as 2.20 Å, 2.21 Å, 2.22 Å, 2.24 Å, showing a little difference to those of Re2X82− dianions in crystal2. The 2a isomer has a distorted cube-like structure with C2 symmetry and the energy is 1.14 eV higher than its ground-state structure 1a. The metastable isomer 3a of Re2F82− has C s symmetry, at 1.71 eV higher than its global minimum 1a. Interestingly enough, the structure of 3a is a small square-bottom boat, and the two rhenium atoms are located in its interior. The point group symmetry of the 4a isomer is C2v, and its energy is 3.36 eV higher than its lowest-energy structure 1a. It is obvious that the two rhenium atoms are exposed outside in the geometry structure of 4a. It can be clearly seen from Fig. 1 that 2b has similar structures with 3a. The isomer of 2b has C1 symmetry with its energy 1.16 eV higher than the ground-state structure 1b. The isomers of 3b and 4b display cage-like structure with the two Re atoms encapsulated in a chlorine framework. They possess C s and C2v symmetry with the energy 1.22 eV and 1.47 eV, respectively, higher than their lowest-energy structures 1b. The isomer 2c has C2v symmetry, with total energy 0.28 eV higher than the ground-state 1c, whose structure is similar to that of 2b. The 3c structure of C2v symmetry looks similar to the structure of 4b, with total energy higher than 1c by 1.31 eV. The C2v symmetry 4c isomer is 3.07 eV less stable than the ground-state 1c. The 2d isomer of C2v symmetry has similar structure to the isomers 2b and 2c with the total energy 0.43 eV higher than 1d structure. The structure of 3d, which possesses D2d symmetry with total energy higher than the 1d one by 1.50 eV, is similar to that of 4b and 3c isomers. The C2v symmetry 4d isomer, at 2.43 eV higher in energy than the ground-state 1d, has similar structure to 4c. It is worth noting that, except for the 4a structure of Re2F82−, the two rhenium atoms are invariably inclined to stay inside for all ground and excited state structures of Re2X82− (X = F, Cl, Br, I). In order to confirm the validity of our calculations, we have also optimized the Re2X82− (X = F, Cl, Br, I) clusters at the BP86 level of theory. The corresponding lowest-energy geometries of Re2X82− clusters are presented in Figure S1 of the supplementary information. From Figure S1 we can see all structures optimized at BP86 functional also have cube-like structures with D4h symmetry and the same electronic state of 1A1g. The respective ground-state structures are in agreement with those obtained by our B3LYP optimization, further supporting our claim for the reliability of our theoretical approach.
Photoelectron Spectra of Re2X8 2−
Photoelectron spectrum (PES) is a powerful tool, which can provide important information about the electronic configuration of ground-state structures. In order to verify the validity of our obtained structures in this work, as shown in Fig. 2, we have simulated the photoelectron spectra of all global minimum geometries of Re2X82− (X = F, Cl, Br, I) and compared to the available experimental PES. Moreover, the values of adiabatic detachment energy (ADE), extracted from the threshold of the first peak, and the values of vertical detachment energy (VDE), obtained from the first peak maximum of the spectra, are summarized in Table S5 together with the available experimental data21.
As shown in Fig. 2, all spectra exhibit rich features, which correspond to transitions from the ground state of Re2X82− to the ground and excited states of singly charged Re2X8−. Overall, the binding energies, spacings and intensities are different in each spectrum, but the spacings and intensities of spectra features for Re2Br82− and Re2I82− are nearly similar to each other. The most prominent spectral feature of Re2F82− is the observation of a lower adiabatic detachment energy measured as 0.05 eV. This phenomenon is normal for multiply charged anions, largely due to the presence of intramolecular Coulomb repulsion33,34. It can be clearly seen that the first two peaks of the Re2F82− spectrum are very weak and appear in very lower binding energies. The following relatively intense peaks locate at 1.25 and 1.70 eV, respectively, and the most intense peak locates at 3.80 eV. For the simulated PES of Re2Cl82−, the ADE, namely the second electron binding energy, is 0.98 eV, which is consistent with the experimental datum of 1.00 eV. The first peak is located at 1.19 eV, in reasonable agreement with the first peak location of the experimental spectrum of Re2Cl82− centered at 1.16 eV. The following three peaks are relatively intense, located at 2.21, 2.80, and 3.24 eV, respectively. In the simulated PES of Re2Br82−, the first peak is quite intense, and emerges at 2.09 eV. In addition, there is a relatively sharp peak, which is the most intense one, located at 3.95 eV. The simulated spectrum of Re2I82− exhibits three obviously intense peaks and the first relatively weak peak emerges at 1.21 eV. The agreement of the ADE and VDE values of the simulated and experimental PES for Re2Cl82− supports the validity of our computational approach. We hope that the simulated PES of dirhenium halides can provide a helpful reference for the spectroscopic studies of Re2X82− (X = F, Br, I) dianions.
Relative Stabilities
To explore the relative stabilities of the ground state structures of the dirhenium halide system, we have calculated the average binding energies (Eb). For Re2X82− (X = F, Cl, Br, I) clusters, the Eb can be defined as follow:
Where E(Re2X82−), E(Re), E(X), and E(X−) represent the energy of Re2X82− clusters, neutral Re atom, neutral X atom, and anionic X−, respectively. The average binding energies of Re2X82− (X = F, Cl, Br, I) clusters are displayed in Fig. 3. From Fig. 3 we can find that Re2F82− is relatively stable due to its large average binding energy value. Besides, the Eb values of Re2X82− decrease monotonically from Re2F82− to Re2I82−, indicating that the relative stabilities of Re2X82− (X = F, Cl, Br, I) decrease with increasing size of the halogen atom.
Another important parameter related to the relative stabilities of the Re2X82− clusters is the HOMO−LUMO energy gap (Egap), which represents the ability of an electron to jump from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). A large value of Egap implies the corresponding molecular structure is chemically inert. The evolution of the HOMO−LUMO energy gap for the ground-state Re2X82− clusters is shown in Fig. 3. It is clearly seen that the Egap decrease monotonically, that is to say, the clusters are relatively less reactive as the halogen atom size increases, in agreement with the obtained results for the average binding energies. However, in contrast to the average binding energy rapid decrease from Re2F82− to Re2I82−, the HOMO−LUMO energy gap decreases less steeply.
Charge Transfer
Electronegativity35,36,37,38,39 is an important chemical property to describe the ability of an atom to attract electrons. A large electronegativity value is interpreted as a strong ability to attract electrons. In order to investigate the charge transfer between Re atoms and halogen atoms for ground-state Re2X82− clusters and compare to the electronegativity, we utilize natural population analysis (NPA) to obtain the charge on each atom. The results are summarized in Table 1. From Table 1 we can see that the negative charge on halogens gradually decreases from Re2F82− to Re2I82−. This phenomenon agrees with the decreasing values of Pauling electronegativity, which are 3.98, 3.16, 2.96 and 2.6640 for F, Cl, Br and I, respectively. Meanwhile, the charge on Re changes from positive to negative and the negative charge on Re is increasing with the halogen atom size increasing. All this indicates that it becomes more competitive for Re to attract electrons as the electronegativity values of halogens decrease. Although the electronegativity value of Re (1.93 on the Pauling scale)36 is lower than that of all halogen atoms, the negative charge on Re atoms is more than that of Br and I for Re2Br82− and Re2I82−, clearly not in accord with the electronegativity. This is perhaps related to the weak ability of Br and I halogen atoms to attract electrons caused by their large atomic radii and the strong intramolecular Coulomb repulsion observed in multiply charged anions34. In summary, the two excess negative charges shift from peripheral halogens to Re atoms in the case of heavier halogen atoms.
Chemical Bonding Analysis
In order to explore the nature of the chemical bonding in Re2X82−, we have carried out a detailed analysis on the HOMO−LUMO molecular orbitals (MOs). Figure 4 shows the molecular orbital diagrams of Re2X82− clusters together with their orbital energy levels, which feature their HOMO−LUMO energy gaps. Herein we take the Re–Re bond as z axis and the Re–Cl bond as ± x and ± y axes to analyze the chemical bonding. As shown in Fig. 4, the HOMO of Re2F82− displays a large overlap between the 5d xy orbitals of the two Re atoms, and the overlap forms a δ bond. The HOMO–1 and HOMO−2 are doubly degenerate, which feature π bonds formed by the overlap of the 5d yz orbitals. From the HOMO of Re2Cl82−, it can be seen that the 5d xy orbitals of the Re atoms overlap and this leads to the formation of the δ bond. In Re2Cl82−, the HOMO-2 and HOMO–3 are doubly degenerate, leading to π bonds formation by the overlap of the 5d yz orbitals. In the HOMO of Re2Br82−, the 5d xy orbitals of Re atoms have an overlap, leading to the formation of the δ bond. As for Re2I82−, there is no bonding between Re and Re in HOMO, while the HOMO-2 reveals an overlap between the 5d xy orbitals of the Re atoms, forming a δ bond. Both the HOMO of Re2X82− (X=F, Cl, Br) and the HOMO−2 of Re2I82− are δ bonds. Compared to σ and π bonds10,13,21, the δ bond is weak and contributes relatively a little to the total strength of the Re–Re bond. Nevertheless, it plays a vital role in geometric structure. The δ bond strength achieves its maximum only when the conformation is eclipsed. Its strength reduces as the conformation becomes staggered19. Thus, we can deduce that the δ bond is the pivotal factor for the ground-state Re2X82− (X = F, Cl, Br, I) clusters to maintain D4h symmetric cube-like structures.
To further understand the bonding mechanism in Re2X82−, we select Re2Cl82− as a representative example in order to perform a chemical bonding analysis using the adaptive natural density partitioning (AdNDP) method, which is particularly suitable to decipher the nature of the chemical bond. The AdNDP results displayed in Fig. 5 reveals 25 localized bonds and 11 delocalized bonds with occupation numbers (ONs) ranging from 1.9684 to 2.0000 |e|, very close or nearly equal to the ideal values (2.000 |e|). There are eight 1c–2e lone pairs (3 s) with the ON of 1.9684 |e|. The seventeen 2c–2e bonds can be divided into three sets, which contain one Re–Re bond (ON = 1.9991 |e|), eight Cl–Cl bonds (ON = 1.9989 |e|), and eight Re–Cl bonds (ON = 1.9947 |e|), respectively. The Re–Re bond is formed by the overlap of 5d orbital between the two Re atoms. For the Cl–Cl bonds, the 3p orbital in the peripheral Cl atoms results in the formation of the 2c–2e bonds. The interaction between Re and Cl is mainly dominated by the 5d orbital of Re atom and the 3p orbital of the Cl atom. The eight 3c–2e bonds with ON = 1.9886 |e| are formed by the 5d orbitals of two Re atoms and the 3p orbital of one Cl atom. There are three 10c−2e bonds with the ONs of 2.0000 |e| between the two Re atoms and the Cl8 framework, which strengthen the interactions between the inside Re atoms and the peripheral Cl atoms. In addition, the high occupation number among the localized and delocalized bonds may point to its stability. Overall, the enhanced stability of Re2Cl82− is mainly caused by the chemical bonding of 5d orbital of Re atoms and 3p orbital of Cl atoms.
Conclusions
We have performed a comprehensive research on the structural and electronic properties of dirhenium halide clusters via unbiased CALYPSO structure searches combined with DFT optimizations. The results clearly reveal that the ground states of Re2X82− (X = F, Cl, Br, I) all possess cube-like geometry with D4h symmetry. This finding has been further tested by performing calculations at the BP86 level. The simulated PES of Re2Cl82− shows reasonable agreement with the experimental spectrum, which further confirms the validity of our computational approach. According to the average binding energy and HOMO−LUMO energy gap, Re2X82− clusters are progressively less stable as halogen atoms become heavier. The chemical bonding analysis indicates that the δ bond is the pivotal factor for the ground-state Re2X82− (X = F, Cl, Br, I) clusters to retain D4h symmetric cube-like structures, and the enhanced stability of Re2Cl82− is mainly due to the chemical bonding of 5d orbital of Re atoms and 3p orbital of Cl atoms. We expect our findings provide stimulations and guidance to researchers for further experimental or theoretical investigations on binuclear transition metal halide clusters.
Computational Method
The low-lying isomers of Re2X82− (X = F, Cl, Br, I) clusters are determined via the CALYPSO method which is based on the particle swarm optimization (PSO) algorithm. This theoretical method has been described in sufficient detail previously41,42,43. In brief, it can explore the global minima of the potential energy surfaces of predicted system only based on the chemical compositions at given external conditions. It has achieved great success in predicting the ground-state structures of various systems44,45,46,47,48,49. Herein, initial structures for Re2X82− clusters are achieved by the CALYPSO method. Each generation contains 50 structures and 60% of those are generated by PSO, while the other structures are generated randomly. We have followed 30 generations for each cluster to achieve convergence to the global minima on the potential energy surfaces. The candidates within 4 eV of the lowest-energy structure are further optimized using the B3LYP50,51 exchange-correlation functional. The 6-311 + G(d) basis set for F and the LANL2DZ52,53 basis with effective core potentials for Cl, Br, I and transition-metal Re are employed throughout all calculations. All these calculations are carried out using the Gaussian 09 software package54. The choice of the B3LYP functional and The LANL2DZ basis leans heavily on experience acquired from the previous investigations11,13,55. Different spin multiplicities are taken into consideration in the geometric optimization process (up to quintet for all clusters). The harmonic vibrational frequencies are calculated in order to ensure that the optimized structures are true minima without any imaginary frequencies. We also perform the natural bond orbital (NBO)56 and adaptive natural density partitioning (AdNDP)57 to get further insight into the chemical bonding mechanism.
In order to identify the reliability of our calculations, we have optimized the structures of dirhenium halide clusters with the non-hybrid BP86 functional and the same basis set as above. It is readily seen that the optimized results of Re2X82− clusters obtained by BP86 method are in accordance with our B3LYP results. In addition, compared with the Re–Re bond length of Re2X82− dianions in previous study2 (Table S4), we can see the results calculated by the B3LYP level agree better than those from the BP86 functional. Thus we conclude that the results obtained at B3LYP level are reliable. To further confirm the reliability of our computational method, we simulate the photoelectron spectra (PES) of all lowest-energy dirhenium halide clusters and compare to the available experimental PES21. The first VDE is obtained based on the energy difference between the singly charged anion and dianion at the ground-state geometry of the dianion. The excited-state energies of the singly charged anion are calculated via the time-dependent density functional theory (TD-DFT) method58. The reasonable agreement between the simulated and the experimental PES of Re2Cl82− strongly supports our choice of B3LYP functional.
References
Cotton, F. A. et al. Mononuclear and polynuclear chemistry of rhenium(III): Its pronounced homophilicity. Science 145, 1305–1307 (1964).
Cotton, F. A., Murillo, C. A. & Walton, R. A. Multiple Bonds Between Metal Atoms. 8, 271−280. (Springer Science and Business Media, Inc., New York, 2005).
Cotton, F. A. Highlights from recent work on metal−metal bonds. Inorg. Chem. 37, 5710–5720 (1998).
Cotton, F. A., Curtis, N. F., Johnson, B. F. G. & Robinson, W. R. Compounds containing dirhenium(III) octahalide anions. Inorg. Chem. 4, 326–330 (1965).
Barder, T. J. & Walton, R. A. Reductive coupling of perrhenate to form the octachlorodirhenate(III) anion: A new, convenient, and high-yield synthetic procedure. Inorg. Chem. 21, 2510–2511 (1982).
Shtemenko, A. V., Kozhura, O. V., Pasenko, A. A. & Domasevitch, K. V. New octachlorodirhenate(III) salts: Solid state manifestation for a certain conformational flexibility of the [Re2Cl8]2− ion. Polyhedron 22, 1547–1552 (2003).
Cotton, F. A. & Harris, C. B. The crystal and molecular structure of dipotassium octachlorodirhenate(III) dihydrate, K2[Re2Cl8]·2H2O. Inorg. Chem. 4, 330–333 (1965).
Cotton, F. A., Frenz, B. A., Stults, B. R. & Webb, T. R. Investigations of quadruple bonds by polarized crystal spectra. I. The interpretation of the spectrum of tetra(n-butylammonium) octachlorodirhenate. The disordered crystal structure. J. Am. Chem. Soc. 98, 2768–2773 (1976).
Cotton, F. A. Metal–metal bonding in [Re2X8 ]2− ions and other metal atom clusters. Inorg. Chem. 4, 334–336 (1965).
Cotton, F. A. & Harris, C. B. Molecular orbital calculations for complexes of heavier transition elements. III. The metal–metal bonding and electronic structure of Re2Cl8 2−. Inorg. Chem. 6, 924–929 (1967).
Ponec, R. & Yuzhakov, G. Metal–metal bonding in Re2Cl8 (2−) from the analysis of domain averaged fermi holes. Theor. Chem. Acc. 118, 791–797 (2007).
Krapp, A., Lein, M. & Frenking, G. The strength of the σ-, π- and δ-bonds in Re2Cl8 2−. Theor. Chem. Acc. 120, 313–320 (2008).
Ponec, R., Bučinský, L. & Gatti, C. Relativistic effects on metal–metal bonding: Comparison of the performance of ECP and scalar DKH description on the picture of metal–metal bonding in Re2Cl8 2−. J. Chem. Theory Comput. 6, 3113–3121 (2010).
Hay, P. J. Ab initio studies of the metal–metal bond in octachlorodirhenate(2−). J. Am. Chem. Soc. 100, 2897–2898 (1978).
Cowman, C. D. & Gray, H. B. Low-temperature polarized spectral study of the lowest electronic absorption band in Re2Cl8 2− and related binuclear complexes. J. Am. Chem. Soc. 95, 8177–8178 (1973).
Mortola, A. P., Moskowitz, J. W., Rōsch, N., Cowman, C. D. & Gray, H. B. Electronic structure of Re2Cl8 2−. Chem. Phys. Lett. 32, 283–286 (1975).
Trogler, W. C., Cowman, C. D., Gray, H. B. & Cotton, F. A. Further studies of the electronic spectra of octachlorodirhenate(2−) and octabromodirhenate(2−). Assignment of the weak bands in the 600−350-nm region. Estimation of the dissociation energies of metal–metal quadruple bonds. J. Am. Chem. Soc. 99, 2993–2996 (1977).
Trogler, W. C. & Gray, H. B. Electronic spectra and photochemistry of complexes containing quadruple metal–metal bonds. Acc. Chem. Res. 11, 232–239 (1978).
Cotton, F. A. Spectroscopic and quantum theoretical studies of species with metal–to–metal bonds. J. Mol. Struct. 59, 97–108 (1980).
Hay, P. J. Electronic states of the quadruply bonded Re2Cl8 2− species: An ab initio theoretical study. J. Am. Chem. Soc. 104, 7007–7017 (1982).
Wang, X. B. & Wang, L. S. Probing the electronic structure and metal–metal bond of Re2Cl8 2− in the gas phase. J. Am. Chem. Soc. 122, 2096–2100 (2000).
Gagliardi, L. & Roos, B. O. The electronic spectrum of Re2Cl8 2−: A theoretical study. Inorg. Chem. 42, 1599–1603 (2003).
Cotton, F. A., Deboer, B. G. & Jeremic, M. Some reactions of the octahalodirhenate (III) ions. VIII. Definitive structural characterization of the octabromodirhenate (III) ion. Inorg. Chem. 9, 2143–2146 (1970).
Huang, H. W. & Martin, D. S. Single-crystal polarized spectra for the δ → δ* band of tetrabutylammonium octachlorodirhenate(III) and tetrabutylammonium octabromodirhenate(III). Crystal structure of the octabromo salt. Inorg. Chem. 24, 96–101 (1985).
Peters, G. & Preetz, W. Synthesis and properties of the octafluorodirhenate(III) anion, [Re2F8 ]2 −. Z. Naturforsch. 34, 1767−1768 (1979).
Conradson, S. D., Sattelberger, A. P. & Woodruff, W. H. X-ray absorption study of octafluorodirhenate(III): EXAFS structures and resonance Raman spectroscopy of octahalodirhenates. J. Am. Chem. Soc. 110, 1309–1311 (1988).
Henkel, G., Peters, G., Preetz, W. & Skowronek, J. Crystal structure and vibration spectra of [(n-C4H9)4N]2[Re2F8]·2(C2H5)2O. Z. Naturforsch. 45, 469–475 (1990).
Balasekaran, S. M. et al. Octafluorodirhenate(III) revisited: Solid-state preparation, characterization, and multiconfigurational quantum chemical calculations. Inorg. Chem. 55, 5417–5421 (2016).
Glicksman, H. D. & Walton, R. A. Studies on metal carboxylates. 14. Reactions of molybdenum(II) and rhenium(III) carboxylates with the gaseous hydrogen halides in alcoholic media. Synthesis, characterization, and reactivity of the new haloanions of molybdenum and rhenium, Mo2Br6 −, Mo4I11 2−, and Re2I8 2−. Inorg. Chem. 17, 3197–3202 (1978).
Preetz, W. & Rudzik, L. Synthesis and properties of tetrabutylammonium octaiododirhenate(III), [(n-C4H9)4N]2[Re2I8]. Angew. Chem. Int. Ed. Engl. 18, 150–151 (1979).
Preetz, W., Peters, G. & Rudzik, L. Resonance Raman spectrum of tetrabutylammonium octaiododirhenate(III), [(n-C4H9)4N]2[Re2I8]. Z. Naturforsch. 34, 1240–1242 (1979).
Cotton, F. A., Daniels, L. M. & Vidyasagar, K. The crystal structure of [(n-C4H9)4N]2Re2I8: Three-fold disorder of the effectively cubic anion. Polyhedron 7, 1667−1672 (1988).
Wang, X. B., Yang, X. & Wang, L. S. Probing solution-phase species and chemistry in the gas phase. Int. Rev. Phys. Chem. 21, 473–498 (2002).
Dreuw, A. & Cederbaum, L. S. Multiply charged anions in the gas phase. Chem. Rev. 102, 181–200 (2002).
Pauling, L. The nature of the chemical bond. IV. The energy of single bonds and the relative electronegativity of atoms. J. Am. Chem. Soc. 54, 3570–3582 (1932).
Gordy, W. & Thomas, W. J. O. Electronegativities of the elements. J. Chem. Phys. 24, 439–444 (1956).
Allred, A. L. & Rochow, E. G. A scale of electronegativity based on electrostatic force. J. Inorg. Nucl. Chem. 5, 264–268 (1958).
Allred, A. L. Electronegativity values from thermochemical data. J. Inorg. Nucl. Chem. 17, 215–221 (1961).
Parr, R. G., Donnelly, R. A., Levy, M. & Palke, W. E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 68, 3801–3807 (1978).
Murphy, L. R., Meek, T. L., Allred, A. L. & Allen, L. C. Evaluation and test of Pauling’s electronegativity scale. J. Phys. Chem. A 104, 5867–5871 (2000).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063−2070 (2012).
Lv, J., Wang, Y. C., Zhu, L. & Ma, Y. M. Particle-swarm structure prediction on clusters. J. Chem. Phys. 137, 084104 (2012).
Zhu, L. et al. Substitutional alloy of Bi and Te at high pressure. Phys. Rev. Lett. 106, 145501 (2011).
Zhu, L., Liu, H. Y., Pickard, C. J., Zou, G. T. & Ma, Y. M. Reactions of xenon with iron and nickel are predicted in the earth’s inner Core. Nat. Chem. 6, 644–648 (2014).
Lv, J., Wang, Y. C., Zhu, L. & Ma, Y. M. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 106, 015503 (2011).
Xing, X. D. et al. Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci. Rep-uk. 6, 19656 (2016).
Jin, Y. Y. et al. Probing the structural evolution of ruthenium doped germanium clusters: Photoelectron spectroscopy and density functional theory calculations. Sci. Rep-uk. 6, 30116 (2016).
Ding, L. P., Shao, P., Lu, C., Zhang, F. H. & Wang, L. Y. Iron-based magnetic superhalogens with pseudohalogens as ligands: An unbiased structure search. Sci. Rep-uk. 7, 45149 (2017).
Becke, A. D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Wadt, W. R. & Hay, P. J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 82, 284–298 (1985).
Hay, P. J. & Wadt, W. R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 82, 299–310 (1985).
Frisch, M. J. et al. Gaussian 09 (Revision C.0). Gaussian, Inc., Wallingford, CT, 2009. URL http://www.gaussian.com.
Taylor, C. J., Wu, B., Nix, M. G. D. & Dessent, C. E. H. Probing the gas-phase stability of the Re2X8 2− (X = Cl, Br) and Re2X n Y8-n 2− (X = Cl, Y = Br, n = 1−3) metal–metal bond complexes. Chem. Phys. Lett. 479, 184–188 (2009).
Read, A. E., Curtiss, L. A. & Weinhold, F. Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint. Chem. Rev. 88, 899–926 (1988).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207–5217 (2008).
Casida, M. E., Jamorski, C., Casida, K. C. & Salahub, D. R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 108, 4439–4449 (1998).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 11574220, 11304167, and 21671114), the 973 Program of China (Grant 2014CB660804), the Special Program for Applied Research on Super Computation of the NSFC–Guangdong Joint Fund (the second phase; Grant U1501501), and the Program for Science & Technology Innovation Talents in Universities of Henan Province (Grant 15HASTIT020).
Author information
Authors and Affiliations
Contributions
C.L. and X.Y.K. conceived the idea. L.H.Z., X.X.X. and C.L. performed the calculations. L.H.Z., X.X.X., W.G.S. B.L.C. and G.M. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, L.H., Xia, X.X., Sun, W.G. et al. Probing the Structural and Electronic Properties of Dirhenium Halide Clusters: A Density Functional Theory Study. Sci Rep 8, 6702 (2018). https://doi.org/10.1038/s41598-018-25027-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-25027-1
This article is cited by
-
Studies on the structural and electronic characteristics of alkaline-earth metal Mgn+1 and BaMgn (n = 2–10) clusters and their anions
Theoretical Chemistry Accounts (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.