Abstract
In binary aluminosilicate liquids and glasses, heterogeneity on intermediate length scale is a crucial factor for optical fiber performance, determining the lower limit of optical attenuation and Rayleigh scattering, but also clustering and precipitation of optically active dopants, for example, in the fabrication of high-power laser gain media. Here, we consider the low-frequency vibrational modes of such materials for assessing structural heterogeneity on molecular scale. We determine the vibrational density of states VDoS g(ω) using low-temperature heat capacity data. From correlation with low-frequency Raman spectroscopy, we obtain the Raman coupling coefficient. Both experiments allow for the extraction of the average dynamic correlation length as a function of alumina content. We find that this value decreases from about 3.9 nm to 3.3 nm when mildly increasing the alumina content from zero (vitreous silica) to 7 mol%. At the same time, the average inter-particle distance increases slightly due to the presence of oxygen tricluster species. In accordance with Loewensteinian dynamics, this proves that mild alumina doping increases structural homogeneity on molecular scale.
Similar content being viewed by others
Introduction
At low temperature (<50 K), the heat capacity Cp of glasses and other non-crystalline materials exhibits a characteristic deviation from the Debye model1. The underlying excess of vibrational states is often taken as a universal signature of structural heterogeneity at intermediate length scale2, resulting from dynamic heterogeneity in the liquid state which leads to spatial gradients in fictive temperature3,4. Heterogeneity then manifests not only in the excess of heat capacity, but also in the terahertz frequency range (0.1–3 THz) which is detectable by low-frequency Raman spectroscopy5, or in the inelastic scattering of X-rays (IXS) and neutrons (INS)6,7. While the exact consequences of such intermediate-range structural features remain unclear, various links have been identified with macroscopic properties, e.g., optical attenuation8, mechanical behaviour9 or ion mobility10.
Here, we consider the binary system of SiO2-Al2O3, both as a fundamental model for a mixed tetrahedral network11 and for the wide relevance of aluminosilicates, ranging from geosciences to optical fiber and high-power laser gain media12. In the latter, alumina is one of the most significant dopants used in silica-based active fiber laser applications. This is primarily for improving the solubility of rare-earth ions and to prevent their clustering13. However, typical strategies for compositional design remain empirical due to the lack of understanding regarding the structural role of alumina on intermediate length scale. On the other hand, high dopant capacity allows for shorter fiber lengths and/or significantly higher power levels14. We now explore the low-frequency modes of binary aluminosilicate glasses through analysis of low temperature heat capacity and low frequency Raman scattering so as to find quantitative scaling parameters and, subsequently, relations between chemical composition, intermediate-range order and the length-scale of elastic heterogeneity. This is to enable a design strategy for glasses with high dopant capacity, but also to provide new insight at the structural origin of the excess in the vibrational density of states and the Boson peak of aluminosilicate materials.
Experimental
Binary (100-x) SiO2 – x Al2O3 glasses with 2.05 < × < 7 mol % were prepared by reactive powder sintering of nanoscale silica15,16,17. Basically, this method is a modification of the solution-doping process such as employed for the production of alumina- or rare-earth-doped silica for optical fiber preforms. In the present case, sample fabrication involved the preparation of a porous green body from Al-doped high-purity silica nanopowder with a BET surface area of ~60–76 m²/g. For this, an aqueous silica slurry was doped with appropriate amounts of aqueous AlCl3 solution (1 M; AlCl3*6H2O 99.9995% metals basis, Alpha Aesar). The slurry mixture was cast into molds, dried and isostatically pressed to yield rod-shaped preform bodies of about 20 mm in diameter and a length of a few centimeters. The subsequent sintering and vitrification process of the preforms was carried-out in silica jacketing tubes (Heraeus F300) by applying mild vacuum and temperatures of up to 2200 °C (obtained from passing an oxygen-hydrogen burner). The subsequent sintering and vitrification process was carried out at temperatures of up to 2200 °C. Chemical analysis of all such-derived samples was conducted through wavelength-dispersive electron probe microanalysis (WD-EMPA). Besides the primary constituents, impurities of chlorine and water were present in the samples with average concentrations in the doped zone of less than 0.15 mol% (SiCl4) and <10 ppm (OH, determined by infrared optical spectroscopy). In the following, samples are denoted according to their Al2O3 concentration, x = 0, 2.05, 3.20 and 7.00, (Table 1). Sample homogeneity was examined by visual inspection, optical microscopy and through transmission electron microscopy (TEM-EDS). It was confirmed that the samples do not contain any kind of crystals, pores or bubbles. Furthermore, on a length-scale of 5–3000 nm, they did not contain any visible fluctuations in chemical composition or density.
To assess structural features on intermediate range, independent analyses were conducted by low-temperature heat-capacity measurements (Cp) and low-frequency Raman spectroscopy. For Cp analyses, a physical property measurement system (PPMS, Quantum Design) was employed at temperatures down to approximately 2.3 K, using liquid 4He. The samples were cut and polished to small discs of about 2 mm in diameter and 1 mm in thickness, corresponding to a mass of about 7 mg. After cleaning, they were fixed on the center of a sapphire platform using ~0.10 mg Apiezon N grease. The estimated error in mass was about ±1 µg, resulting from balance precision. The data of Cp were measured with the relaxation technique every 10 K within 300 K to 50 K, every 5 K within 50 K to 30 K, every 2 K from 30 K to 20 K, and every 0.5 K from 20 K to about 2 K, applying a logarithmically varying step-size. Within the interval between experimental data points, linear interpolation was conducted as required.
Low-frequency Raman spectroscopy was conducted at room temperature on a confocal micro-Raman spectrometer (Renishaw Invia) equipped with a notch filter for low frequencies (to ~10 cm−1). For excitation, a 514.5 nm Argon laser was used. The Raman signal was collected with a CCD camera in the range of 10 to 1375 cm−1 with a resolution of 2 cm−1, using a 50× objective.
For further reference, infrared reflectance spectra were collected at room temperature on an attenuated total reflection-Fourier transform infrared spectrometer (ATR-FTIR, Perkin Elmer) across the spectral range of 450–7800 cm−1 with a resolution of 0.5 cm−1, averaged over two individual scans. From these, absorption spectra were derived by Kramers-Kronig transformation, α(v) = 4πvk(v), where α(v) is the absorption coefficient, k(v) is the imaginary part of the complex refractive index and v is the infrared frequency.
Supplementary physical data were collected on density (buoyancy, using ethanol as immersion liquid), elastic constants and sound velocity (ultrasonic echography). For the latter, we used polished discs of ~20 mm in diameter and ~1 mm in thickness. The longitudinal v L and transversal v T sound velocities were obtained from the longitudinal and transversal sound wave propagation times, measured with an accuracy of ±1 ns by means of piezoelectric transducers (Echometer 1077, Karl Deutsch, operating at frequencies 8 to 12 MHz). The bulk modulus K, Young’s modulus E and Poisson’s ratio ν were calculated from these data as described elsewhere18. All physical data were recorded at room temperature.
Results
General
IR absorbance spectra of the binary glasses and a silica reference are shown in Fig. 1a. All glasses exhibit similar band shape, dominated by the characteristic vibrations of vitreous silica, i.e., asymmetric stretching of O-Si-O (~1120 cm−1 and 1230 cm−1 19) and O-Si-O bending (~800 cm−1). The lower band is observed to shift slightly (to lower frequency) when Al2O3 is present, while the second band broadens somewhat at the same time20,21. It was previously suggested that this is related to the extent of disorder in the SiO2 network22, which seems to increase with the addition of Al2O3. This interpretation agrees with the gradually disappearing shoulder at 1200 cm−1 23.
Corresponding Raman spectra are shown in Fig. 1b. Once again, all glasses exhibit similar band shape, except for the range from 1050 up to 1250 cm−1. In the lower frequency region, the band at around 430 cm−1 is related to rocking and symmetric bending motions of bridging oxygen (BO) species24. The position of this band remains unchanged during the addition of Al2O3. This indicates that there is no substantial change in the Si-O-Si bond angle.19 The sharp peaks at approximately 490 and 600 cm−1 correspond to symmetric bridging oxygen bending vibrations in 4- and 3-membered rings25. We observe that for both peaks, the relative intensity decreases with increasing Al2O3 content, further indicating that the addition of Al2O3 affects the ring-size distribution in the SiO2 glass system. In the mid-frequency region, the band at about 800 cm−1 results from the motion of Si atoms in their tetrahedral oxygen cage26. The high-frequency bands at about 1050–1250 cm−1 are usually assigned to Si-O stretching vibrations of tetrahedral SiO4 groups. The increasing intensity with addition of Al2O3 suggests that an interconnected Si-O-Al network is formed.19 Also, a new band is arising at around 1100 cm−1. It was suggested that this band is associated to Si-O stretching vibrations in SiO4 tetrahedra connected to one Al polyhedron.
Since there are no distinct variations in the shape of the characteristic band envelope, we assume here that Al speciation is dominated by four-fold coordination, IVAl. There are several studies that found evidence for the predominance of this coordination state in low-alumina aluminosilicate glasses. For example, Al ions implanted into silica glass (1 × 1015–1 × 1017 Al+ ions cm2) were found to simply substitute on Si-positions27. Nuclear magnetic resonance (NMR) and extended X-ray absorption fine structure (EXAFS) have shown that for ≤ 0.4 mol% of Al2O3, the Al ions are predominantly four-fold coordinated28,29. Amorphous thin films were investigated by X-ray emission spectroscopy, from which it was concluded that all Al ions are coordinated tetrahedrally for samples containing up to 5 mol % of Al2O330. Schmücker31 has shown by NMR that aluminosilicate glasses containing up to 10 mol% of Al2O3 contain predominantly four-fold coordinated Al. Finally, Pfleiderer32 arrived at the same conclusion through computational simulation of ensembles with up to 13 mol% of Al2O3.
Replacement of one silicon ion for one aluminum ion, without further charge compensation and in tetrahedral coordination, incites one oxygen to bridge three tetrahedra (instead of two) to maintain the charge balance19,31,33,34. While the existence of such triclusters is still debated, evidence for their presence in aluminosilicate glasses has been obtained in experiment35,36 and through computational simulation37,38,39. In effect, the presence of triclusters in aluminosilicate glasses would induce a tightening of the silica tetrahedral rings and, potentially, initiate crystallization.34,35 While triclusters could be bonded either to two Al and one Si or to two Si and one Al40, according to the principle of aluminum avoidance proposed by Loewenstein41, it is assumed that the latter species is usually dominant. In Fig. 2, an illustration of the structure of binary Al2O3-SiO2 glasses is provided in accordance with these arguments.
Drawing of the network topology in a binary aluminosilicate glass based on the assumption that all cations are in fourfold coordination and a certain fraction of oxygen triclusters is present. The structure was drawn using the Avogadro software package42.
Vibrational Density of States and Boson Peak
The binary of Al2O3-SiO2 exhibits a miscibility gap ranging from ~2–60 mol.% of Al2O343, giving rise to microscopic heterogeneity of melt-derived glasses34,44,45. As for the present case, the presence of phase separation was excluded by high-resolution transmission electron microscopy (TEM) down to a length scale of about 5 nm. Also, on microscopic scale, visible light scattering, Raman microscopic mapping and polarization microscopy did not reveal any heterogeneity. The following observations of low-frequency Raman scattering and low-temperature heat capacity are therefore directly resulting from structural heterogeneity at the nanometric length scale.
Specific heat
Historically, the attempt to understand non-crystalline environments started from direct comparison with the Debye model of crystals1. According to the Debye model, one usually expects a cubic temperature-dependence of the specific heat46. However, experimental studies showed a deviation from this behaviour, apparently for the vast majority of non-crystalline materials. This was denoted one of the two thermal anomalies of glasses. An early demonstration by Zeller and Pohl47 was conducted in vitreous silica. In Fig. 3, a cubic temperature scaling of the heat capacity is displayed for the present samples. The Debye contribution was calculated for each sample according to Eq. (1) and is shown for reference. This uses experimental data of density ρ, and transversal v T and longitudinal v L sound velocities48.
Debye scaling of the temperature dependence of the specific heat of silica and binary aluminosilicate glasses (alumina content indicated in labels). The solid lines in the lower left present the Debye level for each sample according to Eq. 1 (see text for details).
In Eq. 1, kB and \(\hslash \) are the Boltzmann and reduced Planck constants, respectively, N A is Avogadro’s number, m is the mean atomic mass in the chemical formula unit, θ D is the Debye temperature and v D is the Debye sound velocity obtained by averaging v L and v T through \((3/{v}_{D}^{3}).(1/{v}_{L}^{3}+2/{v}_{T}^{3})\). The parameters used for the calculation and the derived values of θ D are listed in Table 1.
All samples exhibit a significant excess of heat capacity over the Debye contribution. This excess takes the form of a broad asymmetric hump, starting at temperatures above 2 K with a maximum intensity at Tmax increasing from about 10.33 to 11.12 K (Tmax values were extracted through a polynomial fit) for increasing alumina content (see Table 1). The shift towards higher temperature is accompanied by a decrease in intensity I(Tmax). The location of Tmax is directly related to the Boson peak through the connection between the specific heat and the low-energy vibrational density of states (VDoS) g(v)48, with \({C}_{V}={(dU/dT)}_{V}\) leading to49
where \(x=hv/{k}_{B}T\). C v can be approximated to C p since glasses are condensed substances in which (C p –C V )/Cp is less than 0.1%50. Eq. 2 presents an ill-posed inverse mathematical problem in which the solution is very instable at perturbations. Following Surovtsev et al.,49 we apply a Tikhonov regularization scheme in order to mathematically stabilize the solution by adding a functional which is weighted with the regularization parameter α49. However, the choice of α is crucial in order to obtain stable solutions without loss of information by excessive smoothing. Knowing that the slope of the reduced density of states g(ω)/ω2 in the present VDoS frequency range switches only once from positive to negative (instead of oscillating), we mathematically filter-out the higher frequency solutions. The choice of α thus presents a kind of low-pass filtering based on physical knowledge. We used two figures of merit in order to optimize α: (i) the relative root-mean-square deviation χ s and (ii) the integral of the squared derivative of g(v)/v2, denoted γ and reflecting oscillatory behavior of the solution. Figure 4a shows the variations of these two parameters over α for sample containing 7.00 mol.% Al2O3. Figure 4b shows the corresponding fit for the same sample.
(a) Relative residual χb and oscillating parameter γ over regularization parameter α. For the further fitting, a value of α is chosen so that γ is minimum while χ b is acceptably small, indicated in (a). (b) Corresponding data fit for a sample with (Al2O3) = 7.00 mol.%, and comparison to experimental data.
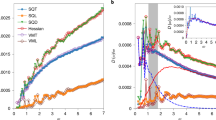
The resulting scalings of VDoS are provided in Fig. 5. There is a clear dependence of the excess vibrational density of states on alumina concentration. For the maximum position of the Boson peak of vitreous silica, we find a value of 32.2 cm−1 (Heraeus F300). This is close to the value of ~33.5 cm−1 as reported in various studies51,52 and taken as a confirmation of the accuracy of the present deconvolution across the low-frequency region (<60 cm−1).
Low-frequency Raman scattering
Prior to the determination of the Boson peak frequency, all Raman spectra were corrected for air scattering and a constant baseline was subtracted individually. In order to compare the intensities of spectra mainly in the low frequency region (ω < 175 cm−1) the intensity of all samples was normalized to the area under the band peaking at 800 cm−1 over the range of 650 cm−1< ω < 870 cm−1 (remaining practically constant with the increasing Al2O3, within the considered range of compositions). As noted before, this vibrational signature is assigned to the symmetric stretching mode of the O-Si-O bond53 or the stretching mode of the Si-O bond.26
The measured intensity I mes (ω, T) was converted into the reduced Raman intensity through the approach of Shuker and Gammon54 (Eq. (3)) to rule-out the temperature-dependence of the Raman spectra. According to the previous model it is possible to connect the reduced density of states g(ω)/ω2 to the reduced intensity by means of a coupling coefficient, C(ω). The reduced intensity of the first order Raman scattering for the Stokes part takes the following form:
Here, \(n(\omega ,T)={[\exp (\hslash \omega /{k}_{B}T)-1]}^{-1}\) is the Bose-Einstein population factor for frequency ω and temperature T; k B and \(\hslash \) are the Boltzmann and reduced Planck constants, respectively. The intensity of Raman scattering depends not only on the vibrational density of states, but also on the coupling between photons and vibrations, expressed by the coupling function C(ω). It is usually calculated by comparison of Raman spectra with neutron inelastic scattering55 or through deconvoluting specific heat data.51 In the following, we now use the VDoS scaling as described in the previous section for this purpose.
Figure 6a shows the Stokes-side of the reduced low-frequency Raman spectra for various samples of silica and binary aluminosilicate glasses. In the low-frequency region (10–175 cm−1) the state density g(ω) of all the samples exceeds the prediction of the Debye model for an isotropic homogeneous continuous medium. This excess of modes appears as a broad peak between 53–60 cm−1 when g(ω)/ω2 is plotted over frequency (with the Debye density of states \({g}_{{\rm{Deb}}}(\omega )\approx {\omega }^{2}\). The maximum of this peak, \({\omega }_{BP}\), shifts toward higher frequency and its intensity decreases with increasing Al2O3 content. To obtain quantitatively the Boson peak frequency, it is necessary to use a function which reproduces-well the reduced intensity Ired (ω) and takes into account the asymmetric shape of the Boson peak. For this, we used a log-normal function56,
(a) Stokes-side of the reduced low-frequency Raman spectra of silica and binary aluminosilicate glasses after subtraction of quasi-elastic scattering (QES) contributions. The solid line represents an exemplary log-normal fit of the experimental data of vitreous silica (type R300) used to estimate the Boson peak frequency. In (b), the computed light-vibration coupling coefficient C(ω) is shown. The alumina content of all samples is given in the labels.
In Eq. 4, H is the amplitude, a is the asymmetry parameter, ω is the width of the log-normal function and I0 is an off-set parameter.
In Fig. 6b the light-vibration coupling coefficient is shown. It varies almost linearly with ω for all samples, similar the earlier observations on other glasses51,57. For the moment, we hence assume that there is no significant effect of C(ω) on the interpretation of the Boson peak in the glass types of this study. Furthermore, we note the uncertainty in C(ω) on the high-frequency tail of the Boson peak which increases with increasing frequency (ω > 60 cm−1). This uncertainty is attributed to the inaccuracy of the computed Cp data according to Eq. 2 as shown in Fig. 4b for T > 40 K.
The evolution of the Boson peak frequency ω BP as extracted from low-frequency Raman scattering and deconvolution of heat capacity data, respectively, can now be explored as a function of Al2O3 content (Fig. 7). We compared the variation of the Boson peak frequency ω BP , extracted from Raman scattering at low frequencies and through deconvolution of heat capacity, as a function of Al2O3 content. In both cases, a clear trend is found where ω BP increases with the addition of Al2O3. Also, for all samples, the values of ω BP extracted from Raman low-frequency data are greater than those extracted from the deconvolution of heat capacity data. However, the absolute shift of the Boson peak frequency \({{\rm{\Delta }}{\rm{\omega }}}_{BP}={{\rm{\omega }}}_{BP}(93\,\,{{\rm{SiO}}}_{2}-7\,{{\rm{Al}}}_{2}{{\rm{O}}}_{3})-{{\rm{\omega }}}_{BP}({{\rm{SiO}}}_{2})\) in both datasets remains unchanged, i.e., \({{\rm{\Delta }}{\rm{\omega }}}_{BP}\approx 6\,c{m}^{-1}\).
Discussion
Vibrational density of states and Boson peak
The excess of heat capacity Cp(T)/T3 relative to the level predicted by the Debye model of thermal properties for silica and aluminosilicate glasses is shown in Fig. 3. Not visible in the present data, due to the limited temperature regime, there are indeed two temperature intervals in which such excess occurs: First, at very low temperatures (<1 K), Cp varies linearly with T (Cp ∝ aT, contrary to the crystallized form of silica in which Cp ∝ aT3)47. This anomaly is commonly explained on the basis of a two-level system (TLS) in which disorder results in structural defects. Tunneling from one configuration to another then causes additional contributions to Cp58,59. As for the present study, the TLS regime is not explored because we did not consider temperatures lower than 2 K. As noted before, we treat the second regime of anomaly in which the Boson peak is found instead.
Both anomalies were successfully explained by the soft potential model (SPM) developed by Karpov and Parshin60,61 and by Yu and Freeman62 over the temperature range of 0 <T <(3Tmin + Tmax)/4 63 (where Tmin and Tmax are the temperature of the minimum and maximum in Cp(T)/T3). This model assumes that the low-frequency dynamics of glasses are characterized by the presence of additional quasi-local harmonic oscillators (soft modes) that coexist and interact with ordinary (delocalized) phonons. The further postulates that the total specific heat can be written as Cp = CTLST + CD T3 + Csm T5 64, where CTLS, CD and Csm represent the contributions of TLS modes, Debye modes and soft mode vibrations, respectively. For an indication, values for amorphous silica were reported at CTLS = 3.15 μJ/gK2, CD = 0.76 μJ/gK4 and CSPM = 0.11 μJ/gK6 63 in the range of 0–4.15 K (with Tmin= 2.1 K65).
In Figs 5 and 6a, the density of states g(ω) for all samples exceeds the prediction of the Debye model. This excess of modes is often also visible in inelastic neutron scattering (INS), X-ray scattering (IXS), hyper-Raman scattering, infrared spectroscopy (IR) and terahertz time-domain spectroscopy (THz-TDS). Its microscopic origin is not well understood. For the specific case of vitreous silica, Buchenau66 argued on the basis of elastic and inelastic neutron scattering that the excess of modes giving rise to the Boson peak is produced by rotational motions of several interconnected tetrahedral SiO4 units. This phenomenon was also demonstrated by Hehlen et al.67 using hyper-Raman spectroscopy. Based on this, Richet68 concluded that the origin of the Boson peak in binary silicate glasses could be the result of the sum of two independent contributions, i.e., rotational motions (liberation modes) of interconnected tetrahedral SiO4 units and localized vibrations of the network modifier cations within oxygen cages. Noteworthy, the latter are different from the common cage rattling modes of modifier cations as they are typically found in the Raman scattering range of 100–300 cm−1 69,70.
Besides the experimental deductions, various theoretical approaches exist to explain the microscopic origin of the excess of modes. For example, the model of the non-continuous structure of Duval et al.71 suggests that amorphous materials comprise of nanometric domains (heterogeneities) in addition to the fundamental building blocks (e.g., SiO4 tetrahedra). The links between two neighboring atoms would be stronger if they belong to the same domain (cohesive domains) as compared to neighbors in distinct domains (soft domains). According to this model, the Boson peak is a signature of hybridization of acoustic and localized modes72.
Heterogeneity and intermediate-range order
Figure 3 shows a negative correlation between excess intensity (Cp/T3)max and Tmax. This observation is in agreement with the study of Liu et al.73 who explored various amorphous materials: inorganic oxide, metallic and organic polymer glasses. According to their results the noted negative correlation is a general feature for amorphous systems. The value of (Cp/T3)max is strongly influenced by the nature and size of the network-modifying cation55,68,74,75. For example, Nakamura75 classified the respective cations according to their ionic radii. However, it was also noted that the ionic radius of the cation cannot be the only factor which is governing the Boson peak intensity because cations with similar ionic radius may exhibit different behavior.69
A clear trend of increasing Boson peak frequency ω BP and decreasing intensity (g(ω)/ω2) max ) (Fig. 5) and \({({I}^{red})}_{max}\) (Fig. 6a) with increasing Al2O3 content is observed. Similar variations have previously been related to increasing stiffness induced by several parameters, including density76, pressure77 or network connectivity78. The intensity decrease with the increase of Al2O3 content could be explained by the fact that the contribution of the localized vibrations of the Al cation relative to non-bridging oxygen species is less important than the contribution of liberation of interconnected tetrahedral SiO4.74 Indeed, when more Al2O3 is introduced into the network the sum of the two contributions becomes less pronounced.
Nakamura et al.79 were interested in the effect of introducing network modifying cations on the nature of the Boson peak, conducting their study on binary alkali and alkaline-earth silicate glasses of the type (100-x) SiO2−xM [M = Li2O, CaO, Na2O, K2O, BaO]. They found two trends in which the size of the ions introduced into the network either increases (rion/rSi<2.5) or decreases (rion/rSi>2.5) the Boson peak. This was similar to an earlier study80 in binary alkali silicate glasses (100-x) SiO2−xM [M = Rb2O, Cs2O]. Nakamura et al. also found79 a linear relationship between the Boson peak frequency ω BP and the mean atomic volume VM/Å3 representative for the interatomic distance: ω BP decreases when VM/Å3 increases. In the present data, we confirm this trend. We have rAl/rSi = 1.25 and VM/Å3 = [15.10, 15.01, 14.98, 14.93] for samples containing [0, 2.05, 3.20, 7.00] Al2O3 mol.%, respectively. For ternary sodium aluminosilicate glasses, it was further noted that Al2O3 replacing Na2O increases the Boson peak frequency due to distortion of the SiO4 tetrahedral network81.
Building on these previous observations, the present trend is explained on the basis of the elastic proprieties of binary aluminosilicate glasses. Al2O3 acts on the local symmetry of tetrahedral SiO4 stretching motions82, decreasing the degrees of freedom in the system and increasing stiffness. This reflects in increasing bulk modulus (Table 1). Further understanding is derived from the inhomogeneity models explained above. Duval71 and Elliott83 independently found a relationship that links the average size of heterogeneities ξ with the position of the Boson peak frequency ω BP through the relation
where v T is the transverse sound velocity. Figure 8 displays the variation of the average length scale of heterogeneity extracted from the deconvolution of heat capacity data as a function of Al2O3 content. We find a decrease of the average size of heterogeneities ξ from 3.88 nm in v-SiO2 (compared to 3.74 nm as reported previously63) to 3.36 nm for an alumina content of 7 mol.%. To understand this behavior, we compare ξ to the mean inter-particle length D \((D={[M(x)/({N}_{A}\times \rho (x))]}^{1/3})\). The results shown in the insets of Fig. 8 indicate that the value of \(D\) increases with increasing content of Al2O3, probably associated with the presence of triclusters. The ratio of \({\rm{\xi }}\)/D decreases with increasing Al2O3 content, which is a signature of the increase of elastic homogenization at the nanometric scale and translates into decreasing contrast between strong and soft domains.
Boson peak shape and scaling
In order to further elaborate on the hypothesis that the decrease of Boson peak intensity and its simultaneous shift to higher frequency (and higher Tmax) are resulting from changes of elastic properties, we consider the shape of the Boson peak as a function of composition. As already noted, it has been found in many studies that changes in chemical composition, chemical bond type (covalent or metallic), density, pressure and temperature lead to changes in the Boson peak. When plotted in reduced form, these changes are universal and can be summarized in a single master curve84. We now carry-out different scaling approaches. First, we consider the Boson peak as function of the scaled frequency \(\upsilon \), obtained by reducing the frequency axis, \({\rm{\upsilon }}={\rm{\omega }}/{{\rm{\omega }}}_{BP}\), and normalization of the VDoS using \(g(\upsilon ){\rm{d}}\upsilon =g(\omega ){\rm{d}}\omega \) (Fig. 9a). This change of variable from \(\omega \) to \(\upsilon \) must be accompanied by a scaling of the reduced Raman intensity. Assuming \(C(\omega ) \sim \omega \), the rescaled intensity can be written as
Normalized master curve of the Boson peak for frequency-scaling of the Raman scattering intensity (a) and temperature-scaling of the isobaric heat capacity (b). (c) Shows the set of curves which are obtained through scaling of the Boson peak with the reduced density of vibrational states after normalizing with the Debye cut-off frequency \({{\rm{\omega }}}_{D}\). Value of \({{\rm{\omega }}}_{D}\) a function of Al2O3 content are provided in Table 1.
In a second approach, the results of the heat capacity were also scaled (Fig. 9b). Here, the scaling was performed by dividing the intensity by the maximum value (Cp T−3) max and T by Tmax. For both approaches, the scaled spectra (corresponding to different glass compositions) fall on a same master curve without introducing any adjustment parameter.
We now compare the evolution of the VDoS to the elastic medium transformations. The latter are quantified by calculating the Debye frequency \({{\rm{\omega }}}_{D}=(6{\pi }^{2}\rho {N}_{A}m/M){}^{1/3}{v}_{D}\) (M is the average molar weight). The excess of vibrational density \(g(\omega )/{\omega }^{2}\) is extracted by subtracting the contribution of the coupling factor already calculated from the reduced intensity \({I}^{red}\) (Eq. 3), and again scaling with the Debye frequency \({{\rm{\omega }}}_{D}\). Therefore, the frequency axis of the excess of VDoS spectra obtained from the conversion of heat capacity data (reported above) was rescaled as Ω = ω/ω D . To conserve the total number of vibrational states85, the intensity of the spectra must be also rescaled as
These rescaled spectra are displayed in Fig. 9c.
In all three scalings, the shape of Boson peak remains practically unchanged across all samples. This agrees with earlier observations on various other glasses. We thus conclude that the vibrational modes responsible for the Boson peak are the same in silica and aluminosilicate glasses. The universal shape observed in the Fig. 9c. can be related to the universality of the spatial distribution of fluctuations in the elastic constants86. Furthermore, the scalability is solely determined by changes occurring in the elastic properties of the material. On the other hand, failure in rescaling of the Boson peak to a single master curve has been attributed microscopic modifications87 such the existence of several phases in the same material (phase separation)88.
Conclusions
In summary, we considered the low-frequency vibrational modes of binary aluminosilicate glasses relative to a reference of vitreous silica. In such materials, heterogeneity on intermediate length scale is a crucial factor for optical fiber performance, determining the lower limit of optical attenuation and Rayleigh scattering, but also clustering and precipitation of optically active dopants, for example, in the fabrication of high-power laser gain media. Using low-temperature heat capacity and low-frequency Raman scattering data, we obtained an accurate scaling of the vibrational density of states and the Boson peak. This allowed for the extraction of the average dynamic correlation length as a function of alumina content. In the absence of macroscopic phase separation, it was found that this value decreases with increasing alumina content. At the same time, the average inter-particle distance increased slightly, assumedly associated with the presence of oxygen tricluster species. In accordance with Loewensteinian dynamics, mild alumina doping therefore increases structural homogeneity on molecular scale.
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Flubacher, P., Leadbetter, A. J., Morrison, J. A. & Stoicheff, B. P. The low-temperature heat capacity and the Raman and Brillouin spectra of vitreous silica. J. Phys. Chem. Solids 12, 53–65 (1959).
De Ligny, D. & Westrum, E. F. Jr. Entropy of calcium and magnesium aluminosilicate glasses. Chem. Geol. 128, 113–128 (1996).
Ediger, M. D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 51, 99–128 (2000).
Chumakov, A. I. et al. Equivalence of the Boson peak in glasses to the transverse acoustic van Hove singularity in crystals. Phys. Rev. Lett. 106, 225501 (2011).
Nakayama, T. Boson peak and terahertz frequency dynamics of vitreous silica. Rep. Prog. Phys. 65, 1195–1242 (2002).
Greaves, G. N. & Sen, S. Inorganic glasses, glass-forming liquids and amorphizing solids. Adv. Phys. 56, 1–166 (2007).
Wondraczek, L. et al. Kinetics of decelerated melting. Adv. Sci. 5, 1700850 (2018).
Champagnon, B., Wondraczek, L. & Deschamps, T. Boson peak, structural inhomogeneity, light scattering and transparency of silicate glasses. J. Non-Cryst. Solids 355, 712–714 (2009).
Wondraczek, L. et al. Towards Ultrastrong Glasses. Adv. Mater. 23, 4578–4586 (2011).
Greaves, G. N. & Ngai, K. L. Reconciling ionic-transport properties with atomic structure in oxide glasses. Phys. Rev. B 52, 6358–6380 (1995).
Kapoor, S. et al. Network glasses under pressure: Permanent densification in modifier-free Al2O3−B2O3−P2O5−SiO2 systems. Phys. Rev. Appl. 7, 54011 (2017).
Tanabe, S. Optical transitions of rare earth ions for amplifiers: how the local structure works in glass. J. Non-Cryst. Solids 259, 1–9 (1999).
Hannon, A. C. & Parker, J. M. The structure of aluminate glasses by neutron diffraction. J. Non-Cryst. Solids 274, 102–109 (2000).
Dragic, P. et al. Mass density and the Brillouin spectroscopy of aluminosilicate optical fibers. Opt. Mater. Express 2, 1641–1654 (2012).
Schuster, K. et al. Evolution of fluorine doping following the REPUSIL process for the adjustment of optical properties of silica materials. Opt. Mater. Express 5, 887–897 (2015).
Schuster, K. et al. Material and technology trends in fiber optics. Adv. Opt. Techn. 3, 447–468 (2014).
Langner, A. et al. A new material for high-power laser fibers. Proc. SPIE 6873, 687311 (2008).
Thieme, A. et al. Structure and properties of alkali and silver sulfophosphate glasses. J. Non-Cryst. Solids 410, 142–150 (2015).
Okuno, M., Zotov, N., Schmücker, M. & Schneider, H. Structure of SiO2–Al2O3 glasses: combined X-ray diffraction, IR and Raman studies. J. Non-Cryst. Solids 351, 1032–1038 (2005).
Sharma, S. K., Matson, D. W., Philpotts, J. A. & Roush, T. L. Raman study of the structure of glasses along the join SiO2 - GeO2. J. Non-Cryst. Solids 68, 99–114 (1984).
Winterstein-Beckmann, A., Möncke, D., Palles, D., Kamitsos, E. I. & Wondraczek, L. A Raman-spectroscopic study of indentation-induced structural changes in technical alkali-borosilicate glasses with varying silicate network connectivity. J. Non-Cryst. Solids 405, 196–206 (2014).
Kirk, C. T. Quantitative analysis of the effect of disorder-induced mode coupling on infrared absorption in silica. Phys. Rev. B 38, 1255–1273 (1988).
Šimon, I. & McMahon, H. O. Study of the structure of quartz, cristobalite, and vitreous silica by reflection in infrared. J. Chem. Phys. 21, 23–30 (1953).
Zotov, N., Ebbsjö, I., Timpel, D. & Keppler, H. Calculation of Raman spectra and vibrational properties of silicate glasses: Comparison between Na2Si4O9 and SiO2 glasses. Phys. Rev. B 60, 6383–6397 (1999).
Galeener, F. L. Planar rings in vitreous silica. J. Non-Cryst. Solids 49, 53–62 (1982).
McMillan, P. Structural studies of silicate glasses and melts-applications and limitations of Raman spectroscopy. Am. Mineral. 69, 622–644 (1984).
Fukumi, K. et al. Refractive index change in Al+-ion-implanted silica glass. J. Appl. Phys. 79, 1060–1064 (1996).
Sen, S. Atomic environment of high-field strength Nd and Al cations as dopants and major components in silicate glasses: a Nd LIII-edge and Al K-edge X-ray absorption spectroscopic study. J. Non-Cryst. Solids 261, 226–236 (2000).
Sen, S. & Youngman, R. E. High-resolution multinuclear NMR structural study of binary aluminosilicate and other related glasses. J. Phys. Chem. B 108, 7557–7564 (2004).
Hanada, T., Bessyo, Y. & Soga, N. Elastic constants of amorphous thin films in the systems SiO2 - Al2O3 and AlPO4 - Al2O3. J. Non-Cryst. Solids 113, 213–220 (1989).
Schmücker, M., MacKenzie, K. J. D., Schneider, H. & Meinhold, R. NMR studies on rapidly solidified SiO2 - Al2O3 and SiO2 - Al2O3 - Na2O-glasses. J. Non-Cryst. Solids 217, 99–105 (1997).
Pfleiderer, P., Horbach, J. & Binder, K. Structure and transport properties of amorphous aluminium silicates: Computer simulation studies. Chem. Geol. 229, 186–197 (2006).
Lacy, E. D. Aluminum in glasses and melts. Phys. Chem. Glasses 4, 234–238 (1963).
Macdowell, J. F. & Beall, G. H. Immiscibility and crystallization in Al2O3-SiO2 Glasses. J. Am. Ceram. Soc. 52, 17–25 (1969).
Schmücker, M. & Schneider, H. New evidence for tetrahedral triclusters in aluminosilicate glasses. J. Non-Cryst. Solids 311, 211–215 (2002).
Stebbins, J. F., Oglesby, J. V. & Kroeker, S. Oxygen triclusters in crystalline CaAl4O7 (grossite) and in calcium aluminosilicate glasses: 17O NMR. Am. Mineral. 86, 1307–1311 (2001).
Winkler, A., Horbach, J., Kob, W. & Binder, K. Structure and diffusion in amorphous aluminum silicate: A molecular dynamics computer simulation. J. Chem. Phys. 120, 384–393 (2004).
Benoit, M., Profeta, M., Mauri, F., Pickard, C. J. & Tuckerman, M. E. First-principles calculation of the 17O NMR parameters of a calcium aluminosilicate glass. J. Phys. Chem. B 109, 6052–6060 (2005).
Tossell, J. A. & Horbach, J. O triclusters revisited: classical MD and quantum cluster results for glasses of composition (Al2O3)2(SiO2). J. Phys. Chem. B 109, 1794–1797 (2005).
Lægsgaard, J. Theory of Al2O3 incorporation in SiO2. Phys. Rev. B 65, 174104 (2002).
Loewenstein, W. The distribution of aluminum in the tetrahedra of silicates and aluminates. Am. Mineral. 39, 92–96 (1954).
Hanwell, M. D. et al. J. Cheminform. 4, 1–17 (2012).
Ban, T., Hayashi, S., Yasumori, A. & Okada, K. Calculation of metastable immiscibility region in the Al2O3–SiO2 system. J. Mater. Res. 11, 1421–1427 (1996).
Ganguli, D. & Saha, P. Macroliquation in the system Al2O3-SiO2. Mat. Res. Bull. 2, 25–36 (1967).
Risbud, S. H. & Pask, J. A. Calculated thermodynamic data and metastable immiscibility in the system SiO2-Al2O3. J. Am. Ceram. Soc. 60, 418–424 (1977).
Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 344, 789–839 (1912).
Zeller, R. C. & Pohl, R. O. Thermal conductivity and specific heat of noncrystalline solids. Phys. Rev. B 4, 2029–2041 (1971).
Kittel, C. Introduction to solid state physics (Wiley, 2005).
Surovtsev, N. V. Evaluation of terahertz density of vibrational states from specific-heat data: Application to silica glass. Phys. Rev. E 64, 61102 (2001).
Huang, B., Bai, H. Y. & Wang, W. H. Relationship between boson heat capacity peaks and evolution of heterogeneous structure in metallic glasses. J. Appl. Phys. 115, 153505 (2014).
Surovtsev, N. V. & Sokolov, A. P. Frequency behavior of Raman coupling coefficient in glasses. Phys. Rev. B 66, 54205 (2002).
Hehlen, B. & Simon, G. The vibrations of vitreous silica observed in hyper-Raman scattering. J. Raman Spectrosc. 43, 1941–1950 (2012).
Shibata, N., Horigudhi, M. & Edahiro, T. Raman spectra of binary high-silica glasses and fibers containing GeO2, P2O5 and B2O3. J. Non-Cryst. Solids 45, 115–126 (1981).
Shuker, R. & Gammon, R. W. Raman-scattering selection-rule breaking and the density of states in amorphous materials. Phys. Rev. Lett. 25, 222–225 (1970).
D’Angelo, G. et al. Boson peak in alkaline borate glasses: Raman spectroscopy, neutron scattering, and specific-heat measurements. Phys. Rev. B 79, 14206 (2009).
Le, Q. H. et al. Formation, structure and properties of fluoro-sulfo-phosphate poly-anionic glasses. J. Non-Cryst. Solids 477, 58–72 (2017).
Fontana, A. et al. The Raman coupling function in amorphous silica and the nature of the long-wavelength excitations in disordered systems. EPL. Europhys. Lett. 47, 56–62 (1999).
Anderson, P. W., Halperin, B. I. & Varma, C. M. Anomalous low-temperature thermal properties of glasses and spin glasses. Philos. Mag. 25, 1–9 (1972).
Phillips, W. A. Tunneling states in amorphous solids. J. Low Temp. Phys. 7, 351–360 (1972).
Karpov, V. G., Klinger, I. & Ignat’Ev, F. N. Theory of the low-temperature anomalies in the thermal properties of amorphous structures. Zh. Eksp. Teor. Fiz 84, 760–775 (1983).
Karpov, V. G. & Parshin, D. A. On the thermal conductivity of glasses at temperatures below the Debye temperature. Zh. Eksp. Teor. Fiz 88, 2212–2227 (1985).
Yu, C. C. & Freeman, J. J. Thermal conductivity and specific heat of glasses. Phys. Rev. B 36, 7620–7624 (1987).
Carini, G., Carini, G., Cosio, D., D’Angelo, G. & Rossi, F. Low temperature heat capacity of permanently densified SiO2 glasses. Philos. Mag. 96, 761–773 (2016).
Vacher, R. et al. The vibrational excitations of glasses in the boson-peak region: application to borates. Phys. Chem. Glasses B 49, 19–25 (2008).
Ramos, M. A. Are the calorimetric and elastic Debye temperatures of glasses really different? Phil. Mag. 84, 1313–1321 (2004).
Buchenau, U. et al. Low-frequency modes in vitreous silica. Phys. Rev. B 34, 5665–5673 (1986).
Hehlen, B., Courtens, E., Yamanaka, A. & Inoue, K. Nature of the Boson peak of silica glasses from hyper-Raman scattering. J. Non-Cryst. Solids 307–310, 87–91 (2002).
Richet, N. F. Boson peak of alkali and alkaline earth silicate glasses: Influence of the nature and size of the network-modifying cation. J. Chem. Phys. 136, 34703 (2012).
Griebenow, K., Bragatto, C. B., Kamitsos, E. I. & Wondraczek, L. Mixed-modifier effect in alkaline earth metaphosphate glasses. J. Non-Cryst. Solids 481, 447–456 (2018).
Griebenow, K., Kamitsos, E. I. & Wondraczek, L. Mixed-modifier effect in (Ca,Mg) metaphosphate glasses. J. Non-Cryst. Solids 468, 74–81 (2017).
Duval, E., Boukenter, A. & Achibat, T. Vibrational dynamics and the structure of glasses. J. Phys. Condens. Matter 2, 10227 (1990).
Duval, E., Mermet, A. & Saviot, L. Boson peak and hybridization of acoustic modes with vibrations of nanometric heterogeneities in glasses. Phys. Rev. B 75, 24201 (2007).
Liu, X. & Löhneysen, Hv Specific-heat anomaly of amorphous solids at intermediate temperatures (1 to 30 K). EPL Europhys. Lett. 33, 617–622 (1996).
Richet, N. F. Heat capacity and low-frequency vibrational density of states. Inferences for the boson peak of silica and alkali silicate glasses. Physica B Condens. Matter 404, 3799–3806 (2009).
Nakamura, K., Takahashi, Y. & Fujiwara, T. Low-temperature excess specific heat in oxide glasses: Comprehensive study of thermometrically observed Boson peak. J. Phys. Soc. Japan 83, 114603 (2014).
Inamura, Y., Arai, M., Otomo, T., Kitamura, N. & Buchenau, U. Density dependence of the boson peak of vitreous silica. Physica B Condens. Matter 284–288, 1157–1158 (2000).
Mantisi, B. et al. Non-Debye normalization of the glass vibrational density of states in mildly densified silicate glasses. J. Phys. Condens. Matter 22, 25402 (2010).
Chen, P. et al. Intermediate phase, network demixing, boson and floppy modes, and compositional trends in glass transition temperatures of binary AsxS1−x system. Phys. Rev. B 78, 224208 (2008).
Nakamura, K., Takahashi, Y., Osada, M. & Fujiwara, T. Low-frequency Raman scattering in binary silicate glass: Boson peak frequency and its general expression. J. Ceram. Soc. Jpn. 121, 1012–1014 (2013).
McIntosh, C., Toulouse, J. & Tick, P. The Boson peak in alkali silicate glasses. J. Non-Cryst. Solids 222, 335–341 (1997).
Le Losq, C., Neuville, D. R., Florian, P., Henderson, G. S. & Massiot, D. The role of Al3+ on rheology and structural changes in sodium silicate and aluminosilicate glasses and melts. Geochim. Cosmochim. Acta 126, 495–517 (2014).
Poe, B. T., McMillan, P. F., Angell, C. A. & Sato, R. K. Al and Si coordination in SiO2-Al2O3 glasses and liquids: a study by NMR and IR spectroscopy and MD simulations. Chem. Geol. 96, 333–349 (1992).
Elliott, S. R. A unified model for the low-energy vibrational behaviour of amorphous solids. EPL Europhys. Lett. 19, 201–206 (1992).
Malinovsky, V. K. & Sokolov, A. P. The nature of boson peak in Raman scattering in glasses. Solid State Commun. 57, 757–761 (1986).
Leonforte, F. Vibrational states and disorder in continuously compressed model glasses. J. Non-Cryst. Solids 357, 552–558 (2011).
Perticaroli, S., Nickels, J. D., Ehlers, G. & Sokolov, A. P. Biophys. J. 106, 2667 (2014).
Orsingher, L. et al. Vibrational dynamics of permanently densified GeO2 glasses: Densification-induced changes in the boson peak. J. Chem. Phys. 132, 124508 (2010).
Wang, Z., Kolesnikov, A. I., Ito, K., Podlesnyak, A. & Chen, S.-H. Pressure effect on the Boson peak in deeply cooled confined water: Evidence of a liquid-liquid transition. Phys. Rev. Lett. 115, 235701 (2015).
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (ERC grant UTOPES, grant agreement no. 681652). The authors gratefully acknowledge Falko Langenhorst for providing TEM-SSD measurements, Pierre Lachkar for technical assistance in Cp data acquisition, Rene Limbach for ultrasonic echography measurements, and Romain Dauliat and Sindy Fuhrmann for fruitful discussions. MFA has obtained a fellowship from the CAPES-Brazilian Federal Agency for Support and Evaluation of Graduate Education within the Ministry of Education of Brazil.
Author information
Authors and Affiliations
Contributions
L.W. initiated and supervised the project. K.W., K.S. and S.G. were responsible for glass synthesis and basic characterization. M.F.A. and J.-L.G. conducted low-temperature experiments. O.B. conducted low-frequency Raman analyses. O.B., Z.P. and L.W. evaluated Boson peak data and performed VDoS scalings. O.B., M.F.A. and L.W. wrote the manuscript with input from all authors. All authors were involved in manuscript revisions.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ando, M.F., Benzine, O., Pan, Z. et al. Boson peak, heterogeneity and intermediate-range order in binary SiO2-Al2O3 glasses. Sci Rep 8, 5394 (2018). https://doi.org/10.1038/s41598-018-23574-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-23574-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.