Abstract
Nd0.05Ce0.95CoIn5 features a magnetic field-driven quantum phase transition that separates two antiferromagnetic phases with an identical magnetic structure inside the superconducting condensate. Using neutron diffraction we demonstrate that the population of the two magnetic domains in the two phases is affected differently by the rotation of the magnetic field in the tetragonal basal plane. In the low-field SDW-phase the domain population is only weakly affected while in the high-field Q-phase they undergo a sharp switch for fields around the a-axis. Our results provide evidence that the anisotropic spin susceptibility in both phases arises ultimately from spin-orbit interactions but are qualitatively different in the two phases. This provides evidence that the electronic structure is changed at the quantum phase transition, which yields a modified coupling between magnetism and superconductivity in the Q-phase.
Similar content being viewed by others
Introduction
Strongly correlated electron systems can feature electronic ground states, in which different electronic charge, spin, orbital and lattice degrees of freedom such as phonons, defects or strain are coupled. Such couplings can trigger novel quantum phenomena, such as unconventional superconductivity, topological and multiferroic phases or heavy-fermion ground states. The understanding of cooperative phenomena is particularly challenging in unconventional superconductors where Cooper pairs are thought to arise from magnetic fluctuations1. Antisymmetric spin-orbit interactions can lead to novel phases with uncommon symmetry such as triplet superconductivity. In CePt3Si, for instance, it is believed that such interactions generate an anomalous spin susceptibility that triggers superconductivity with mixed spin-singlet and triplet Cooper pairs2,3.
A direct way to gain insight in non-phonon driven superconductivity is to study the coupling of magnetic order and superconductivity. Magnetic superconductors feature a variety of different behavior when tuned via external parameters, such as pressure, chemical substitution or magnetic fields4,5,6. In most materials a competition between both phenomena is observed4,5,6, but there also exist cases in which magnetic order and superconductivity cooperate7,8,9. Examples include the heavy-fermion compound UGe2, where superconductivity is only stable in the presence of ferromagnetic order7, or CeCoIn5 where magnetism only appears inside the superconducting phase8,9. The latter phenomena has been discussed theoretically already for some time10,11,12,13,14,15,16,17,18,19,20,21,22,23,24, but it remains an open question how magnetic order can emerge from superconductivity.
The series Nd1−xCe x CoIn5 reveals a competition between static magnetic order and superconductivity for x > 0.78 at zero field25. 5% Nd doped CeCoIn5, however, features an auxiliary field-induced magnetic phase (Q-phase) that is only stable within the superconducting condensate and that collapses in a first-order transition at the upper critical field26. This behavior provides evidence for a cooperative magneto-superconducting ground state in the Q-phase with a coupling that is similar to the one of undoped CeCoIn5. The high-field Q-phase of 5% Nd doped CeCoIn5 is separated from its low-field SDW-phase via a quantum phase transition at μ0H* ≈ 8 T26. Both magnetic phases feature the same amplitude modulated spin-density wave (SDW) order with an ordered magnetic moment, μ ≈ 0.15μ B , that is oriented along the c-axis. The magnetic propagation vector, Q1,2 = (q, ±q, 0.5) with q ≈ 0.445, is similar to the one of the Q-phase in CeCoIn5 and directed along the nodal direction of the \({d}_{{x}^{2}-{y}^{2}}\)-superconducting order parameter26. However, it is currently an open question how the symmetry of superconductivity is affected in the Q-phase.
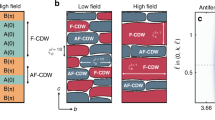
Here, we study the population of the two magnetic domains, Q1,2, in the SDW- and Q-phase of Nd0.05Ce0.95CoIn5 by means of neutron diffraction for magnetic fields oriented close to H ||[0 1 0] and along the [1 \(\bar{1}\) 0]-direction in reciprocal lattice units (r.l.u.). We find a field-induced redistribution of the domain-population for H ||[1 \(\bar{1}\) 0], where the intensity in Q2 is suppressed at μ0H d = 3.6(6) T. The Q-phase features a single spin-density modulation direction except for a small field range of ±2.5° around H ||[0 1 0], where a continuous crossover of populated domains is observed. The behavior is different in the SDW-phase, where the magnetic domains remain equally populated for magnetic fields close to the a-axis.
Results
Figure 1 displays two magnetic Bragg peaks that belong to the magnetic domains Q1 and Q2. The diffracted neutron intensity was measured for wave-vector transfers, (±q, q, \(\mp \,0.5\)), along the tetragonal plane in the Q-phase of Nd0.05Ce0.95CoIn5. The magnetic field equals μ0H = 10.4 T and is oriented along ψ = 2.5 and −2° relative to the a-axis. The neutron diffraction results show a populated Q1-domain for ψ = 2.5°, while Q2 is suppressed. When rotating the field to ψ = −2° the domain population is switched. A tunable mono-domain state is also found in the Q-phase of CeCoIn527.
Figure 2 depicts the angular dependence of the background subtracted peak intensity of both domains inside the Q-phase at μ0H = 10.4 T. When rotating the magnetic field through [0 1 0] one domain continuously depopulates while the other one is populated. The neutron diffraction results reveal a crossover region of Δψ ≈ 5° where both domains are at least partly populated. Although this is much broader than in undoped CeCoIn5, this is relatively sharp considering that the Q-domain must be pinned to the Nd dopants27.
We further studied the magnetic domain population in the SDW-phase. Diffracted neutron intensity along the tetragonal plane of Q1 and Q2 at μ0H = 2 T is shown in Fig. 3. The gray dots denote the background that was measured at μ0H = 11.9 T > \({\mu }_{0}{H}_{{c}_{2}}\). Within the SDW-phase no change in the domain population is observed in the vicinity of H ||[0 1 0]. This is in strong contrast to the Q-phase, where only one of both domains is populated for ψ = ±2.5°.
The field dependence of the integrated Bragg peak intensity at (0.56, 0.44, 0.5) is represented by orange circles in Fig. 4 for H ||[1 \(\bar{1}\) 0]. It demonstrates that the magnetic Q2-domain gradually weakens with increasing magnetic field and is suppressed at μ0H d = 3.6(6) T. This is in strong contrast to the field dependence of the Q1-domain, whose intensity increases at small fields and reveals a broad maximum around μ0H ≈ 4 T26.
Field-induced Domain imbalance. Field dependence of the two magnetic domains, Q1 and Q2, in Nd0.05Ce0.95CoIn5 for H ||[1 \(\bar{1}\) 0] and the total intensity I tot = \({I}_{{Q}_{1}}\) + \({I}_{{Q}_{2}}\). The curve is reconstructed from the data presented here and the ones reported in ref.26 The Solid lines represent weighted linear fits.
In addition, Fig. 4 compares the scaled, integrated intensity of the two magnetic domains, \({I}_{{Q}_{1}}\) and \({I}_{{Q}_{2}}\), with the total integrated intensity I tot = \({I}_{{Q}_{1}}\) + \({I}_{{Q}_{2}}\) for H ||[1 \(\bar{1}\) 0]. This plot combines new measurements with those published earlier26. The normalization of the integrated intensity was chosen to have equal population at zero field, respecting the tetragonal symmetry.
The field dependence of \({I}_{{Q}_{1}}\) and \({I}_{{Q}_{2}}\) show that fields smaller than H d trigger a redistribution of the domain population. The intensity in Q1 is enhanced, while the magnetic domain in the plane along the field Q2 is reduced, such that the total integrated intensity remains constant. Increasing the field further yields a mono-domain state, where only the Q1-domain is populated.
Discussion
5% Nd substituted CeCoIn5 features magnetic order with a moment orientation along the tetragonal c-axis26. The Zeeman coupling (MH) vanishes for fields applied in the tetragonal basal plane and cannot drive the field and angular dependent population of Q1 and Q2.
An anisotropic spin susceptibility can originate from spin-orbit interactions as observed, for instance, in the non-centrosymmetric superconductor CePt3Si2,3. It has been suggested that a similar phenomena can appear in a multiband metal with tetragonal symmetry, such as CeCoIn5, when the spin-orbit coupling reduces the space group symmetry by a basal in-plane field23. Based on this microscopic theory, Kim et. al. developed a phenomenological Landau model, which includes a weak spin-orbit coupling term in its free energy density24. It considers a magnetic moment arrangement perpendicular to the basal plane, as found in the two antiferromagnetic phases of Nd0.05Ce0.95CoIn5. Depending on the Landau parameters, the model predicts either (A) the coexistence of the Q-domains whose population is tuned with the field direction, or (B) the presence of only one Q-domain with a sharp switching24.
Scenario A yields an equal domain population for ψ = 0° and a maximal difference for ψ = 45°. This is consistent with the neutron diffraction results at μ0H = 2 T, where two populated domains are found that feature a comparable intensity for H ||[0 1 0] and a 80% suppression of Q2 for H ||[1 \(\bar{1}\) 0]. Our data in the SDW phase can thus be explained with spin-orbit couplings mediating a field-induced repopulation of the Q-domains. The much sharper switching at high fields, however, is not consistent with scenario A and suggest qualitatively different behavior more consistent with scenario B. This means that the Landau theory by Kim et al.24 can describe the SDW and Q-phase separately, but not both phases simultaneously, and different phenomenological parameters would be needed for the low- and high-field phases. This points towards a qualitative change of the electronic structure at H*.
Alternatively it has been suggested that d-wave superconductivity and magnetic order is coupled via a spatially modulated spin-triplet superconducting order parameter19,20. The formation of triplet superconductivity also relies on spin-orbit interactions and the additional order parameter supports a sharp switch of the modulation direction for a field around the a-axis20,27. A supplementary superconducting gap is consistent with a non-magnetic primary order parameter in the Q-phase that is postulated by the identical magnetic symmetry in the SDW- and the Q-phase26. Such a scenario can also account for the thermal conductivity results of the Q-phase in CeCoIn5 that reveal a reduced quasiparticle excitation spectrum perpendicular to the populated Q-domain28. A symmetry analysis suggests that the two modulation directions belong to different irreducible representations and that a p-wave order parameter is aligned along the suppressed domain27,28. As a result, the switching has to be sharp, albeit it may be broadened by pinning to Nd-ions.
It has been suggested that the Q-phase arises from the condensation of a superconducting exciton that creates a novel superconducting state22. The superconducting spin resonance that is observed in CeCoIn5 at zero field appears at the same wave-vector as static magnetic order in the Q-phase29. Under magnetic field the resonant splits and the lowest mode may condense into the ground state at the Q-phase boundary22,30,31,32. In 5% Nd doped CeCoIn5 the resonance is not affected by the onset of static magnetic order at zero field, which provides evidence for a decoupling of these fluctuations from magnetic order in the SDW-phase33.
In summary, we demonstrate that an in-plane rotation of the magnetic field in Nd0.05Ce0.95CoIn5 triggers a magnetic domain imbalance that is distinct in the SDW- and the Q-phase. We find two domains with no preferable spin-density modulation direction in the low-field SDW-phase, for fields close to the a-axis. At low fields, a field-induced change of the relative domain population is observed when the field is applied along the diagonal direction of the tetragonal plane. The selection of a mono-domain state becomes relatively sharp in the high-field Q-phase, where the spin-density modulation direction can be switched by a few-degree rotation of the field around the a-axis. The low- and high-field behavior cannot be simultaneously explained by the available phenomenological theories, and requires a modification in the coupling between superconductivity and magnetic order at H*. We suggest that an additional superconducting order parameter of p-wave symmetry emerges at high fields and intertwines magnetic order with d-wave superconductivity.
Methods
The neutron diffraction experiments at T = 40 mK and up to μ0H = 11.9 T were carried out on the thermal neutron lifting-counter two-axis spectrometer D23 at the Institut Laue Langevin, Grenoble France. The single crystal (m = 64 mg) was placed in a vertical-field magnet with dilution insert and exposed to an incident neutron wavelength of λ = 1.27 Å. The crystal was oriented either with the vertical axis parallel to [1 \(\bar{1}\) 0] or along [0 1 0]. In the latter setup the tetragonal a-axis was tilted into the basal plane using a non-magnetic piezoelectric sample rotator (type ANGt50 from attocube system AG) inside the dilution refrigerator (see Supplementary Materials of ref.27). The relative field direction was directly measured via the vertical tilt of the structural (2, 0, 0) Bragg peak. The relative angle between the magnetic field direction H and the tetragonal a-axis, [0 1 0], is denoted as ψ.
The solid lines in Figs 1 and 3 represent Gaussian fits to the neutron diffraction data. Magnetic Bragg peaks at (q, q, −0.5) were fitted using a Gaussian line shape on a linear background. The background at (−q, q, 0.5) and ψ ≤ −2° could not be described satisfactorily by a linear behavior solely. We used an additional Gaussian component centered at q = 0.427. The width of the magnetic Bragg peaks in each domain was fixed to the mean value of all corresponding fits.
The integrated intensity at (0.56, 0.44, 0.5) for μ0H = 0, 1, 2, 3 and 4 T and T = 40 mK along H ||[1 \(\bar{1}\) 0] was obtained from scans along (q + h, q, 0.5), where h was chosen such that the scan was centered at (1, 0, 1) - Q2. The integrated intensity at μ0H = 0.5, 1.5, 2.5 and 3.5 T was determined from the background subtracted Bragg peak intensity multiplied with the averaged peak width found in the q-scans. A weighted linear fit to these results yields μ0H d = 3.6(6) T.
References
Monthoux, P., Pines, D. & Lonzarich, G. G. Superconductivity without phonons. Nature 450, 1177–1183 (2007).
Frigeri, P. A., Agterberg, D. F., Koga, A. & Sigrist, M. Superconductivity without Inversion Symmetry: MnSi versus CePt3Si. Phys. Rev. Lett. 92, 097001 (2004).
Fåk, B. et al. Anomalous Spin Response in the Non-Centrosymmetric Metal CePt3Si. J. Phys. Soc. Jpn. 83, 063703 (2014).
Norman, M. R. The Challenge of Unconventional Superconductivity. Science 332, 196–200 (2011).
Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 81, 1551 (2009).
White, B. D., Thompson, J. D. & Maple, M. B. Unconventional superconductivity in heavy-fermion compounds. Physica C 514, 246–278 (2015).
Huxley, A. D. Ferromagnetic superconductors. Physica C 514, 368–377 (2015).
Kenzelmann, M. et al. Coupled Superconducting and Magnetic Order in CeCoIn5. Science 321, 1652 (2008).
Kenzelmann, M. Exotic magnetic states in Pauli-limited superconductors. Rep. Prog. Phys. 80, 034501 (2017).
Fulde, P. & Ferrell, R. A. Superconductivity in Strong Spin-Exchange Field. Phys. Rev. 135, A550 (1964).
Larkin, A. I. & Ovchinnikov, Y. N. Inhomogeneous state of superconductors. Soviet Physics JEPT-USSR 20, 762 (1965).
Psaltakis, G. C. & Fenton, E. C. Superconductivity and spin-density waves: organic superconductors. J. Phys. C: Solid State Phys. 16, 3913–3932 (1983).
Shimahara, H. Coexistence of singlet and triplet at- tractive channels in the pairing interactions mediated by antiferromagnetic fluctuations. J. Phys. Soc. Jpn. 69, 1966–1969 (2000).
Lebed, A. G. Cooper Pairs with Broken Parity and Spin-Rotational Symmetries in d-Wave Superconductors. Phys. Rev. Lett. 96, 037002 (2006).
Aperis, A., Varelogiannis, G., Littlewood, P. B. & Simons, B. D. Coexistence of spin density wave, d-wave singlet and staggered π-triplet superconductivity. J. Phys.: Condens. Matter. 20, 434235 (2008).
Yanase, Y. & Sigrist, M. Antiferromagnetic order and π-triplet pairing in the Fulde-Ferrell-Larkin-Ovchinnikov state. J. Phys. Soc. Jpn. 78, 114715 (2009).
Kato, Y., Batista, C. D. & Vekhter, I. Antiferromagnetic Order in Pauli-Limited Unconventional Superconductors. Phys. Rev. Lett. 107, 096401 (2011).
Hatakeyama, Y. & Ikeda, R. Antiferromagnetic order oriented by Fulde-Ferrell-Larkin-Ovchinnikov superconducting order. Phys. Rev. B 91, 094504 (2015).
Hosoya, K.-I. & Ikeda, R. Possible Triplet Superconducting Order in Magnetic Superconducting Phase induced by Paramagnetic Pair-Breaking. Phys. Rev. B 95, 224513 (2017).
Agterberg, D. F., Sigrist, M. & Tsunetsugu, H. Order Parameter and Vortices in the Superconducting Q phase of CeCoIn5. Phys. Rev. Lett. 102, 207004 (2009).
Suzuki, K. M., Ichioka, M. & Machida, K. Theory of an inherent spin-density-wave instability due to vortices in superconductors with strong Pauli effects. Phys. Rev. B 83, 140503(R) (2011).
Michal, V. P. & Mineev, V. P. Field-induced spin-excitation, condensation in the dx2−y2-wave superconductor CeCoIn5. Phys. Rev. B 84, 052508 (2011).
Mineev, V. P. Antiferromagnetic order in CeCoIn5 oriented by spin-orbital coupling. Low Temp. Phys. 43, 11 (2017).
Kim, D. Y. et al. Switching dynamics of the spin density wave in superconducting CeCoIn5. Phys. Rev. B 95, 241110(R) (2017).
Hu, R., Lee, Y., Hudis, J., Mitrovic, V. F. & Petrovic, C. Composition and field-tuned magnetism and superconductivity in Nd1−xCe x CoIn5. Phys. Rev. B 77, 165129 (2008).
Mazzone, D. G. et al. Field-induced magnetic instability within a superconducting condensate Sci. Adv. 3, e1602055 (2017).
Gerber, S. et al. Switching of magnetic domains reveals evidence for spatially inhomogeneous superconductivity. Nat. Phys. 10, 126–129 (2014).
Kim, D. Y. et al. Intertwined Orders in Heavy-Fermion Superconductor CeCoIn5. Phys. Rev. X 6, 041059 (2016).
Raymond, S. & Lapertot, G. Ising Incommensurate Spin Resonance of CeCoIn5: A Dynamical Precursor of the Q Phase. Phys. Rev. Lett. 115, 037001 (2015).
Stock, C. et al. Magnetic Field Splitting of the Spin Resonance in CeCoIn5. Phys. Rev. Lett. 109, 167207 (2012).
Raymond, S., Kaneko, K., Hiess, A., Steffens, P. & Lapertot, G. Evidence for Three Fluctuation Channels in the Spin Resonance of the Unconventional Superconductor CeCoIn5. Phys. Rev. Lett. 109, 237210 (2012).
Akbari, A. & Thalmeier, P. Field-induced spin exciton doublet splitting in dx2−y2-wave CeMIn5(M = Rh, Ir, Co) heavy-electron superconductors. Phys. Rev. B 86, 134516 (2012).
Mazzone, D. G. et al. Spin Resonance and Magnetic Order in an Unconventional Superconductor. Phys. Rev. Lett. 119, 187002 (2017).
Acknowledgements
We acknowledge the Institut Laue-Langevin for the allocated beam time on D23. We thank P. Fouilloux for technical assistance. Discussions with Duk Young Kim and Roman Movshovich are acknowledged. In addition, we thank the Swiss National Foundation (grant No. 200021_147071, 206021_139082 and 200021_138018). This work was also supported by the Swiss State Secretariat for Education, Research and Innovation (SERI) through a CRG-grant.
Author information
Authors and Affiliations
Contributions
D.G.M., S.R., J.L.G. and M.K. planed and led the project. The experiments were carried out by D.G.M., R.Y., M.B., J.L.G., S.R., E.R., and M.K. The sample was grown by G.L. and the data analyzed by D.G.M. The manuscript was written by D.G.M., S.R., J.L.G. and M.K. with the input of all co-authors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mazzone, D.G., Yadav, R., Bartkowiak, M. et al. Distinct domain switching in Nd0.05Ce0.95CoIn5 at low and high fields. Sci Rep 8, 1295 (2018). https://doi.org/10.1038/s41598-018-19555-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-19555-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.