Introduction

Size based separation and sorting of microparticles and cells improves a variety of biomedical processing steps used in diagnostics and pharmaceutical purification and the study of cell biology1,2,3,4,5. Unfortunately, commercially available size based sorting techniques have disadvantages including being labor intensive, deficient in accuracy, and high in cost6. A variety of microfluidics approaches have been applied to this problem, including field-flow fractionation7,8,9,10,11,12, and active separation methods which utilize forces from external sources such as dielectric, magnetic, acoustic and optical manipulation13,14,15,16,17,18,19,20,21. Additional passive methods use hydrodynamic effects induced by channel geometry and microstructure22,23,24,25, membrane filters (MF)26,27, deterministic lateral displacement devices (DLD)28, and inertial microfluidics22,29,30,31,32,33,34,35. Inertial microfluidics (IM) features high accuracy and high throughputs comparable to MF31,32,33. An advantage of methods such as IM is use of continuous separation without any external control22,24,36. Inertial hydrodynamic methods also utilize non-linear inertial effects in microfluidic channels that provoke cross-stream migration of solid particles. One disadvantage of these methods is that the multiple equilibrium positions of particles in the z-direction37 may lead to inaccurate spatial trajectories during separation. Another problem of inertial sorting is that the size-dependent trajectory differences of particles is relatively small and is comparable to particle size. One approach to increase spatial separation in trajectories is using a combination of inertial particle focusing and cross-stream Dean flows generated by channel curvature29,38,39. This method, however, requires the use of relatively large spiral microchannels that may be difficult to integrate in lab-on-a-chip devices and employ in parallel settings. Alternatively, continuous size separation devices have used periodically arranged diagonal ridges to create helical flow fields, which leverage transverse flow fields to amplify minute inertial effects and alter the particle trajectory in a size-dependent manner40,41,42,43,44,45. The diagonal ridges create a vortex in which the fluid near the bottom of the channel is transported in the negative y direction, whereas the fluid located near top wall, moves in the positive y direction (lateral direction is along y -axis). The cross-sectional flow pattern is illustrated in Fig. 1d. Thus small vertical displacements of particles caused by size differences can be amplified by larger transverse displacements. However an unsolved problem of size-based sorting by transverse flows is that inaccuracies in particle heights at the entrance lead to variations in particle trajectories.

Figure 1
figure 1

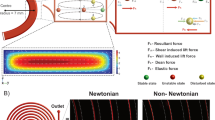
Device Working Principle: (a) Image of the sorting device to control the z-position of the particles as they enter the ridged channel using vertical sheath. H and Hf are the heights of the channel and focused streamline respectively. (b) COMSOL simulations for different sample to sheath flow rate ratio (f). As the vertical sheath flow rate increases the sample flow streamlines are pushed down. (c) COMSOL simulations show the velocity field under the ridge and the lateral deviation of streamlines as they enter the ridged part of channel at different heights. (d) Cross-stream velocity distribution.

Full size image

We demonstrate a novel approach to continuous size-dependent separation of particles that uses a vertical sheath to focus particles to a consistent and optimal position within hydrodynamic flows for enhanced size-dependent enrichment. The separation device consists of a microchannel with periodically arranged diagonal ridges that create helical flow fields. Particles are located to the bottom of the microchannel using vertical focusing, to be then exposed to secondary flows created by diagonal ridges. The incorporation of vertical sheath solves the uncontrolled variation in particle height that leads to variation in transverse flow and thus different trajectory. The height-dependent secondary flows then cause particles with different sizes to migrate transversely with unique trajectories. We use a novel 3D imaging approach46,47 to demonstrate that variability of vertical position affects particle trajectories in a manner detrimental to accurate particle sorting. By incorporating z-axis (vertical direction or channel height is along z-axis) focusing of the sample inlet so as to position all particles to the bottom of the channel, we optimize particle exposure to transverse flow fields for size-dependent sorting. With this key innovation we substantially improve the efficiency and accuracy of size based sorting.

Using the new device we have demonstrated the ability to enrich large particles 8-fold and small particles 35-fold. We demonstrate a form of leukapheresis in which leukocytes are separated from whole blood samples—an essential step to reduce the white blood cell count in treating leukemic patients as well as to retrieve blood stem cells in patient with hematologic malignancies48,49. We demonstrate size based leukapheresis which offers higher or comparable throughput than other cutting edge techniques and with high recovery and no pre or post processing of samples for analysis and isolation.

Results and Discussion

Figure 1a shows the schematic of the vertical focusing device, consisting of a microchannel with diagonal ridges decorating the top of the channel. Four inlets provide sheath focusing of the sample, two for horizontal and two for the vertical directions. The distance between the ridge and bottom wall of the channel is defined as gap size Hg. Particles are considered small if their diameter is less or equal to half the gap size and are considered large if their diameter is greater than half the gap size. By varying the ratio of sample to vertical sheath flow rates, f, streamlines could be focused vertically as shown in in the simulation in Fig. 1b. For these simulations we have assumed point particles and that the particles follow the streamlines. The results indicate that as we decrease f, the focused sample streamlines are positioned to the bottom of the channel. While optimizing the inlet design we examined the critical parameters including the distance between the sample and vertical sheath inlets and their alignment, as the former can increase the negative pressure from the vertical sheath to sample inlet and convolute the particles within the inlet sample flow. The accurate alignment of the sample and vertical sheath inlets ensures no particle can escape the vertical sheath focusing due to inlet misalignment. Figure 1c shows the simulated streamlines at different heights in the device. The diagonal ridges within the channel create helical flow fields and particles at different vertical heights result in different transverse displacements. Figure 1d shows the cross-stream velocity distribution in a channel with ridged walls (see Methods). The velocity is averaged over one period of the wall structure. The arrows show the direction of fluid velocity, whereas the color represents the normalized magnitude of lateral fluid velocity. Note that the diagonal ridges create circulatory flows that transport fluid to the positive y direction in the channel mid plane and near top wall and to the negative y direction close to the bottom wall. Supplementary Fig. S1 which is generated using COMSOL (see Methods) further shows a single velocity slice and direction of flow under and outside the ridge. In the absence of vertical focusing of the particles, differences in particle positioning exposes each particle to different secondary flows. Additionally, the height-dependent secondary flows also cause particles with different sizes to migrate transversely with unique trajectories43. Our simulation results in Fig. 2a and b and experimental data in Fig. 2c,d reveal that microparticles with different sizes separate laterally as they flow in the ridged microchannel, using the separation device with 8 µm gap size to pairwise study the behavior of 7 µm and 4 µm particles42,46,47. We demonstrate that there exists a z-position dependent phenomenon which leads to dispersity of smaller particle trajectories. As shown in Fig. 2c, the smaller particles (4 µm in diameter) entering the ridged part of the channel arrive at different vertical positions as determined from out-of-focus images acquired at a constant focal plane. Hence smaller particles at different z-positions, as indicated by different color markers (red for 2 µm, blue for 4 µm, and green for 5 µm heights) move in either positive or negative y-direction trajectories. In contrast, Fig. 2d shows that the larger particles (7 µm diameter) entering the ridged part of the channel uniformly remain in focus at same vertical height and move in the positive y-direction. The histogram of large particle heights in Fig. 2d shows that unlike the smaller 4 µm size particles, most of the larger 7 µm particles enter the ridged channel at same height due to steric hindrance of the ridged features. Figure 2e shows the plot between the Δy/ridge (lateral displacement per ridge) and the diameter of bright diffraction ring, a surrogate for the height of the particle inside the channel using calibrated images of particles at different heights to determine the z position46,47. That particles of different heights move with different transverse trajectories results from the vortex flow fields created by the diagonal ridge, such that the fluid at the channel center is transported in the positive y direction, whereas the fluid located near the vertical channel walls moves in the negative y direction as shown by computational fluid dynamics simulations43. The particles at different z-positions not only move in different directions but also with different speeds (Fig. 2e), as is expected from the simulated height-dependent velocity gradient43. This effect is harnessed to create the separation among particles with different z positions. Supplementary videos S1 and S2 show particles (4 µm) entering the ridged channel at different heights and move in opposite lateral directions.

Figure 2
figure 2

Demonstration of height dependency of lateral positions of particles in a ridged channel: (a and b) Simulated trajectories showing particles released at different height in a ridged channel will follow different lateral streamlines. (c) Experimental trajectories of small particles at different heights. The scale on left shows the reference images of 4 µm particles at different heights inside the channel. The trajectories on the right shows the 4 µm particles at different height which is determined by comparing it to the reference scale on left. (d) Experimental trajectories of large particles at different heights. The reference scale for 7 µm particles is shown on left and the trajectory of 7 µm at 4 µm heights on right. The histogram on top right shows that most of 7 µm particles are at a height range of 4 to5.5 µm inside the microchannel. (e) Left figure shows Δy/ridge of 4 µm particles at different height in Fig. 2c and right shows their velocity inside the channel.

Full size image

The goal of the vertical sheath is to position all small particles in the channel to the same z position such that they follow the same trajectory. To mathematically and experimentally determine the height of smaller particles (4 µm) entering the ridged part of the channel after vertical sheath focus, we use theoretical model for predicting the height of two-dimensional hydrodynamically focused streams in rectangular microchannels (details can be found in Supplementary Fig. S2) and video microscopy to examine the vertical position of particles. For video microscopy, still-frame images of particles are cropped from the videos recorded at different sample to vertical sheath rates of f = 0.9, 0.8, and 0.7. Figure 3a describes the procedure we used to estimate the z position of particle inside the channel. Each particle in the channel is compared to two reference images for the cross correlation analysis at a vertical focal plane of 5 µm and 2 µm. The templates at different f are shown in Fig. 3b. The particles with square boxes in calculated cross correlation template in Fig. 3a show that they are at different z-position as compare to the z position of the reference image. The cross correlation coefficient calculated from the algorithm in Fig. 3a is plotted in Fig. 3c,d. As the flow rate of vertical sheath is increased, the particles are positioned more narrowly to the 2 µm z-position, validating the focusing procedure. This result suggests increase in the enrichment of large particles with increased flow rate of vertical sheath results as more small particles confined to bottom of the channel move in opposite y-direction compared to large particles. Supplementary videos S3 and S4 show the 2 µm particles entering the ridged part of the channel without and with vertical sheath respectively. In case of with vertical sheath, particles are more focused at single z position as all have same diffraction ring pattern.

Figure 3
figure 3

Experimental determination of particle height: (a) Algorithm showing how height of particles is estimated using cross correlation with a reference image at a known height. (b) Templates showing the particles entering the ridged part of the channel at different vertical sheath flow rates. (c) Cross correlation data estimating the height of the particles at different vertical sheath flow rates by comparing the templates in Fig. 3b with reference image at height 5 µm and (d) 2 µm.

Full size image

For this study we have optimized our device design for channel width and inclination angle of ridges for a given channel length for pairwise sorting of 2 µm and 7 µm particles. Enrichment suffers due to a reversal of particle trajectories that occurs once particles reach the channel walls in an unoptimized design, as shown in Supplementary Fig. S3. This effect is due to the circulating velocity vortex formed by diagonal ridges inside the channel, which can be solved by reducing the channel length to avoid the reversal of particle translation due to circulating flow at the edges of the channel for a given width. To study the optimal width, we tested channel widths of 560 and 317 µm with standard 20 µm ridge width and the distance between the two consecutive ridges is 180 µm and ridge inclination angle of 45 degree. For inclination angle study, 45 degree and 30 degree angles of ridges were tested with the 560 µm channel width. Figure 4a shows the enrichment factor (the enrichment factor is defined as the ratio of targeted to non-targeted particles at outlet and inlet) of small and large particles at f = 0.5. The smaller width channel device has significantly lower enrichment as compare to 560 µm channel width device. Increased enrichment with channel width can be related to more prominent circulation flows that develop in wider microchannel increasing the relative size based lateral displacement. This can also be seen in experimental data in Fig. 4b and can also be confirmed from simulated trajectories in Fig. 4c. Due to smaller difference in lateral velocity there is not much separation between 2 µm and 7 µm particle trajectories which led to the decrease in relative depth difference between two sized particles as they move along the channel, hence decreasing the efficiency of the device. Reynolds number for a microchannel is given by Re = u ρH/µ, where µ is the fluid viscosity, ρ is the density, H is the height of channel and u is the average velocity. Reynolds numbers for 560 and 317 µm channel widths are 5.3 and 9.6 and channel average velocities are 0.216 m/s and 0.383 m/s, respectively. The enrichment factors for different inclination angles show that 30 degree device has significantly high enrichment and almost 100% purity for small particles. This high purity can be explained by examination of the experimental trajectories. Small and large particles experience opposing velocity fields, as seen in Fig. 2e, at same y position inside the channel in case of 30 degree device and hence are separated quickly with relatively high resolution.

Figure 4
figure 4

Device geometry optimization: Small and large particle enrichment factors for (a) width optimization (top) and angle optimization (bottom). Enrichment factor is the ratio of (targeted particles/non-targeted particles at outlet) to (targeted particles/non-targeted particles at inlet).Error bars represent standard deviation from repeated experiments. Each experiment is repeated 5 times. (b) Shows the experimental and (c) simulated particle trajectories for different combinations of channel widths and ridge angles.

Full size image

We have also optimized the vertical sheath flow rate ratio for best sorting efficiency. The estimated height of small particles was calculated using the model described in Supplementary Fig. S2 for different flow rate ratios. The device design used was 560 µm in width and 45 degree inclination angle. The gap size was 8 µm. Figure 5a shows the enrichment of small (117.8) and large (19.5) particles was highest at f = 0.5.

Figure 5
figure 5

Device flow rate optimization and sorting resolution study: Small and large particle enrichment factors for (a) Different flow rates with and without vertical sheath study. The gap size for these studies was 8 µm and the particles were 7 µm and 2 µm. (b) Sorting particles with different size differences to evaluate sorting resolution. The gap size is 10.5 µm and the particle sizes are 9.94 µm and 7 µm with f equal to 5/9. Error bars represent standard deviation from repeated experiments. Each experiment is repeated 5 times.

Full size image

Figure 5a also shows the improvement of sorting enrichment with and without vertical sheath for 8 µm gap size, 560 µm width and 45 degree inclination angle. Small particles are enriched to 117.8 fold from 3.4 with purity of 99.9% and large particles are enriched to 19.5 fold from 2.5 with purity of 70% after incorporating vertical sheath focusing. The purity of large particles in the large particle outlet is less as compared to >99% purity of small particle at small particle outlet that decrease the enrichment of large particles. It is because large particles show decreased transverse displacement per unit length due to their exposure to a velocity field with a small net magnitude compare to vertically focused small particles.

The resolution of sorting was also studied using a 10.5 µm gap size device with 560 µm width and 45 degree ridge inclination angle. Particles of diameter 9.94 µm and 7 µm were sorted with an enrichment of 23 and purity of 90% for large particles and 2.4 and 99% for small particles as shown in Fig. 5b. The throughput of the device with a single channel was 2.8 × 106 particles per minute which is superior as compared to many recent microfluidic studies (Supplementary Table S1).

Depletion of White Blood Cells (WBCs) Leukapheresis

The design used for this application has a gap size of 10.5 µm with channel width of 560 µm and ridge inclination angle of 30 degrees. A 10.5 µm gap size was selected as red blood cells and platelets are in the range of 2–8 µm and white blood cells are greater than 8 µm. Hence, WBCs are sorted and collected at the top outlet. The throughput is calculated for the blood sample (including RBCs, WBCs and platelets). The WBCs were removed at a depletion of 87 fold and at a high throughput of 0.1 × 108 cells per minute with recovery of 73% as shown in Fig. 6. Cells were analyzed with and without microfluidic processing as shown in Supplementary Fig. 4. No RBC lysing was observed as cells collected after microfluidic processing were intact. Peak wall shear stress for the device was calculated (see Methods) and was 230 Pa. A maximum threshold shear stress value of RBCs is reported to be 450 Pa50,51, thereby confirming that the shear stress is not expected to cause hemolysis.

Figure 6
figure 6

Leukapheresis: (a) Enrichment factors for WBCs (top) and platelets and RBCs (middle) and recovery rate of WBCs (bottom). Recovery rate is defined as the % of WBCs at targeted outlet to total number of WBCs collected. (b) Flow cytometer characterization of WBC sorting. Error bars represent standard deviation from repeated experiments. Sorting experiments were repeated 5 times.

Full size image

These results suggest that a microfluidic approach can be developed for leukapheresis with high depletion and recovery rate of WBCs with ease of batch fabrication and low cost, especially if parallelization scaled the throughput and any toxicity of PDMS is addressed. Removal of leukocytes before performing a blood transfusion minimizes transmission of cell-associated infectious agents (cytomegalovirus, herpes virus, human T-cell lymphoma virus), graft rejection rates and prevents febrile transfusion reactions52. Conventional macroscale WBCs sorting techniques include centrifugation, apheresis, chemical lysis, and antibody based techniques including fluorescence-activated cell sorting (FACS) and magnetic-activated cell sorting (MACS)53,54,55,56,57,58,59,60 all face drawbacks. Centrifugation is commercially available, easy to conduct and viability of fractionated blood cells is very high but it does not allow for high separation resolution, is an open process exposed to contamination, and requires milliliters of blood for analysis and dedicated labs and trained users are pre -requisites. Microscale flow-based protocols such as FACS or solid-state immobilization and capture of cells using MACS offers advantages like high specificity, high-throughput, commercial availability but are expensive and cannot reliably handle small numbers of cells. Our device operates simply with a small foot print, label-free, and offers a clog-free and self-cleaning platform61 with high throughput and high purity and enrichment. Comparison with other cutting edge technologies can be found in Supplementary Tables S1 and S2. The proposed z-focusing approach may be extended to separate nanoparticles by using smaller gap size and using an optimized vertical flow rate ratio. Due to its small dimensions, the proposed device can easily be implemented with parallel channels32 to increase throughput.

Conclusions

We have described a novel microfluidic device capable of improved purity of size-dependent separation of particles by positioning particles at the optimal position in three-dimensional space to exaggerate the size-dependent trajectory differences. The unique aspect of this sorting design is the use of three-dimensional focusing of the sample to a position that optimizes the differential secondary flows. Using vertical focusing, we are able to separate 2 µm particles from 7 µm with a substantial improvement in enrichment of sorted number density in comparison to unfocused flow. We demonstrate 8-fold increase of the purity of the larger particles (from 2.5 to 19.5–fold enrichment factor) and a 35–fold increase in the purity of smaller particles (from 3.4–fold to 117.8–fold). This is the first time that a device with 3D focusing has been reported to improve the purity of samples using size sorting. The proposed technology can further be improved for higher purity enrichment of particles by modifying channel geometry and gap size43. It can also be integrated with separation techniques using different biomarkers like stiffness and viscoelastic deformation44,61.

Methods

Experimental section

Microfluidic Device Fabrication

The microfluidic devices with different gap size were fabricated by replica molding Polydimethylsiloxane (PDMS) (Sylgard 184 Dow Corning Corp) on a permanent mold. The mold is made from SU-8 2007 using a two mask photolithography process. The mold dimensions were characterized with profilometry (Dektak 150 profiler) and verified with confocal microscopy imaging (Olympus LEXT). Uncured PDMS was mixed in a 10:1 ratio of elastomer to curing agent, then poured onto the SU-8 molds to a thickness of 1 cm and cured in an oven at 60 °C for 6 hours. The cured PDMS layer was cut and peeled off the mold and inlet and outlet holes were formed with a 1 mm biopsy punch. The PDMS device was treated with oxygen plasma (Harrick plasma cleaner PDS 32G) for 2 minutes then bonded to a glass microscope slide. The separation device consists of a microchannel with periodically arranged diagonal ridges. We designed devices with two sets of dimensions: 5.5 mm channel length and 560 µm channel width and 25 ridges and 2.5 mm channel length and 317 µm channel width and 11 ridges. All devices have 22 µm channel height. The ridges are 20 µm wide and distance between two consecutive ridges is 180 µm. The ridges are at the top of the microchannel and are inclined at either a 30 or 45 degrees.

Sample Preparation

Spherical polystyrene particles of 2.19, 4, 7.06 and 9.94 µm diameters (Bangs Laboratories Inc.) were used in the flow experiments. Dispersions were prepared in phosphate buffered saline (PBS) solution with a concentration of approximately 2 × 104 particles/µL. To prevent bead adhesion, 0.01% v/v Tween 20 was added to flow media. For white blood cell separation, discarded fresh human blood was withdrawn from healthy donors using protocols approved by the Georgia Institute of Technology Institute Review Board43. Blood samples were collected in citrate coated vials and used immediately after collection. The blood sample was diluted 1:10 in PBS before separation experiments.

Experimental Setup

Syringe pumps (PHD 2000 Harvard Apparatus) were used to control the flow rates of the sample and sheath flows for the experiment. Dispersed particles were contained in a plastic syringe and infused into the microfluidic device through polyethylene tubes. The particle flow within the microfluidic device was observed with an inverted microscope (Nikon Eclipse Ti) and the videos were recorded using a high-speed camera (Phantom v7.3 Vision Research). Both x-y positions of particles were collected as well as the vertical position of the particles using an out-of-focus tracking algorithm developed previously47. This algorithm matches each particle image to a reference library of identical particles imaged at various degrees of defocus in order to determine the vertical position of the particle. In order to accurately capture the cell trajectories with sufficient accuracy to determine the vertical position, we operated the high speed camera at a minimum of 3000 frames per second with a minimum resolution of 640 by 480 pixels for all videos and images. Separated particles and cells were collected at the outlets and were analyzed with an Accuri C6 flow cytometer (BD Biosciences). Purity of leukocytes is determined using the antibody cocktail - anti CD45 -APC anti CD61-PE, and anti CD235a-FITC (GlycophorinA) from Biolegend, following manufacturer’s protocols.

Finite Element Simulation

Finite element simulations were performed using COMSOL Multiphysics software (COMSOL Inc., Burlington, MA). Simulations were performed for channel widths of 317 and 560 µm and ridge inclination angles of 30 and 45 degrees. PDMS was selected as material of interfacing structure. Sample to vertical sheath flow rates ratios of 0.22, 0.71 and 2.3 were used in the simulation to determine their effect on sample vertical confinement. The flow profiles in the channel were obtained by solving the Navier-Stokes equations for incompressible fluid using Fluid-Structure Interaction physics. At the outlet, the pressure was set to zero with no viscous stress on the boundary. Due to low Reynolds’s number of fluid, it was assumed that the suspended particles would follow the fluid streamlines.

Three-dimensional computational fluid dynamic simulations were performed to obtain cross-stream velocity distribution in the channel. A pressure-driven flow in a periodic microfluidic channel of height H and width W was considered.The top channel walls were lined with symmetrical solid ridges. In current implementation, the channel was periodic in the x direction. A constant pressure gradient is imposed in the negative x direction via a uniform body force to create a Poiseuille flow in the channel. The velocity is averaged over one period of the wall structure.

Wall Shear Stress Calculation

The maximum wall shear stress inside the channel is estimated (assuming Poiseuille flow) using relation τ = 6 μQ/WHg 2, where τ is the wall shear stress, W and Hg are channel width and gap size respectively and µ is viscosity of the buffer62.