Abstract
Understanding the spatial distribution of tree species in subtropical evergreen-deciduous broadleaf karst forest is fundamental to studying species coexistence and karst species diversity. Here, complete spatial randomness and heterogeneous Poisson process models were used to analyze the spatial distribution patterns of 146 species with at least one individual per ha in a 25-ha plot in southwest China. We used canonical correspondence analysis (CCA) and the torus-translation test (TTT) to explain the distributions of observed species. Our results show that an aggregated distribution was the dominant pattern in Mulun karst forests; the percentage and intensity of aggregated decreased with increasing spatial scale, abundance, mean diameter at breast height (DBH), and maximum DBH. Rare species were more aggregated than intermediately abundant and abundant species. However, functional traits (e.g., growth form and phenological guild) had no significant effects on the distributions of species. The CCA revealed that the four analyzed topographic variables (elevation, slope, aspect, and convexity) had significant influences on species distributions. The TTT showed that not all species have habitat preferences and that 68.5% (100 out of 146 species) show a strongly positive or negative association with at least one habitat. Most species were inclined to grow on slopes and hilltops.
Similar content being viewed by others
Introduction
The spatial distributions of tree species in forests and their influencing mechanisms have always been a hot topic in research, as such information can help us to understand the potential ecological processes that control species coexistence and community structure1,2. Tree species can be distributed in an aggregated, a random, or a regular pattern, with aggregated distributions being widespread in natural forests, particularly tropical forsts1,3,4,5. Over the past few decades, a number of mechanisms have been found to contribute to species aggregation in forests, including niche segregation6, habitat heterogeneity7, dispersal limitation8, intra- and inter-species competition9, and negative density dependence10.
Habitat heterogeneity and dispersal limitation are among the most influential ecological processes. Recently, numerous studies have demonstrated that many species are limited to a range of habitats11. Worldwide, research in forest plots has shown that habitat factors and microhabitat heterogeneity (e.g., topographical factors, rock outcrops, and soil heterogeneity) play vital roles in the spatial patterns of tree species7,12,13, and some studies have shown that many species have a significantly positive or negative relationship with slope, elevation, or aspect7,14,15. Furthermore, spatial distribution can also be affected by differences in functional traits (e.g., growth form, shade tolerance, and seed dispersal limitation) and ecological strategies16,17,18,19. For example, the mode of seed dispersal affects the spatial distribution of trees, with species dispersed by animals being less aggregated than those dispersed by wind or gravity3,4. Moreover, species’ attributes also influence spatial patterns. For example, trees with larger trunk diameters are less aggregated3,4, indicating self-thinning. Therefore, the distribution patterns of tree species are controlled by multiple factors in the forest ecosystem.
The current knowledge regarding spatial distributions and their underlying mechanisms in species-rich communities has mostly been derived from tropical20,21,22 and subtropical4,11 forests. Similar studies on the species spatial distributions of species and species-habitat associations in other specific forest types (e.g., karst forest) are insufficient due to a lack of large forest plots. The karst landscape is mainly found in Eastern Europe, the European Mediterranean, North America, and southwest China, the latter of which has the largest and widest karst area in the world23. Mixed evergreen-deciduous broadleaf forest is unique and representative of the karst landscape in southwest China. This forest type has a complicated community structure, rich biodiversity, and high habitat heterogeneity23,24,25,26, making it an ideal community in which to study spatial patterns. However, our current understanding of spatial patterns in karst forests has mainly been derived from studies conducted at small scales ( ≤ 1 ha). Consequently, the community-wide patterns of the spatial distributions of species and species-habitat associations and the underlying mechanisms of species coexistence are not well understood in karst forests5.
The last undisturbed remnants of karst forest in China (and possibly around the world) are mainly located in Mulun National Natural Reserve and Maolan National Natural Reserve in Guangxi and Guizhou province. Mixed evergreen-deciduous broadleaf forest is a typical subtropical forest in the karst region of southwest China. According to the census measure for the Barro Colorado Island (BCI) plot in Panama, a 25 ha dynamic forest plot was established and surveyed in Mulun in 2014. The Mulun plot is a component of the Chinese Forest Biodiversity Monitoring Network (CForBio) and is also the largest forest plot in the karst region. The main objectives of this study were to (1) analyze the spatial distribution patterns of tree species at different scales in the 25 ha plot using the complete spatial randomness (CSR) null model and homogeneous Poisson process (HPP) null model, (2) examine whether species attributes (e.g., species abundance, diameter at breast height (DBH) class, growth form, etc.) are related to their spatial distribution patterns, and (3) examine species-habitat associations in different habitat types. This study will contribute to our understanding of species coexistence and diversity in subtropical karst forests.
Results
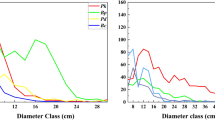
All species were aggregated at small scales, some even up to 50 m, and no species showed regular patterns under the CSR null model, with two exceptions: Loropetalum chinense, which showed a regular pattern at from 45 to 48 m, and Clerodendrum japonicum, which showed a regular pattern at from 44 to 48 m (See Appendix Table S1 for details and Fig. 1). The percentage of aggregated species decreased with an increase in the spatial scale: 146 species (100%) were aggregated at a scale of 6 to 11 m, 145 species (99.3%) were aggregated at 0 to 19 m, 139 species (95.2%) were aggregated at 36 m, and 126 species (86.3%) were aggregated at 50 m (Fig. 1). In contrast, the percentage of species occurring randomly increased at scales of 12 to 50 m. Additionally, the species showed different aggregation intensities, with the four dominant species being suited to different habitats (Fig. 2). Cryptocarya microcarpa was aggregated in depressions, Platycarya longipes on hilltops, and Brassaiopsis glomerulata on slopes.
Four examples of species distributions in the Mulun plot. Left panels show corresponding distribution patterns. Middle and right panels show the relationship between the univariate pair-correlation function (g(r)) and scale for the four species. The lines represent g(r); the gray areas indicate the simulation envelopes generated from 999 Monte Carlo simulations under the null hypothesis of complete spatial randomness (CSR, the middle panels) and heterogeneous Poisson process (HPP, the right panels). The figures were created using R 3.3.2 software31 (https://www.r-project.org/).
To obtain a rough estimate of the magnitude of the large-scale effects of habitat heterogeneity on local tree density, all species distributions were examined and contrasted with the HPP null model. More than 45.9% of the species showed random patterns at 50 m, fewer than 23.5% of the species showed aggregated patterns at 50 m, and five species (3.4%) showed significant regularity at all scales (0 to 50 m). The percentages of aggregated and randomly occurring species decreased with increasing scale, whereas the percentage of regularly occurring species increased with scale (Fig. 1).
Based on the CSR null model, aggregation intensity showed a negative relationship with species abundance, mean DBH, and maximum DBH, i.e., the aggregation intensity declined with these factors (Fig. 3). There was a clear trend that aggregation intensity declined with species abundance (Spearman’s rho = −0.580, p < 0.01): rare species (<4 individuals/ha, n = 43, mean = 33.16, SE = 4.3) were more aggregated than intermediate (4–40 individuals/ha, n = 78, mean = 18.5, SE = 2.48) and abundant species ( ≥ 40 individuals/ha, n = 24, mean = 7.6, SE = 1.06). The results of the Kruskal-Wallis test show that the aggregation intensity of rare species was significantly different from that of intermediate and abundant species (Kruskal-Wallis χ2 = 39.913, p < 0.001).
The average aggregation intensity of (g0-10) of canopy species (n = 26, mean = 8.07, SE = 5.47) was lower than that of midstory species (n = 64, mean = 20.42, SE = 2.97) and understory species (n = 55, mean = 23.23, SE = 3.00) for the CSR null model. However, there were no significant differences among the three growth forms (ANOVA; F = 0.473, p = 0.624).
The mean g0-10 of evergreen species (n = 95, mean = 24.6, SE = 2.7) was higher than that of deciduous species (n = 50, mean = 14.2, SE = 2.1) for the CSR null model. However, the aggregation intensities of deciduous and evergreen species were not significantly different (W = 3,145, p = 0.999) based on the CSR null model. The average g0-10 of endemic species (n = 18, mean = 22.1, SE = 4.2) was higher than that of non-endemic species (n = 127, mean = 20.8, SE = 2.2) for the CSR null model. However, the aggregation intensities of endemic species and non-endemic species were not significantly different (t = 0.266, p = 0.792) based on the CSR null model.
Our results show that four selected topographic factors significantly affect the species distributions, with the four factors explaining 17.29% of the variation in tree species distributions (Table 1). The spatial distributions of the tree species were significantly negatively correlated to these topographic factors on the first axis and significantly positively correlated to slope and aspect but not elevation and convexity on the second axis (Fig. 4).
Different species were suited to different habitat types (Fig. 5). Based on the torus-translation tests (TTT), 95 (65.06%), 110 (75.34%), 31 (21.23%), and 14 (9.59%) out of 146 species were significantly positively associated with hilltops, steep slopes, gentle slopes, and depressions, respectively, while 46 (31.51%), 36 (24.66%), 103 (70.55%), and 86 (58.90%) species were significantly negatively associated with these habitat types.
Discussion
An aggregated distribution was the main spatial pattern in natural forests, while only a few species were randomly distributed, and few species showed a regular distribution2,3,4,27,28,29,30. Aggregation was also the main distribution pattern among dominant species in this study. Among 146 species (with at least one individual/ha), 145 (approximately 99.3%) were aggregated at scales of from 0 to 19 m. Compared with other studies, the intensity of aggregation in the Mulun plot was higher than that in temperate forests and similar to that in subtropical and tropical forests. For example, approximately 99.2% of species were aggregated at scales of from 0 to 10 m in six tropical forest plots3, 99.3% and 98% of species were aggregated in two subtropical forests4,28, and 90.5% of species were aggregated in a temperate forest31. The percentage of aggregated species and the intensity of aggregation species declined with an increase in spatial scale. Similar results were also found in subtropical28 and temperate forests27. These phenomena fully confirm the existence of scale separation.
To test the effects of habitat heterogeneity, we used HPP as the null model. Based on the HPP model, only seven of the 146 species were aggregated at all scales from 0 to 50 m, while five species were regularly distributed at these scales. After eliminating topographic factors (elevation, slop, convexity, and aspect), fewer than 23.5% species were aggregated, and random was the most common distribution pattern. In comparison to other studies, the percentage of species showing an aggregated pattern at scales of from 0 to 10 m (17.81%) in this study was lower than that observed in tropical karst seasonal rainforest (28.85%)32 and far lower than that recorded in a subtropical mixed evergreen-deciduous broadleaf forest in a non-karst region (58%)28. The considerable habitat heterogeneity in karst regions is perhaps the main factor driving species distributions. Therefore, habitat heterogeneity is an important mechanism regulating species aggregation patterns based on the results of the CSR and HPP null models.
Numerous factors play a vital role in determining the spatial patterns of trees in a plant community. Such spatial patterns could arise from many biotic and abiotic processes, such as regeneration, habitat heterogeneity, dispersal limitation, and disturbance3,33,34. Our study showed that species abundance, DBH, growth form, and phenological guild were important factors affecting the spatial patterns of trees in a subtropical karst forest. We analyzed the relationships between species’ attributes (abundance, mean DBH, and maximum DBH) and aggregation intensity for the 145 species aggregated at scales of from 0 to 10 m based on the CSR null model. This analysis indicated that rare species were more aggregated than intermediate and abundant species, a result that is consistent with those from other studies2,3,4,5,27,28. However, not all species showed a similar trend: the rare species Toona sinensis and Choerospondias axillaris, with 74 and 47 individuals, respectively, had relatively low g0-10 values of 7.12 and 7.95, respectively, while the abundant species Tirpitzia ovoidea had a relatively high g0-10 value of 24.61 with 1,299 individuals. One of the most important reasons for such patterns is that the spatial distributions of some species can arise from strong habitat preferences23. Thus, species distribution patterns are species-specific and may occur as a result of a variety of biological and ecological processes, such as stochastic recruitment, clonality, competition, patchy habitat heterogeneity, disturbance, and other stochastic events32,35,36. Our results show that the aggregation intensity g0-10 decreased with increasing DBH due to self-thinning or density-dependent mortality30, which is consistent with previous studies2,28. Water and soil were the limiting resources in karst forest26, and adjacent trees are likely to compete with one another for these limiting resources. Furthermore, larger trees competitively inhibit conspecifics over a larger area of influence than smaller trees5. Thus, small-sized trees were more clumped than larger trees.
Tree height is important for seed dispersal because the distance traveled by seeds is a function of the height of reproductive structures. The higher the stature, the longer and more variable the dispersal distance37. Previous studies have shown that understory species usually have more aggregated patterns than canopy species due to inefficient seed dispersal27. We also found that understory species were the most aggregated species in the Mulun plot, followed by midstory and canopy species, but there were no significant differences among these growth forms. Furthermore, evergreen species were more aggregated than deciduous species in our study, which is consistent with other studies28,32, but the distributions of deciduous and evergreen species were not significantly different. This discrepancy between this and other studies might be related to high habitat heterogeneity and the unique geology of the karst region, which may form strong associations between species habitats and their distributions.
The canonical correspondence analysis (CCA) results show that the spatial distributions of species in Mulun plot can be significantly explained by four topographic factors (elevation, slop, convexity, and aspect). The combination of these factors explained 17.29% of the species distributions; however, edaphic or other environmental factors can also play an important role in governing species distributions7. Furthermore, the TTT results show that not all species have habitat preferences, which is consistent with other studies2,7,14,38. Approximately 68.5% (100 out of 146) species showed strongly positive or negative associations with at least one habitat, demonstrating that habitat heterogeneity plays a vital role in regulating the spatial distributions of species in subtropical karst forest.
Our results show that over 134 species in the Mulun plot have a distinctly positive or negative correlation with hilltops (141 species), steep slopes (146 species), and gentle slope (134 species), while only 100 species were significantly positively or negatively associated with depressions. Moreover, we also found that greater numbers of species were positively associated with hilltops (67.4%) and steep slopes (75.3%) and negatively associated with gentle slopes (76.8%) and depressions (86.0%). These results indicate that most species were inclined to grow on slopes and hilltops; similar results have been found in tropical karst seasonal rain forest39 due to the high light and temperatures at higher elevations. The ecological conditions of different habitat types, along with topographic factors of the terrain, may influence species distribution patterns through the redistribution of light, temperature, soil moisture, and nutrients2. At our study site, complex terrain conditions may lead to habitat specialization, and each species has its preferred habitat. For example, Platycarya longipes establishes more successfully on hilltops. Therefore, habitat partitioning caused by topography may be a major mechanism allowing the coexistence of trees in the Mulun plot. Our results provide evidence that species attributes and habitat heterogeneity jointly contribute to the regulation of their spatial distributions in subtropical evergreen deciduous broadleaf karst forest in southwest China.
Methods
Study site
The study was conducted at the Mulun National Reserve (Mulun Reserve) (107°54′01″-108°05′51″E, 25°07′01″-25°12′22″N), in Huanjiang county, northwestern China’ Guangxi Province. Mulun Reserve was established in 1991 to protect the subtropical mixed evergreen–deciduous broadleaf forest ecosystem that has developed on the limestone substrate. In this 10, 800 ha reserve, the topography is characterized by steep hills separated by lowland depressions with numerous potholes and caves and extensive underground streams. This area has a subtropical climate with an average annual temperature of 19.38 °C and average annual precipitation of 1,500 mm, occurring mainly from April to August. The mean annual frost-free period lasts 310 days, and the mean annual relative humidity is 79%.
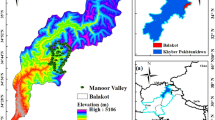
A 25 ha (500 m × 500 m) plot (25°8′N, 108°0′E) was established in Mulun Reserve in April 2014, with the first census completed in December 2014 following the standard field protocol of the CTFS (Center for Tropic Forest Sciences, http://www.ctfs.si.edu). The plot is characterized by rugged terrain (Fig. 6): the altitude varies from 442.6 m to 651.4 m, and the slope ranges from 0.12° to 66.97°, with a mean of 31.4°. The average rock exposure ratio is greater than 60%.
Contour map of the 25 ha Mulun forest plot. The numbers in the map represent elevation (m). The map was created using R3.3.2 software31 (https://www.r-project.org/).
Data collection
The plot was divided into a grid composed of 625 20 × 20 m cells, and all woody stems with a DBH ≥ 1 cm were identified, tagged, measured, and mapped following standard field procedures40. According to the first census, the plot had 144,552 individuals belonging to 51 families, 127 genera, and 228 species. Important species included Cryptocarya microcarpa, Itoa orientalis, Platycarya longipes, and Lindera communis. Species abundances varied to a great extent, from 1 to 31,486 individuals. To obtain a sufficient sample size for point pattern analyses, we chose 146 common species with no fewer than 25 individuals28.
Data analyses
Spatial point pattern analysis
Spatial point pattern analyses have been widely used to analyze the spatial patterns of tree distribution2. In this paper, we used g(r) to study the spatial distributions of the study species on a 0 to 50 m scale28,41 and mean g0-10 as a measure of the mean conspecific aggregation density within 10 m of a tree3. The g function is derived from Ripley’s K function, which is the probability density of the K function. It is a non-cumulative distribution function and presents the expected density of trees in a circular ring of a given distance r around a focal tree, divided by the intensity of the pattern37.
We used CSR and HPP as null models. The former null model is widely used for univariate point patterns; it assumes no interactions between points and indicates that trees can occur at any position without the influence of biological processes42. The latter is used to investigate the significant second-order effects of the spatial distribution of tree species. It can predict the probability of occurrence of a tree of a given species in space, as a function of environmental covariates. In this study, four topographic variables represented the environmental covariates in each 10 × 10 m quadrat: elevation, slope, aspect, and convexity28. Elevation was the mean elevation of the corners of the quadrat; slope was the true value obtained through measurement at the central points in each subplot; aspect was the compass direction to which the slope faced; and convexity was the difference between the mean elevation of a focal quadrat and the average elevation of the eight surrounding quadrats7,38. The significance of departure from a null model was tested using 999 random Monte Carlo simulations in the “spatstat” package43 in R. If the observed value fell outside the 5th and 95th quartiles, the null model could not be rejected and the species is considered to be aggregated.
We used the mean g0-10 to compare the distribution patterns of different growth forms, phenological guilds (evergreen species and deciduous species), and endemic and non-endemic species and then used the Kruskal-Wallis or Wilcoxon rank sum test to test the significance. The observed species were divided into three growth forms according to their mean DBH28: understory species (<4 cm DBH; 55 species), midstory species (≥4 and <8 cm DBH; 64 species), and canopy species (≥8 cm DBH; 26 species). Additionally, we divided the abundance into three levels: abundant (with abundance ≥ 40 individuals/ha), intermediate (4–40 individuals/ha), and rare (<4 individuals/ha).
Analyses of topographic factors and habitat preference
The elevation, slope, aspect, and convexity of each 20 × 20 m grid were selected as topographic variables for use in a species-habitat association analysis2. We used a multivariate regression tree technique to divide the 625 cells into four habitat types: hilltop, steep slope, gentle slope, and depression (Fig. 7) using package “rpart” in R39.
We performed a CCA to analyze the relationship between topography and the spatial distribution of woody plants and employed a Monte Carlo permutation test to evaluate the significance of these relationships using the “vegan” package in R. Each topographic variable was tested at the 5% significance level using 1,000 random permutations. Due to the autocorrelation among species distributions, we used the TTT method to analyze the relationship between species and habitat7. Detailed descriptions of the TTT can be found in Harms et al.7.
All analyses were performed using R3.3.231 (R Development Core Team) and Microsoft Excel 2013.
References
Hai, N. H., Wiegand, K. & Getzin, S. Spatial distributions of tropical tree species in northern Vietnam under environmentally variable site conditions. Journal of forestry research 25(2), 257–268 (2014).
Song, H. et al. Investigating distribution pattern of species in a warm-temperate conifer-broadleaved-mixed forest in China for sustainably utilizing forest and soils. Science of The Total Environment 578, 81–89 (2017).
Condit, R. et al. Spatial patterns in the distribution of tropical tree species. Science 288, 1414–1418 (2000).
Li, L. et al. Spatial distributions of tree species in a subtropical forest of China. Oikos 118, 495–502 (2009).
Zhang, Z. H., Hu, G., Zhu, J. D. & Ni, J. Aggregated spatial distributions of species in a subtropical karst forest, southwestern China. Journal of Plant Ecology 6, 131–140 (2012).
Pielou, E. C. Segregation and symmetry in two-species populations as studied by nearest-neighbour relationships. The Journal of Ecology, 255–269 (1961).
Harms, K. E., Condit, R., Hubbell, S. P. & Foster, R. B. Habitat associations of trees and shrubs in a 50-ha Neotropical forest plot. Journal of Ecology 89, 947–959 (2001).
Hubbell, S. P. Tree dispersion, abundance, and diversity in a tropical dry forest. Science 203, 1299–1309 (1979).
Bruno, J. F., Stachowicz, J. J. & Bertness, M. D. Inclusion of facilitation into ecological theory. Trends in Ecology & Evolution 18, 119–125 (2003).
Wright, J. S. Plant diversity in tropical forests: a review of mechanisms of species coexistence. Oecologia 130, 1–14 (2002).
Lai, J., Mi, X., Ren, H. & Ma, K. Species‐habitat associations change in a subtropical forest of China. Journal of Vegetation Science 20, 415–423 (2009).
Gunatilleke, C. V. S. et al. Species–habitat associations in a Sri Lankan dipterocarp forest. Journal of Tropical Ecology 22, 371–384 (2006).
Queenborough, S. A., Burslem, D. F., Garwood, N. C. & Valencia, R. Habitat niche partitioning by 16 species of Myristicaceae in Amazonian Ecuador. Plant Ecology 192, 193–207 (2007).
Ye, J., Hao, Z. Q., Xie, P. & Li, J. G. Habitat associations of saplings and adults in an old-growth temperate forest in the Changbai mountains, northeastern China. Forestry Studies in China 13, 13–22 (2011).
Svenning, J. C. Environmental heterogeneity, recruitment limitation and the mesoscale distribution of palms in a tropical montane rain forest (Maquipucuna, Ecuador). Journal of Tropical Ecology 17, 97–113 (2001).
Peters, H. A. Neighbour‐regulated mortality: the influence of positive and negative density dependence on tree populations in species‐rich tropical forests. Ecology letters 6, 757–765 (2003).
Stoll, P. & Newbery, D. M. Evidence of species‐specific neighborhood effects in the Dipterocarpaceae of a Bornean rain forest. Ecology 86, 3048–3062 (2005).
Murrell, D. J. On the emergent spatial structure of size‐structured populations: when does self‐thinning lead to a reduction in clustering? Journal of Ecology 97, 256–266 (2009).
Lin, Y. C., Chang, L. W., Yang, K. C., Wang, H. H. & Sun, I. F. Point patterns of tree distribution determined by habitat heterogeneity and dispersal limitation. Oecologia 165, 175–184 (2011).
Condit, R. et al. Beta-diversity in tropical forest trees. Science 295, 666–669 (2002).
Lan, G., Hu, Y., Cao, M. & Zhu, H. Topography related spatial distribution of dominant tree species in a tropical seasonal rain forest in China. Forest Ecology and Management 262, 1507–1513 (2011).
Nishimura, S., Yoneda, T., Fujii, S., Mukhtar, E. & Kanzaki, M. Spatial patterns and habitat associations of Fagaceae in a hill dipterocarp forest in Ulu Gadut, West Sumatra. Journal of tropical ecology 24, 535–550 (2008).
Zhang, Z. H., Hu, G., Zhu, J. D., Luo, D. H. & Ni, J. Spatial patterns and interspecific associations of dominant tree species in two old-growth karst forests, SW China. Ecological research 25, 1151–1160 (2010).
Zhang, Z. G. Karst types in China. GeoJournal 4, 541–570 (1980).
Zhou, Y. C., Wang, S. J., Lu, H. M., Xie, L. P. & Xiao, D. A. Forest soil heterogeneity and soil sampling protocols on limestone outctops: example from SW China. Acta Carsologica 39, 115–122 (2010).
Du, H. et al. Spatial pattern of woody plants and their environmental interpretation in the karst forest of southwest China. Plant Biosystems 149, 121–130 (2015).
Wang, X. et al. Spatial distributions of species in an old-growth temperate forest, northeastern China. Canadian Journal of Forest Research 40, 1011–1019 (2010).
Guo, Y. L. et al. Spatial distribution of tree species in a species-rich subtropical mountain forest in central China. Canadian journal of forest research 43, 826–835 (2013).
Fibich, P. et al. Spatial patterns of tree species distribution in New Guinea primary and secondary lowland rain forest. Journal of vegetation science 27, 328–339 (2016).
Nguyen, H. H., Uria‐Diez, J. & Wiegand, K. Spatial distribution and association patterns in a tropical evergreen broad‐leaved forest of north‐central Vietnam. Journal of vegetation science 27, 318–327 (2016).
R Core Team. R: A language and environment for statistical computing. (R Foundation for Statistical Computing. Vienna, Austria, 2017).
Wiegand, T., Gunatilleke, S., Gunatilleke, N. & Okuda, T. Analyzing the spatial structure of a Sri Lankan tree species with multiple scales of clustering. Ecology 88, 3088–3102 (2007).
Zhu, Y., Mi, X. C., Ren, H. B. & Ma, K. P. Density dependence is prevalent in a heterogeneous subtropical forest. Oikos 119, 109–119 (2010).
Guo, Y. L. et al. Spatial distribution of tree species in a tropical karst seasonal rainforest in Nonggang, Guangxi, southern China. Biodiversity. Science. 23, 183–191 (2015). (In Chinese).
Law, R. et al. Ecological information from spatial patterns of plants: insights from point process theory. Journal of Ecology 97, 616–628 (2009).
Tuomisto, H., Ruokolainen, K. & Yli-Halla, M. Dispersal, environment, and floristic variation of western Amazonian forests. Science 299, 241–244 (2003).
Stoyan, D. & Stoyan, H. Fractals, random shapes, and point fields: methods of geometrical statistics (Vol. 302). John Wiley & Sons Inc (1994).
Valencia, R. et al. Tree species distributions and local habitat variation in the Amazon: large forest plot in eastern Ecuador. Journal of Ecology 92, 214–229 (2004).
Guo, Y. L. et al. Topographic species–habitat associations of tree species in a heterogeneous tropical karst seasonal rain forest, China. Journal of Plant Ecology 10, 450–460 (2017).
Condit, R. Tropical forest census plots: Methods and results from Barro Colorado Island, Panama and a Comparion with other plot. Texas: Springer-Verlag (1998).
Ripley, B. D. The second-order analysis of stationary point processes. Journal of applied probability 13, 255–266 (1976).
Wiegand, T. & A Moloney, K. Rings, circles, and null‐models for point pattern analysis in ecology. Oikos 104, 209–229 (2004).
Baddeley, A. & Turner, R. Spatstat: an R package for analyzing spatial point patterns. Journal of statistical software 12, 1–42 (2005).
Acknowledgements
This work was supported by the National Key Research and Development Program of China (2016YFC0502405), and the National Natural Science Foundation of China (31400412, 31370485, 31370623), the Guangxi Key Research and Development Program (AB17129009, AB16380255), and the Guangxi Provincial Program of Distinguished Expert in China.
Author information
Authors and Affiliations
Contributions
H.D., F.Z., L.W. and T.S. conceived and designed the experiments. H.D., F.H. and W.P. conducted the experiments. H.D., F.H., H.Z., F.Z. and Z.Z. discussed the results. H.D and F.H. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Du, H., Hu, F., Zeng, F. et al. Spatial distribution of tree species in evergreen-deciduous broadleaf karst forests in southwest China. Sci Rep 7, 15664 (2017). https://doi.org/10.1038/s41598-017-15789-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15789-5
This article is cited by
-
Positive effects of plant species diversity on organic carbon accumulation in soil aggregates driven by mineral protection in a subtropical forest in southwest China
Journal of Soils and Sediments (2024)
-
Exploring potential relationships between acoustic indices and ecosystem functions: a test on insect herbivory
Oecologia (2024)
-
Environmental and spatial contributions to tree community assembly across life stages and scales in evergreen-deciduous broadleaf karst forests, southwest China
Journal of Forestry Research (2023)
-
Spatial point-pattern analysis as a powerful tool in identifying pattern-process relationships in plant ecology: an updated review
Ecological Processes (2021)
-
Plant apparency drives leaf herbivory in seedling communities across four subtropical forests
Oecologia (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.