Abstract
Glassiness is ubiquitous and diverse in characteristics in nature. Understanding their differences and classification remains a major scientific challenge. Here, we show that scaling of magnetic memories with time can be used to classify magnetic glassy materials into two distinct classes. The systems studied are high temperature superconductor-related materials, spin-orbit Mott insulators, frustrated magnets, and dilute magnetic alloys. Our bulk magnetization measurements reveal that most densely populated magnets exhibit similar memory behavior characterized by a relaxation exponent of \(1-n\approx 0.6(1)\). This exponent is different from \(1-{\boldsymbol{n}}\approx 1/3\) of dilute magnetic alloys that was ascribed to their hierarchical and fractal energy landscape, and is also different from \(1-{\boldsymbol{n}}=1\) of the conventional Debye relaxation expected for a spin solid, a state with long range order. Furthermore, our systematic study on dilute magnetic alloys with varying magnetic concentration exhibits crossovers among the two glassy states and spin solid.
Similar content being viewed by others
Introduction
Magnetic glassy systems present a unique opportunity for searching possible universal phenomena associated with glassy behaviors. This is because glass phase exists in a wide range of magnetic materials that are described by seemingly very different spin interactions. The most well-known common features of the magnetic glassy behaviors are the lack of long range magnetic order and the field-cooled (FC) and zero-field-cooled (ZFC) hysteresis found in the bulk susceptibility1,2. The term spin glass was coined in 1970s to describe the low temperature behaviors of dilute magnetic alloys that are made of nonmagnetic metals with low concentrations of magnetic impurities1,3. The canonical glassy behaviors are manifested in intriguing phenomena called aging, rejuvenation, and memory effects4. While aging simply refers to the time-span dependence of relaxation phenomena in the glassy state, rejuvenation describes the re-thermalization whenever the system is further cooled after waiting at some temperature. The states accessed while aging can be retrieved upon re-heating, which is called memory effect. Several theories have been proposed to understand the physics of the spin glass.
Various systems other than the dilute magnetic alloys also exhibit the aforementioned characteristic glassy behaviors at low temperatures, even when the magnetic moments are densely populated. For example, glassy behaviors have been observed in the phase diagrams of high temperature superconducting materials, cuprates5,6 and iron-based superconductors7. Another example is the so-called spin-orbit Mott insulators, Li2RhO3 8,9 and Na2Ir1−xTixO3 10, which exhibit anisotropic Kitaev-type exchange interactions. Yet another is a set of geometrically frustrated magnets, pyrochlores such as Y2Mo2O7 11, spinels such as ZnFe2O4 12, and the quasi-two-dimensional bi-pyramid compounds SrCr9pGa12-9pO19 (SCGO)13,14,15,16,17 and BaCr9pGa12−9pO19 (BCGO)18. We emphasize that the magnetic interactions of these systems seem to be quite different in nature. For instance, the parent compound of high-Tc superconductors La2−xSrxCuO4 (LSCO) is a Mott insulator with a conventional Neel spin order19. The entire magnetic excitation spectrum of La2CuO4 can be understood by an effective spin Hamiltonian with dominant nearest neighbor antiferromagnetic coupling constant \(J=104\) meV20. The iron chalcogenide Fe1±yTe displays a bi-collinear antiferromagnetic stripe order21,22. Magnetic interactions in the two spin-orbit Mott insulators, Li2RhO3 and Na2Ir1−xTixO3 are dominated by highly anisotropic Kitaev exchange couplings23,24. Remarkably, despite their different nature of magnetic interactions, all the systems show the same FC-ZFC hysteresis at low temperatures. A natural question to ask is whether or not there is a unifying concept that can unite and also classify these various glassy magnets.
Here, we address this issue by investigating memory effects of several of the aforementioned exemplary systems using the bulk magnetization measurements. We performed thermo-remanent magnetization (TRM)25,26,27 measurements on five different compounds, which can be divided into three categories: (1) the high temperature superconducting materials, cuprates and Fe-chalcogenides, (2) Kitaev-model-related systems Li2RhO3 and Na2Ir1−xTixO3, and (3) a semi-conducting pyrochlore Y2Mo2O7. Intriguingly, despite their distinct microscopic Hamiltonians, all of them exhibit unconventional glassy behaviors in the TRM measurements, that are weak and broad shoulder-like memory effects as in the prototype spin jam compounds SCGO/BCGO, starkly contrasting the strong and dip-like memory effects observed in the canonical spin glass such as CuMn2%. Interestingly, all the data can be well reproduced by a modified stretched exponential function of \(\{1-\exp (-{(\frac{{t}_{w}}{\tau })}^{1-n})\}\). More importantly, all the densely populated magnets except Y2Mo2O7 yield an exponent of \(1-n\approx 0.6(1)\). This value is different from \(1-{\boldsymbol{n}}\approx 1/3\) of dilute magnetic alloys28,29,30 that was ascribed to their hierarchical and fractal energy landscape31,32,33,34, and is also different from \(1-n=1\) of the conventional Debye relaxation expected for a crystal. Based on these results, we argue that the glass magnets can be categorized into two distinct classes with different relaxation behaviors characterized by the exponent: \(1-{\boldsymbol{n}}\approx 1/3\) for glassy magnets with hierarchical energy landscape and \(1-n\approx 0.6(1)\) for the ones with non-hierarchical energy landscape.
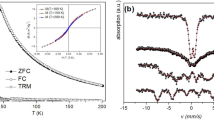
The TRM measurement is the most effective way to probe the memory effects in detail as explained in Supplementary Information and as shown most recently in the comparative study35 of SCGO/BCGO and the canonical spin glass CuMn2%. While a dip-like memory effect with clear rejuvenation was observed, as expected, in CuMn2%, a shoulder-like memory effect seen in SCGO/BCGO implies lack of rejuvenation. Figure 1 shows the TRM data obtained from five different compounds: (a) Fe1.02Se0.15Te0.85, (b) La1.96Sr0.04CuO4 (LSCO(x = 0.04)), (c) Li2RhO3, (d) Na2Ir0.89Ti0.11O3, and (e) Y2Mo2O7. These TRM data were taken after waiting at the waiting temperature \({T}_{w} \sim \,0.7\,{T}_{f}\) for several different waiting times ranging from 1.5(5) min to maximally 100 hours. For all systems aging and memory effect appears, i.e., the magnetization decreases near \({T}_{w}\) when the measurements were performed after waiting. The memory effect gets enhanced as the waiting time, \({t}_{w}\), increases. Surprisingly, Fe1.02Se0.15Te0.85 and LSCO(x = 0.04) whose parent compounds, FeTe and La2CuO4, respectively, are long-range ordered state, i.e., spin solid, exhibit very weak memory effects. The memory effects in both systems are negligible for short waiting time \({t}_{w}\le 6\) min. For \({t}_{w}\gtrsim 1\) hr, both systems show a very weak and broad shoulder appearing around \({T}_{w}\) (see Fig. 1a,b), regardless of how large \({t}_{w}\) is. For Fe1.02Se0.15Te0.85, the memory effect even seems to saturate for \({t}_{w}\gtrsim \,30\) hrs (Fig. 1a). Similar weak shoulder-like memory effects were also observed in the spin-orbit Mott insulators, Li2RhO3 and Na2Ir0.89Ti0.11O3 (see Fig. 1c,d, respectively). Note that, similarly to the two superconductivity-related systems, the two Kitaev-model-related systems also exhibit negligible memory effects for short waiting time \({t}_{w}\le 6\) min.
Memory Effect as a function of waiting time. Bulk susceptibility, \({\chi }_{DC}=\,M/H\), where \(M\) and \(H\) are magnetization and applied magnetic field strength, respectively, obtained from (a) Fe1.02Se0.15Te0.85 (b) La1.96Sr0.04CuO4, (c) Li2RhO3 (d) Na2Ir0.89Ti0.11O3 and (e) Y2Mo2O7, with H = 3 Oe. Symbols and lines with different colors indicate the data taken with different waiting times, \({t}_{w}\), ranging from zero to 100hrs, at \({T}_{w}/{T}_{f} \sim 0.7\) where \({T}_{w}\) and \({T}_{f}\) are the waiting and the freezing temperature, respectively. For Fe1.02Se0.15Te0.85, the Curie-Weiss Temperature \({\theta }_{cw}\) was estimated by fitting its high-T susceptibility data as shown in Fig. S1a in the Supplementary Information. For La1.96Sr0.04CuO4, the high-T susceptibility does not follow the simple Curie-Weiss law (see Fig. S1b in Supplementary Information). In order to show how strong the magnetic interactions are in LSCO, we quote the coupling constants of the parent compound La2CuO4 that were experimentally determined by inelastic neutron scattering (ref.20); the antiferromagnetic nearest-neighbor \(J\approx 104\,meV\) and the ferromagnetic next-nearest-neighbor \({J}^{\text{'}}\approx -18\,meV\). \({\theta }_{cw}\) for Li2RhO3, Na2Ir0.89Ti0.11O3 and Y2Mo2O7 were taken from refs9,24,36 respectively.
The weak shoulder-like memory effects have been recently observed in frustrated magnets, SCGO and BCGO, that are in vicinity of spin liquid, and here we show that another frustrated magnet, Y2Mo2O7, also exhibits similar features (Fig. 1e). These data clearly show that the weak shoulder-like memory effect is universal in these densely populated magnets, regardless of their magnetic interactions. It is in stark contrast to the canonical spin glass such as CuMn2%, where the memory effects in the magnetization curve were readily seen even for such short waiting times as \({t}_{w}=1.5(5)\) min (see Fig. S2 in the Supplementary Information), and the effects become sharp and strong, appearing as a large dip at \({T}_{w}\) for \({t}_{w}\ge 3\) hrs35.
Figure 2a summarizes the \({t}_{w}\) dependence of the memory effect for the densely populated magnets along with the canonical spin glass CuMn2%. The relative change of the magnetization \({\rm{\Delta }}{M}_{rel}=({M}_{ref}-M)/{M}_{ref}\) induced by the aging, in which \(M\) and \({M}_{ref}\) are the magnetizations with and without waiting, respectively, is plotted. Overall, it is clear that the memory effect is much weaker in densely populated magnets than in the canonical spin glass. Firstly, \({\rm{\Delta }}{M}_{rel}\) of \({t}_{w}\ge 30\) hrs for all the densely populated magnets except Y2Mo2O7 is smaller than \({\rm{\Delta }}{M}_{rel}\) of \({t}_{w}=6\) min for CuMn2%. Secondly, for \({t}_{w}\le 6\) min, most of them show negligible memory effects as shown in Fig. 2a and Fig. 1. Thirdly, the memory effect of the spin jams except Y2Mo2O7 seems to saturate for \({t}_{w}\ge 30\) hrs, while for CuMn2% it seems to keep increasing with increasing \({t}_{w}\) over the time period. It is interesting that the densely populated Y2Mo2O7 exhibits both spin glass and spin jam behaviors. This is probably due to the fact that Y2Mo2O7 is a semi-conductor evidenced by its resistivity of \(\rho \sim {10}^{-2}\,{\rm{\Omega }}\,{\rm{cm}}\) at 300 K, and has an unquenched orbital degree of freedom36,37. As a result, Y2Mo2O7 is not a typical frustrated antiferromagnet, which is manifested in the relatively small frustration index \(f={{\rm{\Theta }}}_{CW}/{T}_{f}\cong 2.3\) that is two orders of magnitude smaller than that of SCGO.
Summarizing the memory effect. From the data shown in (a) Fig. 1 and (b) Fig. 3, the aging effect was quantified for the eleven systems by plotting the relative change of the magnetization \({\rm{\Delta }}{M}_{rel}=({M}_{ref}-M)/{M}_{ref}\) where \({M}_{ref}\) is the magnetization without waiting, and it was plotted as a function of \({t}_{w}\) in a log scale. The aging effects of a spin jam prototype, SrCr9pGa12-9pO19 (SCGO(p = 0.97)), and a spin glass prototype CuMn2% were taken from ref.35, except the \({t}_{w}=1.5(5)\,min\) data are new (see Fig. S2 in the Supplementary Information), and are also plotted here for comparison. Each set of \({\rm{\Delta }}{M}_{rel}({t}_{w})\) for each sample shown in panels (a) and (b) was fitted to the modified stretched exponential function, Eq. (1). After the fitting, in (c) \(-\mathrm{log}(1-{\rm{\Delta }}{M}_{rel}/A)\) was plotted as a function of \({({t}_{w}/\tau )}^{1-n}\) in a log-log scale. (d) The degree of aging, \(A\), and the inverse exponent, \(1/(1-n)\), obtained for all the samples are plotted against each other.
In search of possible underlying scaling behavior, we have fitted the \({t}_{w}\) dependence of \({\rm{\Delta }}{M}_{rel}\) to the following phenomenological function
which is modified from the stretched exponential function that was proposed to describe relaxation phenomena in glassy systems28,29,30,31,32,33,34. The modification made here is to take into account the experimental observation that \({\rm{\Delta }}{M}_{rel}\) seems to saturate for long waiting times. Here \(A={\rm{\Delta }}{M}_{rel}({t}_{w}\to \infty )\) is a measure of degree of aging, \(\tau \) is a microscopic time scale for relaxation dynamics. A positive non-zero exponent \(n\) would tell us how much the relaxation deviates from the conventional Debye behavior (\(n=0\)). The exponent \(1-n\) can be related to critical exponents for the spin glass transition within the framework of a random cluster model32,33. For example, assuming that the growth of clusters involves no conserved mode, the droplet model predicts an exponent \(1-n=1/2\) 38. The dashed lines in Fig. 2a are the fits of the experimental data to Eq. (1) for all the materials. It is remarkable that the same phenomenological function, albeit with different parameters, reproduces all the data of both spin jams and spin glass over the wide range of the waiting time. This indicates that a universal scaling may be in play in the aging or relaxation phenomena of all glassy magnets, as shown in Fig. 2c.
The difference between the spin glass and spin jam is clearly manifested in different parameters in Fig. 2d. For spin glass CuMn2%, the exponent \(1-n\approx 1/3\) that deviates significantly from the conventional Debye behavior of \(1-n=1\). This is consistent with the previous studies on several other dilute magnetic alloys such as CuMn1% and AgMn2.6%28, NiMn23.5%29, Au90Fe10 30. This deviation observed in the spin glasses was ascribed to the underlying hierarchically constrained dynamics31,32,33,34. On the other hand, the densely populated glassy magnets, SCGO, Fe1.02Se0.15Te0.85, LSCO, and the two spin-orbit Mott insulators, yield the exponent of \(1-n\approx 0.6(1)\), indicating a smaller deviation from the conventional Debye relaxation. This implies that their energy landscapes are not hierarchical as in the canonical spin glass. These are summarized in Fig. 2d in which the exponent \(1-n\) is plotted as a function of the degree of aging, \(A\). We note that there is a positive correlation between the deviation from the Debye limit and the degree of aging.
To further support the aforementioned scenario, we have performed the TRM measurements on Cu1-x Mn x as a function of the Mn concentration, x. This series of compounds provides an excellent platform also to investigate how the spin glass is connected with the spin jam, and eventually magnetic ordered states. On one hand, Cu1-xMnx is a canonical spin glass for small x. On the other hand, pure Mn exhibits a long-range spin-density wave (SDW) order at low temperatures. The magnetic ground state of samples with large x thus can be viewed as large domains of SDW order disrupted by non-magnetic Cu atoms, similar to that observed in the densely populated magnets such as Fe1.02Se0.15Te0.85 and La1.96Sr0.04CuO4.
As shown in Fig. 3a,b,c,d, for dilute alloys with small values of \(x\lesssim 0.45\), the data exhibits prominent dip behaviors, i.e., the presence of rejuvenation. As x increases further, the dip behavior is gradually replaced with the shoulder behaviors, i.e., lack of rejuvenation, similar to spin jam (see Fig. 3e,f). The crossover seems to occur at x ~0.45 that is close to the percolation threshold for a three-dimensional system39. Note the non-monotonic behavior of the degree of aging \(A={\rm{\Delta }}{M}_{rel}({t}_{w}\to \infty )\) that maximizes at \(x\sim 0.15\). The initial growth of A for small x is related to the increasing number of magnetic impurities, giving rise to a stronger magnetic signal. For very large x where the system is in the spin jam regime, the degree of aging is expected to decrease as observed for x = 0.75 and 0.85 shown in Fig. 3e,f respectively. Thus, even though the exact value of x for the maximal A is determined by the balancing between the exact nature of the magnetic interactions and the magnetic concentration, the maximum of A should occur most likely somewhere close to the middle of x = 0 and the percolation threshold, which is qualitatively consistent with the observed value of \(x\sim 0.15\).
Memory Effect of Cu −x at.% Mn samples as a function of waiting time. Bulk susceptibility, \({\chi }_{DC}=M/H\), where \(M\) and \(H\) are magnetization and applied magnetic field strength, respectively, obtained from Cu 1-x Mn x with (a) x = 0.02, (b) x = 0.15, (c) x = 0.30, (d) x = 0.45, (e) x = 0.75 and (f) x = 0.85, with H = 3 Oe. Symbols and lines with different colors indicate the data taken with different waiting times, \({t}_{w}\), ranging from zero to 100 hrs, at \({T}_{w}/{T}_{f} \sim 0.7\) where \({T}_{w}\) and \({T}_{f}\) are the waiting and the freezing temperature, respectively.
Surprisingly, regardless of x, \({\rm{\Delta }}{M}_{rel}\) of Cu1-x Mn x follows the same stretched exponential relaxation function, as shown in Fig. 2b, but with varying values of the exponent, \(1-n\), from 0.34(1) for x = 0.02 to 0.66(9) for x = 0.85 (see Fig. 2d). And thus, all their \({\rm{\Delta }}{M}_{rel}\) can be collapsed into a same function, once the waiting time is properly scaled, and it is so even with those of the densely populated glassy systems, as shown in Fig. 2c. The change in the exponent, \(1-n\), as a function of x clearly shows that the glassy state of the dilute magnetic alloy (for small x) is replaced by a glassy state for large x similar to the one observed in the densely populated magnets (see Fig. 2d) Interesting, the crossover occurs as the magnetic concentration go beyond the percolation threshold39. This clear crossover phenomenon strongly indicates that there are two distinct glassy states: spin glass and spin jam.
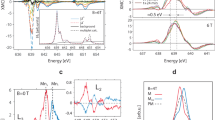
Why do the densely populated systems exhibit the large exponent \(1-n\approx 0.6(1)\) similar to the quantum-fluctuation-induced spin jam SCGO, compared to the canonical spin glass state of dilute magnetic alloys? A clue comes from neutron scattering studies; the magnetic structure factor, \(I(Q)\), of all the densely populated magnets studied here exhibit prominent peaks that are centered at a non-zero momentum (\(Q\)) corresponding to short-range spin correlations, as those of the frustrated magnets SCGO17,40 and BCGO18. This indicates that those systems have dominant antiferromagnetic interactions between localized spins and short-range spin correlations. For example, the cuprate41,42 and iron chalcogenide43,44 exhibit strong incommensurate peaks near the antiferromagnetic ordering wave vector of their parent compounds. As shown in Fig. 4b, the spin-orbit Mott insulator Na2Ir0.89Ti0.11O3 exhibit a prominent peak centered at \(Q=0.87(2)\,\)Å−1. The common characteristics of the antiferromagnetic and short-range magnetic structure factor starkly contrast with the nearly featureless magnetic structure factor of the spin glass CuMn2%, as shown in Fig. 4d. In the dilute magnetic alloys such as CuMn2%, magnetic impurities interact among themselves through the Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions that are mediated by the itinerant electrons. The RKKY interactions are long-ranged, and oscillate from ferromagnetic to antiferromagnetic as a function of the distance. As a result, the random distances among the magnetic moments lead to their random interactions that even change the sign, resulting in the featureless magnetic structure factor.
Neutron scattering measurements. (a) T-dependence, \({I}_{elas}\,(T)\), and (b) Q-dependence, \({I}_{elas}\,(Q)\), of elastic magnetic neutron scattering intensity obtained from Na2Ir0.89Ti0.11O3. The measurements were done at the Cold Neutron Chopper Spectrometer (CNCS) at the Spallation Neutron Source (SNS). (c) T-dependence, \({I}_{elas}\,(T)\), and (d) Q-dependence, \({I}_{elas}\,(Q)\), of elastic magnetic neutron scattering intensity obtained from the magnetic alloy CuMn2%. The measurements were done at the Backscattering Spectrometer (BASIS) at SNS. For both \({I}_{elas}\,(Q)\) in (b) and (d), the non-magnetic background was determined from the data above the freezing temperature and subtracted from the base temperature data. The black solid line in (b) is the fit of the magnetic peak centered at \(Q\,=\,0.87\,\) Å−1 to a simple Gaussian, while the line in (d) is a guide to eyes. The red horizontal bar at the center of the peak in (b) represents the instrument Q-resolution, \(dQ\approx 0.06\) Å−1, that was determined by fitting a nearby Bragg peak centered at 1.2 Å−1.
The featureless \(I(Q)\) of CuMn2% is consistent with the real-space droplet model for spin glass38,45 in which low-energy excitations are dominated by connected spin clusters of arbitrary length scales. The real-space clusters or droplets correspond to the meta-stable ground states or local minima in the energy landscape. Their arbitrary length scales and random RKKY interactions yield a multitude of energy scales, resulting in the complex hierarchical fractal energy landscape35,46,47,48. As a consequence, the spin glass exhibits the observed strong dip-like memory effect. In contrast to the droplet model for spin glass, the clusters in spin jams are more uniform in size, as evidenced by the prominent peak of \(I(Q)\). This feature, combined with the short-range exchange spin Hamiltonian, leads to a narrowly distributed energy scale, and the weak memory effect as observed in our susceptibility measurements.
The distinct nature of the two magnetic glass phases, spin glass and spin jam, also manifests in their characteristically different low energy excitations. The thermodynamic behavior of canonical spin glass at low temperatures is dominated by thermally active clusters or droplets, particularly those with a free energy less than or of the same order of \({k}_{B}T\) where \({k}_{B}\) is the Boltzmann constant. The fact that there is a finite density of clusters with limiting zero free energy naturally leads to the linear-T specific heat38,49, which is a signature of canonical spin glass. On the other hand, the low-energy excitations in spin jam are the Halperin-Saslow (HS) spin waves with finite spin stiffness over large length scales (often larger than the typical cluster sizes)50,51,52. These gapless HS modes exhibit a linear dispersion relation and are the source of a \({T}^{2}\) dependence of the specific heat for a two-dimensional system. Indeed, such \({T}^{2}\) behavior has been observed in the glass phase of SCGO14, Li2RhO3 8,9, and doped Na2IrO3 10.
The memory effect measurements provide crucial information about the nature of relaxation dynamics in different magnetic states, which allows us to classify the semi-classical magnetic glassy materials as shown in Fig. 5. At the lower left corner of the triangle lies the spin solid that is realized in densely populated semi-classical magnetic materials with small disorder and weak frustration that order long-range at low temperatures with Debye relaxation. The typical energy landscape associated with spin solid is a smooth vase with a global minimum. At the lower right corner of the triangle lies the spin glass that is realized in dilute magnetic alloys with random magnetic interactions. Its typical energy landscape is dominated by hierarchical meta-stable states that correspond to spin clusters of arbitrary length scales in real space, exhibiting hierarchical rugged funnels and fractal geometry, and the observed strong deviation from the conventional Debye relaxation. Finally, at the top corner is the new magnetic state dubbed spin jam that encompasses many densely populated compounds with short-range exchange magnetic interactions, disorder and frustration. Disorder can be either extrinsic as in LSCO, FeTeSe and Na2Ir1-xTixO3, or intrinsic due to quantum fluctuations as in SCGO and BCGO15,16. One salient feature of the spin jam, represented by a nonhierarchical energy landscape with a wide and nearly flat but rough bottom, is the lack of widely distributed energy and time scales. This in turn leads to a significantly weaker memory effect and the relaxation exponent that is closer to the Debye exponent than that of the spin glass, as observed in our experiments. Remarkably, the canonical spin glass Cu1−x Mn x with small x crosses over to the spin jam state when the magnetic concentration x increases beyond the percolation threshold.
Our classification of a wide range of semi-classical glassy magnets based on nonequilibrium relaxation dynamics to two distinct states has implication to other non-magnetic structural glasses. Indeed, recent studies have found two distinct low frequency modes in structural glass: one related to a hierarchical energy landscape and the other related to jamming53,54,55. The rather distinct aging and memory behaviors observed in the spin glass and jam might also shed light on the relationship between nonequilibrium dynamics and connectivity among elementary interacting agents in networks and socio-economic systems56.
References
Mydosh, J. A. Spin Glasses: An Experimental Introduction (Taylor & Francis, 1995).
Cannella, V. & Mydosh, J. A. Magnetic Ordering in Gold-Iron Alloys. Phys Rev B 6, 4220 (1972).
Anderson, P. W. Spin Glass. Phys Today 41, 9 (1988).
Dupuis, V. et al. Aging, rejuvenation, memory phenomena in spin glasses. Pramana 64(6), 1109–1119 (2005).
Wakimoto, S. et al. Direct observation of a one-dimensional static spin modulation in insulating La1.95Sr0.05CuO4. Phys Rev B 61(5), 3699–3706 (2000).
Matsuda, M. et al. Static and dynamic spin correlations in the spin-glass phase of slightly doped La2− xSrxCuO4. Phys Rev B 62(13), 9148–9154 (2000).
Katayama, N. et al. Investigation of the Spin-Glass Regime between the Antiferromagnetic and Superconducting Phases in Fe1+ySexTe1-x. J Phys Soc Jpn 79, 113702 (2010).
Luo, Y. et al. Li2RhO3: A spin-glassy relativistic Mott insulator. Phys Rev B 87(16), 161121(R) (2013).
Khuntia, P. et al. Local Magnetism and Spin Dynamics of the Frustrated Honeycomb Rhodate Li2RhO3. arXiv 1512, 04904 (2015).
Manni, S., Tokiwa, S. Y. & Gegenwart, P. Effect of nonmagnetic dilution in the honeycomb-lattice iridates Na2IrO3 and Li2IrO3. Phys Rev B 89, 241102 (2014).
Gingras, M. J. P., Stager, C. V., Raju, N. P., Gaulin, B. D. & Greedan, J. E. Static Critical Behavior of the Spin-Freezing Transition in the Geometrically Frustrated Pyrochlore Antiferromagnet Y2Mo2O7. Phys Rev Lett 78(5), 947–950 (1997).
Mamiya, H. et al. Slow dynamics in the geometrically frustrated magnet ZnFe2O4: Universal features of aging phenomena in spin glasses. Phys Rev B 90, 014440 (2014).
Obradors, X. et al. Magnetic frustration and lattice dimensionality in SrCr8Ga4O19. Solid State Commun 65(3), 189–192 (1988).
Ramirez, A. P., Espinosa, G. P. & Cooper, A. S. Strong frustration and dilution-enhanced order in a quasi-2D spin glass. Phys Rev Lett 64(17), 2070–2073 (1990).
Iida, K., Lee, S. H. & Cheong, S. W. Coexisting Order and Disorder Hidden in a Quasi-Two-Dimensional Frustrated Magnet. Phys Rev Lett 108, 217207 (2012).
Klich, I., Lee, S. H. & Iida, K. Glassiness and exotic entropy scaling induced by quantum fluctuations in a disorder-free frustrated magnet. Nat Comm 5, 3497 (2014).
Yang, J. et al. Spin jam induced by quantum fluctuations in a frustrated magnet. Proc Nat Acad Sci USA 112, 11519 (2015).
Yang, J. et al. Glassy Behavior and Isolated Spin Dimers in a New Frustrated Magnet BaCr9pGa12-9pO19. J Phys Soc Jpn 85, 094712 (2016).
Aeppli, G. et al. Magnetic dynamics of La2CuO4 and La2-xBaxCuO4. Phys Rev Lett 62, 2052–2055 (1989).
Coldea, R. et al. Spin Waves and Electronic Interactions in La2CuO4. Phys Rev Lett 86(23), 5377–5380 (2001).
Bao, W. et al. Tunable (δπ, δπ)-Type Antiferromagnetic order in α-Fe(Te,Se) Superconductors. Phys Rev Lett 102, 247001 (2009).
Dai, P., Hu, J. & Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nature Phys 8, 709 (2012).
Katukuri, Y. M. et al. Strong magnetic frustration and anti-site disorder causing spin-glass behavior in honeycomb Li2RhO3. Scientific Reports 5, 14718 (2015).
Choi, S. K. et al. Spin Waves and Revised Crystal Structure of Honeycomb Iridate Na2IrO3. Phys Rev Lett 108, 127204 (2012).
Mamiya, H. & Nimori, S. Memory effects in Heisenberg spin glasses: Spontaneous restoration of the original spin configuration rather than preservation in a frozen state. J Appl Phys 111, 07E147 (2012).
Ladieu, F., Bert, F., Dupuis, V., Vincent, E. & Hammann, J. The relative influences of disorder and of frustration on the glassy dynamics in magnetic systems. J Phys: Condens Matter 16, S735–S741 (2004).
Dupuis, V. et al. Aging and memory properties of topologically frustrated magnets. J Appl Phys 91, 8384 (2002).
Chamberlin, R. V., Mozurkewich, G. & Orbach, R. Time decay of the remanent magnetization in spin-glasses. Phys Rev Lett 52, 867–870 (1984).
Roshko, R. M. & Ruan, M. Thermoremanent relaxation in a reentrant NiMn ferromagnet close to the tricritical point. J Mag Mag Mat 104, 1613–1614 (1992).
Mitchler, P., Roshko, R. M. & Ruan, W. Crossover from equilibrium to nonequilibrium dynamics in a reentrant AuFe ferromagnet. Journal de Physique I 2, 2299–2309 (1992).
Palmer, R. G., Stein, D. L., Abrahams, E. & Anderson, P. W. Models of hierarchically constrained dynamics for glassy relaxation. Phys Rev Lett 53(10), 958 (1984).
Continentino, M. A. & Malozemoff, A. P. Dynamic scaling and the field-dependent critical line in a fractal cluster model of spin glasses. Phy Rev B 33(5), 3591 (1986).
Campbell, I. A. Critical exponents of spin-galss systems. Phys Rev B 37(16), 9800 (1988).
Ogielski, A. T. Dynamics of three-dimensional Ising spin glasses in thermal equilibrium. Phys Rev B 32(11), 7384 (1985).
Samarakoon, A. M. et al. Aging, memory, and nonhierarchical energy landscape of spin jam. Proc Nat Acad Sci USA 113, 11806 (2016).
Silverstein, H. J. et al. Liquidlike correlations in single-crystalline Y2Mo2O7: An unconventional spin glass. Phys Rev B 89, 054433 (2014).
Shinaoka, H., Motome, Y., Miyake, T. & Ishibashi, S. Spin-orbital frustration in molybdenum pyrochlores A2Mo2O7 (A = rare earth). Phys Rev B 88(17), 174422 (2013).
Fisher, D. & Huse, D. Equilibrium behavior of the spin-glass ordered phase. Phys Rev B 38, 386–411 (1988).
Henley, C. L. Effective Hamiltonians and dilution effects in Kagome and related anti-ferromagnets. Can J Phys 79(11–12), 1307–1321 (2001).
Lee, S. H. et al. Isolated Spin Pairs and Two-Dimensional Magnetism in SrCr9pGa12−9pO19. Phys Rev Lett 76(23), 4424–4427 (1996).
Cheong, S. W. et al. Incommensurate magnetic fluctuations in La2-xSrxCuO4. Phys Rev Lett 67(13), 1791–1794 (1991).
Emery, V. J., Kivelson, S. A. & Tranquada, J. M. Stripe phases in high-temperature superconductors. Proc Natl Acad Sci USA 96, 8814–8817 (1999).
Lee, S. H. et al. Coupling of spin and orbital excitations in the iron-based superconductor FeSe0.5Te0.5. Phys Rev B 81(22), 220502(R) (2010).
Liu, T. J. et al. From (π, 0) magnetic order to superconductivity with (π, π) magnetic resonance in Fe1.02Te1−xSex. Nat Mater 9, 716–720 (2010).
Bouchaud, J. P., Dupuis, V., Hammann, J. & Vincent, E. Separation of time and length scales in spin glasses: Temperature as a microscope. Phys Rev B 65, 024439 (2001).
Lederman, M., Orbach, R., Hammann, J. M., Ocio, M. & Vincent, E. Dynamics in spin glasses. Phys Rev B 44(14), 7403–7412 (1991).
Fontanari, J. F. & Stadler, P. F. Fractal geometry of spin-glass models. J Phys A: Math Gen 35(7), 1509–1516 (2002).
Charbonneau, P., Kurchan, J., Parisi, G., Urbani, P. & Zamponi, F. Fractal free energy landscapes in structural glasses. Nat Comm 5, 3725 (2014).
Anderson, P. W., Halperin, B. I. & Varma, C. M. Anomalous low-temperature thermal properties of glasses and spin glasses. Philos Mag 25, 1 (1972).
Halperin, B. I. & Saslow, W. M. Hydrodynamic theory of spin waves in spin glasses and other systems with noncollinear spin orientations. Phys Rev B 16(5), 2154–2162 (1977).
Sachdev, S. Kagomé- and triangular-lattice Heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys Rev B Condens Matter 45(21), 12377–12396 (1992).
Podolsky, D. & Kim, Y. B. Halperin-Saslow modes as the origin of the low-temper- ature anomaly in NiGa2S4. Phys Rev B 79(14), 140402 (2009).
Franz, S., Parisi, G., Urbani, P. & Zamponi, F. Universal spectrum of normal modes in low-temperature glasses. Proc Nat Acad Sci USA 112, 14539 (2015).
Chen, K. et al. Low-frequency vibrations of soft colloidal glasses. Phys Rev Lett 105(2), 025501 (2010).
Liu, A. J. & Nagel, S. R. The jamming transition and the marginally jammed solid. Annu Rev Condens Matter Phys 1(1), 347–369 (2010).
Albert, R. & Barabasi, A.-L. Statistical mechanics of complex networks. Rev Mod Phys 74, 47–97 (2002).
Acknowledgements
Work at University of Virginia by S.H.L. and A.S. was supported by US National Science Foundation (NSF) Grant DMR-1404994 and Oak Ridge National Laboratory, respectively. The work at Tohoku University was partly supported by Grants-in-Aid for Scientific Research (24224009, 23244068, and 15H05883) from MEXT of Japan. The work at University of Tennessee was supported by the US National Science Foundation (NSF) grant DMR-1350002.
Author information
Authors and Affiliations
Contributions
S.-H.L. designed the research. J.Y., N.K., R.S., H.D.Z., S.W. and K.Y. synthesized the samples. A.S., T.J.S. and M.T. performed the memory effect measurements. A.S., D.Z., G.E., S.O.D. and D.A.T. performed the neutron scattering experiments. G.-W.C. and S.-H.L. wrote the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Samarakoon, A.M., Takahashi, M., Zhang, D. et al. Scaling of Memories and Crossover in Glassy Magnets. Sci Rep 7, 12053 (2017). https://doi.org/10.1038/s41598-017-12187-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-12187-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.