Main

Ordered phases tend towards disorder with increasing temperature, resulting from entropy. There are a few exceptions to such intuition, as exemplified by the ferroelectric Rochelle salt. In this material there are two relevant Curie temperatures (TC), and for both T < TC1 and T > TC2, the material exhibits a disordered paraelectric phase, but oddly an ordered ferroelectric phase stabilizes for TC1 < T < TC2 (ref. 1). For magnetic systems, the presence of re-entrant spin glasses in alloys shows similar order from disorder behaviour, but the source of this phenomena is still being heavily debated owing to the coexistence of both glassy behaviour and long-range order2. Moreover, a study on Y2Ni7 was initially interpreted to show thermally induced spontaneous magnetization3, but was later found to be flawed by sample impurities4. Theoretically, there are mechanisms that predict the appearance of ferromagnetic order at increasing temperature5. For example, in itinerant electron systems, ferromagnetic order may arise if a peak in the density of states shifts such that the Stoner criterion is satisfied at finite temperature, but not at T = 0. Another heavily discussed mechanism to create magnetic order from an increase in temperature is known as order from disorder, and is related to a macroscopic degeneracy of the ground state that is broken by finite-temperature contributions of spin excitations to the free energy6,7. For example, the observation of a spiral phase seen in PrPtAl was connected to the concept of order from disorder8. These proposed mechanisms provide counterexamples to basic thermodynamic intuition, where increasing temperature, and thus increasing entropy, should produce more disorder.

Spin glasses are a special class of magnets that exhibit a critical temperature while lacking long-range order below this temperature. They are often considered to be disordered magnets. Spin glasses are distinguished from both equilibrium and conventional non-equilibrium systems by exhibiting aging; that is, the presence of peculiar dynamics characterized by a very broad distribution of relaxation times9,10. The latter distinguishes a spin glass state from other frustrated magnets, such as spin ices and spin liquids11,12. Spin glass behaviour was traditionally thought to originate in the combination of competing magnetic interactions and non-negligible disorder13,14,15,16. Recently, the so-called self-induced spin glass17,18,19 was discovered to be the magnetic ground state of elemental crystalline Nd20. Unlike conventional spin glasses, the self-induced spin glass state is caused solely by competing interactions derived from the lattice structure itself; that is, in the absence of disorder. In the rare-earth element Nd, these competing exchange interactions lead to a multiplicity of low-energy states defined by a reciprocal lattice vector, or magnetic wavevector, Q. Hence, Nd shows local spin correlations related to these Q states and Q-dependent aging, but no preferential long-range order defined by one of these Q states. In contrast to conventional spin glasses, various experimental methods have identified numerous disputed phase transitions below the ordering temperature (Néel temperature, TN) of Nd21,22,23,24,25,26. These phases have been interpreted as long-range magnetic order, which is at odds with the observation of a low-temperature self-induced spin glass20.

Here, we show that the self-induced spin glass state of elemental Nd exhibits long-range multi-Q order at temperatures above the apparent glass transition temperature. Using temperature-dependent spin-polarized scanning tunnelling microscopy (SP-STM), we imaged the emergence of long-range order from the spin-Q glass state as a function of increasing temperature. Using atomic-scale imaging, we quantified the various short-range and long-range Q states. To analyse the emergence of long-range order, we developed two analytical tools that quantify the observed phase transition temperature on the basis of statistical analysis of the spatially dependent magnetization images. Using atomistic spin dynamics simulations, we qualitatively reproduced the two observed magnetic phases below TN, and related this complex behaviour to the competing interactions driven by the two sublattices of the double hexagonal close-packed (dhcp) crystal structure.

The spin-Q glass state of Nd is characterized by the presence of so-called Q pockets19,20, which are each defined by a distribution of favourable Q states. The favourability of multiple Q states is driven by the competing exchange interactions, linked to the dhcp structure of Nd (Fig. 1a). The self-induced spin glass behaviour can be measured by magnetization images taken on the Nd(0001) surface using SP-STM (Fig. 1b) (Methods). The spin-Q glass state can be distinguished by small spatial regions with a length scale on the order of 10–100 nm (as schematically depicted in Fig. 1c) with well-defined local periodicity (Fig. 1e–g). However, the multiplicity of Q states leads to a varying spectral distribution of Q states, depending on the local region, and varies spatially across the surface (Fig. 1c). The local periodicity can be extracted using fast Fourier transforms (FFT) of the magnetization images, or so-called Q-space images, which reveal the periodicities of the local magnetic order in a given region (Fig. 1h–j). By imaging regions with a statistically significant number of spins, Q-space imaging reveals the relevant Q pockets at a given temperature (Fig. 1d). For sufficiently low defect densities (here ~0.0025 ML, where 1 ML corresponds to a monolayer of Nd(0001)), all relevant Q pockets (QA = 1.1–1.5 nm−1, QB = 1.75–2.9 nm−1 and QC = 4.1–5.5 nm−1) are visible at T = 5.1 K, including the smallest Q pockets, which were previously only observed at lower temperatures20. We note that the reciprocal atomic lattice would have corresponding spots in a given Q-space image at magnitudes of 19.83 nm−1, which is too large to be illustrated in the Q-space maps.

Fig. 1: Spin-Q glass state of Nd(0001) at 5 K.
figure 1

a, The dhcp structure of Nd(0001) characterized by magnetic interactions between both cubic (cub, red) and hexagonal (hex, blue) sublattices . b, Magnetization image based on SP-STM of Nd(0001) at T = 5.2 K. Mz corresponds to the projection of the sample magnetization along the direction of the tip magnetization (tunnelling current It = 100 pA) Scale bar, 50 nm. c, False-colour schematic representing the different distributions of local Q order present in the magnetization image in b. d, Corresponding Q-space image of b illustrating the various Q pockets observed at T = 5.2 K. Scale bar, 3 nm−1. e–j, Close-up real-space (e–g) and Q-space (h–j) images of b showing regions of local Q order defined by a particular set of Q vectors. Scale bars, 10 nm (e–g) and 3 nm−1 (h–j). The coloured dots correspond to the marked regions in c.

Source data

Full size image

To quantify the phase diagram of the spin-Q glass state, we performed temperature-dependent magnetization imaging on a given area below the reported TN (19.9 K)27. In Fig. 2, we illustrate the same imaged area from Fig. 1b (200 × 200 nm2), first measured at T = 11 K (Fig. 2b) and reimaged at T = 5.1 K (Fig. 2a). In comparison to the low-temperature spin-Q glass phase, the 11 K image exhibits large-scale domains, separated by well-defined domain walls (shown by dashed lines in Fig. 2b), with long-range and well-defined multi-Q order. At first glance, all low Q states have disappeared. Using the Q-space image (Fig. 2d), we quantified the values of the multi-Q states, which we describe as diamond-like and stripe-like patterns in the magnetization image, respectively. Close-up views of these patterns and their respective multi-Q states are shown in Fig. 2e–f. We emphasize that from the resolution of the FFT (Fig. 2d), the accuracy of the q value is about ±0.07 nm−1, whereas the angular precision is about ±1.4°. Within this accuracy, we found that the multi-Q state of the diamond-like patterns (Fig. 2g) can be described as a combination of the Q vectors \({{{{{\mathbf{q}}}}}}_1^{\mathrm{D}}\) and \({{{{\mathbf{q}}}}}_2^{\mathrm{D}}\), both with magnitudes of 2.64 nm−1 and oriented along the \(\left[ {\bar 12\bar 10} \right]\) and \(\left[ {\bar 1\bar 120} \right]\) directions, respectively. The multi-Q state of the stripe-like patterns (Fig. 2h) can be expressed as a combination of three Q vectors: \({{{{{\mathbf{q}}}}}}_1^{\mathrm{S}}\) and \({{{{{\mathbf{q}}}}}}_2^{\mathrm{S}}\) with magnitudes of 2.41 nm−1 and 2.69 nm−1 and oriented near the \(\left[ {2\bar 1\bar 10} \right]\) and \(\left[ {\bar 1\bar 120} \right]\) directions, respectively, as well as \({{{{{\mathbf{q}}}}}}_3^{\mathrm{S}}\) with a magnitude of 5.12 nm−1 and oriented close to the \(\left[ {\bar 12\bar 10} \right]\) direction. Different from the Q vectors that describe the diamond order, these Q vectors were not exactly aligned with the crystallographic directions. The angles of the Q vectors corresponding to the stripe order varied between 115° and 120°. We note that the Q vectors of the two observed domains presented similar vectors, which led to an apparent blurring/splitting of certain spots when averaging over all domains (Supplementary Fig. 4). We also note that the observed Q vectors in the multi-Q phase fell within the QB and QC pockets observed for the spin-Q glass phase described above. After cooling back to T = 5.1 K (Fig. 2a), the long-range ordered multi-Q state disappeared and the spin-Q glass state reappeared with an aged Q-state distribution that, when compared with the pre-annealed sample, exhibited aging. With further temperature cycling (Supplementary Section 2), we observed the same ordered multi-Q state at higher temperature, without any indications of aging, whereas we always observed aging of the spin-Q glass states at the lowest temperatures. This observation clearly indicates that there is a glass transition temperature (TG) at a temperature below TN that separates the glassy state from a well-defined ordered state.

Fig. 2: Emergence of long-range multi-Q order from the spin-Q glass state at elevated temperature.
figure 2

a,b, Magnetization images of the same region at T = 5.1 K (a) and 11 K (b) (It = 100 pA). Scale bars, 50 nm. The dotted lines mark the domain walls between the two observed domains. c,d, Corresponding Q-space images, illustrating the changes from strong local Q order (that is, a lack of long-range order) towards multiple large-scale domains with well-defined long-range multi-Q order. Scale bars, 3 nm−1. e,f, Close-up images of the diamond-like (e) and stripe-like (f) patterns. Scale bar, 5 nm. The locations of these images are shown by the white squares in b. g,h, Display of multi-Q state maps of the two apparent domains in the multi-Q ordered phase; g corresponds to the diamond-like pattern and h corresponds to the stripe-like pattern. Scale bar, 3 nm−1. Those multi-Q state maps were extracted from the close-up views (40 × 40 nm2) and their FFT shown in Supplementary Fig. 4. A similar filtering procedure to that described in Supplementary Section 4 was performed. The arrows mark the irreducible Q vectors describing the order in each domain.

Source data

Full size image

To quantify TG and the multi-Q phase, we measured magnetization images of the same spatial area at several temperatures. The relevant Q-space images for T = 5.1 K, 6.6 K, 7.5 K, 8.9 K and 11 K are presented in Fig. 3a–e. The corresponding magnetization images can be found in Supplementary Fig. 5. For T < 8 K, the observed Q pockets were extremely sensitive to the given sample temperature. There was a smooth trend with increasing temperature towards fewer and sharper Q pockets. The lowest- and highest-magnitude Q spots faded with increasing temperature, eventually leading to the well-defined multi-Q state. This behaviour can be seen in the temperature evolution of line cuts of the FFT as shown in Fig. 3f. We observed that the QA pocket intensity vanished while the variance in the QB and QC pockets reduced, leading to sharp peaks for T > 8 K. The observation of a multi-Q state with well-defined domains can be seen from T = 8.3 K and remains robust up to the highest measured temperatures (T = 15.6 K). This is consistent with the ‘double-q’ phase observed in neutron diffraction26,28,29. Furthermore, the Q-vector values we measured on the surface were in good agreement with the values in the range of 2.54–2.78 nm−1 measured by neutron diffraction for bulk Nd. We note that above 15.6 K we observed an increase in surface contamination along with the diffusion of defects, limiting the temperature range (T < 15.6 K) over which we could image and properly compare.

Fig. 3: Multi-Q magnetic transition and extracted TG.
figure 3

a–e, Q-space images of the same 200 × 200 nm2 region at the indicated temperatures. Scale bars, 3nm−1. f, Line cuts across the QA pocket (left, marked orange in a) and the QB and QC pockets (right, marked green in a) at the indicated temperatures. The coloured lines represent Savitzky–Golay filtered versions of the black lines with a frame length of five data points. g, Q-state divergence as a function of the temperature extracted from the real-space images used for a–e. The blue/red lines correspond to linear fits in the spin-Q glass phase and multi-Q phase, respectively. The background shading in g is a qualitative guide to illustrate the two different phases. The dashed line in g correlates with the critical temperature. The definition of the error bars can be found in the Supplementary Information.

Source data

Full size image

To quantify the transition from the glass phase to the multi-Q phase, we developed an analytical sampling method. This is based on the observation that in the spin-Q glass phase, there is strong local Q order, but no long-range order. In contrast, the multi-Q phase exhibits clear long-range order defined by fewer select Q vectors than the glass phase. To this end, one can analyse sections of the Q-space maps as a function of temperature, as done in Fig. 3f. However, it is not sufficient to analyse the Q-space maps as a function of temperature, as the development of long-range order is only indirectly related to the changes in the intensity and variance. On the basis of this observation, we developed a method that uses both the real-space and reciprocal-space magnetization, labelled M(r) and M(Q), respectively. First, we randomly sampled a given area in M(r), and extracted the relevant local Q vectors from the corresponding M(Q) (Supplementary Information). The corresponding M(Q) of this randomly sampled area was then compared to subsequent randomly sampled areas. On the basis of the statistical sampling, we used the computed Jensen–Shannon divergence of the various distributions produced from the sampled areas and calculated the total Q-state divergence (\({{{\mathcal{D}}}}_Q(T)\)) for all the randomly sampled areas at a given temperature. Figure 3g illustrates \({{{\mathcal{D}}}}_Q(T)\) for all measured temperatures. The value of \({{{\mathcal{D}}}}_Q(T)\) was maximally one when the sampled distributions of Q vectors were maximally dissimilar, or minimally zero when these distributions were identical. From Fig. 3g, it can be seen that there was a reduction of the value of \({{{\mathcal{D}}}}_Q(T)\) with increasing temperature and an eventual plateau, consistent with the development of long-range order as a function of temperature that persists above a given temperature (T > 8 K). The reduction in \({{{\mathcal{D}}}}_Q(T)\) can be understood resulting from the fact that a randomly sampled area at higher temperature better represents the total image as long-range order developed. We note that \({{{\mathcal{D}}}}_Q(T)\) approached a finite non-zero value due the presence of multiple domains and defects in the analysed images. From this analysis, we could extract TG = 8.1 ± 0.3 K using linear fitting and analysing where the slope of \({{{\mathcal{D}}}}_Q(T)\) approached zero. We also utilized a second complementary method, based on the recent development of complexity30 that is detailed in the Supplementary Information, which yields a similar value of TG (7.9 ± 0.2 K).

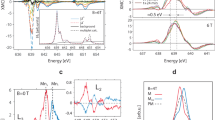
To further understand the physical origin of the spin-Q glass to multi-Q transition, we performed atomistic spin dynamics and Monte Carlo simulations based on exchange parameters obtained from ab initio electronic structure calculations (for a review, see ref. 31). We simulated the magnetic ground states and thermodynamic properties for a range of temperatures between 1 K and 15 K. The specific heat, which was obtained from the derivative of the total energy with respect to temperature31, is shown in Fig. 4a and exhibits two distinct peaks. As a peak in the specific heat indicates a magnetic phase transition, our spin simulations could thus identify two different phase transitions with increasing temperature. The low-temperature state was identified as the spin-Q glass state in ref. 20. An analysis of the two-time autocorrelation function (Supplementary Section 6), which can be extracted from the simulations, confirmed that Nd exhibits the spin-Q glass phase in the whole range of T = 0–4 K. In contrast, for the intermediate temperature range 4 K < T < 11 K, the simulations did not indicate any signs of glassy dynamics. The magnetic order in this range was determined by the static correlation function S(Q) (see Methods for computational details) and could be characterized as a traditional multi-Q phase, as we discuss further below. Above the second predicted phase transition temperature at T = 11.5 K, the system becomes paramagnetic. Although there were discrepancies between these precise temperatures and the experimental data, the phase diagram shows strong qualitative agreement with the experimental findings. Namely, below the computed TN (11.5 K), there is first an ordered phase driven by broken frustration and ultimately a self-induced spin glass phase.

Fig. 4: Atomistic spin dynamics simulations of the specific heat and sublattice-resolved S(Q).
figure 4

a, Specific heat (CV) as a function of temperature. Each peak corresponds to a phase transition at the indicated temperature. b–d, Total (S(Q)total; b) and sublattice-resolved S(Q) for the the cubic–cubic (S(Q)cub–cub; c) and hexagonal–hexagonal (S(Q)hex–hex; d) interactions at the indicated temperatures selected for each phase. The Brillouin zone (BZ) for all plots are indicated. Darker contrast corresponds to higher values, the background shading corresponds to the labelled regions in a. e, Line cuts of S(Q)total along the (Γ–M) direction for T = 1 K (blue) and T = 6 K (red). The Q pockets and Q vectors correlated to the values in the experimentally observed glass and ordered phase are indicated by grey boxes and dashed lines, respectively. The direction of the line cuts is marked on the corresponding S(Q)total plots in b. f–h, Two-time autocorrelation functions (C(tw,t)) for T = 1 K (f), 6 K (g) and 14 K (h).

Source data

Full size image

To explain what drives the spin-Q glass behaviour and causes the transition to the multi-Q state, we investigated the role of the two different sublattices present in the dhcp structure. In ref. 20, a notable difference between the magnetic interactions for the different sublattice sites was identified. For reference, these interactions have been plotted in Supplementary Fig. 12 and decomposed into the various sublattice contributions. The difference in stacking provided a sufficiently important difference in electronic structure to produce drastically different exchange values. The interaction between Nd atoms at cubic positions and atoms at other cubic positions (cub–cub in Supplementary Fig. 12) was different from that of Nd atoms at hexagonal positions that interact with other Nd atoms at hexagonal positions (hex–hex in Supplementary Fig. 12). Cross interactions between cubic and hexagonal positions (cub–hex) were also unique, which simply implies that the local symmetry gives unique short- and long-range interactions.

We investigated the sublattice effect further by studying the temporal and spatial correlations between Nd atoms at different sublattice sites. In Fig. 4b–d we show static correlation functions obtained by considering only the correlations between atoms on the same sublattice; that is, atoms at cubic and hexagonal sites in the system. For comparison, we also show the total S(Q), which shows: (1) intensity at T = 1 K at multiple locations in Q-space, which is substantially broadened compared with the multi-Q phase accentuating the spin-Q glass phase; (2) intensity at T = 6 K at few locations in Q-space with a smaller variance than at T = 1 K, indicative of a long-range ordered state, and (3) minimal intensity at T = 14 K, indicative of a transition to a paramagnetic phase. When comparing the sublattice decomposition for S(Q), we observed notable differences between the sublattice correlations: the cubic–cubic sublattice correlations (S(Q)cub–cub)) exhibited not only different maxima than the hexagonal–hexagonal sublattice correlations (S(Q)hex–hex)) but also different temperature behaviour. From our simulations we observed that the cubic–cubic correlations vanished at the first phase transition temperature, whereas the hexagonal–hexagonal correlations prevailed up to the paramagnetic transition. These results can be interpreted as follows: at low temperatures, both sublattice magnetizations have different tendencies towards magnetic order; that is, they would prefer two different magnetic orderings. It is the competition between these ordering tendencies that effectively results in the spin-Q glass behaviour. The effective strength of the exchange interactions on the cubic sublattice is weaker than the interactions on the hexagonal sublattice, which results in the cubic correlations vanishing at a lower temperature (that is, the first phase transition at T = 4 K. Without the competition from the magnetic atoms on the cubic sublattice, the magnetic order driven by the atoms on the hexagonal sites dominates and the result is then a non-glassy multi-Q state that persists up to the paramagnetic transition. The transition from the spin-Q glass phase to the ordered phase at intermediate temperature can also be seen by taking a line cut of S(Q) along (Γ–M) (Fig. 4e). An overall broadened intensity can be seen near the experimentally determined QC pocket, for T = 1 K, which substantially sharpens at T = 6 K. We note that in the calculations, only one Q state was observed in the intermediate phase, whereas a multi-Q phase was seen with both neutron diffraction (T < 19.1 K)26,27 and our STM-based studies. Although there are deviations in both the precise temperature and the Q values seen between experiments and calculations (Supplementary Section 6), the overall trends of both experimentally observed phases are reproduced in the simulations.

To identify the presence (or lack) of glassy dynamics in the magnetic phases of Nd, we studied the two-time autocorrelation function \({{C}}\left( {{{t}}_{{{\mathrm{w}}}},{{t}}} \right) = \left\langle {{{m}}_{{i}}\left( {{{t}} + {{t}}_{{{\mathrm{w}}}}} \right) \times {{m}}_{{i}}\left( {{{t}}_{{{\mathrm{w}}}}} \right)} \right\rangle\), where mi is the magnetic moment of site i, which depends on the simulated time t and the waiting time tw. In practice, the simulations start from a random distribution of atomic spins that are allowed to relax according to the atomistic Landau–Lifshitz–Gilbert equation for a time tw. After that the two-time autocorrelation was calculated for a time period t. The results of the autocorrelation simulations are shown in Fig. 4f–h, where the results for temperatures T = 1 K, 6 K and 14 K are presented. At T = 1 K the autocorrelation functions show multiple relaxation times depending on tw, which is a typical signal of spin glass behaviour20. In contrast, at T = 6 K, the relaxation behaviour was similar regardless of tw, as with a long-range ordered state. The relaxation behaviour at T = 6 K exhibited different saturation values, which can be explained by the fact that the finite-size simulations performed have no anisotropy or other considerations that keep the system from performing global rotations due to the thermal fluctuations. At T = 14 K, the system was paramagnetic and the rapid relaxation rate came from the thermally induced disorder in the simulated system.

Our experimental finding and theoretical analysis partly support, but also expand, the interpretations from neutron diffraction, susceptibility, heat capacity, thermal expansion and other measurements21,22,23,24,25,26. First, we confirm that there is an ordered multi-Q phase above TG ≈ 8.1 K (which has been referred to as T3 in the literature), driven by coupling of the hexagonal site spins. Although the neutron diffraction data was interpreted as showing that the multi-Q phase was a relatively simple double-q structure32, our data clearly show that various domains with a total of five different q vectors exist. The fact that these (and their higher harmonic) vectors are very close to each other can easily obscure their presence in reciprocal space when averaging over many domains (as exemplified in Supplementary Fig. 4e). This may explain the interpretation of the neutron diffraction data, and underscores the need for a spatially resolved technique to unravel the complex magnetic structure of Nd. Second, we confirm that the phase transition is driven by the onset of coupling of the cubic site spins. This also illustrates that the surface magnetization pattern, as probed by SP-STM, is representative of the bulk. However, the phase below 8 K was interpreted as a ‘triple-q’ magnetic structure21,24, we identified it as the glass transition point, below which no long-range order can be found. We note that we did not observe notable changes in the magnetic structure around 6 K in comparison to higher temperatures, whereas previous studies identified another phase transition near 6 K that was interpreted as a ‘quadrupole-q’ structure22,23,24,26. We merely observed gradual changes in the distribution of, and within, the various Q pockets. The most important effect is the gradual appearance with decreasing temperature of QA pockets, as well as pockets at angles far from the crystallographic axes. Although the former was not observed in neutron diffraction studies, the latter could be easily misinterpreted as stemming from a fourth vector. We would like to emphasize that the spin-Q glass phase is very sensitive to even small defect concentrations. In a previous study with a typical surface defect concentration of ~0.010 ML (ref. 20), we found that the QA pockets had already ‘melted’ away at 4.2 K. In the present data, with four times lower defect concentration, the QA pockets were visible up to TG. The defect-induced pinning of Q vectors, leading to ‘less glassiness’, may also account for the deviating observations found in neutron diffraction experiments.

In conclusion, we have demonstrated the emergence of an ordered phase when the spin-Q glass observed for elemental Nd is heated above TG. This phenomenon is distinct from the debated re-entrant spin glasses2, with the important distinction that the phase observed here is not driven by disorder, a clear coexistence phase or linked to cluster or impurity densities that may influence the magnetism. The origin of this unexpected multi-Q ordering can be traced to quenching of one set of sublattice spin correlations, which is the essential ingredient for driving the spin-Q glass phase. In magnetic systems, it is known that frustration induced by competing interactions can lead to both complicated (for example, noncollinear) magnetic ordering and to spin glassiness. We demonstrate an example of a phase transition between these states and show that the combination of frustration and temperature can lead to very counter-intuitive behaviour, with the emergence of regular and ordered magnetic patterns at relatively higher temperatures. The example of Nd provides a unique platform to investigate complex magnetization dynamics in a system with strong short-range spin correlations that can be tuned by temperature. This could be extended to various other magnetic materials that exhibit temperature-dependent modulations, such as antiferromagnetic-to-ferromagnetic transitions in FeRh (ref. 33), as well as metallic materials that are candidates for fluctuation induced order34, for example PrPtAl (ref. 8). Nd may also provide a platform to study the dynamical behaviour present in glass systems, such as dynamic heterogeneity. This gives a solid experimental and material-specific theoretical background for the concept of order from disorder, which is claimed to be of importance far beyond physics19,35.

Methods

Experimental methods

Nd islands were epitaxially grown using the Stranski–Krastanov method on a cleaned W(110) (Supplementary Section 1). The thicknesses of the islands were around 100 ML and represent bulk-like structural, electronic and magnetic properties20. The experimental study was performed in a commercial Createc low-temperature scanning tunnelling microscope/atomic force microscope, operating at a base temperature of 5 K. The temperature-dependent study was done by means of a Zener diode attached to the SPM head, allowing us to reach stable conditions between 5 K and 20 K. To obtain spin contrast we used both Cr bulk tips and Nd-coated W tips. They showed similar results, and all data shown in the main text were acquired using Cr tips, while the aging study (Supplementary Section 2) was performed using Nd-coated W tips. The magnetization images were produced by subtracting majority and minority SP-STM images20, and a median filter (1 × 6 pixels) was applied before calculating the FFT. No further data processing was applied to the Q-space images shown. The image data processing was performed using MATLAB.

Simulation methods

The simulations for the static correlation functions were done on a slab of 196 × 196 atoms with a thickness of 16 dhcp layers. The system was described using the same spin model as in ref. 20; that is, with a Heisenberg Hamiltonian using scalar Heisenberg exchange interactions calculated from density functional theory. The simulation protocol consists of first equilibrating the system using 5 × 105 Monte Carlo sweeps and then performing atomistic spin dynamics simulations to obtain a thermal average of the static correlation function S(Q). The atomistic spin dynamics simulation time was set to 100 ps, which was found to be needed to properly capture the glassy dynamics when sampling S(Q). The specific heat data were obtained by taking the numerical derivative with respect to the temperature of the total energy obtained from the same simulations used to calculate S(Q). The simulations were performed using the UppASD 5.0-867 software36, and all algorithms used are given in full detail in ref. 31.