Abstract
Modern theories of quantum magnetism predict exotic multipolar states in weakly interacting strongly frustrated spin-1/2 Heisenberg chains with ferromagnetic nearest neighbor (NN) inchain exchange in high magnetic fields. Experimentally these states remained elusive so far. Here we report strong indications of a magnetic field-induced nematic liquid arising above a field of ~13 T in the edge-sharing chain cuprate LiSbCuO4 ≡ LiCuSbO4. This interpretation is based on the observation of a field induced spin-gap in the measurements of the 7Li NMR spin relaxation rate T 1 −1 as well as a contrasting field-dependent power-law behavior of T 1 −1 vs. T and is further supported by static magnetization and ESR data. An underlying theoretical microscopic approach favoring a nematic scenario is based essentially on the NN XYZ exchange anisotropy within a model for frustrated spin-1/2 chains and is investigated by the DMRG technique. The employed exchange parameters are justified qualitatively by electronic structure calculations for LiCuSbO4.
Similar content being viewed by others
Introduction
Strong electronic correlations in solids may give rise to novel ground states of matter such as electronic liquid crystal phases in correlated metals or spin liquid states in insulating quantum magnets1, 2. Theory predicts that in the latter systems conventional long-range magnetic dipolar order can be suppressed down to T = 0 due to frustration of magnetic interactions and/or quantum fluctuations (for a review see, e.g., ref. 3). Though individual spins remain non-ordered in the spin liquid, higher rank magnetic multipoles (quadrupoles, octupoles etc.) can order under favorable conditions4. Such an exotic multipolar (MP) order does not break the time-reversal symmetry and is often referred to as a “hidden order” since it is difficult to detect experimentally by most of the available techniques sensitive to magnetic dipole moments, only. However, the spin rotational symmetry is broken in this hidden phase which is therefore also called a spin-nematic state in the simplest quadropolar case, in analogy with the nematic order in liquid crystals, where the translational crystalline order is absent but the rotational symmetry is broken.
A prominent example of a spin liquid is a single Heisenberg spin-1/2 chain with the nearest neighbor (NN) antiferromagnetic (AFM) interaction whose ground state is described by the so-called gapless Tomonaga-Luttinger (TL) spin liquid5. Further complexity can be brought in the problem by including an AFM next-nearest neighbor (NNN) interaction J 2. Irrespective of the sign of the NN coupling J 1, AFM J 2 causes spin frustration and may yield different phases depending on the frustration ratio α = |J 2/J 1|6,7,8. In particular, pioneering theoretical works8,9,10,11,12,13,14,15,16 devoted mainly to one-dimensional (1D) isotropic frustrated J 1(FM) − J 2(AFM) chain models have predicted unusual field-induced MP states near the saturation field H sat above which at T = 0 all spins are aligned by an external magnetic field H. These states form a TL-liquid of multiple p-bound states of magnons corresponding to nematic, triatic, quartic MP phases (\(p=2,3,4,\ldots \)). For interacting chains within 2D or 3D arrangements, the MP phases strongly compete with collinear longitudinal H-dependent incommensurate spin density wave (SDW p ) phases predominant at lower fields17. (Here the index p indicates the neighboring MP state.) Albeit MP phases might coexist with non-collinear strongly fluctuating dipolar states18.
Low-D spin networks can be found in 3D transition metal (TM) oxides. A specific geometry of the chemical bonds can yield chains of TM ions magnetically coupled mainly via oxygen ligands in one direction. A sizable and still increasing number of frustrated CuO2 spin-1/2 chain compounds is currently available. Nevertheless, the very existence of an MP state is not yet proved. Also the possibility of a coexistence of an MP state (and even of an ordered phase) with some other dipolar magnetic phases or corresponding strong fluctuations of them remains unclear up to now. The quest for MP phases focussed in the last years mainly on two compounds, namely LiCuVO4 19,20,21 and PbCuSO4(OH)2 (linarite)22. Both materials exhibit at ambient fields a 3D-non-collinear spiral type dipolar order at low T due to residual interchain couplings. Various field-induced collinear SDW p phases were detected but the theoretically proposed neighboring MP phases at higher fields remain elusive. In particular, in the case of LiCuVO4 it was concluded that the spin-nematic phase, if it exists at all, could be established only in a very narrow field range of 1 T below \({\mu }_{0}{H}_{{\rm{sat}}}\approx 41.4\,\,{\rm{T}}\) 20. For completeness we note, that a suggested “bond-nematic” phase with a coexisting collinear SDW2-magnetic structure and nematic fluctuations proposed in ref. 23 has been arguably questioned in ref. 17 based on the analysis of an isotropic quasi-2D field-theory model for interacting chains. The very broad phase below μ0 H sat ~ 43 T was ascribed instead to the mentioned above SDW2-phase, only. Indeed, from the theoretical side it has become clear that the interchain coupling that causes dipolar magnetic order can easily destroy fragile MP phases whereas easy-axis exchange anisotropy may stabilize them24, 25. In this context the recent synthesis and the first physical study of a novel member of the frustrated CuO2-chain family, the strongly frustrated J 1(FM) − J 2(AFM) quasi-1D compound LiCuSbO4 (Fig. 1), is noteworthy26. It exhibits short-range incommensurate spin correlations below T ~ 9 K but, in contrast to the spiral spin-chain compounds LiCuVO4 and LiCuZrO4 27, 28, does not show long-range magnetic order at H = 0 down to T ~ 0.1 K. This points to a very weak or specific interchain coupling in LiCuSbO4. Moreover, a sizeable exchange anisotropy was estimated here, too.
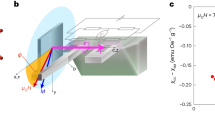
Top: crystallographic structure of LiSbCuO4 ≡ LiCuSbO4. Cu2+ ions (orange) are bonded covalently to four nonequivalent O2− ligands and form buckled non-planar CuO4 plaquettes. Edge-shared CuO4 plaquettes form non-ideal alternatingly tilted stacks (along the c-axis) of CuO2 chains (colored yellow and brown, respectively) running along the a-axis. The chains are interconnected with SbO6 octahedra shown in blue-green. The Li+ ions (bright blue balls) occupy two positions. The split Li1 position is shown with overlapping balls. Bottom: Schematic view of two neighboring individual CuO2 chains within the ab-plane ignoring their tilting and buckling (cf. Top). The relevant intrachain exchange paths are indicated by black arcs. The four nonequivalent O2− ions within a CuO4-plaquette give rise to different left and right Cu-Cu bonds along the a-axis causing this way an alternated \(({J}_{1},{J}_{1}^{^{\prime} })\) − J 2 spin chain with small nonequivalent third neighbor couplings \(({J}_{3},{J}_{3}^{^{\prime} })\). Black arrows denote the magnetically active spins and bright blue arrows the DM vectors that are confined to the (bc)-plane ⊥ to the chain axis whereas their mutual orientation can be arbitrary. For illustration the two limiting configurations, uniform and staggered are depicted that have been studied theoretically in single-chain approximation. Dark dashed line: the frustrated weak interchain couplings J int and \({J}_{int}^{^{\prime} }\sim 1\,{\rm{K}}\ll {J}_{2} < |{J}_{1}|\), \(|{J}_{1}^{^{\prime} }|\) in the basal (ab)-plane (see also Top).
Here we report the results of 7Li NMR relaxation rate \({T}_{1}^{-1}\) measurements in LiCuSbO4 in a broad field range of 3–16 T. A surprising contrasting behavior of \({T}_{1}^{-1}\) vs. T is observed around a special crossover field \({\mu }_{0}{H}_{{\rm{c}}1}\approx 13{\rm{T}}\) within a rather narrow field range. At H < H c1, \({T}_{1}^{-1}\) (T) exhibits a diverging power-law behavior suggesting a static magnetic order at lower temperatures. In contrast, in higher magnetic fields H > H c1, \({T}_{1}^{-1}\) (T) turns into an exponential decrease indicative of the opening of a spin gap above the narrow crossover high-field region. Our analysis of the static magnetization and ESR data rules out saturation of the magnetization or Dzyaloshinskii-Moriya (DM) couplings as possible conventional reasons for the opening of this spin gap. We argue that this gap should be considered as one of the signatures of a distinctive but nevertheless naturally “hidden” for a dipolar sensitive probe MP state. In particular, we argue that such a peculiar behavior of \({T}_{1}^{-1}\) is due to the occurrence of a dipolar spin-liquid state confined to a certain field range below H c1 which crosses over to the competing anisotropic spin-nematic liquid state which is stabilized above H c1. Our theoretical analysis employing the density matrix renormalization group (DMRG) technique indeed reveals a broad stability region of an unconventional spin-nematic liquid state in LiCuSbO4 setting in above ~13 T and extending to \({\mu }_{0}H\gtrsim 20\,{\rm{T}}\). Altogether, our experimental observations and model calculations provide strong arguments to identify a long-sought nematic state in LiCuSbO4 and stress the importance of anisotropic exchange for its relevance.
Results
Magnetization measurements
The T-dependence of the static magnetic susceptibility \(\chi (T)=M/H\) of LiCuSbO4 measured at a field μ 0 H = 3 T is shown in Fig. 2. It appears to be in accord with the data of ref. 26. In particular, a characteristic maximum of χ(T) is observed at ~9 K. The dependence of the static magnetization M on the magnetic field H measured in pulsed fields up to 20 T at a low T = 0.45 K is shown in Fig. 3(a). The M(H) curve exhibits a characteristic S-shape. At fields below ~6 T M increases almost linearly and develops an upward curvature at higher fields as expected for a simple isotropic 1D-chain29. However, by approaching ~12 T the M(H) dependence weakens but surprisingly no saturation is observed up to the highest field of 20 T. Such a peculiar M(H) dependence appears to be a remarkable feature of LiCuSbO4 as discussed in detail below. (Linarite and some other anisotropic CuO2 chain systems with a low crystallographic symmetry30 show the similar feature but at unconvenient for experimental studies higher fields above 30 T in the latter case).
Scaling of Knight shift (K(3 T) ◾, K(9 T)  , and K(15 T)
, and K(15 T)  ) and macroscopic susceptibility (χ(3 T) —, χ(16 T)
) and macroscopic susceptibility (χ(3 T) —, χ(16 T)  ). The susceptibility at 16 Tesla has been reproduced from Dutton et al.26.
). The susceptibility at 16 Tesla has been reproduced from Dutton et al.26.
Field dependence of the magnetization at T = 0.45 K (a). Selected ESR spectra at different temperatures at frequencies ν = 95 GHz (b), and ν = 360 GHz (c), and a summary of the frequency vs. field dependence of the ESR peaks at a low T plotted together with a spectrum at ν = 405 GHz (d). Note the satellite peaks in the spectra in panel (c) that develop at T < 20 K. In (d), symbols - experimental peak positions P1, P2 and P3, solid and dashed lines are linear fits. The main peak P2 follows a linear gapless branch \({\nu }_{2}=({\mu }_{{\rm{B}}}/h)gH\) with g = 2.18, whereas the satellite branches P1 and P3 \({\nu }_{\mathrm{1,3}}={{\rm{\Delta }}}_{\mathrm{1,3}}+({\mu }_{{\rm{B}}}/h)gH\) exhibit offsets \({{\rm{\Delta }}}_{1}\approx 35\,{\rm{GHz}}\) and \({{\rm{\Delta }}}_{3}\approx -27\,{\rm{GHz}}\). (see the text).
ESR measurements
High-field ESR spectra of LiCuSbO4 at all measured frequencies at temperatures T > 20 K consist of a symmetrical single line with the shape close to a Lorentzian [Fig. 3(b,c)]. Considering the polycrystalline form of our samples, this suggests that the anisotropy of the g-factor, which otherwise produces a characteristic asymmetric pattern of the spectrum31, is smaller than the width of the signal. The g-factor of 2.18 obtained from the slope of the ν(H) dependence \(g=(h/{\mu }_{{\rm{B}}})\,\nu /H\) [Fig. 3(d)] is a typical powder-averaged value for a Cu2+ ion in a distorted octahedral ligand coordination32. At ν = 95 GHz which corresponds to the resonance field \({\mu }_{0}{H}_{{\rm{res}}}\approx 3.1\,\,{\rm{T}}\) the signal remains practically a single line down to the lowest temperature. At \(T\mathop{ < }\limits_{ \tilde {}}20\,{\rm{K}}\) it merely exhibits a rather small shift to smaller fields and slightly broadens, but shows no indication of an onset of a static magnetic ordering. In contrast, at ν ≥ 270 GHz and \({\mu }_{0}{H}_{{\rm{res}}}\ge 8.8\,\,{\rm{T}}\) the satellite peaks P1 and P3 begin to develop besides the central peak P2 at \(T\mathop{ < }\limits_{ \tilde {}}20\,{\rm{K}}\) [Fig. 3(c,d)]. Their offset of ~0.8–1 T from the main peak remains practically constant, whereas the intensity increases with increasing ν (and H) and decreasing T. The frequency vs. field dependence of P1 and P3 approximately follows the relation \({\nu }_{1,3}={{\rm{\Delta }}}_{\mathrm{1,3}}+({\mu }_{{\rm{B}}}/h)\,gH\) with \({{\rm{\Delta }}}_{1}\approx 35\,{\rm{GHz}}\) and \({{\rm{\Delta }}}_{3}\approx -27\,{\rm{GHz}}\).
NMR measurements
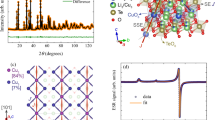
Frequency swept 7Li NMR spectra in a field of 3, 9, and 15 Tesla are shown in Fig. 4 (see methods). The width of the spectra (square root of the second moment) in 3 T and at 296 K is 26.5 kHz, indicating that any quadrupolar broadening or splitting must be significantly smaller than this value. Therefore, the shape of the powder pattern is solely determined by the anisotropic dipolar hyperfine coupling of the two different Li sites in LiCuSbO4 times the susceptibility in the paramagnetic state. The width of the spectra scales perfectly linear with the magnetic field, indicating that the broadening of the spectra is entirely of magnetic origin. The scaling holds also at low temperatures, evidencing the absence of magnetic ordering in all fields down to ~2 K. The dipolar hyperfine coupling tensor has been obtained by lattice sum calculation and is given in the Supplement.
NMR spectra at 3, 9 and 15 Tesla. Note that the width of the x-axis is scaled by a factor 9/3 and 15/3 for 9 and 15 Tesla with respect to the x-axis of the 3 Tesla spectra. This way, this figure shows that the broadening is paramagnetic, and that there is no magnetic order down to ~2 K in any field.
The Knight shift, K, has been extracted from the maximum of the spectra. According to the calculated dipolar hyperfine coupling tensor, both Li sites contribute to the maximum with different elements of the tensor. K is plotted together with the macroscopic susceptibility, in Fig. 2. The scaling of the Knight shift with χ, i.e., K = A hyp · χ, is good down to ~15 K. Below 15 K, the K shows qualitatively the same T-dependence but the error bars of K become large at low temperatures due to the strong magnetic broadening. However, the similar T-dependences indicate that both, K and χ, are dominated by the intrinsic susceptibility and that impurity contributions are small.
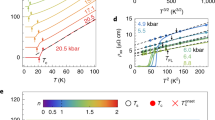
The results of the measurements of the 7Li nuclear spin-lattice relaxation rate \({T}_{1}^{-1}\) at the central peak of the NMR spectrum33 are shown in Fig. 5. In Fig. 5(a) \({T}_{1}^{-1}\) vs. temperature is plotted on a log-log scale for six different fields from 3 to 16 Tesla. At high T, \({T}_{1}^{-1}\) is almost constant and field-independent as expected for a 1D spin system. However, at low T, below ~30 K, a dramatic field dependence develops, resulting in a difference of almost three orders of magnitude between 3 and 16 T at the lowest temperatures. For low fields below 12 T (Fig. 5(b)), \({T}_{1}^{-1}\) diverges at low temperatures (for 3 T, \({T}_{1}^{-1}\) increases below 7 K, for 9 and 12 T, \({T}_{1}^{-1}\) increases already below 15 K). In contrast, for fields above 13.5 T, \({T}_{1}^{-1}\) decreases almost exponentially at low T. This is highlighted in Fig. 5(c,d), where \({T}_{1}^{-1}\) is plotted vs. the inverse temperature T −1.
(a) \({T}_{1}^{-1}\) vs. temperature for different magnetic fields; (b) The \({T}_{1}^{-1}\) (T) dependence at T < 20 K for 3 T, 9 T and 12 T; (c,d) \({T}_{1}^{-1}\) vs. inverse temperature T −1 at T < 20 K for fields >13 T. Solid lines in (b–d) are model curves according to Eq. (3).
Discussion
The central experimental result of this work is an observation of distinct temperature and magnetic field dependences of the 7Li NMR relaxation rate \({T}_{1}^{-1}\) in the short-range ordered (SRO) state of LiCuSbO4 below ~10 K, as shown in Fig. 5, which will be discussed in the following.
NMR relaxation in magnetic solids
In magnetic materials, the nuclear spin lattice relaxation rate, \({T}_{1}^{-1}\), is typically caused by the transverse (i.e. ⊥ to the nuclear spin quantization axis) components of the time-dependent fluctuating field exerted on the nuclei by the electron spin system. It can be expressed in terms of the Fourier transforms \({S}^{z,\pm }(q,\omega )\) of the time-dependent longitudinal and transverse spin-spin correlation functions \(\langle {S}_{j}^{z}(t){S}_{0}^{z}\mathrm{(0)}\rangle \), \(\langle {S}_{j}^{+}(t){S}_{0}^{-}\mathrm{(0)}\rangle \) and \(\langle {S}_{j}^{-}(t){S}_{0}^{+}\mathrm{(0)}\rangle \), respectively34:
Here q is the wave vector, \({\langle \cdots \rangle }_{T}\) means the thermal average, γ e/n are the gyromagnetic ratios of the electron and the probed nucleus, and \({A}_{\parallel ,\perp }(\overrightarrow{q})\) are the hyperfine form factors of the probed nucleus. The subscripts \(\parallel \) and \(\perp \) denote the hyperfine tensor components generating the transversal components of the fluctuating local field at the nuclear site due to the longitudinal 〈zz〉 and transversal 〈+ −〉 spin-spin correlations, respectively. For \(\hslash {\omega }_{{\rm{NMR}}}\ll {k}_{{\rm{B}}}T\), \({S}^{z,\pm }(q,\omega )\propto {\chi }_{z,\pm }^{^{\prime\prime} }(q,\omega ){k}_{{\rm{B}}}T/\hslash {\omega }_{{\rm{NMR}}}\), where \({\chi }_{z,\pm }^{^{\prime\prime} }(q,\omega )\) is the imaginary part of the dynamical electron spin susceptibility, \({\omega }_{{\rm{NMR}}}\) is the NMR frequency, k B and ħ are the Boltzmann’s constant and the reduced Planck constant, respectively. Thus at small NMR frequencies, \(1/{T}_{1}\propto {\sum }_{q}\,\chi ^{\prime\prime} (q,\omega \to 0)T\).
Generally, filtering effects may occur such that the hyperfine coupling is peaked (or zero) for certain q-vectors. However, the crystal structure of LiCuSbO4 indicates that both Li sites are coupled to several Cu sites from different chains, suggesting a rather weak dependence of \({A}_{\parallel ,\perp }\) on q. Since the coupling between the 7Li nuclear spin and the Cu spins is of dipolar nature both the longitudinal and the transversal terms in Eq. (1) are expected to contribute to the relaxation. Indeed, our estimates with the dipolar hyperfine model have revealed comparable contributions from 〈zz〉 and 〈+ −〉 correlations to the transversal field at both Li sites (see, Suppl.).
Field dependence of T1 −1
In weakly coupled unfrustrated critical simple AFM Heisenberg chains in the paramagnetic state far above the Neél ordering temperature \({T}_{{\rm{N}}}\ll T\ll J/{k}_{{\rm{B}}}\), the rate \({T}_{1}^{-1}\) in general continuously increases with decreasing T and/or increasing the magnetic field H up to the saturation field and tends to diverge by approaching T N. This is mainly due to the growth of the \(\langle {S}_{j}^{+}(t){S}_{0}^{-}\mathrm{(0)}\rangle \) correlation function with increasing H and decreasing T whereas \(\langle {S}_{j}^{z}(t){S}_{0}^{z}\mathrm{(0)}\rangle \) decays smoothly following a power law35,36,37.
In LiCuSbO4, however, \({T}_{1}^{-1}\) shows a non-monotonous and even contrasting behavior with respect to temperature and magnetic field. At relatively small fields the low-temperature region is determined by a more or less sharp increase of \({T}_{1}^{-1}\) (T) (Fig. 5) pointing to the vicinity of a critical magnetically ordered state at a lower temperature. Especially at μ 0 H = 9 T the increase is substantially more pronounced than at lower fields such as for 3 T indicating an increase of the ordering temperature of the presumable magnetic phase. Such a behavior is not expected for an ordinary antiferromagnetic Neél state where T N is usually suppressed by an external magnetic field. In fact, the field region around 9 T is also identified by the low-temperature anomaly in the magnetic specific heat in ref. 26. It has been conjectured in that work to be a signature of an unusual field-induced magnetic phase in LiCuSbO4.
One further and even more striking feature, which can be easily recognized in Fig. 5, is the occurrence of a threshold field of ~13 T that separates the upturn behavior from a drastic suppression of \({T}_{1}^{-1}\) vs. T. Indeed, plotting these data points for fixed temperatures as a function of the field, yields a set of curves with a sharp general crossing point at \({\mu }_{0}{H}_{{\rm{c}}1}\approx 13\,{\rm{T}}\), usually denoted in the literature as an isosbestic point (IBP)38 (Fig. 6). Since the nuclear \({T}_{1}^{-1}\) is governed by fluctuating fields at the nuclear site produced by electron spins, the IBP at 13 T may be identified as the critical field that separates two regimes with different types of magnetic fluctuations to be discussed in detail below. Indeed, at low-temperatures T ≤ 10–15 K which are of special interest here, the observed IBP coincides also with an inflection point (IFP). Using the generic linear field dependence \(1/{T}_{1}-const\propto (H-{H}_{{\rm{c}}1})\) in the vicinity of an IFP at H c1, it is tempting to generalize that linear behavior further into the nonlinear region at higher fields employing a quasi-exponential expression that captures also the field region slightly smaller than H c1:
Here \(1/{T}_{1}({\mu }_{0}{H}_{{\rm{c}}1}=13\,{\rm{T}})=110\,{{\rm{s}}}^{-1}\) and A is a dimensional constant taken as 1 T. As can be seen in Fig. 6, Eq. (2) describes the data in the considered field region for the lowest available temperature T = 2.2 K quite well. This way we arrive at a smooth transition across H c1 to a pronounced exponential-type behavior at high magnetic fields and low temperature.
The extracted spin-lattice relaxation rate 1/T 1 vs. external magnetic field for selected temperatures. Full lines are guides for the eye. The isosbestic point (IBP) near ~13 T is indicated by the vertical dashed line. The dashed orange curve is the fit to Eq. (2). (see the text).
Temperature dependence of T1 −1
Importantly, as can be seen in a logarithmic plot of \({T}_{1}^{-1}\) vs. T −1 in Fig. 5(c,d), a similar predominantly exponential behavior develops for the strongest fields also in the T-dependence of \({T}_{1}^{-1}\) suggesting the opening of an energy gap for spin excitations. For a consistent analysis of the whole set of experimental \({T}_{1}^{-1}\) (T) curves we have used a phenomenological combined gapped and power-law ansatz which takes into account theoretical predictions in refs 36 and 37 (see discussion below):
Here, C 1 and C 2 are the weighting factors of the two contributions, Δ is the gap, and T c and β are the critical temperature and the exponent of the power-law contribution, respectively. Possible T-dependences of the prefactors C i remain unknown so far and have been not considered here. Though polycrystallinity of the samples and a certain distribution of the relaxation rates at highest fields and lowest temperatures (Suppl., Fig. S2) are complicating factors for the analysis, the \({T}_{1}^{-1}\) (T) dependences for all applied fields can be consistently modelled yielding a good description of the experimental data as shown in Fig. 5. The field dependences of the parameters of Eq. (3) are plotted in the Suppl., Fig. S3. The critical power-law behavior of \({T}_{1}^{-1}\) (T) at 3 T which sets in at \(T\mathop{ < }\limits_{ \tilde {}}7\,{\rm{K}}\) is fully consistent with the growth of the short-ranged incommensurate correlations reported for this temperature regime in ref. 26. The fit requires a very small T c ~ 0.2 K suggesting that the 3D long-range magnetic order, if present at all, is shifted to very low temperatures. At 9 T, however, T c is pushed up to ~1.5 K indicating the proximity to a new, field-induced magnetic state that has been revealed in the specific heat data in ref. 26. Further increase of the field up to 12 T yields a reduction of T c down to ~1 K, again consistent with the fading of the magnetic anomaly in the specific heat26. Interestingly, the best agreement with experiment for H = 12 T requires a non-zero gap value Δ ~ 2 K in the first term of Eq. (3) implying the contrasting gapped and critical power-law contributions to \({T}_{1}^{-1}\) (T) with Δ > 0 and β < 1. By crossing the IBP \({\mu }_{0}{H}_{{\rm{c}}1}\approx 13\,{\rm{T}}\) the critical growth of \({T}_{1}^{-1}\) (T) by lowering T turns into a decay corresponding to the sign change of the exponent β (Fig. 7, inset). Concomitantly the weight C 1 of the gapped term in Eq. (3) increases on expense of the decreasing weight C 2 of the power-law term (Suppl., Fig. S3). At the same time Δ increases non-linearly (Fig. 7). Despite the smallness of the weighting factor C 2 at H > H c1, the finite power law contribution T β in Eq. (3) with positive β, in contrast to β < 0 for H < H c1, is required to achieve the best fit of \({T}_{1}^{-1}\) (T).
Magnetic field dependence of the gap Δ (squares) evaluated using Eq. (3). Dashed line connecting the data points is guide for the eye. Dotted line is a linear fit revealing the slope Δ/H = 1.56 K/T; Inset: the same for the exponent β in Eq. (3) (circles). Vertical dashed lines denote the isosbestic point H c1 ≈ 13 T. Shaded bar indicates a crossover region between the two distinct regimes of the 7Li T 1 relaxation. (see the text).
Exclusion of an ordinary spin gap
In principle, there is a variety of conventional reasons for the opening of a gap in the spin excitation spectrum of a quantum magnet exposed to an external field. Generally, above saturation where the spins are fully polarized, all excitations acquire a gap that linearly scales with H. In the frustrated J 1(FM) − J 2(AFM) chain a two-magnon excitation is expected to have the lowest energy (see, e.g., ref. 16). In the case of LiCuSbO4, neglecting the non-linearity of the Δ(H) dependence in the crossover region, the increase of Δ amounts to Δ/μ0 H = 1.56 K/T (Fig. 7). This slope is in accord with the Zeeman energy of the flip of a single spin, i.e. a one-magnon excitation, which with the g-factor g = 2.18 obtained in the ESR experiment would amount to gμ B/μ 0 k B = 1.47 K/T. Correspondingly, the two-magnon slope should be ~3 K/T. Anyhow, we note that it would be unreasonable to identify \({\mu }_{0}{H}_{{\rm{c}}1}\approx 13\,{\rm{T}}\) as an effective saturation field. Our measurements of the static magnetization at very low T did not reveal a saturation of M(H) even in 20 T [Fig. 3(a)]. This finding is supported by our DMRG results (see below) showing that in a situation of the symmetric exchange anisotropy present in LiCuSbO4, there is no well defined saturation field at all in a literal sense, i.e. the full saturation at T = 0 is achieved only asymptotically [Fig. 8(a)].
(a) Experimental magnetization curve at 0.45 K and theoretical magnetization curve calculated for \(({J}_{1}^{x},{J}_{1}^{y},{J}_{1}^{z})=(-1.07,-0.99,-1)\) and J 2 = 0.28. Inset: enlarged figure around kink in the theoretical curve. (b) Nematic correlation for a homogeneous DM coupling γ = 0, 0.02, 0.04, and 0.06. (c) The same for a staggered DM coupling. (d) Temperature dependence of the nematic correlation. The shaded area depicts the field range where a spin gap was observed in the NMR experiment.
Another possible reason for a field induced gap could be the presence of staggered antisymmetric Dzyaloshinskii-Moriya (DM) interactions. Due to the low crystallographic symmetry, various DM interactions are generally allowed in LiCuSbO4 (see below). Their magnitude in LiCuSbO4 can be judged from the ESR data, because ESR is very sensitive to magnetic anisotropies. Assuming that the strongest antisymmetric DM coupling is present for the intra-chain NN bond with the DM vectors perpendicular to the Cu chain (see Fig. 1 and Suppl.), a strongly anisotropic gap should open for fields applied along the chain39. Such a gap results in a shift of the ESR signal for this field direction proportional to H 3 at low temperatures \(T < J/{k}_{{\rm{B}}}\) 40, 41. However, experimentally the frequency vs. magnetic field dependence of the ESR signal is linear within the error bars over a broad field range [Fig. 3(c)] which suggests that the staggered DM component of the antisymmetric exchange is small in LiCuSbO4. The uniform component of the DM exchange can give rise to a field independent anisotropic gap which for certain field orientations may yield a splitting of the ESR signal42, 43. Such a fine structure of a powder ESR spectrum of LiCuSbO4 is indeed found at high fields [Fig. 3(c)]. Its extend of the order ≈±30 GHz = ±1.5 K could give then the energy scale of the uniform DM component which is of a percent order of the isotropic and symmetric anisotropic exchange couplings as estimated from the magnetization data (see below).
Evidence for spin-nematicity
Ruling out the above discussed ordinary grounds for the field-dependent spin gap in LiCuSbO4 enables us now to focus on a possible, more sophisticated reason for the gap opening by approaching the IBP \({\mu }_{0}{H}_{{\rm{c}}1}\approx 13\,{\rm{T}}\) from the low-field side. According to the proposed theoretical precursor phase diagram of the isotropic frustrated J 1 − J 2 spin chain11, 12, 14, sufficiently high magnetic fields yet smaller than the saturation field induce a multicomponent spin liquid including multi-magnon bound states. The two-magnon bound state (p = 2), corresponding to a precursor of a quadrupolar (spin-nematic) phase with a finite four-spin correlation function \(\langle {S}_{j}^{+}{S}_{j+1}^{+}{S}_{0}^{-}{S}_{1}^{-}\rangle \) is the simplest one. At the lower side of this field region a collinear and incommensurate quasi long-range ordered SDW2-phase is stabilized since \(\langle {S}_{j}^{z}{S}_{0}^{z}\rangle \) is the slowest decaying correlator. At the higher field side, above a certain crossover field, the quadrupolar 〈+ + − −〉 correlations might become nevertheless dominant yielding a competing quasi long-range ordered pronounced spin-nematic state11, 12, 14. In both SDW2 and the spin-nematic parts of the quadrupolar TL liquid, the transverse spin correlation function \(\langle {S}_{j}^{+}{S}_{0}^{-}\rangle \) is expected to be gapped. This was demonstrated qualitatively for the special quasi-2D isotropic model case at T = 017 which might probably hold in the case of relevant 3D interchain couplings at finite T, too. Finally, at very low fields magnon bound states as well as the collinear SDW fluctuations/order will be suppressed. Instead, a vector chiral order, which typically arises in a spin chain due to magnetic frustration somewhat modified quantitatively by possible DM couplings, turns out to be the ground state. In this phase the gap closes and the transverse \(\langle {S}_{j}^{+}{S}_{0}^{-}\rangle \) correlation becomes dominant.
Since quadrupolar correlations do not generate any fluctuating fields at a nuclear site, Sato et al.36, 37 have proposed an indirect way to identify the quadrupolar phase of the isotropic J 1(FM) − J 2(AFM) chain and to distinguish between its SDW2 and the spin-nematic dominated regions. It is predicted that \({T}_{1}^{-1}\) due to longitudinal 〈zz〉 correlations should follow the power law ~T 2κ−1, where κ is the TL parameter. In the SDW2 precursor phase κ < 1/2 and \({T}_{1}^{-1}\) diverges with decreasing temperature whereas in the spin-nematic state κ > 1/2 and \({T}_{1}^{-1}\) decays as T → 0. In both regimes transverse 〈+ −〉 correlations yield a gapped contribution to \({T}_{1}^{-1}\) ~ exp(−Δ/T).
It is reasonable to attribute incommensurate spin correlations observed in LiCuSbO4 as well as a weak magnetic anomaly in the specific heat at low fields26 with the onset of a conventional short-range ordered vector chiral phase. The proximity to this phase is reflected in an increase of the 7Li relaxation rate at low T due to the growth of 〈+ −〉 correlations. From the fit with Eq. (3) a long-range vector chiral order due to interchain coupling could be realized only at very low temperatures T c ~ 0.2 K and in fact was not observed down to 0.1 K26. A new field-induced magnetic phase at higher fields and higher temperatures yielding a strong anomaly in the magnetic specific heat26 can thus be naturally ascribed to the short-range ordered SDW2 phase. In this regime the observed strong enhancement of \({T}_{1}^{-1}\) (T) should be due to the dominant longitudinal 〈zz〉 correlations which according to the modelling of the 9 T data with Eq. (3) should yield a long-range SDW2 order below T c ~ 1.5 K.
Further increasing the field up to 12 T yields a weakening of the 〈zz〉 power law contribution on which background a gapped 〈+ −〉 contribution to the \({T}_{1}^{-1}\) (T) dependence with Δ ~ 2 K becomes distinguishable. This clearly suggests the destabilization of the SDW2 state which is also reflected in the decreased value of T c ~ 1 K in the model dependence (Suppl., Fig. S3).
The vanishing of the power-law contribution at the critical IBP H c1 ≈ 13 T signals then a crossover to the distinctive spin-nematic state with dominant quadrupolar 〈+ + − −〉 correlations. In this regime the 〈zz〉 correlations are decaying with lowering T which corresponds to the sign change of the power-law exponent κ 36, 37. This is indeed the case for LiCuSbO4 (Fig. 7, inset). The now decaying power law contribution to \({T}_{1}^{-1}\) loses progressively its weight with increasing field whereas the gapped contribution becomes dominant (Suppl., Fig. S3). Indeed, as it has been emphasized in ref. 17 the gapped excitation spectrum is a distinct feature of the spin-nematic state of the weakly coupled 1D-chains with only a weak soft mode in the longitudinal 〈zz〉 channel17, 44. Thus, regardless of the specific details the above analysis points at a rather broad stability range of the spin-nematic liquid state in LiCuSbO4 above the narrow crossover region at the IBP field μ 0 H c1 ≈ 13 T. This state can be considered as a precursor of the envisaged spin nematic long-range ordered phase likely to occur in LiCuSbO4 at comparable magnetic fields and at still lower temperatures beyond those available in the present study. The SDW2 and the spin-nematic states, as well as the isosbestic field H c1 and the parameter window measured by NMR are visualized in the schematic phase diagram of LiCuSbO4 in Fig. 9. Certainly, there must be also a second “upper” critical field H c2 framing the stability region of the strong nematic state in LiCuSbO4. This calls for further experimental studies of LiCuSbO4 at higher fields and also at lower temperatures beyond the scope of the present work.
Schematic phase diagram of LiCuSbO4. Blue, dark green, and dark red regions reproduce approximately the diagram of Dutton et al. based on the analysis of the specific heat and magnetization data (Fig. 3 in ref. 26). The dark red area is suggested to present an anomalous SDW phase, whereas the dark yellow area depicts an envisaged stability region of the proposed nematic state. The region measured by the NMR in the present work is marked by the black rectangle. The blue dashed line denotes the isosbestic field H c1 (cf. Fig. 6). The brown closed circles labelled \({H}_{{\rm{sn}}}^{max}\) connected with the dashed line depict the field of the maximum of the spin-nematic correlation function as found in the DMRG analysis (cf. Fig. 8).
Band structure calculations
As in other related materials (see., e.g., refs 20,21,22 and 27), the edge-sharing geometry of the CuO4 plaquettes in the CuO2 chains in LiCuSbO4 (Fig. 1) is expected to give rise to the usual frustrated magnetism due to the presence of oxygen mediated frustrated AFM NNN intra-chain couplings. The nearly 90° Cu-O-Cu bond angle, i.e. 93°, points to FM NN intra-chain interactions due to the presence of a sizable direct FM coupling K pd ~ 100 meV between two holes residing on neighboring sites with Cu 3d and O 2p orbitals and a significant compensation of the AFM NN superexchange contributions.
We have performed DFT and DFT+U band structure calculations with the aim to understand (i) the amount of interchain couplings and (ii) the magnitude of the intra-chain couplings. With respect to (i) we have analyzed the dispersion of bands and found pronounced 1D van Hove singularities near the Fermi level. Thus, we have confirmed the nearly 1D behavior of LiCuSbO4. Then, in general, the exchange coupling strength can be estimated simply by the AFM contribution \({J}_{1}=4{t}_{1}^{2}/{U}_{{\rm{eff}}}\), where \({U}_{{\rm{eff}}}\sim {{\rm{\Delta }}}_{pd}\approx 3\) to 4 eV is the effective Coulomb repulsion within a single-band type approach for the Cu-sites with NN transfer integral t 1. The frustrating J 2 is measured by the analogous expression using the NNN transfer integral t 2 instead ignoring a much weaker direct FM contribution as compared to that of the NN bond (\({K}_{pd}\gg {K}_{pp}\)) and the small hole occupation at O 2p orbitals. Note that applying such a simple model to charge transfer insulators as cuprates, one is left with an effective onsite repulsion U of the order of the Cu 3d-O 2p onsite energy difference which is significantly smaller than the U d ~ 5.5 eV at Cu sites employed in the DFT+U calculations or in more sophisticated five-band pd Hubbard models45, 46 to be considered for to the case of LiCuSbO4 elsewhere. To check this simple first approach, we have determined the Cu-Wannier functions which contain also the essential O 2p contributions. Their tails point to the important coupling directions. In fact, a closer inspection of the crystal structure reveals nonequivalent “left” and “right” NN intra-chain bonds (Fig. 1). This gives rise to alternating NN transfer integrals (\({t}_{1}\ne {t}_{1}^{^{\prime} }\)). The one-band fit results in the following transfer integrals (given in meV): \({t}_{1}=-95.51,\,{t}_{1}^{^{\prime} }=\mathrm{56.44,}\,{t}_{2}=56.96\), and \({t}_{3}=-11.88,\,{t}_{3}^{^{\prime} }=-16.57\). Then the mean NN transfer integral \({\bar{t}}_{1}\) would provide an AFM superexchange contribution to \({J}_{1}^{e}\) for an equidistant chain of about 67 K which for a typical \({J}_{1}^{e}\) of about −80 K like in linarite (see, refs 22 and 47 and references therein) corresponds to an FM contribution of −147 K. As a result we arrive at a sizable splitting of the two NN exchange integrals: \({J}_{1}\approx -160\,{\rm{K}}\) and \({J}_{1}^{^{\prime} }\approx -90\,{\rm{K}}\), whereas J 2 ≈ 37.6 K, only. Thus, within a 1D picture we are left with a dominant FM total NN coupling and an unrenormalized mean frustration parameter \(\bar{\alpha }={J}_{2}/[({J}_{1}+{J}_{1}^{^{\prime} })/2]\sim 0.3\). This value is close to that (α = 0.28) estimated from the fitting of the observed magnetization curve by the DMRG calculations (see below).
Symmetry analysis and the role of DM interactions
The crystal structure of LiCuSbO4 is described by the polar space-group Cmc21 26. The low symmetry implies modifications of the standard J 1 − J 2 spin-model to describe the chains of the edge-shared CuO4 square-like plaquettes runnning in a-direction. More details of our symmetry analysis are given in the Supplement. In particular, because of the low symmetry, antisymmetric Dzyaloshinskii-Moriya (DM) interactions are allowed for the NN bonds along the spin-chains, \({E}_{D}={{\bf{D}}}_{\nu }\cdot ({{\bf{S}}}_{i}\times {{\bf{S}}}_{i+\nu })\) and have both a homogeneous and a staggered component. These microscopic antisymmetric exchange interactions are caused by the relativistic spin-orbit interactions and compete with the isotropic exchange interactions.
To fit the experimental data for LiCuSbO4, Dutton et al.26 assumed in their model the presence of this exchange anisotropy for the NN bond, while neglected the anisotropic terms linear in |D ν |. However, this could yield an unrealistic picture for the basic magnetic couplings in LiCuSbO4. The determined strength of the effective anisotropic coupling constant is large and would imply an unusual order of magnitude \(|{{\bf{D}}}_{1}|/|{J}_{1}|\sim 1\). The presence of the relativistic antisymmetric exchange in crystals belonging to the crystal classes 2 mm or C 2ν may give rise to two rather different states48: weak ferromagnetism or more generally canting of spins with a net magnetization can be derived by the staggered DM couplings. Besides, the acentric crystal structure also allows for the presence of ‘inhomogeneous DM couplings’48, that derive from the homogeneous part of the DM interaction. It is known that this type of couplings can suppress any long-range ordered states and may be related to the absence of magnetic ordering down to ~0.1 K in LiCuSbO4.
DMRG-calculations
The main aim of this part is to present an analysis of a novel anisotropy mechanism based on the low-symmetric NN exchange anisotropy, which in addition to the J 1 − J 2 frustration, stabilizes a nematic phase in a moderate high-field region to be specified below. We present a first brief analysis also of the effect of weak homogeneous and staggered NN DM couplings which were found not to destroy the nematicity although some weakening has been observed.
Figure 8(a) shows the magnetization curve M(H) measured at T = 0.45 K. Noteworthy, a full saturation is not reached even in the highest accessible field of 20 T. Although this is reminiscent of a typical feature of M(H) at high temperature, the observation temperature is now low enough to prevent a significant finite-temperature effect. To provide a reasonable explanation for this feature, we introduce a 1D frustrated Heisenberg model with an xyz exchange anisotropy and a magnetic field H along the z axis. The Hamiltonian is then given by
where \({J}_{1}^{\gamma }\) and J 2 are the NN FM and the NNN AFM exchange couplings, respectively, and \({S}_{i}^{\gamma }\) is the γ-component of the spin-operator S i . When \(H\gg {J}_{1}^{\gamma }\), J 2, by taking the fully polarized FM state as non-perturbative state, its energy is lowered by \({\rm{\Delta }}E={({J}_{1}^{x}-{J}_{1}^{y})}^{2}/\mathrm{[32(}H-{J}_{1}^{z}-{J}_{2})]\) through the second-order process of an individual double spin-flip. Therefore, the magnetization behaves like \({M}_{S}-M\propto {({J}_{1}^{x}-{J}_{1}^{y})}^{2}/H\) at high fields and saturates at its maximum value M S only at \(H=\infty \), only. We have calculated the magnetization curve using the DMRG technique. By fitting the experimental curve, we have found a possible parameter set: \({J}_{1}^{z}=-546\,{\rm{K}}\), \(({J}_{1}^{x}/{J}_{1}^{z},{J}_{1}^{y}/{J}_{1}^{z})=(1.07,0.99)\), and J 2 = 153 K. Note that these numbers are effective values in the 1D limit, which can be significantly different from the bare values of NN and NNN exchange couplings determined by the DFT+U calculations. Other contributions such as the interchain and longer-range exchange couplings are renormalized into them. As a related similar example we refer the reader to linarite22, 47.
More interestingly, an exotic nematic state is established by the xyz exchange anisotropy. The xy components of the first term of Eq. (4) can be divided into an exchange term \(\frac{{J}_{1}^{x}+{J}_{1}^{y}}{4}({S}_{i}^{+}{S}_{i+1}^{-}+{h}.{c}\mathrm{.)}\) and a double spin-flip term \(\frac{{J}_{1}^{x}-{J}_{1}^{y}}{4}({S}_{i}^{+}{S}_{i+1}^{+}+h.c\mathrm{.)}\). The latter seems to create an attractive interaction among the parallel spins. Therefore, a 2-magnon bound state, i.e., a nematic state, may be naively expected at high fields in the presence of xyz exchange anisotropy. To check this possibility, we have calculated the nematic correlation function as an indicator of magnon pairing
Note that this correlation vanishes for lacking xyz exchange anisotropy, because there is no overlap between different S z sectors. Furthermore, there is an important difference of the two-magnon instability within our unconventional nematicity scenario as compared to the usual isotropic counterpart mentioned above: namely, the total momentum q of a bound two-magnon pair equals to zero just as in a standard BCS superconductor whereas in the isotropic counterpart it equals to q a = π which resembles the behavior of a Pauli-limited strongly paramagnetic superconductor in an extremely inhomogeneous Fulde-Ferrel-Larkin-Ovchinnikov (FFLO) state. In this context, the recently proposed isotropic multipolar field theory based scenario by Balents and Starykh49 with a two-magnon pair with a finite but very small total momentum of \(0 < {q}_{a}\ll \pi \) is noteworthy. The present single chain Hamiltonian with the involved specific exchange anisotropy describes a 1D system with a distinctive nematically ordered ground state at T = 0 and at high enough magnetic fields in contrast with simple AFM Heisenberg chains. With increasing finite T this distinct order is more and more suppressed. The stability of the former generalized also to 2D or 3D with respect to interchain couplings and various DM couplings will be investigated in detail in forthcoming work.
The nematic correlation for our parameter set is plotted as a function of H in Fig. 8(b). It is significantly enhanced just above the kink position of the theoretical magnetization curve. This field range with the enhanced correlation agrees well with that region where the spin gap has been experimentally observed, namely, in between μ 0 H = 13–16 T. A similar nematicity scenario has been proposed in our recent work devoted to linarite22, but there yet not fully confirmed experimentally due to a phase separation and other experimental and physical difficulties. Furthermore, we have also studied the effect of additional uniform or staggered DM couplings allowed by the crystallographic symmetry as mentioned above \({ {\mathcal H} }_{{\rm{DM}}}={\sum }_{i}\,{\bf{D}}\cdot ({{\bf{S}}}_{i}\times {{\bf{S}}}_{i+1})\) with D = (0, 0, γ). As a result we found that the nematic state is hardly affected by a weak DM coupling for γ < 0.05. The effect of a staggered DM interaction is even weaker than that of a uniform one. For simplicity, the dimerization of the NN exchange couplings, suggested by the DFT, was not taken into account in the present DMRG calculations. However, the stability of the nematic state is mostly related to the magnitude of the exchange anisotropy and is less affected by the dimerization. Also, the T-dependence of the correlation is plotted in Fig. 8(d). We can see that the sharp enhancement of the correlation around μ 0 H = 13 T at T = 0 disappears for higher T which points to existence of the mentioned above upper critical field.
Thus, we are confronted with a somewhat unusual situation: the pronounced spin gap and the strongly enhanced nematic correlations are, in a literal sense, not the result of the occurrence of a novel order parameter associated with symmetry breaking due to a second order phase transition from a high temperature and low-field para-phase, since at low fields the nematic order at T = 0 already exists albeit at a low level. Instead, based on our calculations and in accord with the experimental data, we suggest a crossover from a weak nematic state in a narrow field range at about 13 T to a pronounced nematic state up to at least 16 T to 20 T to be followed by a broad field range where it decreases again (Figs 8 and 9).
Such transitions without a symmetry change of the macroscopic order parameter are reminiscent of mesoscopic liquid-liquid transitions in ordinary liquids such as, for instance, in phosphorus and water. It has been found that those single-component liquids may have different liquid states with distinct correlation functions. A transition between them driven by some external control parameter, such as temperature or pressure, is characterized by the quantitative change of a correlation function, only50,51,52. In the case of LiCuSbO4, with increasing T these changes are smeared out and the consequences of the suppressed nematic order parameter are difficult to be observed. In such a complex situation further experimental and theoretical studies beyond the scope of the present work are necessary to refine the parameters of our proposed model and to take into account explicitly the weaker couplings and modifications suggested by the real structure including also impurities or defects.
Summary
In conclusion, we have presented strong experimental and theoretical indications of the occurrence of a distinctive spin-nematic state in the frustrated anisotropic spin chain cuprate LiCuSbO4. This state emerges above an isosbestic point μ 0 H c1 ≈ 13 T detected in the field dependence of the 7Li NMR relaxation rate \({T}_{1}^{-1}\) at low temperatures. The analysis of the temperature dependences of \({T}_{1}^{-1}\) reveals that H c1 separates a lower-field regime with strong enhancement of \({T}_{1}^{-1}\) at low T from a higher-field regime with a sharp decrease of \({T}_{1}^{-1}\) (T). The former is ascribed to diverging longitudinal spin correlations typical for a multipolar SDW liquid whereas the latter is due to the power-law like decaying longitudinal and gapped transverse spin correlations characteristic of the spin-nematic liquid. Theoretical analysis justifies the occurrence of this “hidden” spin-nematic state in LiCuSbO4 in an extended field range above H c1. A broad range of stability of this spin-nematic state unexpected in the corresponding isotropic spin-chain model can be ascribed to the presence of exchange anisotropies. Indeed, as is found in the DMRG calculations it can be due to a special low-symmetry symmetric exchange anisotropy which is reflected in the high-field magnetization data. The missing SDW-type magnetic ordering at lower fields might be ascribed to some structural disorder and/or frustrated interchain interactions caused by DM couplings allowed in this low-symmetry crystal structure in general. The small but finite DM coupling favoring a noncollinear spin arrangement could be responsible for the suppression of the otherwise strongly competing anomalous collinear SDW2 phase. On the other hand, according to complete diagonalization and DMRG studies in high magnetic fields the presence of a weak DM interaction, uniform or staggered, identified in the symmetry analysis of LiCuSbO4 and assessed with ESR, are not detrimental for nematicity. Merely an alteration of the two NN exchange couplings may somewhat reduce the binding energy of two-magnon bound states as compared to equal NN bonds. The remarkable interplay of symmetric and antisymmetric exchange anisotropies with sizable frustration is of general interest in modern quantum magnetism and calls for deeper theoretical and experimental studies.
Methods
Sample synthesis and characterization
Green polycrystalline sample of LiCuSbO4 was prepared through solid-state reaction using stoichiometric mixture of dried Li2CO3 (99.98%, Chempur), CuO (99.95%, Aldrich) and Sb2O5 (99.9%, Alfa Aesar). The mixture of the precursor compounds was homogenized by grinding in a mortar and pestle, followed by a 16 h sintering at 700 °C. The sample was subsequently grounded, pressed into pellets and fired at 1000 °C for 48 h. Pure LiCuSbO4 phase was obtained after annealing of the pellets at 1050 °C for 24 h under dried oxygen flow. Phase purity of the products was assessed by powder X-ray diffraction, by using a STOE Stadi P powder diffractometer with Mo K α1 radiation. The diffractometer is equipped with a curved Ge (111) monochromator and a 6° linear position sensitive detector (DECTRIS MYTHEN 1 K detector). Powder x-ray diffraction data were analyzed with the Rietveld method using the FULLPROF in the WinPlotR program package program53. The background was fitted using linear interpolation between selected points. The March-Dollase model for preferred orientation was used in all of the refinements, and a pseudo-Voigt function was used as the peak-shape model. As refinable parameters background, scale factor, half width, Caglioti variables (U, V, W), lattice parameters, asymmetries and the overall temperature factor were allowed. Based on Rietveld analysis of the powder x-ray diffraction data (Fig. 10), the main phase is LiCuSbO4 96.93(6) wt% (orthorhombic, Cmc21, \(a=\mathrm{5.7493(1)}\,\AA \), \(b=\mathrm{10.8828(2)}\,\AA \), \(c=\mathrm{9.7429(1)}\,\AA \)). LiSbO3 2.36(5) wt% (orthorhombic, Pnma, \(a=\mathrm{5.1756(4)}\,\AA \), \(b=\mathrm{4.9092(3)}\,\AA \), \(c=\mathrm{8.4887(6)}\,\AA \)) and 0.72(1) wt% CuO are two minor impurity phases. The amount of foreign phase is very similar to the previous report in ref. 26.
Calculated and observed X-ray diffraction pattern of the Rietveld refinement for LiCuSbO4. The difference curve is shown in blue; reflection positions are indicated by the vertical lines for LiCuSbO4 (blue), LiSbO3 [2.36(5) wt%] (red) and CuO [0.72(1) wt%] (green) impurity phases. (\(\lambda =0.70932\,{\AA }\), Bragg R-factor: 3.38%; Rf-factor = 3.49%; Bragg R-factor = \(\sum |{I}_{{\rm{ko}}}-{I}_{{\rm{kc}}}|/\sum {I}_{{\rm{ko}}}\); Rf-factor = \({[(N-P)/\sum {w}_{{\rm{i}}}{y}_{{\rm{io}}}2]}^{\mathrm{1/2}}\)). The inset shows optical image of a typical green pellet of polycrystalline sample of LiCuSbO4 after annealing in dried oxygen flow.
Nuclear magnetic resonance
NMR spectra were obtained with a Tecmag Apollo spectrometer and a standard sample probe from NMR Service GmbH. The magnetic field has been applied by a 16 T Oxford Instruments superconducting magnet. Temperatures were regulated by a 4He variable temperature insert (VTI). Temperatures below 4.2 K were achieved by pumping on the VTI. At high temperatures and small fields, Fourier transformations (FFT) of the spin echo covered the whole spectral width. At lower temperatures, we swept the frequency and summed up the FFT’s to obtain the complete spectrum. The spectra at 15 T below 10 K have been obtained by field sweeps, and converting into frequency sweeps. This is easily possible due to the negligible quadrupole interaction. We have confirmed the correctness of this procedure at higher temperatures. The spin lattice relaxation rate, \({T}_{1}^{-1}\), has been measured by standard saturation recovery at the peak of the spectra. The nuclear magnetization, M 0, has been saturated by a train of radio frequency pulses, before measuring the recovered nuclear magnetization, M(τ), depending on the time τ between the saturation train and the spin echo sequence.
Electron spin resonance
ESR spectra were measured with the Terahertz ESR Apparatus (TESRA-IMR) installed in the magnetism division of Institute of Materials Research, Tohoku University54. As sources of the microwave radiation up to 450 GHz conventional Gunn oscillators were employed. The signals were detected with an InSb detector. Pulse magnetic fields up to 20 T were generated with a solenoid magnet and a 90 kJ capacitor bank. The sample temperature was regulated with a 3He cryostat. Additional ESR measurements were performed at the IFW Dresden with a home-made multi-frequency high-field ESR spectrometer at magnetic fields up to 16 T and at frequencies ν up to 400 GHz55. For the generation and detection of the microwave radiation millimeter wave backward oscillators and an InSb bolometer from QMC Insruments Ltd., as well as a millimeter wave network analyzer from AB Millimetre, have been used. DC magnetic fields were obtained with a solenoid superconducting magnet from Oxford Instruments equipped with a 4He variable temperature insert.
Static magnetization
Temperature dependence of the static magnetic susceptibility in fields up to 5 T in the temperature range T = 2–300 K was measured with the SQUID magnetometer from Quantum Design. Static magnetization in fields up to 20 T was measured with a standard inductive method using compensated pickup coils and a nondestructive pulse magnet (for details see ref. 56). The sample was immersed into liquid 3He to reach a temperature as low as 0.45 K.
Density functional calculations
Relativistic density functional (DFT) electronic structure calculations were performed using the full-potential local orbital FPLO code57, 58 (http://www.fplo.de), version fplo14.00-49. For the exchange-correlation potential, within the local density (LDA) and the the general gradient approximation (GGA) the parametrizations of Perdew-Wang59 and Perdew-Burke-Ernzerhof60 were chosen, respectively. Both exchange-correlation potential yielded essentially the same band structure. To obtain precise band structure information, the final calculations were carried out on a well converged mesh of 4800 k-points (20 × 20 × 12 mesh, 1332 points in the irreducible wedge of the Brillouin zone). For our calculations, we used the experimental crystal structure of ref. 26. However, to model the Li split positions Li1a (4a), Li1b (4a) and Li2 (8b), we used averaged coordinates: Li1 (4a) 0.0 0.3610 0.6974 or the coordinates of the nearby high symmetry position Li2 (4a) 0. 0.0002 0.2660; Li split positions have been successfully modeled this way for the related edge-sharing chain compound LiZrCuO4 61.
References
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic Fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153 (2010).
Sachdev, S. Quantum magnetism and criticality. Nature Physics 4, 173 (2008).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199 (2010).
Penc, K. & Läuchli, A. M. Spin nematic phases in quantum spin systems. In Lacroix, C., Mendels, P. & Mila, F. (eds) Introduction to Frustrated Magnetism, vol. 164 of Springer Series in Solid-State Sciences, 331 (Springer-Verlag, Berlin, Heidelberg, 2011).
Mikeska, H.-J. & Kolezhuk, A. One-dimensional magnetism. In Schollwöck, U., Richter, J., Farnell, D. J. & Bishop, R. (eds) Quantum Magnetism, vol. 645 of Lect. Notes Phys., 1 (Springer-Verlag, Berlin, Heidelberg, 2004).
Majumdar, C. K. & Ghosh, D. K. On next-nearest-neighbor interaction in linear chain. I. J. Math. Phys. 10, 1388 (1969).
Haldane, F. Spontaneous dimerization in the S = 1/2 Heisenberg antiferromagnetic chain with competing interactions. Phys. Rev. B 25, 4925(R) (1982); Erratum - Phys. Rev. B 26, 5257 (1982).
Chubukov, A. Chiral, nematic, and dimer states in quantum spin chains. Phys. Rev. B 44, 4693 (1991).
Kecke, L., Momoi, T. & Furusaki, A. Multimagnon bound states in the frustrated ferromagnetic one-dimensional chain. Phys. Rev. B 76, 060407 (2007).
Kuzian, R. & Drechsler, S.-L. Exact one- and two-particle excitation spectra of acute-angle helimagnets above their saturation magnetic field. Phys. Rev. B 75, 024401 (2007).
Vekua, T., Honecker, A., Mikeska, H.-J. & Heidrich-Meisner, F. Correlation functions and excitation spectrum of the frustrated ferromagnetic spin-1/2 chain in an external magnetic field. Phys. Rev. B 76, 174420 (2007).
Hikihara, T., Kecke, L., Momoi, T. & Furusaki, A. Vector chiral and multipolar orders in the spin-1/2 frustrated ferromagnetic chain in magnetic field. Phys. Rev. B 78, 144404 (2008).
Läuchli, A., Sudan, J. & Lüscher, A. The frustrated ferromagnetic S = 1/2 Heisenberg chain in a magnetic field – how multipolar spin correlations emerge from magnetically ordered states. J. Phys. Conf. Ser. 145, 012057 (2009).
Sudan, J., Lüscher, A. & Läuchli, A. Emergent multipolar spin correlations in a fluctuating spiral: The frustrated ferromagnetic spin-1/2 Heisenberg chain in a magnetic field. Phys. Rev. B 80, 140402(R) (2009).
Ueda, H. & Totsuku, K. Magnon Bose-Einstein condensation and various phases of three-dimensonal quantum helimagnets under high magnetic field. Phys. Rev. B 80, 14417 (2009).
Zhitomirsky, M. & Tsunetsugu, H. Magnon pairing in quantum spin nematic. EPL 92, 37001 (2010).
Starykh, O. & Balents, L. Excitations and quasi-one-dimensionality in field-induced nematic and spin density wave states. Phys. Rev. B 89, 104407 (2014).
Smerald, A. & Shannon, N. Theory of NMR 1/T1 relaxation in a quantum spin nematic in an applied field. Phys. Rev. B 93, 184419 (2016).
Nawa, K., Takigawa, M., Yoshida, M. & Yoshimura, K. Anisotropic spin fluctuations in the quasi one-dimensional frustrated magnet licuvo4. Journal of the Physical Society of Japan 82, 094709 (2013).
Büttgen, N. et al. Search for a spin-nematic phase in the quasi-one-dimensional frustrated magnet LiCuVO4. Phys. Rev. B 90, 134401 (2014).
Prozorova, L. et al. Magnetic field driven 2d–3d crossover in the s = 1/2 frustrated chain magnet LiCuVO4. Phys. Rev. B 91, 174410 (2015).
Willenberg, B. et al. Complex field-induced states in linarite PbCuSO4(OH)2 with a variety of high-order exotic spin-density wave states. Phys. Rev. Lett. 116, 047202 (2016).
Mourigal, M. et al. Evidence of a bond-nematic phase in LiCuVO4. Phys. Rev. Lett. 109, 027203 (2012).
Nishimoto, S., Drechsler, S.-L., Kuzian, R., Richter, J. & van den Brink, J. Interplay of interchain interactions and exchange anisotropy: Stability and fragility of multipolar states in spin-1/2 quasi-one-dimensional frustrated helimagnets. Phys. Rev. B 92, 214415 (2015).
Onishi, H. Effects of magnetic anisotropy on spin dynamics of ferromagnetic frustrated chain. J. Phys. Conf. Ser. 592, 012109 (2015).
Dutton, S. et al. Quantum Spin Liquid in Frustrated One-Dimensional LiCuSbO4. Phys. Rev. Lett. 108, 187206 (2012).
Drechsler, S.-L. et al. The route of frustrated cuprates from antiferromagnetic to ferromagnetic spin-1/2 Heisenberg chains: Li2ZrCuO4 as a missing link near the quantum critical point. Phys. Rev. Lett. 98, 077202 (2007).
Vavilova, E. et al. Quantum electric dipole glass and frustrated magnetism near a critical point in Li2ZrCuO4. EPL 88, 27001 (2009).
Griffits, R. B. Magnetization curve at zero temperature for the antiferromagnetie Heisenberg linear chain. Phys. Rev. 133, A768 (1964).
Hase, M. et al. Confirmation of a one-dimensional spin-1/2 heisenberg system with ferromagnetic first-nearest-neighbor and antiferromagnetic second-nearest-neighbor interactions in rb2cu2mo3o12. Phys. Rev. B 70, 104426 (2004).
Poole, C. P. Electron Spin Resonance: A Comprehensive Treatise on Experimental Techniques (Dover Publications, Mineola, NY, 1996).
Abragam, A. & Bleaney, B. Electron paramagnetic resonance of transition ions (Clarendon Press, Oxford, 1970).
Measurements of T 1 −1 at positions in the NMR spectrum left and right from the central peak reveal similar values of T 1 −1.
Moriya, T. Nuclear magnetic relaxation in antiferromagnetics. Prog. Theor. Phys. 16, 23 (1956).
Chitra, R. & Giamarchi, T. Critical properties of gapped spin-chains and ladders in a magnetic field. Phys. Rev. B 55, 5816–5826 (1997).
Sato, M., Momoi, T. & Furusaki, A. NMR relaxation rate and dynamical structure factors in nematic and multipolar liquids of frustrated spin chains under magnetic fields. Phys. Rev. B. 79, 060406(R) (2009).
Sato, M., Hikihara, T. & Momoi, T. Field and temperature dependence of NMR relaxation rate in the magnetic quadrupolar liquid phase of spin-1/2 frustrated ferromagnetic chains. Phys. Rev. B. 83, 064405 (2011).
Greger, M., Kollar, M. & Vollhardt, D. Isosbestic points: How a narrow crossing region of curves determines their leading parameter dependence. Phys. Rev. B 87, 195140 (2013).
Oshikawa, M. & Affleck, I. Field-induced gap in s = 1/2 antiferromagnetic chains. Phys. Rev. Lett. 79, 2883 (1997).
Oshikawa, M. & Affleck, I. Low-temperature electron spin resonance theory for half-integer spin antiferromagnetic chains. Phys. Rev. Lett. 82, 5136 (1999).
Oshikawa, M. & Affleck, I. Electron spin resonance in s = 1/2 antiferromagnetic chains. Phys. Rev. B 65, 134410 (2002).
Povarov, K. Y., Smirnov, A. I., Starykh, O. A., Petrov, S. V. & Shapiro, A. Y. Modes of magnetic resonance in the spin-liquid phase of Cs2CuCl4. Phys. Rev. Lett. 107, 037204 (2011).
Smirnov, A. I., Soldatov, T. A., Povarov, K. Y. & Shapiro, A. Y. High-field magnetic resonance of spinons and magnons in the triangular lattice s = 1/2 antiferromagnet Cs2CuCl4. Phys. Rev. B 91, 174412 (2015).
Syromyatnikov, A. V. Spin nematic phase in one-dimensional and quasi-one-dimensional frustrated magnets in a strong magnetic field. Phys. Rev. B 86, 014423 (2012).
Málek, J., Drechsler, S.-L., Nitzsche, U., Rosner, H. & Eschrig, H. Temperature dependent optical conductivity of undoped cuprates with weak exchange. Phys. Rev. B 78, 165118 (2008).
Monney, M. et al. Probing inter- and intrachain zhang-rice excitons in li2cuo2 and determining their binding energy interaction and weak ferromagnetism. Phys. Rev. B 94, 165118 (2016).
Rule, K. C. et al. Dynamics of linarite: Observations of magnetic excitations. Phys. Rev. B 95, 024430 (2017).
Bogdanov, A., Rößler, U., Wolf, M. & Müller, K. Magnetic structures and reorientation transitions in noncentrosymmetric uniaxial antiferromagnets. Phys. Rev. B 66, 214410 (2002).
Balents, L. & Starykh, O. A. Quantum lifshitz field theory of a frustrated ferromagnet. Phys. Rev. Lett. 116, 177201 (2016).
Katayama, Y. et al. A first order liquid-liquid phase transition in phosphorus. Nature 403, 170 (2000).
Kurita, R. & Tanaka, H. Critical-like phenomena associated with liquid-liquid transition in a molecular liquid. Science 306, 845 (2004).
Tanaka, H. Importance of many-body orientational correlations in the physical description of liquids. Faraday Discuss. 167, 9 (2013).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B: Condensed Matter 192, 55–690 (1993).
Nojiri, H., Ajiro, Y., Asano, T. & Boucher, J.-P. Magnetic excitation of s = 1/2 antiferromagnetic spin chain Cu benzoate in high magnetic fields. New J. Phys. 8, 218 (2006).
Golze, C. et al. Tuning the magnetic ground state of a tetranuclear Nickel(II) molecular complex by high magnetic fields. Phys. Rev. B 73, 224403 (2006).
Nojiri, H., Taniguchi, T., Ajiro, Y., Müller, A. & Barbara, B. Quantum dynamics of molecular magnets in ultra-fast sweeping magnetic fields. Physica B 246–247, 216 (2004).
Koepernik, K. & Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 59, 1743 (1999).
Ophale, I., Koepernik, K. & Eschrig, H. Full-potential band-structure calculation of iron pyrite. Phys. Rev. B 60, 14035 (1999).
Perdew, J. & Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244 (1992).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Schmitt, M., Málek, J., Drechsler, S.-L. & Rosner, H. Electronic structure and magnetic properties of Li2ZrCuO4: A spin-1/2 Heisenberg system close to a quantum critical point. Phys. Rev. B 80, 205111 (2009).
Acknowledgements
The authors thank C. Blum and L. Giebeler for assistance with the XRD measurements, and A. Wolter-Giraud, F. Hammerath, Y. Utz and A. Smirnov for useful discussions. This work has been supported in part by the Deutsche Forschungsgemeinschaft through grants SFB 1143 (S.N.), KA 1694/8-1 (V.K.), GR 3330/4-1 (H.-J.G.), through the Emmy Noether Programme in the projects WU595/3-1, and WU595/3-2 (S.W.). The work of E.V. and M.I. has been supported in part by project RFBR 14-02-01194. V.K. gratefully acknowledges his stay at Tohoku University supported by ICC-IMR. H.N. acknowledges Kakenhi 16H01060. S.-L.D. and S.N. thank R.O. Kuzian, J. van den Brink, C. Agrapidis, A. Tsirlin, A. Zvyagin, P. Mendels, H. Kühne, S. Zvyagin, M. Zhitomirsky, and especially O. Starykh for critical and valuable discussions and stimulating interest. The publication of this article was funded by the Open Access Fund of the Leibniz Association.
Author information
Authors and Affiliations
Contributions
H.-J.G., M.I. and E.V. conducted the NMR studies. H.N., V.K., and A.A. conducted the ESR studies. H.N. performed the high-field magnetization measurements. M.I.S. and S.W. synthesized and characterized the samples. S.N. performed the DMRG-calculations and invented the nematicity scenario based on the special anisotropic NN exchange. J.R. carried out the complete diagonalizations to study effects of the DM interactions. H.R. performed the LDA-FPLO electronic structure calculations for LiCuSbO4, invented its \(({J}_{1},{J}_{1}^{^{\prime} })-{J}_{2}\) model, and estimated the leading exchange couplings. U.R., H.R. and S.-L.D. made the symmetry and phenomenological analysis including the isosbestic point. L.S. calculated the hyperfine tensor. V.K., E.V., S.-L.D. and B.B. designed the project. All coauthors participated actively in the discussion and selection of the various experimental and theoretical results presented in this paper and worked out the final concept of the paper. V.K. and S.-L.D. wrote the paper with important contributions to all its parts from all other coauthors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grafe, HJ., Nishimoto, S., Iakovleva, M. et al. Signatures of a magnetic field-induced unconventional nematic liquid in the frustrated and anisotropic spin-chain cuprate LiCuSbO4 . Sci Rep 7, 6720 (2017). https://doi.org/10.1038/s41598-017-06525-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-06525-0
This article is cited by
-
Milestones of low-D quantum magnetism
npj Quantum Materials (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.