Abstract
Optimal materials to induce bulk photovoltaic effects should lack inversion symmetry and have an optical gap matching the energies of visible radiation. Ferroelectric perovskite oxides such as BaTiO3 and PbTiO3 exhibit substantial polarization and stability, but have the disadvantage of excessively large band gaps. We use both density functional theory and dynamical mean field theory calculations to design a new class of Mott multiferroics–double perovskite oxides A 2VFeO6 (A = Ba, Pb, etc). While neither perovskite AVO3 nor AFeO3 is ferroelectric, in the double perovskite A 2VFeO6 a ‘complete’ charge transfer from V to Fe leads to a non-bulk-like charge configuration–an empty V-d shell and a half-filled Fe-d shell, giving rise to a polarization comparable to that of ferroelectric ATiO3. Different from nonmagnetic ATiO3, the new double perovskite oxides have an antiferromagnetic ground state and around room temperatures, are paramagnetic Mott insulators. Most importantly, the V d 0 state significantly reduces the band gap of A 2VFeO6, making it smaller than that of ATiO3 and BiFeO3 and rendering the new multiferroics a promising candidate to induce bulk photovoltaic effects.
Similar content being viewed by others
Introduction
The lack of inversion symmetry caused by ferroelectric ordering in certain transition metal oxides can separate electrons and holes generated by photo-excitation, making these materials promising candidates for photovoltaic devices1,2,3,4. However, many known ferroelectric perovskite oxides including BaTiO3 and PbTiO3 have very large band gaps (~3–5 eV)5, significantly limiting their absorption efficiency in the visible frequency range. The large band gap is intrinsic: it is set by the energy difference between the Ti-d and O-p levels, which is large because Ti and O have substantially different electronegativity. Intensive research in perovskite oxides has focused on reducing band gaps while maintaining ferroelectric polarization. One approach is to replace a fraction of transition metal ions with a different cation, with one transition metal species driving ferroelectricity and the other providing lower energy states that reduce the band gap6,7,8,9,10,11. Using this approach, band gap reductions of ~1 eV have been attained10 and a high power conversion efficiency has been experimentally achieved in Bi2FeCrO6 11. In another method, a class of layered double perovskite oxides AA′BB′O6 has been theoretically proposed, in which a large in-plane polarization is found via nominal d 0 filling on the B-site, A-site cations bearing lone-pair electrons, and A′ ≠ A size mismatch; the band gap is controlled by B/B′ electronegativity difference12.
In this work, we propose a simple design scheme. We introduce a new class of double perovskite oxides A 2VFeO6 where A is a divalent cation (A = Ba, Pb, etc) and demonstrate that a ‘complete’ charge transfer (nominally one electron transfer) between the two transition metal ions13,14,15,16,17,18 can induce desirable properties for bulk photovoltaics. First-principles calculations show that while neither bulk perovskite AVO3 nor AFeO3 is ferroelectric, a ‘complete’ charge transfer occurs from V to Fe, rendering the new double perovskite oxides a Mott multiferroic: at zero temperature a ferroelectric antiferromagnet and around room temperatures a ferroelectric Mott insulator. The ferroelectric polarization is substantial, comparable to ATiO3, but the band gap is significantly lower, smaller than that of ATiO3 and BiFeO3.
We first focus on Ba2VFeO6 (similar results are obtained for Pb2VFeO6 and Sr2VFeO6, see section 4). Figure 1a and b show the atomic and electronic structures for perovskite BaVO3 and BaFeO3, respectively. Bulk perovskite BaVO3 has been recently synthesized at high pressure and has been found to remain cubic and metallic to the lowest temperature19. Bulk BaFeO3 normally crystallizes in a hexagonal structure but cubic perovskite BaFeO3 can be stabilized in powders20 and in epitaxial thin films21,22,23,24 and exhibits a robust ferromagnetism20,21,22,23,24. Both metallic20, 23 and insulating21, 22, 24 behaviors have been reported.
Design principles for charge-transfer-driven Mott multiferroics. (a) Energy diagram and atomic structure of cubic BaVO3. The dashed line is the Fermi level. δ VO is the V-O displacement along the [001] direction. (b) Energy diagram and atomic structure of cubic BaFeO3. The dashed line is the Fermi level. δ FeO is the Fe-O displacement along the [001] direction. (c) Energy diagram and atomic structure of double perovskite Ba2VFeO6. The dashed line is the Fermi level, which lies in the gap between V d and Fe d states. ‘LHB’ (‘UHB’) means lower Hubbard bands (upper Hubbard bands). The red arrow indicates the charge transfer from V atoms to Fe atoms due to electronegativity difference. In the double perovskite Ba2VFeO6, a polar distortion is developed (δ VO > 0 and δ FeO > 0) because of the new charge configuration V d 0 and Fe d 5.
Formal valence considerations imply that in BaVO3 the V adopts a d 1 configuration while in BaFeO3 the Fe is d 4. In the double perovskite Ba2VFeO6, however, we expect that the large electronegativity difference between V and Fe leads to complete charge transfer from V to Fe, resulting in V-d 0 and Fe-d 5 configurations as illustrated in Fig. 1c. Similar phenomena have been predicted and observed in many different transition metal oxide heterostructures15,16,17,18, 25. The particular relevance here is that the empty V-d shell and half-filled Fe-d shell are both susceptible to noncentrosymmetric distortions (for the empty d shell case, see refs 26 and 27 and for the half-filled d shell cases see refs 28–30) while Ba2+-O2− coupling stabilizes the ferroelectric phase over anti-ferroelectric phases, as in BaTiO3 31. The half filled Fe-d shell leads to magnetic ordering and Mott insulating behavior, while the position of the V-d level leads to a reduced band gap (a similar strategy to reduce band gap has been discussed in refs 12, 26, 27. Therefore as Fig. 1c shows, double perovskite Ba2VFeO6 is predicted to be Mott multiferroic (paramagnetic ferroelectric at high temperatures and long-range magnetically ordered at sufficiently low temperatures). Furthermore, as illustrated in Fig. 1c, the band gap of double perovskite Ba2VFeO6 is set by the filled lower Hubbard band of Fe-d states (strongly hybridized with O-p states) and empty V-d states (conduction band edge).
We note that the double perovskite structure is much more stable than the layered configuration proposed in ref. 12, because charge transfer generically results in substantial metal-oxygen bond disproportionation25. Due to geometry consideration, the bond disproportionation inevitably induces internal strain in the layered structure but is naturally accommodated by the double perovskite structure, explaining the relative phase stability25. Although previous work has suggested that rock-salt ordering of B-site atoms suppresses polarization in A 2 BB′O6 12, 32, our work shows that it is possible to induce robust ferroelectricity in double perovskite oxides Ba2VFeO6.
In the rest of this paper we present calculations substantiating this picture. In Section II we outline the computational details. In Section III we present results for double perovskite Ba2VFeO6. Section IV extends the calculations to the double perovskite Pb2VFeO6 and Sr2VFeO6, in which we discuss the similarities and differences. Section V is a summary and conclusion.
Computational Details
Our first-principles calculations are performed using density functional theory (DFT)33 and dynamical mean field theory (DMFT)34. Structural relaxation is performed within DFT. Gaps are calculated using both DFT and DFT+DMFT. It has been established that structural and magnetic properties of multiferroic oxides strongly depend on the choice of exchange correlation functionals5, 30, 35. We use three exchange correlation functionals to test the robustness of our predictions: i) charge-density-only generalized gradient approximation with Perdew-Burke-Ernzerhof parametrization36 plus Hubbard U and Hund’s J corrections (PBE+U+J)37, (ii) charge-only local density approximation with Hubbard U and Hund’s J corrections (LDA+U+J)37, 38; (iii) spin-polarized generalized gradient approximation with Perdew-Burke-Ernzerhof parametrization revised for solids (sPBEsol)39. In order to investigate Mottness and effects of long-range magnetic ordering, we use DMFT to study both paramagnetic and long-range magnetic ordered states.
The DFT calculations are performed using a plane-wave basis33, as implemented in the Vienna Ab-initio Simulation Package (VASP)40, 41. The Projector Augmented Wave (PAW) approach is used42, 43. We use an energy cutoff of 600 eV. All the supercells of double perovskite oxides A 2VFeO6 consist of 40 atoms to accommodate different magnetic orderings. We consider ferromagnetic ordering, [001] antiferromagnetic ordering, [010] antiferromagnetic ordering and [100] antiferromagnetic ordering (see the Supplementary Materials for their definitions). We note that since in A 2VFeO6 the Fe ions form a face-centered-cubic lattice which has intrinsic ‘geometry frustration’, novel magnetism such as non-collinear magnetic ordering is possible in the ground state44, 45. However, at finite temperatures, [001] antiferromagnetic ordering has been observed in various double perovskite oxides46,47,48,49. In this study, we only consider collinear magnetic orderings. A 6 × 6 × 6 Monkhorst-Pack grid is used to sample the Brillouin zone. Both cell and internal coordinates are fully relaxed until each force component is smaller than 10 meV/Å and the stress tensor is smaller than 0.1 kbar.
In the PBE+U+J/LDA+U+J as well as DMFT calculations, we use U Fe = 5 eV, J V = J Fe = 0.7 eV, following previous studies50, 51. The choice of U V needs comment. While U V of about 5 eV has been accepted in literature50, we find that U V = 5 eV induces an off-center displacement δ VO in perovskite BaVO3, while in experiment perovskite BaVO3 (which experimentally is stable only at pressures P > 15GPa) is a cubic structure19. The calculated off-center displacement of V is closely related to orbital ordering (\({d}_{xy}^{1}{d}_{xz}^{0}{d}_{yz}^{0}\)) stabilized by a large U V in the DFT+U method. Therefore we use a smaller U V = 3 eV which stabilizes a cubic structure in perovskite BaVO3 in our calculations of double perovskite Ba2VFeO6. This ensures that a non-zero δ VO in Ba2VFeO6 is not a consequence of a large U V, but rather is induced by charge transfer. We repeated all the DFT calculations on Ba2VFeO6 using U V = 5 eV and found qualitatively similar results in structural properties. On the other hand, U V controls the energy level of V-d states, which may affect the band gap of Ba2VFeO6. Therefore, in our DMFT calculations, we also studied a range of U V (from 3 to 6 eV) to estimate the variation of energy gap in the spectral function.
We perform single-site DMFT calculations with Ising-like Slater-Kanamori interactions. The impurity problem is solved using the continuous-time quantum Monte Carlo algorithm with a hybridization expansion52, 53. The correlated subspace and the orbitals with which it mixes are constructed using maximally localized Wannier functions54 defined over the full 10 eV range spanned by the p-d band complex, resulting in a well-localized set of d-like orbitals. All the DMFT calculations are performed at the temperature of 290 K. For each DMFT iteration, a total of 3.8 billion Monte Carlo steps is taken to converge the impurity Green function and self energy. In double perovskite oxides, since V-d states are empty, we treat V-t 2g orbitals with the DMFT method and V-e g orbitals with a static Hartree-Fock approximation. Because the Fe-d states are half-filled, we treat all the five Fe-d orbitals with the DMFT method. The two self energies (one for V sites and the other for Fe sites) are solved independently and then coupled at the level of self-consistent conditions.
To obtain the spectral functions, the imaginary axis self energy is continued to the real axis using the maximum entropy method55. Then the real axis local Green function is calculated using the Dyson equation and the spectral function is obtained following:
where i is the label of a Wannier function. 1 is an identity matrix, H 0(k) is the DFT-PBE band Hamiltonian in the matrix form using the Wannier basis. Σ(ω) is understood as a diagonal matrix only with nonzero entries on the correlated orbitals. μ is the chemical potential. V dc is the fully localized limit (FLL) double counting potential, which is defined as in ref. 56:
where N d is the d occupancy of a correlated site.
Results for Ba2VFeO6
Structural properties
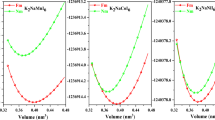
We first discuss the fully relaxed atomic structure of double perovskite Ba2VFeO6, obtained using DFT calculations with three different exchange correlation functionals (PBE+U+J, LDA+U+J and sPBEsol). For each exchange correlation functional, we test ferromagnetic (F), [001] antiferromagnetic, [010] antiferromagnetic and [100] antiferromagnetic orderings (see the Supplementary Materials for precise definitions). For each case, we start from a crystal structure with rotations and tilts of VO6 and FeO6 (space group P21/n) and then perturb the V and Fe atoms along [001] or [011] or [111] directions. Next we perform atomic relaxation with all the symmetry turned off. After atomic relaxation, we find that the rotations and tilts of VO6 and FeO6 are strongly suppressed while the polarization along [001] or [011] or [111] direction is stabilized. Comparing the total energy of the three polarizations, we find the ground state of Ba2VFeO6 has the polarization along the [001] direction. The ground state structure has tetragonal symmetry (space group I4/m). We note that based on the symmetry analysis57 and all the available experimental data for double perovsite oxides compiled in the review49, there are altogether seven tilting patterns which are allowed in a double perovskite structure A 2 BB′O6 and have been observed in experiment. They are: a 0 a 0 a 0(Fm-3m), a + b − b −(P21/n), a 0 a 0 c −(I4/m), a − a − a −(R-3), a 0 b − b −(I2/m), a 0 a 0 c +(P4/mnc) and a − b − c −(I-1) (the last two tilting patterns are much rarer in experiment). Among them, the most common tilting is a + b − b −(P21/n) with over 300 compounds49. We tested different initial guesses with these and other allowed symmetries, perturbed the system with ferroelectric distortions, and after relaxation we always obtained similar results. On the magnetic properties, given the U and J values, we find that the ground state is always of the [001] antiferromagnetic ordering (among the collinear magnetic orderings). Using the same methods and parameters, perovskite BaVO3 and BaFeO3 have cubic symmetry. The resulting lattice constant a, tetragonality c/a ratio and cation-displacement δ BO along the [001] direction (see in Fig. 1c) are shown in Table 1 for each exchange correlation functional. The full crystal structure data are provided in the Supplementary Materials. We observe that the reason that rotations and tilts of VO6/FeO6 octahedra are strongly suppressed in Ba2VFeO6 is due to the large ionic size of Ba ions, which is known to prohibit rotations and tilts of oxygen octahedra in perovskite Ba-compounds and to induce robust ferroelectricity in BaTiO3 and BaMnO3 29, 58.
For comparison, we also calculated the atomic structure of fully relaxed tetragonal BaTiO3, a known ferroelectric perovskite. Since BaTiO3 is a d 0 band insulator with no magnetic properties, we do not add Hubbard U and Hund’s J correction to PBE/LDA and we use PBEsol instead of spin-polarized PBEsol (sPBEsol). We find that the calculated c/a ratio and ion-displacement (δ VO and δ FeO) of Ba2VFeO6 are comparable to those of BaTiO3. The ground state of tetragonal double perovskite Ba2VFeO6 is an insulator (we will discuss the gap properties in details in the following subsections). The ground state of high-symmetry cubic double perovskite Ba2VFeO6 is also an insulator (see Table 1). Therefore a switching path for ferroelectric polarization is well-defined and we can use the Berry phase method54 to calculate the polarization of the tetragonal structure. We find that for each exchange-correlation function the calculated polarization of Ba2VFeO6 is comparable to that of BaTiO3 (see Table 1).
We comment here that our recent studies30, 35 of perovskite manganites show that PBE+U+J and sPBEsol yield the most accurate predictions of structural and magnetic properties of magnetic ferroelectrics, while LDA+U+J sets a conservative estimation for the lower bound of polarization. Therefore we believe that the polarization of Ba2VFeO6 is larger than 18 μC/cm2, which is substantial enough to induce bulk photovoltaic effects4.
Electronic properties
The results of the previous subsection indicate that the double perovskite Ba2VFeO6 has a noncentrosymmetric tetragonal distortion not found in the component materials bulk BaVO3 and BaFeO3. In this section we consider the electronic reconstruction arising in this double perovskite.
Figure 2a shows the band structure of double perovskite Ba2VFeO6 with the [001] antiferromagnetic ordering (only one spin channel is shown here), calculated using the PBE+U+J method. We see that a gap is clearly opened in Ba2VFeO6 while using the same method with the same parameters, perovskite BaVO3 and BaFeO3 are found to be metallic with V-d and Fe-d states at the Fermi surface (see Section II in the Supplementary Materials for details). The gap opening in Ba2VFeO6 is a strong evidence of a nominally “complete” charge transfer from V to Fe. A similar charge-transfer-driven metal-insulator transition is predicted14 and observed17 in LaTiO3/LaNiO3 superlattices.
Comparison of band structure and optical conductivity between Ba2VFeO6 and BaTiO3. The results for Ba2VFeO6 are calculated using DFT-PBE+U+J method. The results for BaTiO3 are calculated using DFT-PBE method. (a) Band structure of tetragonal Ba2VFeO6. The blue arrow indicates the threshold of optical transition. (b) Band structure of tetragonal BaTiO3. The blue arrow indicates the threshold of optical transition. (c) Optical conductivity σ of tetragonal Ba2VFeO6 (solid lines) and tetragonal BaTiO3 (dashed lines). The red lines are for the xx-component and the blue lines are for the zz-component. The green arrows indicate the fundamental gap of band structures.
For comparison, we also calculated the band structure of tetragonal BaTiO3 using PBE (Fig. 2b). We note that while the polarization of double perovskite Ba2VFeO6 is comparable to that of BaTiO3, the band gap of Ba2VFeO6 (0.78 eV) is significantly smaller than that of BaTiO3 (1.75 eV). Using other exchange correlation functionals, we find similar properties that the band gap of Ba2VFeO6 is smaller than that of BaTiO3 by about 1 eV (see ‘fundamental gap’ Δ0 in Table 1).
For photovoltaic effects the relevant quantity is the optical gap Δoptical. We calculate the optical conductivity of both Ba2VFeO6 and BaTiO3 using standard methods59 and show the results in Fig. 2c. Due to the tetragonal symmetry, the off-diagonal matrix elements of the optical conductivity vanish and only two diagonal elements are independent (σ xx = σ yy and σ zz ). For BaTiO3 the minimum optical gap is in the xx channel and is given by the direct (vertical in momentum space) gap (shown for BaTiO3 as the blue arrow in Fig. 2b). In BaTiO3 the optical gap is larger than the fundamental gap, which is indirect (momentum of lowest conduction band state differs from momentum of highest valence band state; the green arrow in Fig. 2c shows the size of the fundamental gap). The optical conductivity of Ba2VFeO6 is also larger than its fundamental gap, which can be understood in a similar manner. If we consider (VFe) as a pseudo-atom X, the hypothetical single perovskite BaXO3 would have an indirect gap (between Γ and R). However, the reduction in translational symmetry due to the V-Fe alternation leads to band folding which maps the original R point to the Γ point, leading to a direct gap of 0.8 eV at the Γ point. However the calculated optical gap is 1.1 eV (blue arrow in Fig. 2a). The difference between the direct and optical gaps is a matrix element effect: the lowest back-folded conduction band state does not have a dipole allowed transition matrix element with the highest-lying valence band state (see the Supplementary Materials for more details).
It is well-known that DFT with semi-local exchange correlation functionals substantially underestimate band gaps. Here we argue that since Ba2VFeO6 and BaTiO3 have similar electronic structures (gap separated by metal d and oxygen p states), the DFT band gap underestimation with respect to experimental values is approximately a constant for BaTiO3 and Ba2VFeO6. The experimental optical gap of BaTiO3 is 3.2 eV and the DFT calculated value is 2.3 eV, about 0.9 eV smaller. The DFT calculated optical gap of Ba2VFeO6 is 1.1 eV, hence we estimate the experimental optical gap of Ba2VFeO6 is 2.0 eV, which is smaller than the optical gap of intensively investigated BiFeO3 (2.7 eV)60.
Our results that Ba2VFeO6 should have a smaller gap than that of BaTiO3 and BiFeO3 are also supported by physical arguments (see Fig. 3). The band gap for transition metal oxides is set by the energy difference between transition metal d states and oxygen p states. This p-d separation is a measure of the relative electronegativity of transition metal and oxygen ions. Ti and V are both first-row transition metals and in BaTiO3 and Ba2VFeO6, Ti and V both have a d 0 configuration. Because V has a larger nuclear charge than Ti, the V-d states have lower energies than the Ti-d states, which leads to a smaller band gap for Ba2VFeO6 than for BaTiO3 (compare panels a and c of Fig. 3). On the other hand, the Fe d states are half-filled in both Ba2VFeO6 and BiFeO3, while V-d states are empty in Ba2VFeO6. Due to Coulomb repulsion and Hund’s coupling effects, adding one more electron in a half-filled d shell generically costs more energy than adding an electron in an empty d shell. Therefore the upper Hubbard band of Fe d states have higher energy than V d states, which results in a larger band gap for BiFeO3 than for Ba2VFeO6 (compare panels b and c of Fig. 3).
Estimation of critical temperatures
Double perovskite Ba2VFeO6 is a type-I multiferroic61, in which ferroelectric polarization and magnetism arise from different origins and they are largely independent of one another. This means that ferroelectric polarization and magnetism have their own critical temperatures and usually the critical temperature of polarization (T C ) is higher than the critical temperature of magnetism (T N )62. In this subsection, we estimate T C and T N for Ba2VFeO6.
Estimation of T C
In order to estimate the ferroelectric Curie temperature T C , we use the predictor \({T}_{C}\propto {P}_{0}^{2}\) where P 0 is the zero-temperature polarization63. This predictor has been successfully applied to a wide range of Pb-based perovskite ferroelectric oxides and it yields an accurate and quantitative estimation for ferroelectric T C 64. We apply this predictor to our Ba-based ferroelectrics, i.e. BaTiO3 and Ba2VFeO6. Here we use tetragonal BaTiO3 as the reference system. The experimental Curie temperature T C for BaTiO3 is about 400 K65. Using the DFT+Berry phase method54, we can obtain the values of the zero-temperature polarization for both BaTiO3 and Ba2 VFe 6 shown in Table 1. Therefore we estimate that T C for Ba2VFeO6 is 473 K (PBE+U+J), 245 K (LDA+U+J) and 425 K (sPBEsol). While different exchange correlation functionals predict a range for T C , we find that T C is near or above room temperature.
Estimation of T N
We use a classical Heisenberg model \(E=\frac{1}{2}{\sum }_{\langle kl\rangle }{J}_{kl}{{\bf{S}}}_{k}\cdot {{\bf{S}}}_{l}\) to estimate the magnetic ordering transition temperature T N , where S k is a unit-length classical spin and 〈kl〉 denotes summation over nearest Fe neighbors. Here we only consider Fe-Fe exchange couplings. Because double perovskite Ba2VFeO6 has a tetragonal structure, there are two exchange couplings of J kl : J in for the short Fe-Fe bonds and J out for the long Fe-Fe bonds. By calculating the total energy for the ferromagnetic ordering, [001] antiferromagnetic ordering and [100] antiferromagnetic ordering, we obtain that the in-plane exchange coupling J in is 2.5 meV (PBE+U+J), 3.7 meV (LDA+U+J) and 3.1 meV (sPBEsol); and the out-of-plane exchange coupling J out is 3.1 meV (PBE+U+J), 4.0 meV (LDA+U+J) and 3.7 meV (sPBEsol). The positive sign means that exchange couplings are all antiferromagnetic. Based on a mean-field theory, the estimated Néel temperature is T N = |4J in − 8J out|. The minus sign is because on a quasi face-centered-cubic lattice, every Fe atom has 8 nearest neighbors that are antiferromagnetically coupled and 4 nearest neighbors that are ferromagnetically coupled. Therefore T N is estimated to be 172 K (PBE+U+J), 200 K (LDA+U+J) and 200 K (sPBEsol). Since mean-field theories usually overestimate magnetic transition temperatures, the actual T N could be lower. An experimental determination of the magnetic ordering temperature would be of great interest.
Effects of long-range order
The estimates for the ferroelectric and magnetic transition temperatures of Ba2VFeO6 suggest that its actual ferroelectric Curie temperature T C is probably higher than its actual Néel temperature T N , as is the case for most type-I multiferroics61. It is therefore important to ask if the magnetically disordered state remains insulating, so that the ferroelectric properties are preserved.
Here we use DFT+DMFT to study both the paramagnetic and magnetically ordered states. The spectral functions for the three magnetic states that we have considered are shown in Fig. 4 along with the spectral function for the paramagnetic state. We find that the paramagnetic state is insulating, with a gap only slightly smaller than that of the ground state with [001] antiferromagnetic ordering, indicating that double perovskite Ba2VFeO6 is a promising candidate for Mott multiferroics62. The calculated spectral functions are consistent with our schematics of Fig. 3.
Spectral functions A(ω) of tetragonal double perovskite Ba2VFeO6 for different magnetic states. The unit of A(ω) is eV−1 per 5-atom. ‘PM’ stands for paramagnetic state, ‘FM’ for ferromagnetic state, ‘[001]-AFM’ for [001] antiferromagnetic state and ‘[100]-AFM’ for [100] antiferromagnetic state. Panels a) spin-resolved spectral function. The positive (negative) y-axis corresponds to spin-up (spin-down). Panels b) total spectral functions (summing over spin-up and spin-down). The red, blue and green curves are for Fe d, V d and O p, respectively. The Fermi level is set at ω = 0 eV.
We also use our DFT+DMFT methodology to investigate how the electronic structure of Ba2VFeO6 evolves as the ferroelectric polarization is suppressed within the paramagnetic state. Figure 5 compares the spectral function of Ba2VFeO6 in the cubic structure (i.e. no polarization) versus in the tetragonal structure (i.e. with polarization). We see that the suppression of polarization reduces the gap by about 0.2 eV. This behavior is very consistent with similar calculations on the nonmagnetic perovskite oxide SrTiO3 in which the presence of ferroelectric polarization can increase the band gap by up to 0.2 eV66.
Spectral functions A(ω) of cubic and tetragonal Ba2VFeO6. The unit of A(ω) is eV−1 per 5-atom. Panel a is for cubic Ba2VFeO6 and panel b is for tetragonal Ba2VFeO6. In both structures, we calculate the paramagnetic state. The red, blue and green curves are for Fe d, V d and O p, respectively. The Fermi level is set at ω = 0 eV.
Hubbard U dependence
Finally we discuss the Hubbard U dependence. As Fig. 4 shows, the conduction band edge is set by V-d states, which is consistent with Fig. 1c and our previous discussion of band gaps. If we change the Hubbard U V, it may affect the energy position of V d states and energy gap. To address this issue, we repeat the DMFT calculations on tetragonal Ba2VFeO6 using several values of U V. The panels a of Fig. 6 show the spectral function of the double perovskite as a function of U V. All the calculations are performed in a paramagnetic state. We note that as U V increases from 4 eV to 6 eV, the band gap is almost unchanged. This is due to the fully localized limit double counting correction which nearly cancels the Hartree shift. Hence, the V-d and O-p energy separation is practically unaffected, which is very consistent with a previous DMFT study of SrVO3 67. If we apply the same method and same Hubbard U parameters to tetragonal BaTiO3, the spectral functions of BaTiO3 (panels b of Fig. 6) show that the energy gap of BaTiO3 is slightly increased. Thus while we have some uncertainty relating to the appropriate values for the Hubbard U, our estimates for energy gap are robust: double perovskite Ba2VFeO6 has an energy gap ~1 eV smaller than that of BaTiO3. The underlying reason is the differing electronegativities of Ti4+ and V5+.
Spectral functions A(ω) of tetragonal Ba2VFeO6 and BaTiO3 as a function of Hubbard U on V and Ti. The unit of A(ω) is eV−1 per 5-atom. Panels a are the results for tetragonal Ba2VFeO6. Panels b are the results for tetragonal BaTiO3. For Ba2VFeO6, the calculations are performed in a paramagnetic state. For BaTiO3, the calculations are performed in a non-magnetic state. In panels a, the green lines are the total spectral functions and the red lines are the spectral functions projected onto V d states. In panels b, the green lines are the total spectral functions and the red lines are the spectral functions projected onto Ti d states. The Fermi level is set at ω = 0 eV.
Related materials Pb2VFeO6 and Sr2VFeO6
In this section we employ the same parameters and methods used for Ba2VFeO6 to discuss double perovskite Pb2VFeO6 and Sr2VFeO6.
We first discuss Pb2VFeO6. Pb has a lone pair of 6s electrons, which favors off-center displacements as was already shown for tetragonal PbTiO3 68. Due to the same mechanism, double perovskite Pb2VFeO6 has substantial cation-displacements, tetragonality and ferroelectric polarization (see Table 2). All these values are comparable to, or even larger than those of tetragonal PbTiO3. We note however that within sPBEsol the polarization of this tetragonal structure is not-well defined because the corresponding high-symmetry cubic structure is metallic and thus the obvious switching path is not available.
While tetragonal double perovskite Pb2VFeO6 has similar structural properties to tetragonal PbTiO3, the fundamental gap Δ0 and optical gap Δoptical are both smaller than those of PbTiO3 by about 1 eV (all three exchange correlation functionals make qualitatively consistent predictions).
We note here that the polarization in Pb2VFeO6 has different origin from the polarization in tetragonal PbVO3 69. In tetragonal PbVO3, V atoms have a d 1 charge configuration and its off-center displacement δ VO and insulating properties are associated with orbital ordering (\({d}_{xy}^{1}{d}_{xz}^{0}{d}_{yz}^{0}\))70. In double perovskite oxide Pb2VFeO6, charge transfer leads to a d 0 configuration on V sites and therefore the off-center displacement δ VO is due to hybridization between V-d and O-p states31. More importantly, perovskite PbVO3 is not ferroelectric because along the switching path (from the tetragonal-to-cubic structure) an insulator-to-metal phase transition is observed71.
Next we discuss Sr2VFeO6. Sr2VFeO6 is more complicated because the ionic size of Sr2+ is smaller than Ba2+ and therefore rotations of oxygen octahedra (so-called antiferrodistortive mode, or AFD mode) can exist in Sr-compounds, such as in SrTiO3. These rotations compete against ferroelectric polarization72. For double perovskite Sr2VFeO6, even if we do not take the AFD mode into account, different exchange correlation functionals predict different structural and electronic properties. Table 3 shows that PBE+U+J predicts that the ground state is tetragonal and ferroelectric. The polarization is sizable (26 μC/cm2) and the DFT-calculated optical gap is 1.36 eV. On the other hand, the LDA+U+J method can not stabilize the tetragonal structure. This method predicts that ground state of Sr2VFeO6 has a cubic structure with no off-center displacements of either V or Fe, and is metallic. The sPBEsol method can stabilize a tetragonal structure with non-zero off-center displacements δ VO and δ FeO, but the ground state is also metallic and therefore the polarization is not well-defined. We may impose epitaxial strain to induce ferroelectricity in Sr2VFeO6, but the critical strain strongly depends on the choice of exchange correlation functional30: PBE+U+J does not require any strain to stabilize the ferroelectric state, while LDA+U+J requires a 3% compressive strain to open the gap and stabilize the tetragonal structure with a sizable polarization. A similar situation occurs for SrTiO3. If we use the same methods and do not take into account the AFD mode, PBE predicts a ferroelectric ground state, while LDA and sPBE predict that the ground state is cubic (i.e. no polarization). Experimentally, SrTiO3 is on the verge of a paraelectric-to-ferroelectric transition73. Thus we conclude that our DFT calculations indicate that double perovskite Sr2VFeO6 is close to the paraelectric-to-ferroelectric phase boundary and probably is on the paraelectric side.
Conclusions
In summary, we use first-principles calculations to design a new class of Mott multiferroics among which double perovskite oxide Ba2VFeO6 stands out as a promising candidate to induce bulk photovoltaic effects because of its large polarization (comparable to BaTiO3); its reduced optical gap (smaller than BaTiO3 by about 1 eV); and its environmentally friendly composition (Pb-free). Our work shows that charge transfer is a powerful approach to engineering atomic, electronic and magnetic structures in complex oxides. New charge configurations not found in bulk materials can occur in oxide heterostructures (including complex bulk forms such as double perovskites), and these charge configurations can produce emergent phenomena and properties not exhibited in constituent compounds. In particular, V5+ is very rare in single perovskite oxides (probably due to its small ionic size). We hope our theoretical predictions can stimulate further experimental endeavors to synthesize and measure these new multiferroic materials for photovoltaic applications.
References
Yang, S. Y. et al. Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 5, 143–147 (2010).
Cao, D. et al. High-efficiency ferroelectric-film solar cells with an n-type CuO cathode buffer layer. Nano Lett. 12, 2803–2809 (2012).
Alexe, M. & Hesse, D. Tip-enhanced photovoltaic effects in bismuth ferrite. Nat. Commun. 2, 256 (2011).
Grinberg, I. et al. Perovskite oxides for visible-light-absorbing ferroelectric and photovoltaic materials. Nature 503, 509–512 (2013).
Bilc, D. I. et al. Hybrid exchange-correlation functional for accurate prediction of the electronic and structural properties of ferroelectric oxides. Phys. Rev. B 77, 165107 (2008).
Bennett, J. W., Grinberg, I. & Rappe, A. M. New highly polar semiconductor ferroelectrics through d8 cation-O vacancy substitution into PbTiO3: a theoretical study. J. Am. Chem. Soc. 130, 17409–17412 (2008).
Gou, G. Y., Bennett, J. W., Takenaka, H. & Rappe, A. M. Post density functional theoretical studies of highly polar semiconductive Pb(Ti1−xNix)O3−x solid solutions: Effects of cation arrangement on band gap. Phys. Rev. B 83, 205115 (2011).
Qi, T., Grinberg, I. & Rappe, A. M. Band-gap engineering via local environment in complex oxides. Phys. Rev. B 83, 224108 (2011).
Choi, T., Lee, S., Choi, Y. J., Kiryukhin, V. & Cheong, S.-W. Switchable ferroelectric diode and photovoltaic effect in BiFeO3. Science 324, 63–66 (2009).
Choi, W. S. et al. Wide bandgap tunability in complex transition metal oxides by site-specific substitution. Nat. Commun. 3, 689 (2012).
Nechache, R. et al. Bandgap tuning of multiferroic oxide solar cells. Nat. Photonics 61, 61–67 (2014).
Kim, C., Park, H. & Marianetti, C. A. New class of planar ferroelectric Mott insulators via first-principles design. Phys. Rev. B 92, 235122 (2015).
Chen, H. et al. Modifying the electronic orbitals of nickelate heterostructures via structural distortions. Phys. Rev. Lett. 110, 186402 (2013).
Chen, H., Millis, A. & Marianetti, C. Engineering correlation effects via artificially designed oxide superlattices. Phys. Rev. Lett. 111, 116403 (2013).
Kleibeuker, J. E. et al. Electronic reconstruction at the isopolar LaTiO(3)/LaFeO(3) interface: an X-ray photoemission and density-functional theory study. Phys. Rev. Lett. 113, 237402 (2014).
Disa, A. et al. Orbital engineering in symmetry-breaking polar heterostructures. Phys. Rev. Lett. 114, 026801 (2015).
Cao, Y. et al. Engineered Mott ground state in LaTiO−{3+/delta}/LaNiO3 heterostructure. Nat. Commun. 7, 10418 (2016).
Grisolia, M. N. et al. Hybridization-controlled charge transfer and induced magnetism at correlated oxide interfaces. Nat. Phys. 12, 484–492 (2016).
Nishimura, K., Yamada, I., Oka, K., Shimakawa, Y. & Azuma, M. High-pressure synthesis of BaVO3: A new cubic perovskite. J. Phys. Chem. Solids 75, 710–712 (2014).
Hayashi, N. et al. BaFeO3: A ferromagnetic iron oxide. Angew. Chemie - Int. Ed. 50, 12547–12550 (2011).
Matsui, T. et al. Structural, dielectric, and magnetic properties of epitaxially grown BaFeO3 thin films on (100) SrTiO3 single-crystal substrates. Appl. Phys. Lett. 81, 2764 (2002).
Matsui, T., Taketani, E., Fujimura, N., Ito, T. & Morii, K. Magnetic properties of highly resistive BaFeO3 thin films epitaxially grown on SrTiO3 single-crystal substrates. J. Appl. Phys. 93, 6993 (2003).
Callender, C., Norton, D. P., Das, R., Hebard, A. F. & Budai, J. D. Ferromagnetism in pseudocubic BaFeO3 epitaxial films. Appl. Phys. Lett. 92, 012514 (2008).
Chakraverty, S. et al. BaFeO3 cubic single crystalline thin film: A ferromagnetic insulator. Appl. Phys. Lett. 103, 142416 (2013).
Chen, H. & Millis, A. Antisite defects at oxide interfaces. Phys. Rev. B 93, 104111 (2016).
Eng, H. W., Barnes, P. W., Auer, B. M. & Woodward, P. M. Investigations of the electronic structure of d0 transition metal oxides belonging to the perovskite family. J. Solid State Chem. 175, 94–109 (2003).
Berger, R. F. & Neaton, J. B. Computational design of low-band-gap double perovskites. Phys. Rev. B 86, 165211 (2012).
Neaton, J. B., Ederer, C., Waghmare, U. V., Spaldin, N. A. & Rabe, K. M. First-principles study of spontaneous polarization in multiferroic BiFeO3. Phys. Rev. B 71, 014113 (2005).
Rondinelli, J. M., Eidelson, A. S. & Spaldin, N. A. Non-d0 Mn-driven ferroelectricity in antiferromagnetic BaMnO3. Phys. Rev. B 79, 205119 (2009).
Chen, H. & Millis, A. J. Spin-density functional theories and their +U and +J extensions: A comparative study of transition metals and transition metal oxides. Phys. Rev. B 93, 045133 (2016).
Benedek, N. A. & Birol, T. ‘Ferroelectric’ Metals Reexamined: Fundamental Mechanisms and Design Considerations for New Materials. Mater. Chem. C 4, 4000–4015 (2016).
Knapp, M. C. & Woodward, P. M. A-site cation ordering in AABBO6 perovskites. J. Solid State Chem. 179, 1076–1085 (2006).
Payne, M. C., Teter, M. P., Allan, D. C., Arias, T. A. & Joannopoulos, J. D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Chen, H. & Millis, A. Comparative study of exchange-correlation functionals for accurate predictions of structural and magnetic properties of multiferroic oxides. Phys. Rev. B 93, 205110 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Liechtenstein, A. I., Anisimov, V. I. & Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467 (1995).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Perdew, J. P. et al. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Chen, G., Pereira, R. & Balents, L. Exotic phases induced by strong spin-orbit coupling in ordered double perovskites. Phys. Rev. B 82, 174440 (2010).
Chen, G. & Balents, L. Spin-orbit coupling in d2 ordered double perovskites. Phys. Rev. B 84, 094402 (2011).
Aharen, T. et al. Magnetic properties of the S = 3/2 geometrically frustrated double perovskites La2LiRuO6 and Ba2YRuO6. Phys. Rev. B 80, 134423 (2009).
Paul, A. K. et al. Magnetically frustrated double perovskites: Synthesis, structural properties, and magnetic order of Sr2BOsO6 (B = Y, In, Sc). Zeitschrift fur Anorg. und Allg. Chemie 641, 197–205 (2015).
Taylor, A. E. et al. Magnetic order and electronic structure of the 5d3 double perovskite Sr2ScOsO6. Phys. Rev. B 91, 100406(R) (2015).
Vasala, S. & Karppinen, M. A2BBO6 perovskites: A review. Prog. Solid State Chem. 43, 1–36 (2015).
Pavarini, E. et al. Mott transition and suppression of orbital fluctuations in orthorhombic 3d1 perovskites. Phys. Rev. Lett. 92, 176403 (2004).
Mosey, N. J., Liao, P. & Carter, E. A. Rotationally invariant ab initio evaluation of Coulomb and exchange parameters for DFT + U calculations. J. Chem. Phys. 129, 014103 (2008).
Werner, P., Comanac, A., De’ Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349–404 (2011).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Silver, R. N., Sivia, D. S. & Gubernatis, J. E. Maximum-entropy method for analytic continuation of quantum Monte Carlo data. Phys. Rev. B 41, 2380–2389 (1990).
Czyżyk, M. T. & Sawatzky, G. A. Local-density functional and on-site correlations: The electronic structure of La2CuO4 and LaCuO3. Phys. Rev. B 49, 14211–14228 (1994).
Lufaso, M. W. et al. Structure prediction of ordered and disordered multiple octahedral cation perovskites using SPuDS. Acta Crystallogr. Sect. B Struct. Sci. 62, 397–410 (2006).
Wu, X., Rabe, K. M. & Vanderbilt, D. Interfacial enhancement of ferroelectricity in CaTiO3/BaTiO3 superlattices. Phys. Rev. B 83, 020104 (2011).
Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J. & Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112 (2006).
Ihlefeld, J. F. et al. Optical band gap of BiFeO [sub 3] grown by molecular-beam epitaxy. Appl. Phys. Lett. 92, 142908 (2008).
Khomskii, D. T. Classifying multiferroics: Mechanisms and effects. Physics (College. Park. Md). 2, 20 (2009).
Puggioni, D., Giovannetti, G., Capone, M. & Rondinelli, J. M. Design of a Mott Multiferroic from a Nonmagnetic Polar Metal. Phys. Rev. Lett. 115, 087202 (2015).
Abrahams, S. C., Kurtz, S. K. & Jamieson, P. B. Atomic Displacement Relationship to Curie Temperature and Spontaneous Polarization in Displacive Ferroelectrics. Phys. Rev. 172, 551–553 (1968).
Grinberg, I. & Rappe, A. M. Local structure and macroscopic properties in PbMg1/3Nb2 3O3-PbTiO3 and PbZn1/3Nb2/3O3-PbTiO3 solid solutions. Phys. Rev. B 70, 220101 (2004).
Megaw, H. D. Crystal structure of double oxides of the perovskite type. Proc. Phys. Soc. 58, 133–152 (1946).
Berger, R. F., Fennie, C. J. & Neaton, J. B. Band gap and edge engineering via ferroic distortion and anisotropic strain: The case of SrTiO3. Phys. Rev. Lett. 107, 146804 (2011).
Dang, H. T., Millis, A. J. & Marianetti, C. A. Covalency and the metal-insulator transition in titanate and vanadate perovskites. Phys. Rev. B 89, 161113 (2014).
Waghmare, U. V. & Rabe, K. M. Ab initio statistical mechanics of the ferroelectric phase transition in PbTiO 3. Phys. Rev. B 55, 6161–6173 (1997).
Shpanchenko, R. V. et al. Synthesis, Structure, and Properties of New Perovskite PbVO3. Chem. Mater. 16, 3267–3273 (2004).
Oka, K. et al. Magnetic ground-state of perovskite PbVO3 with large tetragonal distortion. Inorg. Chem. 47, 7355–7359 (2008).
Belik, A. A., Azuma, M., Saito, T., Shimakawa, Y. & Takano, M. Crystallographic Features and Tetragonal Phase Stability of PbVO3, a New Member of PbTiO3 Family. Chem. Mater. 17, 269–273 (2005).
Fleury, P. A., Scott, J. F. & Worlock, J. M. Soft Phonon Modes and the 110 K Phase Transition in SrTi O 3. Phys. Rev. Lett. 21, 16–19 (1968).
Müller, K. A. & Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 19, 3593–3602 (1979).
Acknowledgements
H. Chen is supported by National Science Foundation under grant No. DMR-1120296. A.J. Millis is supported by National Science Foundation under grant No. DMR-1308236. Computational facilities are provided via Extreme Science and Engineering Discovery Environment (XSEDE), through Award No. TGPHY130003 and via the National Energy Research Scientific Computing Center (NERSC).
Author information
Authors and Affiliations
Contributions
H. Chen conceived the project and performed numerical calculations. A.J.M. supervised the project. H. Chen and A.J.M. analyzed the data, discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, H., Millis, A. Design of new Mott multiferroics via complete charge transfer: promising candidates for bulk photovoltaics. Sci Rep 7, 6142 (2017). https://doi.org/10.1038/s41598-017-06396-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-06396-5
This article is cited by
-
Study of disorder in pulsed laser deposited double perovskite oxides by first-principle structure prediction
npj Computational Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.