Abstract
Recently, advanced designs and materials emerge to study biologically inspired neuromorphic circuit, such as oxide semiconductor devices. The existence of mobile ions in the oxide semiconductors could be somewhat regarded to be similar with the case of the ions movements among the neurons and synapses in the brain. Most of the previous studies focus on the spike time, pulse number and material species: however, a quantitative modeling is still needed to study the voltage dependence of the relaxation process of synaptic devices. Here, the gate pulse stimulated currents of oxide semiconductor devices have been employed to mimic and investigate artificial synapses functions. The modeling for relaxation process of important synaptic behaviors, excitatory post-synaptic current (EPSC), has been updated as a stretched-exponential function with voltage factors in a more quantitative way. This quantitative modeling investigation of representative synaptic transmission bias impacts would help to better simulate, realize and thus control neuromorphic computing.
Similar content being viewed by others
Introduction
In recent years, a lot of advanced architectures have emerged as potential candidates for new generation of integrated circuits for various applications such as neuron computing, including three dimentional (3-D) integration1,2,3, quantum cellular automata4,5,6,7,8, defect tolerant architecture9, 10, molecular architecture and quantum computing11,12,13. However, they all have some limitations for use in the large scale circuits. For example, 3-D integration has difficulty to be test and measured. Quantum architectures have low temperature operation requirement and are sensitive to background noise. Defect tolerant architecture requires pre-computing tests. Molecular architecture has unclear mechanism and thus have limited the functionality to date. Complementary Metal Oxide Semiconductor (CMOS) transistors have been employed to simulate the representative synaptic transmission behaviors of synaptic devices such as excitatory post-synaptic current (EPSC)14,15,16,17,18,19,20,21. By modifying ionic fluxes in neurons and synapses, synaptic behaviors could be established in the human brain, such as signal processing, memory, and learning functions. A potential spike signal in a presynaptic neuron can trigger an ionic EPSC through a synapse, which may last for as much as milli-seconds in a postsynaptic neuron. The semiconductor materials devices with mobile ions can somewhat mimic the representative synaptic behaviors with fast increase signal and subsequently slower decade including EPSC, spike-timing-dependent plasticity (STDP), etc15, 16, 21. However, the appropriate control such as voltage dependence of representative synaptic transmission behaviors are rarely studied in details. Most of the plasticity behaviors studies generally focus on the spike time, spike pulse number, and neuron materials16,17,18,19,20,21.
Meanwhile, amorphous oxide semiconductor materials and transistors have a combination advantages of transparency, flexibility, a relatively fair mobility (>10 cm2/V · s) and room temperature processing with uniform properties in large scale production22,23,24,25,26. Therefore, these device structures are the promising candidate for electronics such as liquid crystal display and light-emitted-diode drivers. In this article, we propose amorphous In-Ga-Zn oxide (α-IGZO) transistors to simulate the synaptic devices14,15,16,17,18,19,20,21. Oxide semiconductor devices have been employed to simulate the synaptic plasticity behaviors and this mechanism could be understood as follows. Neurons and synapses are two basic computational units in the brain, whose plasticity transmissions depend on the existence of ions. For instance, a synatic transmission could be regarded as initiating with the opening of voltage-gated calcium ion channels, where Ca+2 ions diffuse inside the neuron. Then neurotransmitters were released from synaptic vesicles and diffuse through the synaptic gap. Subsequently, they bind to the receptor sites of Na+ gated ion channels at the post-synaptic neuron, which enable Na+ ions to diffuse inside the cell. Amorphous oxide semiconductor devices have metal ions components, which could be regarded to be similar with the case of neurons and synapses which also depends on the ion transport. Therefore, the ions transport inside the amorphous oxide devices could be used to investigate the transmission of synapse and neurons signals21, 22, 27. EPSC is one of the common behaviors of the synaptic plasticity behaviors which has been investigated14,15,16,17,18,19,20,21. Previous research studies have generally focused on stimula time, cycles or neuron categories. Leveraging these intriguing features, typical and tunable synaptic behaviors are investigated in our design, suggesting voltage dependency of these behaviors. This study could help better controlling the artificial synaptic devices, which are the fundamental components for neuromorphic computing systems.
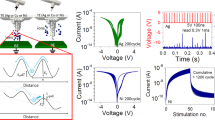
A 3D schematic idea of our artificial synaptic device is shown in Fig. 1a. The synaptic TFTs device based on In-Ga doped Zn-O (IGZO) was fabricated using AOS TFTs method4. Fig. 1b is a photo of the device which is actually fabricated. This typical representative EPSC records behavior in neuron rises immediately and falls relatively more gradually than when it rises in the time ranging from microseconds to miliseconds15, 21. Especially when the semiconductor has mobile ions, which shows similar trend as charging and discharging in a transistor or capacitor14, 15, 21. The EPSC is measured and investigated from the drain in our IGZO device after applying a trapezoidal voltage pulse at the bottom gate terminal as shown in Figure 1c. When the drain voltage is fixed, after a pulse applied on the gate terminal, the measured EPSC from the drain reaches a peal value and decreases gradually, which is similar to that in a biological excitatory synapse14. Here, IGZO is employed as the semiconductor channel of the TFTs. Therefore, the mechanism for the decaying EPSC could be attributed to the oxygen species diffusion/migration, which is suggested as the working mechanism for electrical properties shift of IGZO TFTs in previous publications21, 22, 27.
(a) The schematic of the 3D structure of the device with bottom gate, source, drain, and semiconductor channel, respectively. The conductive electrodes made of Ni/Au were used. The connection line between the drain and source is the semiconductor channel. (b) A representative image form the fabricated device with the bright white metal electrode as long as 800 μm. (c) EPSC triggered by presynaptic spike on bottom gate BG. (d) EPSC decay behavior with a fitting by stretched exponential function.
As shown in Fig. 1d, the decay of measured EPSC can generally fit well the line calculated by a stretched-exponential function17. This suggests that EPSC could be described as a stretched-exponential function. Here, we use EPSC as a representative synaptic transmission to study the voltage dependence of the synaptic plasticity relaxation behaviors. A standard stretched-exponential function is described as Eq. 1 17.
where τ is the retention time, t0 is the time when the presynaptic spike finishes, I0 is the triggered maximum EPSC, and I∞ is the EPSC at the end of the presynaptic spike. τ is found to be voltage dependent. The drain current, measured from the drain electrode, was shown to be a stretched exponential hump like EPSC when we applied drain voltage on the drain electrode terminal and gate pulse on the gate terminal of a transistor with the source voltage fixed at 0 V. We define the drain voltage as Vd, gate pulse maximum amplitude as Vg, and source as 0.
In order to investigate the impact of voltage on the synaptic transmission behaviors, the voltage on different terminals, i.e., drain electrode and gate electrode, were adjusted and the corresponding transmission behaviors were recorded. The voltage on one terminal was set at a wide voltage value range for CMOS which involve the low working voltage less than 1 V and high working voltage up to 3.3 V, i.e., 0.1~3.3 V. After a pulse applied on the gate terminal, the EPSC current, measured from the drain, was recorded and compared. As shown in Fig. 2a,b, EPSC retention time had uniform and obvious drain voltage amplitude, i.e., V1d, dependence linearly. Therefore, Eq. 1 could be updated as Eq. 2 at a fixed gate voltage.
Similarly, according to Fig. 2c,d, the retention time of EPSC had a gate spike amplitude, i. e. Vg, dependence and Eq. 1 could be updated as Eq. 3 at a fixed drain voltage.
where a, b, c and d are experimental constants. These behaviors are critical as they enable the devices in neuromorphic computers to reach a lot of behaviors such as EPSC with adjustable retention times under the different voltages. Figure 2a,c show that the voltage dependence on drain is less than the gate. It is constant due to the fact that the spike as shown in Fig. 1c could be applied on drain also with a DC gate voltage, but the behaviors are less obvious than those applied on voltage.
Memory is an essential function in biological system. In previous biological counterpart, the memory loss is a typical behavior, which can be transformed from short-term memory (STM) into long-term memory (LTM) by the increasing number of stimuli27. These behaviors are found in our devices and are expounded in detail. A set of device samples with different pulse number N, i.e., N = 5, 10, 20, 50 and 150 are shown in Fig. 3, suggesting the memory behaviors transfer through repeated stimulation. It is shown in Fig. 3a that the retention loss is correlated with the stimulation pulse numbers. When the pulse number rises, the retention loss increases. This is consistent with the reported memory behaviors for synaptic devices, i.e., the amplitude of which could be adjusted with pulse numbers21, 27. The results in Fig. 3b indicate that the retention time increases with increasing the number of stimuli, indicating a decreased forgetting rate. This trend is also consistent to and similar with the memory trends in previous studies, suggesting that amorphous oxide semiconductor transistors would be used as the artificial synaptic devices for investigation and the important role of voltage dependency for the development of nueromorphic computing21, 27. Figure 3c shows that upon the application of each stimulation,the off-current increases when the time interval between the stimulation is relatively short. Such behaviors bear resemblance to memory loss in biological system suggests that these devices could to be optimized for memory applications.
Memory enhancement with repeated stimulation. (a) Memory retention data recorded after different numbers of identical stimuli. (b) Characteristic relaxation time (τ) obtained through the fitting in panel a and the prefactor (I0) with respect to the number of stimuli (N). (c) The corresponding current through the memory device data recorded continuously throughout the test. The spontaneous decay after each pulse (in black lines) and the overall conductor enhancement can be observed. The voltage profile (in red) applied to the memory device consisting of ten 20 V 1.55 s pulses and a constant 0.5 V read voltage.
The voltage dependence of I∞ is also investigated. As shown in Fig. 2, the gate voltage doesn’t change I∞ as much as the drain voltage does, whereas the drain voltage have an impact as shown in Fig. 2c. This suggests that Vd could significantly change I∞. However, as shown in Fig. 3, I∞ also increases when the gate pulse number or the gate voltage stress time, i.e., Vg stress rises. Therefore, Vd, Vg and voltage stress time would impact I∞. I∞ increases with increasing Vd. Hence the equation could be updated as
where \({{\rm{I}}}_{\infty }=({\rm{e}}\cdot {\rm{Vd}}+{\rm{f}}\cdot {\rm{Vg}})\cdot {{\rm{I}}}_{\infty 0}\), a, b, c, d, e and f are positive experimental constants.
Besides, as shown in Fig. 3a, the pulse number seems to have less impact on I∞ and retention time as compared to previous studies14, 15. This illustrates that, under such number of pulses, the amount of mobile charges movements corresponding to the signal is not large enough to cause significant change of retention time. A greater number of pulses or a larger stress is needed in order to obtain an obvious memory effects in our samples. This suggests a high quality of the sample devices without many defects, which may facilitate the carriers and mobile ions to diffuse or transport. This conclusion could be verified with the small gate leakage current which is measured and shown in Fig. 4. In Fig. 4, the gate leakage current is at least 1 order of magnitude smaller than EPSC, which could be excluded. The small gate leakage current suggests a high quality of the devices, without significant damage by the mobile ions injection and transport.
In summary, voltage dependence of retention time is investigated in synaptic transistors. These behaviors suggest that the retentions time are voltage dependent and this voltage dependence could be suitable not only for transistors but also other synaptic devices. The voltage dependence of the synaptic relaxation behaviors under one stimulating pulse could help to obtain a clearer understanding and better controlling of the transition from STM to LTM in synaptic devices.
Experimental Section
The fabrication process is described subsequently. Using radio-frequency magnetron sputtering method, 30 nm thick IGZO channels were deposited and patterned by lithography on the isolation layer. The channel width and length were about 100 μm and 90–120 μm, respectively. Afterwards, 90 nm thick Ti/Au metal electrodes (i.e., source and drain) were deposited by electron beam evaporation techniques.
Change history
10 June 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41598-021-91377-y
References
Lee, D. et al. Three-Dimensional Fin-Structured Semiconducting Carbon Nanotube Network Transistor. ACS Nano 10, 10894–10900 (2016).
Dai, X., Nguyen, B. M., Hwang, Y., Soci, C. & Dayeh, S. A. Novel Heterogeneous Integration Technology of III-V Layers and InGaAs FinFETs to Silicon. Advanced Functional Materials 24, 4420–4426 (2014).
Kaleli, B., Hueting, R. J. E., Nguyen, M. D. & Wolters, R. A. M. Integration of a Piezoelectric Layer on Si FinFETs for Tunable Strained Device Applications. IEEE Transactions on Electron Devices 61, 1929–1935 (2014).
Imre, A. et al. Majority Logic Gate for Magnetic Quantum-Dot Cellular Automata. Science 311, 205–208 (2006).
Du, H. K., Lv, H. J., Zhang, Y. Q., Peng, F. & Xie, G. J. Design and Analysis of New Fault-Tolerant Majority Gate for Quantum-Dot Cellular Automata. Journal of Computational Electronics 15, 1484–1497 (2016).
Meyer, D. A. & Shakeel, A. Quantum Cellular Automata Without Particles. Physical Review A 93, 012333 (2016).
Christie, J. A. et al. Synthesis of a Neutral Mixed-Valence Diferrocenyl Carborane for Molecular Quantum-Dot Cellular Automata Applications. Angewandte Chemie International Edition. 54, 15448–15451 (2015).
Avalle, M. & Serafini, A. Noisy Quantum Cellular Automata for Quantum versus Classical Excitation Transfer. Physical Review Letters 112, 170403 (2014).
Mirzaeifar, R., Dimas, L. S., Qin, Z. & Buehler, M. J. Defect-Tolerant Bioinspired Hierarchical Composites: Simulation and Experiment. ACS Biomaterials Science & Engineering 1, 295–304 (2015).
Brunel, D. et al. Integrating Multiple Resistive Memory Devices on a Single Carbon Nanotube. Advanced Functional Materials 23, 5631–5637 (2013).
Benjamin, S. C. et al. Towards a Fullerene-Based Quantum Computer. Journal of Physics: Condensed Matter. 18, S867–883 (2006).
Twamley, J. Quantum-Cellular-Automata Quantum Computing with Endohedral Fullerenes. Physical Review A 6, 052318 (2003).
Jenkins, M. D. et al. A Scalable Architecture for Quantum Computation with Molecular Nanomagnets. Dalton Transactions. 45, 16682–16693 (2016).
Kim, K., Chen, C., Truong, Q., Shen, A. M. & Chen, Y. A Carbon Nanotube Synapse with Dynamic Logic and Learning. Adv. Mater. 25, 1693–1698 (2013).
Lai, Q. et al. Ionic/Electronic Hybrid Materials Integrated in a Synaptic Transistor with Signal Processing and Learning Functions. Adv. Mater. 22, 2448–2253 (2012).
Song, J., Ampatzis, K., Rebecka Björnfors, E. & Manira, A. E. Motor neurons control locomotor circuit function retrogradely via gap junctions. Nature 529, 399–407 (2016).
Huang, Z. et al. TRIP8b-Independent Trafficking and Plasticity of Adult Cortical Presynaptic HCN1 Channels. J Neurosci. 32, 14835–14848 (2012).
Xua, X., Chen, Z., Li, N., Hui, S. & Wang, G. The decrease of NMDAR subunit expression and NMDAR EPSC in hippocampus by neonatal exposure to desflurane in mice. Behavioural Brain Research 317, 82–87 (2017).
Malkin, S. L., Kim, K. K., Tikhonov, D. B. & Zaitsev, A. V. Properties of Spontaneous and Miniature Excitatory Postsynaptic Currents in Neurons of the Rat Prefrontal Cortex. Journal of Evolutionary Biochemistry and Physiology 50, 506–514 (2014).
Sciamanna, G., Ponterio, G., Mandolesi, G., Bonsi, P. & Pisani, A. Optogenetic stimulation reveals distinct modulatory properties of thalamostriatal vs corticostriatal glutamatergic inputs to fast spiking interneurons. Scientific Reports 5, 16742 (2015).
Kuzum, D., Yu, S. & Wong, H.-S. P. Synaptic electronics: materials, devices and applications. Nanotechnology 24, 382001 (2013).
Fortunato, E. et al. Oxide semiconductor thin-film transistors: A review of recent advances. Adv. Mater. 24, 2945–2986 (2012).
Nomura, K. et al. Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors. Nature 432, 488–492 (2004).
Dai, M. & Dai, N. Logic circuit function realization by one transistor. Nano Lett. 12, 5954–5956 (2012).
Kimura, M. et al. Trap densities in amorphous-InGaZnO4 thin-film transistors. Appl. Phys. Lett. 92, 133512 (2008).
Jeon, S. et al. Corrigendum: Gated three-terminal device architecture to eliminate persistent photoconductivity in oxide semiconductor photosensor arrays. Nat. Mater. 14, 301–305 (2015).
Wang, Z. et al. Synaptic learning and memory functions achieved using oxygen ion migration/diffusion in an amorphous InGaZnO memristor. Adv. Func. Mater. 22, 2759–2765 (2012).
Acknowledgements
This work was supported by the Zhejiang Provincial Natural Science Foundation for Distinguished Young Scholar (No. LR17F040002), National Natural Science Foundation of China (Grant Nos 61106090, 61574147, 61474068), Ningbo Municipal Natural Science Foundation (No. 2014A610011), the Ningbo Natural Science Foundation of China (Grant Nos 2015A610034, 2011A610110, No. 2014B82004, Y10814VA0, 2016A610280), the State Key Basic Research Program of China (2013CB922300), Youth Innovation Promotion Association, Chinese Academy of Sciences and Royal Academy of Engineering, UK. The author appreciates the K.C. Wong Magna Fund in Ningbo University.
Author information
Authors and Affiliations
Contributions
M.D. conceived the research and wrote the main manuscript text. W.W. performed the experiments. P.W., M.Z.I., N.A., K.K. and N.A. reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this Article was revised: The original version of this Article contained errors. Modifications have been made to the Figure 1 and the Acknowledgements section. Full information regarding the corrections made can be found in the correction for this Article.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dai, M., Wang, W., Wang, P. et al. Realization of tunable artificial synapse and memory based on amorphous oxide semiconductor transistor. Sci Rep 7, 10997 (2017). https://doi.org/10.1038/s41598-017-04641-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-04641-5
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.